A ZVS Bidirectional Inverting Buck-Boost Converter Using Coupled Inductors
Abstract
:1. Introduction
- Higher efficiency than the CCM BIBBC in most power ranges and higher efficiency than the TCM BIBBC in the medium and low power range;
- A simpler control method and lower cost than ZVT converters;
- Lower core losses and filter capacitance than the TCM BIBBC.
- In short, this paper provides the following contributions:
- Proposal of a new ZVS BIBBC using a coupled inductor with abovementioned advantages;
- Detailed theoretical analysis and design guidelines of the new ZVS BIBBC;
- Experimental analysis and comparison between the proposed ZVS BIBBC and two other BIBBCs.
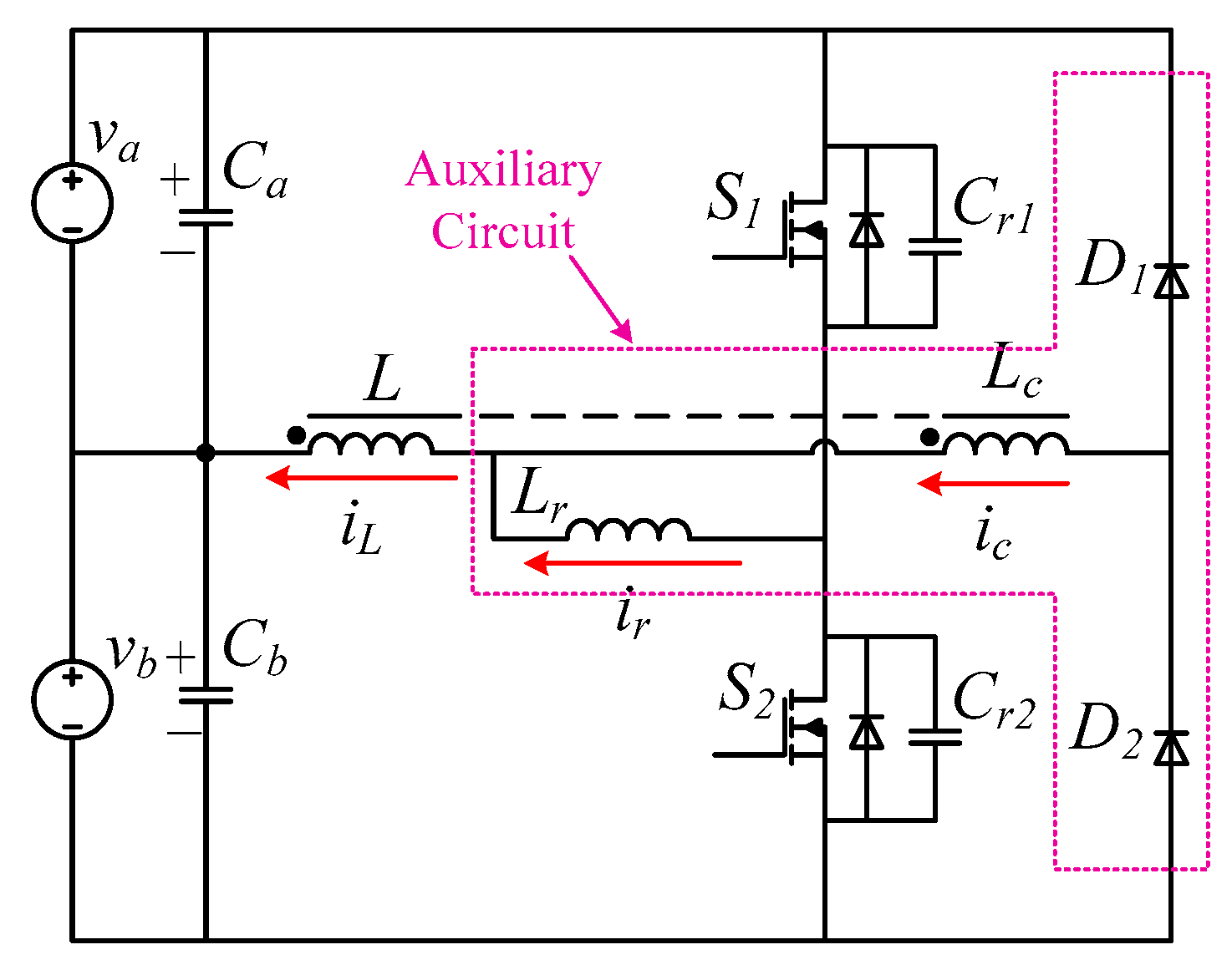
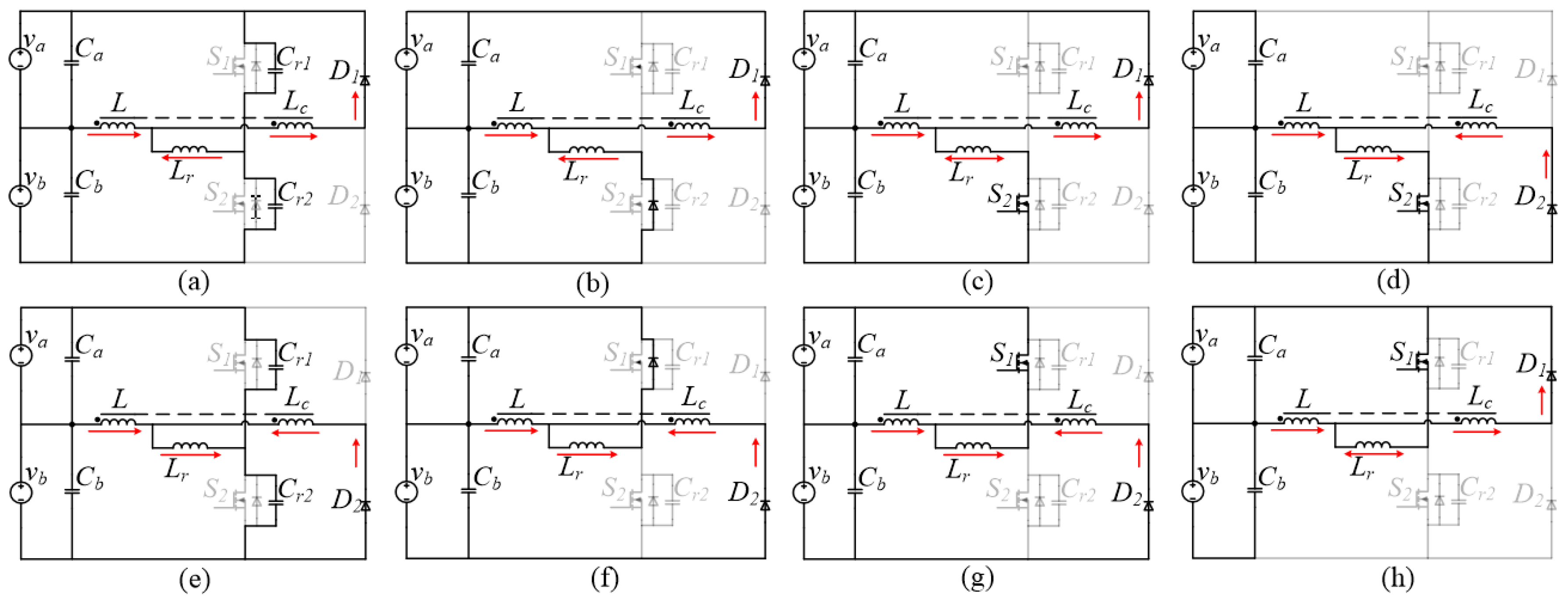
2. Topology and Its Principle
2.1. Proposed Converter
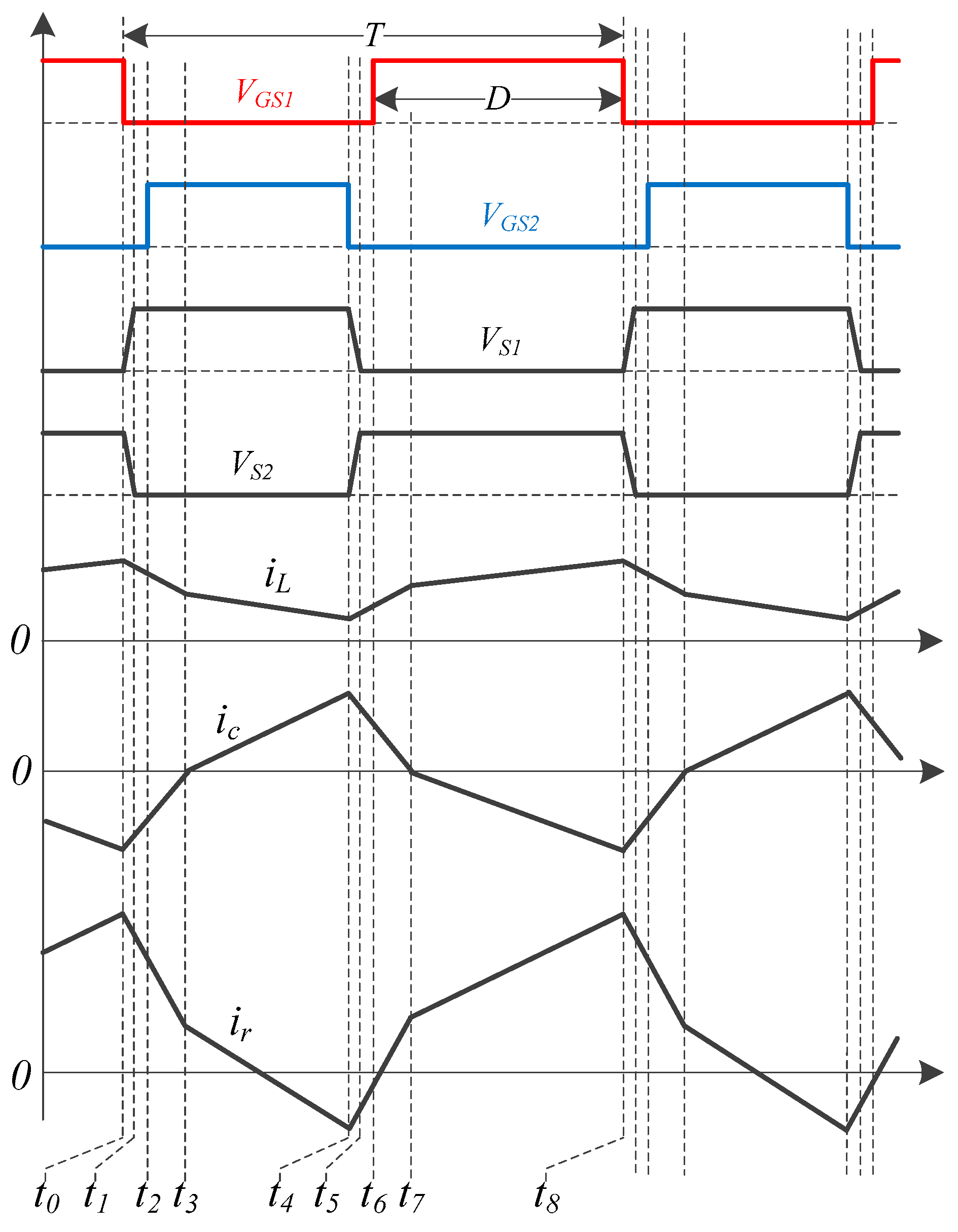
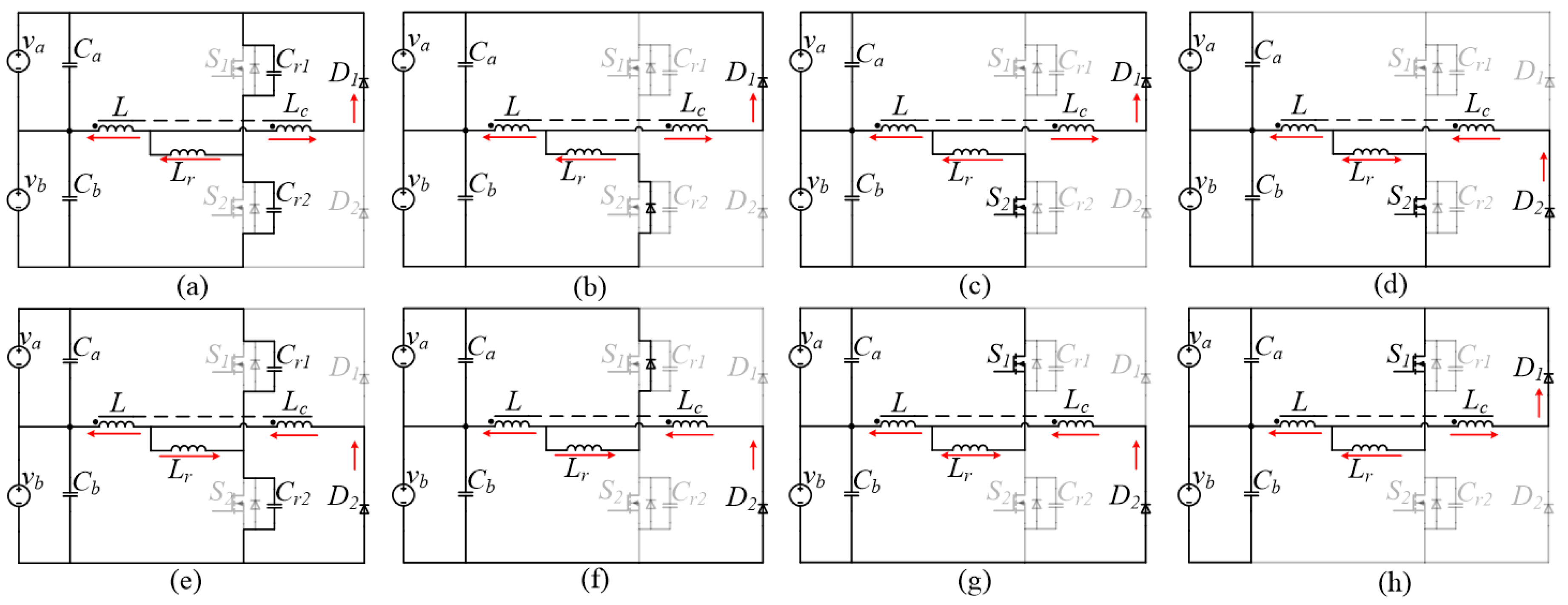
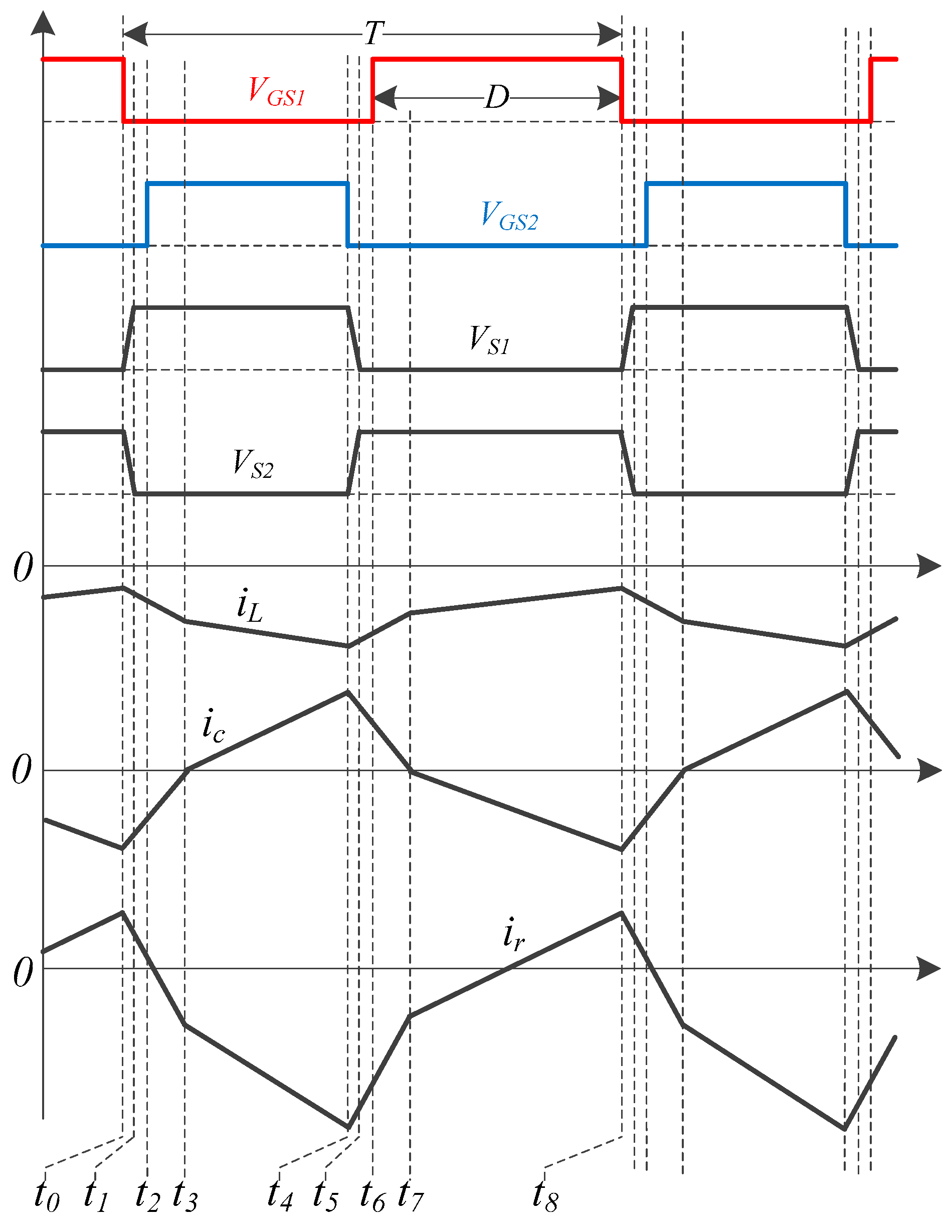
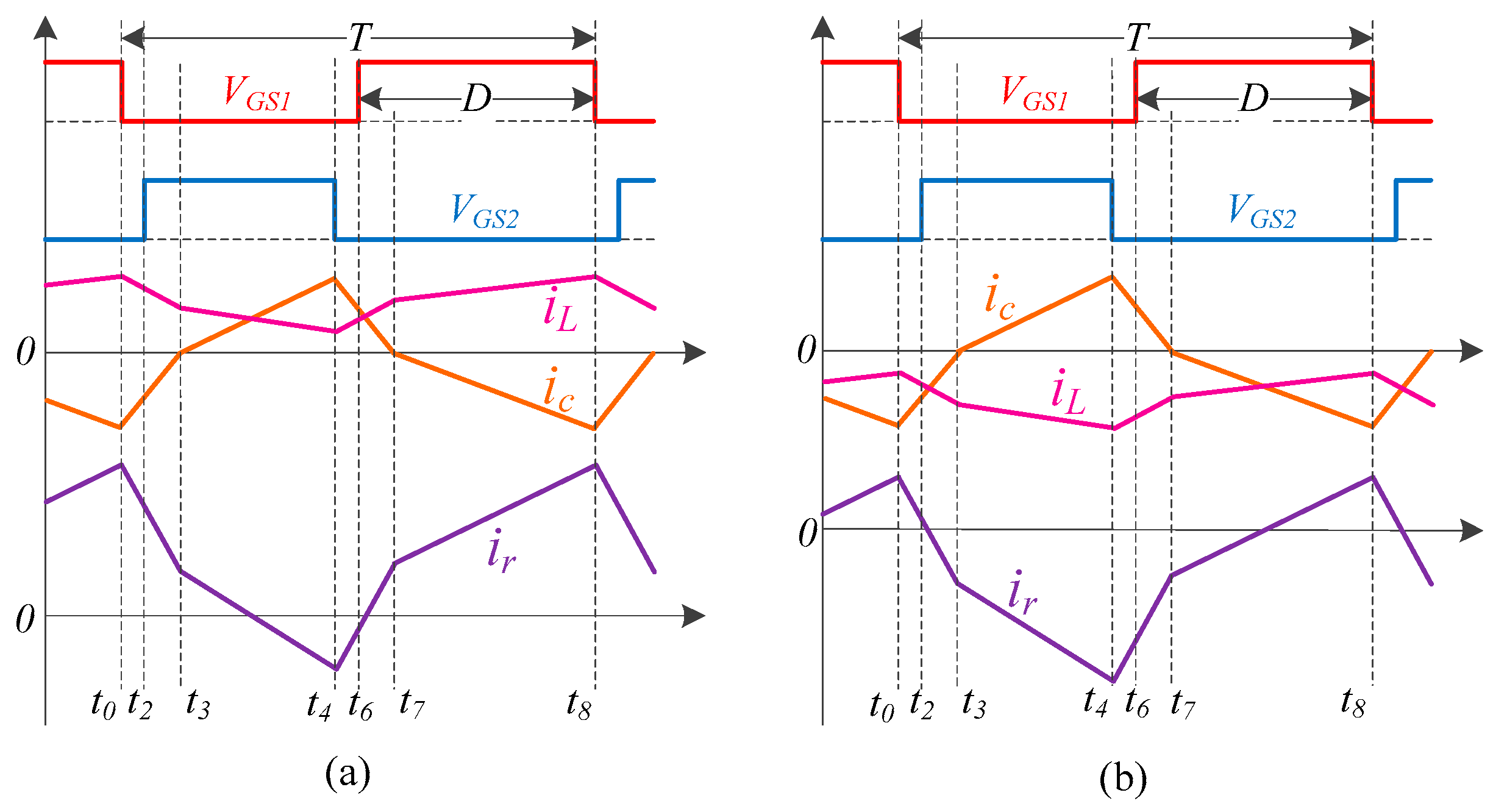
2.2. Positive Operation
2.3. Negative Operation
3. Converter Analysis and Design
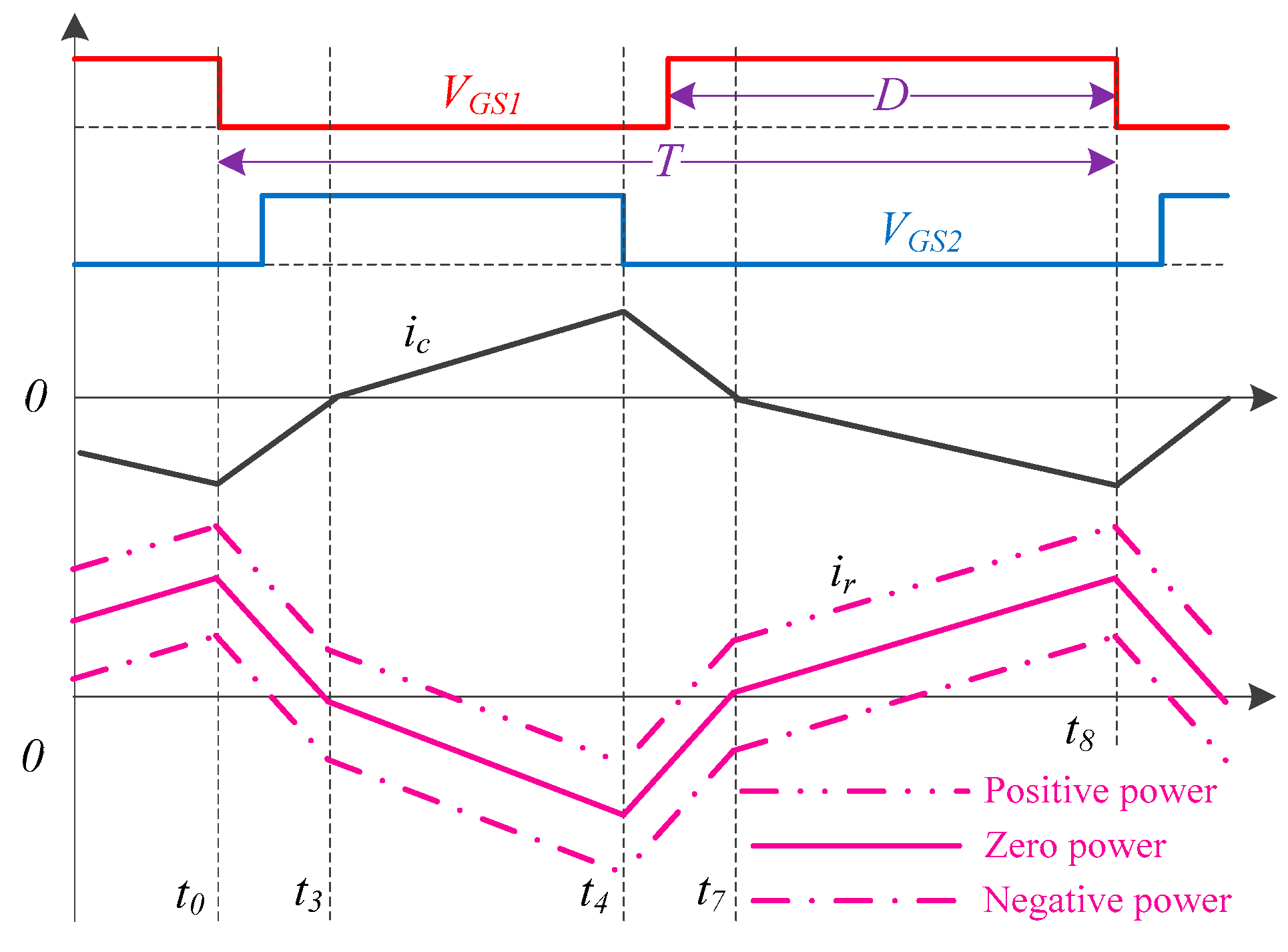
3.1. Soft-Switching Conditions
3.2. Stress and Losses Analysis
3.3. Design Guidelines
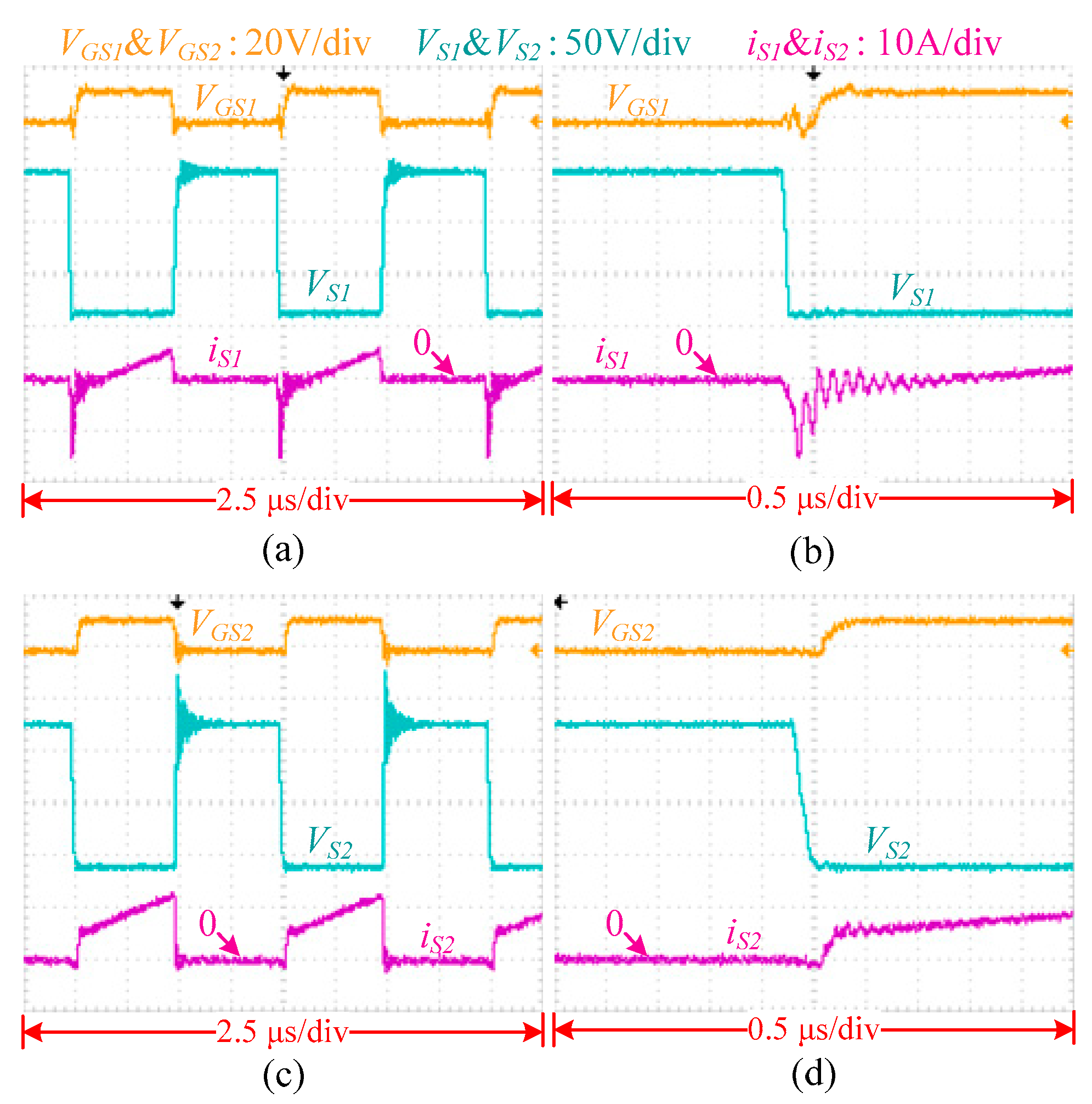
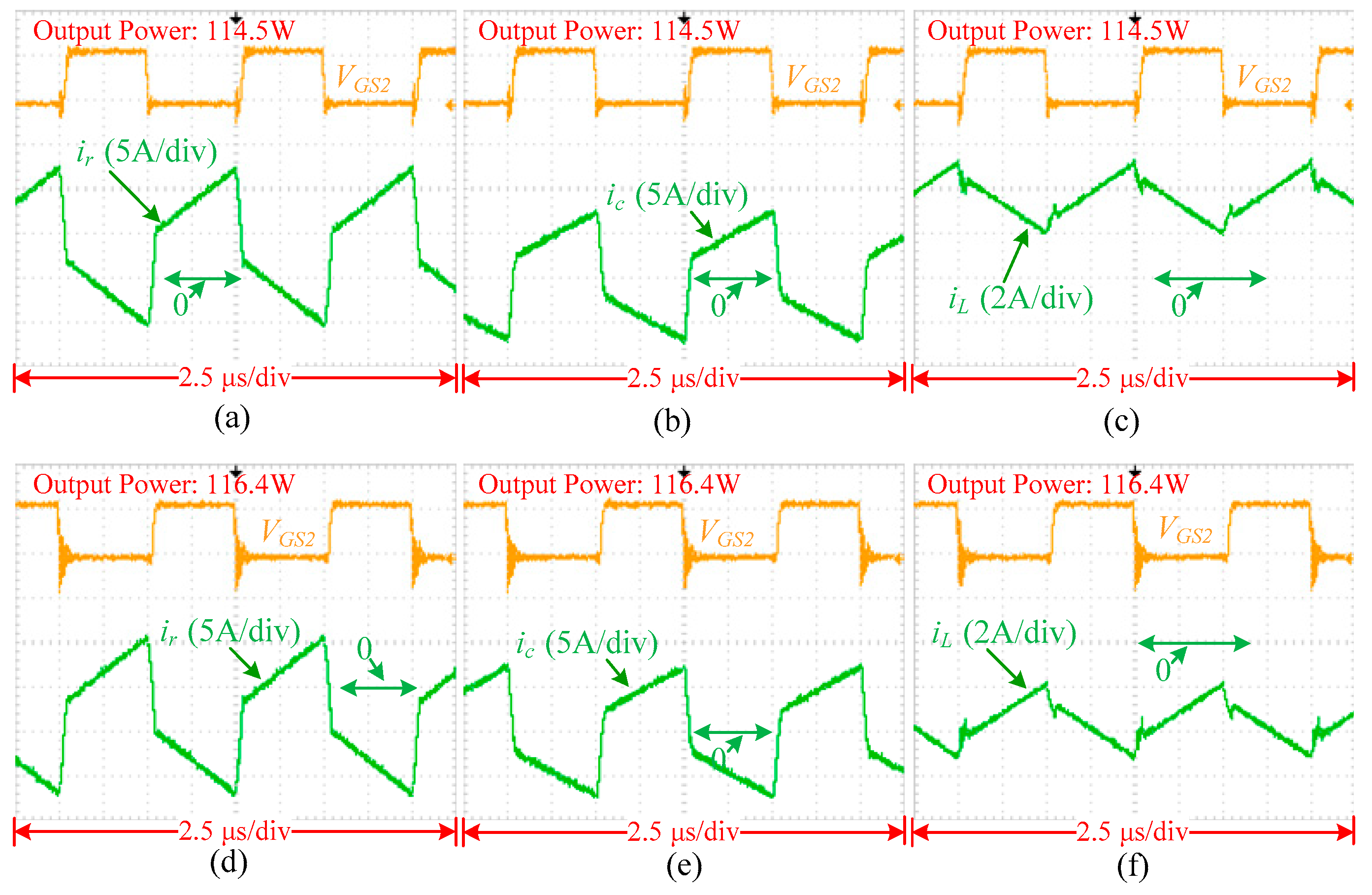
4. Experimental Results
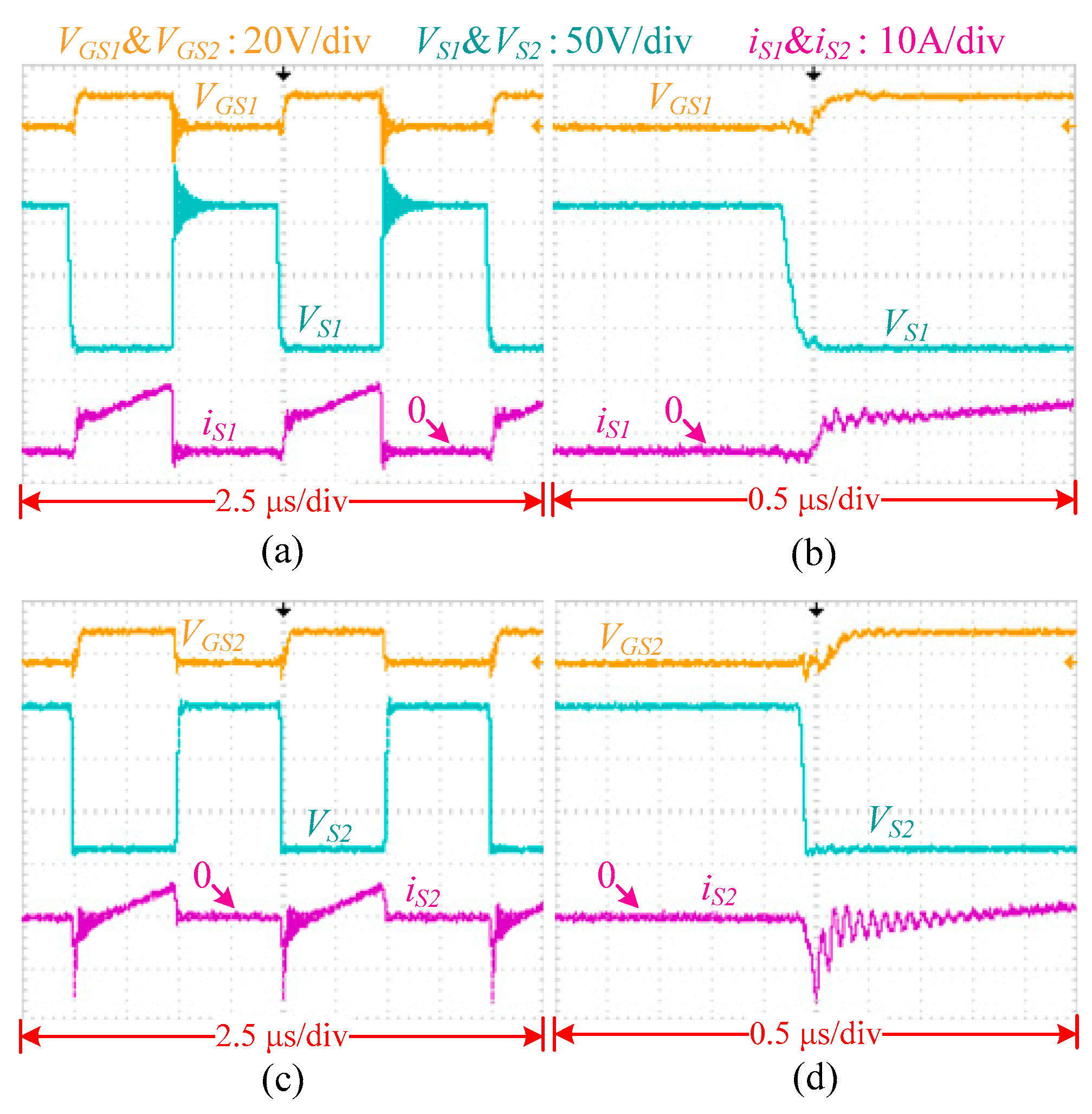
4.1. Experimental Setup
4.2. Results Analysis
4.3. Power Supply and Extended Converter
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moshirvaziri, M.; Li, C.; Trescases, O. A quasi-resonant bi-directional tri-mode DC-DC converter with limited valley current. In Proceedings of the Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition, Orlando, FL, USA, 5–9 February 2012. [Google Scholar]
- Du, Y.; Zhou, X.; Bai, S.; Lukic, S.; Huang, A. Review of non-isolated bi-directional DC-DC converters for plug-in hybrid electric vehicle charge station application at municipal parking decks. In Proceedings of the Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition, Palm Springs, CA, USA, 21–25 February 2010. [Google Scholar]
- Kong, Z.; Zhu, C.; Yang, S.; Cheng, S. Study of Bidirectional DC-DC Converter for Power Management in Electric Bus with Supercapacitors. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Windsor, UK, 6–8 September 2006. [Google Scholar]
- Kumar, B.V.; Singh, R.K.; Mahanty, R. A modified non-isolated bidirectional DC-DC converter for EV/HEV’s traction drive systems. In Proceedings of the 2016 IEEE International Conference on Power Electronics, Drives and Energy Systems, Trivandrum, India, 14–17 December 2016. [Google Scholar]
- Cao, J.; Emadi, A. A New Battery/UltraCapacitor Hybrid Energy Storage System for Electric, Hybrid, and Plug-In Hybrid Electric Vehicles. IEEE Trans. Power Electron. 2012, 27, 122–132. [Google Scholar] [CrossRef]
- Kouchachvili, L.; Yaïci, W.; Entchev, E. Hybrid battery/supercapacitor energy storage system for the electric vehicles. J. Power Sources 2018, 374, 237–248. [Google Scholar] [CrossRef]
- Capassoa, C.; Lauriab, D.; Veneria, O. Experimental evaluation of model-based control strategies of sodium-nickel chloride battery plus supercapacitor hybrid storage systems for urban electric vehicles. Appl. Energy 2018, 228, 2478–2489. [Google Scholar] [CrossRef]
- Veneria, O.; Capassoa, C.; Patalanob, S. Experimental investigation into the effectiveness of a super-capacitor based hybrid energy storage system for urban commercial vehicles. Appl. Energy 2018, 227, 312–323. [Google Scholar] [CrossRef]
- Tytelmaier, K.; Husev, O.; Veligorskyi, O.; Yershov, R. A review of non-isolated bidirectional dc-dc converters for energy storage systems. In Proceedings of the 2016 II International Young Scientists Forum on Applied Physics and Engineering (YSF), Kharkiv, Ukraine, 10–14 October 2016. [Google Scholar]
- Rodriguez, A.; Vazquez, A.; Rogina, M.R.; Briz, F. Synchronous Boost Converter with High Efficiency at Light Load using QSW-ZVS and SiC MOSFETs. IEEE Trans. Ind. Electron. 2018, 65, 386–393. [Google Scholar] [CrossRef]
- Mohammadi, M.R.; Farzanehfard, H. New Family of Zero-Voltage-Transition PWM Bidirectional Converters with Coupled Inductors. IEEE Trans. Ind. Electron. 2012, 59, 912–919. [Google Scholar] [CrossRef]
- Mohammadi, M.R.; Farzanehfard, H. Analysis of Diode Reverse Recovery Effect on the Improvement of Soft-Switching Range in Zero-Voltage-Transition Bidirectional Converters. IEEE Trans. Ind. Electron. 2015, 62, 1471–1479. [Google Scholar] [CrossRef]
- Mohammadi, M.R.; Farzanehfard, H. A New Family of Zero-Voltage-Transition Nonisolated Bidirectional Converters with Simple Auxiliary Circuit. IEEE Trans. Ind. Electron. 2016, 63, 1519–1527. [Google Scholar] [CrossRef]
- Beltrame, R.C.; Zientarski, J.R.R.; Martins, M.L.D.S.; Pinheiro, J.R.; Hey, H.L. Simplified zero-voltage-transition circuits applied to bidirectional poles: concept and synthesis methodology. IEEE Trans. Power Electron. 2011, 26. [Google Scholar] [CrossRef]
- Chen, G.; Deng, Y.; Chen, L.; Hu, Y.; Jiang, L.; He, X.; Wang, Y. A Family of Zero-Voltage-Switching Magnetic Coupling Nonisolated Bidirectional DC–DC Converters. IEEE Trans. Ind. Electron. 2017, 64, 6223–6233. [Google Scholar] [CrossRef]
- Ahmadi, M.; Shenai, K. New, efficient, low-stress buck/boost bidirectional DC-DC converter. In Proceedings of the IEEE Energytech, Cleveland, OH, USA, 29–31 May 2012. [Google Scholar]
- Das, P.; Laan, B.; Mousavi, S.A.; Moschopoulos, G. A nonisolated bidirectional ZVS-PWM active clamped dc–dc converter. IEEE Trans. Power Electron. 2009, 24, 553–558. [Google Scholar] [CrossRef]
- Das, P.; Mousavi, S.A.; Moschopoulos, G. Analysis and Design of a Nonisolated Bidirectional ZVS-PWM DC–DC Converter with Coupled Inductors. IEEE Trans. Power Electron. 2010, 25, 2630–2641. [Google Scholar] [CrossRef]
- Lee, Y.S.; Cheng, G.T. Quasi-Resonant Zero-Current-Switching Bidirectional Converter for Battery Equalization Applications. IEEE Trans. Power Electron. 2006, 21, 1213–1224. [Google Scholar] [CrossRef]
- Broday, G.R.; Nascimento, C.B.; Lopes, L.A.C.; Agostini, E. Analysis and simulation of a buck-boost operation in a bidirectional ZVS DC-DC converter. In Proceedings of the International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference, Toulouse, France, 2–4 November 2016. [Google Scholar]
- Zhang, Y.; Sen, P.C. A new soft switching technique for buck, boost and buck-boost converters. IEEE Trans. Ind. Appl. 2003, 39, 1775–1782. [Google Scholar] [CrossRef]
- Chen, G.; Deng, Y.; Tao, Y.; He, X.; Wang, Y.; Hu, Y. Topology derivation and generalized analysis of zero-voltage-switching synchronous dc–dc converters with coupled inductors. IEEE Trans. Ind. Electron. 2016, 63, 4805–4815. [Google Scholar] [CrossRef]
- Qiu, G.Y.; Luo, X.J. Circuit, 5th ed.; Higher Education Press: Beijing, China, 2006; pp. 126–131. [Google Scholar]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| va | DC 70 V | Cr1, Cr2 | 2.2 nF |
| vb | DC 70 V | Ca, Cb | 1000 μF |
| D | 0.5 | M | 18.9 μH |
| f | 100 kHz | Lc | 4.1 μH |
| L | 159.2 μH | S1, S2 | IRFP4668 |
| Lr | 2.4 μH | L, Lc core | Kool mu |
| D1, D2 | DSSK60-02A | Lr core | Kool mu |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, X.-F.; Zhang, Y.; Yin, C. A ZVS Bidirectional Inverting Buck-Boost Converter Using Coupled Inductors. Electronics 2018, 7, 221. https://doi.org/10.3390/electronics7100221
Cheng X-F, Zhang Y, Yin C. A ZVS Bidirectional Inverting Buck-Boost Converter Using Coupled Inductors. Electronics. 2018; 7(10):221. https://doi.org/10.3390/electronics7100221
Chicago/Turabian StyleCheng, Xu-Feng, Yong Zhang, and Chengliang Yin. 2018. "A ZVS Bidirectional Inverting Buck-Boost Converter Using Coupled Inductors" Electronics 7, no. 10: 221. https://doi.org/10.3390/electronics7100221
APA StyleCheng, X.-F., Zhang, Y., & Yin, C. (2018). A ZVS Bidirectional Inverting Buck-Boost Converter Using Coupled Inductors. Electronics, 7(10), 221. https://doi.org/10.3390/electronics7100221




