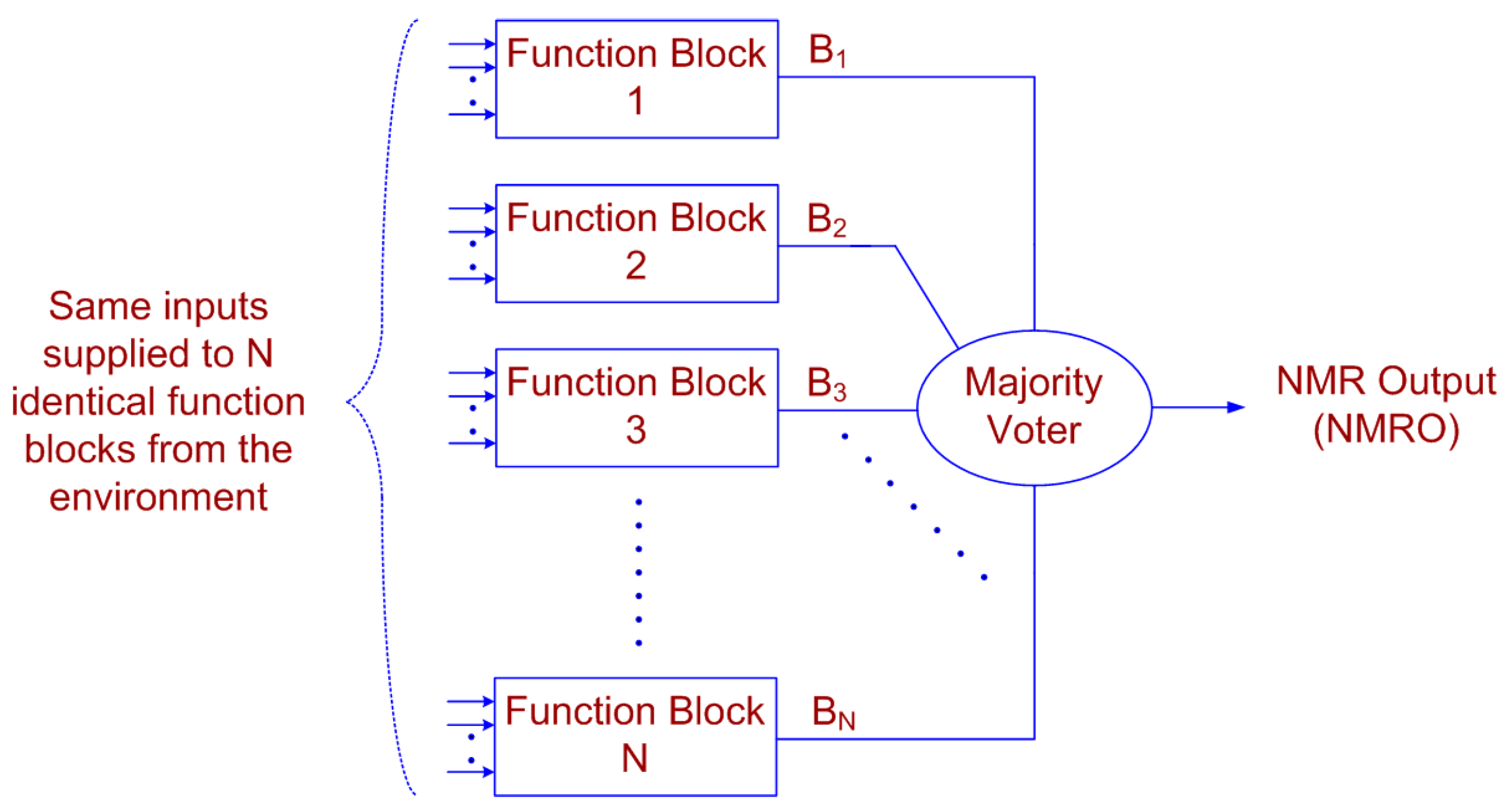
1. Introduction
Nanoelectronic circuits and systems are found to be more prone to multiple faults or failures [
1] due to harsh environmental phenomena such as radiation [
2,
3,
4,
5,
6] and/or aging [
7,
8]. Hence, when such circuits or systems are deployed in safety-critical applications such as aerospace, defense, nuclear plants, etc., redundancy is incorporated by default to cope with the arbitrary fault(s) or failure(s) of constituent function blocks, which are subject to a pre-defined fault tolerance bound. Redundancy implies the use of identical function block(s) in additional to the original function block while designing a circuit or a system for a safety-critical application, where the function block may be a sub-circuit or a sub-system. Redundancy is important in safety-critical circuits and systems to cope with the arbitrary fault(s) or failure(s) of the constituent function blocks. In this context, the N-modular redundancy (NMR) scheme, which is well known, is widely used [
9,
10]. However, the drawbacks with the NMR are: (i) in order to increase the redundancy by an order of magnitude, two extra function blocks should be introduced, which would exacerbate the weight, cost, and design metrics; and (ii) the sizes of the majority of voters that were used in the NMR scheme would substantially increase with increases in the level of redundancy.
To mitigate the impact of multiple faults or failures on nanoelectronics circuits and systems, higher levels of redundancy are suggested to be used. Since it will be exorbitant to implement high levels of redundancy for an entire circuit or system (say, based on the NMR), the progressive module redundancy (PMR) approach was suggested [
11]. PMR is an architectural suggestion that vouches for the selective implementation of high levels of redundancy for the more vulnerable portions of a circuit or system and the implementation of minimum redundancy for the less vulnerable portions of a circuit or system. However, the implementation of higher-order NMR for the more vulnerable portions of a circuit or system would still be expensive. Hence, as an efficient alternative to NMR, the majority and minority voted redundancy (MMR) scheme was proposed in [
12] targeting safety-critical applications. However, just the basic implementation of the MMR scheme was considered in [
12] with no provision for indicating the correct or the incorrect operation of the MMR through error/no-error signaling logic (ESL). In this article, we build upon our previous work [
12] by presenting an ESL for the MMR scheme.
In [
13], an ESL for the NMR scheme was presented. The ESL is important for any redundancy scheme, because if the ESL signals no error, then the outputs of the redundancy scheme are reliable, i.e., dependable, and if the ESL signals error, then the outputs of the redundancy scheme are not reliable i.e., non-dependable. Hence, without the ESL, the correct operation of a redundancy scheme is only assumed, which may be incorrect and may even cause a catastrophic failure. Hence, the ESL avoids assuming the correct operation of a redundancy scheme and thereby contributes to the safety of a circuit or system. However, there are bounds associated with the operation of the ESL, which will be discussed later.
The rest of the article is organized as follows.
Section 2 discusses the NMR scheme and briefs the operation of the NMR circuits without and with the ESL (NMRESL).
Section 3 describes the example MMR circuits without and with the proposed ESL, i.e., the MMRESL. Example NMR and NMRESL circuits, and their counterpart MMR and MMRESL circuits, were considered for physical implementation, and their design metrics are given in
Section 4 and compared. Finally,
Section 5 provides the conclusions.
3. MMR Scheme and MMRESL
The basic MMR scheme was proposed by us in an earlier paper [
12], without the ESL. The generic architecture of the MMR scheme, including the ESL, is shown in
Figure 6. The blue lines depict the basic MMR architecture and the red lines depict the ESL of the MMR (MMRESL).
In the MMR scheme, (M − 1) copies of the original function block are used, and the M identical function blocks are split into two clusters, namely the ‘majority cluster’ and the ‘minority cluster’, as shown in
Figure 6. Three function blocks comprise the majority cluster, and the remaining (M − 3) function blocks comprise the minority cluster. The Boolean majority condition is imposed on the function blocks constituting the majority cluster, which implies that at least two out of the three function blocks 1, 2, and 3 should maintain the correct operation. The relaxed Boolean minority condition is imposed on the function blocks constituting the minority cluster, and thus it would suffice even if any one of the function blocks in the minority cluster operates correctly. Overall, at least three out of the M function blocks should maintain the correct operation in the MMR scheme, and hence the fault tolerance of the MMR scheme is specified as (M − 3).
The MMR voter is marked in
Figure 6. For every output of the function block, the MMR voter would consist of an AO222 complex gate, a (M − 3)-input AND gate, a (M − 3)-input OR gate, and a 2:1 multiplexer (i.e., 2:1 MUX). The outputs of the function blocks 1, 2, and 3 are given to the AO222 gate [
17], which performs majority voting on the three inputs B
1, B
2, and B
3, and produces the internal output MAJ. The outputs of the remainder of the function blocks 4 to M are given to an AND gate and an OR gate, which have the same fan-in of (M − 3). T
1 represents the output of the (M − 3)-input AND gate, and T
2 represents the output of the (M − 3)-input OR gate. T
1 and T
2 are given as inputs to the 2:1 MUX, whose select input is MAJ. Hence, if MAJ = 0, T
1 is selected, and its value is forwarded to the output of the 2:1 MUX, which is labeled MIN. If MAJ = 1, then T
2 is selected, and MIN = T
2. The logical conjunction of MAJ and MIN yields the primary output of the MMR implementation viz. MMRO. The ESL of the MMR scheme consists of an inverter that complements MIN. The ESL also consists of a two-input AND gate, and the logical conjunction of MAJ and the complement of MIN yields the MMRESL output i.e., MMRESLO. If function blocks with multiple outputs are used in an MMR implementation, then the ESL will contain as many two-input AND gates and inverters as are commensurate with the number of outputs from the function blocks. The outputs of all of the ESL circuitry can be combined using an OR gate, which may be decomposed arbitrarily, to produce the ESL output of the MMR implementation.
We will use the notation K-of-M while referring to the MMR scheme for our discussion, which signifies that K out of the M function blocks in a MMR implementation operate correctly. Hence, a three-of-five MMR implementation can mask the faults or failures of a maximum of two function blocks similar to the 5MR implementation; a three-of-six MMR implementation can mask the faults or failures of maximum of three function blocks similar to the 7MR implementation; and a three-of-seven MMR implementation can mask the faults or failures of maximum of four function blocks similar to the 9MR implementation. The three-of-six and three-of-seven MMR implementations provide the same degrees of fault tolerance as the 7MR and 9MR implementations despite requiring one and two function blocks less than their counterparts. This could help to reduce the cost, weight, and design metrics of the former compared to the latter.
The reliabilities of the three-of-five, three-of-six, and three-of-seven MMR implementations are given by Equations (5)–(7) based on the assumption of perfect MMR voters. Let us interpret the reliability components of the three-of-five MMR implementation for an example. In Equation (5), the first term on the right side specifies the condition of any two function blocks in the majority cluster and any one function block in the minority cluster operating correctly. The second term specifies the condition of either of any two function blocks in the majority cluster and both the function blocks in the minority cluster operating correctly, or the correct operation of all three function blocks in the majority cluster and just one function block in the minority cluster. The third term on the right side specifies the (ideal) condition of all five function blocks in the three-of-five MMR implementation maintaining the correct operation:
The reliabilities of the NMR and counterpart MMR implementations are plotted in
Figure 7 as a function of the reliability of the constituent function blocks, and they exhibit a close correlation. Considering the reliability of a function block to be in the range of 0.9 to 0.99, which is quite common for a safety-critical application, the MMR implementations were found to have 1.12% less reliability than the NMR implementations, on average. This is the trade-off that is involved in achieving reductions in the number of function blocks, design metrics, weight, and cost.
A higher priority is inherently accorded to the majority cluster compared to the minority cluster in the MMR scheme. This is because the Boolean majority condition is unambiguous, while the Boolean minority condition may be ambiguous. To understand why this is so, let us presume that the function blocks 1, 2, and 4 in
Figure 6 produce the correct output, and that function block 3 and function blocks 5 to M are faulty or have failed. Given this, since two out of the three function blocks produce the same correct output in the majority cluster, the Boolean majority condition will unambiguously determine the output of the majority cluster as MAJ = B
1 = B
2. On the other hand, given that only function block 4 produces the correct output, this cannot be unambiguously interpreted as the output of the minority cluster. This is because it can be argued that the outputs of the function block 5 to M also correspond to the Boolean minority, since the Boolean minority condition primarily specifies at least one correct output. Hence, there arises an ambiguity in determining the correct output of the minority cluster based on the Boolean minority condition. For example, if B
4 = 0, and B
5 up to B
M assumes 1, both 0 and 1 can correspond to the Boolean minority, since B
4 is 0 and at least one of B
5 up to B
M is 1. For this input combination, T
1 = 0 and T
2 = 1. So, the choice of T
1 or T
2 as the correct output of the minority cluster should have to be decided, and a decision should be taken based on the value of MAJ, which is the output of the majority cluster. This explains why
the correct operation of the majority cluster is crucial in an MMR implementation and cannot be compromised (to overcome the ambiguity with the Boolean minority condition), while the correct operation of the minority cluster may not always be crucial. In fact, a complete failure of the minority cluster can be successfully masked under certain circumstances, and this will be explained through
Table 1.
Under the minority cluster column in
Table 1, ‘B
4–B
M’ represented by ‘0–0’ implies that B
4 up to B
M assume 0; ‘B
4–B
M’ represented by ‘0–1’ implies that B
4 assumes 0, and B
5 up to B
M may assume 1; and ‘B
4–B
M’ represented by ‘1–0’ implies that B
4 assumes 1, and B
5 up to B
M may assume 0. The possible operational scenarios for the MMR scheme are captured in
Table 1.
Scenario 1 indicates the ideal condition of both the majority and minority clusters operating perfectly i.e., the function blocks in both the clusters maintain the correct operation. Obviously, in this scenario, the state of the MMR output (i.e., MMRO) would be correct. Scenario 2 highlights the condition where the majority cluster is imperfect due to a faulty function block and outputs 0 due to any two out of the three function blocks outputting 0, and the minority cluster is imperfect. However, at least one of the function blocks in the minority cluster maintains the correct operation and outputs 0. In this scenario, MAJ = 0, and T1 is selected, which implies that MIN equates to 0. Hence, MMRO = 0, which is correct. Scenario 3 is similar to Scenario 2, except that MMRO = 1 because MAJ = MIN = 1, since two of the function blocks in the majority cluster output 1, and at least one of the function blocks in the minority cluster also outputs 1. With respect to scenarios 1, 2, and 3, the MMRESL output (MMRESLO) is 0, thus implying no-error.
Scenarios 4 and 5 depict the conditions where the majority cluster is imperfect, and the minority cluster fails completely. Although the MMR implementation is not warranted to operate correctly under scenarios 4 and 5, Scenario 4 showcases the innate error resiliency of the MMR scheme, which is captured by the proposed ESL, and Scenario 5 showcases the importance and the need for the ESL. With respect to Scenario 4, if the majority cluster is not perfect and outputs 0 due to any two of the constituent function blocks outputting 0 and given that the minority cluster has completely failed (i.e., all of its constituent function blocks output 1), MAJ = 0 and MIN = 1, and hence MMRO = 0, which is factually correct, since the output of the MMR scheme is primarily dictated by the output of the majority cluster. The correct state of the MMR output under Scenario 4 is confirmed by the MMRESL, where MMRESLO = 0, thus implying no-error. This shows the MMR scheme maintains the correct operation even under an undesirable and unwarranted Scenario 4. Supposing Scenario 5 occurs, where the majority cluster is not perfect and outputs 1 due to two of its function blocks outputting 1 and that the minority cluster has completely failed (i.e., all of its function blocks output 0), MAJ = 1 and MIN = 0. This implies that MMRO = 0, which is incorrect, since the output of the MMR scheme does not tally with the output of the majority cluster i.e., MMRO ≠ MAJ. Under this scenario, the proposed MMRESL would output 1 on MMRESLO, implying the error in the operation of the MMR scheme. Considering all five scenarios which were discussed, it may be evident that the proposed MMRESL provides useful information about the correct or the incorrect operational state of a MMR implementation while encompassing the error resiliency of the MMR scheme.
Figure 8 shows an example three-of-five MMR implementation along with the ESL. Comparing this with the 5MR implementation featuring the ESL that is shown in
Figure 5, it may be noted that the former requires a considerably smaller number of gates than the latter while featuring the same fault tolerance, which is expected to translate into reductions in the design metrics for a physical implementation.
4. Results and Discussion
5MR, 7MR, and 9MR circuits, and three-of-five MMR, three-of-six MMR, and three-of-seven MMR circuits with and without the ESL were physically implemented using a 32/28 nm CMOS standard digital cell library [
15]. A 4 × 4 array multiplier was considered as the function block, which has eight input bits and produces eight output bits. The array multiplier requires 16 two-input AND gates, four half adders, and eight full adders for physical realization. The AND gate, half-adder, and full-adder cells from the library [
15] were utilized to construct the array multiplier, which consumes 84.38 µm
2 of silicon. Functional simulations were performed to verify the functionalities of the redundant circuits using test benches, which included all of the distinct input vectors corresponding to the multiplier. The test benches were supplied at time intervals of 2.5 ns (400 MHz). The switching activity data captured through the functional simulations were used to estimate the average power dissipation using Synopsys tools. Default wire loads were included while performing the simulations, and the areas and the critical path delays were also estimated. The design metrics corresponding to the example NMR and MMR circuits without and with the ESL are given in
Table 2.
The power-delay product (PDP) is a well-known and widely used low power metric for digital circuits and systems. Hence, the PDP of the redundant circuits were calculated and normalized. To perform normalization, the highest PDP value of a redundant circuit corresponding to a specific degree of fault tolerance was chosen as the reference, and this reference value was used to divide the actual PDP values of all of the redundant circuits without and with the ESL, which correspond to the same degree of fault tolerance. The normalized PDP values are given in
Table 1. Although the least value of PDP is desirable, the PDP is traded-off for the provision of the ESL here. The provision of the ESL is important, as it infuses a confidence into interpreting the correct or the incorrect operation of a redundancy scheme, and the absence of the ESL would lead to presuming the correct operation of a redundancy scheme, which may not always be true.
The critical path delays of the NMR circuits are given by the sum of the propagation delays of a function block and the corresponding majority voters. Since the majority voters of the NMR circuits would differ in structure due to increases in the logic gates and the logic levels with increases in the order of redundancy (as portrayed by
Figure 2,
Figure 3 and
Figure 4), the critical path delays of the NMR circuits would increase with increases in the order of redundancy, as noticed in
Table 2. The critical path delays of the NMRESL circuits are given by the sum of the propagation delays of a function block, the corresponding majority voters, and the corresponding ESL circuits. The ESL portion of the NMRESL circuits would considerably increase with increases in the order of redundancy. As a result, the critical path delays of the NMRESL circuits are also expected to increase with increases in the order of redundancy, as seen in
Table 2. In the case of the MMR circuits, their critical path delays are dependent upon the propagation delay of a function block and the propagation delay of the corresponding MMR voter. The propagation delay of a MMR voter is dependent on the propagation delays of an AO222 gate, a 2:1 MUX, and a final two-input AND gate. Given this, the critical path delays of the MMR circuits would be the same, thanks to the regularity implicit in the MMR architecture. In the case of the MMRESL circuits, their critical path delays comprise the propagation delays of a function block, the corresponding MMR voter, and the corresponding ESL portion. The ESL part of the MMR circuits feature a uniform logic realization comprising an inverter and a two-input AND gate with respect to each primary output of the function block. The internal outputs of the MMRESL (for example, MMRESLO1 and MMRESLO2, as shown in
Figure 8) can be combined using an OR gate or an OR gate tree, depending upon the number of primary outputs produced by the function blocks. The ESL portion of the MMRESL circuits would be the same, regardless of the order of redundancy, and hence the critical path delays of the MMRESL circuits will be the same, as noticed in
Table 2.
The critical path delays of the NMRESL and MMRESL circuits will be greater than the critical path delays of the basic NMR and MMR circuits due to the presence of the ESL in the former, which are absent in the latter. From
Table 2, it is found that the averaged critical path delay of the 5MR, 7MR, and 9MR circuits is less than the averaged critical path delay of the 5MRESL, 7MRESL, and 9MRESL circuits by 25%, and the averaged critical path delay of the three-of-five, three-of-six, and three-of-seven MMR circuits is less than the averaged critical path delay of the three-of-five, three-of-six, and three-of-seven MMESL circuits by 15.8%. Also, the averaged critical path delay of the three-of-five, three-of-six, and three-of-seven MMRESL circuits is less than the averaged critical path delay of the 5MRESL, 7MRESL, and 9MRESL circuits by 18.9%.
From
Table 2, it is seen that the areas of the NMR circuits are larger than the areas of the MMR circuits. This is due to two reasons: (i) the 7MR and 9MR circuits require 1 and 2 function blocks more than the three-of-six and three-of-seven MMR circuits, respectively; and (ii) the areas of the NMR majority voters are larger than the areas of the counterpart MMR voters. The normalized areas of the various NMR and counterpart MMR voters are depicted in
Figure 9a. The area of the 9MR majority voter is the maximum among the various voters, and this was considered as the baseline value to divide the actual areas of all of the NMR and MMR voters to perform normalization. On average, the MMR voters require a 63.5% smaller silicon footprint compared to their counterpart NMR voters. Further, the areas of the ESL of the MMR circuits represent a very small percentage compared to the area occupancies of the ESL part of the counterpart NMR circuits.
Figure 9b shows the normalized area occupancies of the NMRESL circuits and the corresponding MMRESL circuits, given in percentages. The ESL portion of the 9MRESL circuit is found to occupy the maximum area, and so this value was used to perform the normalization. On average, the ESL part of the MMRESL circuits requires 26× less area than the ESL part of their counterpart NMRESL circuits. From
Table 2, it is found that on average, the MMR circuits occupy 30.8% less area than the corresponding NMR circuits, and the MMRESL circuits occupy 64.8% less area than the corresponding NMRESL circuits. The proposed MMRESL circuits require 26.8% less silicon than even the corresponding NMR circuits without ESL, which is a notable advantage.
Since the averaged area of the NMR and NMRESL circuits is greater than the averaged area of the MMRESL circuits, the latter are likely to dissipate less power than the former. From
Table 2, it is found that on average, the MMRESL circuits dissipate 25.1% less power compared to the NMR circuits, and 49.5% less power than the NMRESL circuits. Further, it is noted that the proposed MMRESL circuits, on average, achieve an 8.7% reduction in the PDP compared to the basic NMR circuits and a 52.9% reduction in the PDP compared to the NMRESL circuits.
5. Conclusions
This article presented a new ESL circuit for the recently proposed MMR scheme, which forms an attractive alternative to the NMR scheme for the efficient design of circuits and systems that are meant for safety-critical applications. The provision of the ESL is important to be able to make an informed judgment about the correct or the incorrect operation of a redundant implementation. However, for the ESL, the correct operation of a redundancy scheme would be assumed, which may not always be true and may be dangerous. The ESL basically provides a clarity into ascertaining the operational state of a safety-critical circuit or system in real-time. This could be useful information to initiate appropriate remedial action, preemptively or during a scheduled maintenance. Example NMR and MMR circuits without and with the ESL, which embed similar degrees of fault tolerance, were physically implemented using a 32/28-nm CMOS technology, and their design metrics were estimated. It is found that on average, the proposed MMRESL circuits achieve: (i) respective reductions in area, power, and PDP by 26.8%, 25.2%, and 8.7% compared to the basic NMR circuits without ESL; and (ii) respective reductions in delay, area, power, and PDP by 18.9%, 64.8%, 49.6%, and 52.9% compared to the NMRESL circuits. Compared to the basic NMR circuits, on average, the NMRESL circuits report increases in the critical path delay, area, and power dissipation by 33.3%, 107.8%, and 48.4% respectively. However, compared to the basic MMR circuits, on average, the MMRESL circuits report respective increases in the critical path delay, area, and power dissipation by just 18.8%, 5.8%, and 7%; these represent the minor trade-offs to be made to obtain useful information about the operational state of a MMR implementation in real-time.