Nonlinearities Associated with Impaired Sensors in a Typical SHM Experimental Set-Up
Abstract
:1. Introduction
2. Materials and Methods
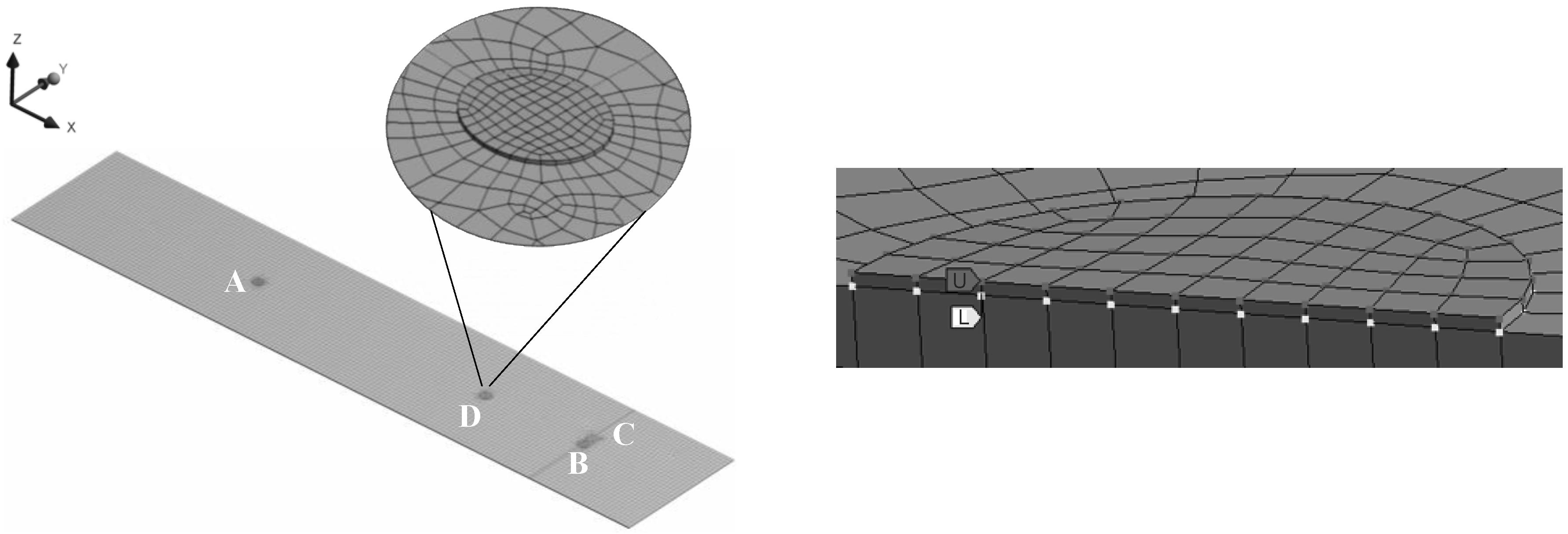
2.1.Experimental Set-Up
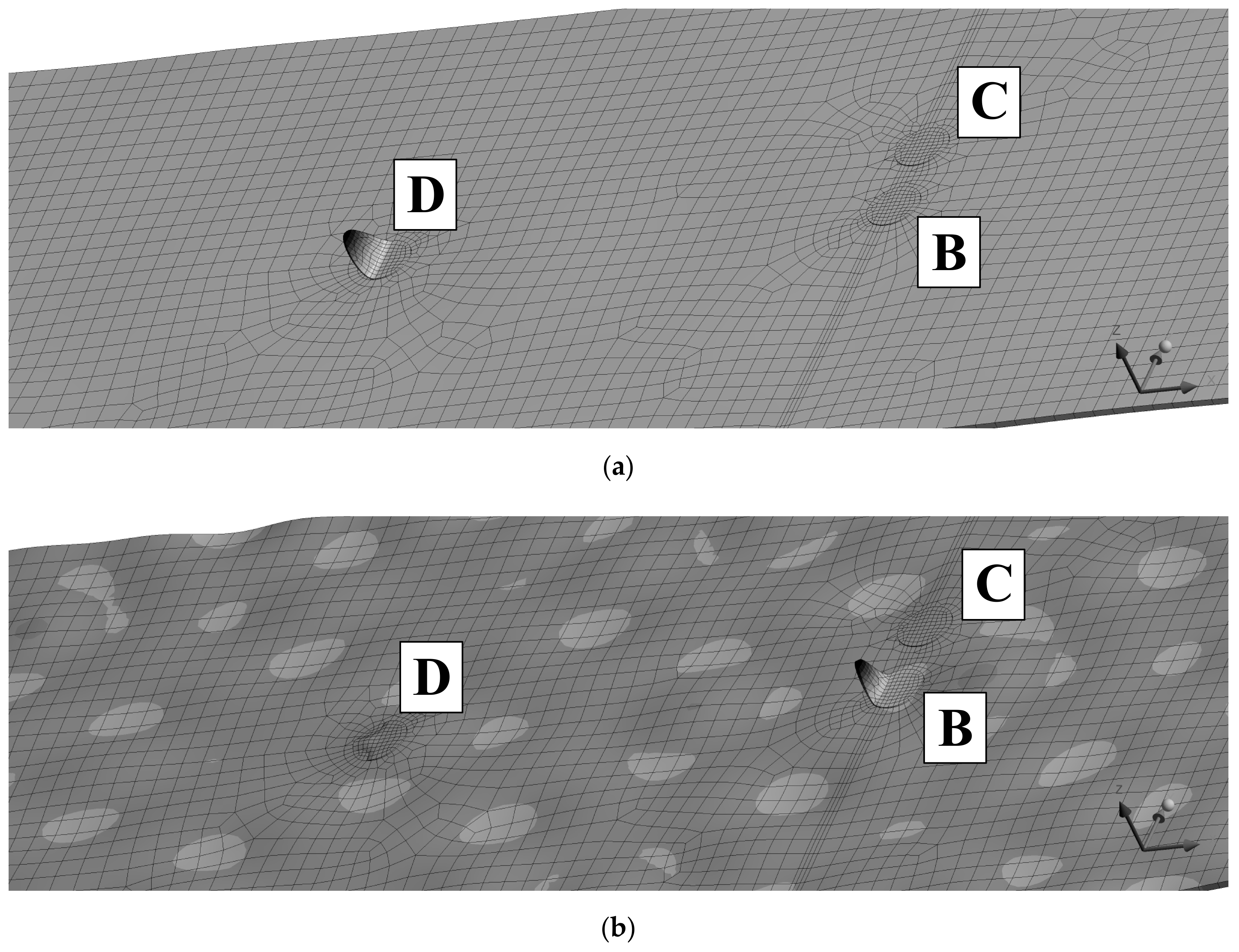
- A and C Are fully bonded;
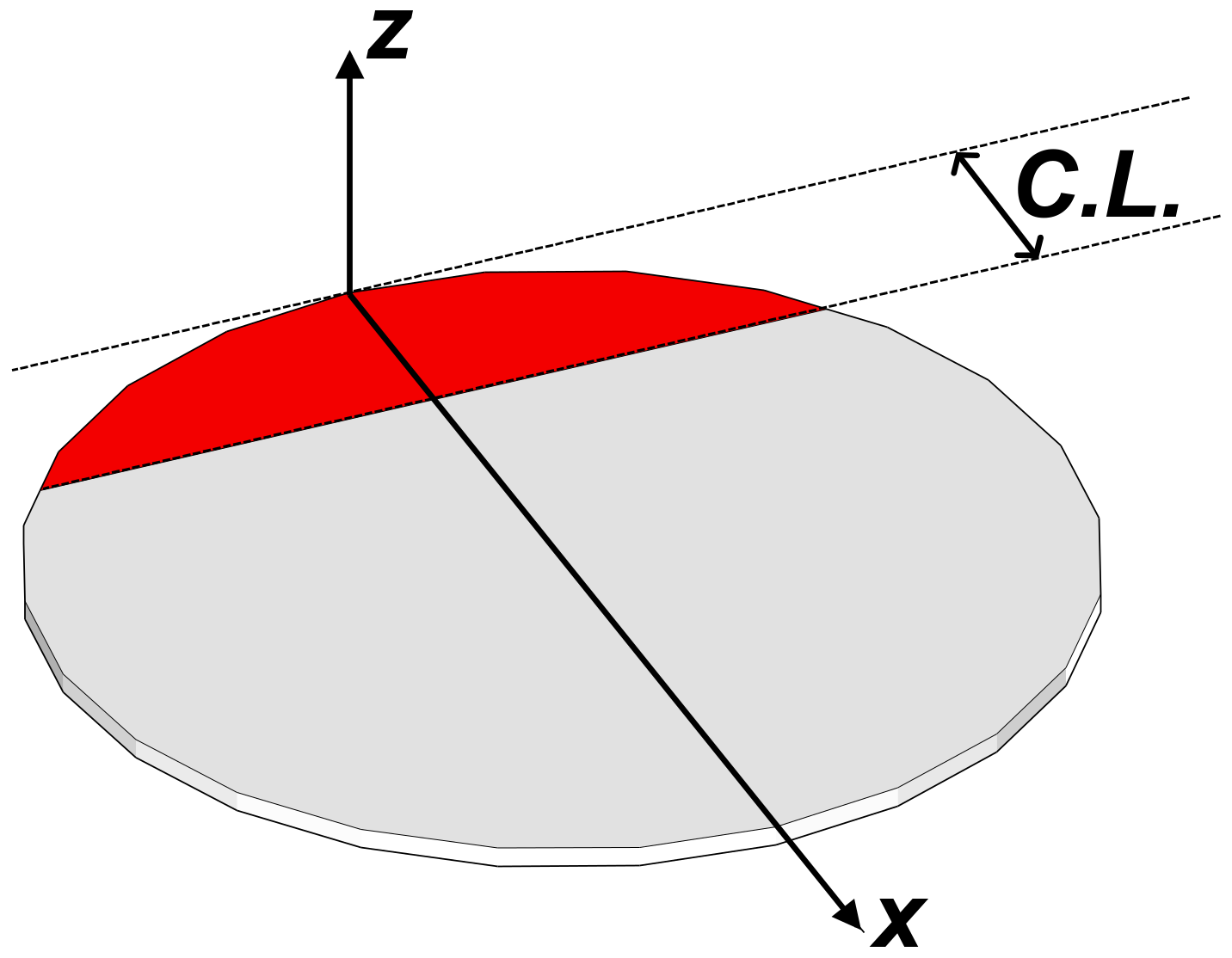
- B is partially bonded, with an adhesive area equal to a circular segment with the “cut off” chord at 75% of the sensor diameter, along x-axis in Figure 3 (Teflon patch in red);
- D is bonded for the half of the contact area.
2.2. SHM Techniques
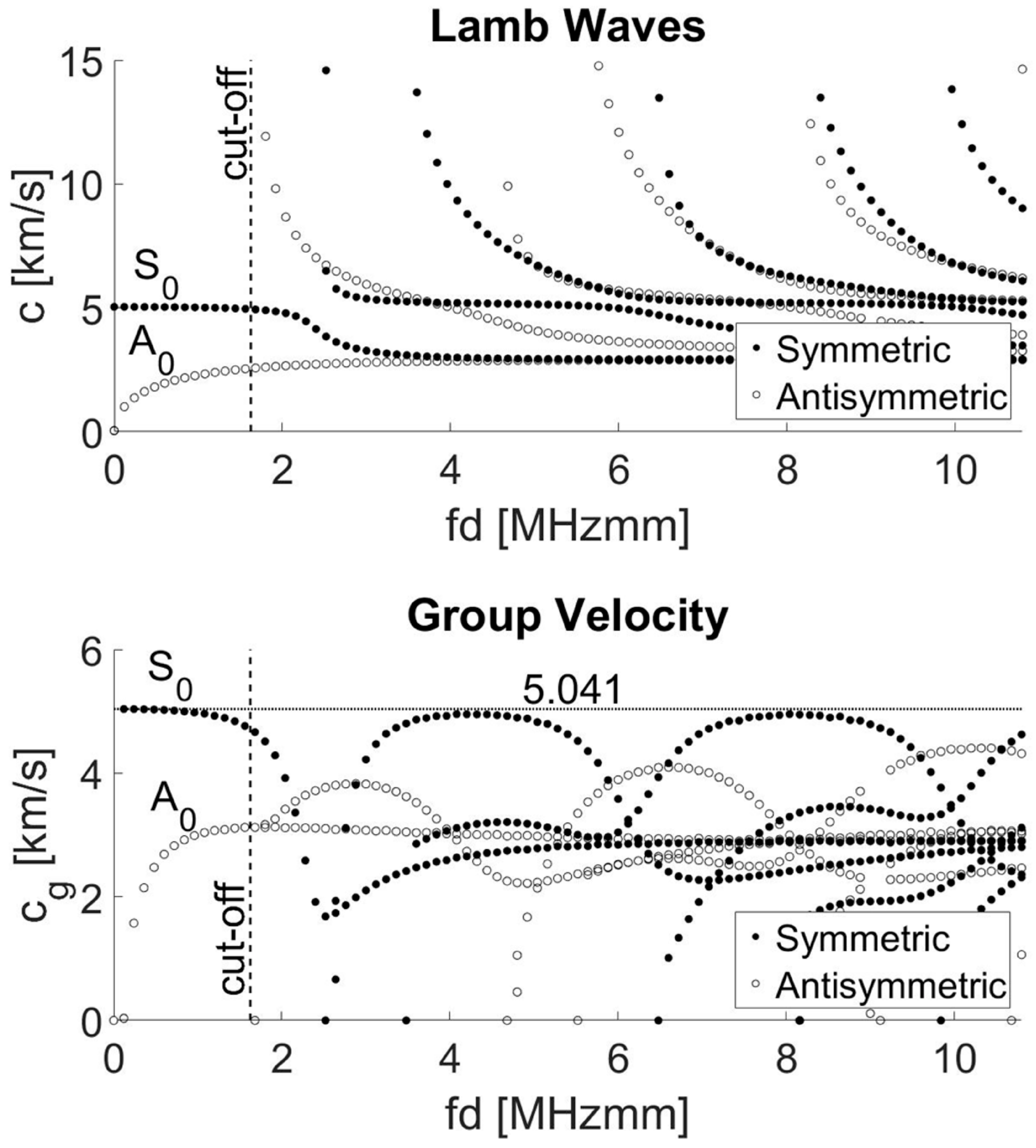
2.2.1. ToF Evaluation Method
2.2.2. Nonlinear Method by Using Subharmonics
- G is the shear modulus of the sensor material; κ is a coefficient to model the short-plate character of this structure and, for a rectangular cross-section, is equal to 5/6;
- Cl is the linear compliance, and is calculated as the ratio between the free-end, out-of-plane deflection and the corresponding force applied at the same point about the same direction; Cl(x) is another linear compliance that is calculated as the ratio of the out-of-plane deflection at a generic point of abscissa x to the force that is applied at the cantilever free end;
- Ca(x), the axial compliance, represents the ratio between the axial displacement at a point of abscissa x and the axial force that would be applied at the cantilever free end;
- Cc(x), the cross compliance, is the ratio of the slope of the deformed cantilever being measured at the point of abscissa x to the free-end, out-of-plane force.
3. Numerical Simulations
4. Results and Discussion
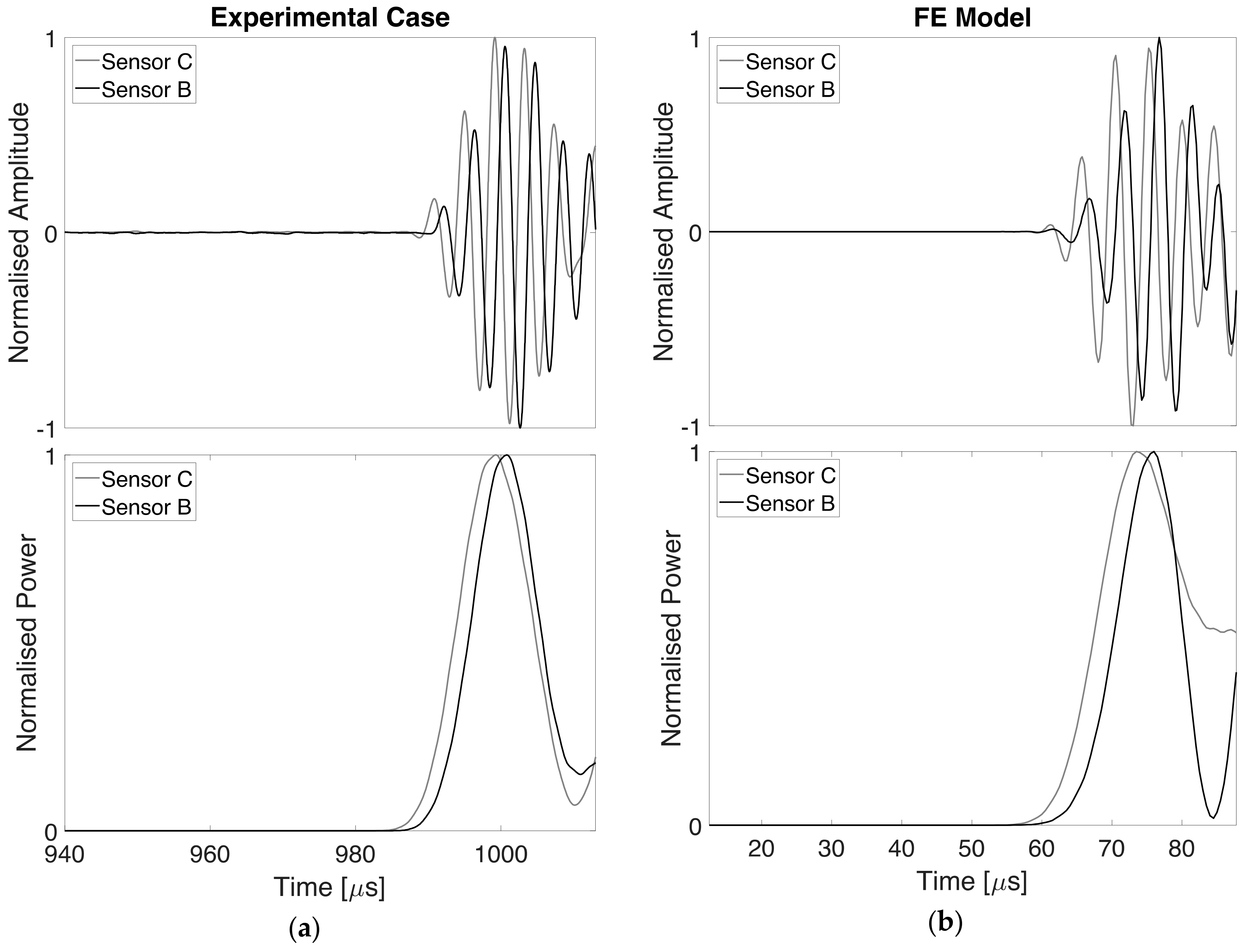
- the ToF associated with the intact (fully bonded) sensor should be known a priori: in this way the time-shift (otherwise wrongly interpreted) allows to identify the damaged sensor;
- the debonded region must be oriented to the exciting sensor like in the present case of investigation: the ToF actually indicates the presence of debonding when it occurs between approaching edge and propagation wavefront as reported also in [22]. If this condition is not satisfied, the ToF can be useless in the identification of impaired sensors;
- a comparison with an undamaged sensor (in this case the sensor C) should be made to evaluate the time-shift, which makes this approach requiring a baseline.
- the excitation at first subharmonic frequency (fe at 5.45 kHz in experiments and fe at 5.13 kHz in numerical simulations) led to voltage peak at sensor D higher than the received one at sensor B. The excitation at first subharmonic frequency (fe at 19.99 kHz in experiments and fe at 20.51 kHz in numerical simulations) led to voltage peak at sensor B higher than the received one at sensor D;
- for every exciting frequency (experimental cases or FE models), the higher voltage peak was produced by the impaired sensor which was characterised by having the damage resonance frequency equal to fe (LDR). This happens because a structure excited at its natural frequency, behaves with abnormal vibrations (as highlighted in Figure 9): in the specific case of the present investigation, the excitation from the sensor A resulted in higher voltage peak of the impaired sensor since its frequency was equal to the first natural frequency of the sensor debonded part that was free to vibrate as a cantilevered plate.
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Abe, M. Structural monitoring of civil structures using vibration measurement Current practice and future. In Artificial Intelligence in Structural Engineering; Springer: Berlin/Heidelberg, Germany, 1998; pp. 1–18. ISBN 978-3-540-68593-7. [Google Scholar]
- Ostachowicz, W.; Kudela, P.; Krawczuk, M.; Zak, A. Guided Waves in Structures for SHM: The Time-Domain Spectral Element Method; John Wiley & Sons: New York, NY, USA, 2011; pp. 233–294. ISBN 978-0-470-97983-9. [Google Scholar]
- De Marchi, L.; Marzani, A.; Miniaci, M. A dispersion compensation procedure to extend pulse-echo defects location to irregular waveguides. NDT E Int. 2013, 54, 115–122. [Google Scholar] [CrossRef]
- Miniaci, M.; Gliozzi, A.S.; Morvan, B.; Krushynska, A.; Bosia, F.; Scalerandi, M.; Pugno, N.M. Proof of concept for an ultrasensitive technique to detect and localize sources of elastic nonlinearity using phononic crystals. Phys. Rev. Lett. 2017, 118, 214301. [Google Scholar] [CrossRef] [PubMed]
- Ciampa, F.; Mankar, A.; Marini, A. Phononic Crystal Waveguide Transducers for Nonlinear Elastic Wave Sensing. Sci. Rep. 2017, 7, 14712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Senesi, M.; Xu, B.; Ruzzene, M. Experimental characterization of periodic frequency-steerable arrays for structural health monitoring. Smart Mater. Struct. 2010, 19, 055026. [Google Scholar] [CrossRef]
- Gliozzi, A.S.; Miniaci, M.; Bosia, F.; Pugno, N.M.; Scalerandi, M. Metamaterials-based sensor to detect and locate nonlinear elastic sources. Appl. Phys. Lett. 2015, 107, 161902. [Google Scholar] [CrossRef] [Green Version]
- Song, G.; Gu, H.; Mo, Y.L.; Hsu, T.T.; Dhonde, H. Concrete structural health monitoring using embedded piezoceramic transducers. Smart Mater. Struct. 2007, 16, 959. [Google Scholar] [CrossRef]
- Giri, P.; Kharkovsky, S.; Zhu, X.; Clark, S.M.; Taheri, S.; Samali, B. Characterization of carbon fiber reinforced polymer strengthened concrete and gap detection with a piezoelectric-based sensory technique. Struct. Health Monit. 2018, 11. [Google Scholar] [CrossRef]
- Wu, F.; Chang, F.K. Debond detection using embedded piezoelectric elements in reinforced concrete structures-part I: Experiment. Struct. Health Monit. 2006, 5, 5–15. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.; Hao, H.; Ou, J. Guided wave propagation and spectral element method for debonding damage assessment in RC structures. J. Sound Vib. 2009, 324, 751–772. [Google Scholar] [CrossRef]
- Adams, R.D.; Adams, R.D.; Comyn, J.; Wake, W.C. Structural Adhesive Joints in Engineering; Springer Science & Business Media: Dordrecht, The Netherlands, 1997; p. 244. ISBN 978-0-412-70920-3. [Google Scholar]
- Viana, G.M.; Costa, M.; Banea, M.D.; da Silva, L.F. A review on the temperature and moisture degradation of adhesive joints. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2017, 231, 488–501. [Google Scholar] [CrossRef]
- Tinoco, H.A.; Serpa, A.L.; Peña, F.M. Debonding estimation of piezoelectric sensors by power consumption analysis in smart structures using the finite element method. In Proceedings of the V Congreso Internacional de Ingenierıa Mecįnica y III de Ingenierıa Mecatronica, Colombia, Bogota, 11–12 August 2011; pp. 1–12. [Google Scholar]
- Overly, T.G.; Park, G.; Farrar, C.R. Development of signal processing tools and hardware for piezoelectric sensor diagnostic processes. Sens. Syst. Netw. Phenom. Technol. Appl. NDE Health Monit. 2007, 6530, 653018. [Google Scholar] [CrossRef]
- Wandowski, T.; Moll, J.; Malinowski, P.; Opoka, S.; Ostachowicz, W. Assessment of piezoelectric sensor adhesive bonding. J. Phys. Conf. Ser. 2015, 628, 012114. [Google Scholar] [CrossRef] [Green Version]
- Lanzara, G.; Yoon, Y.; Kim, Y.; Chang, F.K. Influence of interface degradation on the performance of piezoelectric actuators. J. Intell. Mater. Syst. Struct. 2009, 20, 1699–1710. [Google Scholar] [CrossRef]
- Park, G.; Farrar, C.R.; Rutherford, A.C.; Robertson, A.N. Piezoelectric active sensor self-diagnostics using electrical admittance measurements. J. Vib. Acoust. 2006, 128, 469–476. [Google Scholar] [CrossRef]
- Lee, S.J.; Sohn, H.; Michaels, J.E.; Michaels, T.E. In situ detection of surface–mounted pzt transducer defects using linear reciprocity. In AIP Conference Proceedings; AIP: Kingston, Rhode Island, 2010; Volume 1211, pp. 1844–1851. [Google Scholar]
- Lee, S.J.; Michaels, J.E.; Sohn, H.; Michaels, T.E. Piezoelectric transducer diagnostics via linear reciprocity for guided wave structural health monitoring. AIAA J. 2011, 49, 621–629. [Google Scholar] [CrossRef]
- Achenbach, J.A.; Achenbach, J.D. Reciprocity in Elastodynamics; Cambridge University Press: Cambridge, UK, 2003; pp. 90–115. ISBN 9780511550485. [Google Scholar]
- Sathyanarayana, C.N.; Ashwin, U.; Raja, S. Effect of sensor debonding on lamb wave propagation in plate structure. ARPN J. Eng. Appl. Sci. 2014, 9, 1358–1366. [Google Scholar]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors; Elsevier: Burlington, MA, USA, 2007; pp. 321–329. [Google Scholar]
- Scarselli, G.; Corcione, C.; Nicassio, F.; Maffezzoli, A. Adhesive joints with improved mechanical properties for aerospace applications. Int. J. Adhes. Adhes. 2017, 75, 174–180. [Google Scholar] [CrossRef]
- Duarte, R.M.; Villanueva, J.M.; Costa, M.M.; Freire, R.C.; Catunda, S.Y.; Costa, W.M. Ultrasonic time of flight estimation for wind speed measurement based on time-frequency domain using STFT. In Proceedings of the 19th IMEKO TC 4Symposium and 17th IWADC Workshop Advances in Instrumentation and Sensors Interoperability, Barcelona, Spain, 15 July 2013; pp. 18–19. [Google Scholar]
- Lobontiu, N.; Ilic, B.; Reissman, T.; Garcia, E.; Nam, Y.; Craighead, H.G. Modeling, Design and Experimental Characterization of Bending Resonant Circular Nano Cantilevers. Micro Nanosyst. 2009, 1, 22–29. [Google Scholar] [CrossRef]
- Lobontiu, N. Compliant Mechanisms: Design of Flexure Hinges; CRC Press: Boca Raton, FL, USA, 2002; pp. 214–215. ISBN 9780849313677. [Google Scholar]
- ANSYS Help. Available online: https://ansyshelp.ansys.com (accessed on 30 August 2018).
- Chien, W.T.; Yang, C.J.; Yen, Y.T. Coupled-field analysis of piezoelectric beam actuator using FEM. Sens. Actuators A Phys. 2005, 118, 171–176. [Google Scholar] [CrossRef]
- Ciampa, F.; Scarselli, G.; Meo, M. On the generation of nonlinear damage resonance intermodulation for elastic wave spectroscopy. J. Acoust. Soc. Am. 2017, 141, 2364–2374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scarselli, G.; Ciampa, F.; Nicassio, F.; Meo, M. Non-linear methods based on ultrasonic waves to analyse disbonds in single lap joints. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 3066–3076. [Google Scholar] [CrossRef]
- Scarselli, G.; Ciampa, F.; Ginzburg, D.; Meo, M. Non-destructive testing techniques based on nonlinear methods for assessment of debonding in single lap joints. In Proceedings of the Structural Health Monitoring and Inspection of Advanced Materials, Aerospace, and Civil Infrastructure, San Diego, CA, USA, 1 April 2015; International Society for Optics and Photonics: San Diego, CA, USA, 2015; p. 943706. [Google Scholar]





| Mechanical Properties | Dielectric Properties | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Density ρ [kg/m3] | 7800 | Elastic Compliance S33 [m2/N] | 20.7 × 10−12 | Curie Temperature [K] | 623 | Relative Permittivity | 1650 | ||
| Elastic Compliance S11 [m2/N] | 16.1 × 10−12 | Elastic Stiffness E33 [N/m2] | 10.0 × 1010 | Relative Permittivity | 1750 | Dielectric Loss Factor | 20 × 10−3 | ||
| Electromechanical properties | |||||||||
| Coupling factor | Piezoelectric charge coefficient | Piezoelectric Voltage Coefficient | |||||||
| kp | 0.62 | k33 | 0.69 | d31 [C/N] | −180 × 10−12 | g31 [Vm/N] | −11.3 × 10−3 | ||
| kt | 0.47 | k15 | 0.66 | d33 [C/N] | 400 × 10−12 | g33 [Vm/N] | 25.0 × 10−3 | ||
| k31 | 0.35 | d15 [C/N] | 550 × 10−12 | ||||||
| Actuator (Exciter) | Receiver | Experimental First Superharmonic Amplitude [dBu] | Numerical First Superharmonic Amplitude [dBu] |
|---|---|---|---|
| A | B | −33.8 | −44.5 |
| D | −40.2 | −43.5 | |
| B | A | −54.0 | −55.7 |
| D | −53.2 | −56.1 | |
| D | A | −52.0 | −56.9 |
| B | −51.6 | −55.3 |
| Actuator (Exciter) | Receiver | Experimental | Numerical | ||
|---|---|---|---|---|---|
| fe [kHz] | Fundamental Amplitude [dBu] | fe [kHz] | Fundamental Amplitude [dBu] | ||
| A | B | 5.45 | −20.2 | 5.13 | −18.7 |
| D | −15.1 | −13.3 | |||
| B | 19.99 | −16.1 | 20.51 | −14.2 | |
| D | −27.4 | −26.3 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrino, S.; Nicassio, F.; Scarselli, G. Nonlinearities Associated with Impaired Sensors in a Typical SHM Experimental Set-Up. Electronics 2018, 7, 303. https://doi.org/10.3390/electronics7110303
Carrino S, Nicassio F, Scarselli G. Nonlinearities Associated with Impaired Sensors in a Typical SHM Experimental Set-Up. Electronics. 2018; 7(11):303. https://doi.org/10.3390/electronics7110303
Chicago/Turabian StyleCarrino, Stefano, Francesco Nicassio, and Gennaro Scarselli. 2018. "Nonlinearities Associated with Impaired Sensors in a Typical SHM Experimental Set-Up" Electronics 7, no. 11: 303. https://doi.org/10.3390/electronics7110303





