Modeling the Hysteresis Characteristics of Transformer Core under Various Excitation Level via On-Line Measurements
Abstract
:1. Introduction
2. Materials and Methods
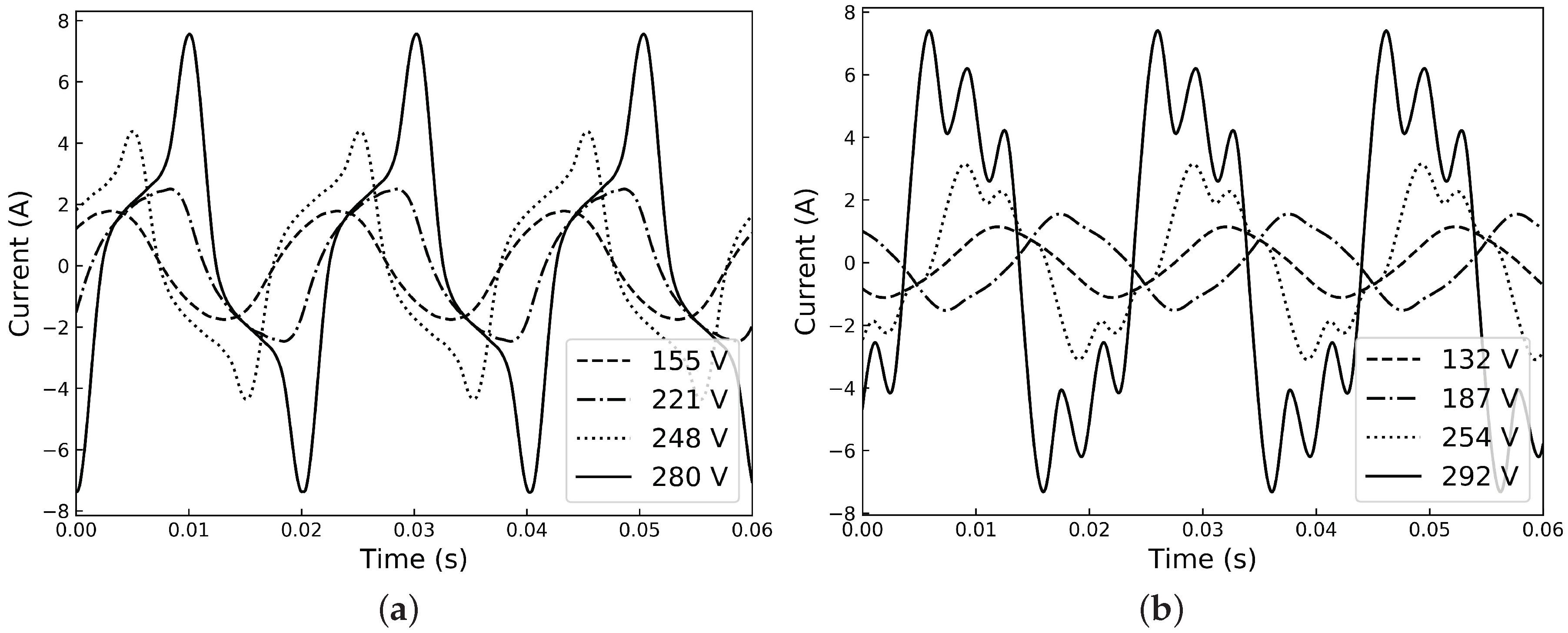
3. Result and Discussion
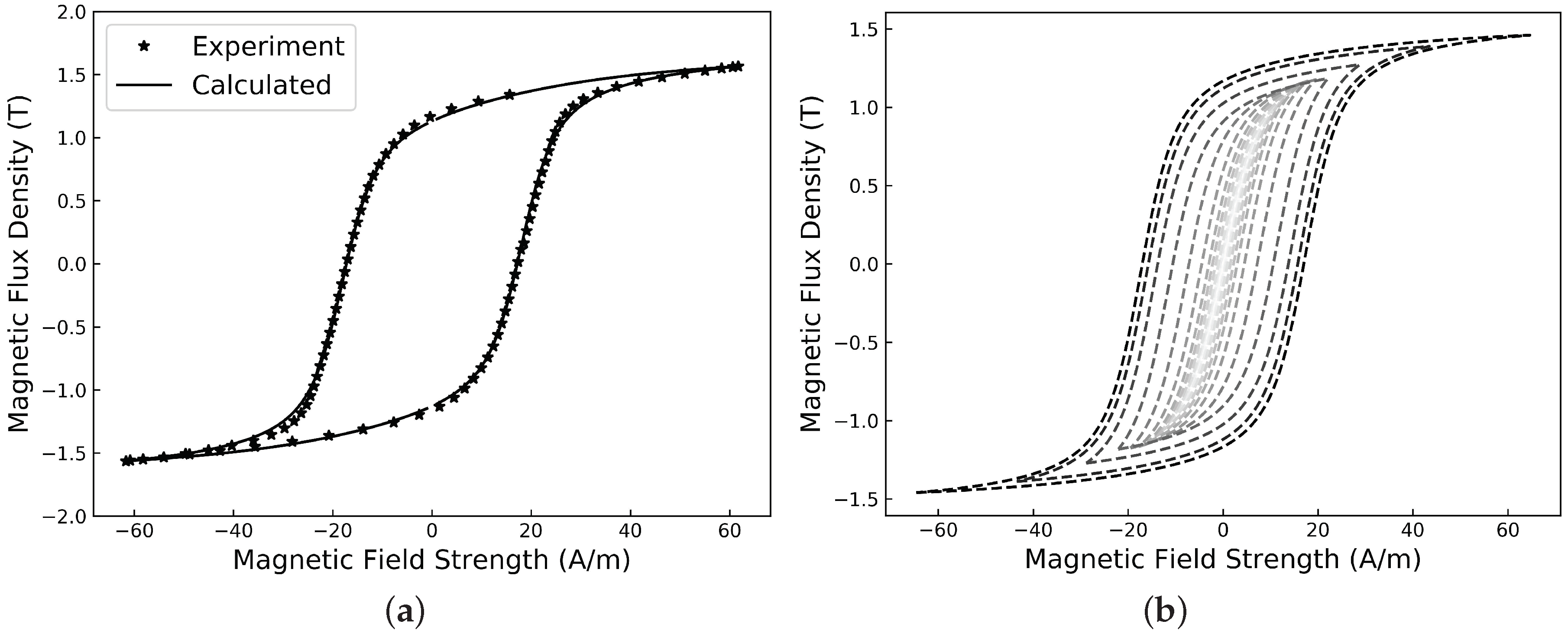
3.1. Magnetization Modeling
3.2. Hysteresis Loop Simulation
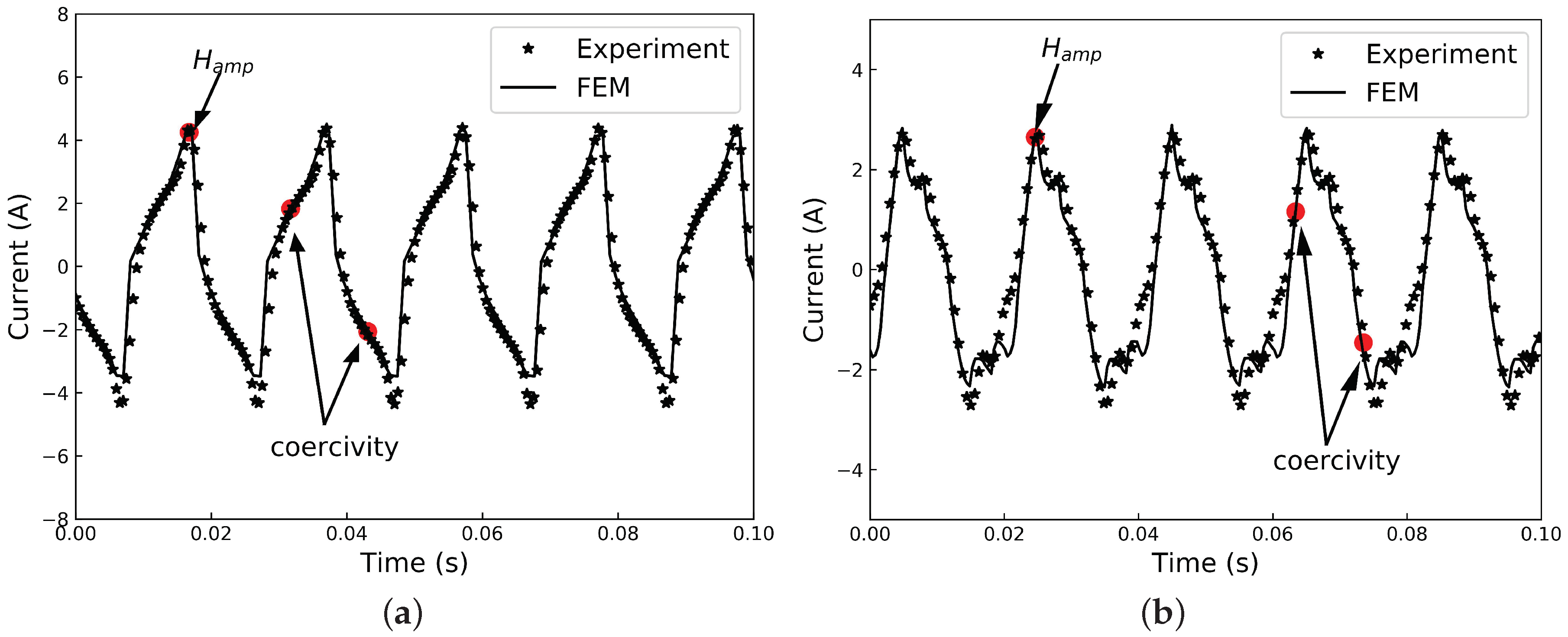
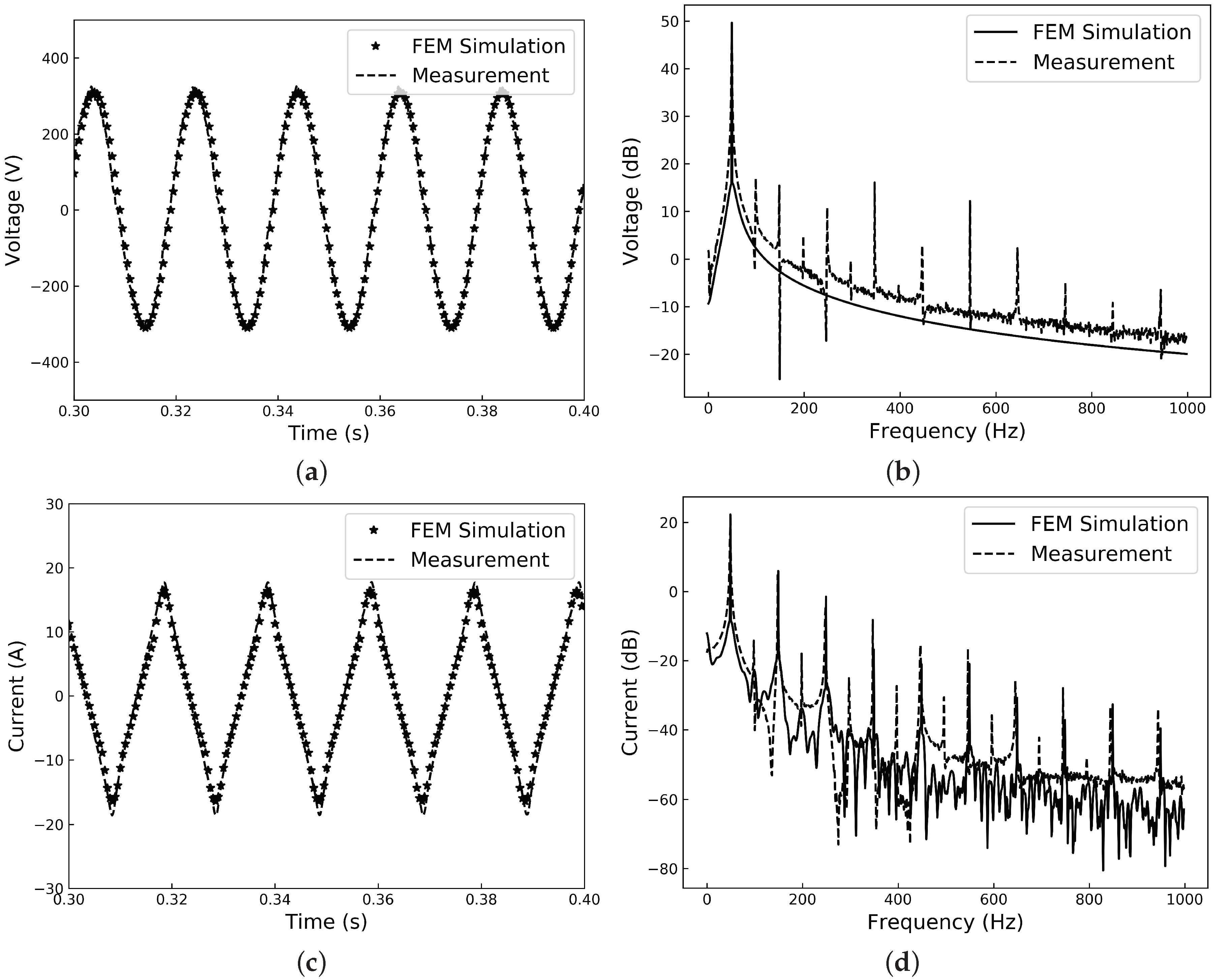
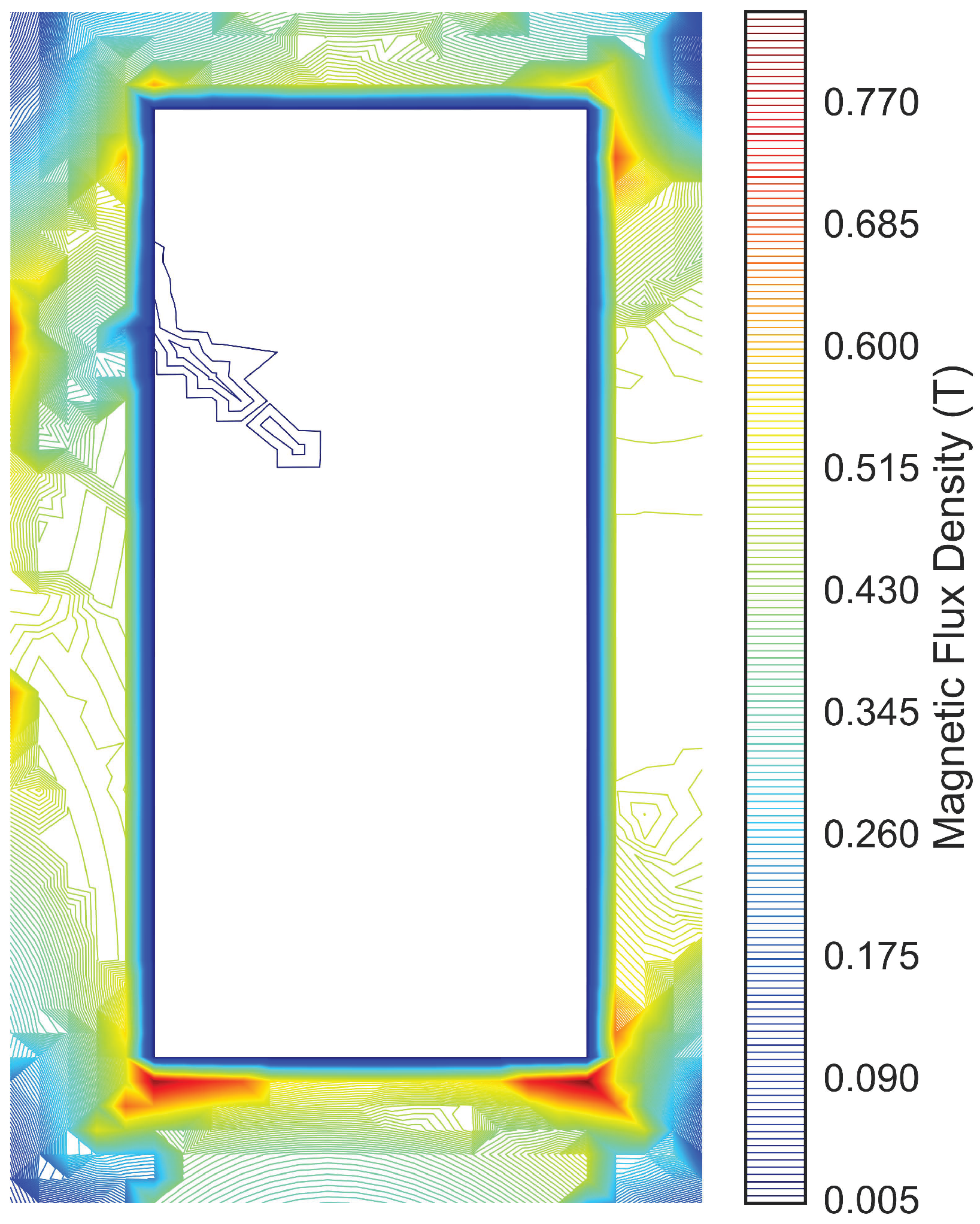
3.3. Applications
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | Finite element model |
| DNN | Deep neural network |
| RMSE | Root mean square error |
| SVR | Support vector regressor |
References
- Schulz, M.; Ringlee, R. Some characteristics of audible noise of power transformers and their relationship to audibility criteria and noise ordinances. Trans. Am. Inst. Electr. Eng. 1960, 79, 316–322. [Google Scholar] [CrossRef]
- Salvini, A.; Fulginei, F.R. Genetic algorithms and neural networks generalizing the Jiles–Atherton model of static hysteresis for dynamic loops. IEEE Trans. Magn. 2002, 38, 873–876. [Google Scholar] [CrossRef]
- Jiles, D.; Ramesh, A.; Shi, Y.; Fang, X. Application of the anisotropic extension of the theory of hysteresis to the magnetization curves of crystalline and textured magnetic materials. IEEE Trans. Magn. 1997, 33, 3961–3963. [Google Scholar] [CrossRef] [Green Version]
- Liorzou, F.; Phelps, B.; Atherton, D. Macroscopic models of magnetization. IEEE Trans. Magn. 2000, 36, 418–428. [Google Scholar] [CrossRef]
- De Leon, F.; Semlyen, A. A simple representation of dynamic hysteresis losses in power transformers. IEEE Trans. Power Del. 1995, 10, 315–321. [Google Scholar] [CrossRef]
- Li, C.; Tan, Y. Modelling Preisach-type hysteresis nonlinearity using neural network. Int. J. Model. Simul. 2007, 27, 233–241. [Google Scholar] [CrossRef]
- Lin, C.E.; Cheng, C.L.; Huang, C.L. Hysteresis characteristic analysis of transformer under different excitations using real time measurement. IEEE Trans. Power Deliv. 1991, 6, 873–879. [Google Scholar] [CrossRef]
- Benšić, T.; Biondić, I.; Marić, P. Single-phase autotransformer modelling and model parameter identification. Electr. Eng. 2018, 100, 625–632. [Google Scholar] [CrossRef]
- Freitag, C.I. Magnetic Properties of Electrical Steel, Power Transformer Core Losses and Core Design Concepts. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2017. [Google Scholar]
- Mayergoyz, I.; Friedman, G. Generalized Preisach model of hysteresis. IEEE Trans. Magn. 1988, 24, 212–217. [Google Scholar] [CrossRef]
- Sadowski, N.; Batistela, N.; Bastos, J.; Lajoie-Mazenc, M. An inverse Jiles–Atherton model to take into account hysteresis in time-stepping finite-element calculations. IEEE Trans. Magn. 2002, 38, 797–800. [Google Scholar] [CrossRef]
- Wlodarski, Z. Modeling hysteresis by analytical reversal curves. Phys. B Condens. Matter 2007, 398, 159–163. [Google Scholar] [CrossRef]
- Wlodarski, Z. Extraction of hysteresis loops from main magnetization curves. J. Magn. Magn. Mater. 2007, 308, 15–19. [Google Scholar] [CrossRef]
- Lin, G.; Song, Q.; Wang, L.; Zhang, D.; Pan, F. A hybrid algorithm based on fish swarm and simulated annealing for parameters identification of modified JA model. In Proceedings of the IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–22 October 2017; pp. 483–488. [Google Scholar]
- Saghafifar, M.; Kundu, A.; Nafalski, A. Dynamic magnetic hysteresis modelling using Elman recurrent neural network. Int. J. Appl. Electromagn. Mech. 2001, 13, 209–214. [Google Scholar]
- Deželak, K.; Pihler, J. Artificial Neural Network as Part of a Saturation-Level Detector within the Transformer’s Magnetic Core. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Dommel, H.W. Electromagnetic Transients Program: Reference Manual: (EMTP Theory Book); Bonneville Power Administration: Portland, OR, USA, 1986.
- Casoria, S.; Sybille, G.; Brunelle, P. Hysteresis modeling in the MATLAB/power system blockset. Math. Comput. Simul. 2003, 63, 237–248. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.r.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; Kingsbury, B. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Liu, L.; Wang, S.; Zhao, Z. Radar Waveform Recognition Based on Time-Frequency Analysis and Artificial Bee Colony-Support Vector Machine. Electronics 2018, 7, 59. [Google Scholar] [CrossRef]
- Sandeep, V.; Murthy, S.; Singh, B. A comparative study on approaches to curve fitting of magnetization characteristics for induction generators. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bengaluru, India, 16–19 December 2012; pp. 1–6. [Google Scholar]
- Tang, Q.; Wang, Z.; Anderson, P.I.; Jarman, P.; Moses, A.J. Approximation and prediction of AC magnetization curves for power transformer core analysis. IEEE Trans. Magn. 2015, 51, 1–8. [Google Scholar] [CrossRef]
- Bertotti, G.; Fiorillo, F.; Soardo, G. The prediction of power losses in soft magnetic materials. J. Phys. Colloq. 1988, 49, C8-1915–C8-1919. [Google Scholar] [CrossRef]
- Štumberger, B.; Goričan, V.; Štumberger, G.; Hamler, A.; Trlep, M.; Jesenik, M. Accuracy of iron loss calculation in electrical machines by using different iron loss models. J. Magn. Magn. Mater. 2003, 254, 269–271. [Google Scholar] [CrossRef]



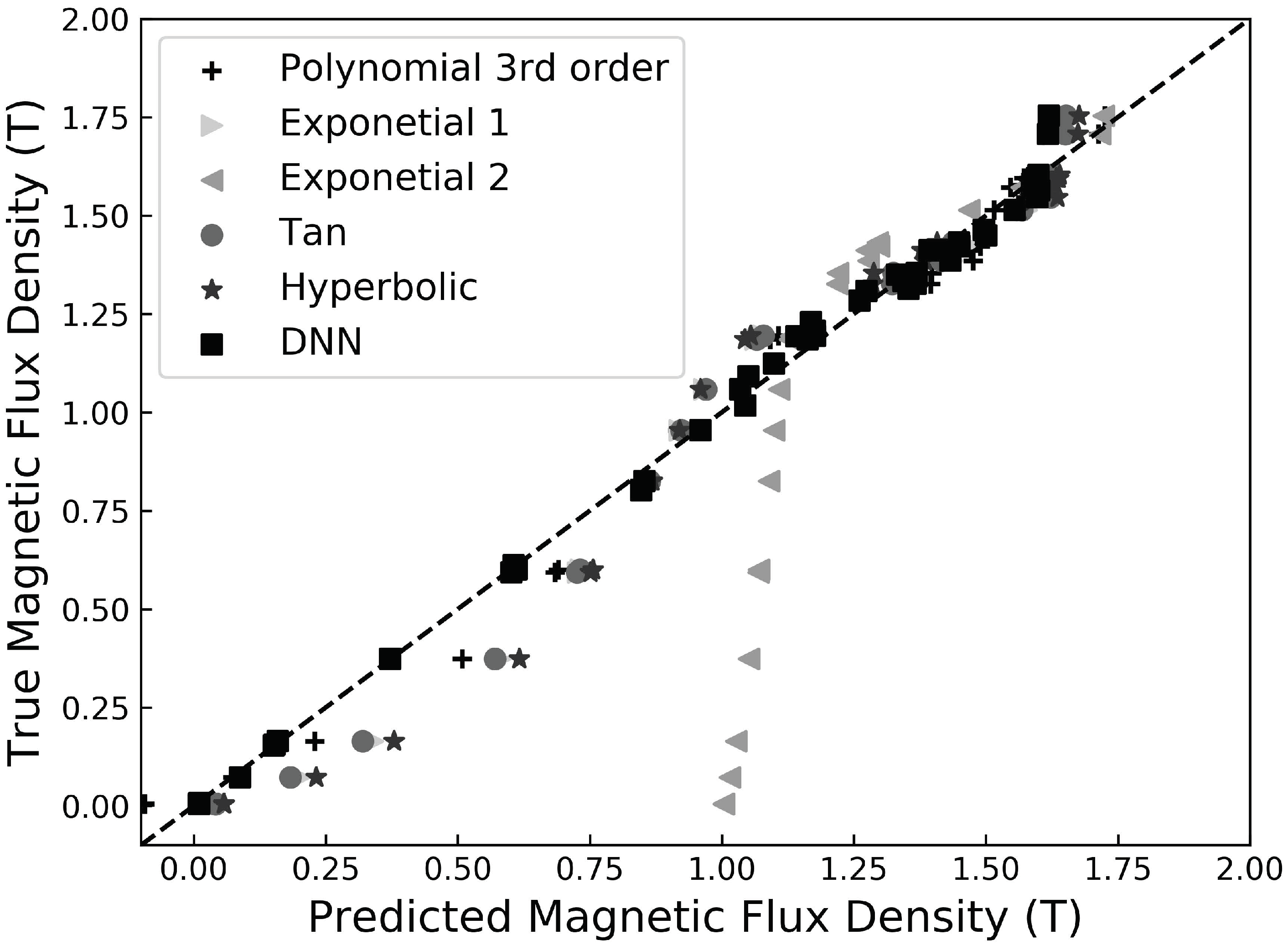


| Model | RMSE | Correlation Coefficient |
|---|---|---|
| Neural Network | 0.0013 | 99.95% |
| Polynomial | 0.0079 | 99.47% |
| Hyperbolic | 0.0236 | 98.09% |
| Exponential 1 | 0.0211 | 98.84% |
| Exponential 2 | 0.1207 | 83.12% |
| Transcendental | 0.0198 | 98.89% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Pan, J.; Guzzomi, A. Modeling the Hysteresis Characteristics of Transformer Core under Various Excitation Level via On-Line Measurements. Electronics 2018, 7, 390. https://doi.org/10.3390/electronics7120390
Du X, Pan J, Guzzomi A. Modeling the Hysteresis Characteristics of Transformer Core under Various Excitation Level via On-Line Measurements. Electronics. 2018; 7(12):390. https://doi.org/10.3390/electronics7120390
Chicago/Turabian StyleDu, Xuhao, Jie Pan, and Andrew Guzzomi. 2018. "Modeling the Hysteresis Characteristics of Transformer Core under Various Excitation Level via On-Line Measurements" Electronics 7, no. 12: 390. https://doi.org/10.3390/electronics7120390





