An Energy-Efficient Fail Recovery Routing in TDMA MAC Protocol-Based Wireless Sensor Network
Abstract
:1. Introduction
2. Network Topology and Energy Model
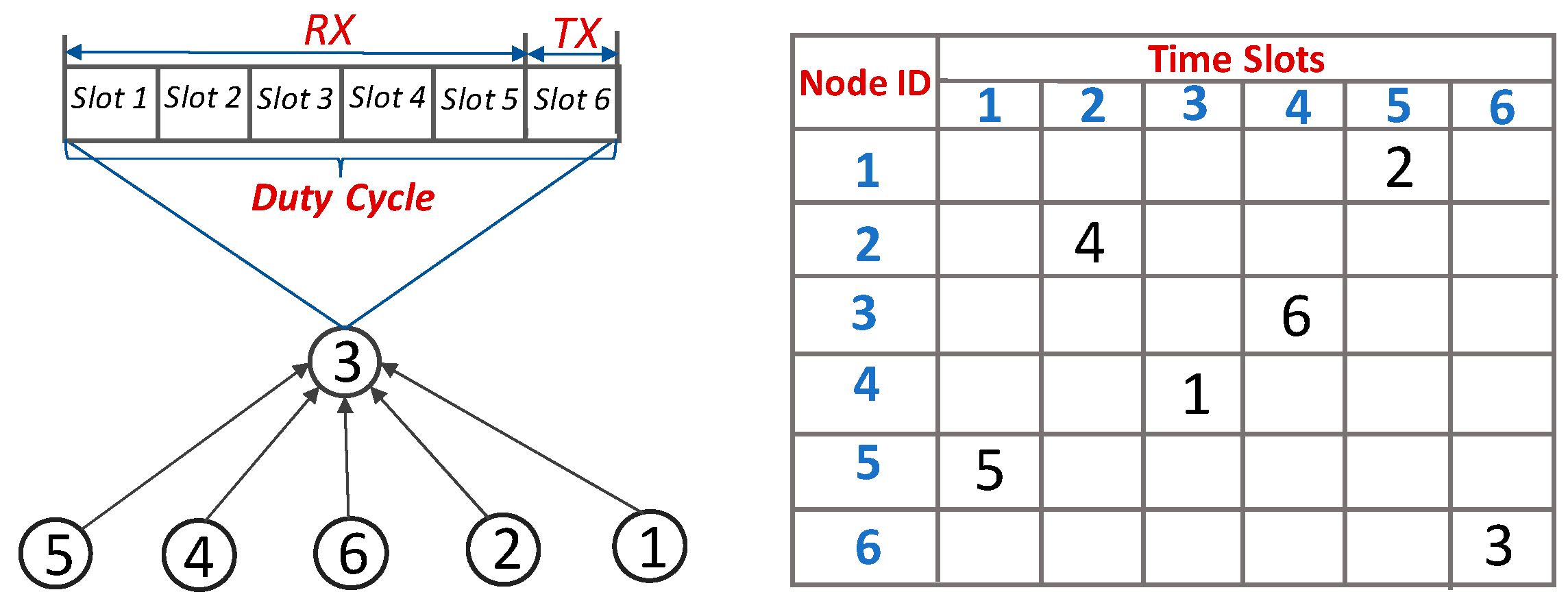
2.1. Network Topology with Time Division Multiplexing
2.2. Energy Model of Convergent Network
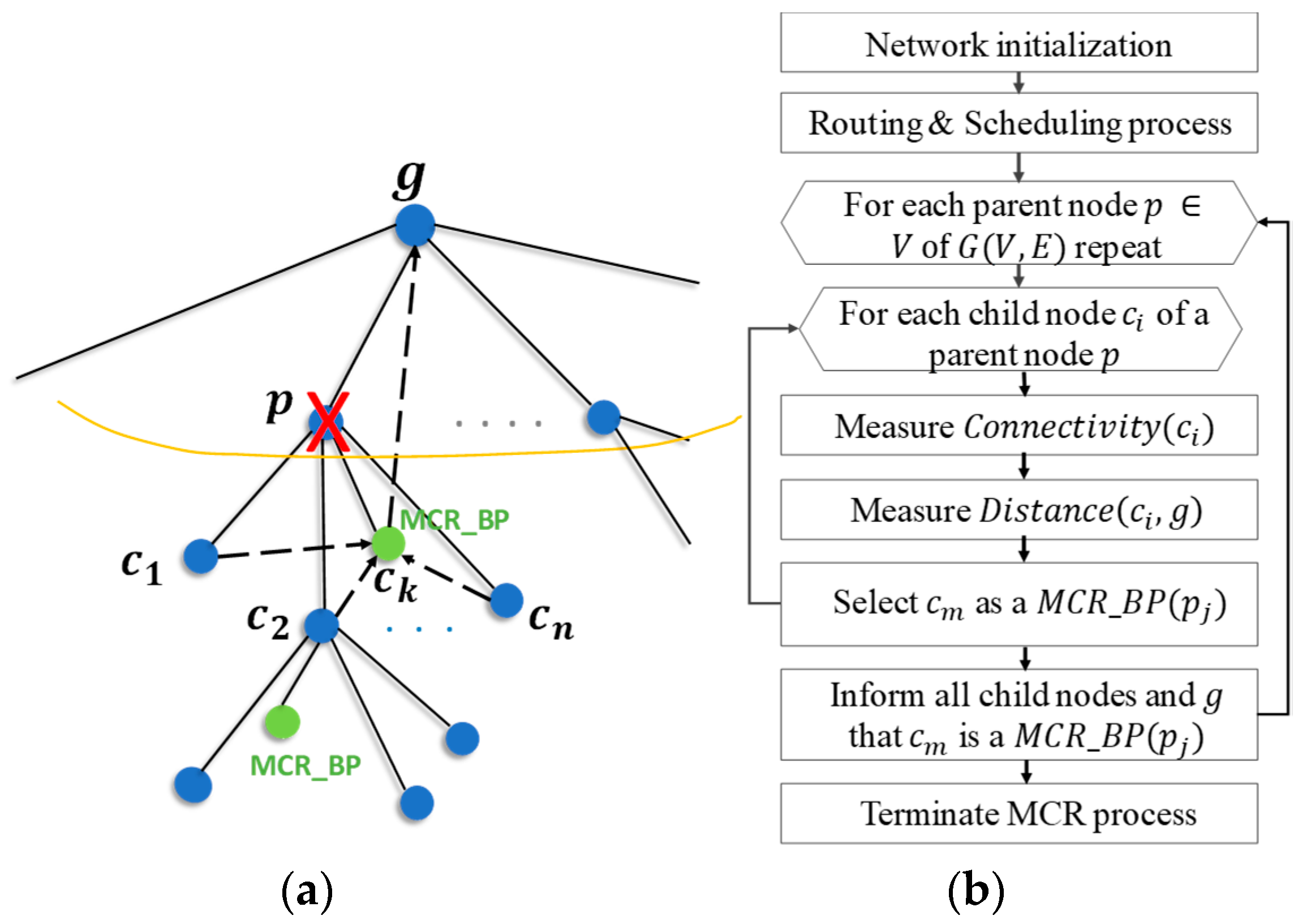
3. Proposed Route-Recovery Algorithms
3.1. Energy Model of Convergent Network
Procedure Select-MCR_BP
- For each child node of a parent node :
- (1)
- Measure = number of other child nodes of such that all are in the wireless range of .
- (2)
- Measure = the distance from to grandparent of (parent of ).
- Select as a MCR backup parent of such that is maximum and , where is the wireless range of .
- If for all child nodes, is unreachable, select the as a and NE-MCR concept to find NE- (details are given in following subsection).
- Inform all ’s and g that is chosen as .
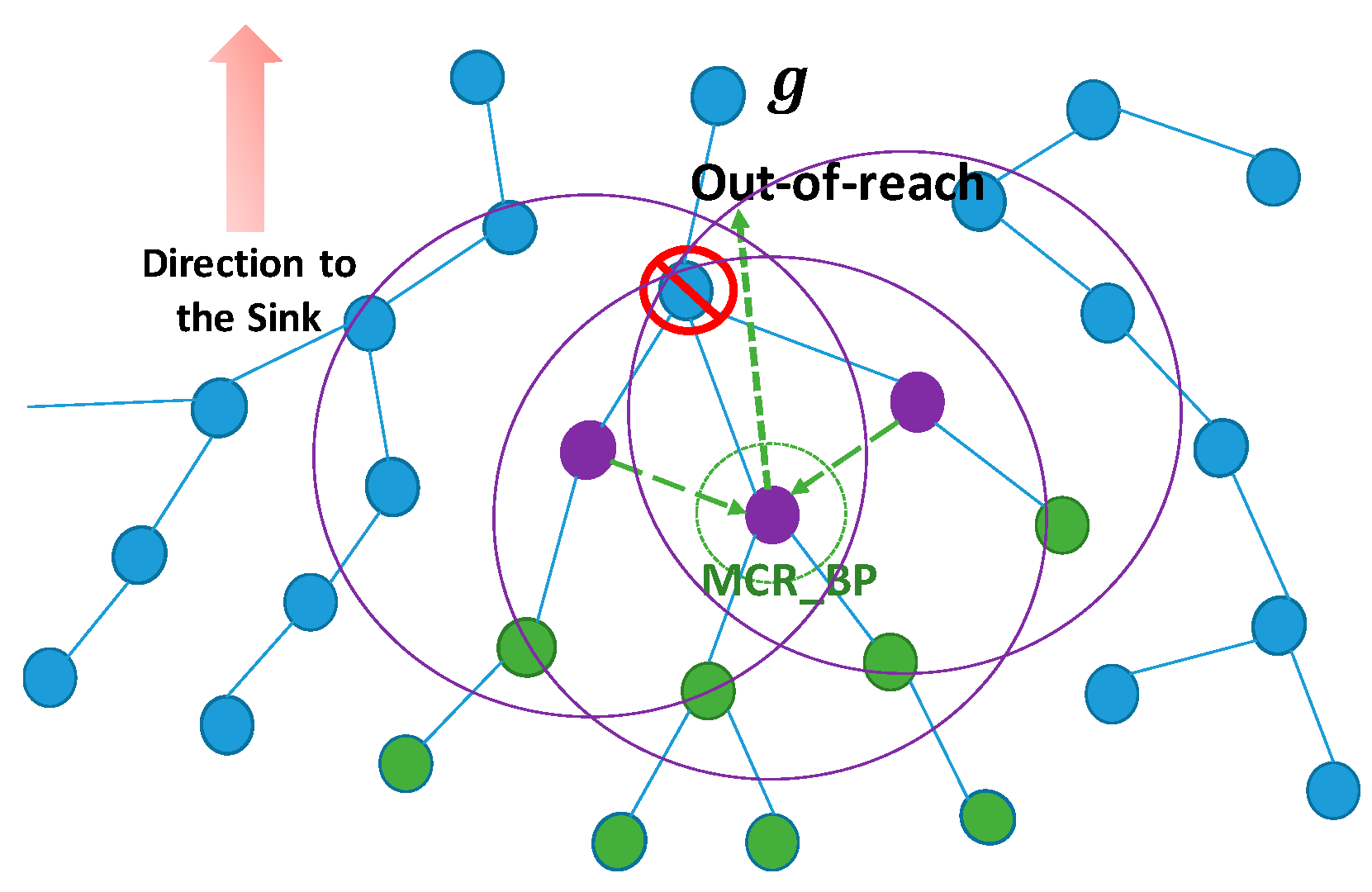
3.2. Neighbor-Extended Maximal Connectivity Routing
Procedure Select-NE-MCR_BP
- For each child node of a parent node :
- Select as a if it has a maximal with other siblings;
- informs its child nodes about the out-of-reach problem;
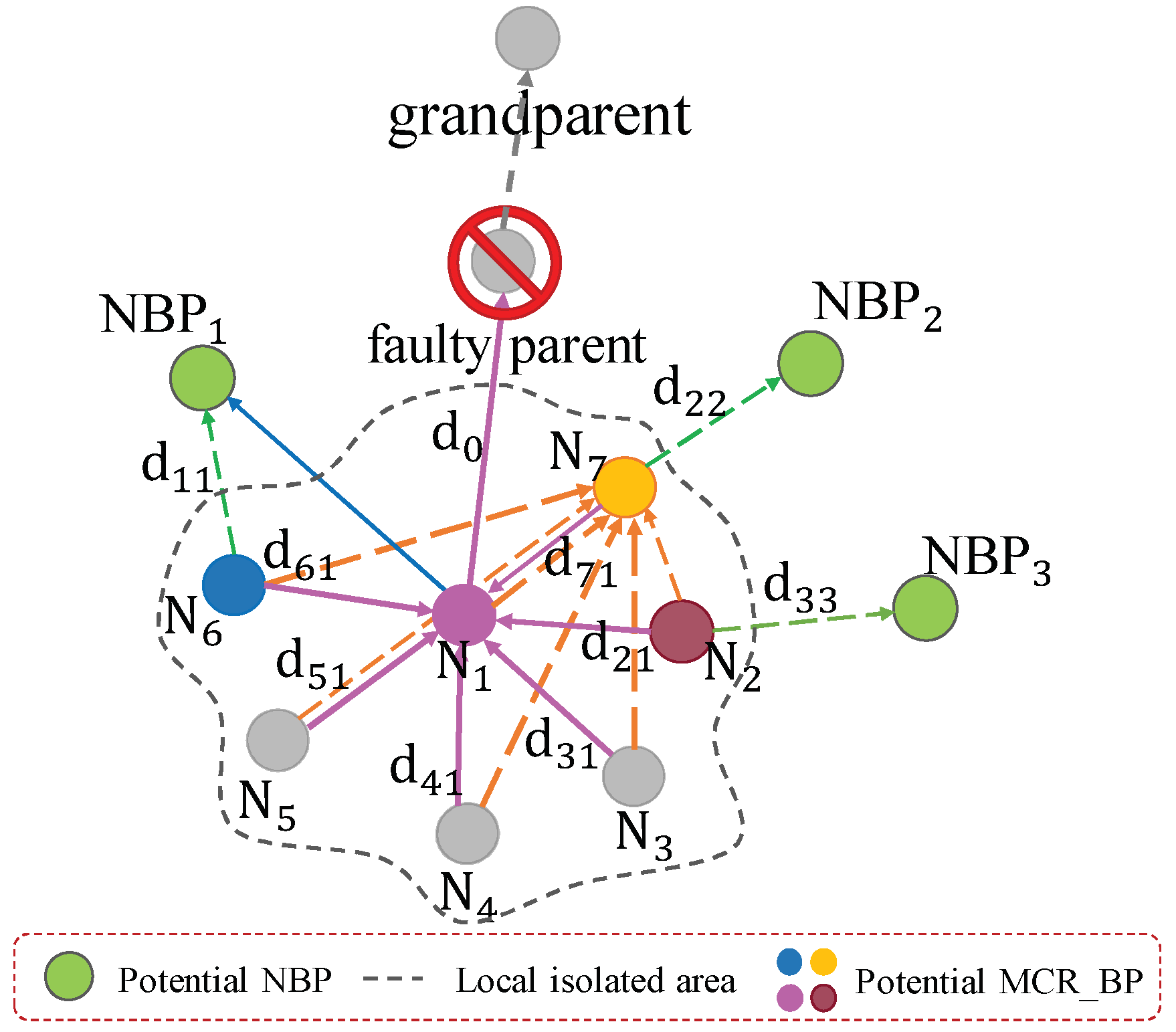
- Every examines each parent’s neighbor () for the following conditions:
- (a)
- Verify if the is minimal;
- (b)
- Verify if the aggregated packet length of is minimal;
- (c)
- Verify if has an extra time slot to receive ’s data;
- If best satisfies all three conditions, it sends to ;
- for each received {} from :
- Determine with conditions (a), (b) and (c);
- If is determined by then assign to ;
- Else, keep assigning to ;
- Send registration request message to .
- Case 1: parent node has only one child c1.
- Case 2: has more than one child nodes ’s.
4. Constraints and Objectives of NE-MCR Algorithm
5. Results and Discussion
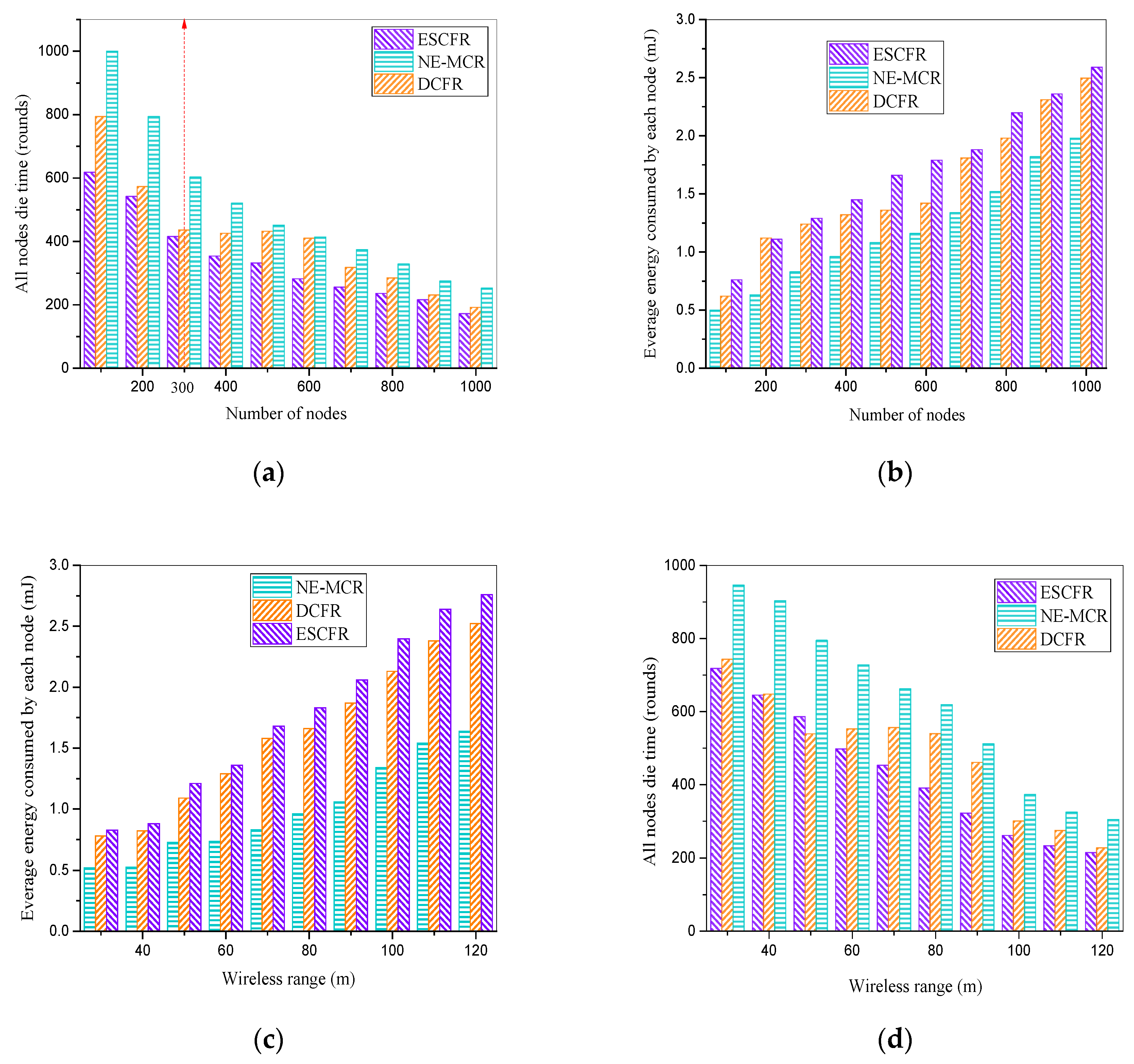
5.1. Analysis of the Performance of NE-MCR
5.2. Energy Efficiency of NE-MCR
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zanella, A.; Bui, N.; Castellani, A.; Vangelista, L.; Zorzi, M. Internet of Things for Smart Cities. IEEE Internet Things J. 2014, 1, 22–32. [Google Scholar] [CrossRef]
- Mois, G.; Folea, S.; Sanislav, T. Analysis of Three IoT-Based Wireless Sensors for Environmental Monitoring. IEEE Trans. Instrum. Meas. 2017, 66, 2056–2064. [Google Scholar] [CrossRef]
- Wu, F.; Rüdiger, C.; Redouté, J.M.; Yuce, M.R. WE-Safe: A Wearable IoT Sensor Node for Safety Applications via LoRa. In Proceedings of the IEEE 4th World Forum on IoT (WF-IoT), Singapore, 5–8 February 2018. [Google Scholar]
- Singh, H.; Biswas, B. Comparison of CSMA Based MAC Protocols of Wireless Sensor Networks. Int. J. Ad Hoc Netw. Syst. (IJANS) 2012, 2. [Google Scholar] [CrossRef]
- Kumar, S.; Lim, H.; Kim, H. Energy Optimal Scheduling of Multi-Channel Wireless Sensor Networks for Wireless Metering. In Proceedings of the International Conference on Electronics, Information and Communication (ICEIC), Danang, Vietnam, 27–30 January 2016. [Google Scholar]
- Rahman, M.N.; Matin, M.A. Efficient Algorithm for Prolonging Network Lifetime of Wireless Sensor Networks. Tsinghua Sci. Technol. 2011, 16, 561–568. [Google Scholar] [CrossRef]
- Ghaffari, M.; Parter, M. Near-Optimal Distributed Algorithms for Fault-Tolerant Tree Structures. In Proceedings of the 28th ACM Symposium on Parallelism in Algorithms and Architectures, Pacific Grove, CA, USA, 11–13 July 2016. [Google Scholar]
- Banerjee, I.; Chanak, P.; Sikdar, B.K.; Rahaman, H. DFDNM: Distributed fault detection and node management scheme in wireless sensor network. In Proceedings of the Springer Link International Conference on Advances in Computing and Communications (ACC-2011), Kochi, India, 22–24 July 2011. [Google Scholar]
- Kamal, A.R.M.; Bleakley, C.J.; Dobson, S. Failure Detection in Wireless Sensor Networks: A Sequence-Based Dynamic Approach. ACM Trans. Sens. Netw. 2014, 10, 35. [Google Scholar] [CrossRef]
- Gupta, G.; Younis, M. Fault tolerant clustering of wireless sensor networks. In Proceedings of the 2003 IEEE Wireless Communications and Networking (WCNC 2003), New Orleans, LA, USA, 16–20 March 2003. [Google Scholar]
- Liu, A.; Ren, J.; Li, X.; Chen, Z.; Shen, X.S. Design principles and improvement of cost function based energy aware routing algorithms for wireless sensor networks. Comput. Netw. 2012, 56, 1951–1967. [Google Scholar] [CrossRef]
- Ok, C.-S.; Lee, S.; Mitra, P.; Kumara, S. Distributed energy balanced routing for wireless sensor networks. Comput. Ind. Eng. 2009, 57, 125–135. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, Y.; Zhang, K.; Liu, A.; Chen, J.; Shen, X.S. Lifetime and Energy Hole Evolution Analysis in Data-Gathering Wireless Sensor Networks. IEEE Trans. Ind. Inf. 2016, 12, 788–800. [Google Scholar] [CrossRef]
- Lee, W.L.; Datta, A.; Cardell-Oliver, R. WinMS: Wireless Sensor Network Management System, an Adaptive Policy-Based Management for Wireless Sensor Networks; Technical Report UWA-CSSE-06-001; University of Western Australia: Crawley, Australia, 2006. [Google Scholar]
- Chessa, S.; Santi, P. Crash faulty identification in wireless sensor networks. Comput. Commun. 2002, 25, 1273–1282. [Google Scholar] [CrossRef]
- Gobriel, S.; Khattab, S.; Mossé, D.; Brustoloni, J.; Melhem, R. Fault Tolerant Aggregation in Sensor Networks Using Corrective Actions. In Proceedings of the 3rd Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks, Reston, VA, USA, 28 September 2006; Volume 2, pp. 595–604. [Google Scholar]
- Chen, J.; Kher, S.; Somani, A. Distributed fault detection of wireless sensor networks. In Proceedings of the 2006 Workshop on Dependability Issues in Wireless ad Hoc Networks and Sensor Networks, Los Angeles, CA, USA, 26 September 2006. [Google Scholar]
- Koren, I.; Krishna, C.M. Fault-Tolerant Systems; Morgan Kaufmann: Burlington, MA, USA, 2007. [Google Scholar]
- Alwan, H.; Agarwal, A. A survey on fault tolerant routing techniques in Wireless Sensor Networks. In Proceedings of the Third International Conference on Sensor Technologies and Applications, Athens, Greece, 18–23 June 2009; pp. 366–371. [Google Scholar]
- Ganesan, D.; Govindan, R.; Shenker, S.; Estrin, D. Highly Resilient, Energy-efficient multipath routing in Wireless Sensor Networks. Mob. Comput. Commun. Rev. 2011, 5, 11–25. [Google Scholar] [CrossRef]
- Ho, J.H.; Shih, H.C.; Liao, B.Y.; Chu, S.C. A ladder diffusion algorithm using ant colony optimization for wireless sensor networks. Inf. Sci. 2012, 192, 204–212. [Google Scholar] [CrossRef]
- Wu, G.; Lin, C.; Xia, F.; Yao, L.; Zhang, H.; Liu, B. Dynamical Jumping Real-Time Fault-Tolerant Routing Protocol for Wireless Sensor Networks. Sensors 2010, 10, 2416–2437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keerthana, S.; Pamila, J.M.J. A Survey on Fault node Detection and Recovery Mechanisms in Wireless Sensor Network. In Proceedings of the International Conference on Advanced Computing and Communication Systems (ICACCS-2015), Coimbatore, India, 5–7 January 2015. [Google Scholar]
- Munir, A.; Antoon, J.; Gordon-Ross, A. Modelling and Analysis of Fault Detection and Fault Tolerance in Wireless Sensor Networks. ACM Trans. Embed. Comput. Syst. 2015, 14, 3. [Google Scholar] [CrossRef]
- Guo, S.; Zhong, Z.; He, T. Find: Faulty Node Detection for Wireless Sensor Networks. In Proceedings of the 7th ACM Conference on Embedded Networked Sensor Systems (SenSys’09), Berkeley, CA, USA, 4–6 November 2009; ACM Press: New York, NY, USA, 2009; pp. 253–266. [Google Scholar]
- Liu, Y.; Liu, K.; Li, M. Passive diagnosis for wireless sensor networks. IEEE/ACM Trans. Netw. 2010, 18, 1132–1144. [Google Scholar]
- Kumar, S.; Kim, H. Low Energy Scheduling of Minimal Active Time Slots for Multi-Channel Multi-Hop Convergence Wireless Sensor Networks. In Proceedings of the International Conference on Computing, Network and Communications (ICNC 2017), Santa Clara, CA, USA, 26–29 January 2017. [Google Scholar]
- Urmonov, O. TDMA Latency Verification in Small-Scale WSN. Available online: https://youtu.be/3RNd491TXzE (accessed on 13 November 2018).
- Rogers, A.; David, E.; Jennings, N.R. Self-organized routing for wireless microsensor networks. IEEE Trans. Syst. Man Cybern. A 2005, 35, 349–359. [Google Scholar] [CrossRef]
- Aouchiche, M.; Hansen, P.; Zheng, M. Variable neighborhood search for extremal graphs 18. Conjectures and results about the Randic index. Commun. Math. Comput. Chem. 2006, 56, 541–550. [Google Scholar]
- Rodoplu, V.; Men, T.H. Minimum energy mobile wireless networks. IEEE J. Sel. Areas Commun. 1999, 17, 1333–1344. [Google Scholar] [CrossRef] [Green Version]
- Aziz, A.A.; Sekercioglu, Y.A.; Fitzpatrick, P.; Ivanovich, M. A Survey on Distributed Topology Control Techniques for Extending the Lifetime of Battery Power Wireless Sensor Networks. IEEE Commun. Surv. Tutor. 2013, 15, 121–144. [Google Scholar] [CrossRef]
- Hu, Y.; Leus, G. Self-Estimation of Path Loss Exponent in Wireless Networks and Applications. IEEE Trans. Veh. Technol. 2015, 64, 5091–5102. [Google Scholar] [CrossRef]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-Efficient Communication Protocol for Wireless Microsensor Networks. In Proceedings of the 33rd Hawaii International Conference on System and Sciences, Maui, HI, USA, 7 January 2000. [Google Scholar]
- Liu, A.F.; Zhang, P.H.; Chen, Z.G. Theoretical analysis of the energy hole in cluster based wireless sensor networks. J. Parallel Distrib. Comput. 2011, 71, 1327–1355. [Google Scholar] [CrossRef]
- Sarioz, D. Geographic Graph Theory and Wireless Sensor Network. Ph.D. Thesis, City University of New York, New York, NY, USA, 2012. [Google Scholar]
- Urmonov, O.; Kumar, S.; Kim, H. Maximal Connectivity Local Routing for Self-Recovery Wireless Sensor Network. In Proceedings of the IEIE 2016 Summer Conference, Jeju Island, South Korea, 27–22 June 2016. [Google Scholar]
- Bagheri, T. DFMC: Decentralized Fault Management mechanism for Cluster Based Wireless Sensor Networks. In Proceedings of the Second International Conference on Digital Information and Communication Technology and its Applications (DICTAP), Bangkok, Thailand, 16–18 May 2012. [Google Scholar]







| Parameter | Value |
|---|---|
| (nJ/bit) | |
| 10 (pJ/bit/) | |
| 0.0013 (pJ/bit/) | |
| Initial energy | 0.5 (J) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urmonov, O.; Kim, H. An Energy-Efficient Fail Recovery Routing in TDMA MAC Protocol-Based Wireless Sensor Network. Electronics 2018, 7, 444. https://doi.org/10.3390/electronics7120444
Urmonov O, Kim H. An Energy-Efficient Fail Recovery Routing in TDMA MAC Protocol-Based Wireless Sensor Network. Electronics. 2018; 7(12):444. https://doi.org/10.3390/electronics7120444
Chicago/Turabian StyleUrmonov, Odilbek, and HyungWon Kim. 2018. "An Energy-Efficient Fail Recovery Routing in TDMA MAC Protocol-Based Wireless Sensor Network" Electronics 7, no. 12: 444. https://doi.org/10.3390/electronics7120444
APA StyleUrmonov, O., & Kim, H. (2018). An Energy-Efficient Fail Recovery Routing in TDMA MAC Protocol-Based Wireless Sensor Network. Electronics, 7(12), 444. https://doi.org/10.3390/electronics7120444






