Modeling and Control of the Starter Motor and Start-Up Phase for Gas Turbines
Abstract
:1. Introduction
- No LLP (Life Limited Parts) penalty when used less than 4 times a year
- Two cycles per 1 penalty when used more than 4 times a year
- Observation and measurement manual should be checked when used more than 4 times a year.
- Initialization, purge of enclosure
- Purge of engine/stack
- Acceleration to reach sync idle
- Synchronization to grid, then warm up
- Acceleration to reach full load
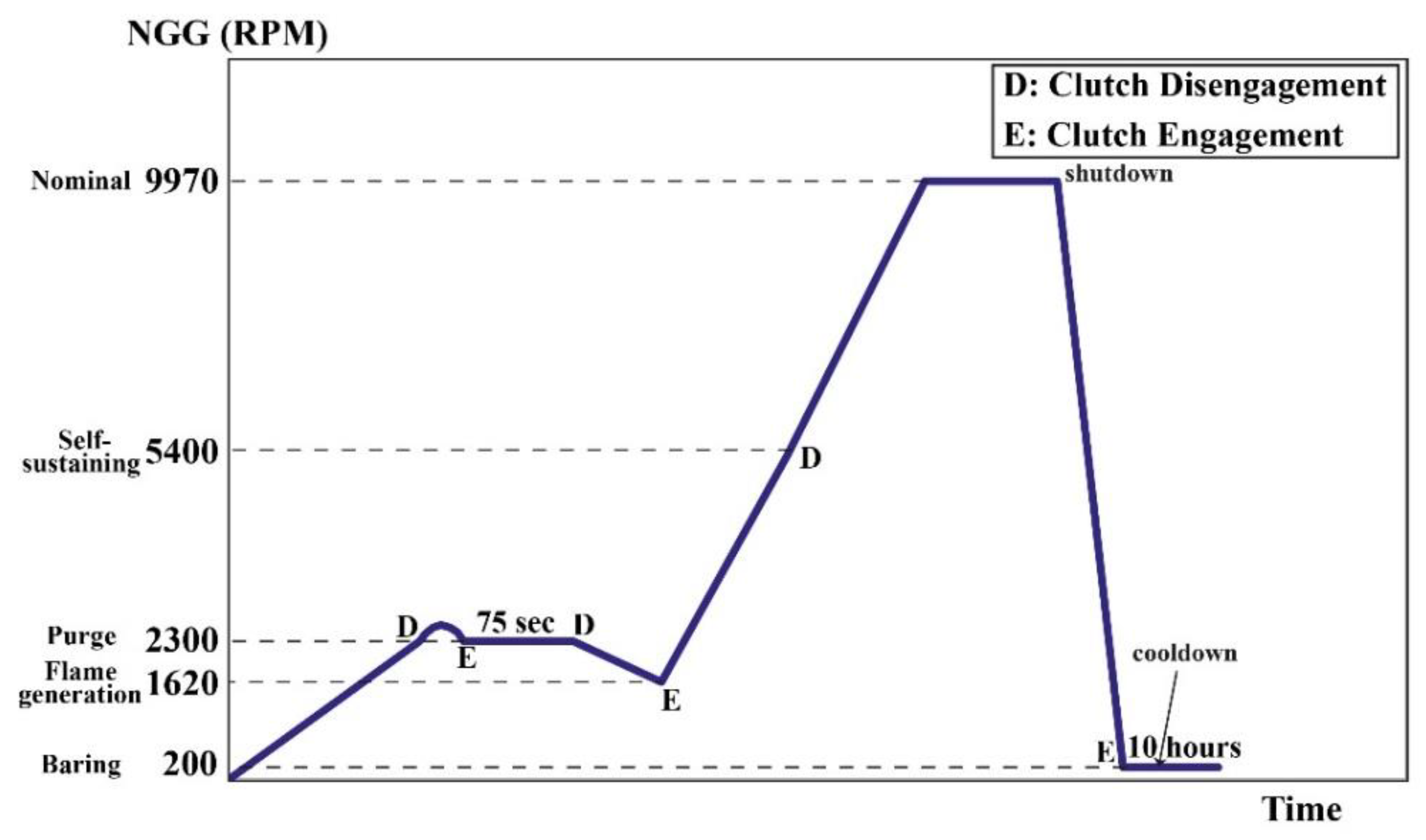
2. Description of Gas Turbine and its Start-Up Process
3. Bond Graph Modeling of Components During Cold Start
3.1. Modeling the Induction Motor and SFC Drive
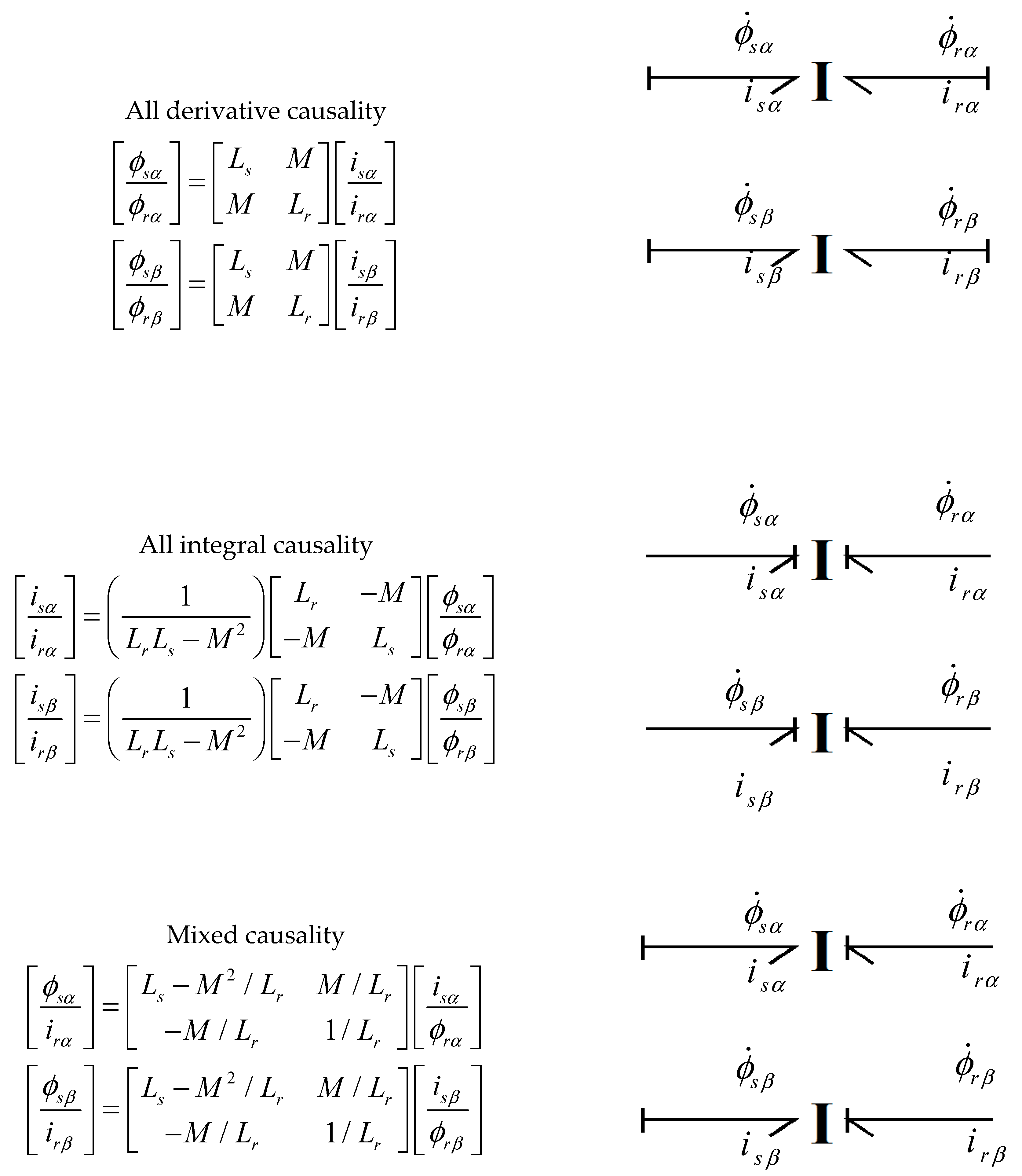
3.1.1. Modeling the Induction Motor Using Bond Graph
Inductive Coupling of Rotor and Stator
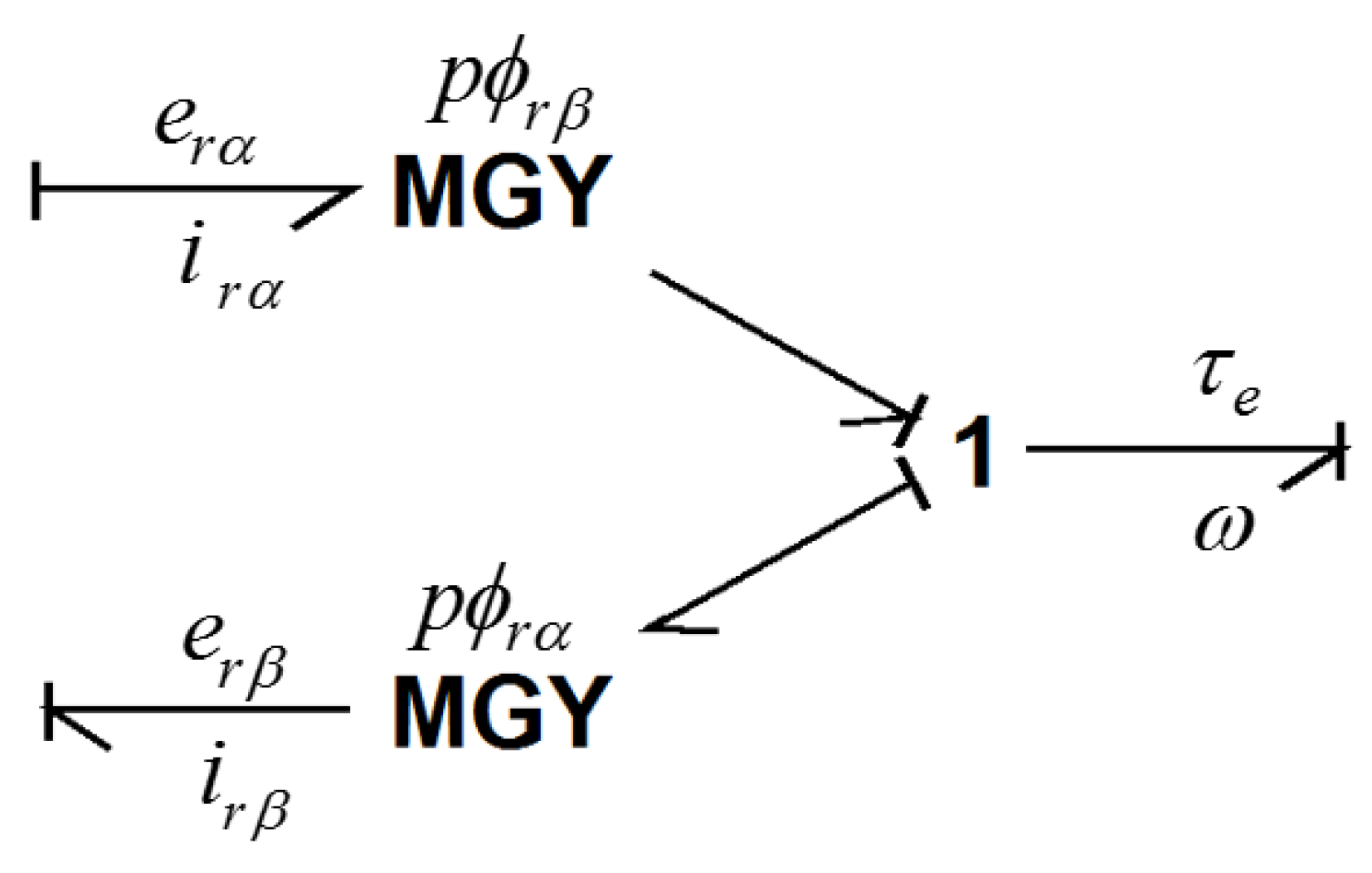
Representation of Torque and Induced Voltage in Bond Graph
Bond Graph for the Induction Motor
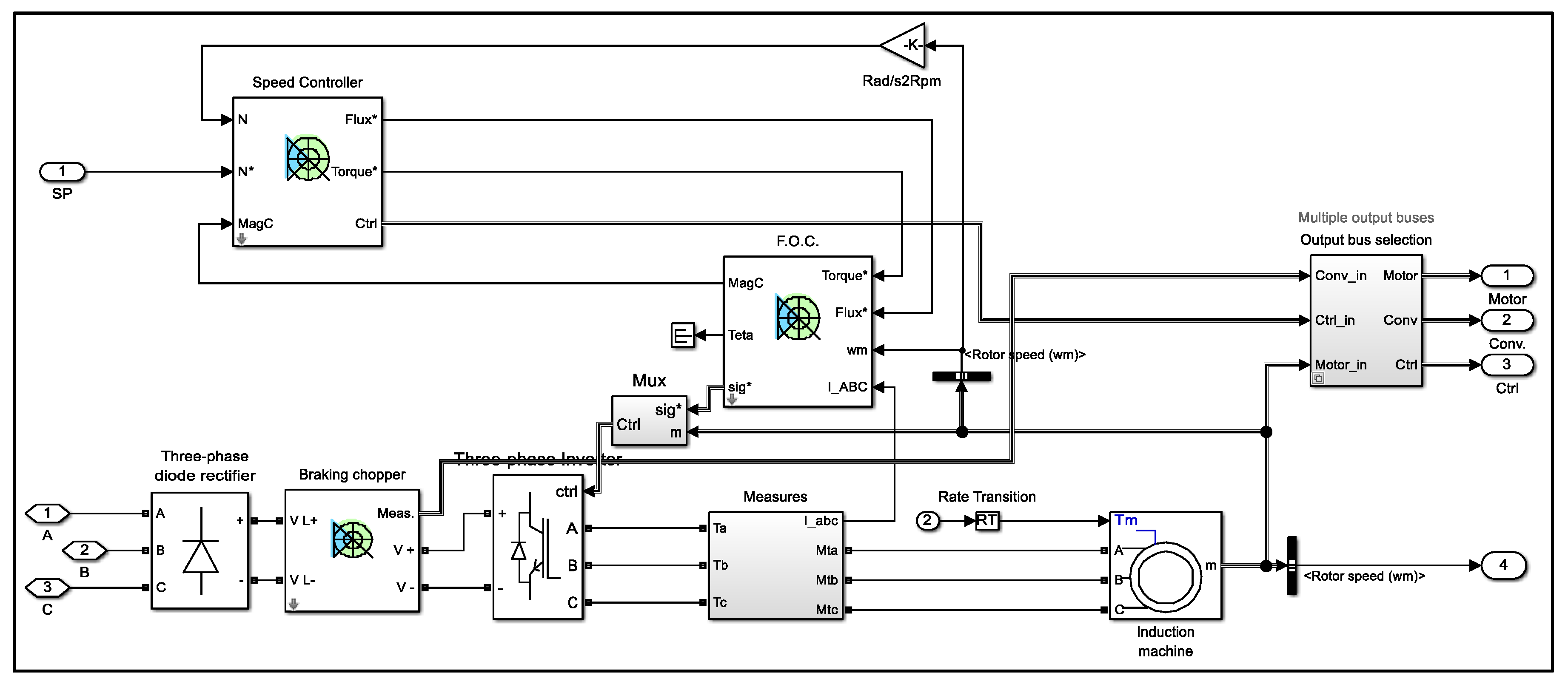
3.1.2. Modeling SFC Drive
3.2. Modeling the Industrial Gas Turbine
4. Completed Model of Gas Turbine in Cold Start-Up Phase
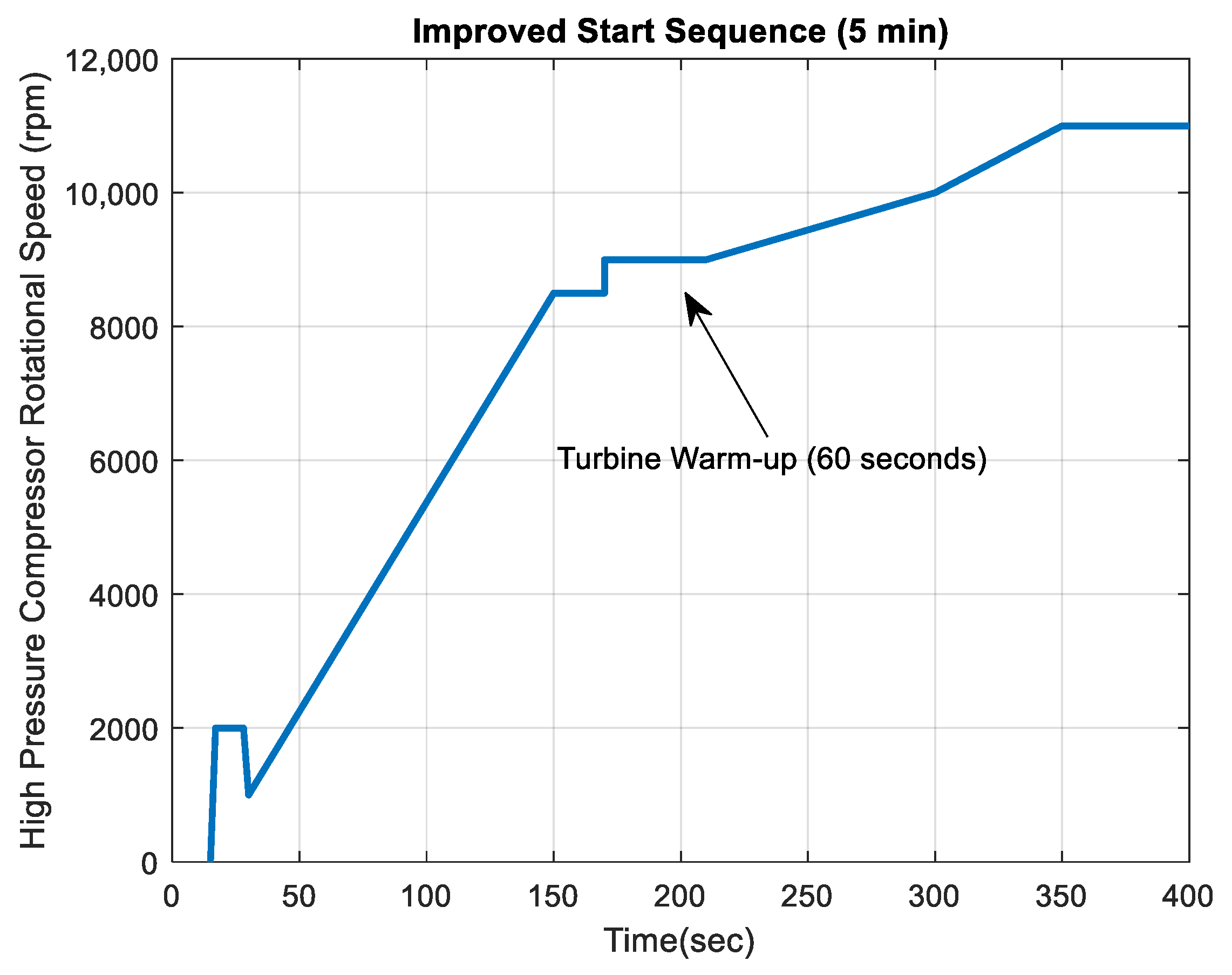
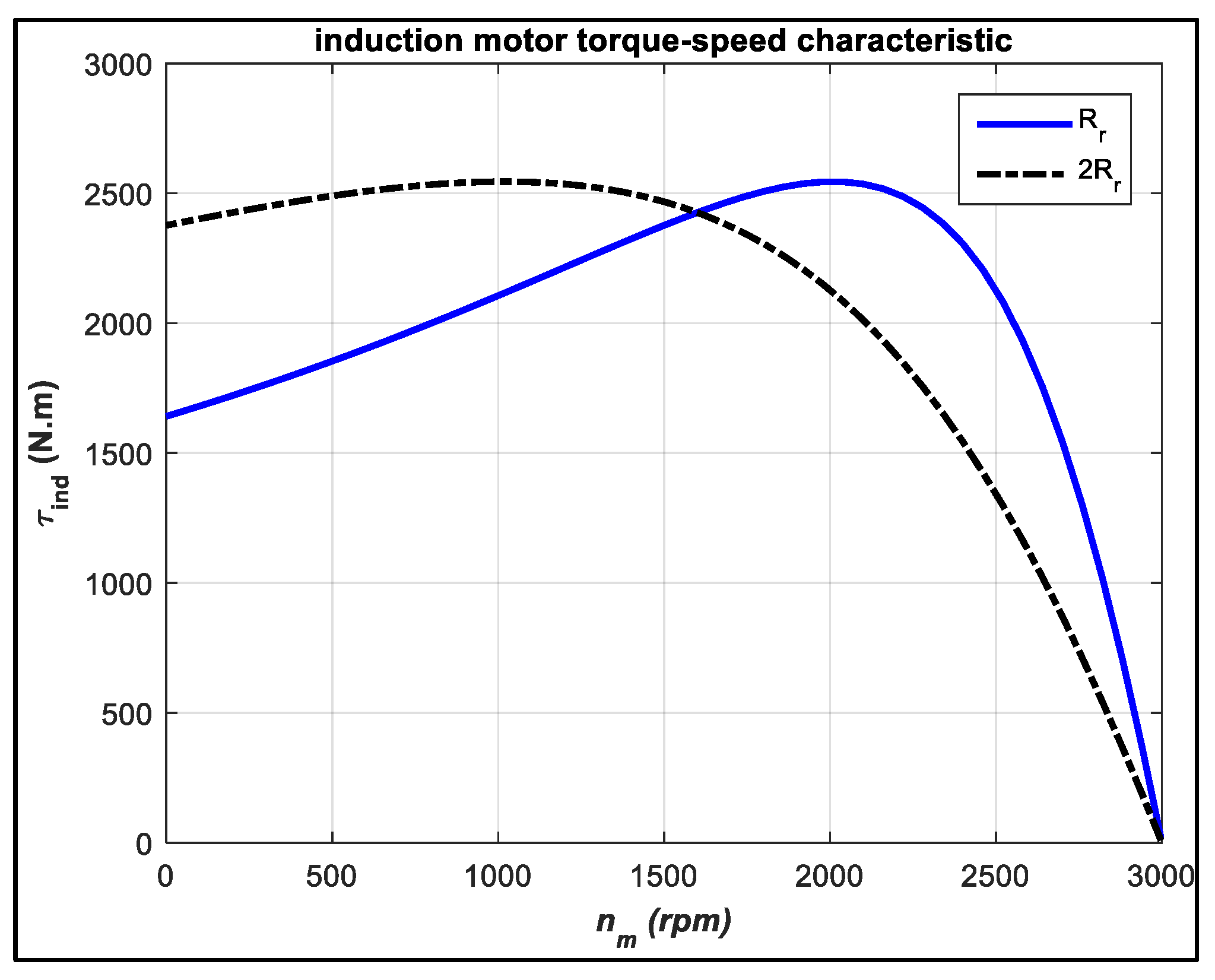
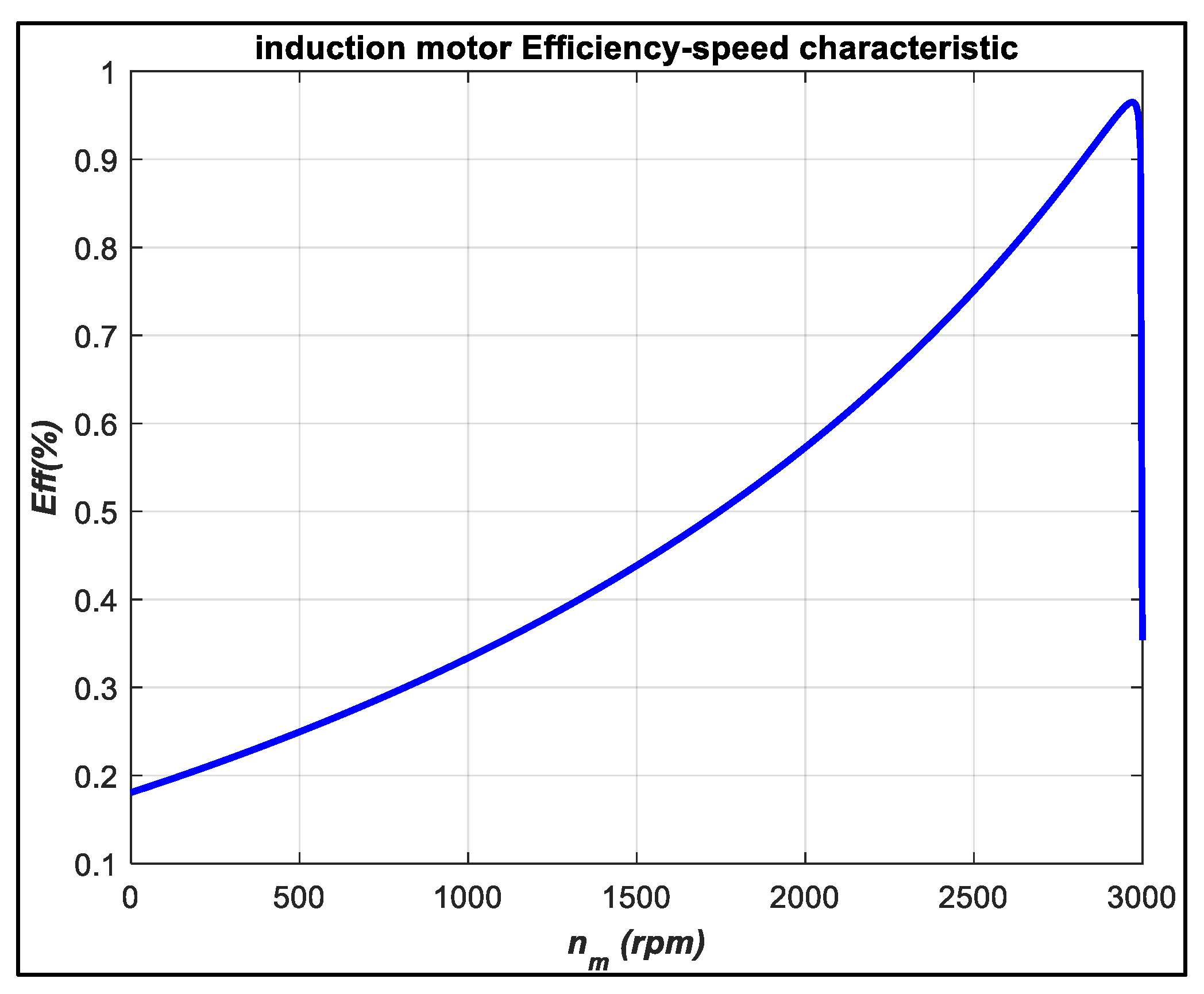
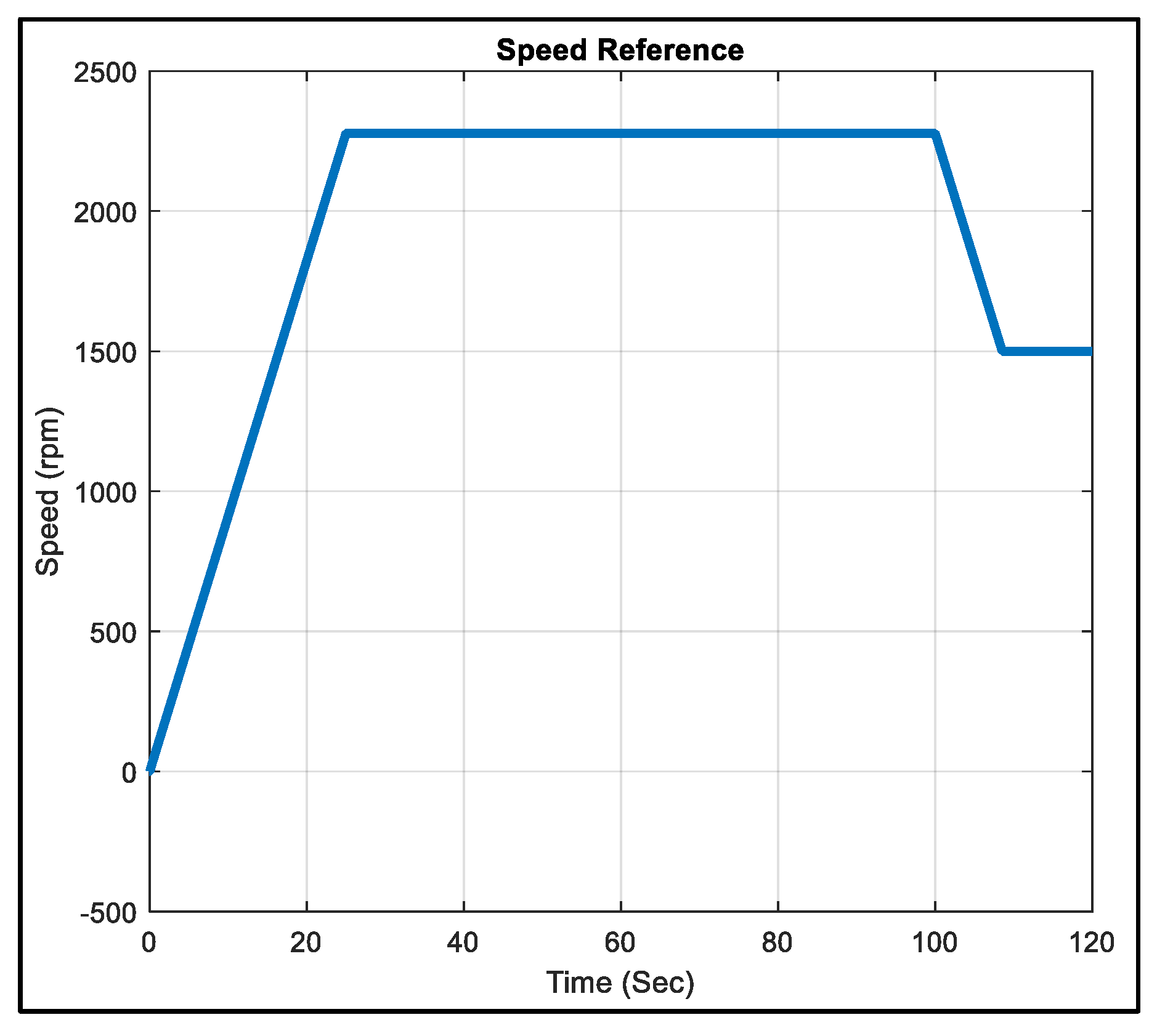
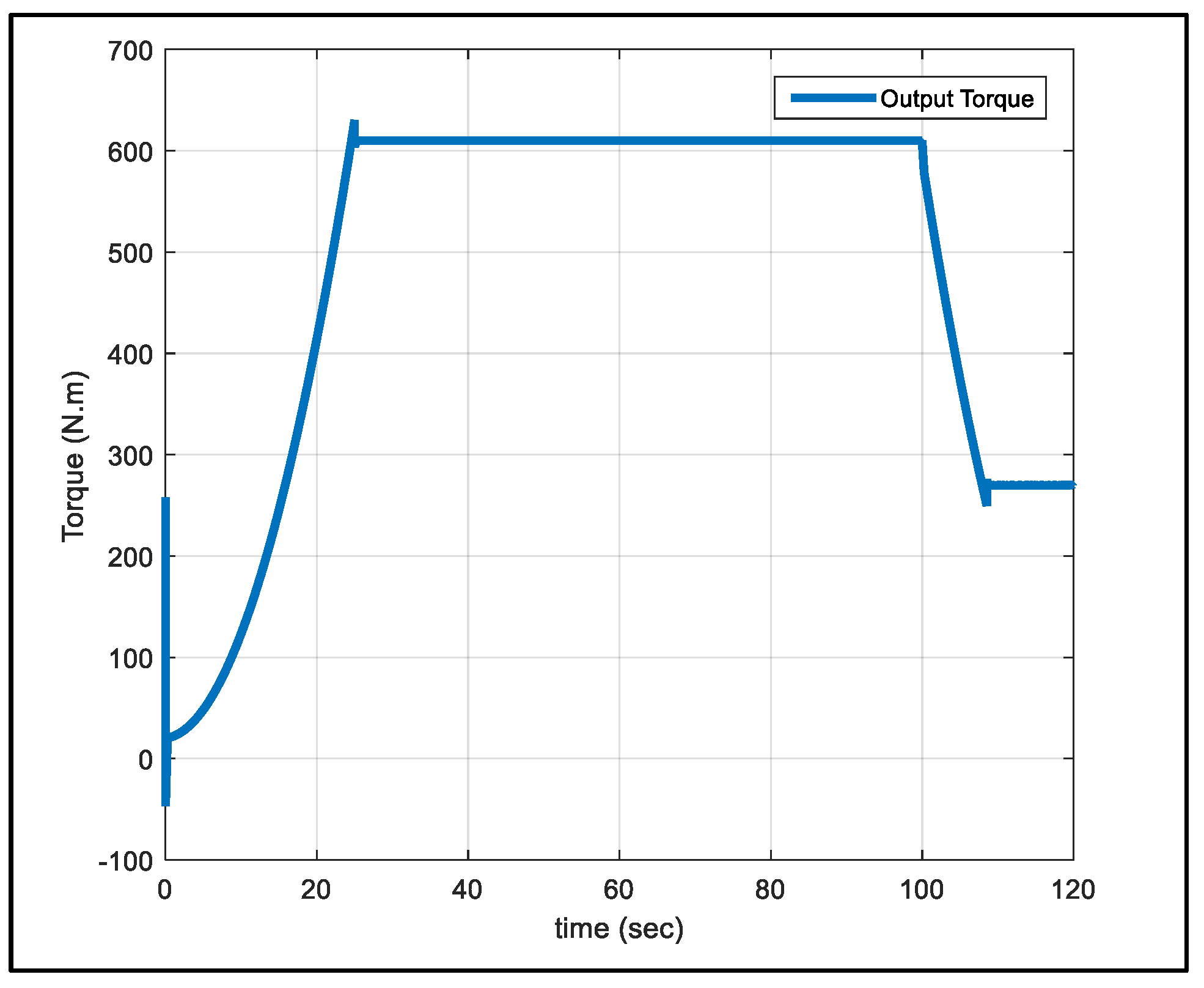
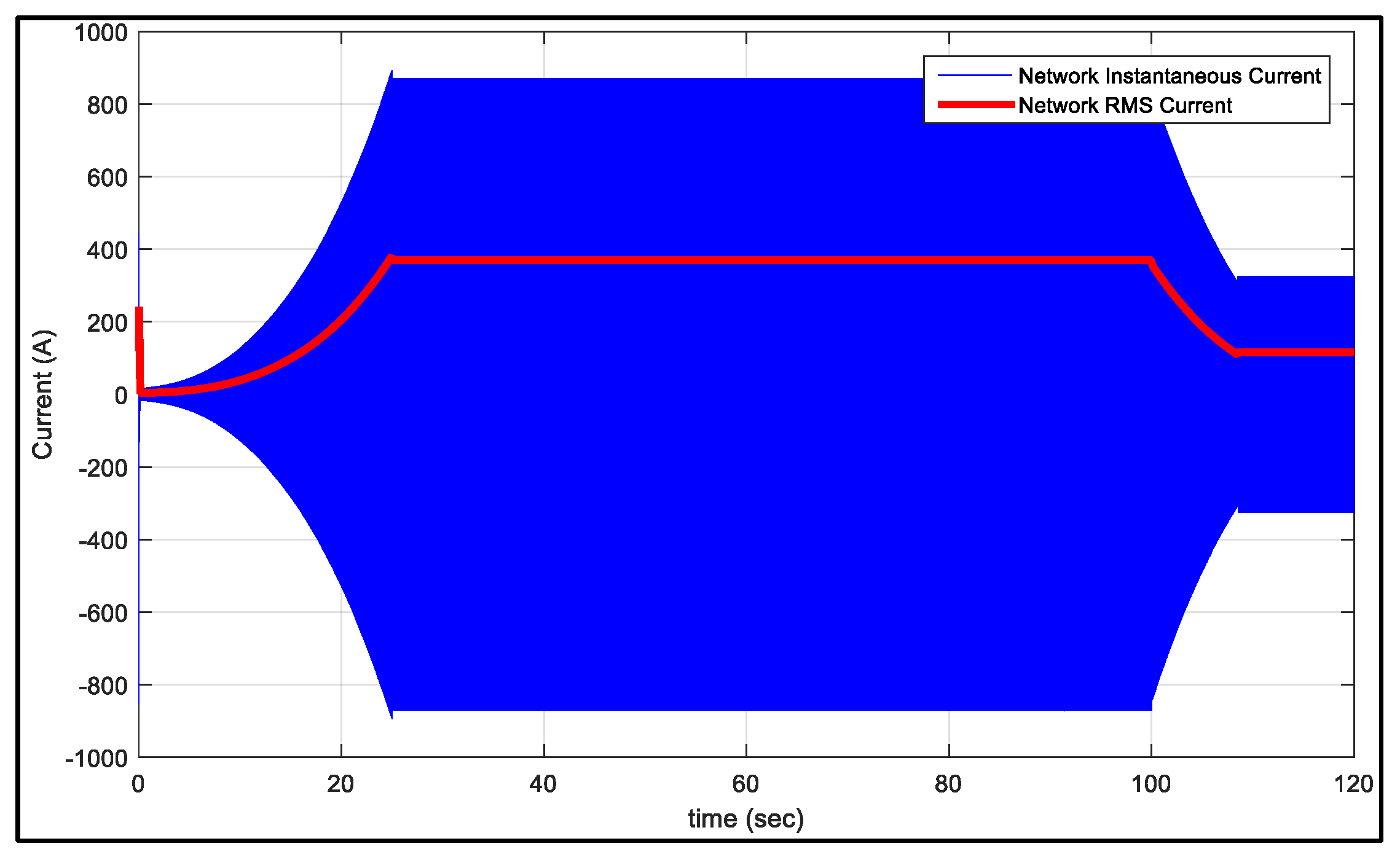
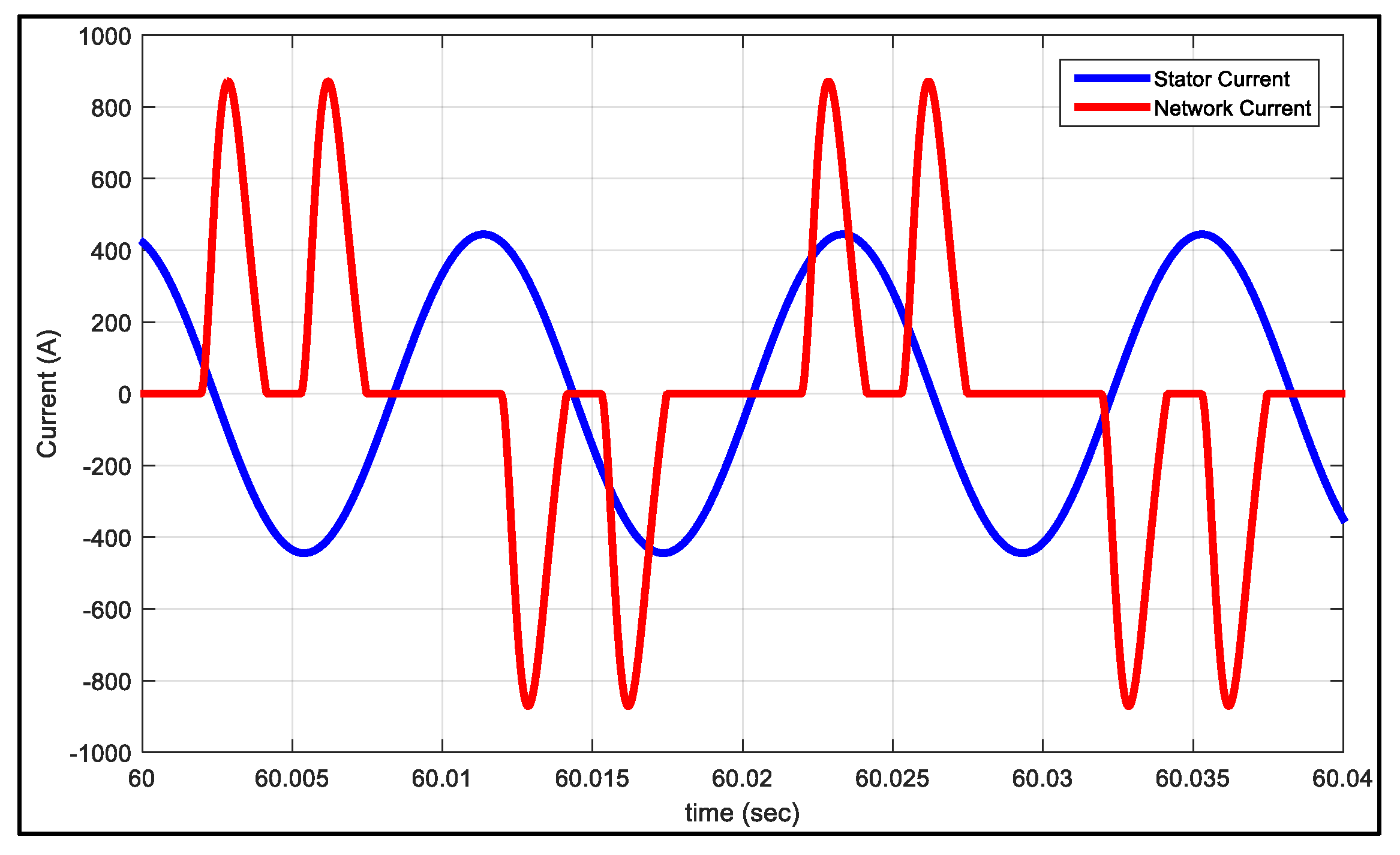
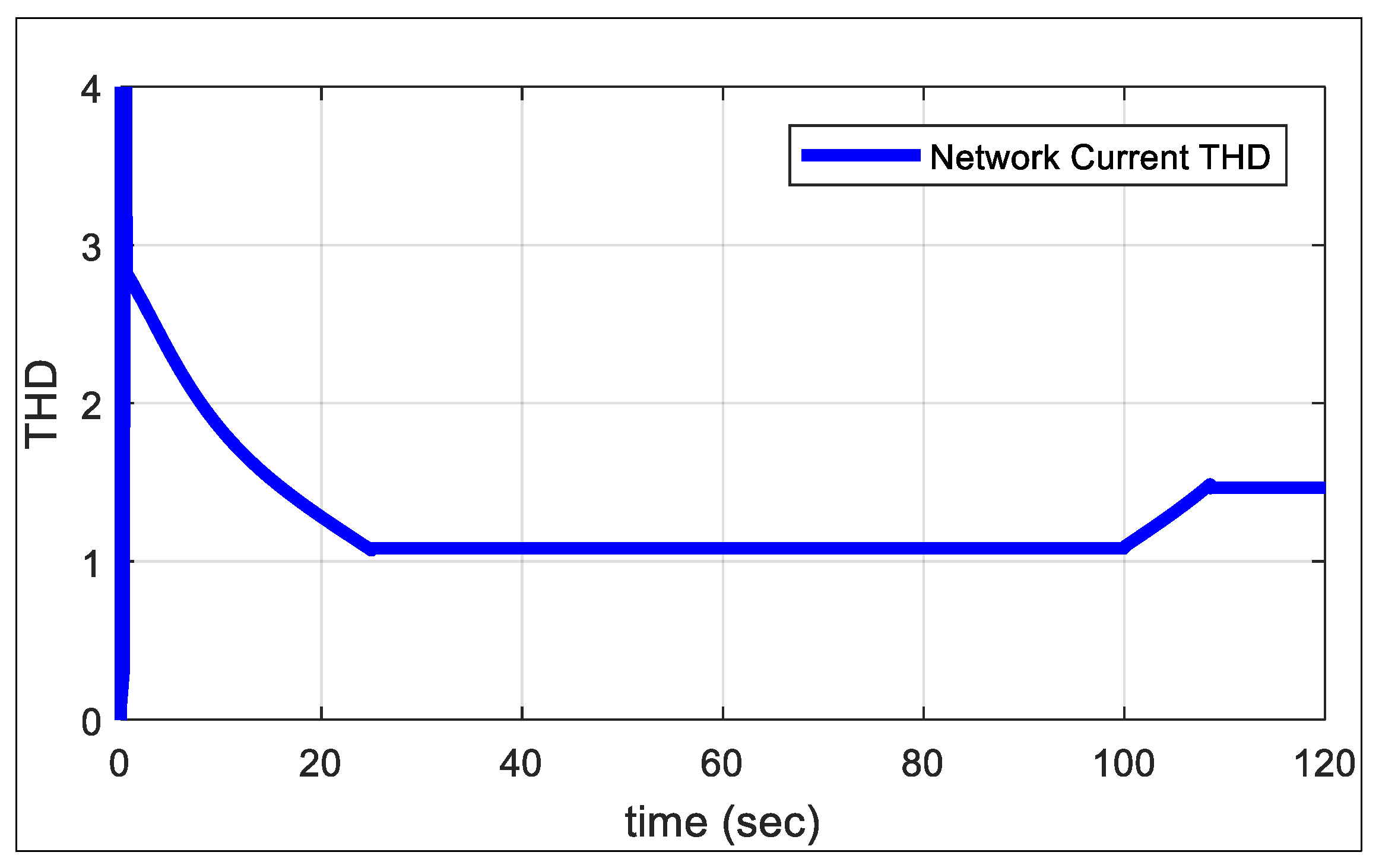
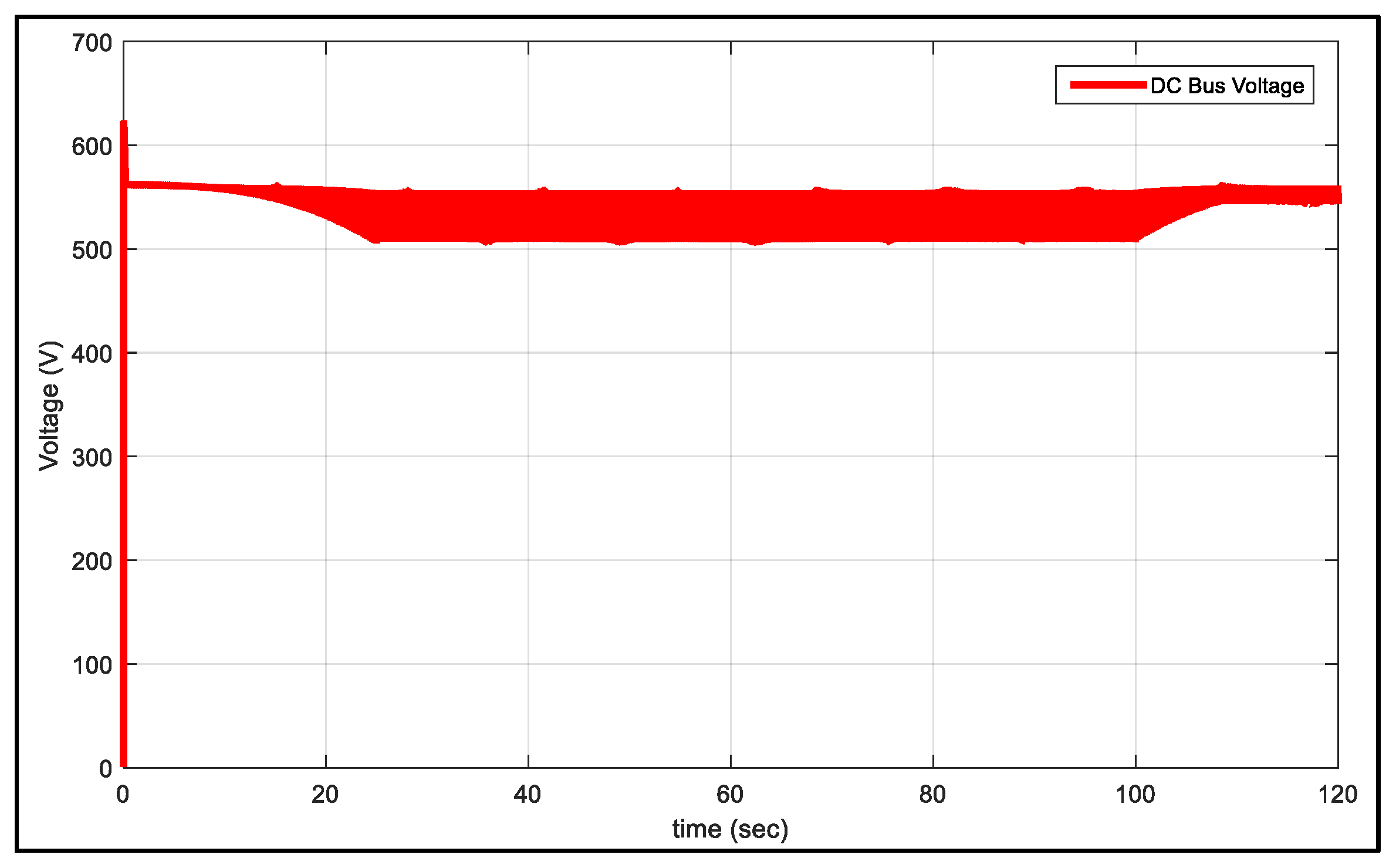
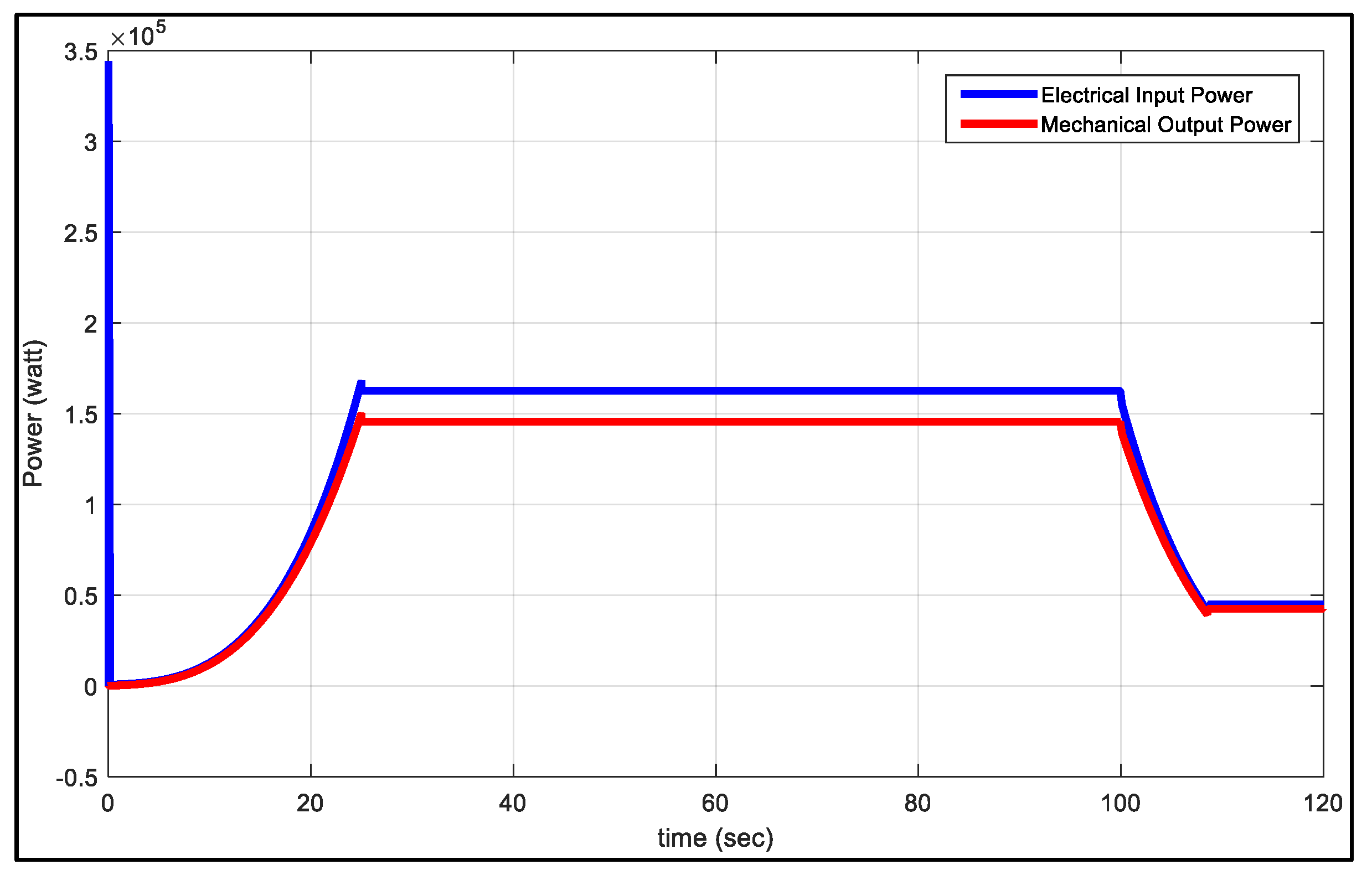
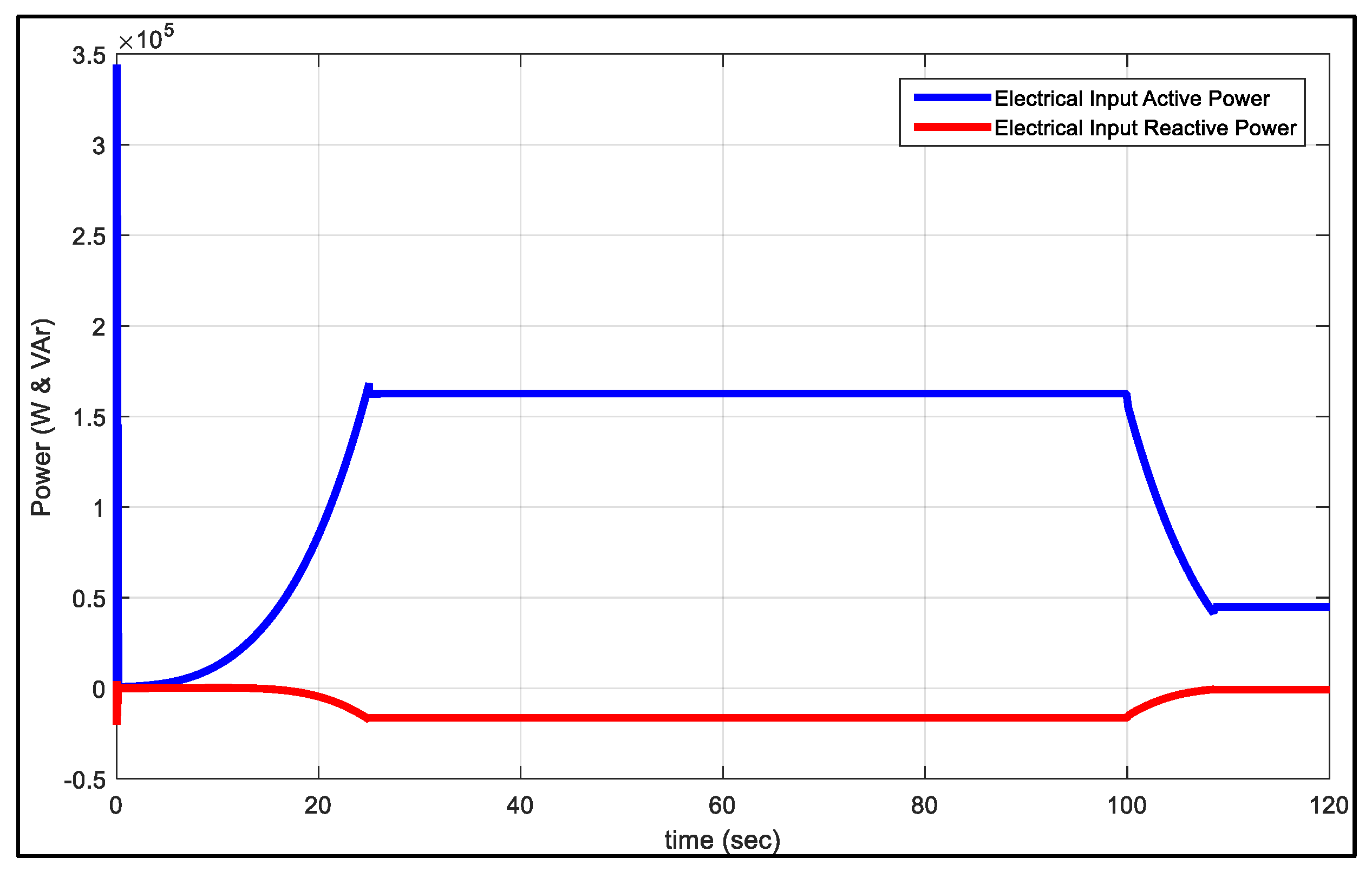
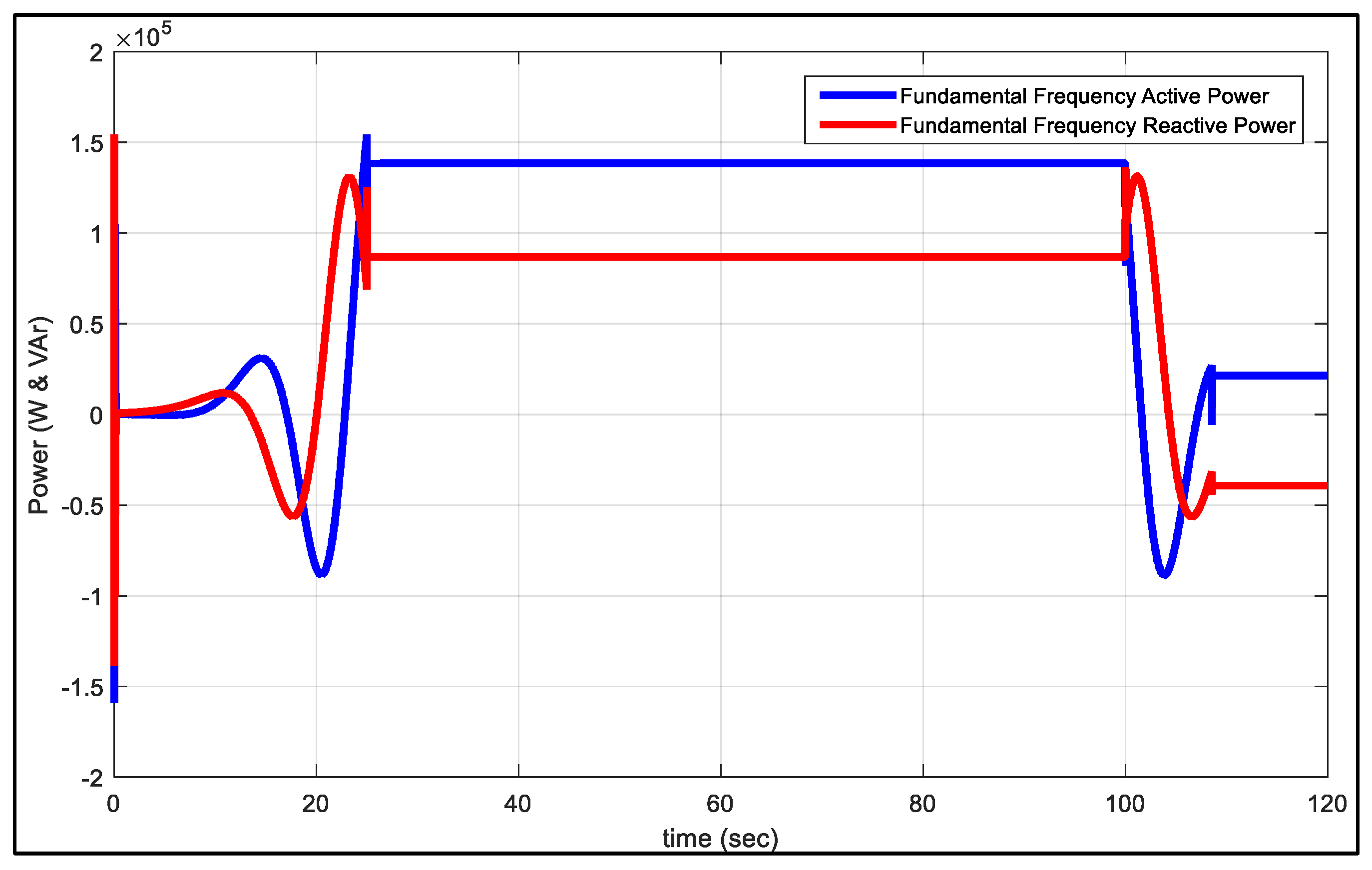
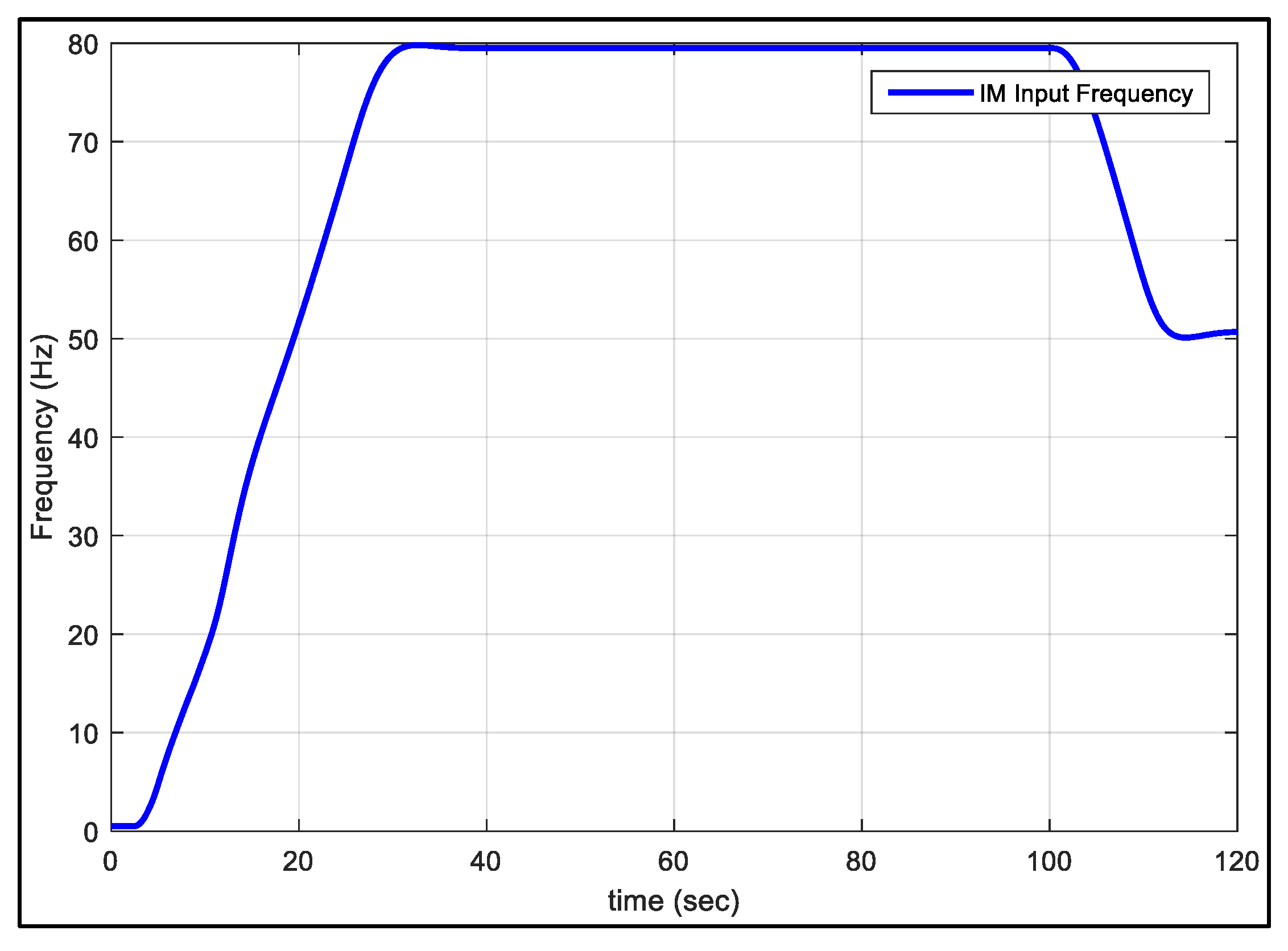
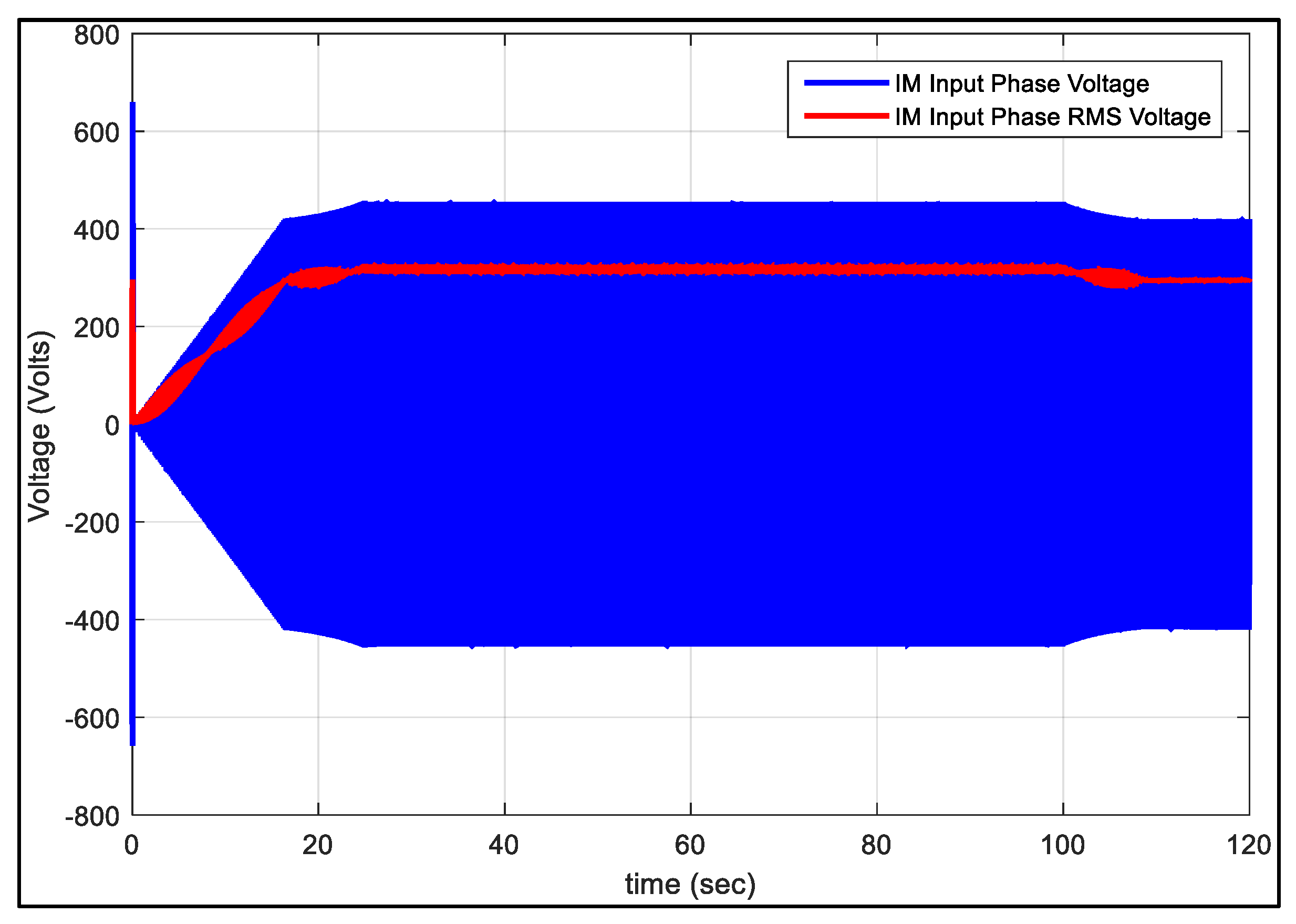
5. Analysis of Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References and Note
- Siemens AG. Modernizations and Upgrades—Siemens. 2018. Available online: https://www.energy.siemens.com/hq/en/services/fossil-power-generation/modernization-upgrades/ (accessed on 10 February 2018).
- General Electric. Aeroderivative & Heavy-Duty Gas Turbines|GE Power. 2018. Available online: https://www.gepower.com/gas/gas-turbines (accessed on 20 January 2018).
- ALSTOM. Alstom’s World Class Gas Turbine Technology Enters Commercial Operation in China. 2014. Available online: http://www.alstom.com/press-centre/2014/3/alstoms-world-class-gas-turbine-technology-enters-commercial-operation-in-china-/ (accessed on 8 December 2017).
- Balling, L. Fast cycling and rapid start-up: New generation of plants achieves impressive results. Mod. Power Syst. 2011, 31, 35–41. [Google Scholar]
- Western Turbine Users. LM6000 Product Breakout Session; General Electric Company: Long Beach, CA, USA, 2015. [Google Scholar]
- Poluéktova, E. Results of Model Studies of the Control System of a Gas-Turbine Unit with a Free Power Turbine. Power Technol. Eng. 2017, 51, 459–463. [Google Scholar] [CrossRef]
- Bahlawan, H.; Morini, M.; Pinelli, M.; Spina, P.R.; Venturini, M. Development of Reliable NARX Models of Gas Turbine Cold, Warm and Hot Start-Up. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; p. V009T027A007. [Google Scholar]
- Asgari, H.; Venturini, M.; Chen, X.; Sainudiin, R. Modeling and simulation of the transient behavior of an industrial power plant gas turbine. J. Eng. Gas Turbines Power 2014, 136, 061601. [Google Scholar] [CrossRef]
- Morini, M.; Cataldi, G.; Pinelli, M.; Venturini, M. A Model for the Simulation of Large-Size Single-Shaft Gas Turbine Start-Up Based on Operating Data Fitting. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007; pp. 1849–1856. [Google Scholar]
- Zhang, Y.; Cruz-Manzo, S.; Latimer, A. Start-up vibration analysis for novelty detection on industrial gas turbines. In Proceedings of the International Symposium on 2016 Industrial Electronics (INDEL), Santa Clara, CA, USA, 8–10 June 2016; pp. 1–6. [Google Scholar]
- Mahdipour, M.; Bathaee, S.M.T. A novel static frequency converter for start-up and shutdown processes of gas turbine power plant units. Int. Trans. Electr. Energy Syst. 2015, 25, 3586–3599. [Google Scholar] [CrossRef]
- An, H.; Han, B.-M.; Cha, H. A new sensorless start-up method of LCI system for gas-turbine. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 6559–6564. [Google Scholar]
- An, H.; Cha, H. A New Start-up Method for a Load Commutated Inverter for Large Synchronous Generator of Gas-Turbine. J. Electr. Eng. Technol. 2018, 13, 201–210. [Google Scholar]
- Bretschneider, S.; Reed, J. Modeling of Start-Up from Engine-Off Conditions Using High Fidelity Turbofan Engine Simulations. J. Eng. Turbines Power 2016, 138, 051201. [Google Scholar] [CrossRef]
- Sheng, H.; Zhang, T.; Jiang, W. Full-Range Mathematical Modeling of Turboshaft Engine in Aerospace. Int. J. Turbo Jet-Engines 2016, 33, 309–317. [Google Scholar] [CrossRef]
- Sukhovii, S.I.; Sirenko, F.F.; Yepifanov, S.V.; Loboda, I. Alternative method to simulate a Sub-idle engine operation in order to synthesize its control system. Int. J. Turbo Jet-Engines 2016, 33, 229–237. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, J.; Dai, Y.; Xie, D. Study of the speed control system of a heavy-duty gas turbine. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; p. V006T005A014. [Google Scholar]
- Hu, Z.; Jiang, B.; Wang, J.; He, X. A generalized method for sub-idle modeling of aircraft engines. In Proceedings of the 2017 8th International Conference on Mechanical and Aerospace Engineering (ICMAE), Prague, Czech Republic, 22–25 July 2017; pp. 527–531. [Google Scholar]
- Agrawal, R.; Yunis, M. A generalized mathematical model to estimate gas turbine starting characteristics. J. Eng. Power 1982, 104, 194–201. [Google Scholar] [CrossRef]
- Kim, J.; Song, T.; Kim, T.; Moverare, J. Dynamic simulation of full start-up procedure of heavy duty gas turbines. In Proceedings of the ASME Turbo Expo 2001: Power for Land, Sea, and Air, New Orleans, LA, USA, 4–7 June 2001; p. V004T004A010. [Google Scholar]
- Blomstedt, M.; Lindgren, H.; Olausson, H.-L.; Moverare, J. Innovative starting procedure of Siemens SGT-600 in cold climate conditions. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; pp. 1021–1026. [Google Scholar]
- Montazeri-Gh, M.; Miran, F.S.A. Application of bond-graph method in microjet engine cold start modeling to investigate the idea of injecting compressed air. Appl. Mech. Mater. 2015, 799–800, 890–894. [Google Scholar] [CrossRef]
- Miran, F.S.A.; Montazeri-Gh, M. Modeling and Simulation of JetQuad Aerial Robot Knowledge-Based Engineering and Innovation (KBEI); Iran University of Science and Technology (IUST): Tehran, Iran, 2017. [Google Scholar]
- Asgari, H.; Chen, X.; Morini, M.; Pinelli, M.; Sainudiin, R.; Spina, P.R.; Venturini, M. NARX models for simulation of the start-up operation of a single-shaft gas turbine. Appl. Therm. Eng. 2016, 93, 368–376. [Google Scholar] [CrossRef]
- Nannarone, A.; Klein, S.A. Start-Up Optimization of a CCGT Power Station Using Model-Based Gas Turbine Control. J. Eng. Gas Turbines Power 2019, 141, 041018. [Google Scholar] [CrossRef]
- Yoshida, Y.; Yoshida, T.; Enomoto, Y.; Osaki, N.; Nagahama, Y.; Tsuge, Y. Start-up optimization of combined cycle power plants: A field test in a commercial power plant. J. Eng. Gas Turbines Power 2019, 141, 031002. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Meskin, N. Dynamic performance simulation and control of gas turbines used for hybrid gas/wind energy applications. Appl. Therm. Eng. 2019, 147, 122–142. [Google Scholar] [CrossRef]
- Borutzky, W. Bond graph modelling and simulation of multidisciplinary systems an introduction. Simul. Model. Pract. Theory 2009, 17, 3–21. [Google Scholar] [CrossRef]
- Karnopp, D.C.; Margolis, D.L.; Rosenberg, R.C. System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Brown, F.T. Engineering System Dynamics: A Unified Graph-Centered Approach; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Uddin, N.; Gravdahl, J.T. Bond graph modeling of centrifugal compression systems. Simulation 2015, 91, 998–1013. [Google Scholar] [CrossRef]
- Munari, E.; Morini, M.; Pinelli, M.; Brun, K.; Simons, S.; Kurz, R. Measurement and Prediction of Centrifugal Compressor Axial Forces During Surge—Part II: Dynamic Surge Model. J. Eng. Gas Turbines Power 2018, 140, 012602. [Google Scholar] [CrossRef]
- Munari, E.; Morini, M.; Pinelli, M.; Spin, P.R. Experimental Investigation and Modeling of Surge in a Multistage Compressor. Energy Procedia 2017, 105, 1751–1756. [Google Scholar] [CrossRef]
- Sanei, A.; Novinzadeh, A.; Habibi, M. Addition of momentum and kinetic energy effects in supersonic compressible flow using pseudo bond graph approach. Math. Comput. Model. Dyn. Syst. 2014, 20, 491–503. [Google Scholar] [CrossRef]
- Yum, K.K.; Pedersen, E. Architecture of model libraries for modelling turbocharged diesel engines. Math. Comput. Model. Dyn. Syst. 2016, 22, 584–612. [Google Scholar] [CrossRef]
- Movaghar, A.S.; Novinzadeh, A. Ideal Turbo charger Modeling and Simulation using Bond Graph Approach. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition: American Society of Mechanical Engineers, Vancouver, BC, Canada, 6–10 June 2011; pp. 871–879. [Google Scholar]
- Vangheluwe, H.; de Lara, J.; Mosterman, P.J. An introduction to multi-paradigm modelling and simulation. In Proceedings of the AIS2002 Conference (AI, Simulation and Planning in High Autonomy Systems), Lisboa, Portugal, 7–10 April 2002; pp. 9–20. [Google Scholar]
- Montazeri-Gh, M.; Fashandi, S.A.M. Application of Bond Graph approach in dynamic modelling of industrial gas turbine. Mech. Ind. 2017, 18, 410. [Google Scholar] [CrossRef]
- Åström, K.J.; Hilding, E.; Dynasim, A.; Sven, E.M. Evolution of Continuous-Time Modeling and Simulation. In Proceedings of the 12th European Simulation Multiconference, Manchester, UK, 16–19 June 1998. [Google Scholar]
- Montazeri-Gh, M.; Miran Fashandi, S.A.; Jafari, S. Theoretical and Experimental Study of a Micro Jet Engine Start-Up Behaviour. Tech. Gaz. 2018, 25, 839–845. [Google Scholar]
- Montazeri-Gh, M.; Miran Fashandi, S.A.; Abyaneh, S. Real-time simulation test-bed for an industrial gas turbine engine’s controller. Mech. Ind. 2018, 19, 311. [Google Scholar] [CrossRef]
- Jafari, S.; Miran Fashandi, S.A.; Nikolaidis, T. Control Requirements for Future Gas Turbine-Powered Unmanned Drones: JetQuads. Appl. Sci. 2018, 8, 2675. [Google Scholar] [CrossRef]
- Nordström, L. Construction of a Simulator for the Siemens Gas Turbine SGT-600; Institutionen för Systemteknik: Linköping, Sweden, 2005. [Google Scholar]
- EMI Induction Motor Data Sheet, Motor Type: EM1-315L2-2 200KW 400 690V 50HZ.
- Bose, B.K. Modern Power Electronics and AC Drives; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Krause, P.C. Analysis of Electric Machinery; McGraw-Hill: New York, NY, USA, 1986. [Google Scholar]
- Sahm, D. A two-axis, bond graph model of the dynamics of synchronous electrical machines. J. Frankl. Inst. 1979, 308, 205–218. [Google Scholar] [CrossRef]
- Benchaib, A.; Rachid, A.; Audrezet, E.; Tadjine, M. Real-time sliding-mode observer and control of an induction motor. IEEE Trans. Ind. Electron. 1999, 46, 128–138. [Google Scholar] [CrossRef]
- Cadism Engineering PObDC. CAMP-G User’s Manual; P Stevens Institute of Technology: Hoboken, NJ, USA, 1999. [Google Scholar]
- Hu, J.; Dawson, D.M.; Qian, Y. Position tracking control for robot manipulators driven by induction motors without flux measurements. IEEE Trans. Robot. Autom. 1996, 12, 419–438. [Google Scholar]
- Karnopp, D. Understanding induction motor state equations using bond graphs. Simul. Ser. 2003, 35, 269–273. [Google Scholar]
- Montazeri-Gh, M.; Fashandi, S.A.M. Modeling and simulation of a two-shaft gas turbine propulsion system containing a frictional plate type clutch. Inst. Mech. Eng. M 2018, in press. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Miran Fashandi, S.A. Bond graph modeling of a jet engine with electric starter. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018. [Google Scholar] [CrossRef]







| Quantity | Value |
|---|---|
| Thermal efficiency, % | 34.2 |
| Compressor pressure ratio | 14 |
| Power, MW | 24.77 |
| Exhaust gas temperature, °C | 543 |
| Exhaust gas flow, kg/s | 80.4 |
| GG turbine speed, rpm | 9705 |
| Power turbine speed, rpm | 7700 |
| Rated IM Voltage | 400 V A.C |
|---|---|
| Rated IM current | 345 A |
| Rated IM power | 200 KW |
| Rated IM power factor | 0.86 |
| IM pole pair number | 1 |
| Synchronous speed | 3000 RPM |
| Efficiency (100% load) | 95.7 |
| Efficiency (75% load) | 95.7 |
| Efficiency (50% load) | 94.9 |
| Number of phases | 3 |
| Frequency (Hz) | 50 Hz |
| IM pole number | 2 |
| Stator connection | Delta |
| Inominal | 345 A |
| Istart/Inominal | 7.7 |
| Tnominal | 640 N.m |
| Tlocked Rotor/Tnominal | 2.6 |
| Tpull out/Tnominal | 4 |
| J (Inertia) kg·m2 | 2.1 kg·m2 |
| Weight | 1290 Kg |
| Sound press level | 78 Db |
| Temperature rise class | F |
| Stator Resistance | 0.01908 Ω |
|---|---|
| Rotor resistance | 0.02545 Ω |
| Stator leakage inductance | 0.000128 H |
| Rotor leakage inductance | 0. 000113 H |
| Mutual inductance | 0. 005195 H |
| Friction factor | 0.1 N-m-s |
| Simulation Method | Discrete |
|---|---|
| Time step | 2 × 10−5 s |
| Network frequency | 50 Hz |
| Run time | 120 s |
| Solver | Ode45 |
| Converter and DC Bus | Rectifier | Snubbers | Resistance (ohm) | 10 × 103 |
| Capacitance (F) | 20 × 10−9 | |||
| Diodes | On-state resistance (ohm) | 1 × 10−3 | ||
| Forward voltage (V) | 1.3 | |||
| DC Bus | Capacitance (F) | 10,000 × 10−6 | ||
| Breaking chopper | Resistance (ohm) | 8 | ||
| Chopper frequency (Hz) | 4000 | |||
| Activation voltage (V) | 700 | |||
| Shutdown voltage (V) | 660 | |||
| Inverter | Source frequency (Hz) | 50 | ||
| On-state resistance (ohm) | 1 × 10−3 | |||
| Controller | Regulation Type | Speed regulation | ||
| Speed Controller | Speed ramps (rpm/s) | Acceleration | 900 | |
| Deceleration | −900 | |||
| PI regulator | Proportional gain | 300 | ||
| Integral gain | 2000 | |||
| Speed cutoff frequency (Hz) | 1000 | |||
| Speed controller sampling time (s) | 120 × 10−6 | |||
| Torque output limit (N-m) | Negative | −1200 | ||
| Positive | 1200 | |||
| Field Oriented Control | Flux controller | Proportional gain | 100 | |
| Integral gain | 30 | |||
| Flux output limit | Negative | −2 | ||
| Positive | 2 | |||
| Low pass filter cutoff frequency (Hz) | 16 | |||
| Sampling time (s) | 60 × 10−6 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari, S.; Miran Fashandi, S.A.; Nikolaidis, T. Modeling and Control of the Starter Motor and Start-Up Phase for Gas Turbines. Electronics 2019, 8, 363. https://doi.org/10.3390/electronics8030363
Jafari S, Miran Fashandi SA, Nikolaidis T. Modeling and Control of the Starter Motor and Start-Up Phase for Gas Turbines. Electronics. 2019; 8(3):363. https://doi.org/10.3390/electronics8030363
Chicago/Turabian StyleJafari, Soheil, Seyed Alireza Miran Fashandi, and Theoklis Nikolaidis. 2019. "Modeling and Control of the Starter Motor and Start-Up Phase for Gas Turbines" Electronics 8, no. 3: 363. https://doi.org/10.3390/electronics8030363
APA StyleJafari, S., Miran Fashandi, S. A., & Nikolaidis, T. (2019). Modeling and Control of the Starter Motor and Start-Up Phase for Gas Turbines. Electronics, 8(3), 363. https://doi.org/10.3390/electronics8030363







