1. Introduction
Presently, LED lighting systems are gaining more importance as they provide a tool for a more rational use of electrical energy on household, public lighting systems, transportation, commercial applications, etc. [
1,
2]. Therefore, one of the major power electronic development fields is related to the enhancement of efficient high-performance electronic lighting systems for LED lamps. The main features to consider when designing an LED driver are its
voltage source behavior (a
driving stage able to limit the LED current must be used), the long operating life (the driver must last at least as long as the LED itself), and the color variations (there are some parameters that affect the color such as the waveforms, the operating temperature, etc.).
For low requirement applications, simple, passive, or cost-effective solutions can be used to deal with the
behavior of the LED lamp [
3]. For instance, [
4] presents a linear regulator integrated with an LED lamp that provides an optimal solution in terms of power density for single LED applications. But generally speaking, linear regulators are not recommended when the application requires a high number of LEDs (as the overall efficiency of the system turns more critical) or when high-performance control schemes are needed. In fact, the driver might also include additional features such as dimming—either Amplitude Modulated (
) dimming or Pulse Width Modulation (
) dimming—, current derating, etc. Linear regulators can be used for implementing
dimming, but in case
dimming is required (to avoid color shift or stability problems at low power, as in higher power LED Lamps), switch-mode regulators are much more adequate. Also, the future deployment of
grids will allow significant simplification in the LED driver topologies used for
applications [
5]. However, taking into account the regulations and standards that lighting equipment must fulfill, in most cases high-performance drivers are required. The LED driving system must provide not only
-
efficient conversion, but also LED current control, Power Factor Correction (
) and input current Total Harmonic Distortion (
) control.
As the lifespan of the driver is expected to match that of the LED lamp [
6], some constraints are derived for the design of the electronic stage [
7]. For instance, large electrolytic capacitors usage is highly inadvisable, considering their shorter operating life compared to the life of the LED lamp [
8]. Many recent works in the literature agree that large capacitance values for the power stage of LED drivers need to be avoided [
9,
10,
11,
12,
13,
14,
15]. In order to achieve this goal, electrolytic capacitors must be discarded. Therefore, researchers have come up with novel control strategies [
16,
17,
18,
19] as well as optimized topologies [
6,
13,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33] that imply smaller capacitances in the
link, to overcome this issue.
Two-stage schemes are the most common approach when designing single-phase LED ballasts. A first active stage controls the power factor and the line current harmonics content. Considering a power factor close to unity, the input power to this active stage pulsates at twice the line frequency. In order to guarantee the instant power balance, this input stage delivers the pulsating power to a second stage, interfaced through an energy storage device. This storage part is usually a capacitive device at the link. The main voltage ripple component at this capacitor, at twice the line frequency, is a function of the capacitance value, taking into account that higher capacitances mean smaller ripple amplitudes. To ensure proper operation of the system, and to effectively control the output power through the LEDs—and hence the emitted light—standard output stages require a low voltage ripple at the link. This guarantees a given constant current through the LEDs. These large capacitance values are implemented by means of electrolytic technology devices, which achieve such high capacitance values in reasonable component size.
In the conventional scheme, each of the stages processes the full amount of power, ensuring enough design flexibility as it decouples the input and the output constraints, allowing for simple solutions. However, this usually results in relatively low efficiencies, higher volume, and components count.
A second strategy divides the output power of the input stage in two different power flows. The largest share of this power is delivered directly to the LED lamp, while the rest of the power (including the
part) is processed by a second stage. This ensures the
power ripple cancellation at the load [
29,
30,
31,
32]. Upon careful design considerations, this scheme provides an overall system efficiency increase, as most of the power is processed only once.
The approach followed in this work delivers all the
part of the output power of the input stage, and uses a second stage to process only the
. Therefore, this bidirectional stage stores energy in some intervals and sends it back to the
link in others. Provided that adequate management of the
power is carried out, the resulting power through the LEDs will be pure
, therefore allowing for higher ripples and smaller capacitances at the
link. This capacitance reduction is the main purpose of the proposed topological scheme. Given that these low capacitance values can be achieved with technologies such as plastic film capacitors, thus avoiding the reliability problems derived from the use of electrolytic parts, therefore extending the lifespan of the system. In particular, this work improves the performance of the system presented in [
33] but including a deeper analysis that allows for an optimal design strategy in terms of power density and efficiency.
The design of the second stage has one degree of freedom, which is related to the inductance value of an inductive energy storage device, . Therefore, the performance of the output stage (size, weight, power losses, dynamic behavior, etc.) largely depends on this value. In a first approach, the design of this inductor is carried out by analyzing the steady state, open loop operation of the circuit, for different inductance values, considering two key dimensions of this performance. These two factors are losses on one hand (both copper and core losses), and size (and therefore weight) on the other hand. A trade-off between those two dimensions is initially achieved, although it is considered to be unfeasible, as it will be justified. After that, a novel closed-loop operation analysis of the output stage has been carried out, and as it will be shown, a smaller, yet more efficient design of the inductor will be achieved, considering the same trade-off approach in terms of losses vs. size than in the steady-state analysis previously discussed. This work shows the detailed procedure of the optimization process, and demonstrates its feasibility through simulations and by experimental validation on a 40 W design example.
The paper is divided as follows.
Section 2 deals with the considered LED driving strategy. Later,
Section 3 presents and discusses the proposed topology and its basic operation.
Section 4 and
Section 5 show the switching and dynamic equations of the open loop operation respectively, in order to obtain the transfer functions of the proposed scheme. A design example for open loop operation is given in
Section 6, while
Section 7 shows the simulation results obtained with this configuration. The control scheme implemented for closed-loop operation is discussed in
Section 8, whereas
Section 9 shows the experimental results of the closed-loop operation of the converter. Finally,
Section 10 shows the main conclusions of this work as well as the future developments.
3. Proposed Topology
Figure 2 shows the block diagram of the full off-line High Frequency (
) LED driver with the followed approach. After being rectified and filtered, the input voltage enters the input
stage, which processes the energy towards the
link capacitor,
. However, the selection and proper design of this input stage is out of the scope of this work. The input of the second stage,
, is connected in series with the LEDs assembly. As a small capacitance value is selected for the capacitor
, in order to avoid electrolytic technologies, a significant
ripple appears at the
link voltage,
.
Figure 2 also depicts the simplified waveforms in the expected operation of the system (pure
voltage at
, and pure
voltage at
as well).
Figure 3a details the topology of the system. A grid-side PFC stage is implemented by means of a Discontinuous Conduction Mode (
) buck-boost converter, in order to provide unity power factor with constant duty ratio. This input stage supplies power from the grid towards the
link. Connected to this DC link, the proposed bidirectional series circuit can be seen. This stage is a current-fed bidirectional buck converter, formed by switches
and
, capacitor
and the storage inductor,
. The input of this stage is considered to be the LEDs current,
, with the output variable being the current through the inductor
,
.
and
have been represented as bipolar transistors for simplicity, as they must be able to block reverse voltages. In the final prototype, they will be implemented by means of MOSFET transistors with a series blocking diode.
Figure 3b depicts again the main
voltage waveforms at the driver, sharing the time axis.
4. HF Analysis of the Proposed Topology
The
and
analysis of the basic topology for this application has already been presented in [
33]. The most important conclusions to this analysis are reviewed in this work. The
analysis employs a fixed frequency control, denoting the switching period as
T. The common
analysis in power electronics is based on considering that the system operates in steady state. Therefore, the significant waveforms of the most relevant devices can be calculated for one switching period, keeping in mind that for any magnitude considered to be a function of time,
, the following equation is fulfilled:
This is achieved through a power balance, as the circuit input power in one period equals the power delivered to the output stage. It must be taken into account that there is not an output load in the proposed stage able to dissipate active power. This implies that the input power in one switching period will not be dissipated. In turn, the energy will be stored within the storage inductor,
, by changing the electric parameters at this device. Therefore, the analysis cannot be based on considering steady state in a switching period, and (
1) is not fulfilled anymore. Instead, this analysis must be focused on finding the variations of the capacitor voltage,
, and the storage inductor current,
, in a switching period, while the LEDs current remains constant.
Figure 4a shows the voltage and current references considered during the analysis. Only complementary operation of switches
and
is considered. The duty ratio,
D, is defined for switch
. Given that the current through the storage inductor will flow either through
or
, thus:
where
is the forward current through
(see
Figure 4a, and the expression
denotes the average value of a generic magnitude
in a switching period,
T. Furthermore, (
2) ultimately states that the current flowing through the storage inductor will always be greater than the LEDs current. The
analysis considers two switching modes in a switching period. While
is turned on and
is turned off, i.e.,
, the system operates in Mode I. On the other hand, for the complementary state of the switches, i.e.,
, the converter operates in Mode II. The full analysis of these modes is given in [
33], and only the main statements are summarized here. At instant
, the values of the storage inductor current and the input capacitor are, respectively:
After a switching period
T, the waveforms are expressed by:
After some calculations [
33], the final expressions for these parameters can be expressed as:
Finally, from (8) and (9):
The expression of the
current ripple through the LEDs can be calculated considering Mode II. In this interval, the capacitor current,
, equals the current through the LEDs. Considering that the
link behaves as a voltage source at
, then the resulting circuit for this subinterval can be seen in
Figure 5, in which the LEDs assembly is modeled by a series connection of an ideal diode
, a dynamic resistor
, and a threshold voltage
. Therefore the
ripple of the current through the LEDs can be calculated considering an exponential discharge through the dynamic resistance of the LEDs,
:
6. Design Example for a 40 W LEDs Assembly
With the previous analysis, a design example is proposed for a XLamp
® XR-E LED (part XREWHT-L1-0000-00D01) from Cree
®, in a series connection assembly of 36 devices, accounting for a nominal power of 40 W. the design parameters of the input PFC stage can be seen in
Table 1. The input values for the design are shown in
Table 2. In order to design the power stage, both values of
and
must be calculated. A target value for the LEDs current ripple will be 10%, considering this parameter is equally split into a 5% at
and a 5% at
.
The value of the
voltage ripple at capacitor
is given by the capacitor charge when
is turned off:
Therefore, the
current ripple through the LEDs will be:
The worst case will be when
. Therefore, from (
15), (
16) and
Table 2, for a 5%
ripple in the output current, the
current ripple through the LEDs will be:
The value of the storage inductor,
, can be calculated considering the performance of the system. The first approach, taken into account in [
33], is to supply the system in open loop, with a constant duty ratio, in this case
, and check the evolution of the waveforms. Upon these conditions, the inductor is chosen as follows. From
Figure 6, for a constant duty ratio, and after referring the inductance value to the primary side of the equivalent transformer, the expression for the current through the LEDs becomes:
This yields an expression of
given by:
Therefore, the value of
depends on the selected fixed duty ratio,
D. The design solution must be optimized in terms of size (core volume of the inductor) and efficiency (losses in the switches and in the inductor). A series of preliminary data has been calculated for four different duty ratio parameters. These figures are represented in
Table 3:
From
Table 3, it can be seen how the larger the duty ratio, the larger the inductance, allowing for larger core sizes. However, this would imply smaller currents through the inductor, which in turn implies smaller losses. On the other hand, smaller duty ratios cause higher effects of non-linear aspects (switching times, etc.) and parasitic elements. In order to take a final decision, an optimal design of the inductor has been carried out for each of these duty ratio values. This design provides the sizes of the cores, the
and
losses in the inductors, the number of turns, air gap, etc. For simplicity, the core geometry has been restricted to the commercial
shape; however, the full series of size has been considered (from
to
). These results are presented in
Table 4,
Table 5,
Table 6 and
Table 7, for
cores, of
magnetic material. The proximity effect has been included within the losses while the skin effect skin-depth which limits the diameter in case it is too large.
As an initial guess, a 10% duty ratio has been selected as the minimum value allowing proper operation of the converter. Assuming the total losses in the inductor of around 10% of the output power levels, then from (
19) and
Table 3:
For this inductance choice,
Table 5 shows the different coil designs that minimize losses for each ETD size considered. Aiming to balance the size and the losses, the ETD44 size has been selected, and it is represented in bold characters.
8. Closed-Loop Control of the Proposed Topology
Figure 9a depicts the equivalent
model of the second stage including the LEDs assembly. The
voltage source models the output voltage behavior of the input
stage, including both the
and the
ripple voltage components at the
link capacitor. As in the previous discussion, the equivalent circuit that models the LEDs assembly is formed by an ideal diode,
, in series with a
source,
, and a resistor,
.
and
account for the total threshold voltage and the total dynamic resistor of the LEDs setup, respectively. After following a small-signal analysis approach (linearize and perturb) [
33], the final small-signal
model of the circuit is shown in
Figure 9b. After some calculations, the transfer functions of the system are finally given by:
where
is the transfer function representing the duty ratio,
, to the LEDs current,
, and
is the transfer function representing the voltage across the capacitor,
, also to
. Capital letters represent steady-state parameters, while lower case letters with the symbol ^ represent small-signal variables.
Figure 9c shows the system block diagram that depicts the current control scheme implemented in the LEDs driver. The current error,
, is the input of the regulator block,
. The output of this block is the control action,
, that corresponds to the duty ratio of switch
. From (
23), it can be seen that the open loop transfer function is a second order system. A PI controller, with a bandwidth of 1 kHz and a phase margin of 45° has been tuned using
of
, resulting in the following parameters:
Figure 10 depicts some simulation waveforms of the closed-loop system with such a controller. As it can be seen, the
ripple results in a much smaller value than the obtained in open loop. Nevertheless, given that the perturbation represented by the
link voltage ripple,
, is continuously changing at twice the grid reference, a complete error cancellation is not possible with a PI regulator. In fact, this error,
, can be calculated as:
The value of this error is a function of the storage inductor,
, and of the parameters of the regulator. This opens an interesting option, which is to optimize the design (including the inductance value and the regulator parameters) for a given target parameter. In this case, the target will be to decrease the inductance value, keeping constant the control parameters (bandwidth and phase margin), and ensuring that the
ripple is equal or smaller than in the open loop case.
Table 8 shows a set of designs for different inductor values, along with the resulting control parameters that ensure relatively similar dynamic performance.
To make a decision, the design solution must be optimized in terms of size (core volume of the inductor), efficiency (losses in the switches and in the inductor) and implementation (allowing enough control margins in the control action variable). For very small
values, the control action gets too high, and the control loop is unable to operate properly in the carried-out simulations. On the other hand, very high values of
yield large size cores, which result in non-practical design values. Thus, the optimal solution has been chosen as
= 300 µH (highlighted in bold characters in
Table 8). For this new value of the inductor, a new design is given in
Table 9. Again, and in order to balance the size and the losses in the core, the ETD34 size has now been selected, and it is represented in bold characters in
Table 9.
Comparing
Table 5 and
Table 9, a theoretical 2 W power losses decrease in the total inductor losses can be achieved, accounting for around a 5% efficiency gain. This is obtained even moving to an
core size, significantly smaller than the first guess, and much more adequate for a 40 W design. The system has been again simulated for the PI controller selected from
Table 8.
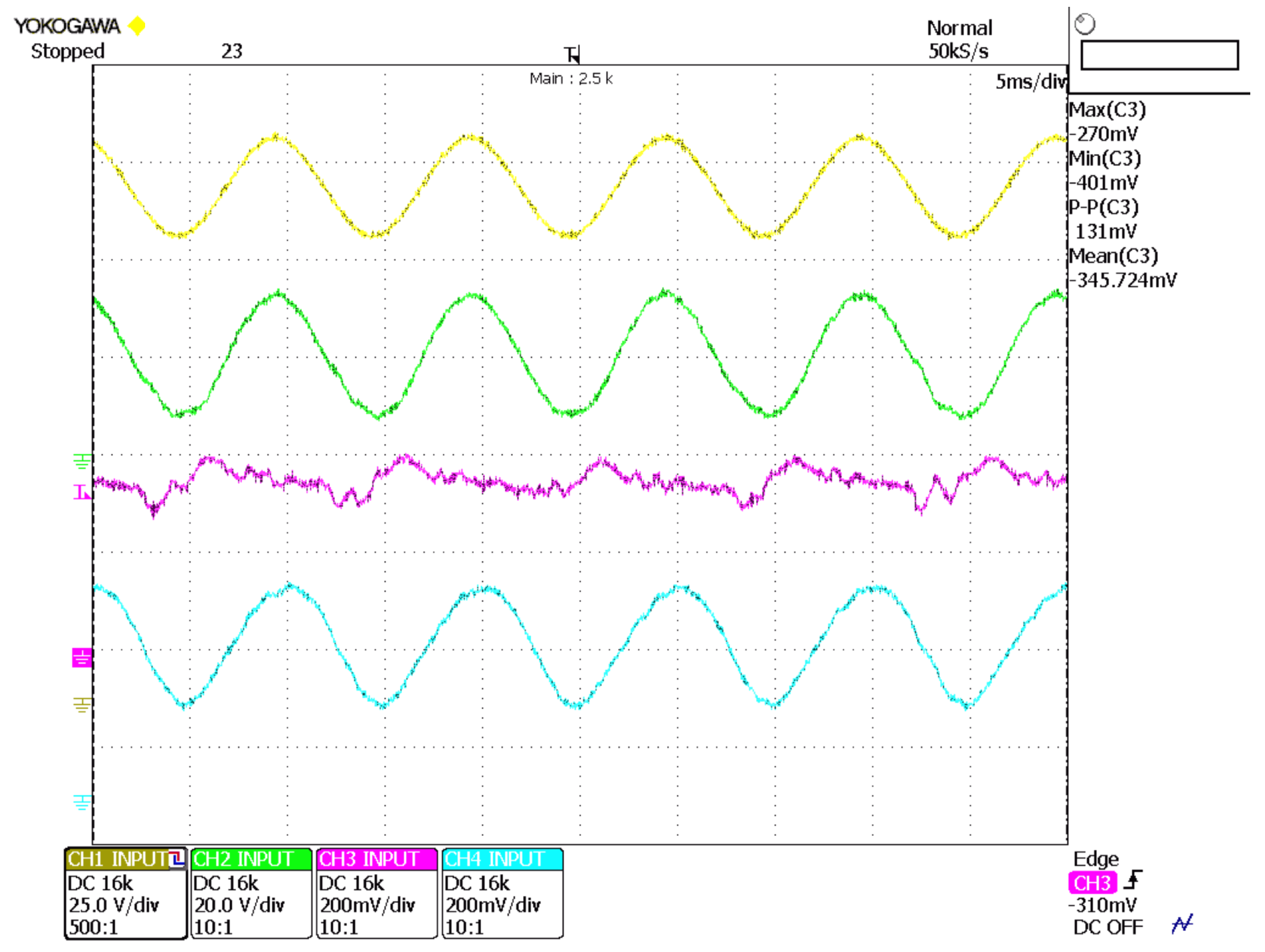
Figure 11 shows the simulated behavior of the system. As it can be seen, the resulting LEDs current ripple has also a smaller value, therefore the design has been optimized in terms of inductor size. However, as the real inductor is much smaller, the inductor average current and LF current ripple is larger. As the system needs to avoid the current to evolve to negative values (as switches
and
cannot withstand negative currents), the capacitor
voltage presents a
offset. This ensures low ripple in the LEDs current, but unfortunately provides a decrease in the system efficiency. These losses are represented, for the inductor values considered, in the last row of
Table 8.
Therefore, with the new inductor, there is an increase of 4.3 W in the system power losses due the capacitance offset required for proper operation of the output stage. However, from
Table 5 and
Table 9, a saving of 2.1 W is obtained in the inductor
(as its inductance decreases by a factor of ten). Therefore, considering the power balance, the global loss increase is around 2.2 W for this solution, but significantly decreasing the size of the inductor (from
to
). Depending on the particular application considered, a trade-off must be carried out, in order to select the optimal size of the inductor.
10. Conclusions and Future Developments
The LED driver topology proposed in [
33] for the output stage of an electronic driver for power LEDs has been deeply analyzed, and a new design methodology for optimizing the converter size has been proposed. This methodology has been validated both by simulations and experimentally. The advantages of this improved methodology are mainly two: first, the optimization of the inductor design which implies that the resulting inductor value can be built in an
core, and secondly, the dynamics of the controller are improved allowing for comparably faster performance which implies that the proposed series scheme is suitable for
dimming control.
The main drawbacks of the proposed driver are the number of components (two extra switches, which in addition must be driven with isolated drivers, as well as the reactive elements and ), plus the mandatory current control loop (including sensor, microcontroller, etc.). Comparing the closed-loop control schemes, in standard LED drivers, the link voltage control is mandatory, while the LED current control can be achieved without a dedicated closed loop (for instance, in open loop by means of a peak current control through the LEDs); however, with the proposed series output stage, the LED current control is also necessary to attain proper operation of the stage. Future developments of the work include the design of a full off-line driver, also considering the input stage in the control system, as well as the experimental validation of the system operating under dimming scheme. Also, alternative control methods such as peak current control or resonant current control can be explored.