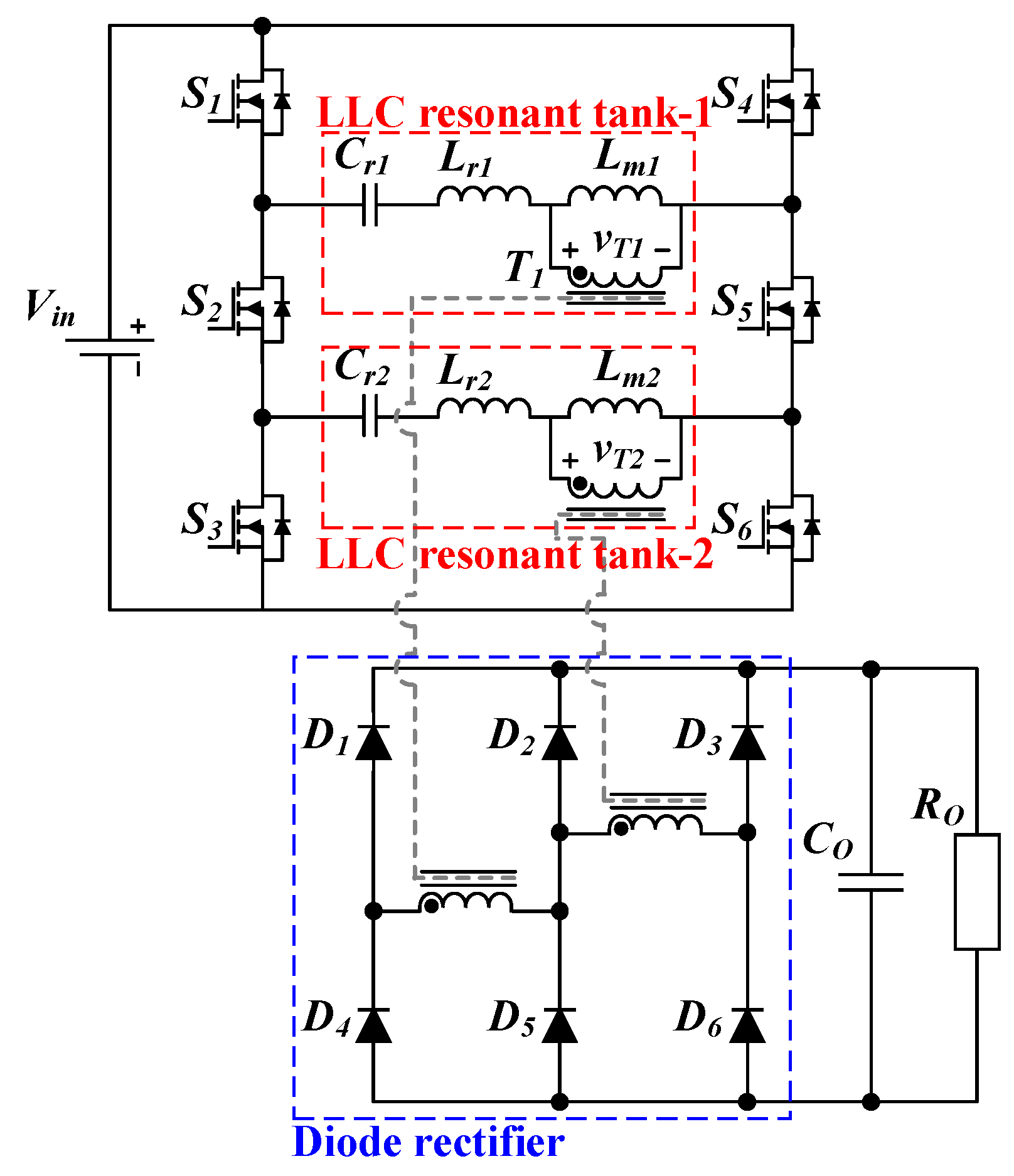
This paper introduces five different switching patterns of DI-LRC for a wide range of output voltages. Switching Patterns 1 and 2 only use one resonant tank in the DI-LRC to obtain the same voltage gain curve as the conventional single full-bridge LLC resonant converter. In Switching Pattern 3, the voltage gain is 0.5-times the nominal voltage gain of the existing LLC resonant converter, since DI-LRC is operated as a full-bridge connecting the two LLC resonant tanks in series. In Switching Pattern 4, two resonant tanks are connected in series in a manner identical to Switching Pattern 3, but they have a voltage gain of 0.25-times the nominal voltage gain, because of the half-bridge operation. In contrast to Switching Patterns 3 and 4, Switching Pattern 5 has the highest voltage gain at twice the nominal voltage, because it performs a full-bridge operation that connects the two LLC resonators in parallel. Detailed mode analysis according to each switching pattern is as follows.
2.2.1. Switching Patterns 1 and 2: Single Full-Bridge Operation
Switching Patterns 1 and 2 perform the same operation as conventional single full-bridge LLC converters, using only the resonance tanks of one of the two LLC resonance tanks, as shown in
Figure 2a,b. In Switching Pattern 1, switches
S1,
S5, and
S6 and switches
S2,
S3, and
S4 operate complementarily at a 0.5 duty ratio to only operate the top full-bridge LLC converter. Conversely, in Switching Pattern 2, switches
S1,
S2, and
S6 and switches
S3,
S4, and
S5 are operated complementarily to only operate the bottom full-bridge LLC converter. Therefore, Switching Patterns 1 and 2 operate on the same principle, so this paper omits any analysis of the operation of Switching Pattern 2.
For Switching Pattern 1, +
Vin is applied to the upper LLC resonance tank when switches
S1,
S5, and
S6 are turned on, while −
Vin is applied when switches
S2,
S3, and
S4 are turned on. Thus, for the DI-LRC operating with Switching Pattern 1, it can be expressed as an equivalent circuit with a square wave input voltage of
Vin, as shown in
Figure 3, and the input square wave
vin_ac can be represented using Fourier transform as follows.
The response characteristics by the switching frequency of the LLC resonant tank affect only the fundamental components of
vin_ac, and the fundamental component
vin_acF is expressed as follows:
The current flowing into the resonant tank is determined by the fundamental component
vin_acF of the input voltage and the characteristic impedance and can be expressed as follows:
where
Ir,peak is the peak value of resonant current and
represents the phase delay component of resonant current. Meanwhile, since the input current
iin has the same waveform as the resonant current
ir before the half-cycle based on the switching half-cycle, the mean value of the input current
iin can be calculated by integrating the resonant current during the switching half-cycle, as follows:
As shown in
Figure 4, an LLC resonant converter has a resonant current of a complete sine wave when the switching frequency and resonant frequency are the same, with magnetizing current having a triangular waveform. In (3), the peak value of resonant current is replaced by the RMS value as follows:
For the current flowing through the magnetizing inductor, the switching half-cycle is subjected to a positive voltage, and the negative voltage is applied for the remainder of the half-cycle, which can be expressed as follows:
where the peak value of magnetized inductor current
Im must be continuous when
t is
Ts/2 at (6), so it can be obtained as follows:
In practice, since the current supplied to the load is the current that passes from the primary to the secondary side of the transformer, the relationship (8) can be obtained based on the mean of the difference between the magnetizing current im and the resonant current ir.
In addition, since the resonant and magnetizing currents have the same value in times
Ts/2 and
Ts, they have the same relationship, as shown in (9).
Using (8) and (9), the effective value
Ir,rms of resonant current can be obtained as follows:
When the LLC resonant converter operates at resonant frequencies, the voltage and current waveforms flowing to the secondary side of the transformer are as shown in
Figure 5 and can be obtained using Fourier series in the same way as on the primary side. The voltage and current peak values on the secondary side of the transformer are as shown in (11) and (12), respectively.
When the output current is obtained using the secondary current as (13), the rectifier section and load shown in
Figure 3a can be modelled as shown in (14), using the secondary voltage and current of the transformer.
The final equivalent circuit of the DI-LRC, operated by Switching Patterns 1 and 2 through circuit interpretation for the resonant tanks and rectifier section as shown above, can be represented as shown in
Figure 3b; where voltage gain
M can be represented by the ratio of input voltage to output voltage, quality factor
Q, the ratio of the magnetizing inductor to the return inductor
m, and normalized switching frequency
Fx.
where
,
,
,
,
2.2.2. Switching Patterns 3: Series Full-Bridge Operation
The current pass of the DI-LRC operating with Switching Pattern 3 is shown in
Figure 2c. Switches
S1,
S3, and
S5 and switches
S2,
S4, and
S6 are operated complementarily at a 0.5 duty ratio, so that two resonant tanks are connected in series to perform full-bridge operation. Therefore, input voltage is applied to each LLC resonant tank by half. In contrast, at the output side of the DI-LRC, three diodes turn on and have a parallel structure. Therefore, Switching Pattern 3 has an input-serial, output-parallel structure, and the equivalent circuit for detailed analysis and for calculating voltage gain is presented in
Figure 6.
As shown in
Figure 6, in an equivalent circuit, due to the series connection of two LLC resonance tanks, the sizes of the magnetized inductor and resonant inductor are reduced by half, the resonant capacitors have doubled, and the input voltage of
Vin/2 is applied. Calculating the quality factor
Qsp3 and the voltage gain using the resonance components value of the equivalent resonance tank can be achieved using (16) and (17), respectively.
The quality factor
Qsp3 of Switching Pattern 3 is halved as compared to the quality factor
Q of Switching Patterns 1 and 2, and under conditions of
Fx = 1 with the same resonant frequency and switching frequency, the voltage gain is also reduced to one-half. As the voltage gain decreases by half, the resonant current and output current also decrease by half, as calculated by (18) and (19), respectively.
As a result, the output voltage and output current are halved, and the output power is eventually reduced to 1/4 as compared to Switching Patterns 1 and 2. However, it is necessary to obtain a quality factor and voltage gain under the same power condition considering that some applications require a constant output current of a certain value, such as a battery charger. In order to operate at the same power, taking into account the half-reduced voltage gain, the output current should be quadrupled; as a result, the load resistance should be reduced to 1/4 as compared to Switching Patterns 1 and 2. Therefore, the equivalent resistance
Rac_sp3_cp and quality factor
Qsp3_cp, considering the same power, can be expressed as follows:
In the equivalent circuit of Switching Pattern 3, the quality factor was reduced by half, but the quality factor was doubled when the same power was taken into account. Therefore, the voltage gain value was calculated again using (21) as shown in (22). At resonant frequencies, the converter has a voltage gain of one-half the size of the voltage gain of Switching Patterns 1 and 2.
A comparison of the voltage gain curves of Switching Patterns 1 and 3 at the same power is shown in
Figure 7. When
m is six and the quality factor is 0.4, the maximum voltage gain for Switching Pattern 1 has a value of approximately 1.2, while that for Switching Pattern 3 is approximately 0.6.
2.2.3. Switching Patterns 4: Series Half-Bridge Operation
As shown in
Figure 2d, Switching Pattern 4 connects the LLC resonant tank in series, as described previously in Switching Pattern 3; however, it always turns on switch
S4 and turns on and off switches
S1 and
S2 complementarily as a half-bridge mode. Thus, for Switching Pattern 4, a quarter of the input voltage is applied to each resonant tank. The secondary diode rectifier has a parallel structure in which three diodes turn on, as shown in Switching Pattern 3. Therefore, DI-LRC has an input-serial output-parallel structure and can be represented as an equivalent circuit, as shown in
Figure 8.
Switching Pattern 4 also requires an adjustment of the load to be analyzed based on the same power as Switching Pattern 1. Switching Pattern 4 causes the series-connected LLC resonance tank to enter half-bridge operation, so it has a 1/4 voltage gain less than Switching Pattern 1, thus reducing the output voltage and current to one quarter. As a result, the output power is reduced to 1/16. For the same power condition, the quality factor can be obtained as shown in (24) by reducing the resistance by 16 times, as shown in (23).
Under the same load condition, the quality factor in Switching Pattern 4 shows an eight-times increase over that pf Switching Pattern 1, while the voltage gain shows a one-quarter reduction in resonant frequency, as follows:
In
Figure 9, the voltage gain curves of Switching Patterns 1 and 4 are compared when
m is six and the quality factor is 0.4. In Switching Pattern 4, the voltage gain is one-quarter at the resonant frequency. The quality factor of Switching Pattern 4 has a value of 3.2 when that of Switching Pattern 1 is 0.4, so it has a curve similar to that of the voltage gain curve of the series resonant converter. However, as actual battery chargers charge the battery by fixing certain current values, the voltage gain curve in Switching Pattern 4 may have a wider voltage gain than that shown in
Figure 9 when charging with an output current that is lower than 16-times the output current of Switching Pattern 1 (equal to Switching Pattern 1).
2.2.4. Switching Patterns 5: Parallel Full-Bridge Operation
The current pass for Switching Pattern 5 is shown in
Figure 10. Switches
S2 and
S5 are always turned on, while switches
S1 and
S6 and switches
S3 and
S4 are operated complementarily in order to perform full-bridge operation connecting the two LLC resonance tanks in parallel. Therefore, each LLC resonator tank has an input-parallel structure in which an input voltage
Vin is applied, and the output stage has an output serial structure in which only two diodes are turned on, making the secondary side of the transformer and the load a series connection.
In the equivalent circuit of Switching Pattern 5, as shown in
Figure 11, the magnetizing inductors and resonant inductors in resonance tanks are twice the value of conventional single resonance tanks, while resonant capacitors are half the value. In addition, an equivalent resonant tank is input with twice the input voltage of a single resonant tank. Similar to Switching Patterns 3 and 4, which operate the LLC resonator tanks in series, the
Q factor is obtained using the resonance components’ value of the resonant tank in Switching Pattern 5.
In contrast to Switching Patterns 3 and 4, the quality factor of Switching Pattern 5 is doubled. However, for Switching Pattern 5, as shown in
Figure 12, the LLC resonance tank is connected in parallel and performs a full-bridge operation, resulting in a voltage gain of twice that of the existing single LLC full-bridge operation. This results in a four-times increase in power over a single LLC full-bridge operation with twice the output voltage and output current. The load adjustment is required to be analyzed under the same power condition as the previous switching pattern analysis.
In Switching Pattern 5, load resistance
Rac_sp5_cp and quality factor
Qsp5_cp are as expressed in (27) and (28), respectively, as the load must be reduced to 1/4 in order to compensate for a four-times increase in power. In addition, the voltage gain of Switching Pattern 5 obtained under the same power condition using (28) is equal to that using (29).
At resonant frequency points, it has twice the voltage gain of the existing single LLC full-bridge operation, and at points other than the resonant frequency, it has another type of voltage gain curve, because the
Q factor is reduced by half. In
Figure 9, the voltage gain curves of Switching Patterns 1 and 5 are compared when
m is six and the quality factor has a value of 0.4. Operating the switching frequency in an area below the resonant frequency with Switching Pattern 5 can result in a higher voltage gain than twice the nominal voltage. Under conditions in which a high range of boost is required, operating with Switching Pattern 5 can satisfy the high output voltage. However, under conditions where voltage gains less than one are required, switching frequencies should be increased to 10-times the resonant frequency, so Switching Pattern 1, 2, or 3 should be operated.