Shunt Active Power Filter: A Review on Phase Synchronization Control Techniques
Abstract
:1. Introduction
2. Shunt Active Power Filter: Working Principle and Control Scheme
- (1)
- Harmonic Extraction Algorithm.The main function of this algorithm is to extract harmonic information from a harmonic-polluted power system and applied the extracted information to form a reference current signal . In this aspect, the distorted load current signal is processed in a way that allows its harmonic and fundamental elements to be separated.After separating the elements, can be derived by using either the harmonic or fundamental elements, each having its own derivation setting. Note that quality of the reference current signal will mainly determine how well the SAPF is going to work, thus it must be generated in a quick and accurate manner. This algorithm is also referred as reference current generation algorithm in some literature, such as in [18,19] due to the reason that reference current is being generated as the final output of this algorithm. Few examples of commonly applied techniques for this algorithm include synchronous reference frame (SRF) or theory [20,21,22], instantaneous power theory [23,24,25], fast Fourier transform (FFT) [26,27], discrete Fourier transform (DFT) [28,29] and artificial neural network (ANN) [30,31,32].
- (2)
- Synchronization Algorithm.The main function of this algorithm is to track angular position of source voltage signal and subsequently generate a phase synchronization angle to match the phase of the generated with the phase of the operating power system. Many harmonic extraction algorithms do not possess a phase tracking feature and are fully dependent on an explicit synchronization algorithm to provide them with an effective synchronization angle. Nevertheless, there are some harmonic extraction algorithms that are inherited with phase tracking ability, for example, the algorithm designed based on instantaneous power theory technique [25,33]. In this case, an explicit synchronization algorithm can be omitted. Further details on the available techniques for this algorithm are presented in the next section.
- (3)
- DC-link Capacitor Voltage Regulation Algorithm.The main function of this algorithm is to estimate the amount of dc-link charging current needed by the SAPF to constantly maintain dc-link voltage at a desired level. This algorithm continuously compares the measured with a predetermined set-point value and minimizes the resulted error by using either proportional-integral (PI) [34,35,36] or fuzzy logic control (FLC) [37,38,39] techniques, via a voltage control loop. When the error between the measured and the predetermined set-point value has been minimized, the effective magnitude of will be generated. Subsequently, by utilizing the phase synchronization angle , can be coordinated in-phase with the operating power system.
- (4)
- Current Control Algorithm.The main function of this algorithm is to convert delivered by harmonic extraction algorithm and delivered by dc-link capacitor voltage regulation algorithm into gate switching pulses via a pulse-width modulation process, while ensuring that the feedback signal or is able to track via a current control loop. This algorithm is also commonly referred as switching algorithm due to its function in generating gate switching pulses. Few examples of commonly applied techniques for this algorithm include hysteresis control [40,41,42,43], sinusoidal pulse-width modulation (SPWM) [44,45,46] and space vector PWM (SVPWM) [47,48,49,50].
3. Phase Synchronization Techniques
3.1. Zero-Crossing Detection (ZCD) Technique
3.2. Phase-Locked Loop (PLL) Technique
3.3. Adaptive Linear Neuron (ADALINE) Technique
- is the weight factor,
- is the fundamental sine and cosine components,
- is the error between the measured and estimated voltage signal, and is the learning rate.
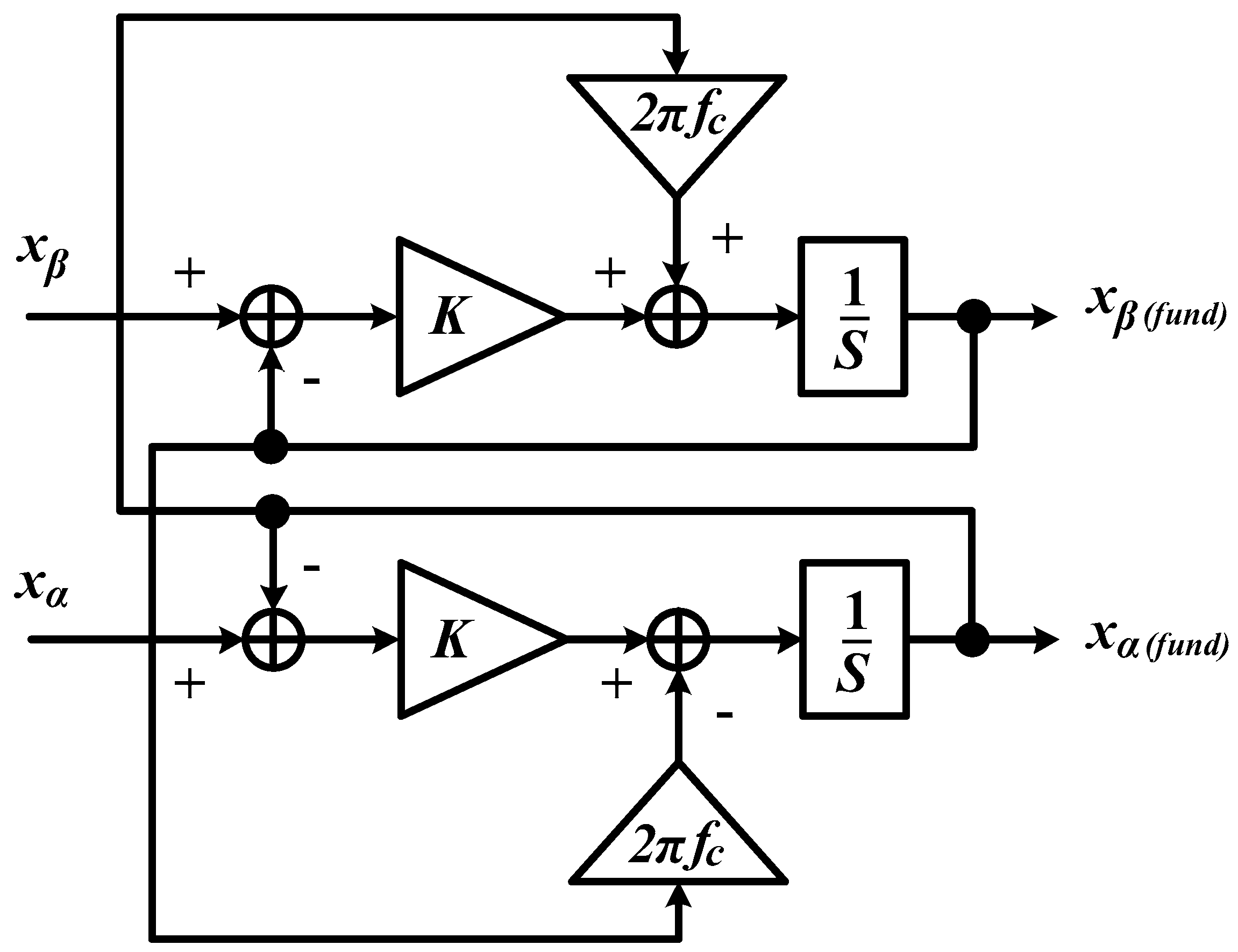
3.4. Fundamental Component Extraction Technique
- Extraction of fundamental (sinusoidal characteristic) source voltage from the measured source voltage . In the first stage, the extraction process is conducted in -domain where a Clarke-transformation ( transformation) is applied according to Equation (4). In -domain, source voltage which is subjected to distortion can be expressed aswhere is the fundamental component and is distorted component of source voltage in α domain, respectively. Similar relation valid for source voltage in β domain, and .Here, a STF (as in Equation (6)) is applied to extract and which is subsequently converted into a pure sinusoidal signal by means of inverse Clarke-transformation ( transformation), as in Equation (10). Note that, the application of STF is only needed when the source voltage is subjected to any distortion. In the case where the source voltage is ideal (balanced-sinusoidal), STF can actually be omitted to reduce structure complexity.
- Magnitude calculation by using the extracted fundamental voltage component ( and ). In this stage, the fundamental magnitude of source voltage is computed as follow
- Direct magnitude division from to obtain its unity form. In the final stage, the desired synchronization signal is obtained as follow
3.5. Unit Vector Generation Technique
4. Comparative Highlights on Phase Synchronization Techniques and Possible Future Works
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kale, M.; Ozdemir, E. An adaptive hysteresis band current controller for shunt active power filter. Electr. Power Syst. Res. 2005, 73, 113–119. [Google Scholar] [CrossRef]
- Soni, M.K.; Soni, N. Review of causes and effect of harmonics on power system. Int. J. Sci. Eng. Technol. Res. 2014, 3, 214–220. [Google Scholar]
- Henderson, R.D.; Rose, P.J. Harmonics: The effects on power quality and transformers. IEEE Trans. Ind. Appl. 1994, 30, 528–532. [Google Scholar] [CrossRef]
- IEEE Standard 519. IEEE recommended practice and requirement for harmonic control in electric power systems. In IEEE Std 519-2014 (Revision of IEEE Std 519-1992); IEEE: Piscataway, NJ, USA, 2014; pp. 1–29. [Google Scholar]
- Das, J.C. Passive filters—Potentialities and limitations. IEEE Trans. Ind. Appl. 2004, 40, 232–241. [Google Scholar] [CrossRef]
- Akagi, H. Active harmonic filters. Proc. IEEE 2005, 93, 2128–2141. [Google Scholar] [CrossRef]
- El-Habrouk, M.; Darwish, M.K.; Mehta, P. Active power filters: A review. IEEE Proc. Electr. Power Appl. 2000, 147, 403–413. [Google Scholar] [CrossRef]
- Singh, B.; Al-Haddad, K.; Chandra, A. A review of active filters for power quality improvement. IEEE Trans. Ind. Electron. 1999, 46, 960–971. [Google Scholar] [CrossRef]
- Jain, B.; Jain, S.; Nema, R.K. Control strategies of grid interfaced wind energy conversion system: An overview. Renew. Sustain. Energy Rev. 2015, 47, 983–996. [Google Scholar] [CrossRef]
- Jaalam, N.; Rahim, N.A.; Bakar, A.H.A.; Tan, C.K.; Haidar, A.M.A. A comprehensive review of synchronization methods for grid-connected converters of renewable energy source. Renew. Sustain. Energy Rev. 2016, 59, 1471–1481. [Google Scholar] [CrossRef] [Green Version]
- Bobrowska-Rafal, M.; Rafal, K.; Jasinski, M.; Kazmierkowski, M.P. Grid synchronization and symmetrical components extraction with pll algorithm for grid connected power electronic converters—A review. Bull. Pol. Acad. Sci. Tech. Sci. 2011, 59, 485–497. [Google Scholar] [CrossRef]
- Green, T.C.; Marks, J.H. Control techniques for active power filters. IEEE Proc. Electr. Power Appl. 2005, 152, 369–381. [Google Scholar] [CrossRef] [Green Version]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. Control algorithms of shunt active power filter for harmonics mitigation: A review. Energies 2017, 10, 2038. [Google Scholar] [CrossRef]
- Schwanz, D.; Bagheri, A.; Bollen, M.; Larsson, A. Active harmonic filters: Control techniques review. In Proceedings of the 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 36–41. [Google Scholar]
- Steela, K.; Rajpurohit, B.S. A survey on active power filters control strategies. In Proceedings of the IEEE 6th India International Conference on Power Electronics (IICPE), Kurukshetra, India, 8–10 December 2014; pp. 1–6. [Google Scholar]
- Rahmani, S.; Hamadi, A.; Al-Haddad, K.; Dessaint, L.A. A combination of shunt hybrid power filter and thyristor-controlled reactor for power quality. IEEE Trans. Ind. Electron. 2014, 61, 2152–2164. [Google Scholar] [CrossRef]
- Trinh, Q.-N.; Lee, H.-H. An advanced current control strategy for three-phase shunt active power filters. IEEE Trans. Ind. Electron. 2013, 60, 5400–5410. [Google Scholar] [CrossRef]
- Terriche, Y.; Golestan, S.; Guerrero, J.M.; Kerdoune, D.; Vasquez, J.C. Matrix pencil method-based reference current generation for shunt active power filters. IET Power Electron. 2018, 11, 772–780. [Google Scholar] [CrossRef]
- Chauhan, S.K.; Shah, M.C.; Tiwari, R.R.; Tekwani, P.N. Analysis, design and digital implementation of a shunt active power filter with different schemes of reference current generation. IET Power Electron. 2014, 7, 627–639. [Google Scholar] [CrossRef]
- Monfared, M.; Golestan, S.; Guerrero, J.M. A new synchronous reference frame-based method for single-phase shunt active power filters. J. Power Electron. 2013, 13, 692–700. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F.; Wahab, N.I.A. A simplified synchronous reference frame for indirect current controlled three-level inverter-based shunt active power filters. J. Power Electron. 2016, 16, 1964–1980. [Google Scholar] [CrossRef]
- Jain, N.; Gupta, A. Comparison between two compensation current control methods of shunt active power filter. Int. J. Eng. Res. Gen. Sci. 2014, 2, 603–615. [Google Scholar]
- Eskandarian, N.; Beromi, Y.A.; Farhangi, S. Improvement of dynamic behavior of shunt active power filter using fuzzy instantaneous power theory. J. Power Electron. 2014, 14, 1303–1313. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. Enhanced instantaneous power theory with average algorithm for indirect current controlled three-level inverter-based shunt active power filter under dynamic state conditions. Math. Probl. Eng. 2016, 2016, 9682512. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chakraborty, C.; Bhattacharya, S. Shunt compensation—Reviewing traditional methods of reference current generation. IEEE Ind. Electron. Mag. 2009, 3, 38–49. [Google Scholar] [CrossRef]
- Vodyakho, O.; Mi, C.C. Three-level inverter-based shunt active power filter in three-phase three-wire and four-wire systems. IEEE Trans. Power Electron. 2009, 24, 1350–1363. [Google Scholar] [CrossRef]
- Chen, K.F.; Mei, S.L. Composite interpolated fast fourier transform with the hanning window. IEEE Trans. Instrum. Meas. 2010, 59, 1571–1579. [Google Scholar] [CrossRef]
- Mattavelli, P.; Marafao, F.P. Repetitive-based control for selective harmonic compensation in active power filters. IEEE Trans. Ind. Electron. 2004, 51, 1018–1024. [Google Scholar] [CrossRef]
- Maza-Ortega, J.M.; Rosendo-Macías, J.A.; Gómez-Expósito, A.; Ceballos-Mannozzi, S.; Barragán-Villarejo, M. Reference current computation for active power filters by running dft techniques. IEEE Trans. Power Deliv. 2010, 25, 1986–1995. [Google Scholar] [CrossRef]
- Abdeslam, D.O.; Wira, P.; Merckle, J.; Flieller, D.; Chapuis, Y.-A. A unified artificial neural network architecture for active power filters. IEEE Trans. Ind. Electron. 2007, 54, 61–76. [Google Scholar] [CrossRef]
- Saribulut, L.; Teke, A.; Tümay, M. Artificial neural network based discrete-fuzzy logic controlled active power filter. IET Power Electron. 2014, 7, 1536–1546. [Google Scholar] [CrossRef]
- Qasim, M.; Khadkikar, V. Application of artificial neural networks for shunt active power filter control. IEEE Trans. Ind. Inform. 2014, 10, 1765–1774. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Blaabjerg, F.; Hansen, S. Detection is key—Harmonic detection methods for active power filter applications. IEEE Ind. Appl. Mag. 2007, 13, 22–33. [Google Scholar] [CrossRef]
- De Araujo Ribeiro, R.L.; Rocha, T.D.O.A.; de Sousa, R.M.; dos Santos, E.C.; Lima, A.M.N. A robust dc-link voltage control strategy to enhance the performance of shunt active power filters without harmonic detection schemes. IEEE Trans. Ind. Electron. 2015, 62, 803–813. [Google Scholar] [CrossRef]
- Afghoul, H.; Krim, F. Comparison between pi and fuzzy dpc control of a shunt active power filter. In Proceedings of the IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 146–151. [Google Scholar]
- Mahanty, R. Indirect current controlled shunt active power filter for power quality improvement. Int. J. Electr. Power Energy Syst. 2014, 62, 441–449. [Google Scholar] [CrossRef]
- Jain, S.K.; Agrawal, P.; Gupta, H.O. Fuzzy logic controlled shunt active power filter for power quality improvement. IEEE Proc. Electr. Power Appl. 2002, 149, 317–328. [Google Scholar] [CrossRef]
- Mekri, F.; Mazari, B.; Machmoum, M. Control and optimization of shunt active power filter parameters by fuzzy logic. Can. J. Electr. Comput. Eng. 2006, 31, 127–134. [Google Scholar] [CrossRef]
- Mikkili, S.; Panda, A.K. Simulation and real-time implementation of shunt active filter id-iq control strategy for mitigation of harmonics with different fuzzy membership functions. IET Power Electron. 2012, 5, 1856–1872. [Google Scholar] [CrossRef]
- Suresh, Y.; Panda, A.K.; Suresh, M. Real-time implementation of adaptive fuzzy hysteresis-band current control technique for shunt active power filter. IET Power Electron. 2012, 5, 1188–1195. [Google Scholar] [CrossRef] [Green Version]
- Vahedi, H.; Sheikholeslami, A.; Bina, M.T.; Vahedi, M. Review and simulation of fixed and adaptive hysteresis current control considering switching losses and high-frequency harmonics. Adv. Power Electron. 2011, 2011, 397872. [Google Scholar] [CrossRef]
- Doǧan, H.; Akkaya, R. A control scheme employing an adaptive hysteresis current controller and an uncomplicated reference current generator for a single-phase shunt active power filter. Turk. J. Electr. Eng. Comput. Sci. 2014, 22, 1085–1097. [Google Scholar] [CrossRef]
- Suul, J.A.; Ljøkelsøy, K.; Midtsund, T.; Undeland, T. Synchronous reference frame hysteresis current control for grid converter applications. IEEE Trans. Ind. Appl. 2011, 47, 2183–2194. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Q.; Zhao, Y.; Li, D.; Xiong, Y. A novel active power filter for high-voltage power distribution systems application. IEEE Trans. Power Deliv. 2007, 22, 911–918. [Google Scholar] [CrossRef]
- Wu, L.; Zhuo, F.; Zhang, P.; Li, H.; Wang, Z. Study on the influence of supply-voltage fluctuation on shunt active power filter. IEEE Trans. Power Deliv. 2007, 22, 1743–1746. [Google Scholar] [CrossRef]
- Rahmani, S.; Al-Haddad, K.; Kanaan, H.Y. Two pwm techniques for single-phase shunt active power filters employing a direct current control strategy. IET Power Electron. 2008, 1, 376–385. [Google Scholar] [CrossRef]
- Gupta, A.K.; Khambadkone, A.M. A space vector pwm scheme for multilevel inverters based on two-level space vector pwm. IEEE Trans. Ind. Electron. 2006, 53, 1631–1639. [Google Scholar] [CrossRef]
- Choi, U.-M.; Lee, K.-B. Space vector modulation strategy for neutral-point voltage balancing in three-level inverter systems. IET Power Electron. 2013, 6, 1390–1398. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, Y.-X.; Huang, W.-P.; Le, J.-Y.; Chen, L. A new svpwm method for single-phase three-level npc inverter and the control method of neutral point voltage balance. In Proceedings of the International Conference on Electrical Machines and Systems, 2008 (ICEMS 2008), Tokyo, Japan, 15–18 November 2009; pp. 1–4. [Google Scholar]
- Raj, P.H.; Maswood, A.I.; Ooi, G.H.P.; Lim, Z. Voltage balancing technique in a space vector modulated 5-level multiple-pole multilevel diode clamped inverter. IET Power Electron. 2015, 8, 1263–1272. [Google Scholar] [CrossRef]
- Radzi, M.A.M.; Rahim, N.A. Neural network and bandless hysteresis approach to control switched capacitor active power filter for reduction of harmonics. IEEE Trans. Ind. Electron. 2009, 56, 1477–1484. [Google Scholar] [CrossRef]
- Vainio, O.; Ovaska, S.J.; Polla, M. Adaptive filtering using multiplicative general parameters for zero-crossing detection. IEEE Trans. Ind. Electron. 2003, 50, 1340–1342. [Google Scholar] [CrossRef]
- Rodriguez, P.; Pou, J.; Bergas, J.; Candela, J.I.; Burgos, R.P.; Boroyevich, D. Decoupled double synchronous reference frame pll for power converters control. IEEE Trans. Power Electron. 2007, 22, 584–592. [Google Scholar] [CrossRef]
- Golestan, S.; Monfared, M.; Freijedo, F.D. Design-oriented study of advanced synchronous reference frame phase-locked loops. IEEE Trans. Power Electron. 2013, 28, 765–778. [Google Scholar] [CrossRef]
- Campanhol, L.B.G.; Silva, S.A.O.; Goedtel, A. Application of shunt active power filter for harmonic reduction and reactive power compensation in three-phase four-wire systems. IET Power Electron. 2014, 7, 2825–2836. [Google Scholar] [CrossRef]
- Zainuri, M.A.A.M.; Radzi, M.A.M.; Soh, A.C.; Mariun, N.; Rahim, N.A.; Hajighorbani, S. Fundamental active current adaptive linear neural networks for photovoltaic shunt active power filters. Energies 2016, 9, 397. [Google Scholar] [CrossRef]
- Zainuri, M.A.A.M.; Radzi, M.A.M.; Soh, A.C.; Mariun, N.; Rahim, N.A. Simplified adaptive linear neuron harmonics extraction algorithm for dynamic performance of shunt active power filter. Int. Rev. Model. Simul. 2016, 9, 144–154. [Google Scholar]
- Rahman, N.F.A.; Radzi, M.A.M.; Soh, A.C.; Mariun, N.; Rahim, N.A. Dual function of unified adaptive linear neurons based fundamental component extraction algorithm for shunt active power filter operation. Int. Rev. Electr. Eng. 2015, 10, 544–552. [Google Scholar]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. Operation of three-level inverter-based shunt active power filter under nonideal grid voltage conditions with dual fundamental component extraction. IEEE Trans. Power Electron. 2018, 33, 7558–7570. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. A self-tuning filter-based adaptive linear neuron approach for operation of three-level inverter-based shunt active power filters under non-ideal source voltage conditions. Energies 2017, 10, 667. [Google Scholar] [CrossRef]
- Elangovan, S.; Thanushkodi, K.; Neelakantan, P.N. A two level shunt active power filter without pll for industrial loads. Aust. J. Basic Appl. Sci. 2014, 8, 71–77. [Google Scholar]
- Musa, S.; Radzi, M.A.M.; Hizam, H.; Wahab, N.I.A.; Hoon, Y.; Zainuri, M.A.A.M. Modified synchronous reference frame based shunt active power filter with fuzzy logic control pulse width modulation inverter. Energies 2017, 10, 758. [Google Scholar] [CrossRef]
- Marques, G.D.; Pires, V.F.; Malinowski, M.; Kazmierkowski, M. An improved synchronous reference frame method for active filters. In Proceedings of the EUROCON 2007—The International Conference on “Computer as a Tool”, Warsaw, Poland, 9–12 September 2007; pp. 2564–2569. [Google Scholar]
- Kanjiya, P.; Khadkikar, V.; Zeineldin, H.H. A noniterative optimized algorithm for shunt active power filter under distorted and unbalanced supply voltages. IEEE Trans. Ind. Electron. 2013, 60, 5376–5390. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Formentini, A.; Gaeta, A.; Degano, M.; Zanchetta, P.; Rabbeni, R.; Pucci, M. Model predictive control for shunt active filters with fixed switching frequency. IEEE Trans. Ind. Appl. 2017, 53, 296–304. [Google Scholar] [CrossRef]
- Tareen, W.U.K.; Mekhilef, S. Three-phase transformerless shunt active power filter with reduced switch count for harmonic compensation in grid-connected applications. IEEE Trans. Power Electron. 2018, 33, 4868–4881. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G.; Galloway, J.J.H. Power converter line synchronization using a discrete fourier transform (dft) based on a variable sample rate. IEEE Trans. Power Electron. 2005, 20, 877–884. [Google Scholar] [CrossRef]
- Timbus, A.; Liserre, M.; Teodorescu, R.; Blaabjerg, F. Synchronization methods for three phase distributed power generation systems—An overview and evaluation. In Proceedings of the IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 16 June 2005; pp. 2474–2481. [Google Scholar]
- Chen, L.-R. Pll-based battery charge circuit topology. IEEE Trans. Ind. Electron. 2004, 51, 1344–1346. [Google Scholar] [CrossRef]
- Lai, M.-F.; Nakano, M. Special section on phase-locked loop techniques. IEEE Trans. Ind. Electron. 1996, 43, 607–608. [Google Scholar]
- Hsieh, G.-C.; Hung, J.C. Phase-locked loop techniques—A survey. IEEE Trans. Ind. Electron. 1996, 43, 609–615. [Google Scholar] [CrossRef]
- Bacon, V.D.; Souza, V.D.; Padim, E.T.; Silva, S.A.O.D. Influence of the pll phase-angle quality on the static and dynamic performance of grid-connected systems. In Proceedings of the 2017 Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Silva, S.A.O.D.; Bacon, V.D.; Campanhol, L.B.G.; Angelico, B.A. An adaptive phase-locked loop algorithm for single-phase utility connected system. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Han, Y.; Xu, L.; Khan, M.M.; Yao, G.; Zhou, L.-D.; Chen, C. A novel synchronization scheme for grid-connected converters by using adaptive linear optimal filter based pll (alof-pll). Simul. Model. Pract. Theory 2009, 17, 1299–1345. [Google Scholar] [CrossRef]
- Abdulsalam, M.; Poure, P.; Karimi, S.; Saadate, S. New digital reference current generation for shunt active power filter under distorted voltage conditions. Electr. Power Syst. Res. 2009, 79, 759–765. [Google Scholar] [CrossRef]
- Djazia, K.; Krim, F.; Chaoui, A.; Sarra, M. Active power filtering using the zdpc method under unbalanced and distorted grid voltage conditions. Energies 2015, 8, 1584–1605. [Google Scholar] [CrossRef]
- Shinnaka, S. A novel fast-tracking d-estimation method for single-phase signals. IEEE Trans. Power Electron. 2011, 26, 1081–1088. [Google Scholar] [CrossRef]
- Shinnaka, S. A robust single-phase pll system with stable and fast tracking. IEEE Trans. Ind. Appl. 2008, 44, 624–633. [Google Scholar] [CrossRef]
- Shinnaka, S. A new characteristics-variable two-input/output filter in d-module-designs, realizations, and equivalence. IEEE Trans. Ind. Appl. 2002, 38, 1290–1296. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chakraborty, C. A shunt active power filter with enhanced performance using ann-based predictive and adaptive controllers. IEEE Trans. Ind. Electron. 2011, 58, 421–428. [Google Scholar] [CrossRef]
- Tey, L.H.; So, P.L.; Chu, Y.C. Improvement of power quality using adaptive shunt active filter. IEEE Trans. Power Deliv. 2005, 20, 1558–1568. [Google Scholar] [CrossRef]
- Biricik, S.; Redif, S.; Özerdem, Ö.C.; Khadem, S.K.; Basu, M. Real-time control of shunt active power filter under distorted grid voltage and unbalanced load condition using self-tuning filter. IET Power Electron. 2014, 7, 1895–1905. [Google Scholar] [CrossRef]
- Zainuri, M.A.A.M.; Radzi, M.A.M.; Soh, A.C.; Mariun, N.; Rahim, N.A. Dc-link capacitor voltage control for single-phase shunt active power filter with step size error cancellation in self-charging algorithm. IET Power Electron. 2016, 9, 323–335. [Google Scholar] [CrossRef]
- Ng, C.H.; Busawon, K.; Putrus, G.A.; Ran, L. Fast-individual-harmonic-extraction technique. IEEE Proc. Gener. Transm. Distrib. 2005, 152, 556–562. [Google Scholar] [CrossRef] [Green Version]







| Synchronization Technique | Single Phase | Three Phase | Non-Ideal Grid | Strengths | Weaknesses |
|---|---|---|---|---|---|
| ZCD | Yes | Yes | No | Simplest control structure [9]. | Require hardware circuit [51]. Sensitive to noise [9]. Poor dynamic response [69]. Poor performance when grid is subjected to harmonics [67]. |
| SRF-PLL | Yes | Yes | No | Easy to implement [10]. Accurate synchronization under ideal grid conditions [10,54]. Most widely applied techniques [54]. | PI controller needs to properly be tuned [35,84]. Unable to cope with distorted and unbalanced grid conditions [10,53,54]. |
| STF-PLL | Yes | Yes | Yes | Suitable for highly distorted and unbalanced grid conditions [55]. | PI controller needs to properly be tuned [35,84]. Gain parameter of STF needs to carefully be selected [59,76]. Integration of STF increases control complexity [55]. |
| DDSRF-PLL | No | Yes | Yes | Suitable for highly distorted and unbalanced grid conditions [53]. | PI controller needs to properly be tuned [35,84]. Additional SRF loops increases computational burden [53]. |
| ADALINE | Yes | Yes | No | Low computational burden [58]. Can be applied for harmonic extraction purposes [58]. | Learning rate needs to be properly tuned [30,58,81]. Unable to cope with distorted and unbalanced grid conditions [58]. |
| Fundamental Component Extraction | No | Yes | Yes | Easy to implement [59,60]. Effective for highly distorted and unbalanced grid conditions [59,60] Can be applied for harmonic extraction purposes [59,60]. | Gain parameter of STF needs to carefully be selected [59,76]. |
| Unit Vector Generation | No | Yes | No | Simple control structure [61,62]. | LPF needs to properly be tuned [85]. LPF imposes additional delay [61,62]. Unable to cope with distortion and unbalanced grid conditions [61,62]. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoon, Y.; Mohd Radzi, M.A.; Mohd Zainuri, M.A.A.; Zawawi, M.A.M. Shunt Active Power Filter: A Review on Phase Synchronization Control Techniques. Electronics 2019, 8, 791. https://doi.org/10.3390/electronics8070791
Hoon Y, Mohd Radzi MA, Mohd Zainuri MAA, Zawawi MAM. Shunt Active Power Filter: A Review on Phase Synchronization Control Techniques. Electronics. 2019; 8(7):791. https://doi.org/10.3390/electronics8070791
Chicago/Turabian StyleHoon, Yap, Mohd Amran Mohd Radzi, Muhammad Ammirrul Atiqi Mohd Zainuri, and Mohamad Adzhar Md Zawawi. 2019. "Shunt Active Power Filter: A Review on Phase Synchronization Control Techniques" Electronics 8, no. 7: 791. https://doi.org/10.3390/electronics8070791
APA StyleHoon, Y., Mohd Radzi, M. A., Mohd Zainuri, M. A. A., & Zawawi, M. A. M. (2019). Shunt Active Power Filter: A Review on Phase Synchronization Control Techniques. Electronics, 8(7), 791. https://doi.org/10.3390/electronics8070791