Analysis of the Critical Bits of a RISC-V Processor Implemented in an SRAM-Based FPGA for Space Applications
Abstract
:1. Introduction
2. Configuration Memory Errors in SRAM-Based FPGAs
2.1. FPGA Error Model
- Open fault: The affected bit interrupts a path creating an unconnected signal.
- Conflict fault: Two signals are connected together creating a short-circuit and, therefore, an undefined output value.
- Antenna fault: The input path is connected to a floating line segment, thus delivering an unknown value to the output.
- Bridge fault: The selection bit of a multiplexer is affected by the SEU connecting a wrong input with the output.
2.2. Characterization of Designs and Fault Tolerance Verification
3. Proposed Analysis
- The unprotected design is characterized. We implement the unprotected design (RISC-V in this case), and, using the ACME tool [15], together with the Xilinx SEM IP Controller [16], we perform an injection campaign in the essential bits of the configuration memory while running some benchmarks (see Section 4 for more details). After each injection, the behavior of the design is observed and compared with the golden outcome (the result that should be produced in the absence of error). With this, we obtain how many bit flips have actually produced a failure and how many have not. The purpose of this is to use the unprotected design to “calibrate” the critical vs. essential bit ratio, assuming that, for an unprotected design, nearly 100% of the critical bits should produce an issue.
- Then, the protected design needs to be characterized. In this work, we have protected a Rocket RISC-V processor with distributed triple modular redundancy (DTMR) for the sake of simplicity, but any other technique can be used. Using the ACME tool, together with the SEM IP, an error injection campaign is performed in all the essential bits, and, again, the number of errors and no errors at the output are logged. The number of errors divided by the total number of injections would give the probability of error of the technique. However, as mentioned above, many of the injections are performed on non-critical bits that would not produce any error whatsoever. That is why the probability of error needs to be normalized, using the critical vs. essential bit ratio calculated in the previous step.
- Now, the number of critical bits of the DTMR-protected design () is normalized as the number of essential bits that are provided by the design tool (), multiplied by the fraction obtained in the first step (percentage of critical bits () within the total number of essential bits ()). That number of critical bits is what we consider a figure of merit of the cross-section of the protected circuit and is presented in Equation (1).In this same way, the probability of error (P) can be also normalized () by dividing this value (calculated in Step 2) by the critical vs. essential bit ratio calculated in Step 1 (the lower the result, the more reliability the protected design offers) as shown in Equation (2).
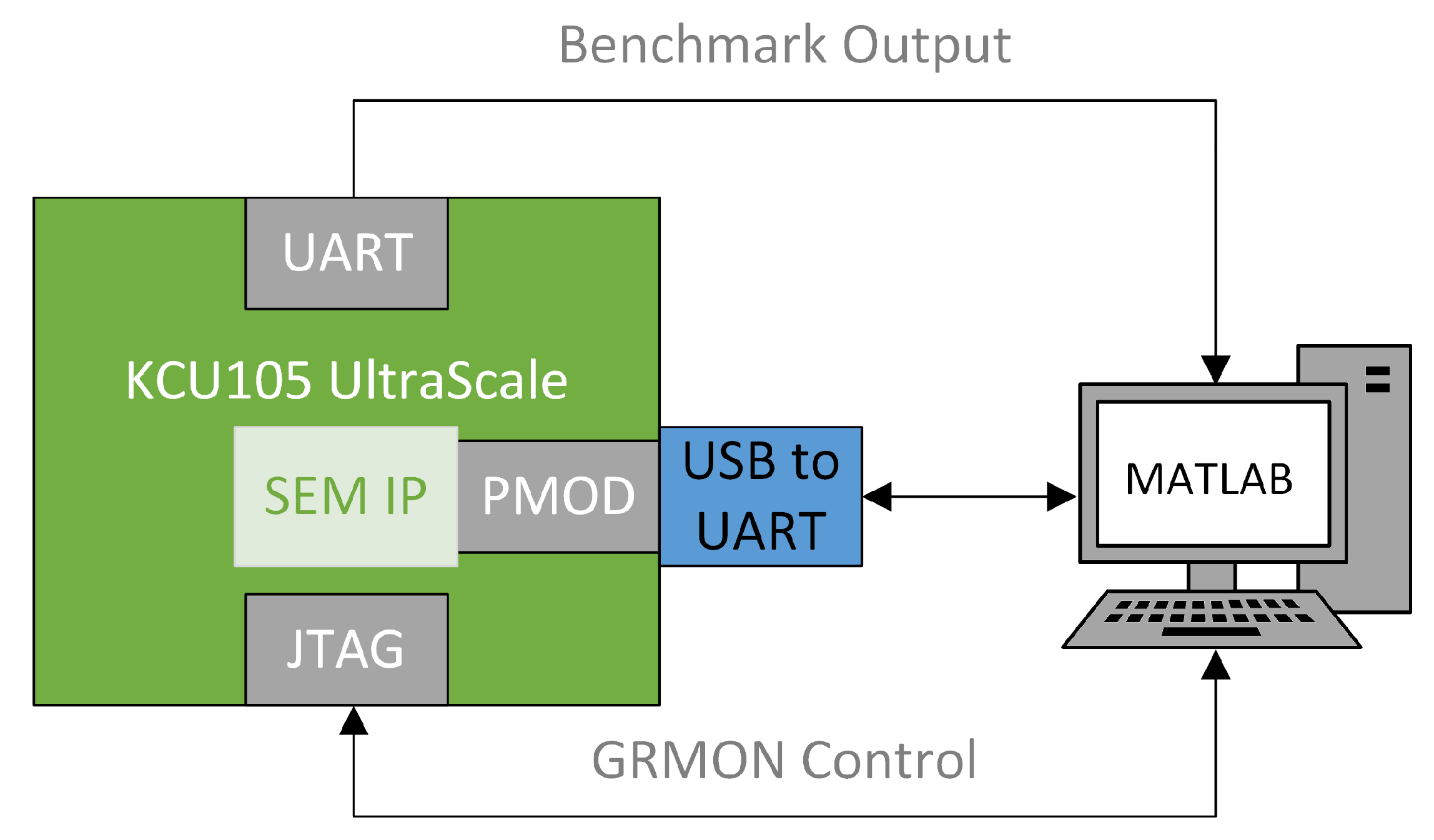
4. Experimental Set-Up
- Dhrystone: A widely used integer benchmark that does not contain any floating point operation
- Systest: An integer benchmark that checks the status of the processor with different tests
- Whetstone: The floating point counterpart of the Dhrystone benchmark that is used to measure the floating point arithmetic performance of a processor
- Linpack: A floating point benchmark that performs several linear algebra operations
- The DUT is programmed in the FPGA of the KCU105 board together with the SEM IP tool.
- A golden simulation is performed where one of the four selected benchmarks is executed in the DUT in the absence of errors to obtain the correct outcome of the benchmark. The golden outcome of the benchmark is stored for later comparisons.
- A command is sent to the SEM IP to inject a bit-flip at a random configuration memory frame.
- A reset signal is sent to the DUT to initialize its internal state.
- The selected benchmark is loaded in the DUT and then executed by using GRMON.
- The outcome of the DUT is received and logged in a text file.
- A command is sent to the SEM IP to correct the injected error.
- Steps 3–7 are repeated until all the configuration memory errors have been injected.
- No error: The outcome of the benchmark matches the golden outcome.
- Error: The outcome of the benchmark does not match the golden outcome.
- Hang: There is no outcome of the benchmark or the execution of the benchmark never ends, receiving continuous garbage information for a long period of time. This case is detected during Step 6 and it is logged in the text file as “hang”. To classify an error as “hang”, the execution time of each benchmark is previously measured in the absence of errors and a proper timeout is implemented in the MATLAB code depending on the current executed benchmark.
5. Experimental Results
5.1. Characterization of the Unprotected Design
5.2. Characterization of the Protected Design
5.3. Critical Bits Calculation
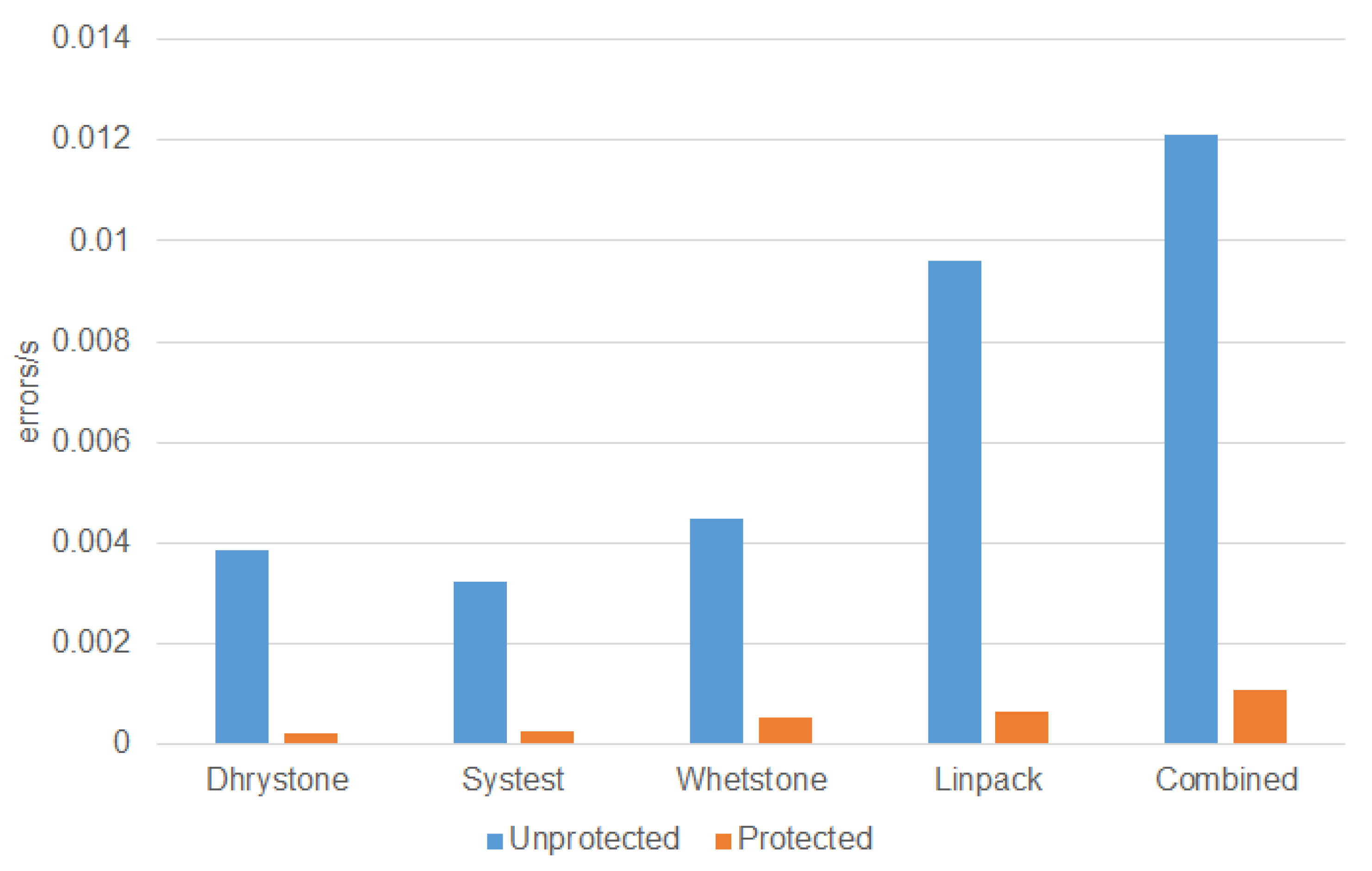
5.4. Application Example: Error Rate Calculation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Howard, J.W.; Hardage, D.M. Spacecraft Environments Interactions: Space Radiation and Its Effects on Electronic Systems; Tech. Report. TP-1999-209373; NASA: Washington, DC, USA, 1999. [Google Scholar]
- Oldham, T.R.; McLean, F.B. Total ionizing dose effects in MOS oxides and devices. IEEE Trans. Nucl. Sci. 2003, 50, 483–499. [Google Scholar] [CrossRef] [Green Version]
- Karnik, T.; Hazucha, P.; Patel, J. Characterization of soft errors caused by single event upsets in CMOS processes. IEEE Trans. Dependable Secur. Comput. 2004, 1, 128–143. [Google Scholar] [CrossRef] [Green Version]
- Lacoe, R.C.; Osborn, J.V.; Roga, R.; Brown, S.; Mayer, D.C. Application of hardness-by-design methodology to radiation-tolerant ASIC technologies. IEEE Trans. Nucl. Sci. 2000, 47, 2334–2341. [Google Scholar] [CrossRef]
- Asadi, H.; Tahoori, M.B. Soft error modeling and remediation techniques in ASIC designs. Microelectron. J. 2010, 41, 506–522. [Google Scholar] [CrossRef]
- Herrera-Alzu, I.; Lopez-Vallejo, M. Design techniques for Xilinx Virtex FPGA configuration memory scrubbers. IEEE Trans. Nucl. Sci. 2013, 60, 376–385. [Google Scholar] [CrossRef] [Green Version]
- Asanović, K.; Avizienis, R.; Bachrach, J.; Beamer, S.; Biancolin, D.; Celio, C.; Cook, H.; Dabbelt, D.; Hauser, J.; Izraelevitz, A.; et al. The Rocket Chip Generator; University of California, Berkeley, Tech. Report. UCB/EECS-2016-17; EECS Department: North York, ON, Canada, 2016. [Google Scholar]
- Entrena, L.; Garcia-Valderas, M.; Fernandez-Cardenal, R.; Lindoso, A.; Portela, M.; Lopez-Ongil, C. Soft error sensitivity evaluation of microprocessors by multilevel emulation-based fault injection. IEEE Trans. Comput. 2010, 61, 313–322. [Google Scholar] [CrossRef]
- Wissel, L.; Pheasant, S.; Loughran, R.; LeBlanc, C.; Klaasen, B. Managing soft errors in ASICs. In Proceedings of the IEEE 2002 Custom Integrated Circuits Conference, Orlando, FL, USA, 15 May 2002; pp. 85–88. [Google Scholar]
- Alderighi, M.; Casini, F.; D’Angelo, S.; Gravina, A.; Liberali, V.; Mancini, M.; Musazzi, P.; Pastore, S.; Sassi, M.; Sorrenti, G. A preliminary study about SEU effects on programmable interconnections of SRAM-based FPGAs. J. Electron. Test. 2013, 29, 341–350. [Google Scholar] [CrossRef]
- SymbiFlow Team. Project X-ray Documentation. Release 0.0-2853-g55ef667. Available online: https://readthedocs.org/projects/prjxray/downloads/pdf/latest/ (accessed on 8 January 2019).
- Alderighi, M.; Casini, F.; D’Angelo, S.; Pastore, S.; Sechi, G.R.; Weigand, R. Evaluation of single event upset mitigation schemes for SRAM based FPGAs using the flipper fault injection platform. In Proceedings of the 20th IEEE International Symposium on Defect and Fault-Tolerance in VLSI Systems (DFT 2007), Rome, Italy, 26–28 September 2007; pp. 105–113. [Google Scholar]
- Mogollon, J.M.; Guzman-Miranda, H.; Napoles, J.; Barrientos, J.; Aguirre, M.A. FTUNSHADES2: A novel platform for early evaluation of robustness against SEE. In Proceedings of the 12th European Conference on Radiation and Its Effects on Components and Systems, Sevilla, Spain, 19–23 September 2011; pp. 169–174. [Google Scholar]
- Le, R. Soft Error Mitigation Using Prioritized Essential Bits; Xilinx: San Jose, CA, USA, 2012. [Google Scholar]
- Aranda, L.A.; Sánchez-Macián, A.; Maestro, J.A. ACME: A tool to improve configuration memory fault injection in SRAM-Based FPGAs. IEEE Access 2019, 7, 128153–128161. [Google Scholar] [CrossRef]
- Xilinx. Soft Error Mitigation Controller; LogiCORE IP Product Guide (PG036). Available online: https://www.xilinx.com/support/documentation/ip_documentation/sem/v4_1/pg036_sem.pdf (accessed on 7 November 2019).
- Xilinx. KCU105 Board User Guide (UG917). Available online: https://www.xilinx.com/support/documentation/boards_and_kits/kcu105/ug917-kcu105-eval-bd.pdf (accessed on 7 November 2019).
- Digilent. PmodUSBUART Reference Manual. Available online: https://reference.digilentinc.com/_media/reference/pmod/pmod-interface-specification-1_2_0.pdf (accessed on 7 November 2019).
- Cobham Gaisler AB. GRMON3 User’s Manual. Available online: https://www.gaisler.com/doc/grmon3.pdf (accessed on 7 November 2019).
- Cochran, W.G. Sampling Techniques, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Tan, Y.C.; Chandrasekara, R.; Cheng, C.; Ling, A. Silicon Avalanche Photodiode Operation and Lifetime Analysis for Small Satellites. Opt. Express 2013, 21, 16946–16954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, D.S.; Allen, G.R.; Swift, G.; Cannon, M.; Wirthlin, M.; George, J.S.; Koga, R.; Huey, K. Single-Event Characterization of the 20 nm Xilinx Kintex UltraScale Field-Programmable Gate Array under Heavy Ion Irradiation. In Proceedings of the 2015 IEEE Radiation Effects Data Workshop (REDW), Boston, MA, USA, 13–17 July 2015; pp. 1–6. [Google Scholar]
| Dhrystone | Systest | Whetstone | Linpack | Combined | |
|---|---|---|---|---|---|
| No errors | 26,162 (96.90%) | 26,297 (97.40%) | 26,025 (96.39%) | 24,921 (92.30%) | 24,385 (90.31%) |
| Errors | 329 (1.22%) | 220 (0.81%) | 494 (1.83%) | 1213 (4.49%) | 1630 (6.03%) |
| Hangs | 509 (1.88%) | 483 (1.79%) | 481 (1.78%) | 866 (3.21%) | 985 (3.65%) |
| Total injections | 27,000 (100%) | 27,000 (100%) | 27,000 (100%) | 27,000 (100%) | 27,000 (100%) |
| Dhrystone | Systest | Whetstone | Linpack | Combined |
|---|---|---|---|---|
| 3.10% | 2.60% | 3.61% | 7.70% | 9.68% |
| Dhrystone | Systest | Whetstone | Linpack | Combined | |
|---|---|---|---|---|---|
| Execution time | 7.5 | 7.2 | 12 | 15.4 | 42 |
| Dhrystone | Systest | Whetstone | Linpack | Combined | |
|---|---|---|---|---|---|
| No errors | 26,986 (99.95%) | 26,984 (99.94%) | 26,968 (99.88%) | 26,960 (99.85%) | 26,960 (99.75%) |
| Errors | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) |
| Hangs | 14 (0.05%) | 16 (0.06%) | 32 (0.12%) | 40 (0.15%) | 67 (0.25%) |
| Total injections | 27,000 (100%) | 27,000 (100%) | 27,000 (100%) | 27,000 (100%) | 27,000 (100%) |
| Dhrystone | Systest | Whetstone | Linpack | Combined | |
|---|---|---|---|---|---|
| 3.10% | 2.60% | 3.61% | 7.70% | 9.68% | |
| 0.05% | 0.06% | 0.12% | 0.15% | 0.25% |
| Dhrystone | Systest | Whetstone | Linpack | Combined | |
|---|---|---|---|---|---|
| 100% | 100% | 100% | 100% | 100% | |
| 1.61% | 2.31% | 3.32% | 1.95% | 2.58% |
| Dhrystone | Systest | Whetstone | Linpack | Combined | |
|---|---|---|---|---|---|
| 206,629 | 173,302 | 240,623 | 513,240 | 645,216 | |
| 714,407 | 599,180 | 831,938 | 1,774,495 | 2,230,793 |
| Dhrystone | Systest | Whetstone | Linpack | Combined | |
|---|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aranda, L.A.; Wessman, N.-J.; Santos, L.; Sánchez-Macián, A.; Andersson, J.; Weigand, R.; Maestro, J.A. Analysis of the Critical Bits of a RISC-V Processor Implemented in an SRAM-Based FPGA for Space Applications. Electronics 2020, 9, 175. https://doi.org/10.3390/electronics9010175
Aranda LA, Wessman N-J, Santos L, Sánchez-Macián A, Andersson J, Weigand R, Maestro JA. Analysis of the Critical Bits of a RISC-V Processor Implemented in an SRAM-Based FPGA for Space Applications. Electronics. 2020; 9(1):175. https://doi.org/10.3390/electronics9010175
Chicago/Turabian StyleAranda, Luis Alberto, Nils-Johan Wessman, Lucana Santos, Alfonso Sánchez-Macián, Jan Andersson, Roland Weigand, and Juan Antonio Maestro. 2020. "Analysis of the Critical Bits of a RISC-V Processor Implemented in an SRAM-Based FPGA for Space Applications" Electronics 9, no. 1: 175. https://doi.org/10.3390/electronics9010175
APA StyleAranda, L. A., Wessman, N.-J., Santos, L., Sánchez-Macián, A., Andersson, J., Weigand, R., & Maestro, J. A. (2020). Analysis of the Critical Bits of a RISC-V Processor Implemented in an SRAM-Based FPGA for Space Applications. Electronics, 9(1), 175. https://doi.org/10.3390/electronics9010175





