A Power-Efficient Pipelined ADC with an Inherent Linear 1-Bit Flip-Around DAC
Abstract
:1. Introduction
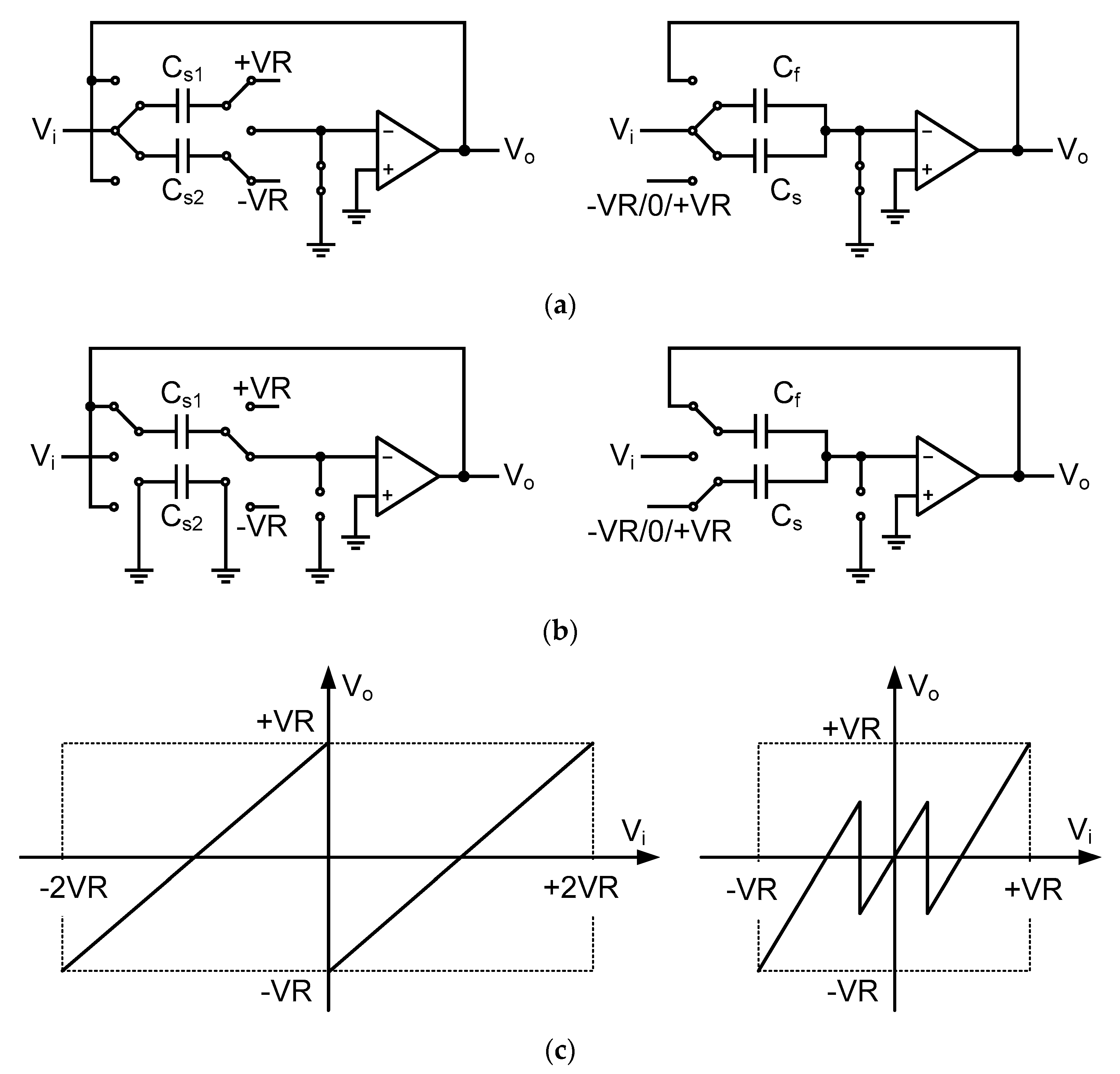
2. Front-end Unity-Gain 1-Bit FADAC
2.1. Unity-Gain 1-Bit FADAC
2.2. Noise Performance Analysis and Compaison
2.3. Digital Foreground Calibration
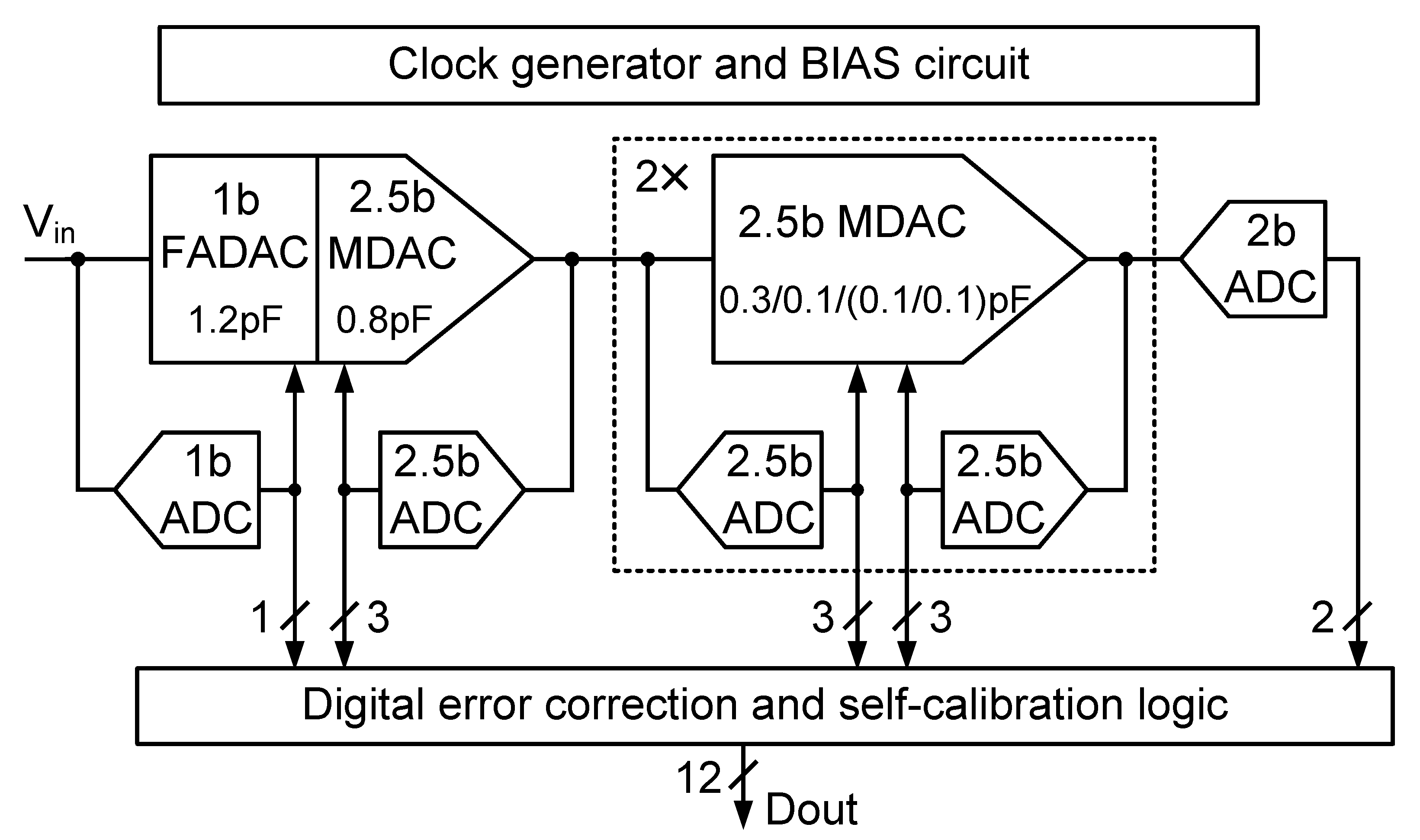
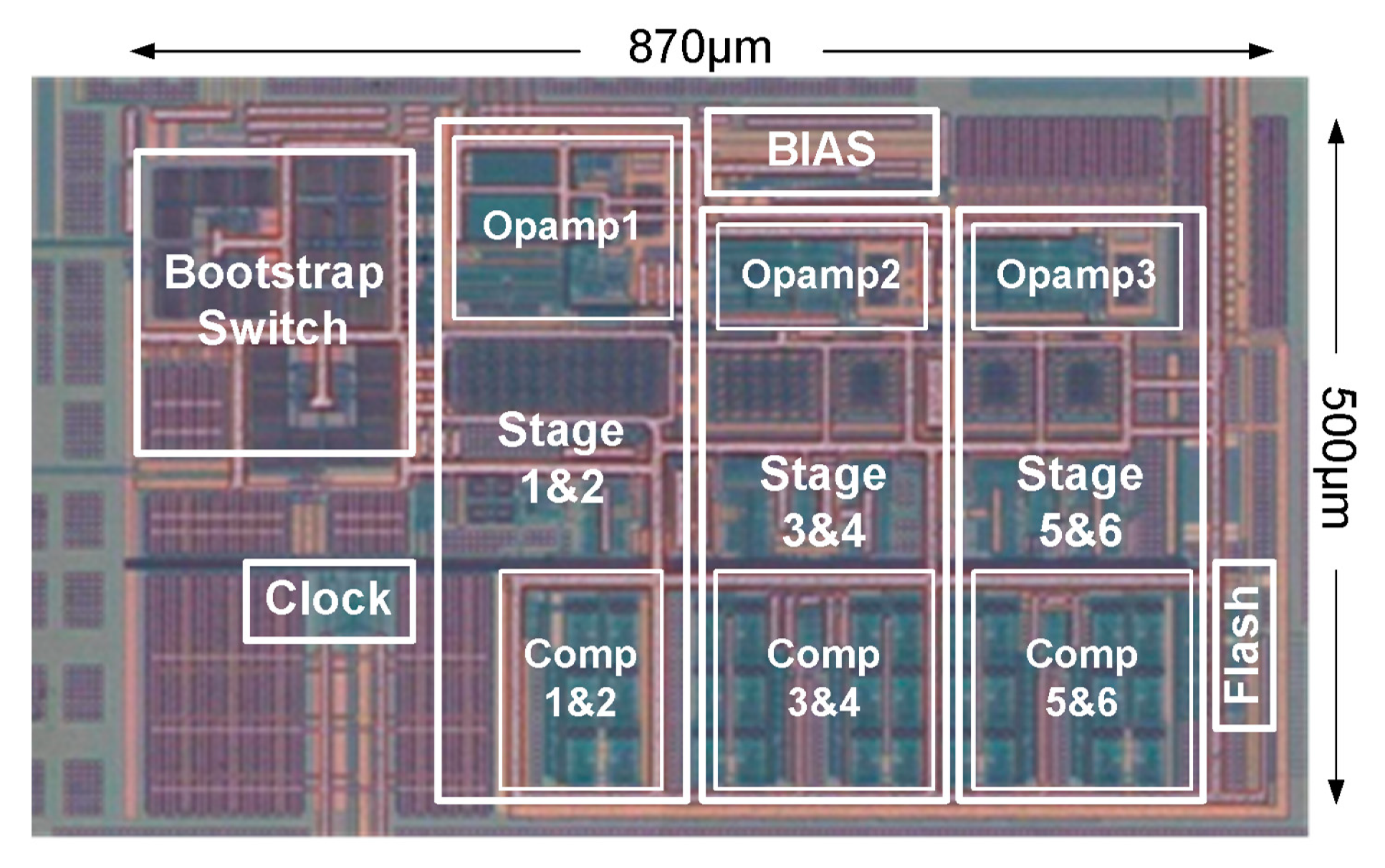
3. Prototype ADC Design
3.1. ADC Architecture
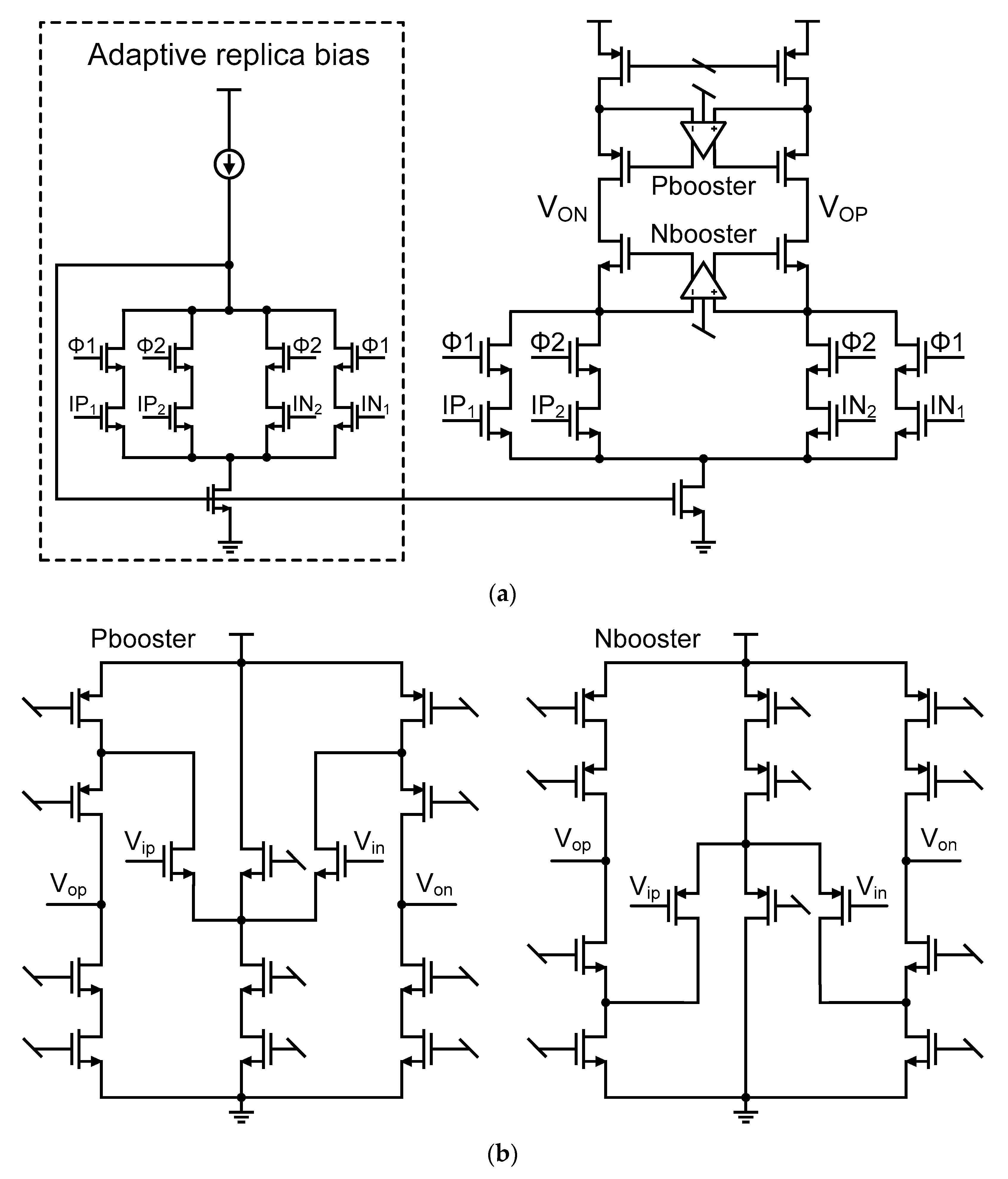
3.2. OPAMP Design
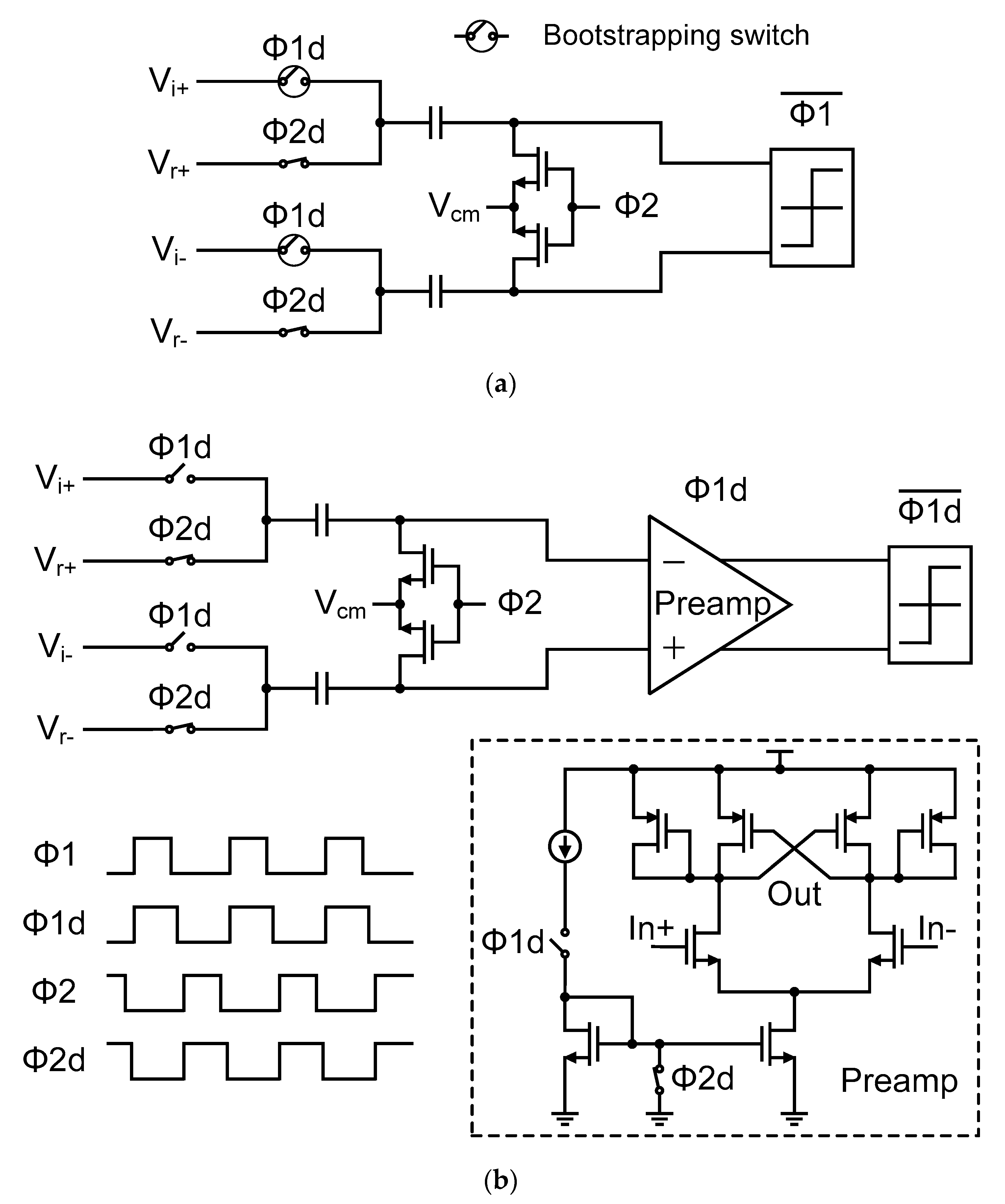
3.3. Comparator Design
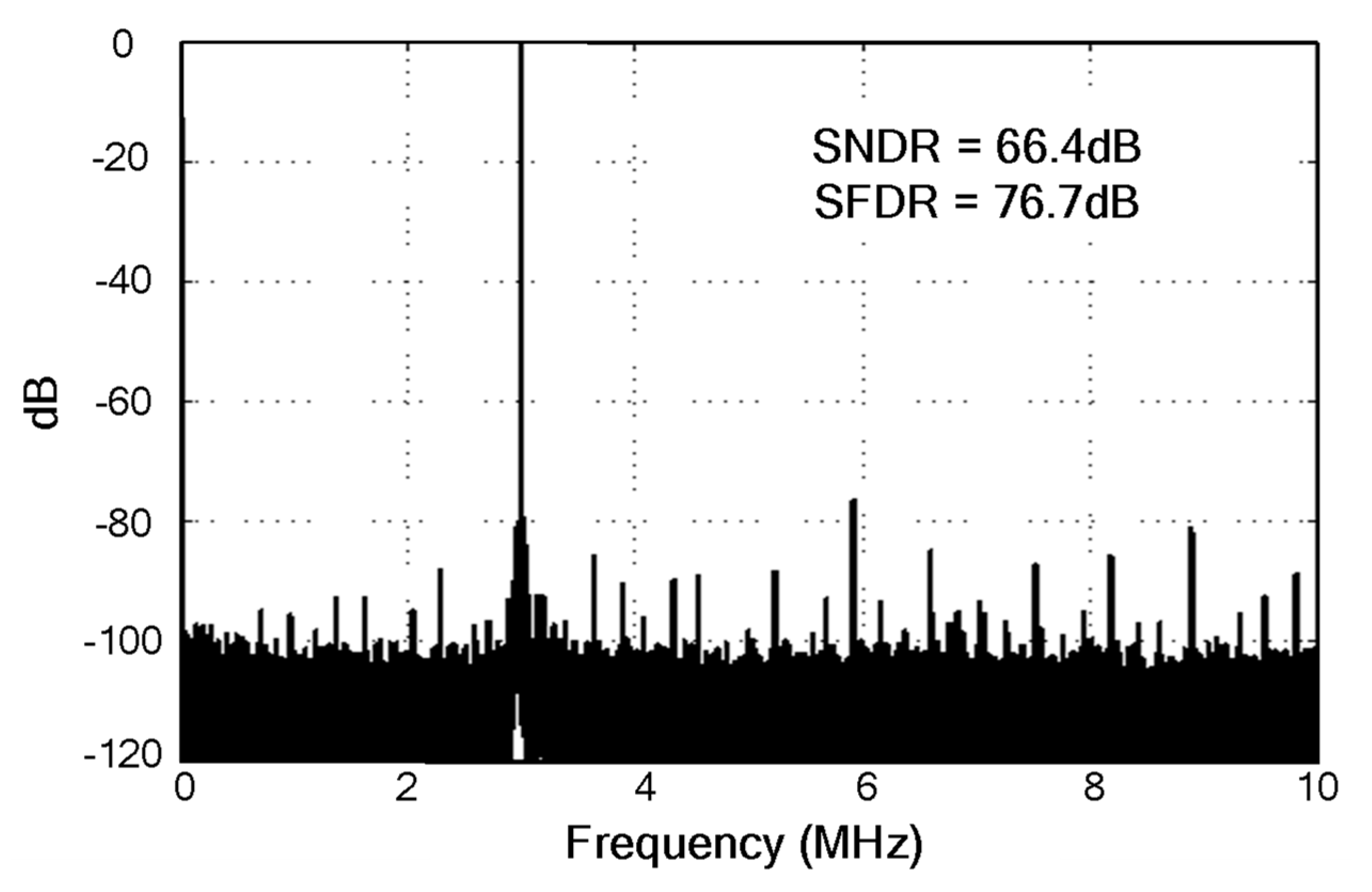
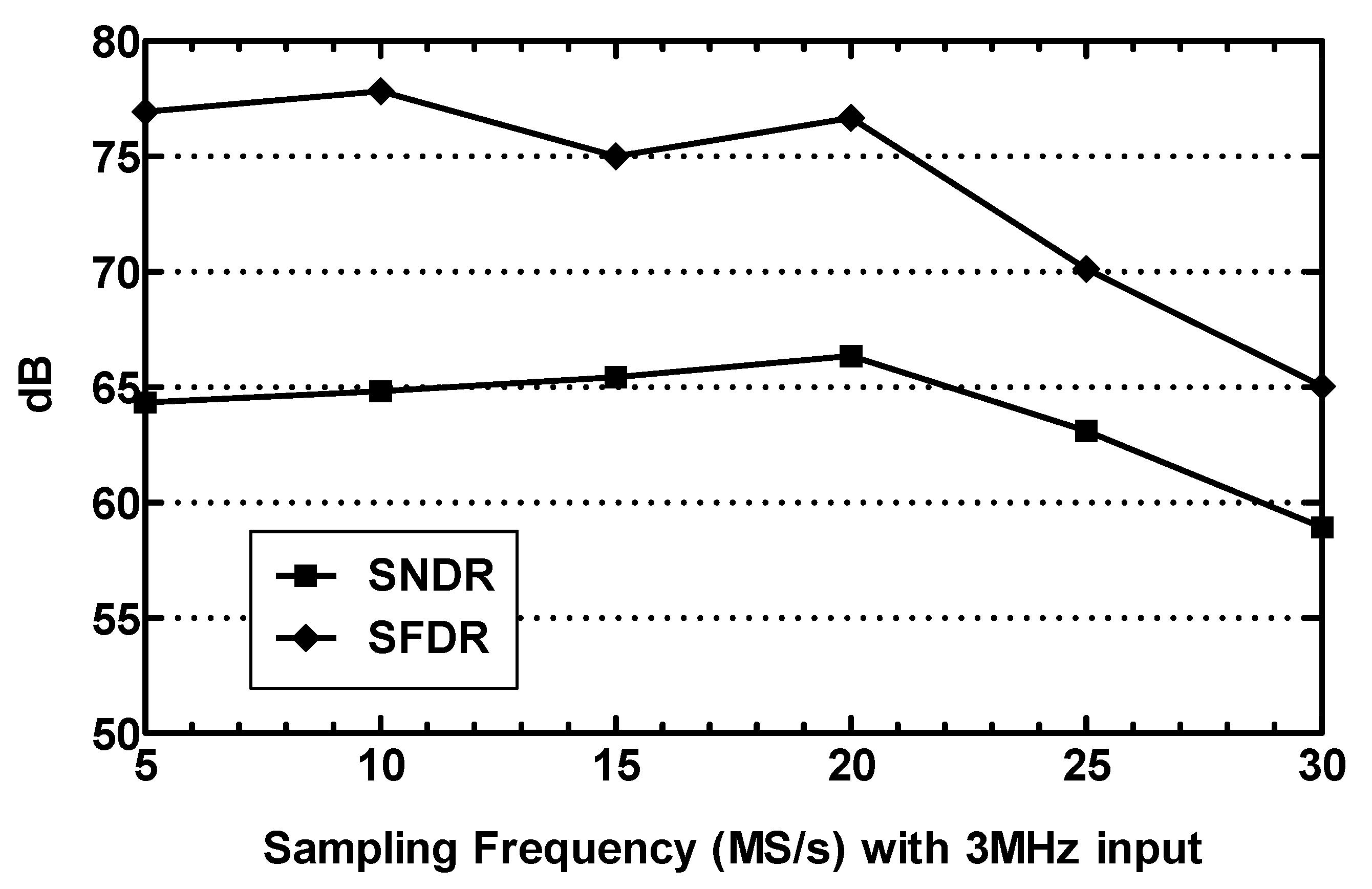
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lagos, J.; Hershberg, B.; Martens, E.; Wambacq, P.; Craninckx, J. Asingle-channel 600Msps 12bit ringamp-based pipelined ADC in 28nm CMOS. In Proceedings of the 2017 Symposium on VLSI Circuits, Kyoto, Japan, 5–8 June 2017; pp. C96–C97. [Google Scholar]
- Boo, H.H.; Boning, D.S.; Lee, H.S. A 12b 250MS/s pipelined ADC with virtual ground reference buffers. In Proceedings of the 2015 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 22–26 February 2015; pp. 282–284. [Google Scholar]
- El-Chammas, M.; Li, X.; Kimura, S.; Coulon, J.; Hu, J.; Smith, D.; Landman, P.; Weaver, M. 90dB-SFDR 14b 500MS/S BiCMOS switched-current pipelined ADC. In Proceedings of the 2015 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 22–26 February 2015; pp. 286–288. [Google Scholar]
- Dolev, N.; Kramer, M.; Murmann, B. A12-Bit,200-MS/s,11.5-mW pipeline ADC using a pulsed bucket brigade front-end. In Proceedings of the 2013 Symposium on VLSI Circuits, Kyoto, Japan, 12–14 June 2013; pp. C98–C99. [Google Scholar]
- Oh, T.; Venkatram, H.; Moon, U.K. A70MS/s69.3dBSNDR38.2fJ/conversion-step time-based pipelined ADC. In Proceedings of the 2013 Symposium on VLSI Circuits, Kyoto, Japan, 12–14 June 2013; pp. C96–C97. [Google Scholar]
- Mohammad, T.S.; Hamoui, A.A. A reconfigurable and power-scalable10–12 bit0.4–44MS/s pipelined ADC with0.35–0.5pJ/Stepin1.2V90nm digital CMOS. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 74–83. [Google Scholar]
- Yuan, J.; Fung, S.W.; Chan, K.Y.; Xu, R.Y. A12-bit20MS/s56.3mW pipelined ADC with interpolation-based nonlinear calibration. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 555–565. [Google Scholar] [CrossRef]
- Hershberg, B.P.; Weaver, S.T.; Moon, U.K. A 1.4V signal swing hybrid CLS-opamp/ZCBC pipelined ADC using a 300mV output swing opamp. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 7–11 February 2010; pp. 302–304. [Google Scholar]
- Ponce-Hinestroza, V.Y.; Castaneda-Camacho, J.; Gonzalez-Diaz, V.R.; Mino-Aguilar, G.; Garcia-Santigao, A. Pipelined A/D converter design for 5G OFDM communication systems. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–5. [Google Scholar]
- Huo, Y.; Dong, X.; Xu, W.; Yuen, M. Enabling multi-functional 5G and beyond user equipment: A survey and tutorial. IEEE Access 2019, 7, 116975–117008. [Google Scholar] [CrossRef]
- Chiu, Y.; Gray, P.R.; Nikolic, B. A 14-b 12-MS/s CMOS pipelined ADC with over 100-dB SFDR. IEEE J. Solid State Circuit 2005, 39, 2139–2151. [Google Scholar] [CrossRef]
- Zhou, Z.K.; Lin, M.; Huang, S.G.; Wang, R.Y.; Dong, Y.M. A 12 bit 120 MS/s SHA-less pipeline ADC with capacitor mismatch error calibration. IEICE Electron. Express 2018, 15, 1–12. [Google Scholar] [CrossRef]
- El-Chammas, M.; Li, X.; Kimura, S.; Coulon, J.; Hu, J.; Smith, D.; Landman, P.; Weaver, M. A 10b 125MS/s 40mW Pipelined ADC in 0.18µm CMOS. In Proceedings of the 2015 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 6–10 February 2005; pp. 282–283. [Google Scholar]
- Yang, C.Y.; Li, F.L.; Li, W.T.; Wang, X.; Wang, Z.H. An 85 mW 14-bit 150MS/s pipelined ADC with 71.3 dB peak SNDR in 130 nm CMOS. In Proceedings of the 2013 Asian Solid State Circuits Conference, Singapore, 11–13 November 2013; pp. 85–86. [Google Scholar]
- Huang, P.L.; Hsien, S.K.; Lu, V.; Wan, P.Y.; Lee, S.C.; Liu, W.B.; Chen, B.W.; Lee, Y.P.; Chen, W.T.; Yang, T.Y.; et al. SHA-Less pipelined ADC with in situ background clock-skew calibration. IEEE J. Solid State Circuits 2011, 46, 1893–1903. [Google Scholar] [CrossRef]
- Huang, P.L.; Hsien, S.K.; Lu, V.; Wan, P.Y.; Lee, S.C.; Liu, W.B.; Chen, B.W.; Lee, Y.P.; Chen, W.T.; Yang, T.Y.; et al. SHA-less pipelined ADC converting 10th Nyquist band with in-situ clock-skew calibration. In Proceedings of the 2011 Custom Integrated Circuits Conference, San Francisco, CA, USA, 19–22 September 2010; pp. 1–4. [Google Scholar]
- Yin, Y.; Wen, X.; Liao, Y.; Zhang, W.; Tang, Z.W. Switch-embedded opamp-sharing MDAC with dual-input OTA in pipelined ADC. IEEE Electron. Lett. 2010, 46, 831–832. [Google Scholar] [CrossRef] [Green Version]
- Peng, B.; Huang, G.Z.; Li, H.; Wan, P.Y.; Lin, P. A 48-mW, 12-bit, 150-MS/s pipelined ADC with digital calibration in 65 nm CMOS. In Proceedings of the 2011 Custom Integrated Circuits Conference, San Francisco, CA, USA, 19–21 October 2011; pp. 1–4. [Google Scholar]
- Karanicolas, A.N.; Lee, H.; Bacrania, K.L. A 15-b 1-Msample/s digitally self-calibrated pipeline ADC. IEEE J. Solid State Circuits 1993, 28, 1207–1215. [Google Scholar] [CrossRef] [Green Version]
- Zhong, J.Y.; Zhu, Y.; Chan, C.H.; Sin, S.W.; Seng-Pan, U.; Martins, R.P. A12b180MS/s0.068 mm2 with full-calibration-integrated pipelined-SARADC. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 1684–1695. [Google Scholar] [CrossRef]
- Huang, H.; Du, L.; Chiu, Y. A1.2-GS/s8-bit two-stepSARADCin65-nmCMOS with passive residue transfer. IEEE J. Solid State Circuits 2017, 52, 1551–1562. [Google Scholar] [CrossRef]
- Yang, W.; Kelly, D.; Mehr, L.; Sayuk, M.T.; Singer, L. A 3-V 340-mW 14-b 75-Msample/s CMOS ADC with 85-dB SFDR at Nyquist input. IEEE J. Solid State Circuits 2001, 36, 1931–1936. [Google Scholar] [CrossRef]
- Li, J.; Guo, X.; Luan, J.; Wu, D.; Zhou, L.; Huang, Y.; Wu, N.; Jia, H.; Zheng, X.; Wu, J.; et al. A 3G 12-bit four-channel time-interleaved pipelined ADC in 40 nm CMOS process. Electronics 2019, 8, 1551. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, I.; Johns, D.A. An 11-bit 45 MS/s pipelined ADC with rapid calibration of DAC errors in a multibit pipeline stage. IEEE J. Solid State Circuits 2008, 43, 1626–1637. [Google Scholar] [CrossRef] [Green Version]
- Sasidhar, N.; Kook, Y.J.; Takeuchi, S.; Hamashita, K.; Takasuka, K.; Hunumolu, P.K.; Moon, U.K. A 1.8V 36-mW 11-bit 80MS/s pipelined ADC using capacitor and opamp sharing. In Proceedings of the 2007 IEEE Asian Solid-State Circuits Conference, Jeju, Korea, 12–14 November 2007; pp. 241–243. [Google Scholar]
- Treichler, J.; Huang, Q.T. A 11.1-bit ENOB 50-MS/s pipelined A/D converter in 130-nm CMOS without S/H front end. In Proceedings of the 2010 IEEE European Solid-State Circuits Conference, Sevilla, Spain, 13–17 September 2010; pp. 374–377. [Google Scholar]



| Parameters | 1.5-Bit MDAC | 1-Bit FADAC |
|---|---|---|
| Resolved bit | 1 | 1 |
| Ideal feedback factor β | 0.5 | 1 |
| Opamp GBW requirement | 1 × | 0.5 × |
| Gain accuracy | ≈2 (Cs and Cf matching issue) | Perfect unity gain |
| Input full swing | 2 VR | 4 VR |
| SNR | / | ~3dB improved |
| Parameters | [6] | [7] | [8] | [14] | [18] | [24] | [25] | [26] | This Work |
|---|---|---|---|---|---|---|---|---|---|
| Architecture | Pipe. | Pipe. | Pipe. | Pipe. | Pipe. | Pipe. | Pipe. | Pipe. | Pipe. |
| Resolution (bit) | 12 | 11 | 12 | 14 | 12 | 11 | 11 | 14 | 12 |
| Sample rate (MS/s) | 44 | 20 | 20 | 150 | 150 | 45 | 80 | 50 | 20 |
| Max. DNL (LSB) | 0.9 | 0.27 | / | 0.8 | 0.3 | 0.45 | 1.3 | / | 0.72 |
| Max. INL (LSB) | 1.26 | 0.2 | / | 2.6 | 1.0 | 1.1 | 3.11 | / | 0.84 |
| Peak SNDR (dB) | 65.1 | 72.5 | 68.3 | 71.3 | 67 | 60.1 | 53.2 | 71.4 | 66.4 |
| Peak SFDR (dB) | 79 | 84.4 | 76.3 | 93.6 | 81 | 70 | 66.7 | 90.5 | 76.7 |
| Power (mW) | 22.9 | 56.3 | 17.2 | 85 | 48 | 81 | 38 | 109.5 | 5.2 |
| FoM1 1 @ low fin | / | 780 | 405 | 138 | 194 | 2179 | 1206 | 991 | 153 |
| FoM2 @ high fin | 350 | / | 528 | 188 | / | / | / | / | 254 |
| CMOS technology | 90 nm | 0.35 µm | 0.18 µm | 0.13 µm | 65 nm | 0.18 µm | 0.18 µm | 0.13 µm | 0.13 µm |
| Supply voltage (V) | 1.2 | 3.3 | 1.4 | 1.3 | 1.2 | 1.8 | 1.8 | 1.2 | 1.1 |
| Active area (mm2) | 1 | 20.64 | 1.11 | 1 | 0.78 | 3.57 | 2.16 | 3.43 | 0.44 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, P.; Su, L.; Zhang, H.; Chen, Z. A Power-Efficient Pipelined ADC with an Inherent Linear 1-Bit Flip-Around DAC. Electronics 2020, 9, 199. https://doi.org/10.3390/electronics9010199
Wan P, Su L, Zhang H, Chen Z. A Power-Efficient Pipelined ADC with an Inherent Linear 1-Bit Flip-Around DAC. Electronics. 2020; 9(1):199. https://doi.org/10.3390/electronics9010199
Chicago/Turabian StyleWan, Peiyuan, Limei Su, Hongda Zhang, and Zhijie Chen. 2020. "A Power-Efficient Pipelined ADC with an Inherent Linear 1-Bit Flip-Around DAC" Electronics 9, no. 1: 199. https://doi.org/10.3390/electronics9010199
APA StyleWan, P., Su, L., Zhang, H., & Chen, Z. (2020). A Power-Efficient Pipelined ADC with an Inherent Linear 1-Bit Flip-Around DAC. Electronics, 9(1), 199. https://doi.org/10.3390/electronics9010199




