A Design of a Dual-Band Bandpass Filter Based on Modal Analysis for Modern Communication Systems
Abstract
:1. Introduction
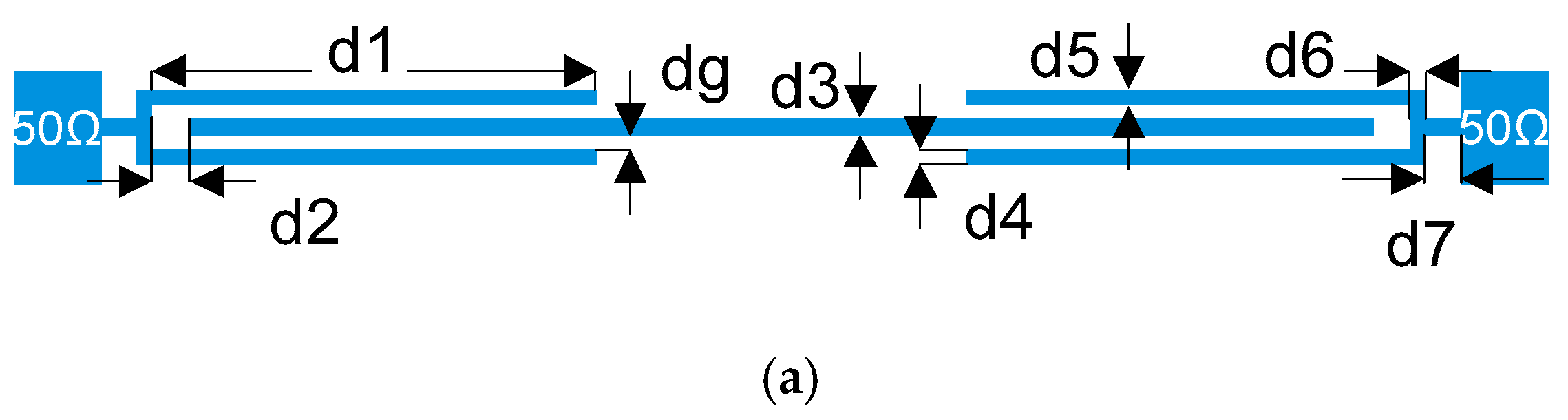
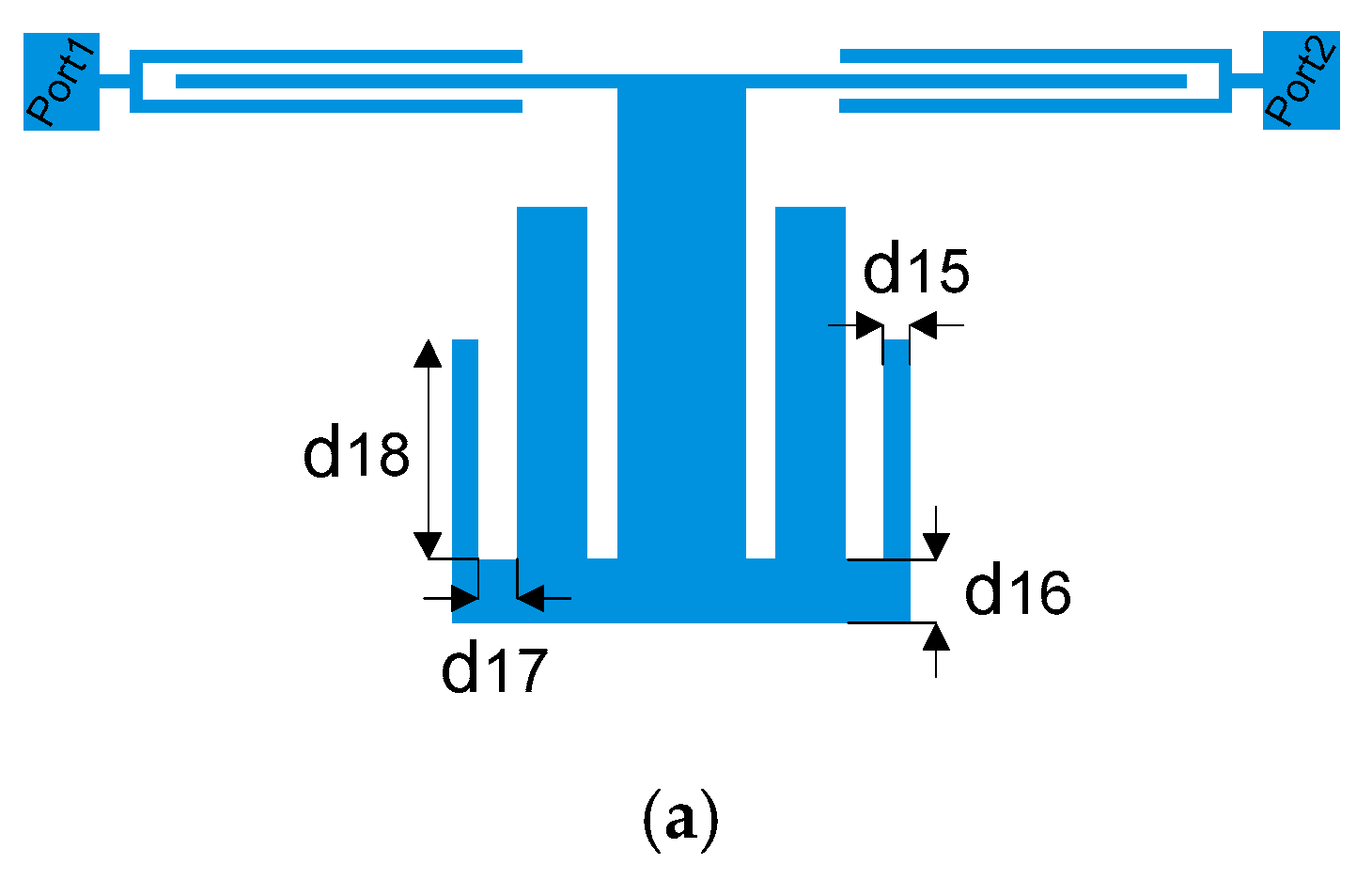
2. BPF Design
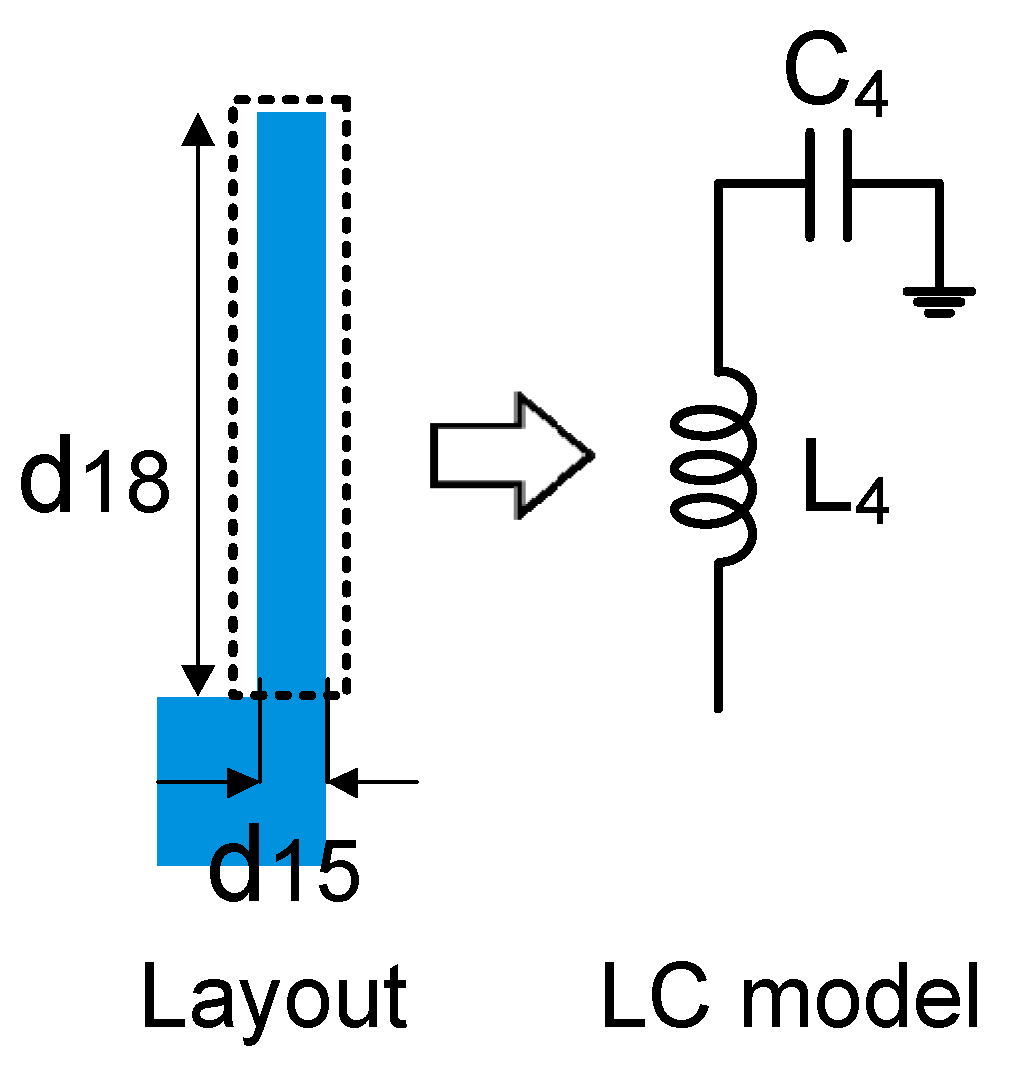
2.1. Coupling Structure
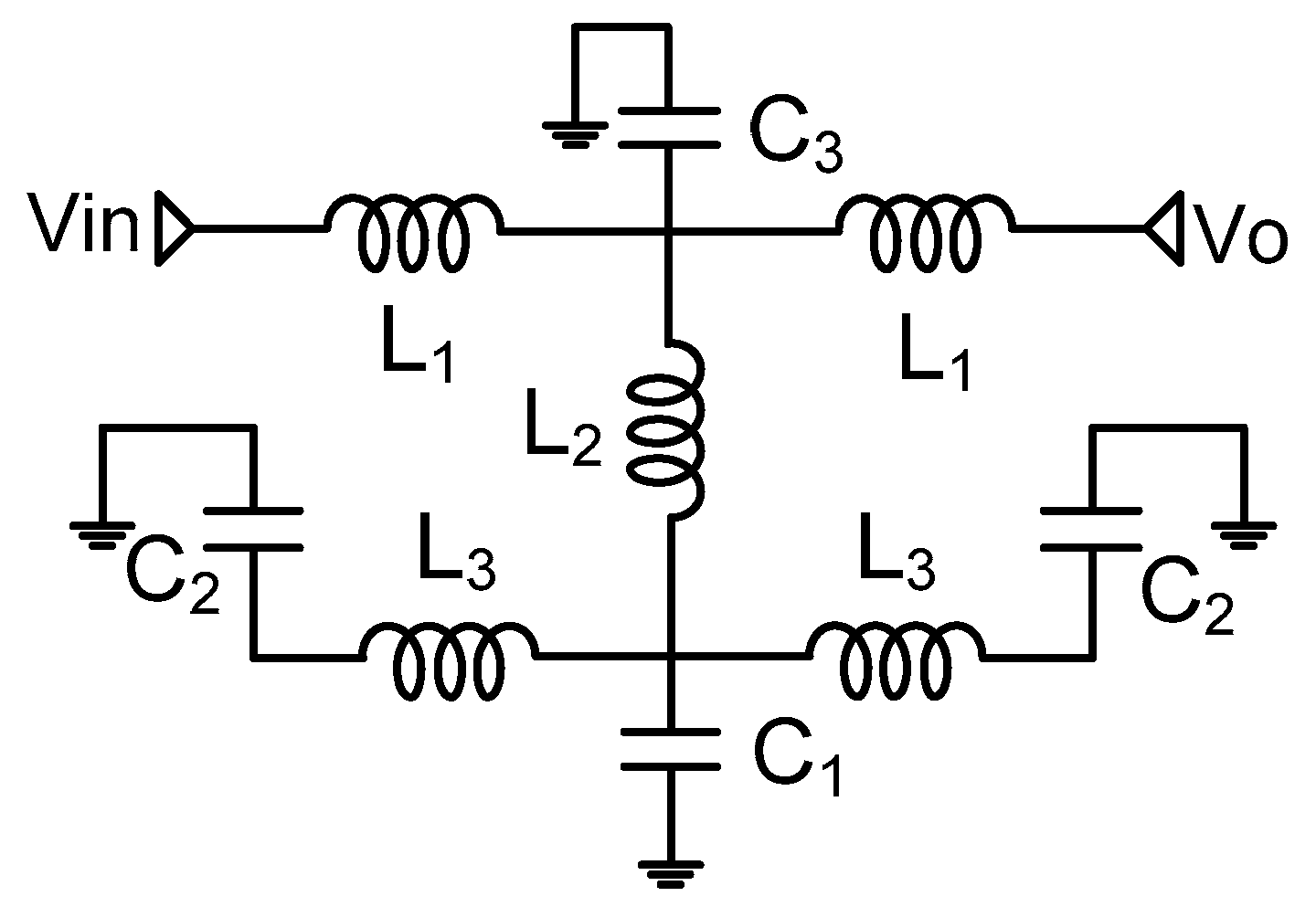
2.2. Single Wide-Band Response
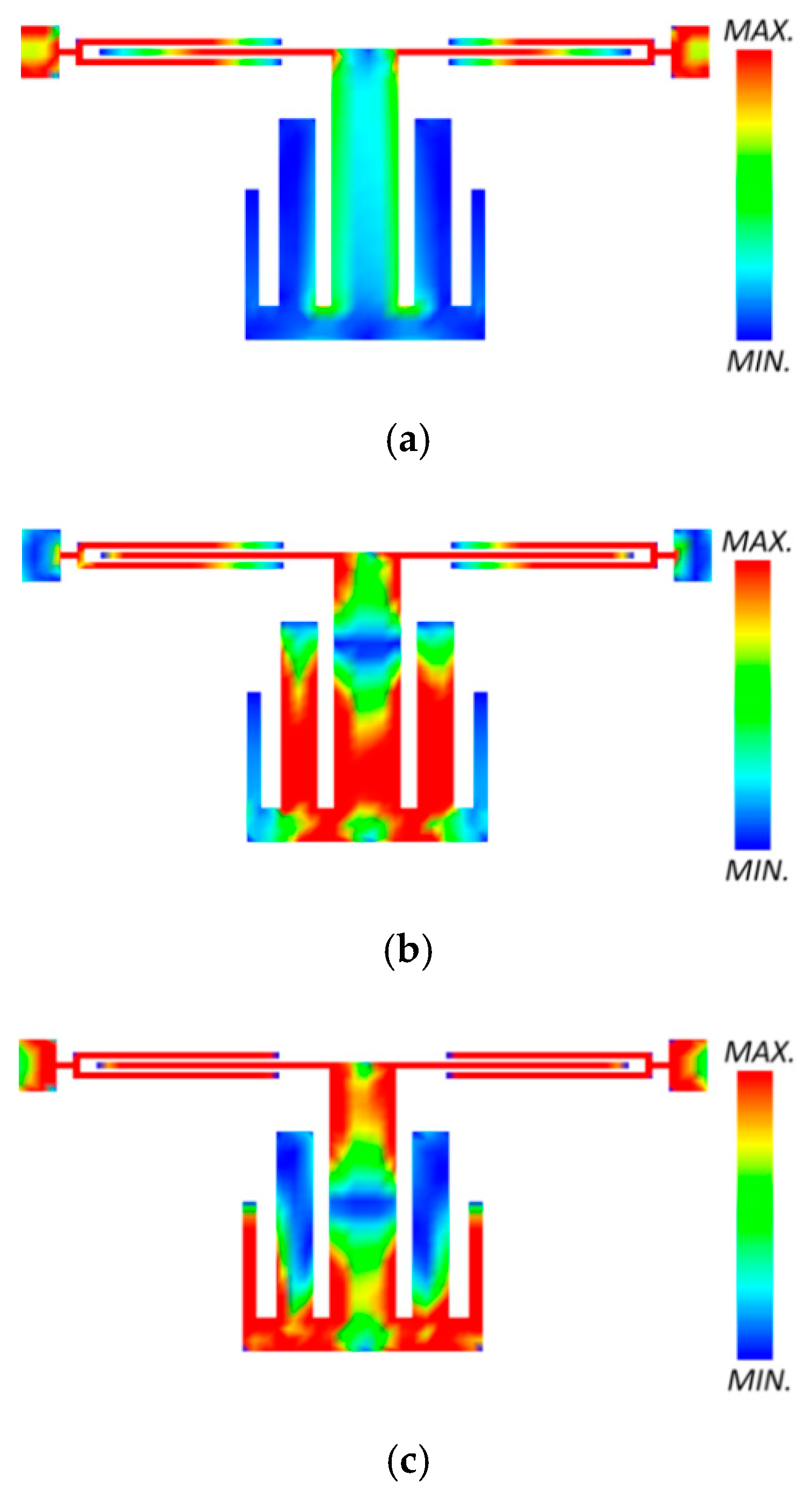
2.3. Current Distribution
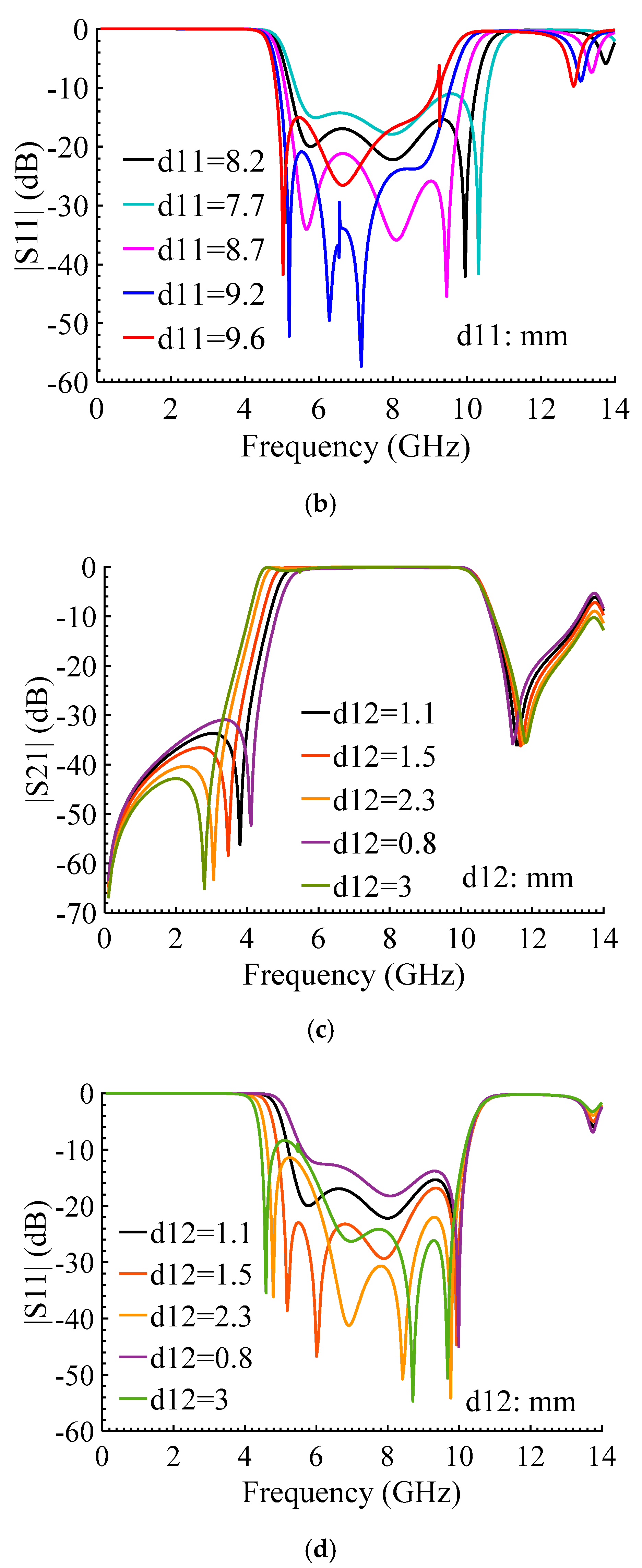
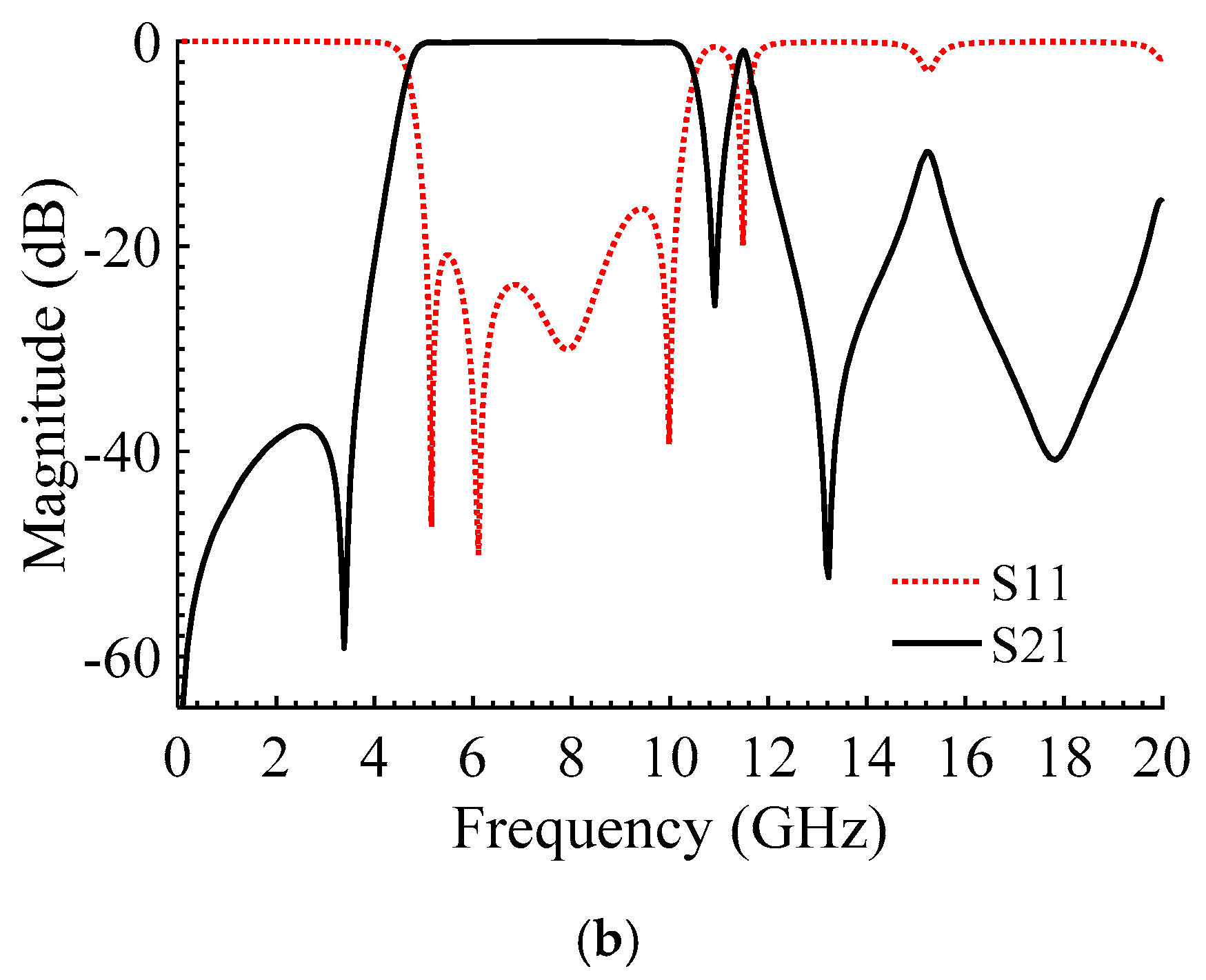
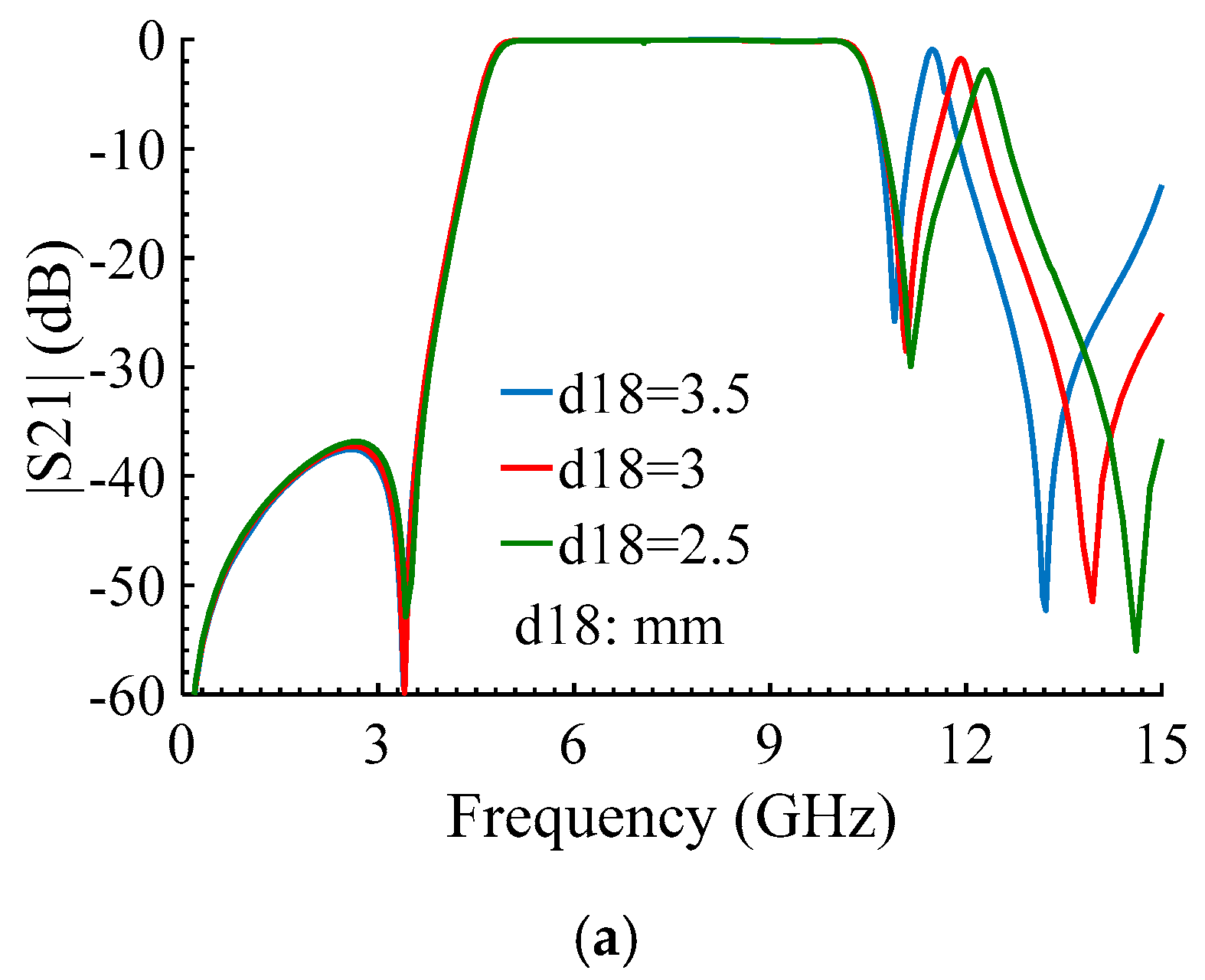
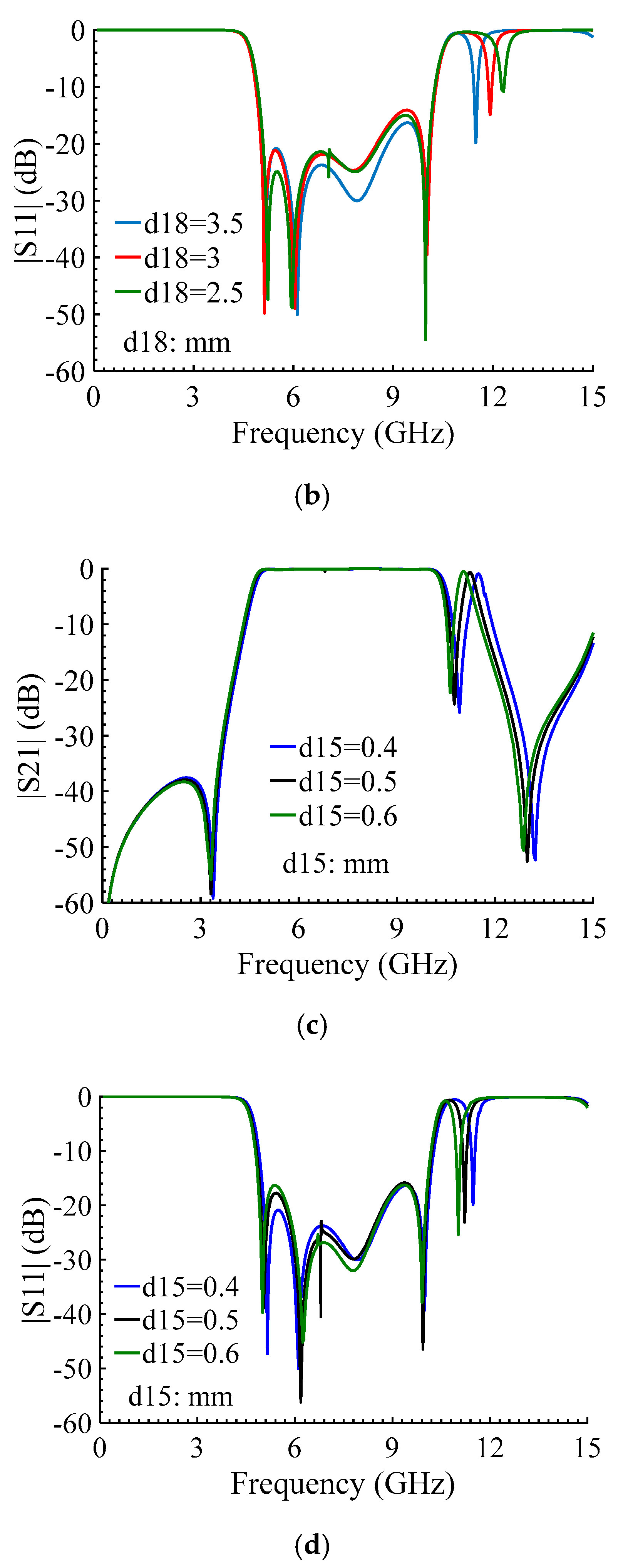
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kumar, L.; Parihar, M.S. Quasi-Lumped Analysis of Wideband Bandpass Filter With High Out-of-Band Rejection Rate. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 1549–1558. [Google Scholar] [CrossRef]
- Xu, K.-D.; Li, D.; Liu, Y. High-Selectivity Wideband Bandpass Filter Using Simple Coupled Lines With Multiple Transmission Poles and Zeros. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 107–109. [Google Scholar] [CrossRef]
- Zakharov, A.; Litvintsev, S.; Ilchenko, M. Trisection Bandpass Filters With All Mixed Couplings. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 592–594. [Google Scholar] [CrossRef]
- Xia, X.; Cheng, X.; Chen, F.; Deng, X. Compact UWB bandpass filter with sharp roll-off using APCL structure. Electron. Lett. 2018, 54, 837–839. [Google Scholar] [CrossRef]
- Zhang, T.; Bao, J.; Cai, Z.; Yang, Y.; Zhu, H.; Zhu, X.; Dutkiewicz, E. A C-Band Compact Wideband Bandpass Filter With High Selectivity and Improved Return Loss. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 1–3. [Google Scholar] [CrossRef]
- Da Xu, K.; Zhang, F.; Liu, Y.; Nie, W. High selectivity seventh-order wideband bandpass filter using coupled lines and open/shorted stubs. Electron. Lett. 2018, 54, 223–225. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Karimi, G.; Sabaghi, F. Triple mode spiral wideband bandpass filter using symmetric dual-line coupling. Electron. Lett. 2017, 53, 795–797. [Google Scholar] [CrossRef]
- Chen, P.; Li, L.; Yang, K.; Chen, Q. Hybrid Spoof Surface Plasmon Polariton and Substrate Integrated Waveguide Broadband Bandpass Filter With Wide Out-of-Band Rejection. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 984–986. [Google Scholar] [CrossRef]
- Pan, B.C.; Luo, G.Q.; Liao, Z.; Cai, J.L.; Cai, B.G. Wideband Miniaturized Design of Complementary Spoof Surface Plasmon Polaritons Waveguide Based on Interdigital Structures. Sci. Rep. 2020, 10, 3258. [Google Scholar] [CrossRef]
- Song, K.; Zhu, Y.; Zhang, F. Single- and dual-band filtering-response power dividers embedded SIW filter with improved output isolation. Sci. Rep. 2017, 7, 3361. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Fumeaux, C.; Lim, C.-C. Folded Substrate-Integrated Waveguide Band-Pass Post Filter. IEEE Microw. Wirel. Compon. Lett. 2016, 27, 22–24. [Google Scholar] [CrossRef]
- Dong, J.; Shi, J.; Xu, K. Compact Wideband Differential Bandpass Filter Using Coupled Microstrip Lines and Capacitors. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 444–446. [Google Scholar] [CrossRef]
- Karimi, G.; Amirian, M.; Lalbakhsh, A.; Ranjbar, M. A new microstrip coupling system for realization of a differential dual-band bandpass filter. AEU Int. J. Electron. Commun. 2019, 99, 186–192. [Google Scholar] [CrossRef]
- Abdalla, M.; Choudhary, D.K.; Chaudhary, R.K. A compact reconfigurable bandpass/lowpass filter with independent transmission zeros based on generalized NRI metamaterial. Int. J. RF Microw. Comput. Eng. 2019, 30. [Google Scholar] [CrossRef]
- Dehghani, K.; Karimi, G.; Lalbakhsh, A.; Maki, S.V. Design of lowpass filter by using a novel Stepped Impedance Resonator. Electron. Lett. 2004, 50, 37–39. [Google Scholar] [CrossRef]
- Hosseinkhani, F.; Roshani, S. A compact branch-line coupler design using low-pass resonators and meandered lines open stubs. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 1164–1170. [Google Scholar]
- Karimi, G.; Siahkamari, H.; Hamedani, F.K.; Lalbakhsh, A. Design of Modified Z-Shaped and T-Shaped Microstrip Filter Based on Transfer Function Analysis. Wirel. Pers. Commun. 2015, 82, 2005–2016. [Google Scholar] [CrossRef]
- Jin, X.; Huang, X.; Chen, D.; Cheng, C. Response Diversity of Stub-Loaded Ring Bandpass Filter Based on Commensurate Line Element: Single- and Dual-Band Applications. IEEE Access 2019, 7, 25681–25689. [Google Scholar] [CrossRef]
- Liang, J.G.; Wang, C.; Kim, N.Y. Implementation of UWB BPF with modularised design based on SQR and DCR. IET Microw. Antennas Propag. 2018, 12, 1175–1184. [Google Scholar] [CrossRef]
- Luo, C.; Wong, S.-W.; Lin, J.-Y.; Yang, Y.; Li, Y.; Yu, X.-Z.; Feng, L.-P.; Tu, Z.-H.; Zhu, L. Quasi-Reflectionless Microstrip Bandpass Filters Using Bandstop Filter for Out-of-Band Improvement. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 1849–1853. [Google Scholar] [CrossRef]
- Bi, X.-K.; Zhang, X.; Wong, S.-W.; Yuan, T.; Guo, S.-H. Design of Equal-Ripple Dual-Wideband Bandpass Filter With Minimum Design Parameters Based on Cross-Shaped Resonator. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 1780–1784. [Google Scholar] [CrossRef]
- Liang, G.Z.; Chen, F.C. A Compact Dual-Wideband Bandpass Filter Based on Open-/Short-Circuited Stubs. IEEE Access 2020, 21, 20488–20492. [Google Scholar] [CrossRef]
- Yun, Y.-C.; Oh, S.-H.; Lee, J.-H.; Choi, K.; Chung, T.-K.; Kim, H.-S. Optimal Design of a Compact Filter for UWB Applications Using an Improved Particle Swarm Optimization. IEEE Trans. Magn. 2015, 52, 1–4. [Google Scholar] [CrossRef]
- Li, Y.S.; Wei, X.C.; Li, E.P. An asymmetric spiral-shaped DGS optimized by genetic algorithm for wideband common-mode suppression. In Proceedings of the 2015 Asia-Pacific Symposium on Electromagnetic Compatibility (APEMC), Taipei, Taiwan, 26–29 May 2015; pp. 681–684. [Google Scholar]
- Jamshidi, M.; Lalbakhsh, A.; Mohamadzade, B.; Siahkamari, H.; Mousavi, S.M.H. A novel neural-based approach for design of microstrip filters. AEU Int. J. Electron. Commun. 2019, 110, 152847. [Google Scholar] [CrossRef]
- Karimi, G.; Lalbakhsh, A.; Dehghani, K.; Siahkamari, H. Analysis of Novel Approach to Design of Ultra-wide Stopband Microstrip Low-Pass Filter Using Modified U-Shaped Resonator. ETRI J. 2015, 37, 945–950. [Google Scholar] [CrossRef]
- Weng, M.-H.; Lan, S.-W.; Chang, S.-J.; Yang, R. Design of Dual-Band Bandpass Filter With Simultaneous Narrow- and Wide-Bandwidth and a Wide Stopband. IEEE Access 2019, 7, 147694–147703. [Google Scholar] [CrossRef]
- Ahmadi, A.; Makki, S.V.; Lalbakhsh, A.; Majidifar, S. A novel dual-mode wideband band pass filter. Appl. Comput. Electromagn. Soc. J. 2014, 29, 735–742. [Google Scholar]
- Zhu, H.; Chu, Q.-X.; Tian, X.-K. Compact UWB bandpass filter using folded-T-shaped resonator with a notch-band. J. Electromagn. Waves Appl. 2012, 26, 1366–1373. [Google Scholar] [CrossRef]




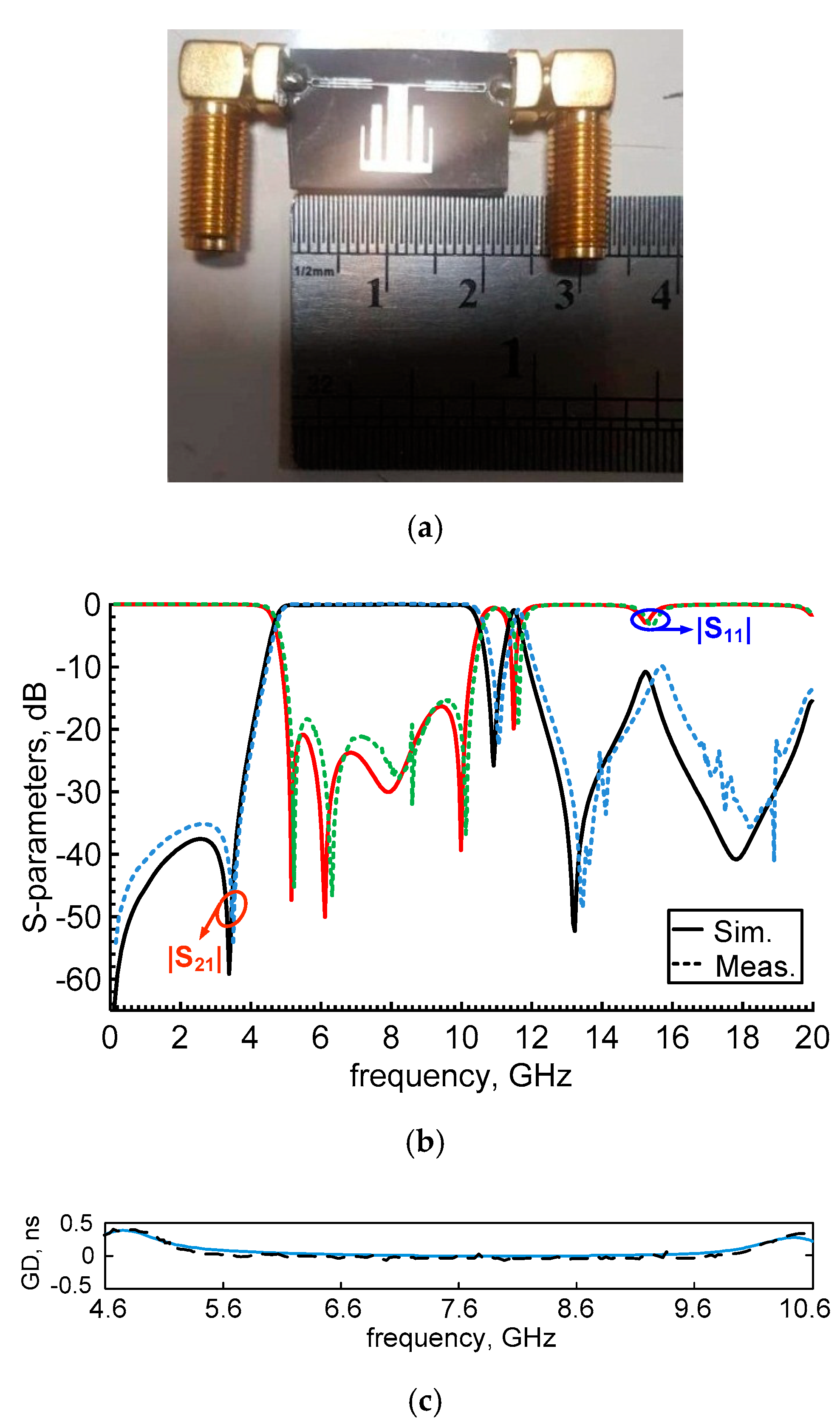
| Refs. | Passbands (GHz) | BW (GHz) | FBW (%) | IL (dB) | RL (dB) | GD (ns) | |
|---|---|---|---|---|---|---|---|
| [1] | 2.15 | 1.4–2.9 | 67.3 | 0.57 | 13 | 5.91 | 0.080 |
| [2] | 2.05 | 1.44–2.66 | 60 | 0.6 | 20 | 2 | 0.115 |
| [3] | 2.05 | 1.96–2.08 | 4.96 | 1.5 | 12.2 | 3 | - |
| [4] | 6.85 | 3.1–10.6 | 109.5 | - | 12 | 0.65 | 0.205 |
| [5] | 5.1 | 3.5–6.7 | 63 | 0.6 | 22 | 0.6 | 0.095 |
| [6] | 1.99 | 1.22–2.77 | 78 | - | 17 | 5 | 0.128 |
| [7] | 7.8 | 4.8–10.8 | 78 | 0.7 | 12 | 0.4 | 0.220 |
| [27] | 2.4/4 | 2.3–2.5/3-5 | 8/39 | 1.4/1 | 16/15 | - | 0.043 |
| This work | 7.6/11.5 | 4.6–10.6/11.35–11.62 | 78.9/2.34 | 0.6/0.92 | 16.32/20 | 0.45 | 0.198 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lalbakhsh, A.; Alizadeh, S.M.; Ghaderi, A.; Golestanifar, A.; Mohamadzade, B.; Jamshidi, M.; Mandal, K.; Mohyuddin, W. A Design of a Dual-Band Bandpass Filter Based on Modal Analysis for Modern Communication Systems. Electronics 2020, 9, 1770. https://doi.org/10.3390/electronics9111770
Lalbakhsh A, Alizadeh SM, Ghaderi A, Golestanifar A, Mohamadzade B, Jamshidi M, Mandal K, Mohyuddin W. A Design of a Dual-Band Bandpass Filter Based on Modal Analysis for Modern Communication Systems. Electronics. 2020; 9(11):1770. https://doi.org/10.3390/electronics9111770
Chicago/Turabian StyleLalbakhsh, Ali, Seyed Morteza Alizadeh, Amirhossein Ghaderi, Alireza Golestanifar, Bahare Mohamadzade, Mohammad (Behdad) Jamshidi, Kaushik Mandal, and Wahab Mohyuddin. 2020. "A Design of a Dual-Band Bandpass Filter Based on Modal Analysis for Modern Communication Systems" Electronics 9, no. 11: 1770. https://doi.org/10.3390/electronics9111770
APA StyleLalbakhsh, A., Alizadeh, S. M., Ghaderi, A., Golestanifar, A., Mohamadzade, B., Jamshidi, M., Mandal, K., & Mohyuddin, W. (2020). A Design of a Dual-Band Bandpass Filter Based on Modal Analysis for Modern Communication Systems. Electronics, 9(11), 1770. https://doi.org/10.3390/electronics9111770








