Improvement of Multilevel DC/DC Converter for E-Mobility Charging Station
Abstract
:1. Introduction
2. Comparison of Diode Series Structure Multilevel Converter (DSS-MLC) and Diode Parallel Structure Multilevel Converter (DPS-MLC) for E-Mobility
2.1. Comparison between Structures and Operational Characteristics of DSS-MLC and DPS-MLC
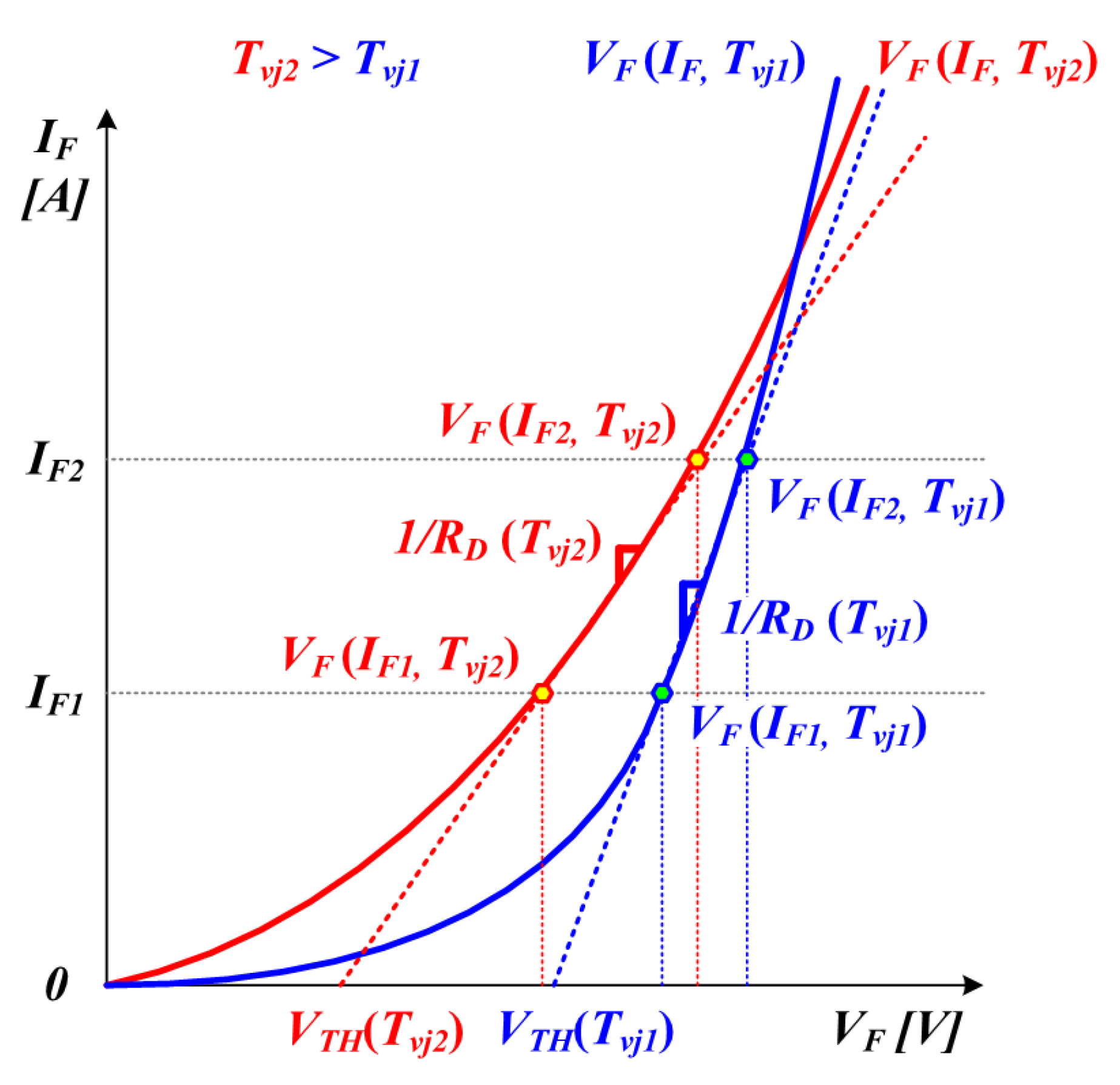
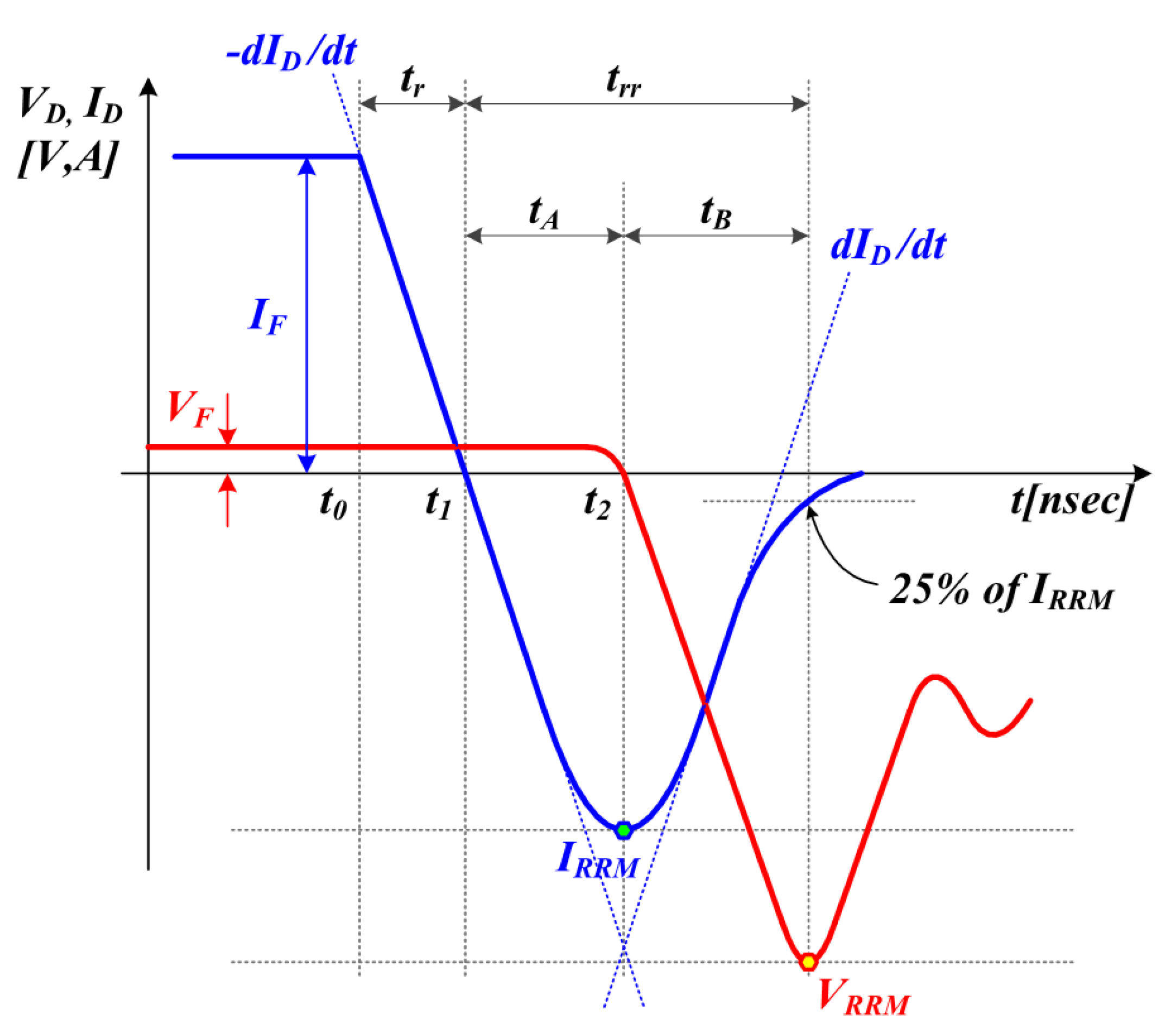
2.2. Comparison between Losses and Output Voltages of DSS-MLC and DPS-MLC
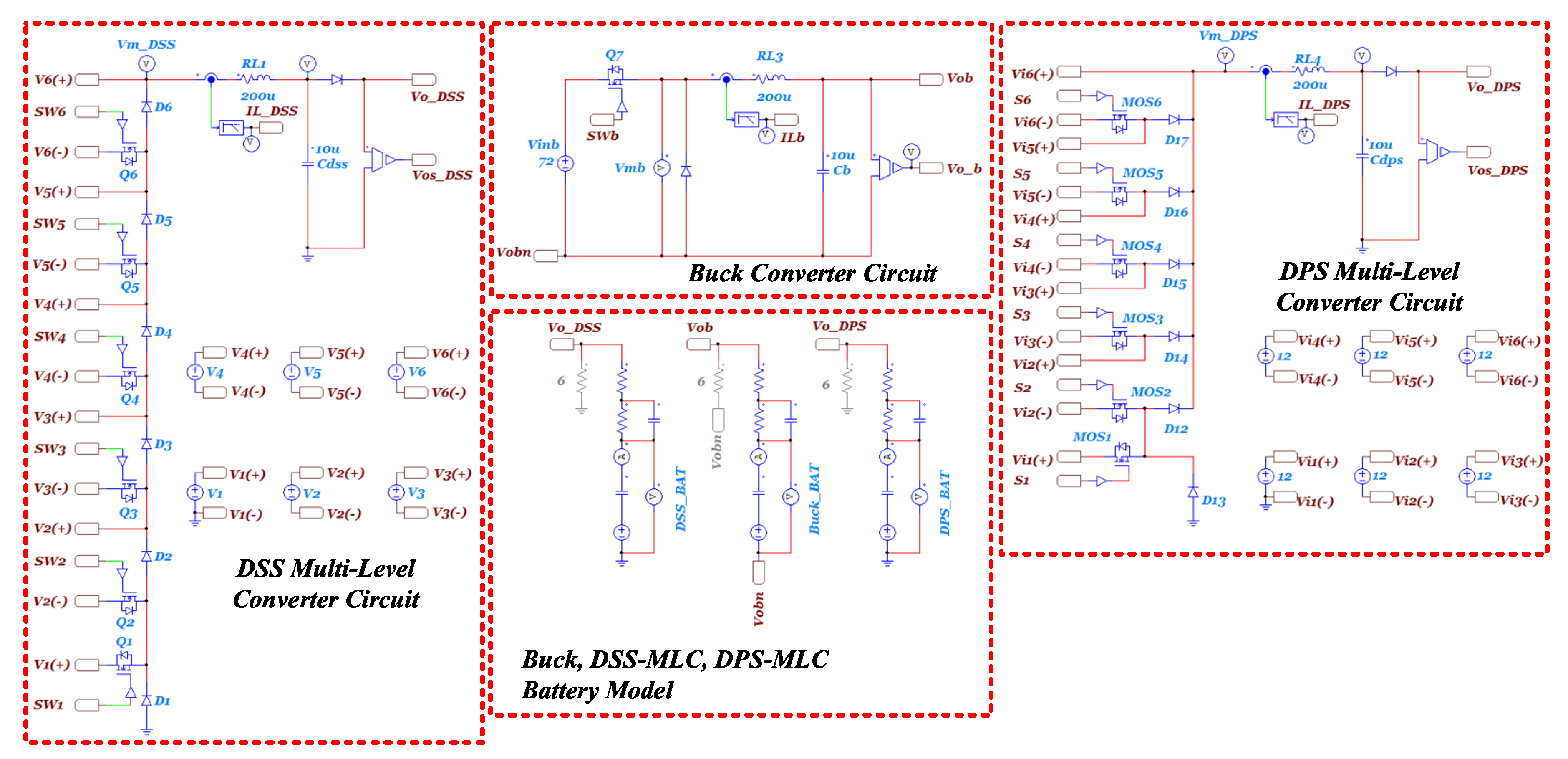
3. Validation of DPS-MLC
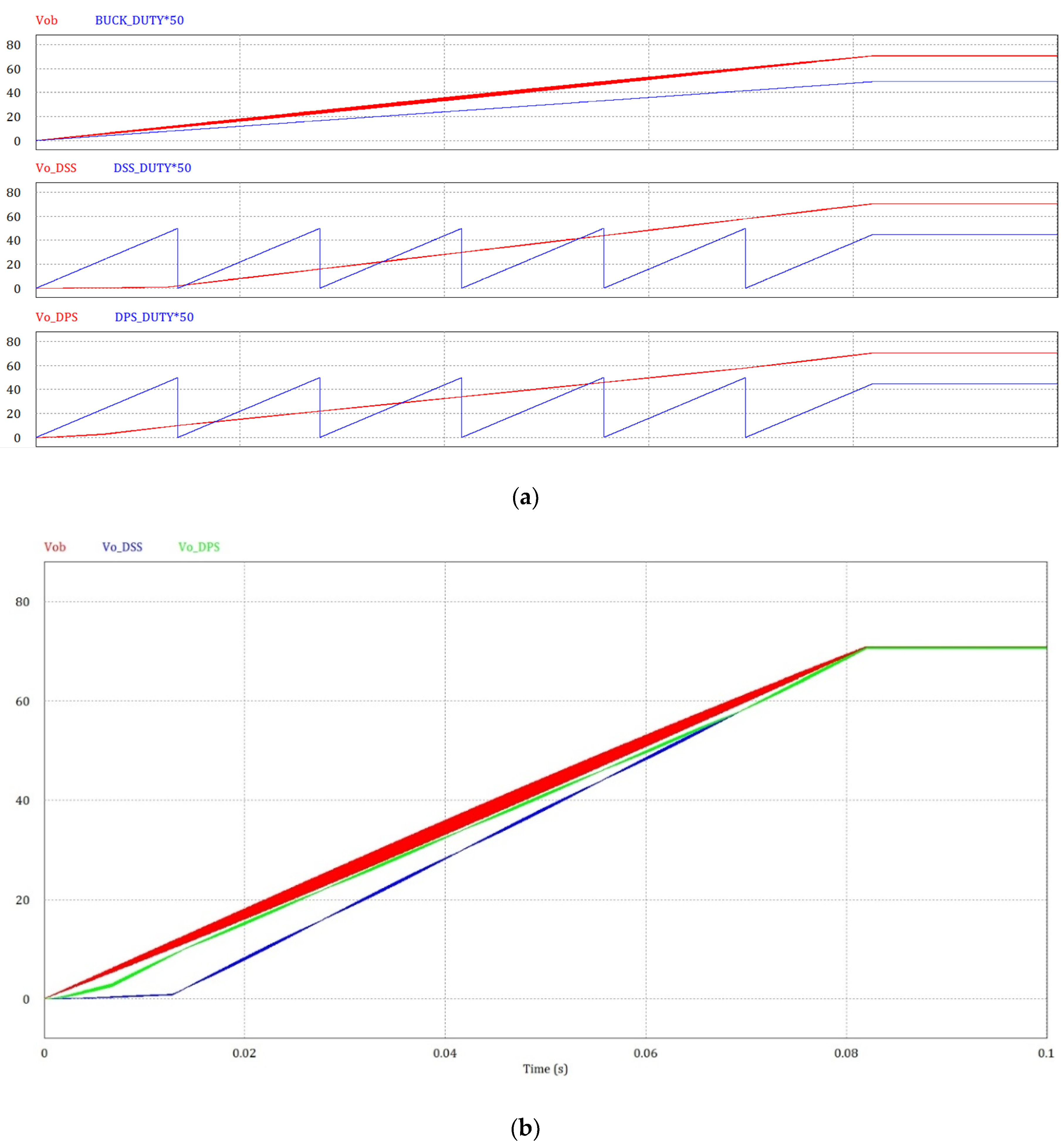
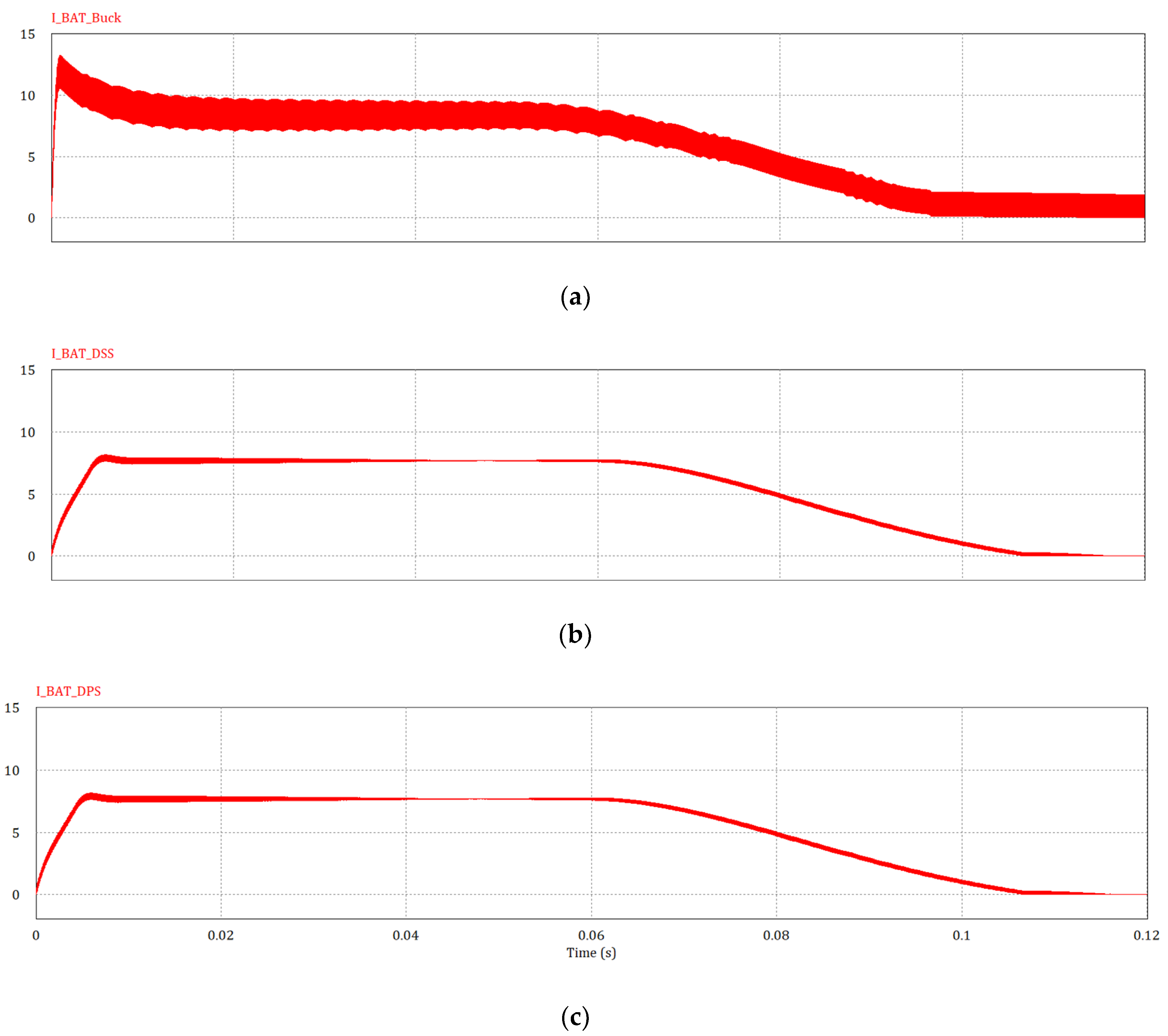
3.1. Simulation
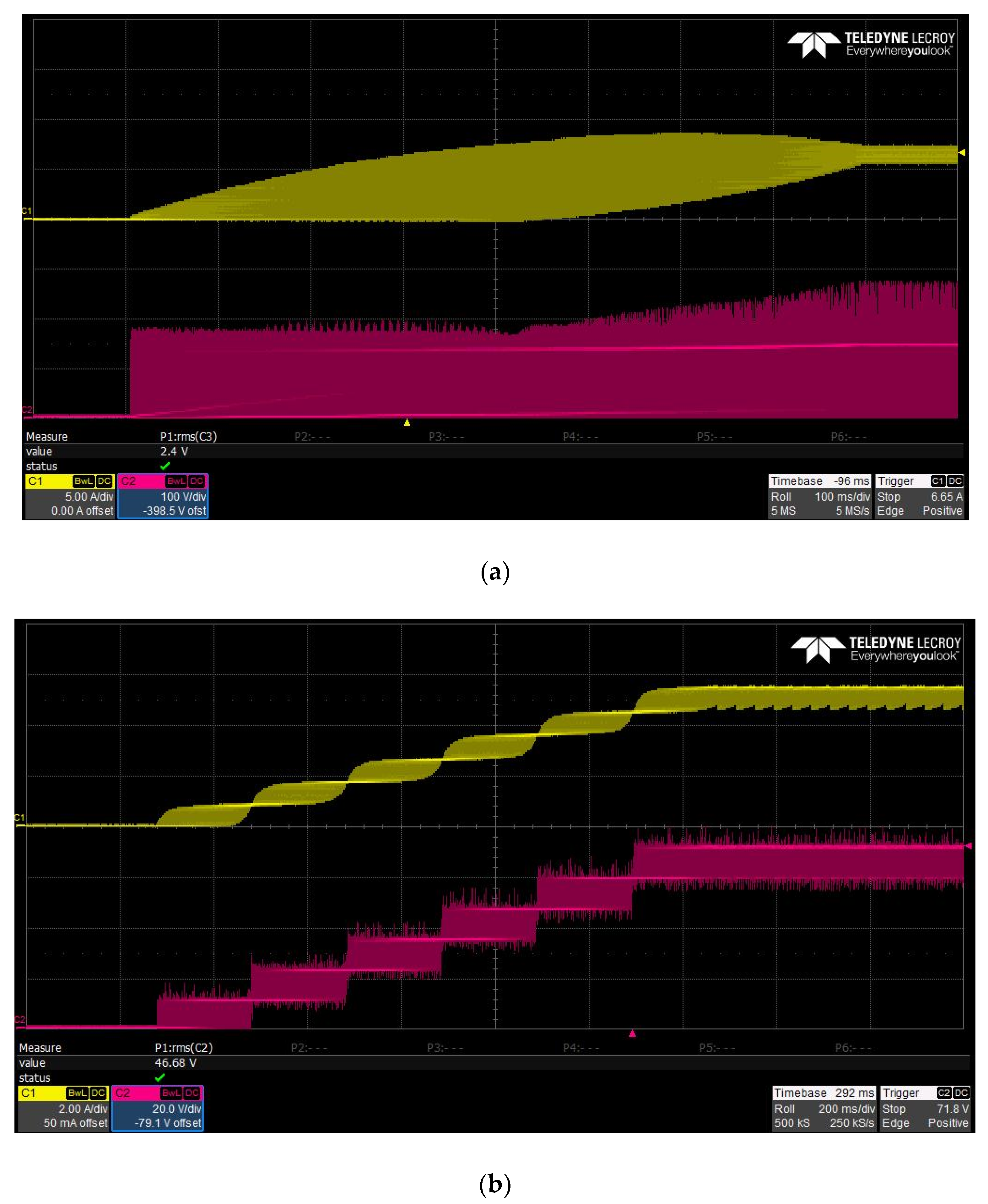
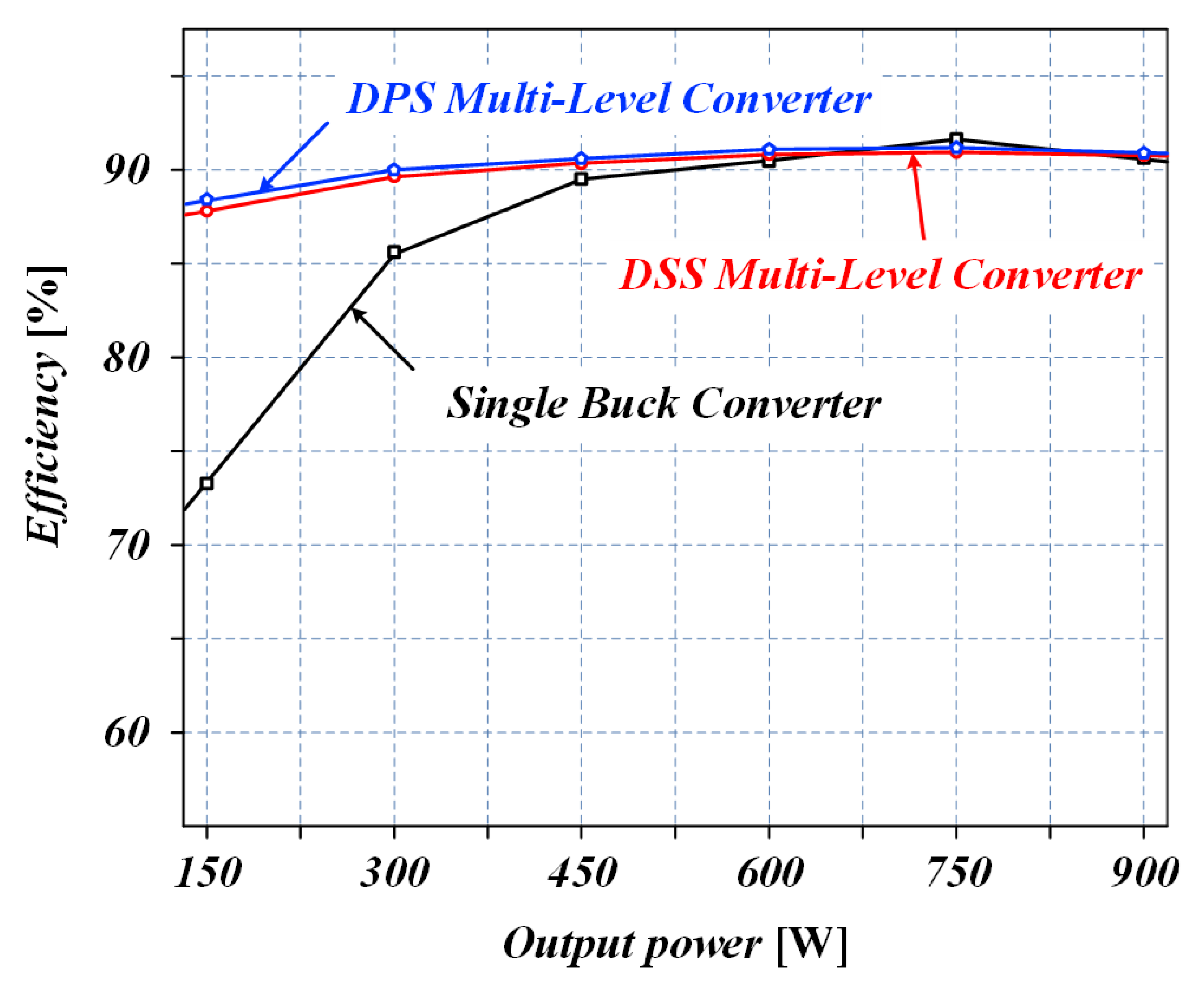
3.2. Experiment
4. Conclusions
- The DPS-MLC exhibits an improved efficiency by reducing the switching loss of the diode while providing the same operational characteristics as the existing multilevel converter DSS-MLC. The serial connection structure of the diodes at the output side of the multilevel design is changed to a parallel connection structure. Therefore, the loss can be reduced regardless of the number of levels by using only one output diode in the freewheeling switching section.
- The voltage drop caused by the diode is minimized to increase the control region of the charging voltage. This region, which can be responsible for each multilevel converter, is expanded to a wider range. As the number of multilevel converters increases, the advantages of the DPS-MLC become more prominent. However, the operation of the DSS-MLC is limited because the voltage drop caused by the diode increases at a lower level. The DPS-MLC solves this problem and can control a wide range of charging voltages regardless of the number of levels. In particular, it has a high efficiency when compared to DSS-MLC in the low output voltage section. It is more advantageous in the PMD field because the charging voltage range of the PMD is from 12 V to 36 V.
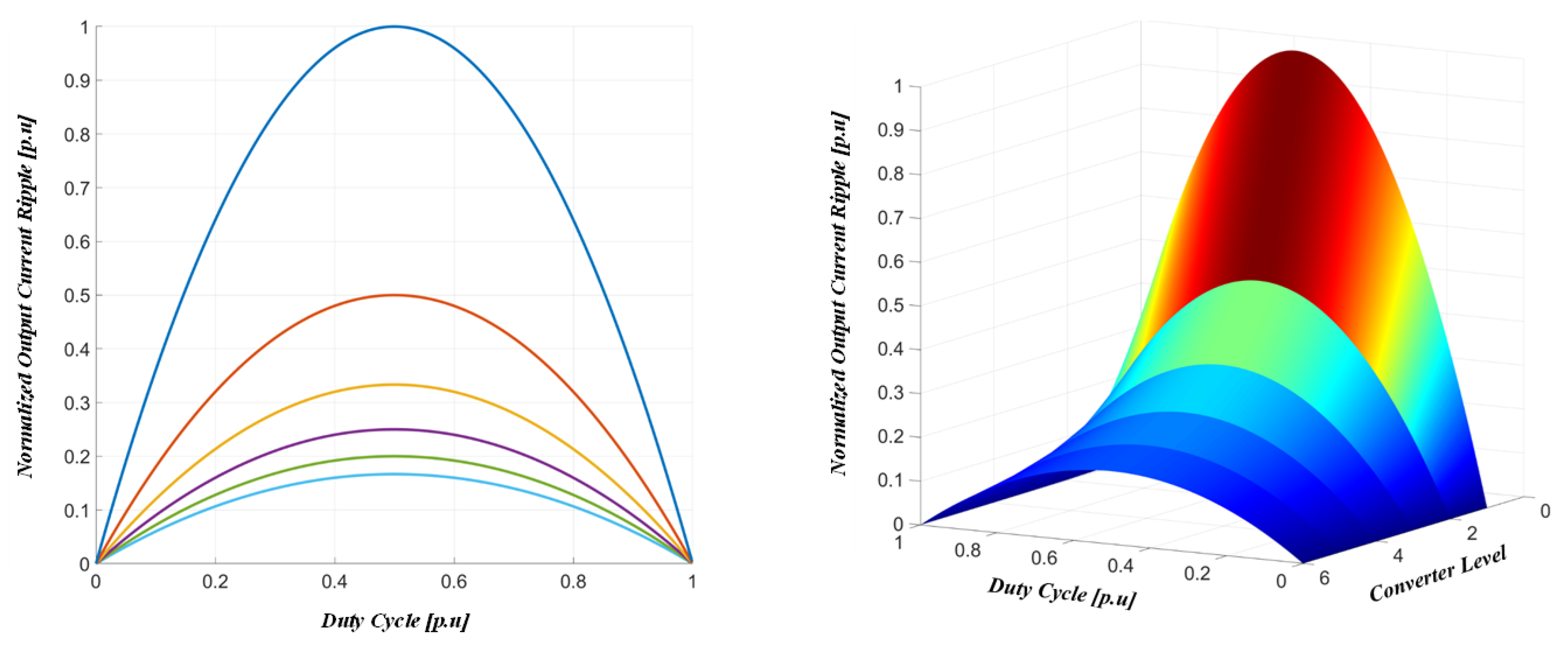
- The DPS-MLC has a considerably better efficiency than the single buck converter and can improve the charging power quality by reducing the current ripple. Furthermore, it can also reduce the electromagnetic interference caused by the charging system by reducing the voltage ripples obtained by PWM.
Author Contributions
Funding
Conflicts of Interest
References
- Rigas, E.S.; Ramchurn, S.D.; Bassiliades, N.; Koutitas, G. Congestion Management for Urban EV Charging Systems. In Proceedings of the 2013 IEEE International Conference on Smart Grid Communications (SmartGridComm), Vancouver, BC, Canada, 21–24 October 2013; pp. 121–126. [Google Scholar]
- ElBanhawy, E.Y. Investigating the evolution of e-mobility in its urban context a longitudinal study in Newcastle-Gateshead area. In Proceedings of the 5th IET Hybrid and Electric Vehicles Conference (HEVC 2014), London, UK, 5–6 November 2014; pp. 1–11. [Google Scholar]
- Creutzig, F.; Baiocchi, G.; Bierkant, R.; Seto, K.C. Global typology of urban energy use and potentials for an urbanization mitigation wedge. Proc. Natl. Acad. Sci. USA 2015, 112, 6283–6288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Momirlan, M.; Veziroglu, T. The properties of hydrogen as fuel tomorrow in sustainable energy system for a cleaner planet. Int. J. Hydrogen Energy 2005, 30, 795–802. [Google Scholar] [CrossRef]
- Li, C.; Cao, Y.; Zhang, M.; Wang, J.; Liu, J.; Shi, H.; Geng, Y. Hidden Benefits of Electric Vehicles for Addressing Climate Change. Sci. Rep. 2015, 5, 9213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hawkins, T.R.; Singh, B.; Majeau-Bettez, G.; Strømman, A.H. Comparative environmental life cycle assessment of conventional and electric vehicles. J. Ind. Ecol. 2013, 17, 53–64. [Google Scholar] [CrossRef]
- Ahmad, F.; Alam, M.S.; Asaad, M. Developments in xEVs charging infrastructure and energy management system for smart microgrids including xEVs. Sustain. Cities Soc. 2017, 35, 552–564. [Google Scholar] [CrossRef]
- Schlund, J.; Steinert, R.; Pruckner, M. Coordinating E-Mobility charging for frequency containment reserve power provision. In Proceedings of the e-Energy ’18: The Ninth International Conference on Future Energy Systems, Karlsruhe, Germany, 12–15 June 2018; pp. 556–563. [Google Scholar]
- Deventer, P.; Steen, M.; Schelven, R.; Rubin, B.; Kotter, R. Large-Scale Deployment of Public Charging Infrastructure: Identifying Possible Next Steps Forward; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 107–124. [Google Scholar]
- Nikulina, V.; Simon, D.; Ny, H.; Baumann, H. Context-adapted urban planning for rapid transitioning of personal mobility towards sustainability: A systematic literature review. Sustainability 2019, 11, 1007. [Google Scholar] [CrossRef] [Green Version]
- Kaya, K.; Poyrazoglu, G. A Platform for Personal E-Mobility with Route Forecasting. In Proceedings of the 2020 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Istanbul, Turkey, 12–13 June 2020; pp. 1–5. [Google Scholar]
- Kuo, J.Y.; Sayeed, A.; Tangirala, N.T.; Han, V.C.Y.; Dauwels, J.; Mayer, M.P. Pedestrians’ acceptance of personal mobility devices on the shared path: A structural equation modelling approach. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 2349–2354. [Google Scholar]
- Thomas, D.; Klonari, V.; Vallée, F.; Ioakimidis, C.S. Implementation of an e-bike sharing system: The effect on low voltage network using pv and smart charging stations. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 572–577. [Google Scholar]
- Mauromicale, G.; Raciti, A.; Rizzo, S.A.; Susinni, G.; Parise, G.; Parise, L. E-mobility: Safety, Service Continuity and Penetration of Charging Systems. In Proceedings of the 2019 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Torino, Italy, 2–4 July 2019; pp. 1–6. [Google Scholar]
- Ivan, P.; Hrvoje, P.; Tomislav, C. Electric vehicle based smart e-mobility system–Definition and comparison to the existing concept. Appl. Energy 2020, 272, 115153. [Google Scholar]
- Lim, S.; Lee, H.; Cha, H.; Park, S. Multi-Level DC/DC Converter for E-Mobility Charging Stations. IEEE Access 2020, 8, 48774–48783. [Google Scholar] [CrossRef]
- Dimitrov, B.; Hayatleh, K.; Barker, S.; Collier, G.; Sharkh, S.; Cruden, A. A Buck-Boost Transformerless DC–DC Converter Based on IGBT Modules for Fast Charge of Electric Vehicles. Electronics 2020, 9, 397. [Google Scholar] [CrossRef] [Green Version]
- Abronzini, U.; Attaianese, C.; D’Arpino, M.; Di Monaco, M.; Genovese, A.; Pede, G.; Tomasso, G. Multi-source power converter system for EV charging station with integrated ESS. In Proceedings of the 2015 IEEE 1st International Forum on Research and Technologies for Society and Industry Leveraging a Better Tomorrow (RTSI), Turin, Italy, 16–18 September 2015; pp. 427–432. [Google Scholar]
- Dahidah, M.S.A.; Liu, H.; Agelidis, V.G. Reconfigurable Converter with Multiple-Voltage Multiple-Power for E-Mobility Charging. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 3215–3222. [Google Scholar]
- Kesler, M.; Kisacikoglu, M.C.; Tolbert, L.M. Vehicle-to-Grid Reactive Power Operation Using Plug-In Electric Vehicle Bidirectional Offboard Charger. IEEE Trans. Ind. Electron. 2014, 61, 6778–6784. [Google Scholar] [CrossRef]
- Malik, M.Z.; Chen, H.; Nazir, M.S.; Khan, I.A.; Abdalla, A.N.; Ali, A.; Chen, W. A New Efficient Step-Up Boost Converter with CLD Cell for Electric Vehicle and New Energy Systems. Energies 2020, 13, 1791. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Abu Qahouq, J.A. Input Voltage Ripple-Based Sensorless Current Sharing Autotuning Controller for Multiphase DC–DC Converters. IEEE Trans. Ind. Appl. 2016, 52, 4117–4125. [Google Scholar] [CrossRef]
- Ferreira, J.A. The Multilevel Modular DC Converter. IEEE Trans. Power Electron. 2013, 28, 4460–4465. [Google Scholar] [CrossRef]
- Nguyen, M.K.; Choi, Y.O. Voltage Multiplier Cell-Based Quasi-Switched Boost Inverter with Low Input Current Ripple. Electronics 2019, 8, 227. [Google Scholar] [CrossRef] [Green Version]
- Ismail, A.A.A.; Elnady, A. Advanced Drive System for DC Motor Using Multilevel DC/DC Buck Converter Circuit. IEEE Access 2019, 7, 54167–54178. [Google Scholar] [CrossRef]
- Thinh, Q.; Ngoc, C.; Lee, S.H.; Kim, S.M.; Kim, H.C.; Eel, H. Analyzing Modulation Techniques for the Modular Multilevel Converter. Int. J. Comput. Electr. Eng. 2016, 8, 259–271. [Google Scholar] [CrossRef] [Green Version]
- Babaei, E. A Cascade Multilevel Converter Topology with Reduced Number of Switches. IEEE Trans. Power Electron. 2008, 23, 2657–2664. [Google Scholar] [CrossRef]
- Prozorov, A.M.; Nikitin, D.A.; Tarasov, A.D. Techniques for reducing output current ripple in a flyback converter with PFC. In Proceedings of the 2019 Ural Symposium on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT), Yekaterinburg, Russia, 25–26 April 2019; pp. 391–393. [Google Scholar]
- Xiong, Y.; Sun, S.; Jia, H.; Shea, P.; John Schen, Z. New Physical Insights on Power MOSFET Switching Losses. IEEE Trans. Power Electron. 2009, 24, 525–531. [Google Scholar] [CrossRef]
- Bazzi, A.M.; Krein, P.T.; Kimball, J.W.; Kepley, K. IGBT and Diode Loss Estimation under Hysteresis Switching. IEEE Trans. Power Electron. 2012, 27, 1044–1048. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, J.; Guo, Y. Calculation of Power Loss in Output Diode of a Flyback Switching DC-DC Converter. In Proceedings of the 2006 CES/IEEE 5th International Power Electronics and Motion Control Conference, Shanghai, China, 14–16 August 2006; pp. 1–5. [Google Scholar]
- Jiang, H.; Wei, J.; Dai, X.; Ke, M.; Zheng, C.; Deviny, I. Silicon carbide split-gate MOSFET with merged Schottky barrier diode and reduced switching loss. In Proceedings of the 2016 28th International Symposium on Power Semiconductor Devices and ICs (ISPSD), Prague, Czech Republic, 12–16 June 2016; pp. 59–62. [Google Scholar]
- Xu, Y.; Ho, C.N.M.; Ghosh, A.; Muthumuni, D. An Electrical Transient Model of IGBT-Diode Switching Cell for Power Semiconductor Loss Estimation in Electromagnetic Transient Simulation. IEEE Trans. Power Electron. 2020, 35, 2979–2989. [Google Scholar] [CrossRef]

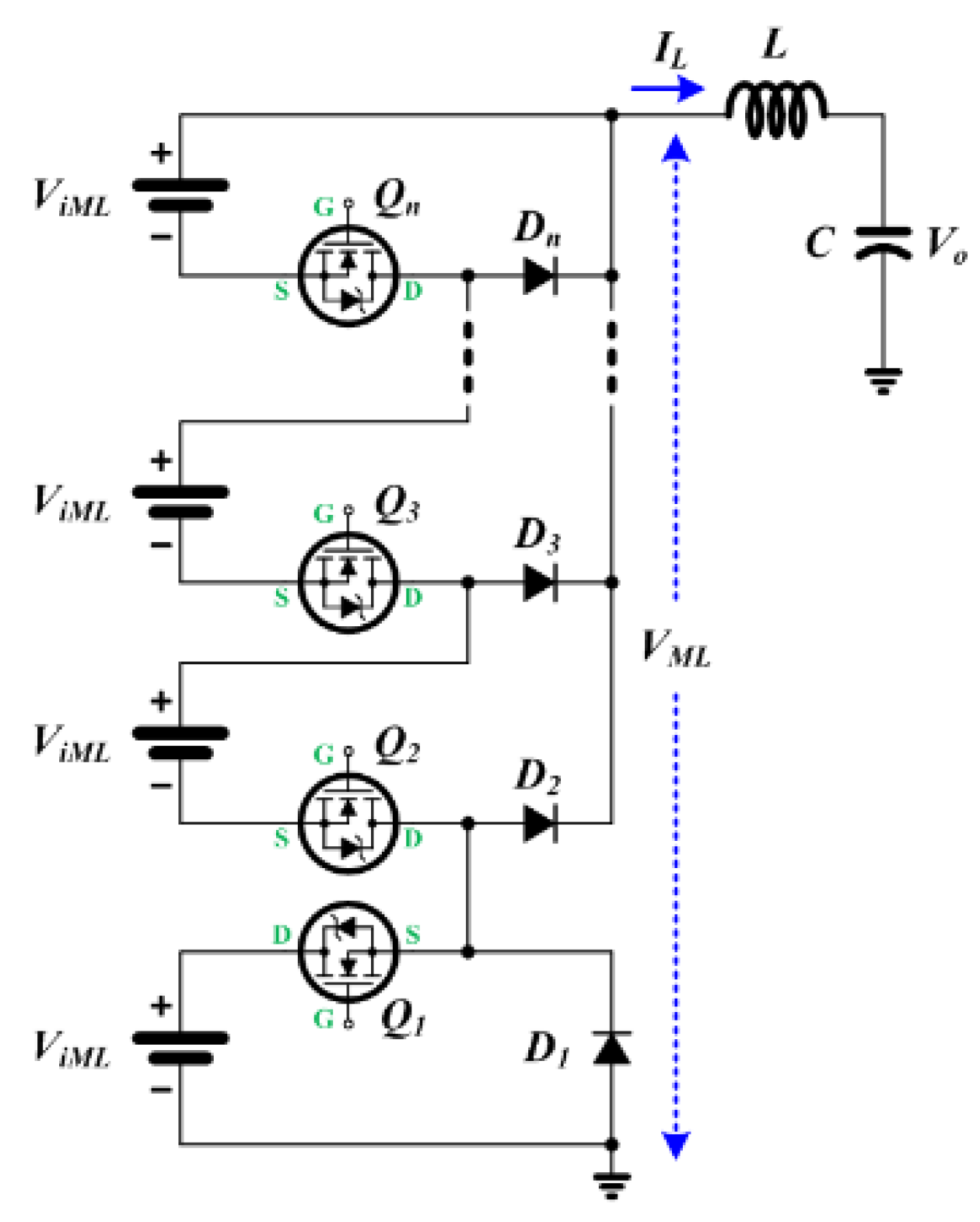
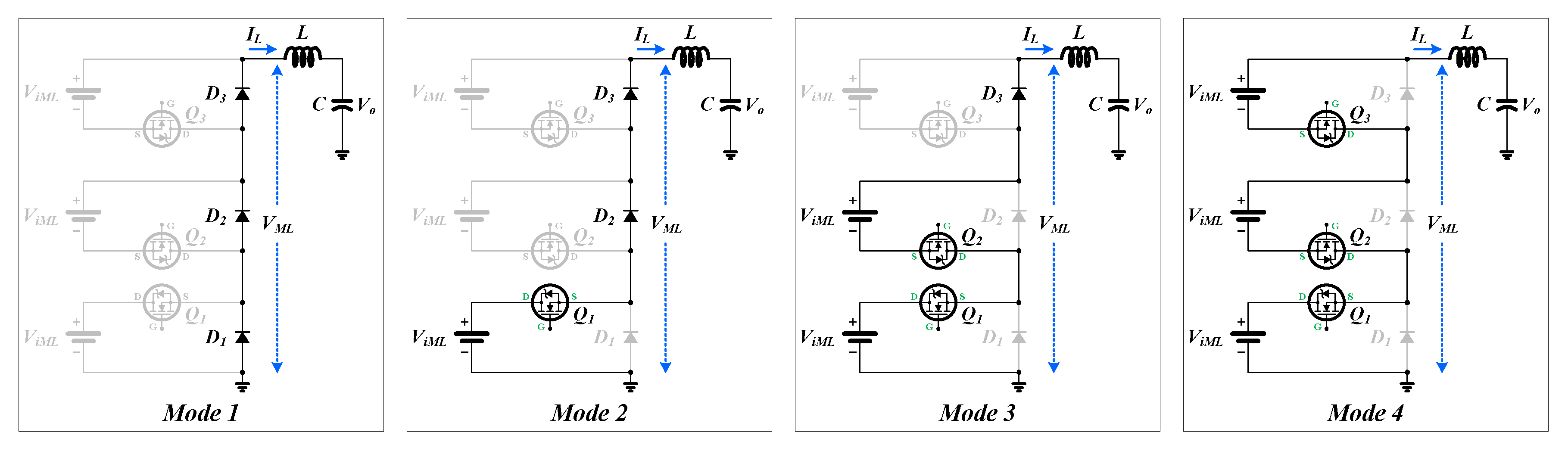






| Q1 | Q2 | Q3 | DSS-MLC | DPS-MLC | |
|---|---|---|---|---|---|
| Mode 1 | 0 | 0 | 0 | 0 | 0 |
| Mode 2 | 1 | 0 | 0 | ||
| Mode 3 | 1 | 1 | 0 | ||
| Mode 4 | 1 | 1 | 1 |
| Parameter | Symbol | Value |
|---|---|---|
| Buck converter input voltage | Vinb | 72 V |
| Multilevel converter input voltage | V1–V6 | 12 V |
| Output reactor inductance | RL1, RL3, RL4 | 200 μH |
| Output capacitor capacitance | Cb, Cdss, Cdps | 10 μF |
| Output load resistance | Rload | 6 Ω |
| Switching frequency | fs | 20 kHz |
| Parameter | Value |
|---|---|
| Output inductor inductance | 200 μH |
| Output capacitor capacitance | 220 μF |
| Output load resistance | 13.5 Ω |
| Switching frequency | 20 kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-H.; Park, S.-J.; Lim, S.-K. Improvement of Multilevel DC/DC Converter for E-Mobility Charging Station. Electronics 2020, 9, 2037. https://doi.org/10.3390/electronics9122037
Lee J-H, Park S-J, Lim S-K. Improvement of Multilevel DC/DC Converter for E-Mobility Charging Station. Electronics. 2020; 9(12):2037. https://doi.org/10.3390/electronics9122037
Chicago/Turabian StyleLee, Jung-Hwan, Sung-Jun Park, and Sang-Kil Lim. 2020. "Improvement of Multilevel DC/DC Converter for E-Mobility Charging Station" Electronics 9, no. 12: 2037. https://doi.org/10.3390/electronics9122037
APA StyleLee, J.-H., Park, S.-J., & Lim, S.-K. (2020). Improvement of Multilevel DC/DC Converter for E-Mobility Charging Station. Electronics, 9(12), 2037. https://doi.org/10.3390/electronics9122037




