Design and Development of BTI Model and 3D InGaAs HEMT-Based SRAM for Reliable and Secure Internet of Things Application
Abstract
:1. Introduction
- Design and simulation of the -based HEMT;
- Calibration of simulation models and HEMT with experimental data;
- Proposed a PBTI/NBTI model for HEMT;
- Proposed model is modified according to the material parameters;
- Use of proposed model for 6T SRAM cell design.
2. State-Of-The-Art BTI Models
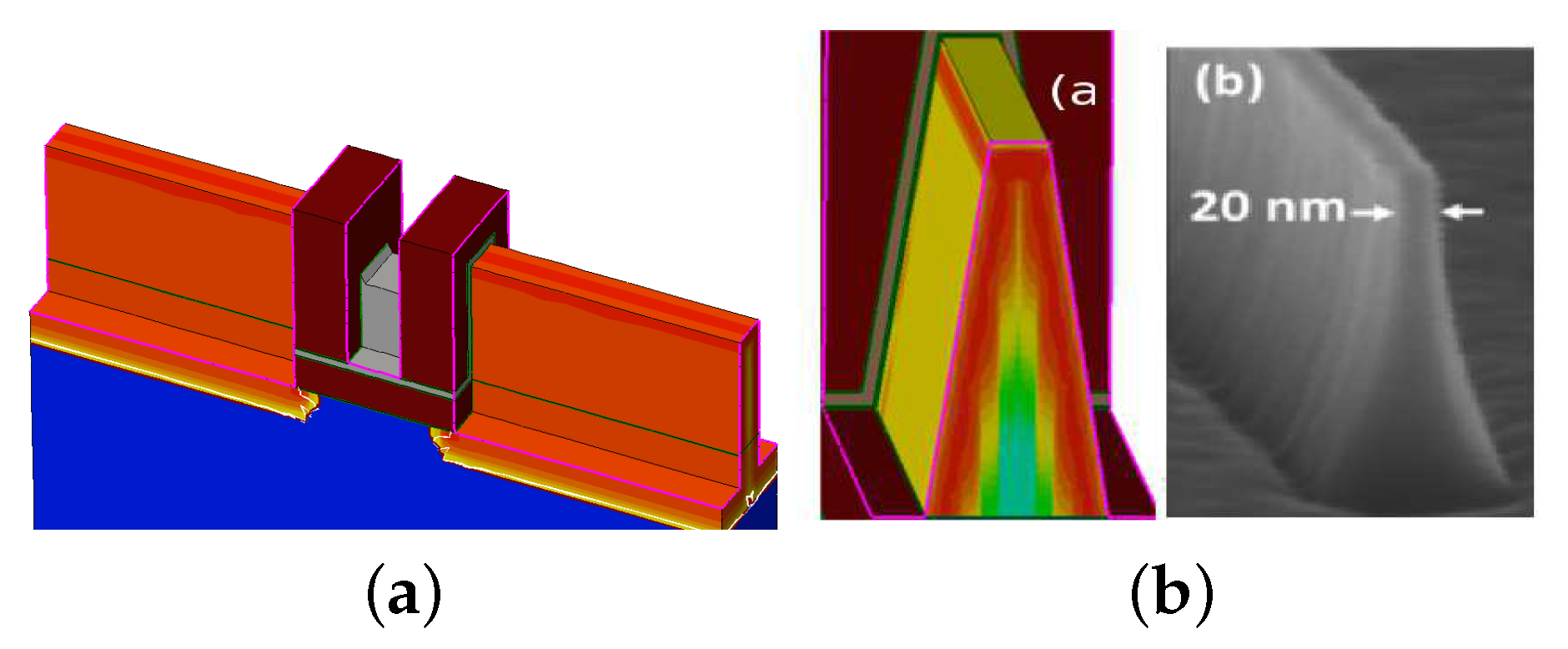
3. Proposed InGaAs HEMT
4. BTI Effects on 6T SRAM Cell
5. Proposed BTI Model for HEMT
6. Modeling of Charge Generation Constant
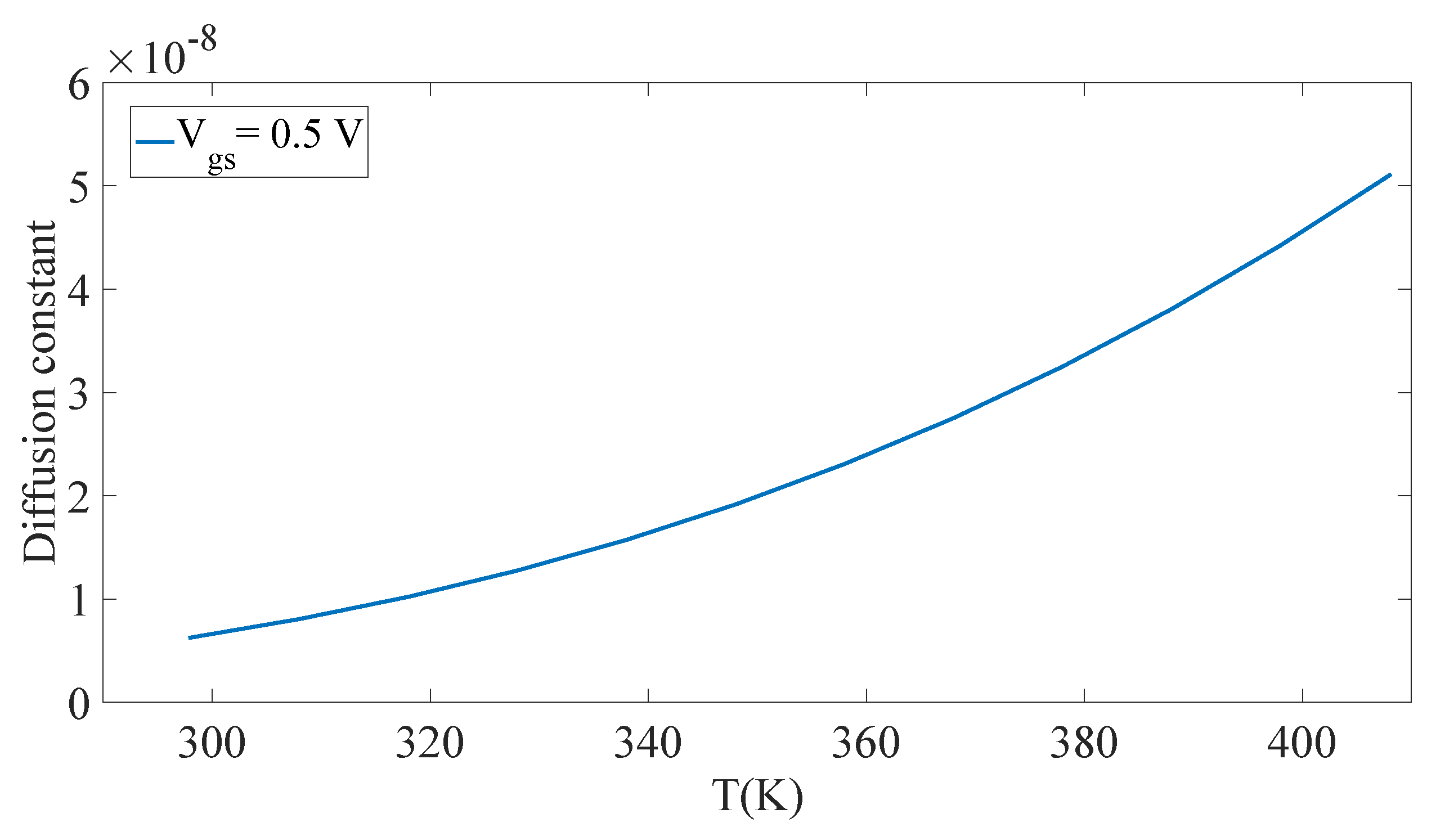
Modeling of Hydrogen Diffusion Constant
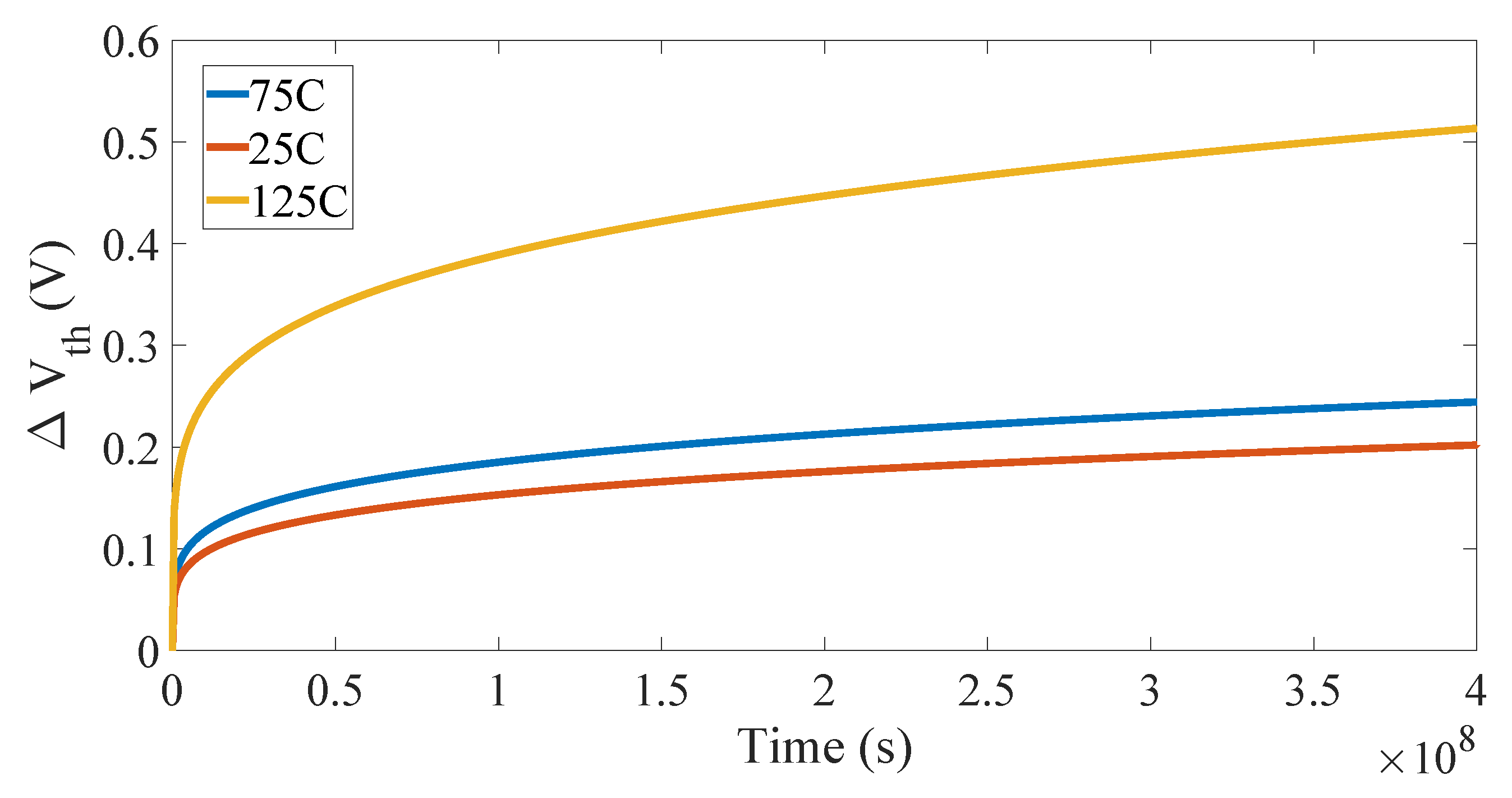
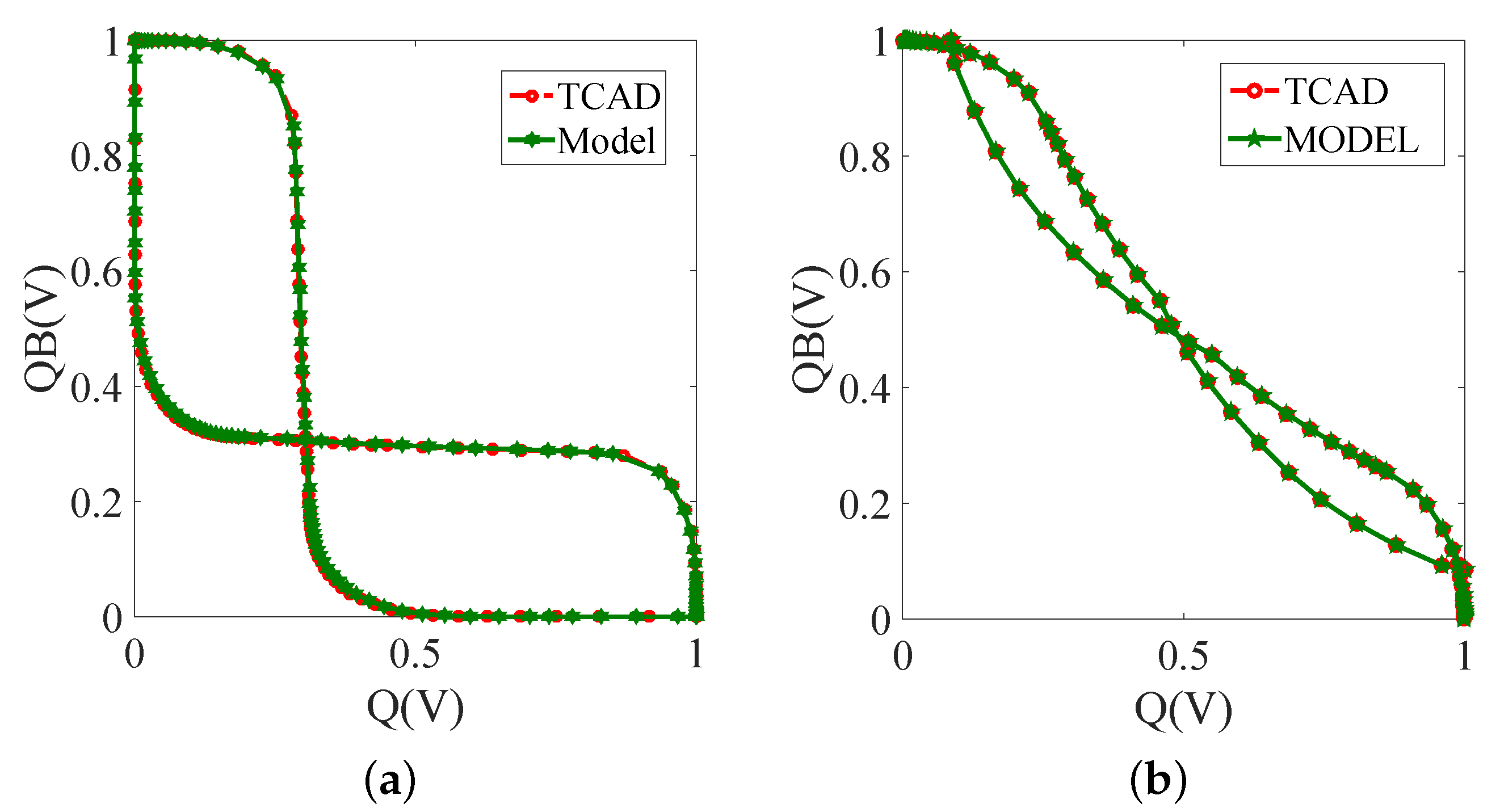
7. Model Verification and Circuit Simulation
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kabashkin, I.; Kundler, J. Reliability of sensor nodes in wireless sensor networks of cyber physical systems. Procedia Comput. Sci. 2017, 104, 380–384. [Google Scholar] [CrossRef]
- Qian, Q.; Lei, J.; Wei, J.; Zhang, Z.; Tang, G.; Zhong, K.; Zheng, Z.; Chen, K.J. 2D materials as semiconducting gate for field-effect transistors with inherent over-voltage protection and boosted ON-current. NPJ 2D Mater. Appl. 2019, 3, 1–9. [Google Scholar] [CrossRef]
- Halfaya, Y.; Bishop, C.; Soltani, A.; Sundaram, S.; Aubry, V.; Voss, P.L.; Salvestrini, J.P.; Ougazzaden, A. Investigation of the performance of HEMT-based NO, NO2 and NH3 exhaust gas sensors for automotive antipollution systems. Sensors 2016, 16, 273. [Google Scholar] [CrossRef] [PubMed]
- Sharma, P.; Sharma, N.; Gupta, R.; Jogi, J. Simulating Optical Behavior of Nano Dimensional InAlAs/InGaAs HEMT for IoT Applications. In Proceedings of the 2018 UKSim-AMSS 20th International Conference on Computer Modelling and Simulation, Cambridge, UK, 27–29 March 2018; pp. 181–185. [Google Scholar]
- Joshi, K.; Mukhopadhyay, S.; Goel, N.; Mahapatra, S. A consistent physical framework for N and P BTI in HKMG MOSFETs. In Proceedings of the 2012 IEEE International Reliability Physics Symposium, Anaheim, CA, USA, 15–19 April 2012; p. 5A-3. [Google Scholar]
- Oktyabrsky, S.; Peide, D.Y. Fundamentals of III-V Semiconductor MOSFETs; Springer: New York, NY, USA, 2010. [Google Scholar]
- Alam, M.A. A critical examination of the mechanics of dynamic NBTI for PMOSFETs. In Proceedings of the IEDM’03 International Technical Digest Electron Devices Meeting, Washington, DC, USA, 8–10 December 2003; pp. 4–14. [Google Scholar]
- Abbasizadeh, H.; Kim, S.Y.; Samadpoor Rikan, B.; Hejazi, A.; Khan, D.; Pu, Y.G.; Hwang, K.C.; Yang, Y.; Kim, D.I.; Lee, K.Y. Design of a 900 MHz Dual-Mode SWIPT for Low-Power IoT Devices. Sensors 2019, 19, 4676. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Puttaswamy, K.; Loh, G.H. 3D-integrated SRAM components for high-performance microprocessors. IEEE Trans. Comput. 2009, 58, 1369–1381. [Google Scholar] [CrossRef]
- Kufluoglu, H.; Alam, M.A. Theory of interface-trap-induced NBTI degradation for reduced cross section MOSFETs. IEEE Trans. Electron Devices 2006, 53, 1120–1130. [Google Scholar] [CrossRef]
- Lee, H.; Lee, C.H.; Park, D.; Choi, Y.K. A comprehensive modeling of dynamic negative-bias temperature instability in PMOS body-tied FinFETs. IEEE Electron Device Lett. 2006, 27, 281–283. [Google Scholar]
- Islam, A.E.; Kufluoglu, H.; Varghese, D.; Mahapatra, S.; Alam, M.A. Recent issues in negative-bias temperature instability: Initial degradation, field dependence of interface trap generation, hole trapping effects, and relaxation. IEEE Trans. Electron Devices 2007, 54, 2143–2154. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Reddy, V.; Krishnan, A.T.; Vattikonda, R.; Krishnan, S.; Cao, Y. Compact modeling and simulation of circuit reliability for 65-nm CMOS technology. IEEE Trans. Device Mater. Reliab. 2007, 7, 509–517. [Google Scholar] [CrossRef]
- Alam, M.A.; Kufluoglu, H.; Varghese, D.; Mahapatra, S. A comprehensive model for PMOS NBTI degradation: Recent progress. Microelectron. Reliab. 2007, 47, 853–862. [Google Scholar] [CrossRef]
- Ma, C.; Li, B.; He, F.; Zhang, X.; Lin, X. A novel Negative Bias Temperature Instability model for nanoscale Finfet. In Proceedings of the 16th IEEE International Symposium on the Physical and Failure Analysis of Integrated Circuits, Suzhou, China, 6–10 July 2009; pp. 117–121. [Google Scholar]
- Wang, Y.; Cotofana, S.D.; Fang, L. Statistical reliability analysis of NBTI impact on FinFET SRAMs and mitigation technique using independent-gate devices. In Proceedings of the 2012 IEEE/ACM International Symposium on Nanoscale Architectures, Amsterdam, The Netherlands, 4–6 July 2012; pp. 109–115. [Google Scholar]
- Mishra, S.; Wong, H.Y.; Tiwari, R.; Chaudhary, A.; Rao, R.; Moroz, V.; Mahapatra, S. TCAD-Based Predictive NBTI Framework for Sub-20-nm Node Device Design Considerations. IEEE Trans. Electron Devices 2016, 63, 4624–4631. [Google Scholar] [CrossRef]
- Yadav, N.; Shah, A.P.; Beohar, A.; Vishvakarma, S.K. Source drain Gaussian doping profile analysis for high ON current of InGaAs based HEMT. In Proceedings of the 2017 International Conference on Electron Devices and Solid-State Circuits, Hsinchu, Taiwan, 18–20 October 2017; pp. 1–2. [Google Scholar]
- Synopsys, T. SDEVICE Manual, Release H-2013.03; Synopsys: Zurich, Switzerland, 2013. [Google Scholar]
- Vardi, A.; del Alamo, J.A. Sub-10-nm Fin-Width Self-Aligned InGaAs FinFETs. IEEE Electron Device Lett. 2016, 37, 1104–1107. [Google Scholar] [CrossRef]
- Kim, E.J.; Chagarov, E.; Cagnon, J.; Yuan, Y.; Kummel, A.C.; Asbeck, P.M.; Stemmer, S.; Saraswat, K.C.; McIntyre, P.C. Atomically abrupt and unpinned Al2O3/In0.53Ga0.47As interfaces: Experiment and simulation. J. Appl. Phys. 2009, 106, 124508. [Google Scholar] [CrossRef]
- Weijtens, C. Reduction of oxide charge and interface-trap density in MOS capacitors with ITO gates. IEEE Trans. Electron Devices 1992, 39, 1889–1894. [Google Scholar] [CrossRef]
- Parihar, N.; Goel, N.; Mukhopadhyay, S.; Mahapatra, S. BTI analysis tool Modeling of NBTI DC, AC stress and recovery time kinetics, nitrogen impact, and EOL estimation. IEEE Trans. Electron Devices 2017, 65, 392–403. [Google Scholar] [CrossRef]
- Reis, R.; Cao, Y.; Wirth, G. Circuit Design for Reliability; Springer: New York, NY, USA, 2015. [Google Scholar]
- Mitonneau, A.; Mircea, A.; Martin, G.; Pons, D. Electron and hole capture cross-sections at deep centers in gallium arsenide. Rev. Phys. Appl. 1979, 14, 853–861. [Google Scholar] [CrossRef]
- Saks, N.S.; Ancona, M.G. Determination of interface trap capture cross sections using three-level charge pumping. IEEE Electron Device Lett. 1990, 11, 339–341. [Google Scholar] [CrossRef] [Green Version]
- Deora, S.; Bersuker, G.; Kim, T.; Kim, D.; Hobbs, C.; Kirsch, P.; Sahoo, K.; Oates, A. Positive bias instability in gate-first and gate-last InGaAs channel n-MOSFETs. In Proceedings of the 2014 IEEE International Reliability Physics Symposium, Waikoloa, HI, USA, 1–5 June 2014; p. 3C-5. [Google Scholar]
- Cartier, E.; Frank, M.M.; Ando, T.; Rozen, J.; Narayanan, V. PBTI in InGaAs MOS capacitors with Al2O3/HfO2/TiN gate stacks: Interface-state generation. In Proceedings of the 2018 IEEE International Reliability Physics Symposium, Burlingame, CA, USA, 11–15 March 2018; p. 5A-4. [Google Scholar]
- Li, Y.; Di, S.; Jiang, H.; Huang, P.; Wang, Y.; Lun, Z.; Shen, L.; Yin, L.; Zhang, X.; Du, G.; et al. Insight into PBTI in InGaAs nanowire FETs with Al2O3 and LaAlO3 gate dielectrics. In Proceedings of the 2016 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 3–7 December 2016; p. 36-5. [Google Scholar]
- Franco, J.; Kaczer, B.; Waldron, N.; Roussel, P.J.; Alian, A.; Pourghaderi, M.A.; Ji, Z.; Grasser, T.; Kauerauf, T.; Sioncke, S.; et al. RTN and PBTI-induced time-dependent variability of replacement metal-gate high-k InGaAs FinFETs. In Proceedings of the 2014 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2014; pp. 20–22. [Google Scholar]







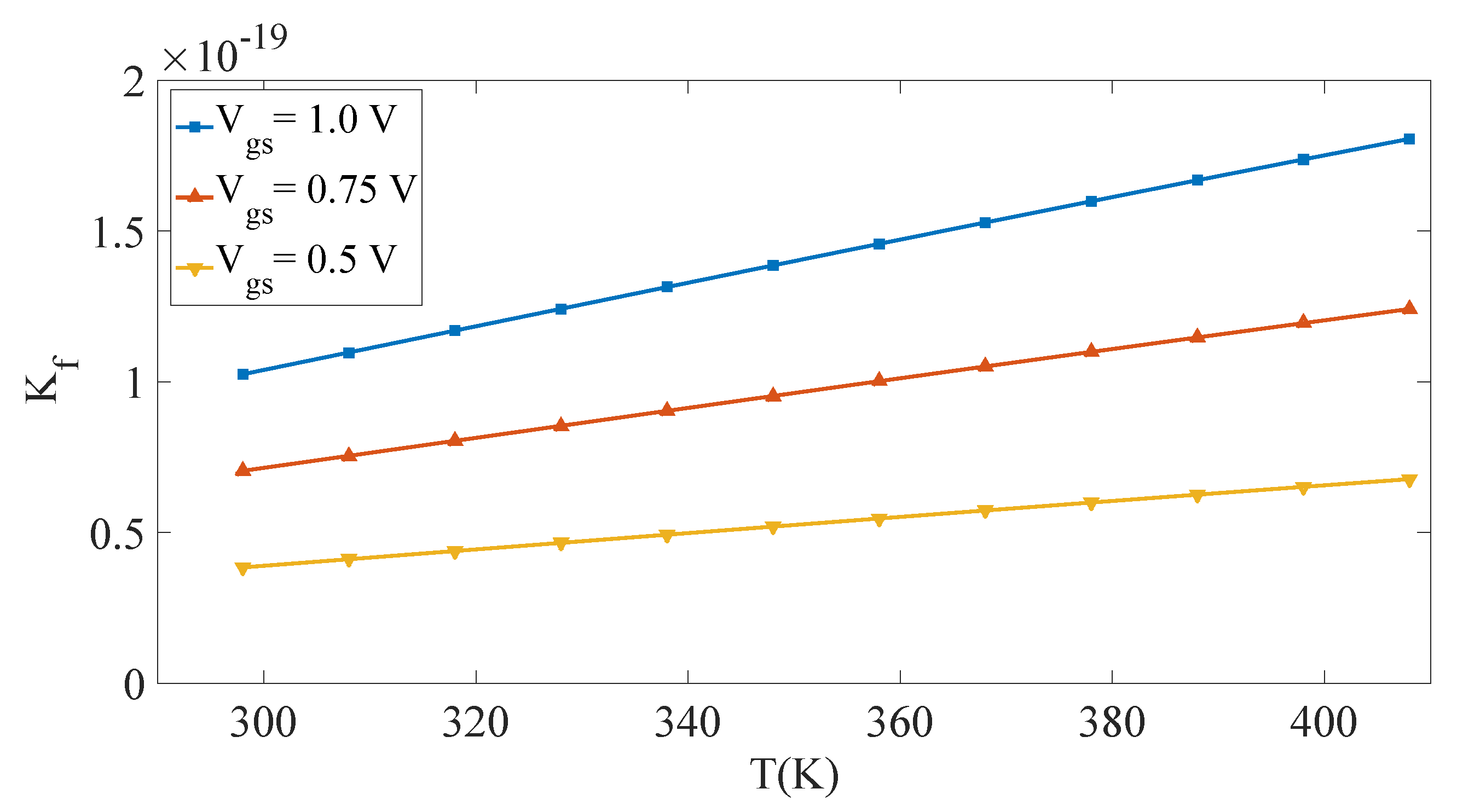



| Operating voltage [V] | 0.5 |
| Operating overdrive =2/3 * [V] | 0.33 |
| EOT [nm] | 1.8 |
| Operating [mV/cm] | 2 |
| [nm] | 35 |
| [nm] | 10 |
| [nm] | 30 |
| PBTI time exponent (n) | 0.1 |
| [mV] | 118 |
| [cm−2] | 2 × 1011 |
| K | |
| 1.8 nm | |
| 9 | |
| 9.56 × 10−11 cm2/s | |
| 0.2 eV | |
| 2 eV | |
| 0.5 eV | |
| 0.58 | |
| 0.054 eV |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadav, N.; Alashi, M.; Choi, K.K. Design and Development of BTI Model and 3D InGaAs HEMT-Based SRAM for Reliable and Secure Internet of Things Application. Electronics 2020, 9, 469. https://doi.org/10.3390/electronics9030469
Yadav N, Alashi M, Choi KK. Design and Development of BTI Model and 3D InGaAs HEMT-Based SRAM for Reliable and Secure Internet of Things Application. Electronics. 2020; 9(3):469. https://doi.org/10.3390/electronics9030469
Chicago/Turabian StyleYadav, Nandakishor, Mahmoud Alashi, and Kyuwon Ken Choi. 2020. "Design and Development of BTI Model and 3D InGaAs HEMT-Based SRAM for Reliable and Secure Internet of Things Application" Electronics 9, no. 3: 469. https://doi.org/10.3390/electronics9030469





