A Spherical Near-to-far-Field Transformation Using a Non-Redundant Voltage Representation Optimized for Non-Centered Mounted Quasi-Planar Antennas
Abstract
:1. Introduction
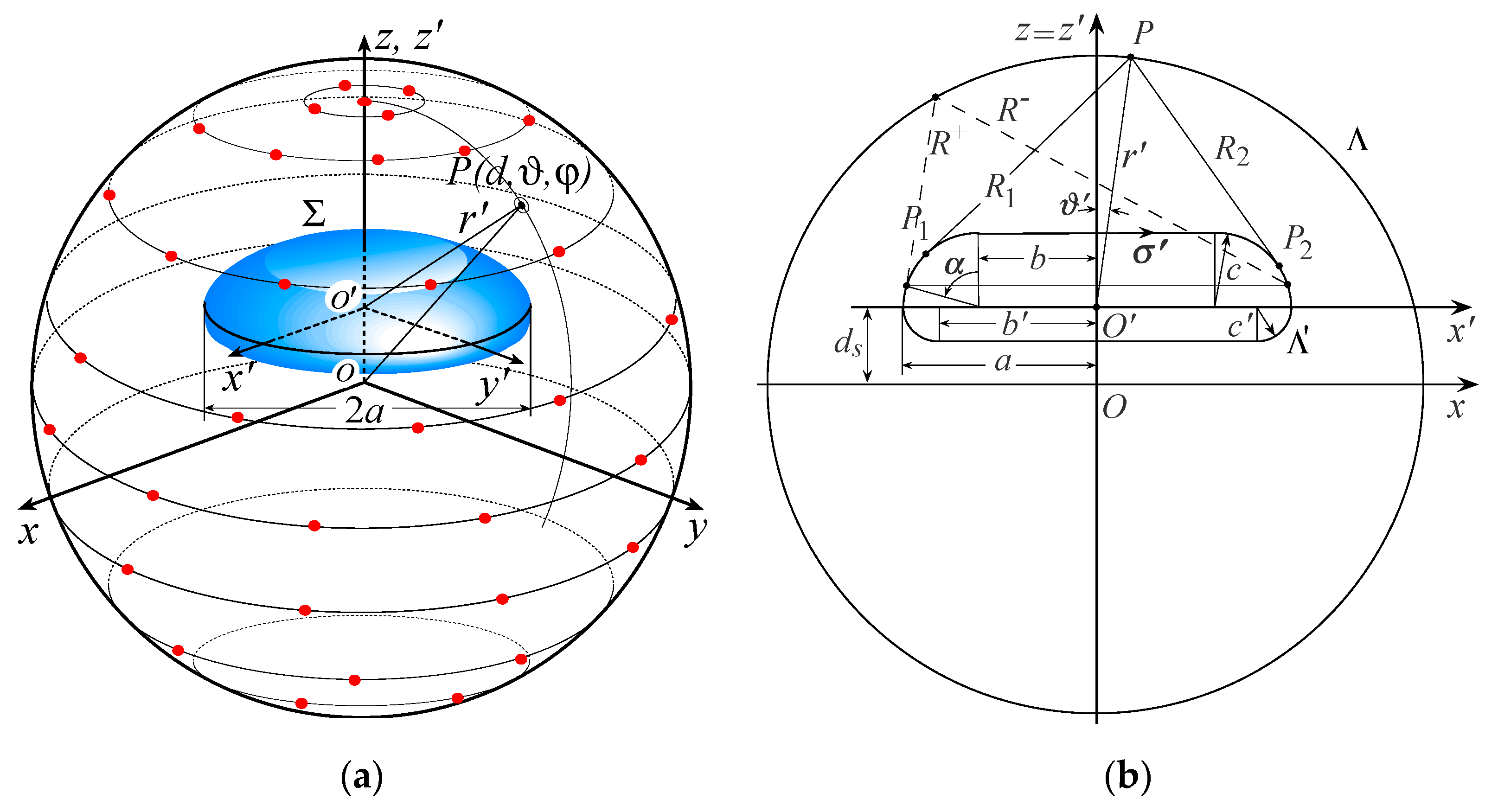
2. Sampling Representation over a Sphere from a Minimum Number of NF Samples
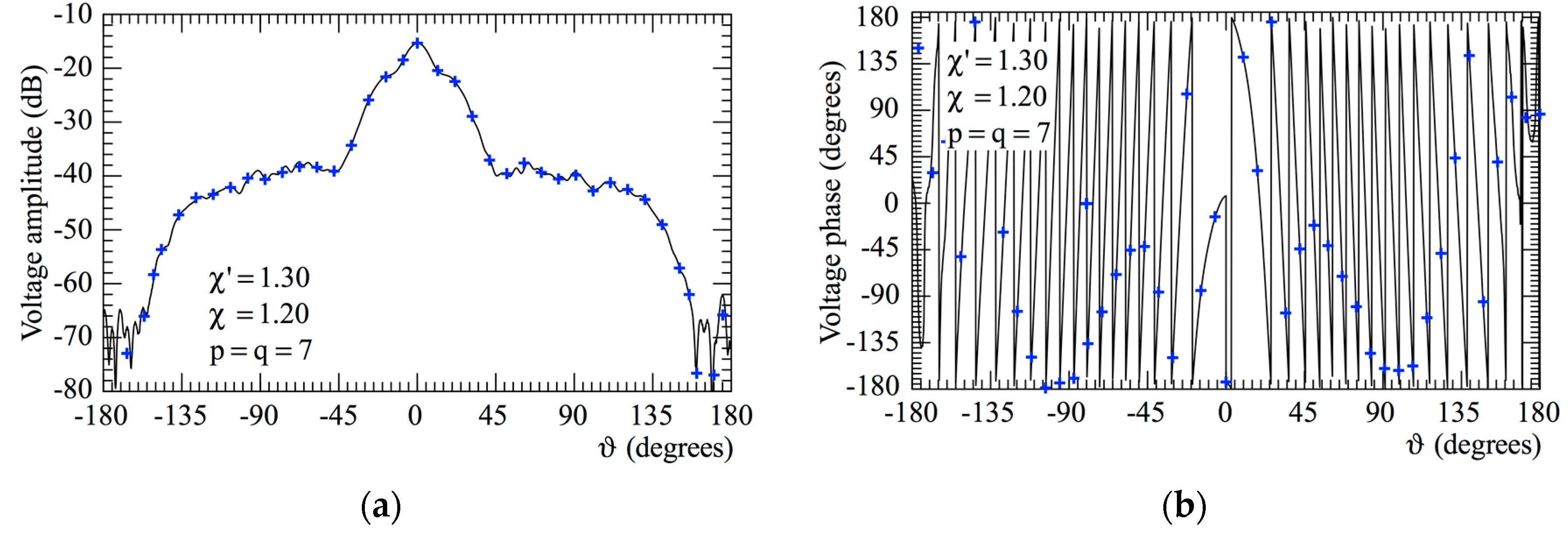
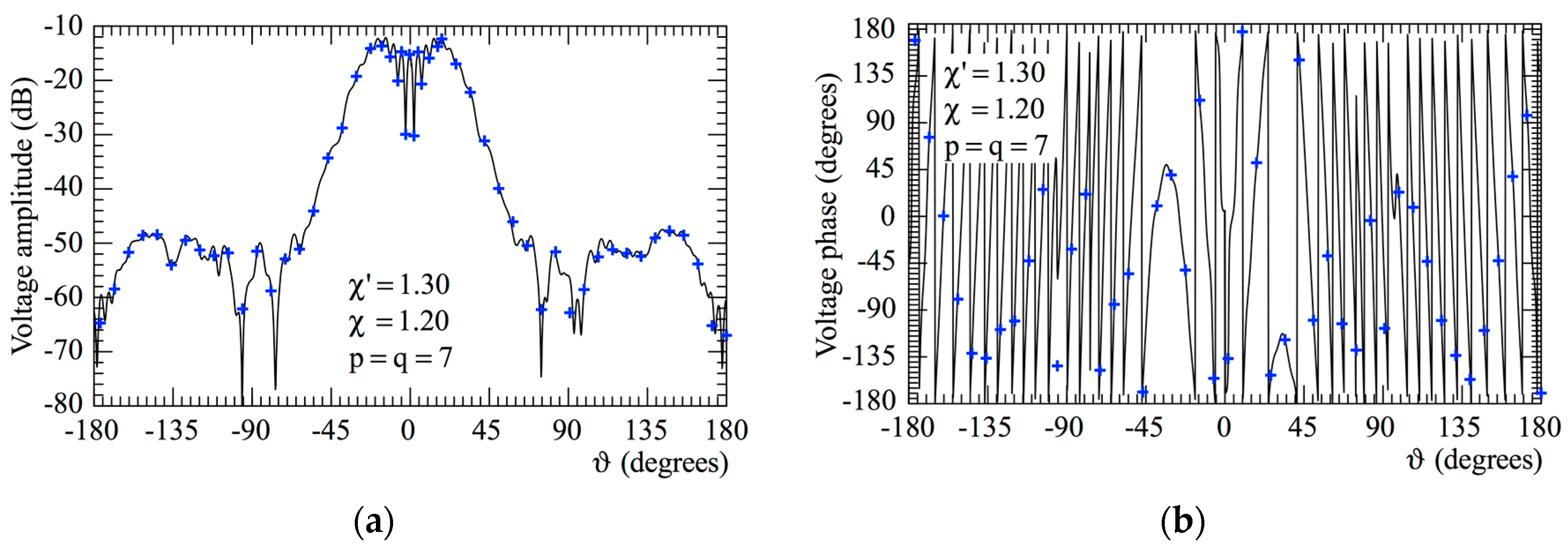
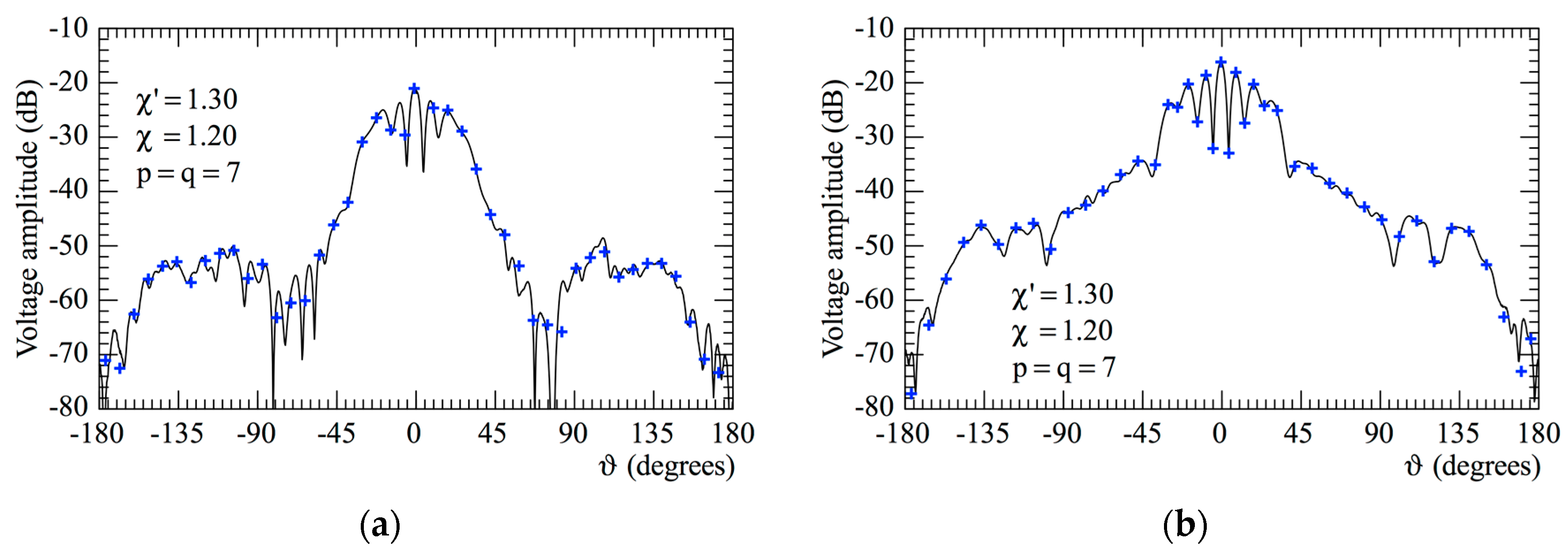
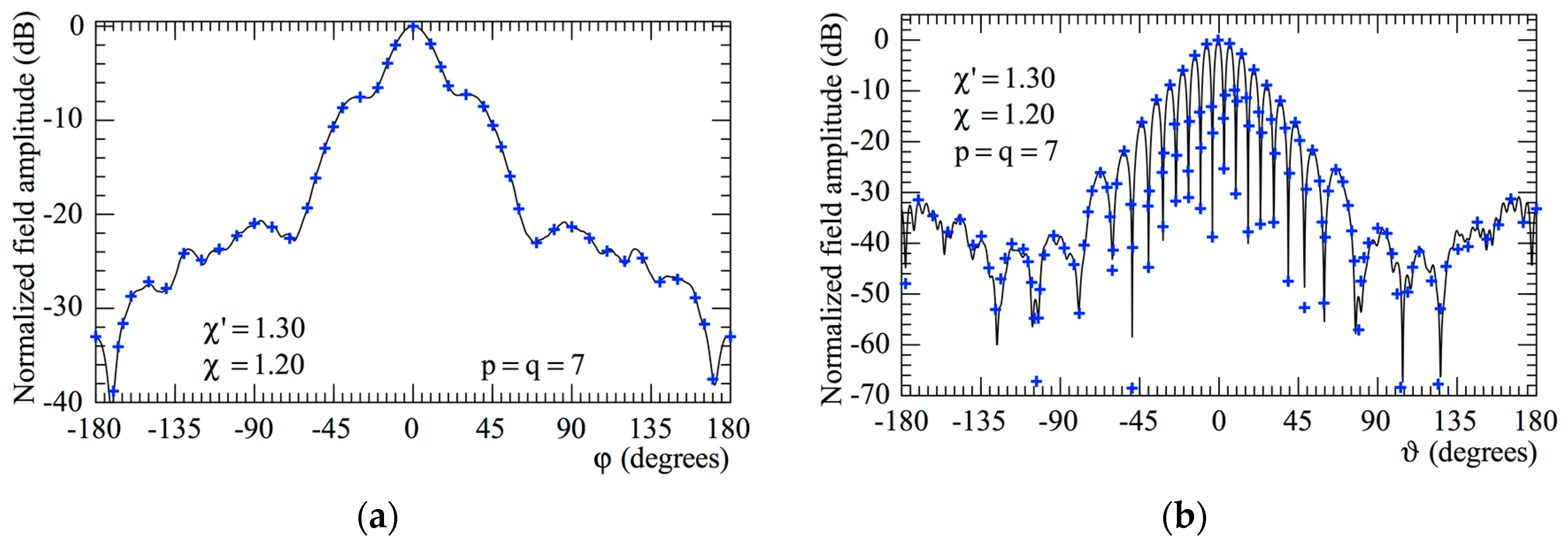
3. Results
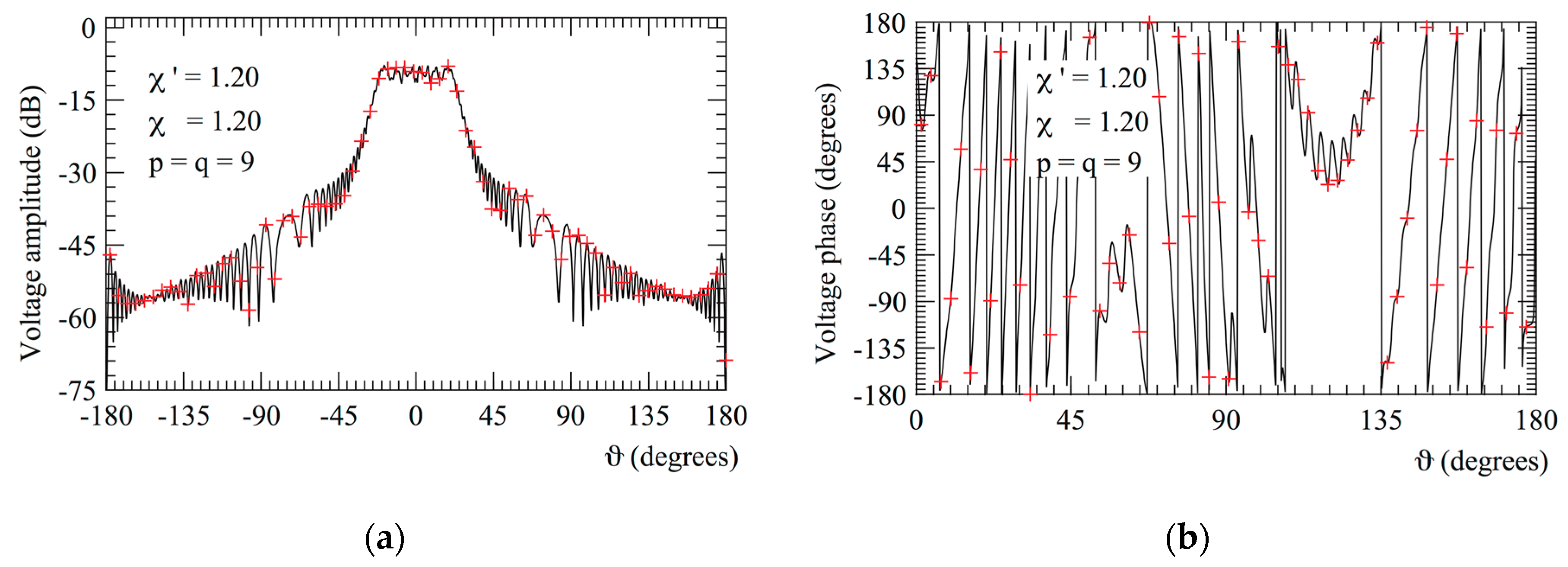
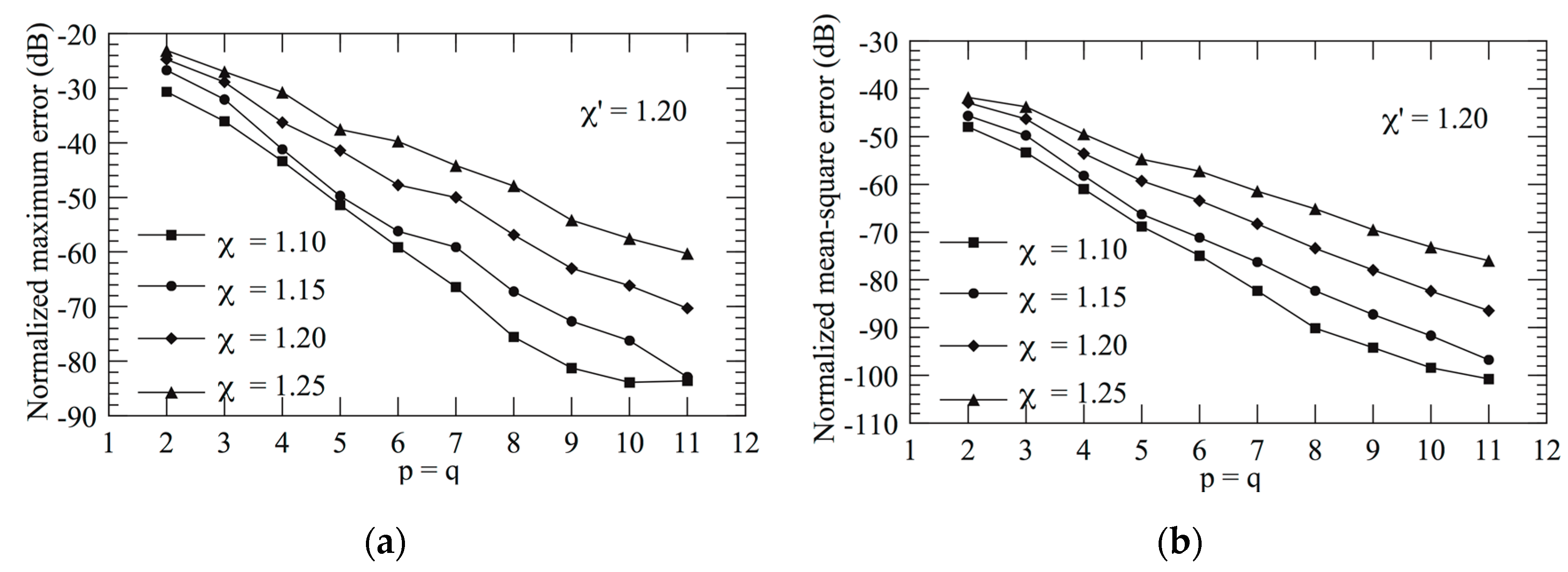
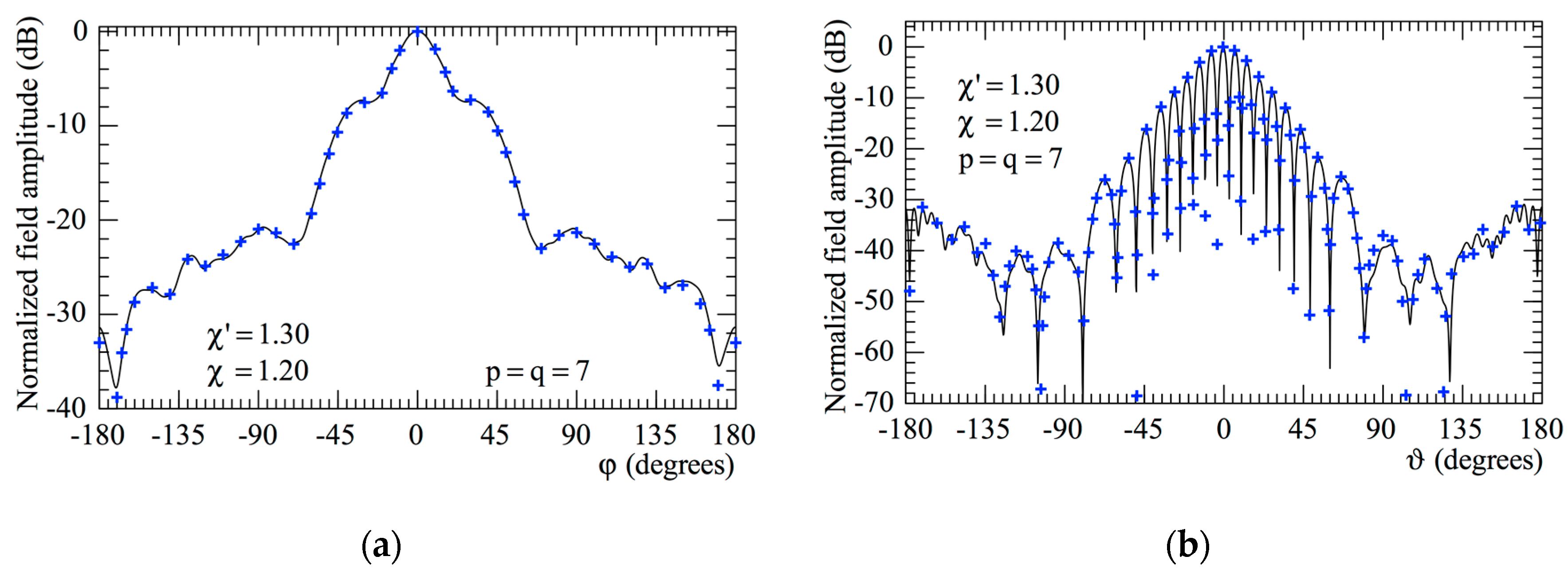
3.1. Numerical Simulations
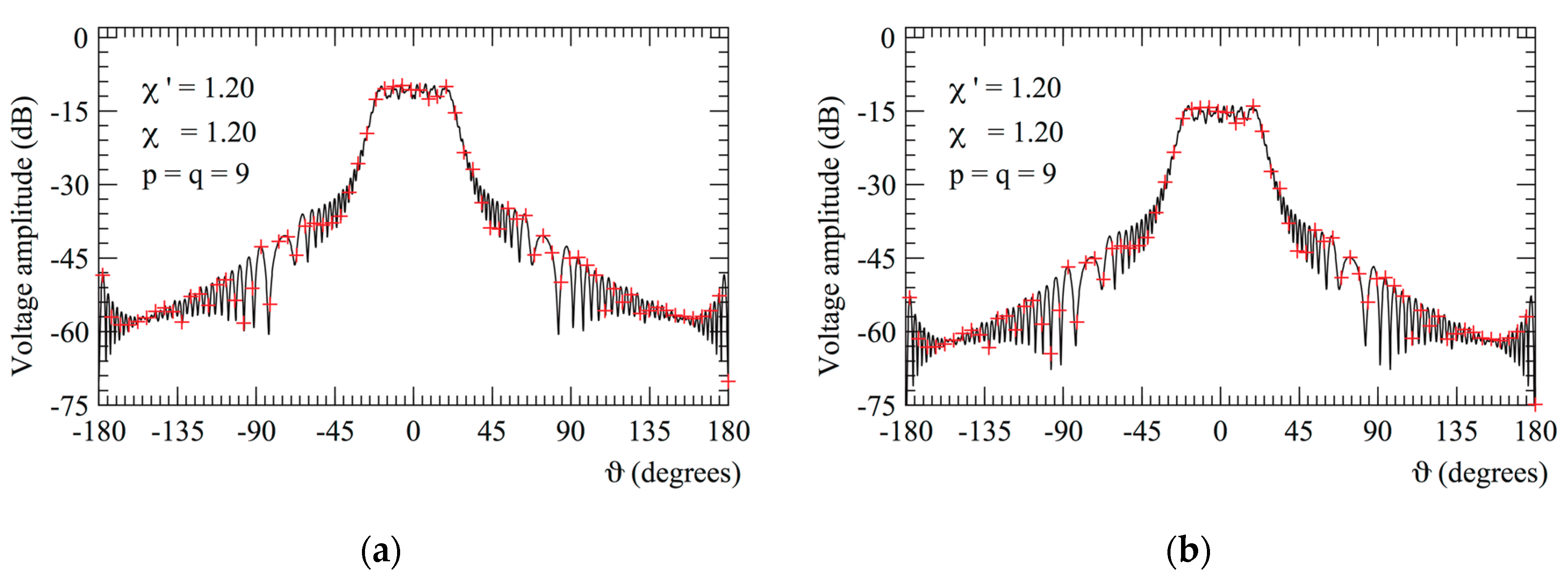
3.2. Experimental Proofs
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yaghjian, A.D. An overview of near-field antenna measurements. IEEE Trans. Antennas Propag. 1986, 34, 30–45. [Google Scholar] [CrossRef] [Green Version]
- Appel-Hansen, J.; Dyson, J.D.; Gillespie, E.S.; Hickman, T.G. Antenna measurements. In The Handbook of Antenna Design; Rudge, A.W., Milne, K., Olver, A.D., Knight, P., Eds.; Peter Peregrinus: London, UK, 1986; pp. 584–694. [Google Scholar]
- Francis, M.H.; Wittmann, R.W. Near-field scanning measurements: Theory and practice. In Modern Antenna Handbook; Balanis, C.A., Ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2008; pp. 929–976. [Google Scholar]
- Gennarelli, C.; Capozzoli, A.; Foged, L.; Fordham, J.; van Rensburg, D.J. Recent advances in near-field to far-field transformation techniques. Int. J. Antennas Propag. 2012, 2012, 1–3. [Google Scholar] [CrossRef]
- IEEE Standard 1720–2012 IEEE Recommended Practice for Near-Field Antenna Measurements; Francis, M.H. (Ed.) IEEE: New York, NY, USA, 2012. [Google Scholar]
- Ferrara, F.; Gennarelli, C.; Guerriero, R. Near-field antenna measurement techniques. In Handbook of Antenna Technologies; Chen, Z.N., Liu, D., Nakano, H., Qing, X., Zwick, T., Eds.; Springer Singapore: Singapore, 2016; pp. 2107–2163. [Google Scholar]
- Yaccarino, R.G.; Rahmat-Samii, Y. Phaseless bi-polar planar near-field measurements and diagnostics of array antennas. IEEE Trans. Antennas Propag. 1999, 47, 574–583. [Google Scholar] [CrossRef]
- Álvarez, Y.; Las-Heras, F.; Pino, M.R. Antenna diagnostics using phaseless NF information. Automatika 2012, 53, 49–55. [Google Scholar] [CrossRef]
- Jensen, F. On the probe compensation for near-field measurements on a sphere. Arch. Elektr. Übertr. 1975, 29, 306–308. [Google Scholar]
- Wacker, P.F. Non-Planar Near-Field Measurements: Spherical Scanning; NBSIR 75-809: Boulder, CO, USA, 1975. [Google Scholar]
- Larsen, F.H. Probe correction of spherical near-field measurements. Electron. Lett. 1977, 13, 393–395. [Google Scholar] [CrossRef]
- Yaghjian, A.D.; Wittmann, R.C. The receiving antenna as a linear differential operator: Application to spherical near-field measurements. IEEE Trans. Antennas Propag. 1985, 33, 1175–1185. [Google Scholar] [CrossRef]
- Hansen, J.E.; Jensen, F. Spherical near-field scanning at the technical university of Denmark. IEEE Trans. Antennas Propag. 1988, 36, 734–739. [Google Scholar] [CrossRef]
- Hald, J.; Hansen, J.E.; Jensen, F.; Larsen, F.H. Spherical Near-Field Antenna Measurements; Hansen, J.E., Ed.; Peregrinus: London, UK, 1998. [Google Scholar]
- Bucci, O.M.; Gennarelli, C.; Riccio, G.; Savarese, C. Data reduction in the NF-FF transformation technique with spherical scanning. J. Electromagn. Waves Appl. 2001, 15, 755–775. [Google Scholar] [CrossRef]
- Laitinen, T.; Pivnenko, S.; Nielsen, J.M.; Breinbjerg, O. Theory and practice of the FFT/matrix inversion technique for probe-corrected spherical near-field antenna measurements with high-order probes. IEEE Trans. Antennas Propag. 2010, 58, 2623–2631. [Google Scholar] [CrossRef] [Green Version]
- Hansen, T.B. Spherical near-field scanning with higher-order probes. IEEE Trans. Antennas Propag. 2011, 59, 4049–4059. [Google Scholar] [CrossRef]
- D’Agostino, F.; Ferrara, F.; Gennarelli, C.; Guerriero, R.; Migliozzi, M. Effective antenna modellings for NF-FF transformations with spherical scanning using the minimum number of data. Int. J. Antennas Propag. 2011, 936781, 1–11. [Google Scholar] [CrossRef]
- Hansen, T.B. Numerical investigation of the system-matrix method for higher-order probe correction in spherical near-field antenna measurements. Int. J. Antennas Propag. 2012, 2012, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, M.A.; Schmidt, C.H.; Eibert, T.F. Adaptive sampling in spherical and cylindrical near-field antenna measurements. IEEE Antennas Propag. Magaz. 2013, 55, 243–249. [Google Scholar] [CrossRef]
- D’Agostino, F.; Ferrara, F.; Gennarelli, C.; Guerriero, R.; Migliozzi, M. Non-redundant spherical NF-FF transformations using ellipsoidal antenna modeling: Experimental assessments. IEEE Antennas Propag. Magaz. 2013, 55, 166–175. [Google Scholar] [CrossRef]
- D’Agostino, F.; Ferrara, F.; Gennarelli, C.; Guerriero, R.; Migliozzi, M. Experimental testing of nonredundant near-field to far-field transformations with spherical scanning using flexible modellings for nonvolumetric antennas. Int. J. Antennas Propag. 2013, 2013, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Cornelius, R.; Heberling, D. Spherical near-field scanning with pointwise probe correction. IEEE Trans. Antennas Propag. 2017, 65, 995–996. [Google Scholar] [CrossRef]
- Cornelius, R.; Heberling, D. Spherical wave expansion with arbitrary origin for near-field antenna measurements. IEEE Trans. Antennas Propag. 2017, 65, 4385–4388. [Google Scholar] [CrossRef]
- Saccardi, F.; Rossi, F.; Mioc, F.; Foged, L.J.; Iversen, P.O. Application of the translated-SWE algorithm for the characterization of antennas installed on cars using a minimum number of samples. In Proceedings of the Antenna Measurement Techniques Association Symposium, Atlanta, GA, USA, 15–20 October 2017; pp. 1–6. [Google Scholar]
- Mauermayer, R.A.M.; Eibert, T.F. Spherical field transformation above perfectly electrically conducting ground planes. IEEE Trans. Antennas Propag. 2018, 66, 1465–1478. [Google Scholar] [CrossRef]
- D’Agostino, F.; Ferrara, F.; Foged, L.J.; Gennarelli, C.; Guerriero, R.; Saccardi, F.; Saporetti, M.A.; Trenta, D. Fast measurement methodology for near field satellite testing. In Proceedings of the European Conference on Antennas and Propagation, Krakow, Poland, 31 March–April 2019; pp. 1–5. [Google Scholar]
- Alavi, R.R.; Mirzavand, R.; Doucette, J.; Mousavi, P. An adaptive data acquisition and clustering technique to enhance the speed of spherical near-field antenna measurements. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2329–2335. [Google Scholar] [CrossRef]
- Almajali, E.; van Rensburg, D.J.; McNamara, D.A. Customized spherical near-field test time reduction for wireless base station antennas. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 172–176. [Google Scholar] [CrossRef]
- Hofmann, B.; Neitz, O.; Eibert, T.F. On the minimum number of samples for sparse recovery in spherical antenna near-field measurements. IEEE Trans. Antennas Propag. 2019, 67, 7597–7610. [Google Scholar] [CrossRef]
- Bucci, O.M.; Franceschetti, G. On the spatial bandwidth of scattered fields. IEEE Trans. Antennas Propag. 1987, 35, 1445–1455. [Google Scholar] [CrossRef]
- Bucci, O.M.; Gennarelli, C.; Savarese, C. Representation of electromagnetic fields over arbitrary surfaces by a finite and nonredundant number of samples. IEEE Trans. Antennas Propag. 1998, 46, 351–359. [Google Scholar] [CrossRef]
- Bucci, O.M.; Gennarelli, C. Application of nonredundant sampling representations of electromagnetic fields to NF-FF transformation techniques. Int. J. Antennas Propag. 2012, 2012, 1–14. [Google Scholar] [CrossRef]
- Bucci, O.M.; Gennarelli, C.; Savarese, C. Optimal interpolation of radiated fields over a sphere. IEEE Trans. Antennas Propag. 1991, 39, 1633–1643. [Google Scholar] [CrossRef]
- Bucci, O.M.; D’Elia, G.; Migliore, M.D. Advanced field interpolation from plane-polar samples: Experimental verification. IEEE Trans. Antennas Propag. 1998, 46, 204–210. [Google Scholar] [CrossRef]
- Foged, L.J.; Iversen, P.O.; Mioc, F.; Saccardi, F. Spherical near field offset measurements using downsampled acquisition and advanced NF/FF transformation algorithm. In Proceedings of the European Conference on Antennas and Propagation, Davos, Switzerland, 10–15 April 2016; p. 1570229473. [Google Scholar]
- D’Agostino, F.; Ferrara, F.; Gennarelli, C.; Guerriero, R.; Migliozzi, M. Non-redundant spherical near-field to far-field transformation for a volumetric antenna in offset configuration. Open Electr. Electron. Engin. J. 2019, 13, 19–29. [Google Scholar] [CrossRef]
- D’Agostino, F.; Ferrara, F.; Gennarelli, C.; Guerriero, R.; Migliozzi, M. A non-redundant sampling repre sentation managing an offset mounting of an elongated antenna in a spherical near-field facility. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2671–2675. [Google Scholar] [CrossRef]
- D’Agostino, F.; Ferrara, F.; Gennarelli, C.; Guerriero, R. A non-redundant sampling representation requiring the same number of spherical near-field measurements for both onset and offset mountings of a quasi-planar antenna. Int. J. Commun. Antenna Propag. 2019, 9, 311–319. [Google Scholar]
- Yaghjian, A.D. Approximate formulas for the far field and gain of open-ended rectangular waveguide. IEEE Trans. Antennas Propag. 1984, 32, 378–384. [Google Scholar] [CrossRef]
- D’Agostino, F.; Ferrara, F.; Gennarelli, C.; Guerriero, R.; Migliozzi, M. Laboratory Proofs on a Nonredundant Spherical NF-FF Transformation for a Quasi-Planar AUT Mounted in Offset Configuration. In Proceedings of the 2018 Antenna Measurement Techniques Association, Williamsburg, VA, USA, 4–9 November 2018; pp. 1–5. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Agostino, F.; Ferrara, F.; Gennarelli, C.; Guerriero, R.; Migliozzi, M. A Spherical Near-to-far-Field Transformation Using a Non-Redundant Voltage Representation Optimized for Non-Centered Mounted Quasi-Planar Antennas. Electronics 2020, 9, 944. https://doi.org/10.3390/electronics9060944
D’Agostino F, Ferrara F, Gennarelli C, Guerriero R, Migliozzi M. A Spherical Near-to-far-Field Transformation Using a Non-Redundant Voltage Representation Optimized for Non-Centered Mounted Quasi-Planar Antennas. Electronics. 2020; 9(6):944. https://doi.org/10.3390/electronics9060944
Chicago/Turabian StyleD’Agostino, Francesco, Flaminio Ferrara, Claudio Gennarelli, Rocco Guerriero, and Massimo Migliozzi. 2020. "A Spherical Near-to-far-Field Transformation Using a Non-Redundant Voltage Representation Optimized for Non-Centered Mounted Quasi-Planar Antennas" Electronics 9, no. 6: 944. https://doi.org/10.3390/electronics9060944
APA StyleD’Agostino, F., Ferrara, F., Gennarelli, C., Guerriero, R., & Migliozzi, M. (2020). A Spherical Near-to-far-Field Transformation Using a Non-Redundant Voltage Representation Optimized for Non-Centered Mounted Quasi-Planar Antennas. Electronics, 9(6), 944. https://doi.org/10.3390/electronics9060944








