Symmetric-Key Cryptographic Routine Detection in Anti-Reverse Engineered Binaries Using Hardware Tracing

Abstract

Software uses cryptography to provide confidentiality in communication and to provide authentication. Additionally, cryptographic algorithms can be used to protect software against cracking core algorithms in software implementation. Recently, malware and ransomware have begun to use encryption to protect their codes from analysis. As for the detection of cryptographic algorithms, previous works have had demerits in analyzing anti-reverse engineered binaries that can detect differences in analysis environments and normal execution. Here, we present a new symmetric-key cryptographic routine detection scheme using hardware tracing. In our experiments, patterns were successfully generated and detected for nine symmetric-key cryptographic algorithms. Additionally, the experimental results show that the false positive rate of our scheme is extremely low and the prototype implementation successfully bypasses anti-reversing techniques. Our work can be used to detect symmetric-key cryptographic routines in malware/ransomware with anti-reversing techniques.

1. Introduction

As security is considered a significant issue in modern software development, various security techniques have been used to protect software products from the threats. Among them, one of the most widely used of techniques is cryptography. Software uses cryptography to provide confidentiality in communication and to provide authentication. Additionally, it can be used to protect software against cracking core algorithms in software implementation.

Recently, malware [1,2] and ransomware [3,4] have begun to use encryption to hide important information from analysis, e.g., ransomware encrypts user’s files and displays messages to persuade users to pay. In order to alleviate the difficulties that analysts face and to increase analysis efficiency, it is necessary to identify cryptographic routines in the target executable and to detect the correct cryptographic algorithm.

There are roughly two approaches of executable analysis that analysts use to detect cryptographic algorithms. The first is static analysis, which detects important features without execution such as specific constant values or machine instructions used by cryptographic algorithms. These characteristics are unique signatures of encryption algorithms, so a static approach is also called a signature-based detection method [5]. Existing signature-based encryption detection tools include KANAL [6], DRACA [7], FindCrypt2 [8], and Signsrch [9]. However, since static detection methods perform analysis without executing a program, accurate analysis cannot be performed for polymorphic/metamorphic malware [10] that uses self-modifying code (which alters its own instructions while it is executing) or code packing (which compresses malware code and combines the compressed data with a decompression routine into a single executable) techniques. Therefore, a second analysis approach, a dynamic analysis method, has appeared to address this problem.

Dynamic analysis, unlike static analysis, analyzes run-time behavior during program execution. Therefore, dynamic analysis can analyze a program with a self-modifying code or code packing techniques. Aligot [5], CryptoHunt [11], and K-HUNT [12] are cryptographic detection tools that adopt dynamic analysis. However, for such dynamic analysis, the target executable must be executed in a secure environment for analysis. The analysis process at this time takes a considerable amount of time due to the creation of a separate execution environment. Additionally, the secure environment is quite different from a runtime environment on an actual native machine [13]. The detection of encryption algorithms using dynamic analysis hits a limit as the executable under analysis begins to detect differences in these execution environments by applying anti-reversing techniques that execute different behaviors than in normal execution. Recently, commercial packers, including Themida [14] and Enigma [15], use anti-reversing and encryption techniques at the same time to protect executables [16].

To overcome this limitation, we present a symmetric-key cryptographic routine detection scheme that uses hardware tracing. Hardware tracing [17,18] is the latest monitoring function supported by CPU hardware and provides execution traces at the CPU level. At this time, because it does not build a separate execution environment like dynamic analysis, it is possible to obtain a trace for the target executable in runtime environment while evading anti-reversing techniques. In this paper, our scheme detects the symmetric-key cryptographic routine from the executable by utilizing these characteristics of hardware tracing.

However, hardware tracing has some limitations. First, it provides a very limited type of information compared to existing analysis tools. The limited information includes timing, program flow information, and program-induced mode-related information [18]. Because hardware tracing records execution information for all instructions executed by the CPU, the size of the trace log is very large, making it difficult to find the exact location of the information to be analyzed. To overcome this limitation, our scheme uses the new feature of the latest CPUs—software trace instrumentation, which allows the analyst to instrument directly into the hardware tracing record. This allows for the analysis of the execution information of the cryptographic routine to generate a certain pattern using the limited information provided by hardware tracing. In this paper, we generate these patterns and propose a scheme of detecting cryptographic algorithms in the executable using the generated patterns.

The cryptographic algorithm can be divided into symmetric-key cryptography and public-key cryptography. Among them, we focused on the symmetric-key cryptographic algorithm. The operation of the symmetric-key cryptographic algorithm can be roughly classified into three processes: key generation, data processing according to the block cipher mode of operation, and encryption round functions. We found out that for most of symmetric-key cryptographic algorithms, these processes perform fixed operations regardless of key or plaintext contents. Hence, we succeeded in using this property to obtain the unique pattern for each of the symmetric-key cryptographic algorithms.

In this paper, we propose a symmetric-key cryptographic routine detection scheme using hardware tracing. This method utilizes the characteristics of a symmetric-key cryptographic algorithm to create a signature pattern that can specify the type of algorithm through hardware tracing. The signature pattern of the encryption operation is generated for each widely used cryptographic library, and it is then integrated and stored in the database. The patterns generated in this way can not only detect the type of cryptographic algorithm but also detect the block cipher mode of operation.

Experiments were conducted on cryptographic libraries to verify the practicality of the scheme proposed in this paper. As a result, patterns were generated and detected for each block cipher mode of operation for nine types of symmetric-key cryptographic algorithms. In addition, we conducted experiments on normal executables that do not perform encryption to measure the rate of false positives. The experiment confirmed that the probability of incorrectly detecting a pattern was 0% when the number of iterations of the encryption routine reached a certain threshold value. Finally, we conducted experiments on target executables using anti-reversing techniques to verify whether our scheme could bypass the anti-reversing techniques. Our experiments showed that the dynamic analysis tools that previous works have relied on are detected by anti-reversing techniques, but the proposed scheme successfully bypassed them.

This paper is organized as follows. First, in Section 2, we mathematically define the problem that our scheme is trying to solve. Section 3 introduces related works. Section 4 describes the proposed scheme. Section 5 explains the implementation of the proposed scheme. Section 6 shows the experimental results, and we conclude in Section 7.

2. Problem Definition

In this section, we mathematically define the problem that we focus on. The problem is defined as follows (which is based on [19]).

Let B denote a binary string (e.g., a text section in a Linux or Windows executable). Let B[i] denote the $i^{th}$ byte of B. A cryptographic routine (CR) in a binary B is a list of bytes corresponding to machine instructions in either a cryptographic routine from the original compiled language or a cryptographic routine introduced directly by the compiler; this is denoted as Equation (1). Note that there are points where the bytes are not continuous.

$$CR=\left\{B\left[i\right], B\left[i+1\left], \dots , B\right[i+j\left], B\right[i+m\left], B\right[i+m+1\left], \dots , B\right[i+n\right]\right\}.$$

(1)

CR performs the cryptographic operation, which is an implementation of a certain algorithm. The function $NAM{E}_{ROUT}()$, which outputs the name of the cryptographic algorithm performed by CR is defined in Equation (2):

$$\begin{gathered} NAM{E}_{ROUT}\left(CR\right)=“Name of CR’s cryptographic algorithm,” \\ NAM{E}_{ROUT}\left(C{R}_{OPENSS{L}_{X_{AE{S}_{{128}_{CBC}}}}}\right)= “OPENSS{L}_{X_{AE{S}_{{128}_{CBC}}}}." \end{gathered}$$

(2)

where CR_OPENSSL_X_AES_128_CBC is the cryptographic routine for the OpenSSL version X of the AES cryptographic algorithm (key size: 128, block cipher mode of operation: CBC). In order to evaluate cryptographic routine detection algorithms, we define the ground truth in terms of oracles. The routine oracle, ${\mathit{O}}_{ROUT}()$, is an oracle that, given a binary B, returns a list of names of cryptographic algorithms in B, where each $NAM{E}_{ROUT}\left(C{R}_i\right)$ is the name of the algorithm of (higher-level) $i^{th}$ cryptographic routine. This function can be expressed as follows:

$${\mathit{O}}_{ROUT}\left(B\right)=\left\{s_1=NAM{E}_{ROUT}\left(C{R}_1\right), \dots ,s_n=NAM{E}_{ROUT}\left(C{R}_n\right)\right\}.$$

(3)

The definition of the problem we are trying to solve is as follows. The cryptographic routine detection (CRD) problem is to output the complete list of names of algorithms of the cryptographic routines $\left\{s_1, s_2, \dots , s_k\right\}$ given binary B compiled from a source containing k cryptographic routines.

Suppose that there is an algorithm A_CRD(B) for the CRD problem that outputs $\mathrm{S}=\left\{s_1, s_2, \dots , s_k\right\}$. Then, the set of true positives (TP), the set of false positives (FP), the set of false negatives (FN), and the set of true negatives (TN) are as follows:

$$\begin{gathered} TP=S\cap {\mathit{O}}_{ROUT}\left(B\right), \\ FP=S-{\mathit{O}}_{ROUT}\left(B\right), \\ FN={\mathit{O}}_{ROUT}\left(B\right)-S, \\ TN={\mathit{O}}_{ROUT}{\left(B\right)}^c-S. \end{gathered}$$

(4)

We also define recall and false positive rate (FPR) as follows:

$$\begin{gathered} Recall=\left|TP\right|/\left(\left|TP\right|+\left|FN\right|\right), \\ FPR=\left|FP\right|/\left(\left|TN\right|+\left|FP\right|\right). \end{gathered}$$

(5)

3. Related Work

In this section, we summarize previous works related to our scheme. In Section 3.1, we first describe the previous works on cryptographic algorithm detection. The methods of identifying cryptographic algorithms can be largely classified into static and dynamic detection. In Section 3.2, we summarize the research conducted using the hardware tracing function. In addition, there have been various recent studies [20,21,22,23,24] to detect ransomware. However, these studies aim not to detect the cryptographic algorithm used by ransomware, but to detect ransomware by taking advantage of the feature that ransomware uses encryption.

3.1. Cryptographic Algorithm Detection

Static detection is a cryptographic algorithm detection method that uses static analysis. The research conducted using the static detection method is as follows. First, KANAL [6] is a cryptographic identification tool that works as a plug-in for PEiD. PEiD is a tool that identifies packers, compilers, etc. KANAL defines a signatures (that are compatible with PEiD) to identify cryptographic algorithms.

DRACA [7] is a tool that detects encryption algorithm in the executable files. The tool is implemented as an 80 × 86/Win32 command line tool, but it can be used for the Unix ELF (executable and linkable format) binary, the Java applet, and the PE (portable executable) file.

FindCrypt2 [8] is a plug-in for IDA Pro, one of the popular disassemblers, that searches for constants known to be associated with the code’s encryption algorithm. Signsrch [9] is also a plug-in for IDA Pro that detects not only encryption algorithms but also compression algorithms, multimedia, and other known strings and anti-debugging techniques based on signatures. Users can also add their own signatures for detection.

These tools must update signatures whenever new or modified encryption algorithms appear. Because they do not execute programs when analyzing, it is not effective for analyzing polymorphic/metamorphic code that has self-modifying code or code packing techniques.

In addition, some of the studies that have analyzed cryptographic algorithms have done so without executing a target use deep learning. Hill et al. [25] introduced a new approach to classify cryptographic primitives in compiled binary executables using deep learning.

Next, dynamic detection is a cryptographic algorithm detection method that uses dynamic analysis. It uses debugger and DBI (dynamic binary instrumentation) [26] for analysis. The cryptographic detection studies adopting the dynamic detection method are as follows. Calvet et al. proposed Aligot [5], which analyzes the parameter values of cryptographic functions to identify them. Input/output, given as a parameter to the encryption function, is used. First, it creates a loop of data flow for the target binary, and then it assigns input/output parameters to it. The same process is performed for the cryptographic reference implementations. Finally, the encryption algorithm is detected by comparing the two assigned results.

In the study of Xu et al. [11], the semantics of possible encryption algorithm was captured using bit-precise symbolic loop mapping [11] from the target binary and reference implementation. They proposed CryptoHunt, a method to detect encryption algorithms by comparing two sets of formulas from loop mapping results after significantly reducing comparison candidates through guided fuzzing.

Lestringant [27] identified cryptographic primitives and modes of operation from a target executable. For this, the trace segments generated through DBI are represented and used as a DFG (data flow graph).

In the study of Li et al. [12], they first defined the insecure crypto key that could be exposed to a threat and then proposed K-HUNT, a method for identifying whether the encryption function used in the target executable uses an insecure key.

The above studies detected most encryption algorithms or identified insecure keys. However, since these techniques use DBI like Intel Pin [28], which inserts code when the target binary is running, there are significant limitations to detection if the target binary contains anti-reversing techniques.

3.2. Hardware Tracing

In this section, we describe the previous studies using hardware tracing. Hardware tracing is the tracing function supported by the CPU. The hardware tracing function supported by the ARM CPU is called ARM CoreSight [17]. CoreSight is an ARM CPU-only hardware feature that provides a solution to debug and trace in complex SoC (system on chip) designs [17]. Intel Processor Trace is another hardware trace function supported by Intel CPUs [18]. Intel Processor Trace is an extension of the Intel architecture that uses CPU hardware features to capture information about software execution [18].

The research conducted through ARM CoreSight is as follows. First, Lee’s work [29] used the ARM CoreSight Program Trace Macrocell (PTM) to detect a code reuse attack (CRA). PTM, a component of CoreSight, allows for the execution of an application running on an ARM processor to be extracted through an external debugger. Since most CRAs violate the normal operation of a program, they are detected by continuously monitoring and analyzing the execution trace of the victim application using PTM.

In [30], Peña-Fernandez et al. used ARM CoreSight PTM to detect program bugs or errors on a commercial off-the-shelf (COTS) ARM microprocessor architecture. Existing techniques for detecting or mitigating errors use a software approach and thus cannot directly access the various resources of processors, and they have a limitation in that a significant performance penalty occurs. This study overcame this limitation by using ARM CoreSight, a hardware monitoring feature.

The following are studies that used the Intel Processor Trace function. In the study of [31,32,33], the control flow integrity (CFI) of the program was verified using branch information provided by Intel Processor Trace.

A simple implementation of Intel Processor Trace (PT) on Linux is simple-pt [34], which decodes the information provided by the Intel Processor Trace and provides a function trace or instruction trace of the target executable. However, the code has not worked properly since the kernel page-table isolation (KPTI) Linux kernel patch caused by the Spectre vulnerability; this issue has yet to be resolved [35].

In [36], they developed a Windows device driver that can analyze the vulnerability of a program using Intel Processor Trace. Then, they combined it with DynamoRIO [37], another popular DBI, to develop a new fuzzing tool, WinAFL. Because it uses Intel Processor Trace, unlike DBI (which needs to emulate the execution environment to create the control flow graph required for fuzzing), it is possible to fuzz in a much faster time than the fuzzing tool made of only DynamoRIO.

In [38], they proposed a method to provide an automatic method to bypass anti-debugging techniques by combining the information provided by DBI and the branch information provided by Intel Processor Trace. This method uses the feature that the Intel Processor Trace is not affected by anti-debugging.

In [39], they created an image of the target malware’s branch information and target address information provided by the Intel Processor Trace, and then they used deep learning to create malware models for malware detection.

4. Proposed Scheme

This section describes the scheme for detecting the cryptographic algorithms proposed in this paper. First, Section 4.1 introduces the features and capabilities of the hardware tracing used by the scheme proposed in this paper. Section 4.2 describes the proposed scheme in detail.

4.1. Hardware Tracing Features and Capabilities

The hardware tracing directly generates a trace of the executable from the CPU hardware without any software interference. Since generated traces are so large and complex and have limited type of information, it is difficult to analyze information without the separate decoding of information and synchronization with an executable [18].

In this paper, therefore, we carried out the detection of a symmetric-key cryptographic algorithm with only limited information provided by hardware tracing. Regardless of the CPU manufacturer, the information that hardware tracing provides in common is the execution flow information for the target executable.

For ARM processors, the Program Flow Trace (PFT) architecture is supported for the execution of the flow trace [40]. The PFT architecture outputs the branch information traces necessary to reconstruct program flows. The module of ARM CoreSight that implements this PFT structure is called Program Trace Macrocell (PTM). The PTM trace generates an atom for the direct branch. An E atom is generated if the branch instruction passes its condition, and an N atom is generated if the branch instruction fails its condition. Additionally, the PTM trace generates a target address packet for indirect branches, exceptions, processor state change commands, etc [40].

For Intel ×86-64, TNT packets are generated through Intel Processor Trace [18]. TNT packets indicate whether the corresponding branch was taken or not taken when the condition branch is executed.

We significantly reduced the amount of the analysis log by limiting the information we intended to analyze in the branch information of the execution flow, but the amount of information was still enormous because branch instructions could be included in most operations that software can perform, as can cryptographic routines. To solve this problem, we needed to instrument the part we wanted to analyze in the traces created by hardware tracing. For this paper, we used software trace instrumentation [41,42].

Software trace instrumentation is a function that enables software to perform instrumentation on traces generated by hardware tracing. In other words, the software allows the analyst to pinpoint the location of the information he/she wants to analyze by using instrumentation at the desired location.

For ARM, CoreSight’s Module Instrumentation Trace Macrocell (ITM) supports SoftWare Instrumentation Trace (SWIT) generation. When instrumentation is performed in a software application, SWIT packets are generated in the CoreSight’s traces [41].

Intel introduced the PTWRITE as a software trace instrumentation feature for Processor Trace [42]. PTWRITE is an instruction that reads the data stored in the source operand and sends them to the Intel Processor Trace hardware to be encoded into PTW packet [42]. This feature requires the PTWRITE assembly instruction to be inserted into the source code of the target executable and then built. Then, when the file is executed through Intel Processor Trace, PTWRITE packets are logged in the trace when the PTWRITE is executed. This allows the analyst to find and analyze the range of packets in the desired portion of the packet log from a very large packet log by inserting the PTWRITE instruction into the source code part.

The C code of Figure 1a demonstrates the insertion of a PTWRITE instruction as inline assembly into the source code of a simple program. Figure 1b shows the packet log output after building Figure 1a. As shown in Figure 1, even though it is a very simple program that only performs simple addition and loop iteration, it can be seen that it generates a packet log of very large size up to 2.0 MB, and PTWRITE packets are recorded in the packet log. It can also be seen that four and six branches are executed before and after PTWRITE packets generated within the trace, respectively, which exactly corresponds to the number of branches in the source code before and after the PTWRITE instruction inserted in Figure 1a.

The scheme proposed in this paper is intended to overcome the limitations of hardware tracing and detect the symmetric-key encryption algorithm by utilizing the features and capabilities of hardware tracing, as discussed above.

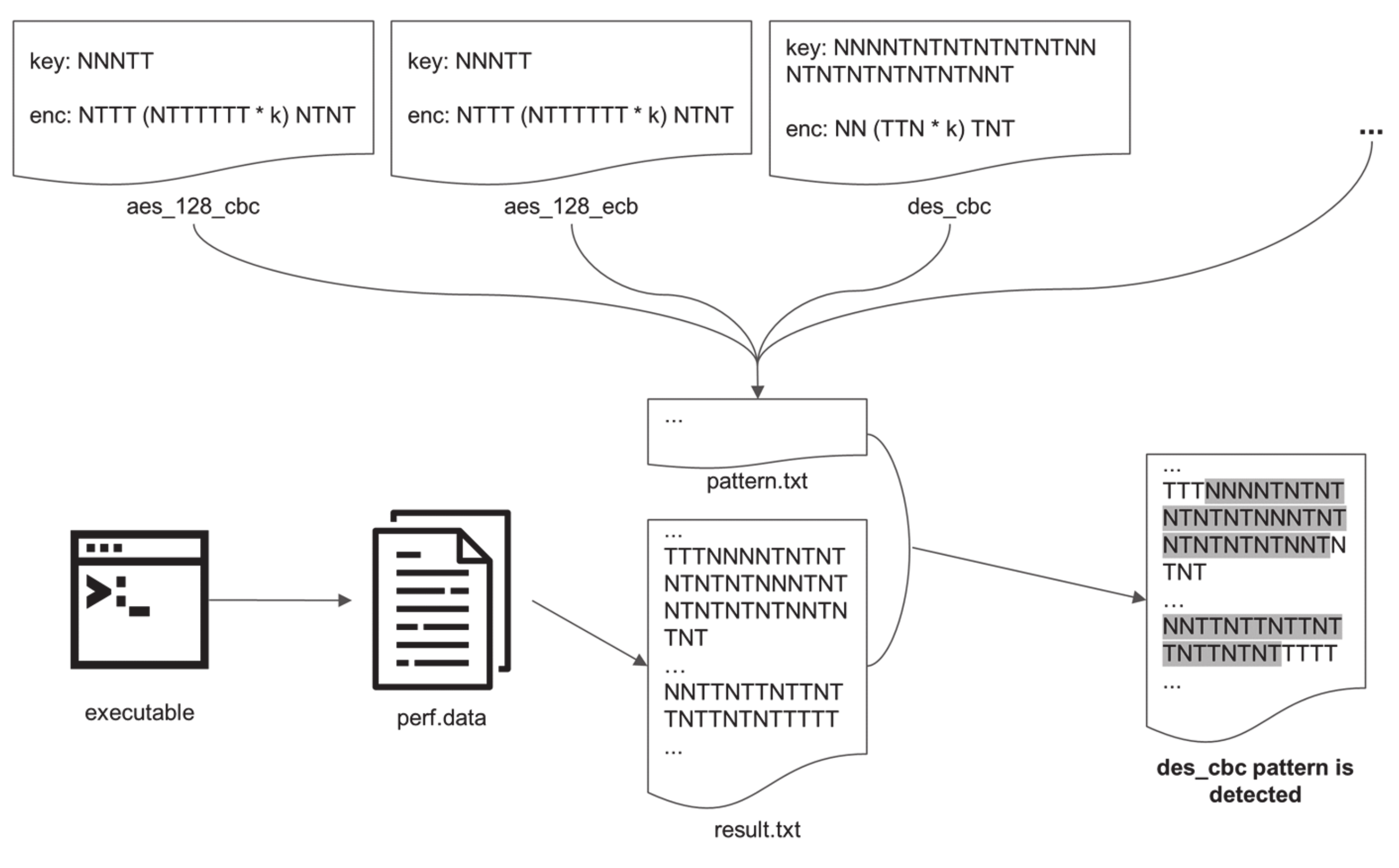
4.2. Symmetric Cryptographic Routine Detection Scheme

Figure 2 is an overview of the scheme proposed in this paper. We describe Figure 2 by dividing (1), (2), and (3) into Section 4.2.1, Section 4.2.2 and Section 4.2.3, respectively. Steps (1) and (2) correspond only to the pattern generation located at the top of Figure 2, and Step (3) includes both the pattern generation and cryptographic detection located at the bottom of Figure 2. Briefly speaking, Step (1) is the procedure for making an instrumented cryptographic library, Step (2) is the procedure for generating patterns for cryptographic routines using hardware tracing, and Step (3) is related to detecting cryptographic algorithms by using generated patterns.

4.2.1. Making Instrumented Cryptographic Library

Step (1) of Figure 2 corresponds to instrumenting work on the cryptographic libraries. The making process is follows. First, the source codes were collected for each version by selecting various cryptographic libraries that could invoke encryption algorithms. Next, the location of the cryptographic routine to be analyzed was found in the source code of the collected library.

The parts we were interested in and wanted to analyze are as follows: cryptographic key generation (e.g., (sub-)keys for AES-256bit), code for block cipher mode operation (e.g., ECB/CBC/OFB), code for encryption/decryption routines (including round functions and encrypting/decrypting functions) In this paper, we call the latter two parts as block cryptographic routines.

After collecting the source codes for widely used cryptographic libraries, software trace instrumentation was performed on the specific routines we were interested in, e.g., in OpenSSL version X, for the AES-128-CBC algorithm, we inserted a special instruction (e.g., PTWRITE) at the beginning and at the end of the following functions: key generation, block cipher mode of operation, and encryption/decryption. Then, in Step (2), after the execution trace was generated, we could easily find this special instruction in the log and could find the execution trace of the cryptographic routines (i.e., this instruction had a role of bookmark, as shown in Figure 2).

4.2.2. Hardware Tracing and Generated Pattern Integration

Step (2) went through the process of performing hardware tracing and integrating generated traces for the libraries where software trace instrumentation was performed. To do this, the instrumented libraries were compiled first (using the source code in Step (1)). At this time, various compilers were used for each version in the build process. In the generated trace, the execution information that we were interested in was information about the branch because the branch information may have varied depending on the code chunk generated by the compiler. Therefore, the instrumented library build was performed with various compilers to include branch patterns in the database that may have varied depending on the compiler.

Then, hardware tracing was generated on library code (built with various compilers that performed instrumentation). Note that the trace contained the special instruction (just as a bookmark) where analysis was required. In the trace w.r.t. each specific symmetric-key cryptographic routine, we observed a unique pattern for branch information, regardless of key contents or plaintext contents. The generated patterns may or may not have been the same, depending on the version of the encryption library. Therefore, if the same pattern was found, we integrated traces for optimization.

The reason that the cryptographic routine formed a constant branch pattern in the pattern generation process was due to the characteristics of the symmetric-key encryption algorithm. A characteristic of symmetric-key encryption algorithm was that key generation, data processing according to the block cipher mode of operation, and the performed encryption round functions were fixed by definition of the algorithm. As we observed, the pattern varied depending on how each library was implemented, but the pattern within a specific version of a library was fixed regardless of key values or plaintext input. For example, a list of actions performed by the DES symmetric-key encryption algorithm included initial/final permutation or computation, P-box, straight P-box, S-box, parity drop, and shift left operation. What these actions had in common is that they only replaced or change input data according to the set rules, but they did not change the plaintext or key contents.

The problem was that it is difficult to generate meaningful patterns when cryptographic routines contains very small number of branches. To solve this problem, we generated patterns not only for the core encryption routine but also for the block cipher mode of operation. We combined these two procedures and now call them block cryptographic routine patterns.

The block cipher mode of operation was designed to encrypt plaintext input of an arbitrary length larger than the size received by the encryption algorithm. Examples for them include ECB, CBC, CFB, OFB, and CTR modes. In our experience, these block cipher modes of operation produced different branching results. Therefore, the proposed scheme extracted/used the pattern of the block cryptographic routine to identify specific cryptographic algorithms. In this way, the proposed scheme not only generated a meaningful pattern that could distinguish the cryptographic algorithm but also enabled the detection of a block cipher mode of operation.

For this reason, branch patterns could be found in trace acquired through hardware tracing. If we take a look at the trace in Step (2) in detail, the generated trace consisting of ‘T,’ ‘N,’ and ‘*’ characters can be seen. In that trace, * is the software trace instrumentation bookmark, T means the ‘branch is taken,’ and N means the ‘branch is not taken.’

In Figure 2, we can see two strings consisting of T and N between *-pair: (a) and (b). First, in the string (a), “NNNTT” was repeated twice in the whole trace. In addition, though it is not shown in Figure 2 due to a lack of space, the same cryptographic algorithm traces using a different block cipher mode operation could also be seen to repeat the same (a) string. Thus, the (a) string was a key generation pattern that could specify the type of cryptographic algorithm.

The next string between another two * characters was (b). Unlike the key generation pattern (a), string (b) took the form of a T and N character with a specific rule that could be represented as a regular expression. Analyzing the string (b), it can be seen that it started with “NTTT,” and then “NTTTTTT” repeated at least k times and ended with the “NTNT” string. This was represented by the meta-character of a regular expression as "NTTT(NTTTTTT){k,}NTNT". The string (b) had an initial pattern, an intermediate repeated pattern, and another pattern at the end, indicating that it took the form of a typical encryption routine consisting of an initial process, an intermediate encryption process and a final padding process. In addition, string (b) was located between two string (a), which was a key generation pattern. Thus, it can be seen that string (b) was a pattern of a block cryptographic routine. At this time, k was the number of iterations in the middle of the block cryptographic routine, depending on the size of the input plaintext. In the proposed scheme, the value of k was set to threshold, which maximized the detection and minimizes false positive rate.

For example, suppose that we obtained the trace “...TNTNT*NNNTT*TNNTNT... *NTTTTNTTTTTTNTTTTTTNTTTTTTNTNT*NT...” as seen in Figure 3. First, we extracted two pattern chunks in between * (PTWRITE)-pairs: “NNNTT” and “NTTTTNTTTTTTNTTTTTTNTTTTTTNTNT.” The first one corresponded to key generation and the second one was a block cryptographic routine pattern. Then we could build a regular expression for these patterns: “NNNTT” and “NTTT(NTTTTTT){k,}NTNT,” which are illustrated in groups #1 and #2 of Figure 3.

4.2.3. Making Database with Generated Patterns and Detecting the Cryptographic Algorithm

Now, in Step (3) in Figure 2, the patterns generated in Step (2) were stored in the database, and the cryptographic algorithm was detected from the target executable using the stored patterns. In the database of Step (3), the stored trace with a part enlarged could be seen. In that trace, cryptographic library, type of cryptographic algorithm, key size, the block cipher mode of operation information, and the corresponding key generation and block cryptographic routine patterns were stored. Now the cryptographic algorithm can be detected from the target executable using a pattern database consisting of these patterns.

The cryptographic detection process is as follows. First, we selected an executable file to detect the cryptographic algorithm. In general, software trace instrumentation to the target was almost impossible because the analyst could not obtain the source code of the executable to be analyzed. Therefore, hardware tracing is performed on the executable without any preprocessing. After that, only the branch packet was parsed from the generated trace, and patterns in the pattern database were searched. If a matching pattern was found, the cryptographic algorithm was detected. It could detect not only the type of cryptographic algorithm but also the block cipher mode of operation.

5. Implementation

This section describes how the proposed scheme is implemented. Section 5.1 introduces the implementation environment, and Section 5.2 describes the details of the implementation approach. We implemented a prototype of our scheme, and the source can be accessed at https://github.com/Juhyunpark-paper.

5.1. Implementation Environment

Implementation was carried out in the Linux 19.10 64bit operating system environment. The Linux kernel version was 5.3.0-51-generic, and the version of perf, a Linux monitoring tool that uses Intel Processor Trace as a Performance Monitoring Unit (PMU), is 5.3.18. The CPU used was Intel (R) Pentium Silver N5000 CPU @ 1.10GHz × 4 (Gemini Lake), which supports PTWRITE instruction [44], the software trace instrumentation feature of Intel Processor Trace (from Broadwell to Sky Lake, Coffee Lake, and Coffee Lake Refresh, did not support PTWRITE in our tests).

5.2. Proposed Scheme Implementation

Figure 4 shows an implementation of the pattern generation process. First, a cryptographic library was selected to generate the cryptographic pattern. In the selected cryptographic library source code, the PTWRITE instruction was inserted into the function that performed key generation (key.c) and cryptographic function with the block cipher mode of operation (enc.c) in the form of inline assembly. The PTWRITE instruction insertion was made before and after the line of the function call or at the beginning of the function code and before the return statement. Depending on the format of the selected cryptographic library, PTWRITE could be inserted using (inline-)assembly language or perl script.

After PTWRITE was inserted into each function code to be analyzed, the source code was compiled to build a library-provided executable. After that, a trace of executable was recorded using Intel Processor Trace. The tool used to utilize the Intel Processor Trace was perf. Perf is a user-level tool included in the Linux kernel that provides various techniques for measuring system performance. The execution information of the target executable was recorded through perf, which selected Intel Processor Trace as a PMU event. The perf.data in Figure 4 are the output recorded through perf. This trace data acquired after recording could be viewed by the perf record or perf script. We used the perf script to convert the entire information into a dump file named result.dump.

Next, we examined the packet log where PTWRITE packets were generated. The section enclosed by PTWRITE packets parsed with ‘*’ contained various information including timing, function call address, exception, and interrupt target address, but only TNT packets were of interest in our scheme. Thus, to obtain the pattern, we implemented the parser with python that only parsed TNT packets between the PTWRITE packet pair and the outputs result.txt. The format of the TNT packet was as follows.

Table 1. Short TNT packet format [18].

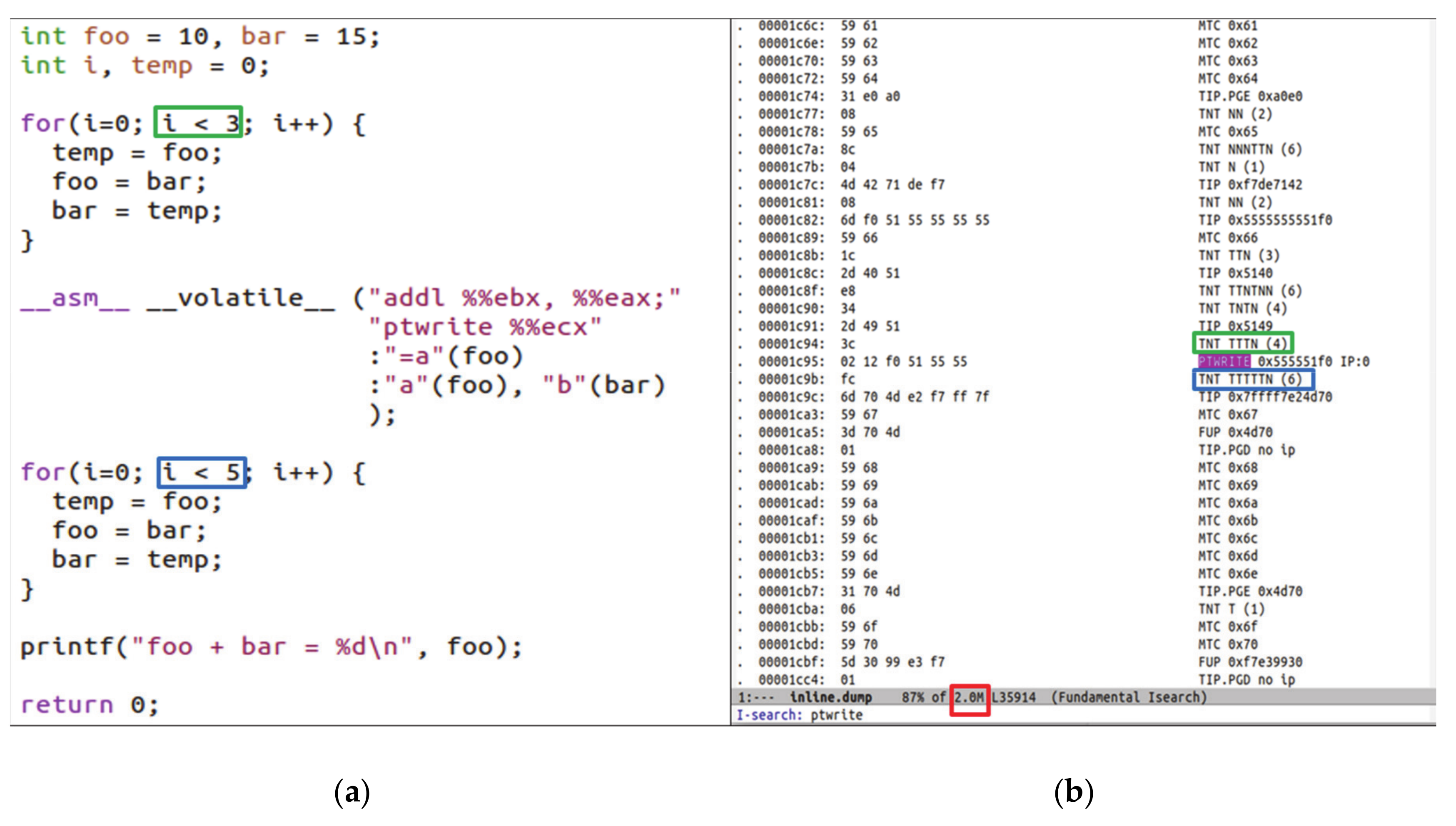
	7	6	5	4	3	2	1	0
0	1	B1	B2	B3	B4	B5	B6	0	Short TNT

shows the format of the short TNT packet among four TNT packet formats (short/long TNT and short/long partial TNT) that could be generated [18]. B1–B6 indicate the last conditional branch or specific return instruction, such that B1 was oldest and B6 was youngest. The short TNT packet could contain 1–6 TNT bits, and the long one could contain 1–47 TNT bits. If the TNT bit value was 1, a conditional branch was taken or a specific return instruction was executed, and if it is 0, a conditional branch was not taken—and the last green field bit was the header bit [18]. In the dump file made through perf script, bit 1 was T and bit 0 was N. The implemented parser parsed T and N between PTWRITE packet pairs from the dump file.

As a result of parsing, a key generation and a block cryptographic routine pattern were enclosed with * characters in result.txt. These patterns were extracted and stored in pattern.txt. By repeating the process so far with other cryptographic algorithms, pattern.txt became a pattern database in which patterns were accumulated. Through these patterns, it was possible to detect the presence of encryption operation and the type of cryptographic algorithm from the target executable. Occasionally, in the case of a block cryptographic routine pattern, although different types of cryptographic algorithms were used, similar or identical patterns were generated when the block cipher modes of operation were the same. However, as we observed, the same key generation pattern and block cryptographic routine pattern were never found in more than two different algorithms. Based on this observation, for conservative point of view, we defined the following rule: the trace contained the routine for the specific cryptographic algorithm only if 1): we found two pattern-matchings, key generation and block cryptographic routine, and 2): the key generation pattern must precede the block cryptographic routine pattern. Note that in block cryptographic routine pattern, at least k times matchings occurred (k: threshold).

Figure 5 shows an implementation of cryptographic algorithm detection process. Using the generated block cryptographic routine patterns and key generation branch patterns, the presence of the encryption operation and the type of cryptographic algorithm were detected from the target executable. To do this, a packet log had to be generated first by using Intel Processor Trace for the target. The packet log dump file creation process was performed using perf script for perf.data in the same way as the above pattern generation (the dump file is omitted from Figure 5 because of insufficient space). However, unlike the cryptographic pattern generation, the analyst could not proceed with the process of inserting the PTWRITE instruction because the source code of the executable to detect cryptographic routine could not be obtained.

Next, necessary information was parsed from the generated packet log dump file. A PTWRITE packet was not generated because PTWRITE instruction was not inserted. Therefore, only TNT packets were parsed from the dump file. As a result of the parsing, a significant amount of TNT packets was parsed into result.txt because all branches executed in the target executable were parsed, unlike the cryptographic pattern generation process that only parsed TNT packets between PTWRITE packet pairs.

If the target executable performed only the encryption operation, both the key generation and the encryption operation were performed once. Otherwise, when both encryption and decryption are performed, key generation was performed twice and the encryption operation was performed once. Additionally, key generation occurred first, and then, after performing an encryption operation, key generation was performed once more. The number and order of execution could vary depending on the implementation method of the cryptographic library, but the commonality of all libraries was to perform the key generation and encryption operation at least once, and the first key generation had to precede the encryption operation. Therefore, when searching for a pattern, a key generation pattern and a block cryptographic routine pattern must be searched in order.

Now, the patterns in the pattern database generated in the previous process (pattern.txt) were searched in the generated TNT packets (result.txt). Both the key generation pattern and the block cryptographic routine pattern had to be searched at least once, and the key generation pattern had to precede the block cryptographic routine pattern. When a search was performed in the TNT packet log of the target executable by applying these conditions, if a matching exists, the target executable was detected as using the cryptographic algorithm corresponding to the matching pattern. For example, in result.txt of Figure 5, the key generation pattern “NNNNTNTNTNTNTNTNNNTNTNTNTNTNTNNT” preceded the block cryptographic routine pattern “NN(TTN){5}TNT” and appeared once each. Because it matched the des_cbc pattern stored in the pattern database, des_cbc was detected from the target executable.

6. Experimental Results

First, in Section 6.1, we show the experimental results on generating patterns for the cryptographic routines on one of the most widely used cryptographic libraries, OpenSSL. Section 6.2 measures the FPR (false positive rate), which is the case when a non-cryptographic executable file is falsely regarded as containing cryptographic routines. Section 6.3 deals with the experimental results on anti-reversing techniques. The experimental environments were already described in Section 5.1.

6.1. Generated and Detected Cryptographic Algorithms

In this experiment, we chose OpenSSL because it is one of the most widely used open-sourced cryptographic libraries. We conducted experiments on pattern generation and encryption algorithm detection. In this experiment, six OpenSSL versions were used: 0.9.8zh, 1.0.0s, 1.0.1u, 1.0.2u, 1.1.0l, and 1.1.1e. For the cryptographic algorithms to generate patterns, 12 of the symmetric key encryption algorithms were selected: AES, AES-NI (Advanced Encryption Standard-New Instructions, extension of x86 instruction set), BF (Blowfish), CAST, DES, DES3 (DES-Triple), IDEA, RC2, RC4, ARIA, SM4, and SEED. In addition, experiments were conducted on all the key sizes and block cipher modes of operation supported by OpenSSL’s enc command for the selected cryptographic algorithms.

Table 2. Successfully generated cryptographic algorithms and the average elapsed time. BF: Blowfish; DES3: DES-Tripe.

Cryptographic Algorithm	AES	AES-NI	BF	CAST	DES	DES3	IDEA	RC2	RC4	ARIA	SEED	SM4	Aver age
Key Generation	O	O	O	O	O	O	X	O	O	O	X	O
Block Crypto Routine	O	O	O	O	O	O	O	O	O	O	O	X
Average Elapsed Time (s)	3.249	3.163	3.177	3.176	3.172	3.177	3.184	3.207	3.183	3.202	3.179	3.177	3.187

lists the cryptographic algorithms that successfully generated patterns for the 6 OpenSSL versions. The plaintext to be encrypted by the cryptographic algorithm was randomly generated through Python. A random string with a length of 1000 bytes was generated by randomly selecting digits, asci letters, and punctuation characters in the string module of python.

In this table, the second and third rows indicate whether key generation and block cryptographic routine patterns were successfully generated, respectively (O: success; X: failure). Experiments showed that for 9 of 12 algorithms, we were able to generate both key generation patterns and block cryptographic patterns. Key generation patterns could not be generated from the IDEA and SEED algorithms and block cryptographic routine patterns could not be generated from the SM4 algorithms. These were the cases when the cryptographic algorithm’s key generation or block cryptographic routine was implemented to perform little or no branch instruction. Therefore, in our scheme, it was difficult to detect the algorithm when it was difficult to generate a pattern because the branch instructions were not sufficiently executed, such as with the IDEA, SEED, and SM4 algorithms of OpenSSL. The full list of the generated patterns is in Appendix A.

The fourth row of Table 2 shows the average of the time taken for each pattern generation after 50 times of pattern generation for each cryptographic algorithm of OpenSSL (only the 1.1.1e version was measured). The time for each pattern generation was a measure of the time taken to generate both key generation and block cryptographic routine pattern. Additionally, time measurement was performed for all key sizes and to block cipher modes of operation. For example, AES had three key sizes and two block cipher modes of operation for each key size. Thus, pattern generation was performed 50 times for a total of six AES encryption algorithms. Thus, the AES average elapsed time at the third row and second column of Table 2 was obtained after the average time of pattern generation for the six AES encryption algorithms was obtained, and then the average of those six values was calculated.

As a result of the experiment, the total average time for 50 pattern generations for each cryptographic algorithm was 3.187 seconds.

Table 3. The number of successfully detected symmetric-key cryptographic algorithms.

Cryptographic Algorithm	# of key size	# of block cipher mode of operation	# of target executable	# of success
AES	3	2	6	6
AES-NI	3	2	6	6
BF	1	4	4	4
CAST	1	4	4	4
DES	1	4	4	4
DES3	2	3 (128 bits), 2 (192 bits)	5	5
RC2	3	1 (40 bits), 1 (64 bits), 4 (128 bits)	6	6
RC4	2	1	1	1
ARIA	3	4 (128 bits), 5 (192 bits), 5 (256 bits)	14	14
Total			50	50

shows experimental results for measuring TP and FN. In this experiment, we set the threshold k as 6. The first column of Table 3 lists the cryptographic algorithms that successfully generated both key generation and block cryptographic routine patterns for the six OpenSSL versions. The second column is the number of key sizes of the algorithm supported by the OpenSSL enc command. The third column shows the number of block cipher modes of operation of the algorithm supported by the OpenSSL enc command. If there are two or more values, the number of block cipher modes of operation supported by the enc command was different for each key size. Therefore, we prepared target executables to include all the cases for different key sizes and different block cipher modes of operation. Additionally, the plaintext encrypted by the target executable was set under the same conditions as the pattern generation experiment in Table 2.

As a result of the experiment, we were able to accurately detect the cryptographic algorithm from all the target executables. The value in the last row of the fourth column is the total number of target executables used in the experiment. The value in the last row of the fifth column is the number of target executables that our scheme successfully detected the cryptographic algorithm. As defined in Section 2, the value of |TP| is the value of the last column in the fifth row, and the value of |FN| is the value of the last column of the fourth row minus the value of the last column of the fifth row. Therefore, since |TP| = 50 and |FN| = 0, the recall was 1 when using these two values.

The time taken for detection is not indicated. The reason for this is that the detection process for the trace of the target executable file was a simple string search with regular expression pattern, and it took a very short time. For example, as a result of performing 50 pattern searches on a target executable executing des-cbc, the average elapsed time was very short at 0.021 seconds.

6.2. Experimental Results for Executable Files That Do Not Use Cryptography

We conducted experiments for detecting cryptographic routines for the general executable files that did not perform any cryptographic operations. The executables used in the experiment were GNU coreutils v8.30 (ls, touch, cat, expr), calculator (bc v1.07.1), calendar (cal), image viewer (feh v3.2.1), text editor (vim v8.1), and telnet, which are the most widely used tools in the Linux and do not perform any cryptographic operations.

In Figure 6, the x-axis represents the threshold value k, and the y-axis represents the percentage of false positive where the encryption algorithm pattern was falsely detected from the general executable files. The line L1 is the case when the encryption algorithm was detected only with the block cryptographic routine pattern, and the line L2 (our scheme) is the case when the encryption algorithm was detected using both the block cryptographic routine pattern and the key generation pattern.

Figure 6 shows that the encryption algorithms were detected regardless of k values in the case of L1, which identified the encryption algorithm from the general executable file through the block encryption routine pattern. Since the normal executable files did not perform any encryption operations, the FPR of L1 was 100%. However, as a result of testing with L2 that added the key generation pattern, it was confirmed that the FPR decreased ask increases. From this experiment, we saw that when k value was more than 6, our scheme had an extremely low FPR, and this was why we set k = 6 in the experiment in Section 6.1.

Table 4. False positive rate (FPR) of normal executable (X: no algorithm was detected).

	L1	L2
		1	2	3	4	5	6 (threshold)
bc	multiple	CAST	CAST	X	X	X	X
cal	multiple	CAST	CAST	CAST	X	X	X
cat	multiple	CAST	CAST	X	X	X	X
expr	multiple	CAST	CAST	X	X	X	X
feh	multiple	CAST, AES, AES-NI	CAST	CAST	CAST	CAST	X
gcc	multiple	CAST, AES, AES-NI	CAST, AES	CAST	CAST	CAST	X
ls	multiple	CAST	CAST	CAST	X	X	X
touch	multiple	CAST	CAST	X	X	X	X
telnet	multiple	CAST	CAST	X	X	X	X
vim	multiple	CAST	CAST	X	X	X	X
FPR	100%	100%	100%	40%	20%	20%	0%

shows the results of the crypto-routine detection for the non-cryptographic executables in Figure 6. Since these executables did not have a cryptographic routine, if our scheme detected a cryptographic routine, it was FP, and if it did not, it was TN. The last row is a calculation of the FPR through these two values, as defined in Section 2.

In the case of L1, since multiple cryptographic algorithms were identified regardless of the number of iterations of the block cryptographic routine, they were marked as multiple. In the case of L2, it was classified according to the number of iterations of the block cryptographic routine, as in the table above. In all cases where an encryption algorithm was detected, a CAST encryption algorithm with a relatively short pattern length was detected. In addition, AES and AES-NI algorithms were detected in feh and gcc, where the size of the hardware tracing result was relatively large.

Through experimentation, it could be confirmed that the block cryptographic routine had to be repeated at least six times in order to reduce the FPR to 0%, such that any false detection of the cryptographic algorithm in the normal executable which did not perform encryption operation. Again, we found that if k value was more than 6, our scheme had an extremely low FPR.

Since each algorithm had different input sizes and processing methods, it was difficult to specify that k became 6 when the input plaintext size was more than a certain value. However, we could see several times that the block cryptographic routine was repeated more than six times even for very short input. For the conservative point of view, it was rare that the block cryptographic routine was executed less than six times in an executable file that performed an encryption operation. Therefore, when the threshold was set to six, it was estimated that true negatives were extremely rare to be undetected by performing less than six block encryption routines, even though encryption was performed.

6.3. Experimental Results for Executables That Use Anti-Reversing Technique

Finally, an experiment was conducted on the executable files using anti-reversing techniques. Recall that previous works have had demerits in the sense that they have used debuggers or DBIs that modify the running environment. The proposed scheme was not detected by the anti-reversing technique because hardware tracing did not modify the running environment. To verify this, experiments were done for each analysis tool on the executable file to which the anti-reverse techniques were applied.

Table 5. Comparison of anti-reversing bypass and dynamic binary instrumentation (DBI) detection results with other detection tools.

	GDB	Valgrind [45]	DynamoRIO	Intel Pin	Proposed Scheme
ptrace	X	O	O	O	O
rdtsc	X	X	X	X	O
PwIN [46]	O	X	X	X	O

shows the result of anti-reversing bypass for each detection tool for the executable file to which the anti-reversing techniques were applied. The first row contains the dynamic analysis tools used by the previous works and the proposed scheme. The first column corresponds to anti-reversing techniques and tools to detect presence of the analysis work. O means that the analysis tool successfully bypassed the anti-reversing techniques/tool. X means that bypassing failed.

Ptrace detects the presence of a debugger in a Linux operating system. rdtsc (read time-stamp counter) assembly instruction detects the presence of an analysis tool using the fact that it is consuming more CPU cycles than when executing a normal instruction. PwIN is not an anti-reversing technique; rather, it is a DBI detection tool implemented in Zhechev et al.’s study [46]. The analysis tools used in the experiment consisted of one debugger (GDB v8.30) and three DBIs (Valgrind v3.15.0, DynamoRIO v8.0.18386, and Intel Pin v3.13) widely used for binary analysis.

As a result of the experiment, GDB was detected in ptrace and rdtsc. Because PwIN was designed to detect only DBIs, it could not detect GDB. Valgrind, DynamoRIO, and Intel Pin were not detected in ptrace. However, rdtsc and PwIN detected them. The proposed scheme in this paper bypassed all anti-reversing techniques and was not detected by the DBI detection tool.

7. Conclusions

In this paper, we proposed a new method to detect symmetric-key cryptographic routines for binary with anti-reversing techniques. To address the problem that the previous works have suffered from bypassing anti-reversing techniques, we utilized the latest CPUs’ hardware-supported functionality: hardware tracing. Since hardware tracing provides very limited type of information and produces large-sized logs, we identified the target cryptographic routines using hardware tracing-related software trace instrumentation to extract the relevant branch information for the cryptographic routine. Then, we generated the patterns in the form of regular expression for each cryptographic routine for matching. We conducted experiments on OpenSSL 0.9.8 zh, 1.0.0 s, 1.0.1 u, 1.0.2 u, 1.1.0 l, and 1.1.1 e—one of the most widely used cryptographic libraries. The experimental results showed that patterns were generated and detected for 9 of the 12 symmetric-key cryptographic algorithms. Experiments were also conducted on GNU coreutils v8.30 (ls, touch, cat, expr), Calculator (bc v1.07.1), Calendar (cal), Image Viewer (feh v3.2.1), text editor (vim v8.1), and telnet, all of which are widely-used non-cryptographic executable files that do not perform encryption operations, and it was confirmed that the FPR became 0% when the number of repetitions of the cryptographic routine reached a certain threshold. Additionally, experiments were conducted on the executable files to which the anti-reversing techniques are applied. As a result, the analysis tools used for previous work could not bypass the anti-reversing techniques. Our method successfully bypassed the anti-reversing techniques. From this, if the proposed scheme is used to find cryptographic routines in malware/ransomware-containing diverse anti-reversing techniques, we expect that analysts can reduce a significant amount of time in analyzing important algorithms or finding cryptographic keys.