Dynamic and Static Calibration of Ultra-Low-Voltage, Digital-Based Operational Transconductance Amplifiers †
Abstract
:1. Introduction
2. Digital-Based OTA
2.1. Basic Operation
2.2. Process Variations and Mismatch
3. Dynamic Digital Calibration
3.1. Digital PWM (DPWM) Modulation
3.2. DDPM Modulation
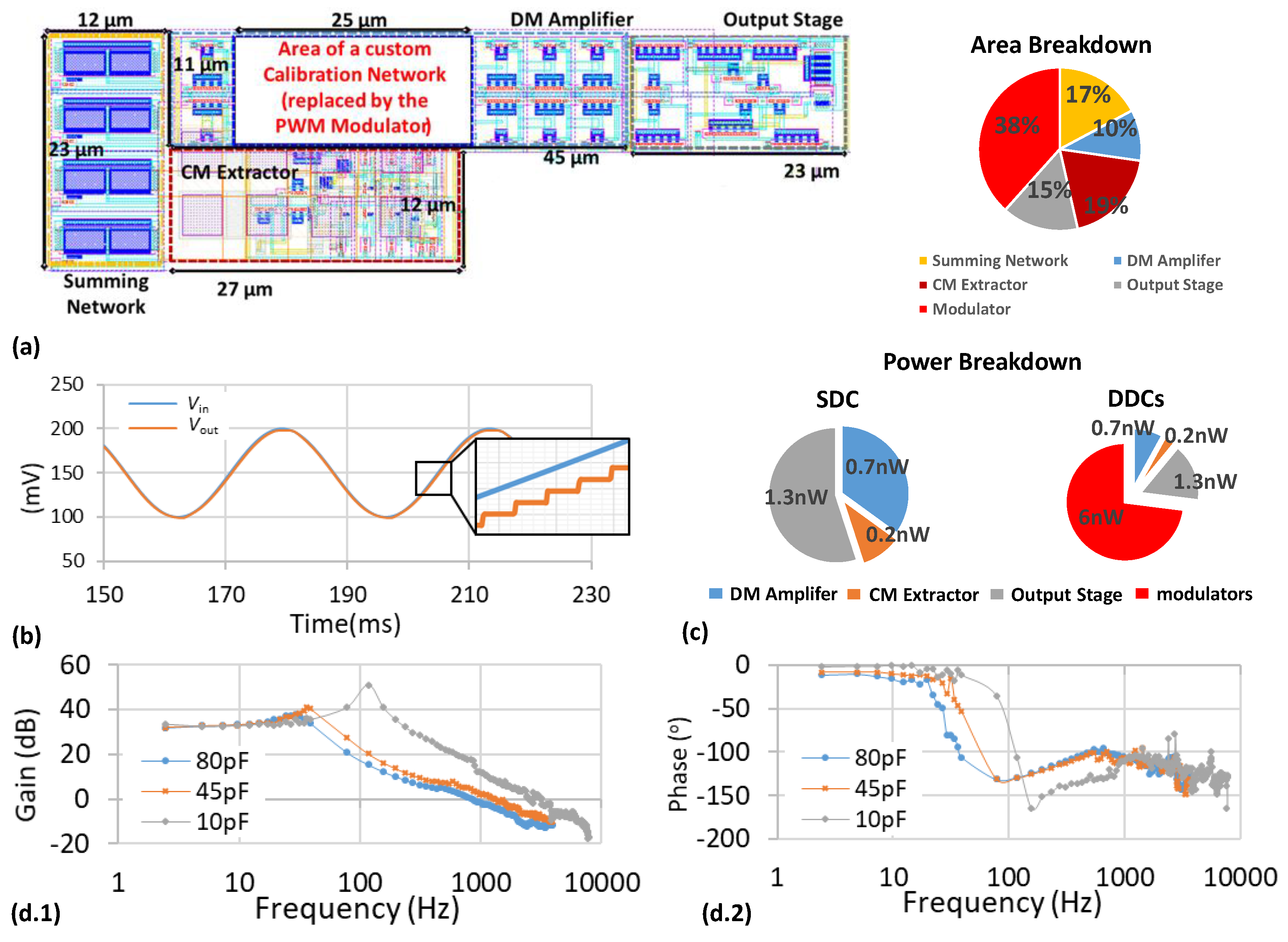
3.3. Static and Dynamic Calibration Networks
3.3.1. Static Digital Calibration (SDC) Network
3.3.2. Dynamic Digital Calibration (DDC)
4. Simulation Results
4.1. Performance under Nominal Conditions
4.2. Process Variations, SDC and DDC comparison
4.2.1. SDC and DDC Simulation Flow
4.2.2. SDC and DDC Statistical Characterization
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| ULV | Ultra Low Voltage |
| DB-OTAs | Digital-Based Operational Transconductance Amplifiers |
| DPWM | Digital Pulse Width Modulation |
| DDPM | Dyadic Digital Pulse5Modulation |
| MC | Monte-Carlo |
| IoT | Internet of Things |
| CMOS | Complementary Metal-Oxide Semiconductor |
| MOS | Metal-Oxide Semiconductor |
| OTA | Operational Transconductance Amplifier |
| VCO | Voltage Controlled Oscillator |
| CMIR | Common Mode Input Range |
| PMU | Power Management Unit |
| AFE | Analog Front-End |
| ULP | Ultra Low Power |
| P | microprocessor |
| MAC | Media Access Control |
| SDC | Static Digital Calibration |
| DDC | Dynamic Digital Calibrations |
| DM | Differential-Mode |
| CM | Common-Mode |
| GBW | Gain Bandwidth Product |
| THD | Total Harmonic Distortion |
| FFT | Fast Fourier Transform |
References
- Kim, S.; Vyas, R.; Bito, J.; Niotaki, K.; Collado, A.; Georgiadis, A.; Tentzeris, M.M. Ambient RF Energy-Harvesting Technologies for Self-Sustainable Standalone Wireless Sensor Platforms. Proc. IEEE 2014, 102, 1649–1666. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, F.; Shakhsheer, Y.; Silver, J.D.; Klinefelter, A.; Nagaraju, M.; Boley, J.; Pandey, J.; Shrivastava, A.; Carlson, E.J.; et al. A Batteryless 19 μW MICS/ISM-Band Energy Harvesting Body Sensor Node SoC for ExG Applications. IEEE J. Solid-State Circuits 2013, 48, 199–213. [Google Scholar] [CrossRef]
- Klinefelter, A.; Roberts, N.E.; Shakhsheer, Y.; Gonzalez, P.; Shrivastava, A.; Roy, A.; Craig, K.; Faisal, M.; Boley, J.; Oh, S.; et al. A 6.45 μW self-powered IoT SoC with integrated energy-harvesting power management and ULP asymmetric radios. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 22–26 February 2015. [Google Scholar]
- Alioto, M. Enabling the Internet of Things—From Integrated Circuits to Integrated Systems, 1st ed.; Springer: Berlin, Germany, 2017. [Google Scholar]
- Lee, J.; Zhang, Y.; Dong, Q.; Lim, W.; Saligane, M.; Kim, Y.; Jeong, S.; Lim, J.; Yasuda, M.; Miyoshi, S.; et al. A Self-Tuning IoT Processor Using Leakage-Ratio Measurement for Energy-Optimal Operation. IEEE Solid-State Circuits Mag. 2020, 55, 87–97. [Google Scholar] [CrossRef]
- Kinget, P.R. Scaling analog circuits into deep nanoscale CMOS: Obstacles and ways to overcome them. In Proceedings of the 2015 IEEE Custom Integrated Circuits Conference (CICC), San Jose, CA, USA, 28–30 September 2015; pp. 1–8. [Google Scholar]
- Richelli, A.; Colalongo, L.; Kovacs-Vajna, Z.; Calvetti, G.; Ferrari, D.; Finanzini, M.; Pinetti, S.; Prevosti, E.; Savoldelli, J.; Scarlassara, S. A Survey of Low Voltage and Low Power Amplifier Topologies. J. Low Power Electron. Appl. 2018, 8, 22. [Google Scholar] [CrossRef] [Green Version]
- Yoon, Y.; Choi, D.; Roh, J. A 0.4 V 63 μW 76.1 dB SNDR 20 kHz Bandwidth Delta-Sigma Modulator Using a Hybrid Switching Integrator. IEEE J. Solid-State Circuits 2015, 50, 2342–2352. [Google Scholar] [CrossRef]
- Dessouky, M.; Kaiser, A. Very low-voltage digital-audio ΔΣ modulator with 88-dB dynamic range using local switch bootstrapping. IEEE J. Solid-State Circuits 2001, 36, 349–355. [Google Scholar] [CrossRef]
- Ferreira, L.; Sonkusale, R. A 60-dB Gain OTA Operating at 0.25-V Power Supply in 130-nm Digital CMOS Process. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 1609–1617. [Google Scholar] [CrossRef]
- Lv, L.; Zhou, X.; Qiao, Z.; Li, Q. Inverter-Based Subthreshold Amplifier Techniques and Their Application in 0.3-V ΔΣ -Modulators. IEEE J. Solid-State Circuits 2019, 54, 1436–1445. [Google Scholar] [CrossRef]
- Michel, F.; Steyaert, M. A 250 mV 7.5 μW 61 dB SNDR SC ΔΣ Modulator Using Near-Threshold-Voltage-Biased Inverter Amplifiers in 130 nm CMOS. IEEE J. Solid-State Circuits 2012, 47, 709–721. [Google Scholar] [CrossRef]
- Kalani, S.; Bertolini, P.; Richelli, A.; Kinget, P. A 0.2 V 492 nW VCO-based OTA with 60 kHz UGB and 207 μVrms noise. In Proceedings of the IEEE International Symposium on Circuits and Systems, Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Kinget, P.; Kalani, S. Zero-Crossing-Time-Difference Model for Stability Analysis of VCO-Based OTAs. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 839–851. [Google Scholar]
- Crovetti, P. A Digital-Based Analog Differential Circuit. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 3107–3116. [Google Scholar] [CrossRef]
- Toledo, P.; Crovetti, P.; Klimach, H.; Bampi, S. A 300 mV-Supply, 2 nW-Power, 80 pF-Load CMOS Digital-Based OTA for IoT Interfaces. In Proceedings of the IEEE International Conference on Electronics, Circuits and Systems, Genoa, Italy, 27–29 November 2019; pp. 170–173. [Google Scholar]
- Crovetti, P.; Musolino, F.; Aiello, O.; Toledo, P.; Rubino, R. Breaking the boundaries between analogue and digital. Electron. Lett. 2019, 55, 672–673. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Alioto, M. Fully Synthesizable, Rail-to-Rail Dynamic Voltage Comparator for Operation down to 0.3 V. In Proceedings of the IEEE International Symposium on Circuits and Systems Letters, Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Drost, B.; Talegaonkar, M.; Hanumolu, P. Analog Filter Design Using Ring Oscillator Integrators. IEEE J. Solid-State Circuits 2012, 47, 3120–3129. [Google Scholar] [CrossRef]
- Cai, G.; Zhan, C.; Lu, Y. A Fast-Transient-Response Fully-Integrated Digital LDO with Adaptive Current Step Size Control. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3610–3619. [Google Scholar] [CrossRef]
- Crovetti, P. A Digital-Based Virtual Voltage Reference. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 1315–1324. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.; Alioto, M. Standard Cell-Based Ultra-Compact DACs in 40-nm CMOS. IEEE Access 2019, 7, 126479–126488. [Google Scholar] [CrossRef]
- Unnikrishnan, V.; Vesterbacka, M. Time-Mode Analog-to-Digital Conversion Using Standard Cells. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 3348–3357. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Hwang, Y.; Jeong, D. A 0.5-V Fully Synthesizable SAR ADC for On-Chip Distributed Waveform Monitors. IEEE Access 2019, 7, 63686–63697. [Google Scholar] [CrossRef]
- Weaver, S.; Hershberg, B.; Moon, M. Digitally synthesized stochastic flash ADC using only standard digital cells. In Proceedings of the Symposium on VLSI Circuits—Digest of Technical Papers, Honolulu, HI, USA, 10–13 June 2014; pp. 266–267. [Google Scholar]
- Crovetti, P.; Rubino, R.; Musolino, F. Relaxation digital-to-analogue converter. Electron. Lett. 2019, 55, 685–688. [Google Scholar] [CrossRef]
- Deng, W.; Yang, D.; Ueno, T.; Siriburanon, T.; Kondo, S.; Okada, K.; Matsuzawa, A. A Fully Synthesizable All-Digital PLL with Interpolative Phase Coupled Oscillator, Current-Output DAC, and Fine-Resolution Digital Varactor Using Gated Edge Injection Technique. IEEE J. Solid-State Circuits 2015, 50, 68–80. [Google Scholar] [CrossRef]
- Park, M.; Perrott, M. A multiphase PWM RF modulator using a VCO-based opamp in 45 nm CMOS. In Proceedings of the IEEE Radio Frequency Integrated Circuits Symposium, Anaheim, CA, USA, 23–25 May 2010; pp. 39–42. [Google Scholar]
- Toledo, P.; Aiello, O.; Crovetti, P. A 300 mV-Supply Standard-Cell-Based OTA with Digital PWM Offset Calibration. In Proceedings of the IEEE Nordic Circuits and Systems Conference, Helsinki, Finland, 29–30 October 2019; pp. 1–5. [Google Scholar]
- Crovetti, P. All-Digital High Resolution D/A Conversion by Dyadic Digital Pulse Modulation. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 573–584. [Google Scholar] [CrossRef] [Green Version]
- Crovetti, P.S.; Usmonov, M.; Musolino, F.; Gregoretti, F. Limit Cycle-Free Digitally Controlled DC-DC Converters based on Dyadic Digital PWM. IEEE Trans. Power Electron. 2020. [Google Scholar] [CrossRef]
- Braga, R.; Ferreira, L.; Coletta, G.; Dutra, O. A 0.25-V calibration-less inverter-based OTA for low-frequency Gm-C applications. Microelectron. J. 2019, 83, 62–72. [Google Scholar] [CrossRef]
- Abdelfattah, O.; Roberts, G.; Shih, I.; Shih, Y. An Ultra-Low-Voltage CMOS Process-Insensitive Self-Biased OTA with Rail-to-Rail Input Range. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 2380–2390. [Google Scholar] [CrossRef]
- Chatterjee, S.; Tsividis, Y.; Kinget, P. 0.5-V analog circuit techniques and their application in OTA and filter design. IEEE J. Solid-State Circuits 2005, 40, 2373–2387. [Google Scholar] [CrossRef]
- Veldandi, H.; Shaik, R. A 0.3-v pseudo-differential bulk-input ota for low-frequency applications. Circuits Syst. Signal Process. 2018, 37, 5199–5221. [Google Scholar] [CrossRef]
- Ferreira, L.; Pimenta, T.; Moreno, R. An Ultra-Low-Voltage Ultra-Low-Power CMOS Miller OTA with Rail-to-Rail Input/Output Swing. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 843–847. [Google Scholar] [CrossRef]
- Woo, K.; Yang, B. A 0.25 V Rail-to-Rail Three-Stage OTA with an Enhanced DC GainA 0.25 V Rail-to-Rail Three-Stage OTA With an Enhanced DC Gain. IEEE Trans. Circuits Syste. II Express Briefs 2020. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F. A 0.3-V 98-dB Rail-to-Rail OTA in 0.18μm CMOS. IEEE Access 2020, 8, 27459–27467. [Google Scholar] [CrossRef]






| Peformance | No Calibration | Static | DPWM | DDPM |
|---|---|---|---|---|
| Voltage Offset (mV) | , | , | , | , |
| THD (%) | , | , | , | , |
| Power (nW) | , | , | , | , |
| GBW (nW) | - | , | , | , |
| FoM () | - | , | , | , |
| This Work | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Calibration of the Worst Sample | ||||||||||||||
| Performance | [10] | [11] | [13] | [33] | [34] | [35] | [36] | [37] | [38] | Typ. | Uncal. | Static | DPWM | DDPM |
| Tech. (nm) | 130 | 130 | 65 | 65 | 180 | 65 | 350 | 65 | 180 | 180 | 180 | 180 | 180 | 180 |
| Supply (mV) | 250 | 300 | 200 | 350 | 500 | 300 | 600 | 250 | 300 | 300 | 300 | 300 | 300 | 300 |
| DC Gain (dB) | 60 | 49.8 | - | 43 | 52 | 60 | 69 | 70 | 98.1 | 35 | - | 32 | 27 | 26 |
| GBW (kHz) | 1.88 | 9100 | 60 | 3600 | 1200 | 70 | 11.4 | 9.5 | 3.1 | 0.85 | - | 0.836 | 0.67 | 0.69 |
| Slew Rate () | 0.7 | 3800 | 10.5 | 5600 | 2890 | 25 | 14.6 | 2 | 9.1 | 0.5 | - | - | ||
| THD (%) | 0.2 | - | - | 0.6 | 1 | - | 0.08 | - | 0.49 | 3 | 77 | 1.32 | 2.73 | 2.35 |
| Phase Margin () | 52.5 | 76 | - | 56 | - | 53 | 65 | 89.9 | 54 | 76 | - | 70 | 67 | 68 |
| (pF) | 15 | 2 | 15 | 3 | 20 | 5 | 15 | 15 | 30 | 80 | 80 | 80 | 80 | 80 |
| Power (nW) | 18 | 1800 | 492 | 17,000 | 110,000 | 51 | 550 | 26 | 13 | 2 | 1.18 | 1.81 | 1.15 | 3.8 |
| Area () | 83,000 | - | - | 5000 | 26,000 | 3000 | 60,000 | 2000 | 9800 | 1426 | 1426 | 1426 | 1426 | 1426 |
| () | 39.2 | 303 | 36.6 | 22.3 | 11 | 205 | 19 | 137 | 215 | 1020 | - | 1108 | 1397 | 434.76 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toledo, P.; Crovetti, P.; Klimach, H.; Bampi, S. Dynamic and Static Calibration of Ultra-Low-Voltage, Digital-Based Operational Transconductance Amplifiers. Electronics 2020, 9, 983. https://doi.org/10.3390/electronics9060983
Toledo P, Crovetti P, Klimach H, Bampi S. Dynamic and Static Calibration of Ultra-Low-Voltage, Digital-Based Operational Transconductance Amplifiers. Electronics. 2020; 9(6):983. https://doi.org/10.3390/electronics9060983
Chicago/Turabian StyleToledo, Pedro, Paolo Crovetti, Hamilton Klimach, and Sergio Bampi. 2020. "Dynamic and Static Calibration of Ultra-Low-Voltage, Digital-Based Operational Transconductance Amplifiers" Electronics 9, no. 6: 983. https://doi.org/10.3390/electronics9060983
APA StyleToledo, P., Crovetti, P., Klimach, H., & Bampi, S. (2020). Dynamic and Static Calibration of Ultra-Low-Voltage, Digital-Based Operational Transconductance Amplifiers. Electronics, 9(6), 983. https://doi.org/10.3390/electronics9060983







