Kilonova-Targeting Lightcurve Classification for Wide Field Survey Telescope
Abstract
:1. Introduction
2. Transients Simulation
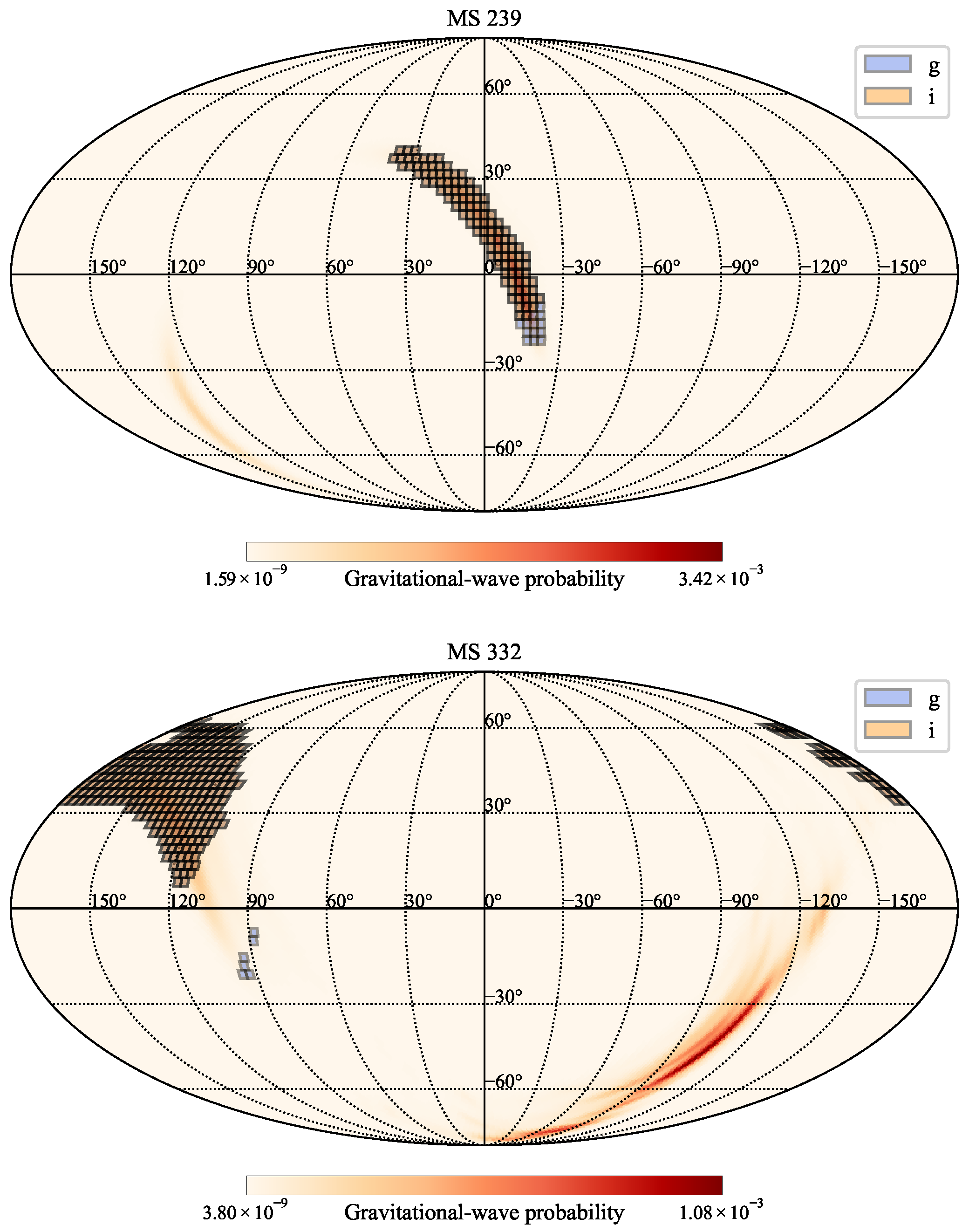
2.1. Survey Simulation
2.2. KN Simulation
2.3. Other Transients Simulation
2.4. Training Set
3. Binary Classification
3.1. TCN Framework
3.2. Training
4. Results
4.1. Performance on Dataset
4.2. Performance on Real Data
4.3. Performance on Mock Survey
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Andreoni, I.; Ackley, K.; Cooke, J.; Acharyya, A.; Allison, J.R.; Anderson, G.E.; Ashley, M.C.B.; Baade, D.; Bailes, M.; Bannister, K.; et al. Follow Up of GW170817 and Its Electromagnetic Counterpart by Australian-Led Observing Programmes. Proc. Astron. Soc. Aust. 2017, 34, e069. [Google Scholar] [CrossRef]
- Li, L.X.; Paczyński, B. Transient Events from Neutron Star Mergers. Astrophys. J. Lett. 1998, 507, L59–L62. [Google Scholar] [CrossRef]
- Metzger, B.; Martínez-Pinedo, G.; Darbha, S.; Quataert, E.; Arcones, A.; Kasen, D.; Thomas, R.; Nugent, P.; Panov, I.; Zinner, N. Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. Mon. Not. R. Astron. Soc. 2010, 406, 2650–2662. [Google Scholar] [CrossRef]
- Paczynski, B. Cosmological gamma-ray bursts. Acta Astron. 1991, 41, 257–267. [Google Scholar]
- Narayan, R.; Paczynski, B.; Piran, T. Gamma-Ray Bursts as the Death Throes of Massive Binary Stars. Astrophys. J. Lett. 1992, 395, L83. [Google Scholar] [CrossRef]
- Nakar, E. Short-hard gamma-ray bursts. Phys. Rep. 2007, 442, 166–236. [Google Scholar] [CrossRef]
- Totani, T.; Panaitescu, A. Orphan Afterglows of Collimated Gamma-Ray Bursts: Rate Predictions and Prospects for Detection. Astrophys. J. 2002, 576, 120–134. [Google Scholar] [CrossRef]
- Roberts, L.F.; Kasen, D.; Lee, W.H.; Ramirez-Ruiz, E. Electromagnetic Transients Powered by Nuclear Decay in the Tidal Tails of Coalescing Compact Binaries. Astrophys. J. Lett. 2011, 736, L21. [Google Scholar] [CrossRef]
- Metzger, B.D.; Berger, E. What is the Most Promising Electromagnetic Counterpart of a Neutron Star Binary Merger? Astrophys. J. 2012, 746, 48. [Google Scholar] [CrossRef]
- Nagakura, H.; Hotokezaka, K.; Sekiguchi, Y.; Shibata, M.; Ioka, K. Jet Collimation in the Ejecta of Double Neutron Star Mergers: A New Canonical Picture of Short Gamma-Ray Bursts. Astrophys. J. Lett. 2014, 784, L28. [Google Scholar] [CrossRef]
- Chornock, R.; Berger, E.; Kasen, D.; Cowperthwaite, P.S.; Nicholl, M.; Villar, V.A.; Alexander, K.D.; Blanchard, P.K.; Eftekhari, T.; Fong, W.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. IV. Detection of Near-infrared Signatures of r-process Nucleosynthesis with Gemini-South. Astrophys. J. Lett. 2017, 848, L19. [Google Scholar] [CrossRef]
- Drout, M.R.; Piro, A.L.; Shappee, B.J.; Kilpatrick, C.D.; Simon, J.D.; Contreras, C.; Coulter, D.A.; Foley, R.J.; Siebert, M.R.; Morrell, N.; et al. Light curves of the neutron star merger GW170817/SSS17a: Implications for r-process nucleosynthesis. Science 2017, 358, 1570–1574. [Google Scholar] [CrossRef]
- Kilpatrick, C.D.; Foley, R.J.; Kasen, D.; Murguia-Berthier, A.; Ramirez-Ruiz, E.; Coulter, D.A.; Drout, M.R.; Piro, A.L.; Shappee, B.J.; Boutsia, K.; et al. Electromagnetic evidence that SSS17a is the result of a binary neutron star merger. Science 2017, 358, 1583–1587. [Google Scholar] [CrossRef]
- Utsumi, Y.; Tanaka, M.; Tominaga, N.; Yoshida, M.; Barway, S.; Nagayama, T.; Zenko, T.; Aoki, K.; Fujiyoshi, T.; Furusawa, H.; et al. J-GEM observations of an electromagnetic counterpart to the neutron star merger GW170817. Proc. Astron. Soc. Jpn. 2017, 69, 101. [Google Scholar] [CrossRef]
- McCully, C.; Hiramatsu, D.; Howell, D.A.; Hosseinzadeh, G.; Arcavi, I.; Kasen, D.; Barnes, J.; Shara, M.M.; Williams, T.B.; Väisänen, P.; et al. The Rapid Reddening and Featureless Optical Spectra of the Optical Counterpart of GW170817, AT 2017gfo, during the First Four Days. Astrophys. J. Lett. 2017, 848, L32. [Google Scholar] [CrossRef]
- Nicholl, M.; Berger, E.; Kasen, D.; Metzger, B.D.; Elias, J.; Briceño, C.; Alexander, K.D.; Blanchard, P.K.; Chornock, R.; Cowperthwaite, P.S.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. III. Optical and UV Spectra of a Blue Kilonova from Fast Polar Ejecta. Astrophys. J. Lett. 2017, 848, L18. [Google Scholar] [CrossRef]
- Shappee, B.J.; Simon, J.D.; Drout, M.R.; Piro, A.L.; Morrell, N.; Prieto, J.L.; Kasen, D.; Holoien, T.W.S.; Kollmeier, J.A.; Kelson, D.D.; et al. Early spectra of the gravitational wave source GW170817: Evolution of a neutron star merger. Science 2017, 358, 1574–1578. [Google Scholar] [CrossRef]
- Soares-Santos, M.; Holz, D.E.; Annis, J.; Chornock, R.; Herner, K.; Berger, E.; Brout, D.; Chen, H.Y.; Kessler, R.; Sako, M.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. I. Discovery of the Optical Counterpart Using the Dark Energy Camera. Astrophys. J. Lett. 2017, 848, L16. [Google Scholar] [CrossRef]
- Pian, E.; D’Avanzo, P.; Benetti, S.; Branchesi, M.; Brocato, E.; Campana, S.; Cappellaro, E.; Covino, S.; D’Elia, V.; Fynbo, J.P.U.; et al. Spectroscopic identification of r-process nucleosynthesis in a double neutron-star merger. Nature 2017, 551, 67–70. [Google Scholar] [CrossRef]
- Smartt, S.J.; Chen, T.W.; Jerkstrand, A.; Coughlin, M.; Kankare, E.; Sim, S.A.; Fraser, M.; Inserra, C.; Maguire, K.; Chambers, K.C.; et al. A kilonova as the electromagnetic counterpart to a gravitational-wave source. Nature 2017, 551, 75–79. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Levan, A.J.; González-Fernández, C.; Korobkin, O.; Mandel, I.; Rosswog, S.; Hjorth, J.; D’Avanzo, P.; Fruchter, A.S.; Fryer, C.L.; et al. The Emergence of a Lanthanide-rich Kilonova Following the Merger of Two Neutron Stars. Astrophys. J. Lett. 2017, 848, L27. [Google Scholar] [CrossRef]
- Arcavi, I. The First Hours of the GW170817 Kilonova and the Importance of Early Optical and Ultraviolet Observations for Constraining Emission Models. Astrophys. J. Lett. 2018, 855, L23. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo during the First Half of the Third Observing Run. Phys. Rev. X 2021, 11, 021053. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration; The KAGRA Collaboration; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; et al. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef]
- Dietrich, T.; Coughlin, M.W.; Pang, P.T.H.; Bulla, M.; Heinzel, J.; Issa, L.; Tews, I.; Antier, S. Multimessenger constraints on the neutron-star equation of state and the Hubble constant. Science 2020, 370, 1450–1453. [Google Scholar] [CrossRef]
- Kasliwal, M.M.; Anand, S.; Ahumada, T.; Stein, R.; Carracedo, A.S.; Andreoni, I.; Coughlin, M.W.; Singer, L.P.; Kool, E.C.; De, K.; et al. Kilonova Luminosity Function Constraints Based on Zwicky Transient Facility Searches for 13 Neutron Star Merger Triggers during O3. Astrophys. J. 2020, 905, 145. [Google Scholar] [CrossRef]
- Andreoni, I.; Goldstein, D.A.; Kasliwal, M.M.; Nugent, P.E.; Zhou, R.; Newman, J.A.; Bulla, M.; Foucart, F.; Hotokezaka, K.; Nakar, E.; et al. GROWTH on S190814bv: Deep Synoptic Limits on the Optical/Near-infrared Counterpart to a Neutron Star–Black Hole Merger. Astrophys. J. 2020, 890, 131. [Google Scholar] [CrossRef]
- Sagués Carracedo, A.; Bulla, M.; Feindt, U.; Goobar, A. Detectability of kilonovae in optical surveys: post-mortem examination of the LVC O3 run follow-up. Mon. Not. R. Astron. Soc. 2021, 504, 1294–1303. [Google Scholar] [CrossRef]
- Zhu, J.P.; Wu, S.; Yang, Y.P.; Zhang, B.; Yu, Y.W.; Gao, H.; Cao, Z.; Liu, L.D. No Detectable Kilonova Counterpart is Expected for O3 Neutron Star–Black Hole Candidates. Astrophys. J. 2021, 921, 156. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2018, 21, 3. [Google Scholar] [CrossRef]
- Weizmann Kiendrebeogo, R.; Farah, A.; Foley, E.; Gray, A.; Kunert, N.; Puecher, A.; Toivonen, A.; VandenBerg, R.; Anand, S.; Ahumada, T.; et al. Updated observing scenarios and multi-messenger implications for the International Gravitational-wave Network’s O4 and O5. arXiv 2023, arXiv:2306.09234. [Google Scholar]
- Petrov, P.; Singer, L.P.; Coughlin, M.W.; Kumar, V.; Almualla, M.; Anand, S.; Bulla, M.; Dietrich, T.; Foucart, F.; Guessoum, N. Data-driven Expectations for Electromagnetic Counterpart Searches Based on LIGO/Virgo Public Alerts. Astrophys. J. 2022, 924, 54. [Google Scholar] [CrossRef]
- Chase, E.A.; O’Connor, B.; Fryer, C.L.; Troja, E.; Korobkin, O.; Wollaeger, R.T.; Ristic, M.; Fontes, C.J.; Hungerford, A.L.; Herring, A.M. Kilonova Detectability with Wide-field Instruments. Astrophys. J. 2022, 927, 163. [Google Scholar] [CrossRef]
- Andreoni, I.; Margutti, R.; Salafia, O.S.; Parazin, B.; Villar, V.A.; Coughlin, M.W.; Yoachim, P.; Mortensen, K.; Brethauer, D.; Smartt, S.J.; et al. Target-of-opportunity Observations of Gravitational-wave Events with Vera C. Rubin Observatory. Astrophys. J. Suppl. 2022, 260, 18. [Google Scholar] [CrossRef]
- Rastinejad, J.C.; Paterson, K.; Fong, W.; Sand, D.J.; Lundquist, M.J.; Hosseinzadeh, G.; Christensen, E.; Daly, P.N.; Gibbs, A.R.; Hall, S.; et al. A Systematic Exploration of Kilonova Candidates from Neutron Star Mergers during the Third Gravitational-wave Observing Run. Astrophys. J. 2022, 927, 50. [Google Scholar] [CrossRef]
- WFST Collaboration; Wang, T.; Liu, G.; Cai, Z.; Gen, J.; Fang, M.; He, H.; Jiang, J.-a.; Jiang, N.; Kong, X.; et al. Sciences for The 2.5-meter Wide Field Survey Telescope (WFST). arXiv 2023, arXiv:2306.07590. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Lin, Z.Y.; Yu, J.M.; Wang, H.Y.; Mourani, G.M.; Zhao, W.; Dai, Z.G. Target-of-Opportunity Observation Detectability of Kilonovae with WFST. Astrophys. J. 2023, 947, 59. [Google Scholar] [CrossRef]
- Salafia, O.S.; Colpi, M.; Branchesi, M.; Chassande-Mottin, E.; Ghirlanda, G.; Ghisellini, G.; Vergani, S.D. Where and When: Optimal Scheduling of the Electromagnetic Follow-up of Gravitational-wave Events Based on Counterpart Light-curve Models. Astrophys. J. 2017, 846, 62. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Tao, D.; Chan, M.L.; Chatterjee, D.; Christensen, N.; Ghosh, S.; Greco, G.; Hu, Y.; Kapadia, S.; Rana, J.; et al. Optimizing searches for electromagnetic counterparts of gravitational wave triggers. Mon. Not. R. Astron. Soc. 2018, 478, 692–702. [Google Scholar] [CrossRef]
- Lei, L.; Zhu, Q.F.; Kong, X.; Wang, T.G.; Zheng, X.Z.; Shi, D.D.; Fan, L.L.; Liu, W. Limiting Magnitudes of the Wide Field Survey Telescope (WFST). Res. Astron. Astrophys. 2023, 23, 035013. [Google Scholar] [CrossRef]
- Deng, L.; Yang, F.; Chen, X.; He, F.; Liu, Q.; Zhang, B.; Zhang, C.; Wang, K.; Liu, N.; Ren, A.; et al. Lenghu on the Tibetan Plateau as an astronomical observing site. Nature 2021, 596, 353–356. [Google Scholar] [CrossRef]
- Andreoni, I.; Coughlin, M.W.; Kool, E.C.; Kasliwal, M.M.; Kumar, H.; Bhalerao, V.; Carracedo, A.S.; Ho, A.Y.Q.; Pang, P.T.H.; Saraogi, D.; et al. Fast-transient Searches in Real Time with ZTFReST: Identification of Three Optically Discovered Gamma-Ray Burst Afterglows and New Constraints on the Kilonova Rate. Astrophys. J. 2021, 918, 63. [Google Scholar] [CrossRef]
- Stachie, C.; Coughlin, M.W.; Christensen, N.; Muthukrishna, D. Using machine learning for transient classification in searches for gravitational-wave counterparts. Mon. Not. R. Astron. Soc. 2020, 497, 1320–1331. [Google Scholar] [CrossRef]
- Muthukrishna, D.; Narayan, G.; Mandel, K.S.; Biswas, R.; Hložek, R. RAPID: Early Classification of Explosive Transients Using Deep Learning. Proc. Astron. Soc. Pac. 2019, 131, 118002. [Google Scholar] [CrossRef]
- Chatterjee, D.; Narayan, G.; Aleo, P.D.; Malanchev, K.; Muthukrishna, D. El-CID: A filter for gravitational-wave electromagnetic counterpart identification. Mon. Not. R. Astron. Soc. 2021, 509, 914–930. [Google Scholar] [CrossRef]
- Biswas, B.; Ishida, E.E.O.; Peloton, J.; Moller, A.; Pruzhinskaya, M.V.; de Souza, R.S.; Muthukrishna, D. Enabling the discovery of fast transients: A kilonova science module for the Fink broker. arXiv 2022, arXiv:2210.17433. [Google Scholar]
- Sravan, N.; Graham, M.J.; Coughlin, M.W.; Ahumada, T.; Anand, S. Machine-directed gravitational-wave counterpart discovery. arXiv 2023, arXiv:2307.09213. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Ahumada, T.; Anand, S.; De, K.; Hankins, M.J.; Kasliwal, M.M.; Singer, L.P.; Bellm, E.C.; Andreoni, I.; Cenko, S.B.; et al. GROWTH on S190425z: Searching Thousands of Square Degrees to Identify an Optical or Infrared Counterpart to a Binary Neutron Star Merger with the Zwicky Transient Facility and Palomar Gattini-IR. Astrophys. J. 2019, 885, L19. [Google Scholar] [CrossRef]
- Antier, S.; Agayeva, S.; Almualla, M.; Awiphan, S.; Baransky, A.; Barynova, K.; Beradze, S.; Blažek, M.; Boër, M.; Burkhonov, O.; et al. GRANDMA observations of advanced LIGO’s and advanced Virgo’s third observational campaign. Mon. Not. R. Astron. Soc. 2020, 497, 5518–5539. [Google Scholar] [CrossRef]
- Anand, S.; Coughlin, M.W.; Kasliwal, M.M.; Bulla, M.; Ahumada, T.; Sagués Carracedo, A.; Almualla, M.; Andreoni, I.; Stein, R.; Foucart, F.; et al. Optical follow-up of the neutron star–black hole mergers S200105ae and S200115j. Nat. Astron. 2021, 5, 46–53. [Google Scholar] [CrossRef]
- Frostig, D.; Biscoveanu, S.; Mo, G.; Karambelkar, V.; Canton, T.D.; Chen, H.Y.; Kasliwal, M.; Katsavounidis, E.; Lourie, N.P.; Simcoe, R.A.; et al. An Infrared Search for Kilonovae with the WINTER Telescope. I. Binary Neutron Star Mergers. Astrophys. J. 2022, 926, 152. [Google Scholar] [CrossRef]
- Bulla, M. POSSIS: Predicting spectra, light curves, and polarization for multidimensional models of supernovae and kilonovae. Mon. Not. R. Astron. Soc. 2019, 489, 5037–5045. [Google Scholar] [CrossRef]
- Doctor, Z.; Farr, B.; Holz, D.E.; Pürrer, M. Statistical gravitational waveform models: What to simulate next? Phys. Rev. D 2017, 96, 123011. [Google Scholar] [CrossRef]
- Almualla, M.; Ning, Y.; Salehi, P.; Bulla, M.; Dietrich, T.; Coughlin, M.W.; Guessoum, N. Using Neural Networks to Perform Rapid High-Dimensional Kilonova Parameter Inference. arXiv 2021, arXiv:2112.15470. [Google Scholar] [CrossRef]
- Pang, P.; Dietrich, T.; Coughlin, M.; Bulla, M.; Tews, I.; Almualla, M.; Barna, T.; Kiendrebeogo, W.; Kunert, N.; Mansingh, G.; et al. NMMA: A nuclear-physics and multi-messenger astrophysics framework to analyze binary neutron star mergers. arXiv 2022, arXiv:2205.08513. [Google Scholar]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M.; Taniguchi, K. Dynamical mass ejection from the merger of asymmetric binary neutron stars: Radiation-hydrodynamics study in general relativity. Phys. Rev. D 2016, 93, 124046. [Google Scholar] [CrossRef]
- Dietrich, T.; Ujevic, M. Modeling dynamical ejecta from binary neutron star mergers and implications for electromagnetic counterparts. Class. Quantum Gravity 2017, 34, 105014. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Hotokezaka, K.; Fromm, S.A.; Bernuzzi, S.; Roberts, L.F. Binary Neutron Star Mergers: Mass Ejection, Electromagnetic Counterparts, and Nucleosynthesis. Astrophys. J. 2018, 869, 130. [Google Scholar] [CrossRef]
- Foucart, F.; Hinderer, T.; Nissanke, S. Remnant baryon mass in neutron star-black hole mergers: Predictions for binary neutron star mimickers and rapidly spinning black holes. Phys. Rev. D 2018, 98, 081501. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Dietrich, T.; Margalit, B.; Metzger, B.D. Multimessenger Bayesian parameter inference of a binary neutron star merger. Mon. Not. R. Astron. Soc. Lett. 2019, 489, L91–L96. [Google Scholar] [CrossRef]
- Nedora, V.; Schianchi, F.; Bernuzzi, S.; Radice, D.; Daszuta, B.; Endrizzi, A.; Perego, A.; Prakash, A.; Zappa, F. Mapping dynamical ejecta and disk masses from numerical relativity simulations of neutron star mergers. Class. Quantum Gravity 2022, 39, 015008. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Dietrich, T.; Doctor, Z.; Kasen, D.; Coughlin, S.; Jerkstrand, A.; Leloudas, G.; McBrien, O.; Metzger, B.D.; O’Shaughnessy, R.; et al. Constraints on the neutron star equation of state from AT2017gfo using radiative transfer simulations. Mon. Not. R. Astron. Soc. 2018, 480, 3871–3878. [Google Scholar] [CrossRef]
- Nicholl, M.; Margalit, B.; Schmidt, P.; Smith, G.P.; Ridley, E.J.; Nuttall, J. Tight multimessenger constraints on the neutron star equation of state from GW170817 and a forward model for kilonova light-curve synthesis. Mon. Not. Roy. Astron. Soc. 2021, 505, 3016–3032. [Google Scholar] [CrossRef]
- Bauswein, A.; Goriely, S.; Janka, H.T. Systematics of Dynamical Mass Ejection, Nucleosynthesis, and Radioactively Powered Electromagnetic Signals from Neutron-star Mergers. Astrophys. J. 2013, 773, 78. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Okawa, H.; Sekiguchi, Y.i.; Shibata, M.; Taniguchi, K. Mass ejection from the merger of binary neutron stars. Phys. Rev. D 2013, 87, 024001. [Google Scholar] [CrossRef]
- Lehner, L.; Liebling, S.L.; Palenzuela, C.; Caballero, O.L.; O’Connor, E.; Anderson, M.; Neilsen, D. Unequal mass binary neutron star mergers and multimessenger signals. Class. Quantum Gravity 2016, 33, 184002. [Google Scholar] [CrossRef]
- Fernández, R.; Kasen, D.; Metzger, B.D.; Quataert, E. Outflows from accretion discs formed in neutron star mergers: Effect of black hole spin. Mon. Not. R. Astron. Soc. 2015, 446, 750–758. [Google Scholar] [CrossRef]
- Siegel, D.M.; Metzger, B.D. Three-Dimensional General-Relativistic Magnetohydrodynamic Simulations of Remnant Accretion Disks from Neutron Star Mergers: Outflows and r -Process Nucleosynthesis. Phys. Rev. Lett. 2017, 119, 231102. [Google Scholar] [CrossRef]
- Fernández, R.; Tchekhovskoy, A.; Quataert, E.; Foucart, F.; Kasen, D. Long-term GRMHD simulations of neutron star merger accretion discs: Implications for electromagnetic counterparts. Mon. Not. R. Astron. Soc. 2019, 482, 3373–3393. [Google Scholar] [CrossRef]
- Christie, I.M.; Lalakos, A.; Tchekhovskoy, A.; Fernández, R.; Foucart, F.; Quataert, E.; Kasen, D. The role of magnetic field geometry in the evolution of neutron star merger accretion discs. Mon. Not. R. Astron. Soc. 2019, 490, 4811–4825. [Google Scholar] [CrossRef]
- Bulla, M. The critical role of nuclear heating rates, thermalization efficiencies, and opacities for kilonova modelling and parameter inference. Mon. Not. R. Astron. Soc. 2023, 520, 2558–2570. [Google Scholar] [CrossRef]
- Shrestha, M.; Bulla, M.; Nativi, L.; Markin, I.; Rosswog, S.; Dietrich, T. Impact of jets on kilonova photometric and polarimetric emission from binary neutron star mergers. arXiv 2023, arXiv:2303.14277. [Google Scholar] [CrossRef]
- Farrow, N.; Zhu, X.J.; Thrane, E. The Mass Distribution of Galactic Double Neutron Stars. Astrophys. J. 2019, 876, 18. [Google Scholar] [CrossRef]
- Woosley, S.E.; Weaver, T.A. The physics of supernova explosions. Annu. Rev. Astron. Astrophys. 1986, 24, 205–253. [Google Scholar] [CrossRef]
- Plewa, T.; Calder, A.C.; Lamb, D.Q. Type Ia Supernova Explosion: Gravitationally Confined Detonation. Astrophys. J. Lett. 2004, 612, L37–L40. [Google Scholar] [CrossRef]
- Hsiao, E.Y.; Conley, A.; Howell, D.A.; Sullivan, M.; Pritchet, C.J.; Carlberg, R.G.; Nugent, P.E.; Phillips, M.M. K-Corrections and Spectral Templates of Type Ia Supernovae. Astrophys. J. 2007, 663, 1187–1200. [Google Scholar] [CrossRef]
- Filippenko, A.V.; Richmond, M.W.; Branch, D.; Gaskell, M.; Herbst, W.; Ford, C.H.; Treffers, R.R.; Matheson, T.; Ho, L.C.; Dey, A.; et al. The Subluminous, Spectroscopically Peculiar Type 1a Supernova 1991bg in the Elliptical Galaxy NGC 4374. Astrophys. J. 1992, 104, 1543. [Google Scholar] [CrossRef]
- Phillips, M.M. The Absolute Magnitudes of Type IA Supernovae. Astrophys. J. Lett. 1993, 413, L105. [Google Scholar] [CrossRef]
- Eldridge, J.J.; Maund, J.R. The disappearance of the helium-giant progenitor of the Type Ib supernova iPTF13bvn and constraints on its companion. Mon. Not. R. Astron. Soc. 2016, 461, L117–L121. [Google Scholar] [CrossRef]
- Nugent, P.; Kim, A.; Perlmutter, S. K-Corrections and Extinction Corrections for Type Ia Supernovae. Proc. Astron. Soc. Pac. 2002, 114, 803–819. [Google Scholar] [CrossRef]
- Smartt, S.J.; Eldridge, J.J.; Crockett, R.M.; Maund, J.R. The death of massive stars—I. Observational constraints on the progenitors of Type II-P supernovae. Mon. Not. R. Astron. Soc. 2009, 395, 1409–1437. [Google Scholar] [CrossRef]
- Lunnan, R.; Chornock, R.; Berger, E.; Laskar, T.; Fong, W.; Rest, A.; Sanders, N.E.; Challis, P.M.; Drout, M.R.; Foley, R.J.; et al. Hydrogen-poor Superluminous Supernovae and Long-duration Gamma-Ray Bursts Have Similar Host Galaxies. Astrophys. J. 2014, 787, 138. [Google Scholar] [CrossRef]
- Chomiuk, L.; Chornock, R.; Soderberg, A.M.; Berger, E.; Chevalier, R.A.; Foley, R.J.; Huber, M.E.; Narayan, G.; Rest, A.; Gezari, S.; et al. Pan-STARRS1 Discovery of Two Ultraluminous Supernovae at z ≈ 0.9. Astrophys. J. 2011, 743, 114. [Google Scholar] [CrossRef]
- Quimby, R.M.; Kulkarni, S.R.; Kasliwal, M.M.; Gal-Yam, A.; Arcavi, I.; Sullivan, M.; Nugent, P.; Thomas, R.; Howell, D.A.; Nakar, E.; et al. Hydrogen-poor superluminous stellar explosions. Nature 2011, 474, 487–489. [Google Scholar] [CrossRef]
- Kessler, R.; Narayan, G.; Avelino, A.; Bachelet, E.; Biswas, R.; Brown, P.J.; Chernoff, D.F.; Connolly, A.J.; Dai, M.; Daniel, S.; et al. Models and Simulations for the Photometric LSST Astronomical Time Series Classification Challenge (PLAsTiCC). Proc. Astron. Soc. Pac. 2019, 131, 094501. [Google Scholar] [CrossRef]
- Feindt, U.; Nordin, J.; Rigault, M.; Brinnel, V.; Dhawan, S.; Goobar, A.; Kowalski, M. Simsurvey: Estimating transient discovery rates for the Zwicky transient facility. J. Cosmol. Astropart. Phys. 2019, 2019, 005. [Google Scholar] [CrossRef]
- Bai, S.; Zico Kolter, J.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Coulter, D.A.; Foley, R.J.; Kilpatrick, C.D.; Drout, M.R.; Piro, A.L.; Shappee, B.J.; Siebert, M.R.; Simon, J.D.; Ulloa, N.; Kasen, D.; et al. Swope Supernova Survey 2017a (SSS17a), the optical counterpart to a gravitational wave source. Science 2017, 358, 1556–1558. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Antier, S.; Agayeva, S.; Aivazyan, V.; Alishov, S.; Arbouch, E.; Baransky, A.; Barynova, K.; Bai, J.M.; Basa, S.; Beradze, S.; et al. The first six months of the Advanced LIGO’s and Advanced Virgo’s third observing run with GRANDMA. Mon. Not. R. Astron. Soc. 2020, 492, 3904–3927. [Google Scholar] [CrossRef]
- Morgan, R.; Soares-Santos, M.; Annis, J.; Herner, K.; Garcia, A.; Palmese, A.; Drlica-Wagner, A.; Kessler, R.; García-Bellido, J.; Bachmann, T.G.; et al. Constraints on the Physical Properties of GW190814 through Simulations Based on DECam Follow-up Observations by the Dark Energy Survey. Astrophys. J. 2020, 901, 83. [Google Scholar] [CrossRef]
- Liang, R.; Liu, Z.; Lei, L.; Zhao, W. Constraints Based on Non-detection of Kilonova Optical Searching. arXiv 2023, arXiv:2308.10545. [Google Scholar] [CrossRef]
- Reitze, D.; Adhikari, R.X.; Ballmer, S.; Barish, B.; Barsotti, L.; Billingsley, G.; Brown, D.A.; Chen, Y.; Coyne, D.; Eisenstein, R.; et al. Cosmic Explorer: The U.S. Contribution to Gravitational-Wave Astronomy beyond LIGO. Bull. Am. Astron. Soc. 2019, 51, 35. [Google Scholar]
- Maggiore, M.; Van Den Broeck, C.; Bartolo, N.; Belgacem, E.; Bertacca, D.; Bizouard, M.A.; Branchesi, M.; Clesse, S.; Foffa, S.; García-Bellido, J.; et al. Science case for the Einstein telescope. J. Cosmol. Astropart. Phys. 2020, 2020, 050. [Google Scholar] [CrossRef]
- Sánchez-Sáez, P.; Reyes, I.; Valenzuela, C.; Förster, F.; Eyheramendy, S.; Elorrieta, F.; Bauer, F.E.; Cabrera-Vives, G.; Estévez, P.A.; Catelan, M.; et al. Alert Classification for the ALeRCE Broker System: The Light Curve Classifier. Astrophys. J. 2021, 161, 141. [Google Scholar] [CrossRef]
- Smith, K. Lasair: The transient alert broker for LSST:UK. In Proceedings of the The Extragalactic Explosive Universe: The New Era of Transient Surveys and Data-Driven Discovery (EEU2019), ESO Garching, Munich, Germany, 16–19 September 2019; p. 51. [Google Scholar] [CrossRef]
- Yuan, W.; Zhang, C.; Feng, H.; Zhang, S.N.; Ling, Z.X.; Zhao, D.; Deng, J.; Qiu, Y.; Osborne, J.P.; O’Brien, P.; et al. Einstein Probe—A small mission to monitor and explore the dynamic X-ray Universe. arXiv 2015, arXiv:1506.07735. [Google Scholar] [CrossRef]
- Weisskopf, M.C.; Tananbaum, H.D.; Van Speybroeck, L.P.; O’Dell, S.L. Chandra X-ray Observatory (CXO): Overview. In Proceedings of the X-ray Optics, Instruments, and Missions III, Munich, Germany, 27 March–1 April 2000; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. Truemper, J.E., Aschenbach, B., Eds.; 2000; Volume 4012, pp. 2–16. [Google Scholar] [CrossRef]








| Object Type | Number Count | Rate |
|---|---|---|
| Bulla KN | 19,694 | - |
| MOSFiT KN | 20,459 | - |
| SNIa | 13,553 | |
| SNIbc | 2988 | |
| SNIIn | 5492 | |
| SNIIP | 926 | |
| SLSN | 4712 | |
| SNIa-91bg | 9180 |
| MD | PM | PMD | |
|---|---|---|---|
| 10 | 1.2629, 0.1234 | 1.2686, 0.1060 | 1.2723, 0.1060 |
| 15 | 1.3745, 0.1332 | 1.3724, 0.1149 | 1.3552, 0.1127 |
| 20 | 1.5154, 0.1445 | 1.440, 0.1184 | 1.4362, 0.1165 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, R.; Liu, Z.; Lei, L.; Zhao, W. Kilonova-Targeting Lightcurve Classification for Wide Field Survey Telescope. Universe 2024, 10, 10. https://doi.org/10.3390/universe10010010
Liang R, Liu Z, Lei L, Zhao W. Kilonova-Targeting Lightcurve Classification for Wide Field Survey Telescope. Universe. 2024; 10(1):10. https://doi.org/10.3390/universe10010010
Chicago/Turabian StyleLiang, Runduo, Zhengyan Liu, Lei Lei, and Wen Zhao. 2024. "Kilonova-Targeting Lightcurve Classification for Wide Field Survey Telescope" Universe 10, no. 1: 10. https://doi.org/10.3390/universe10010010






