- Article
Gauge-Invariant Gravitational Wave Polarization in Metric f(R) Gravity with Cosmological Implications
- Ramesh Radhakrishnan,
- David McNutt and
- Gerald Cleaver
- + 4 authors
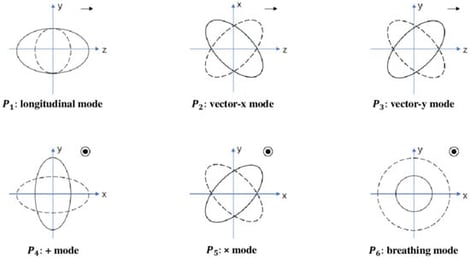
We develop a fully gauge-invariant analysis of gravitational-wave polarizations in metric gravity with a particular focus on the modified Starobinsky model
5 February 2026