Comparing Numerical Relativity and Perturbation Theory Waveforms for a Non-Spinning Equal-Mass Binary
Abstract
1. Introduction
2. NR and ppBHPT Data at
3. Comparing NR and ppBHPT at
3.1. Model Calibration Setup
3.2. Setting a Common Mass Scale
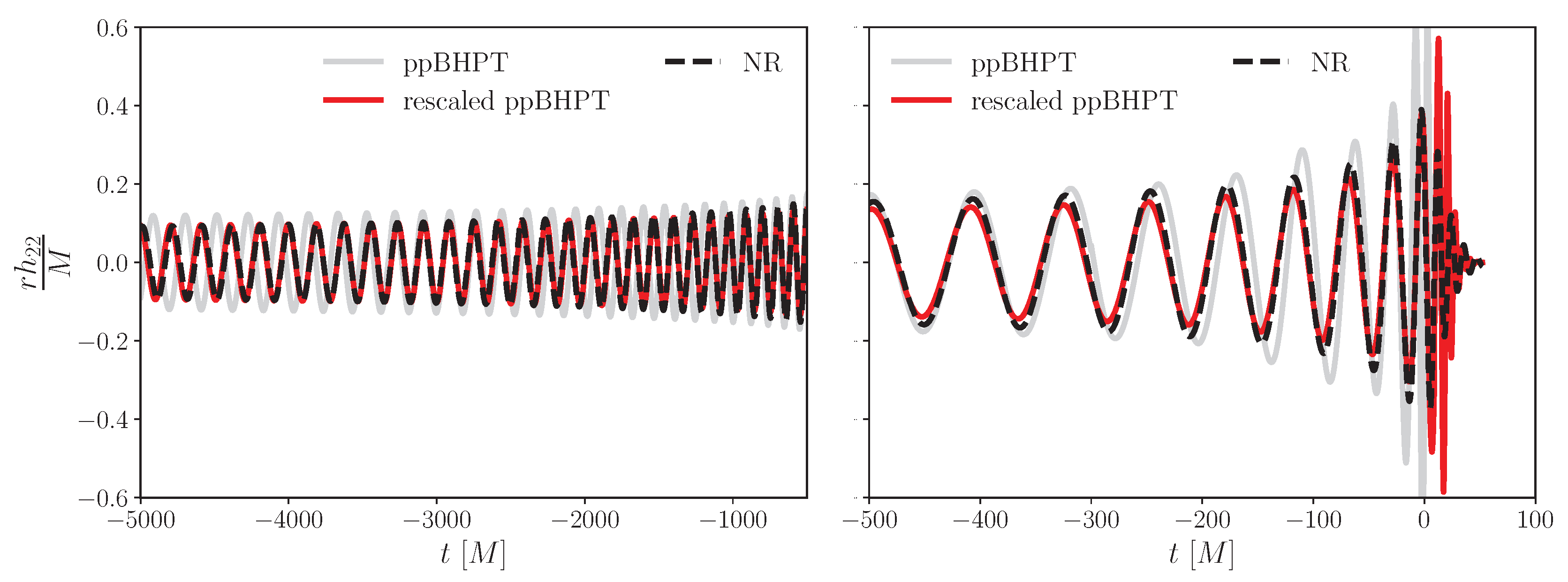
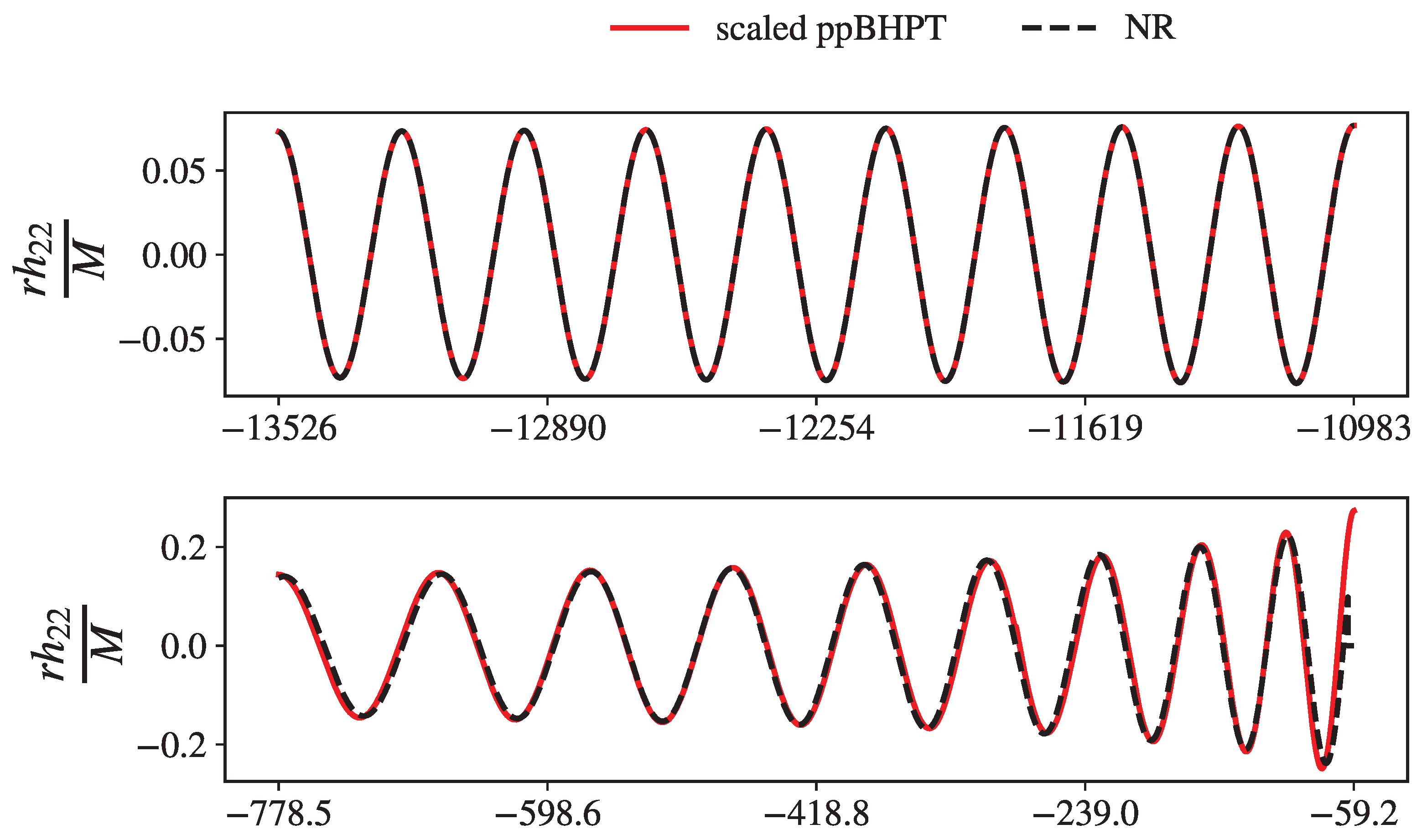
3.3. Effectiveness of the - Scaling at
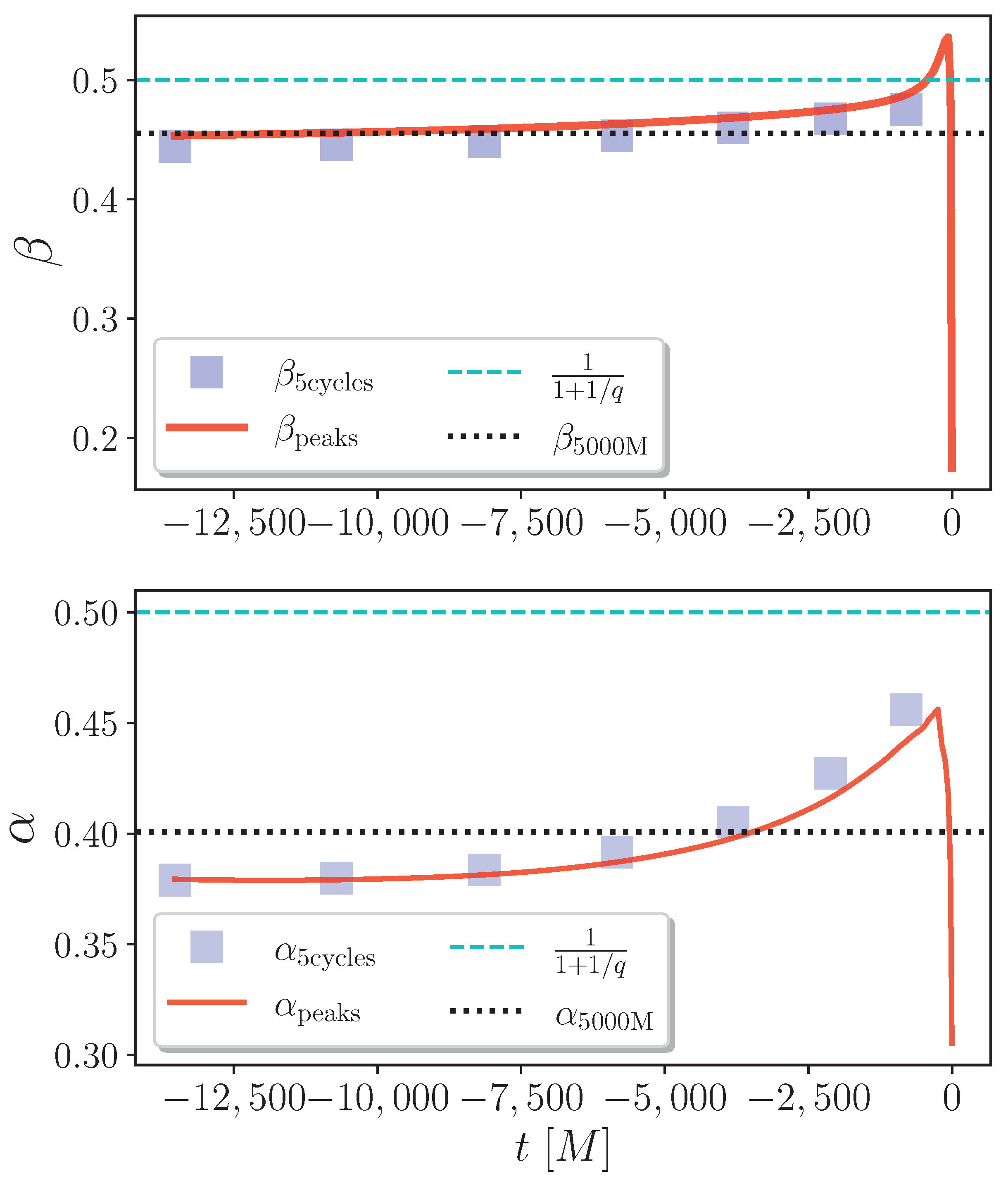
3.4. Exploring the Time Dependence of - Parameters from Different Methods
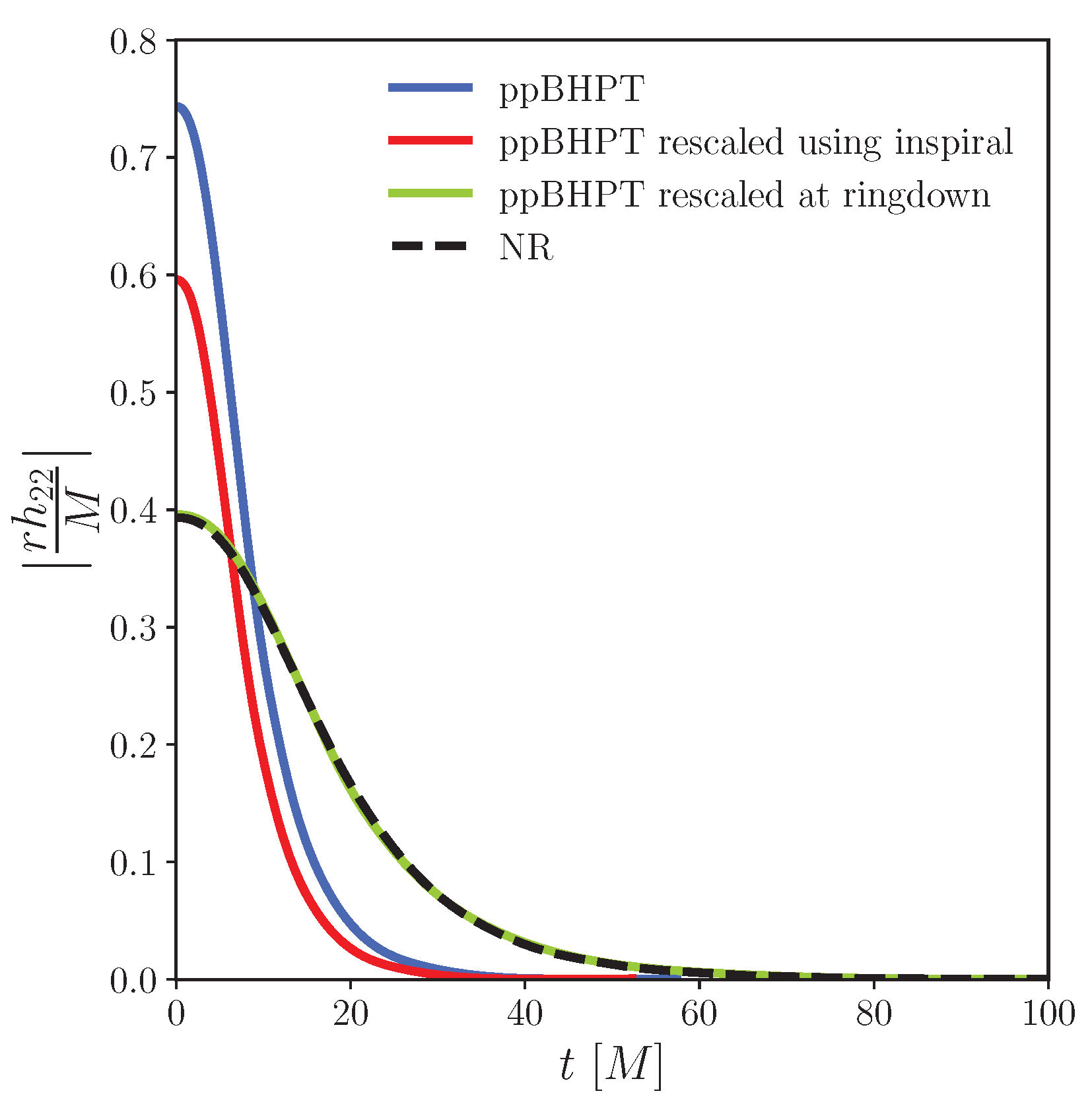
3.5. Understanding - Values at the Ringdown
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blackman, J.; Field, S.E.; Galley, C.R.; Szilágyi, B.; Scheel, M.A.; Tiglio, M.; Hemberger, D.A. Fast and Accurate Prediction of Numerical Relativity Waveforms from Binary Black Hole Coalescences Using Surrogate Models. Phys. Rev. Lett. 2015, 115, 121102. [Google Scholar] [CrossRef]
- Blackman, J.; Field, S.E.; Scheel, M.A.; Galley, C.R.; Ott, C.D.; Boyle, M.; Kidder, L.E.; Pfeiffer, H.P.; Szilágyi, B. Numerical relativity waveform surrogate model for generically precessing binary black hole mergers. Phys. Rev. 2017, D96, 024058. [Google Scholar] [CrossRef]
- Blackman, J.; Field, S.E.; Scheel, M.A.; Galley, C.R.; Hemberger, D.A.; Schmidt, P.; Smith, R. A Surrogate Model of Gravitational Waveforms from Numerical Relativity Simulations of Precessing Binary Black Hole Mergers. Phys. Rev. D 2017, 95, 104023. [Google Scholar] [CrossRef]
- Varma, V.; Field, S.E.; Scheel, M.A.; Blackman, J.; Kidder, L.E.; Pfeiffer, H.P. Surrogate model of hybridized numerical relativity binary black hole waveforms. Phys. Rev. 2019, D99, 064045. [Google Scholar] [CrossRef]
- Varma, V.; Field, S.E.; Scheel, M.A.; Blackman, J.; Gerosa, D.; Stein, L.C.; Kidder, L.E.; Pfeiffer, H.P. Surrogate models for precessing binary black hole simulations with unequal masses. Phys. Rev. Res. 2019, 1, 033015. [Google Scholar] [CrossRef]
- Islam, T.; Varma, V.; Lodman, J.; Field, S.E.; Khanna, G.; Scheel, M.A.; Pfeiffer, H.P.; Gerosa, D.; Kidder, L.E. Eccentric binary black hole surrogate models for the gravitational waveform and remnant properties: Comparable mass, nonspinning case. Phys. Rev. D 2021, 103, 064022. [Google Scholar] [CrossRef]
- Bohé, A.; Shao, L.; Taracchini, A.; Buonanno, A.; Babak, S.; Harry, I.W.; Hinder, I.; Ossokine, S.; Pürrer, M.; Raymond, V.; et al. Improved effective-one-body model of spinning, nonprecessing binary black holes for the era of gravitational-wave astrophysics with advanced detectors. Phys. Rev. D 2017, 95, 044028. [Google Scholar] [CrossRef]
- Cotesta, R.; Buonanno, A.; Bohé, A.; Taracchini, A.; Hinder, I.; Ossokine, S. Enriching the Symphony of Gravitational Waves from Binary Black Holes by Tuning Higher Harmonics. Phys. Rev. D 2018, 98, 084028. [Google Scholar] [CrossRef]
- Cotesta, R.; Marsat, S.; Pürrer, M. Frequency domain reduced order model of aligned-spin effective-one-body waveforms with higher-order modes. Phys. Rev. D 2020, 101, 124040. [Google Scholar] [CrossRef]
- Pan, Y.; Buonanno, A.; Taracchini, A.; Kidder, L.E.; Mroué, A.H.; Pfeiffer, H.P.; Scheel, M.A.; Szilágyi, B. Inspiral-merger-ringdown waveforms of spinning, precessing black-hole binaries in the effective-one-body formalism. Phys. Rev. D 2014, 89, 084006. [Google Scholar] [CrossRef]
- Babak, S.; Taracchini, A.; Buonanno, A. Validating the effective-one-body model of spinning, precessing binary black holes against numerical relativity. Phys. Rev. D 2017, 95, 024010. [Google Scholar] [CrossRef]
- Husa, S.; Khan, S.; Hannam, M.; Pürrer, M.; Ohme, F.; Jiménez Forteza, X.; Bohé, A. Frequency-domain gravitational waves from nonprecessing black-hole binaries. I. New numerical waveforms and anatomy of the signal. Phys. Rev. D 2016, 93, 044006. [Google Scholar] [CrossRef]
- Khan, S.; Husa, S.; Hannam, M.; Ohme, F.; Pürrer, M.; Jiménez Forteza, X.; Bohé, A. Frequency-domain gravitational waves from nonprecessing black-hole binaries. II. A phenomenological model for the advanced detector era. Phys. Rev. D 2016, 93, 044007. [Google Scholar] [CrossRef]
- London, L.; Khan, S.; Fauchon-Jones, E.; García, C.; Hannam, M.; Husa, S.; Jiménez-Forteza, X.; Kalaghatgi, C.; Ohme, F.; Pannarale, F. First higher-multipole model of gravitational waves from spinning and coalescing black-hole binaries. Phys. Rev. Lett. 2018, 120, 161102. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Chatziioannou, K.; Hannam, M.; Ohme, F. Phenomenological model for the gravitational-wave signal from precessing binary black holes with two-spin effects. Phys. Rev. D 2019, 100, 024059. [Google Scholar] [CrossRef]
- Mroue, A.H.; Scheel, M.A.; Szilágyi, B.; Pfeiffer, H.P.; Boyle, M.; Hemberger, D.A.; Kidder, L.E.; Lovelace, G.; Ossokine, S.; Taylor, N.W.; et al. Catalog of 174 Binary Black Hole Simulations for Gravitational Wave Astronomy. Phys. Rev. Lett. 2013, 111, 241104. [Google Scholar] [CrossRef]
- Boyle, M.; Hemberger, D.; Iozzo, D.A.B.; Lovelace, G.; Ossokine, S.; Pfeiffer, H.P.; Scheel, M.A.; Stein, L.C.; Woodford, C.J.; Zimmerman, A.B.; et al. The SXS Collaboration catalog of binary black hole simulations. Class. Quant. Grav. 2019, 36, 195006. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O.; Zlochower, Y.; Campanelli, M. The RIT binary black hole simulations catalog. Class. Quant. Grav. 2017, 34, 224001. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O.; Lange, J.; O’Shaughnessy, R.; Zlochower, Y.; Campanelli, M. Second RIT binary black hole simulations catalog and its application to gravitational waves parameter estimation. Phys. Rev. D 2019, 100, 024021. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O. Third RIT binary black hole simulations catalog. Phys. Rev. D 2020, 102, 104018. [Google Scholar] [CrossRef]
- Healy, J.; Lousto, C.O. Fourth RIT binary black hole simulations catalog: Extension to eccentric orbits. Phys. Rev. D 2022, 105, 124010. [Google Scholar] [CrossRef]
- Jani, K.; Healy, J.; Clark, J.A.; London, L.; Laguna, P.; Shoemaker, D. Georgia Tech Catalog of Gravitational Waveforms. Class. Quant. Grav. 2016, 33, 204001. [Google Scholar] [CrossRef]
- Hamilton, E.; Fauchon-Jones, E.; Hannam, M.; Hoy, C.; Kalaghatgi, C.; London, L.; Thompson, J.E.; Yeeles, D.; Ghosh, S.; Khan, S.; et al. A catalogue of precessing black-hole-binary numerical-relativity simulations. arXiv 2023, arXiv:2303.05419. [Google Scholar]
- Yoo, J.; Varma, V.; Giesler, M.; Scheel, M.A.; Haster, C.J.; Pfeiffer, H.P.; Kidder, L.E.; Boyle, M. Targeted large mass ratio numerical relativity surrogate waveform model for GW190814. Phys. Rev. D 2022, 106, 044001. [Google Scholar] [CrossRef]
- Lousto, C.O.; Healy, J. Study of the intermediate mass ratio black hole binary merger up to 1000: 1 with numerical relativity. Class. Quantum Grav. 2023, 40, 09LT01. [Google Scholar] [CrossRef]
- Lopez-Aleman, R.; Khanna, G.; Pullin, J. Perturbative evolution of particle orbits around Kerr black holes: Time domain calculation. Class. Quant. Grav. 2003, 20, 3259. [Google Scholar] [CrossRef]
- Khanna, G. Teukolsky evolution of particle orbits around Kerr black holes in the time domain: Elliptic and inclined orbits. Phys. Rev. D 2004, 69, 024016. [Google Scholar] [CrossRef]
- Burko, L.; Khanna, G. Accurate time-domain gravitational waveforms for extreme-mass-ratio binaries. Europhys. Lett. 2007, 78, 60005. [Google Scholar] [CrossRef]
- Sundararajan, P.A.; Khanna, G.; Hughes, S.A.; Drasco, S. Towards adiabatic waveforms for inspiral into Kerr black holes: II. Dynamical sources and generic orbits. Phys. Rev. D 2008, 78, 024022. [Google Scholar] [CrossRef]
- Sundararajan, P.A.; Khanna, G.; Hughes, S.A. Binary black hole merger gravitational waves and recoil in the large mass ratio limit. Phys. Rev. D 2010, 81, 104009. [Google Scholar] [CrossRef]
- Zenginoglu, A.; Khanna, G. Null infinity waveforms from extreme-mass-ratio inspirals in Kerr spacetime. Phys. Rev. X 2011, 1, 021017. [Google Scholar] [CrossRef]
- Fujita, R.; Tagoshi, H. New numerical methods to evaluate homogeneous solutions of the Teukolsky equation. Prog. Theor. Phys. 2004, 112, 415–450. [Google Scholar] [CrossRef]
- Fujita, R.; Tagoshi, H. New Numerical Methods to Evaluate Homogeneous Solutions of the Teukolsky Equation II. Solutions of the Continued Fraction Equation. Prog. Theor. Phys. 2005, 113, 1165–1182. [Google Scholar] [CrossRef]
- Mano, S.; Suzuki, H.; Takasugi, E. Analytic solutions of the Teukolsky equation and their low frequency expansions. Prog. Theor. Phys. 1996, 95, 1079–1096. [Google Scholar] [CrossRef]
- Throwe, W.W.T. High Precision Calculation of Generic Extreme Mass Ratio Inspirals. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2010. [Google Scholar]
- O’Sullivan, S.; Hughes, S.A. Strong-field tidal distortions of rotating black holes: Formalism and results for circular, equatorial orbits. Phys. Rev. D 2014, 90, 124039. [Google Scholar] [CrossRef]
- Drasco, S.; Hughes, S.A. Gravitational wave snapshots of generic extreme mass ratio inspirals. Phys. Rev. D 2006, 73, 024027, Erratum in Phys. Rev. D 2013, 88, 109905; Erratum in Phys. Rev. D 2014, 90, 109905. [Google Scholar] [CrossRef]
- Price, R.H.; Pullin, J. Colliding black holes: The Close limit. Phys. Rev. Lett. 1994, 72, 3297–3300. [Google Scholar] [CrossRef]
- Lousto, C.O.; Nakano, H.; Zlochower, Y.; Campanelli, M. Intermediate Mass Ratio Black Hole Binaries: Numerical Relativity meets Perturbation Theory. Phys. Rev. Lett. 2010, 104, 211101. [Google Scholar] [CrossRef]
- Lousto, C.O.; Nakano, H.; Zlochower, Y.; Campanelli, M. Intermediate-mass-ratio black hole binaries: Intertwining numerical and perturbative techniques. Phys. Rev. D 2010, 82, 104057. [Google Scholar] [CrossRef]
- Nakano, H.; Zlochower, Y.; Lousto, C.O.; Campanelli, M. Intermediate-mass-ratio black hole binaries II: Modeling Trajectories and Gravitational Waveforms. Phys. Rev. D 2011, 84, 124006. [Google Scholar] [CrossRef]
- Pound, A.; Wardell, B. Black hole perturbation theory and gravitational self-force. In Handbook of Gravitational Wave Astronomy; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Miller, J.; Pound, A. Two-timescale evolution of extreme-mass-ratio inspirals: Waveform generation scheme for quasicircular orbits in Schwarzschild spacetime. Phys. Rev. D 2021, 103, 064048. [Google Scholar] [CrossRef]
- Wardell, B.; Pound, A.; Warburton, N.; Miller, J.; Durkan, L.; Le Tiec, A. Gravitational waveforms for compact binaries from second-order self-force theory. Phys. Rev. Lett. 2021, 130, 241402. [Google Scholar] [CrossRef] [PubMed]
- Islam, T.; Field, S.E.; Hughes, S.A.; Khanna, G.; Varma, V.; Giesler, M.; Scheel, M.A.; Kidder, L.E.; Pfeiffer, H.P. Surrogate model for gravitational wave signals from nonspinning, comparable-to large-mass-ratio black hole binaries built on black hole perturbation theory waveforms calibrated to numerical relativity. Phys. Rev. D 2022, 106, 104025. [Google Scholar] [CrossRef]
- Rifat, N.E.M.; Field, S.E.; Khanna, G.; Varma, V. Surrogate model for gravitational wave signals from comparable and large-mass-ratio black hole binaries. Phys. Rev. D 2020, 101, 081502. [Google Scholar] [CrossRef]
- Anninos, P.; Price, R.H.; Pullin, J.; Seidel, E.; Suen, W.M. Headon collision of two black holes: Comparison of different approaches. Phys. Rev. D 1995, 52, 4462–4480. [Google Scholar] [CrossRef] [PubMed]
- Baker, J.G.; Abrahams, A.; Anninos, P.; Brandt, S.; Price, R.; Pullin, J.; Seidel, E. The Collision of boosted black holes. Phys. Rev. D 1997, 55, 829–834. [Google Scholar] [CrossRef]
- Nollert, H.P.; Baker, J.G.; Price, R.; Pullin, J. A Slightly less grand challenge: Colliding black holes using perturbation techniques. In Proceedings of the 18th Texas Symposium on Relativistic Astrophysics, Chicago, IL, USA, 15–20 December 1996; pp. 604–606. [Google Scholar]
- Khanna, G.; Baker, J.G.; Gleiser, R.J.; Laguna, P.; Nicasio, C.O.; Nollert, H.P.; Price, R.; Pullin, J. Inspiralling black holes: The Close limit. Phys. Rev. Lett. 1999, 83, 3581–3584. [Google Scholar] [CrossRef]
- Khanna, G.; Gleiser, R.; Price, R.; Pullin, J. Close limit of grazing black hole collisions: Nonspinning holes. New J. Phys. 2000, 2, 3. [Google Scholar] [CrossRef]
- Sundararajan, P.A.; Khanna, G.; Hughes, S.A. Towards adiabatic waveforms for inspiral into Kerr black holes. I. A New model of the source for the time domain perturbation equation. Phys. Rev. D 2007, 76, 104005. [Google Scholar] [CrossRef]
- Field, S.; Islam, T.; Khanna, G.; Rifat, N.; Varma, V. BHPTNRSurrogate. Available online: http://bhptoolkit.org/BHPTNRSurrogate/ (accessed on 7 December 2022).
- Black Hole Perturbation Toolkit. Available online: http://bhptoolkit.org/ (accessed on 7 December 2022).
- Islam, T.; Khanna, G. Interplay between numerical relativity and perturbation theory: Finite size effects. Phys. Rev. D 2023, 108, 044012. [Google Scholar] [CrossRef]
- Islam, T.; Field, S.E.; Khanna, G. Remnant black hole properties from numerical-relativity-informed perturbation theory and implications for waveform modelling. arXiv 2023, arXiv:2301.07215. [Google Scholar]
- Islam, T.; Khanna, G. On the approximate relation between black-hole perturbation theory and numerical relativity. arXiv 2023, arXiv:2307.03155. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, T.; Field, S.E.; Khanna, G. Comparing Numerical Relativity and Perturbation Theory Waveforms for a Non-Spinning Equal-Mass Binary. Universe 2024, 10, 25. https://doi.org/10.3390/universe10010025
Islam T, Field SE, Khanna G. Comparing Numerical Relativity and Perturbation Theory Waveforms for a Non-Spinning Equal-Mass Binary. Universe. 2024; 10(1):25. https://doi.org/10.3390/universe10010025
Chicago/Turabian StyleIslam, Tousif, Scott E. Field, and Gaurav Khanna. 2024. "Comparing Numerical Relativity and Perturbation Theory Waveforms for a Non-Spinning Equal-Mass Binary" Universe 10, no. 1: 25. https://doi.org/10.3390/universe10010025
APA StyleIslam, T., Field, S. E., & Khanna, G. (2024). Comparing Numerical Relativity and Perturbation Theory Waveforms for a Non-Spinning Equal-Mass Binary. Universe, 10(1), 25. https://doi.org/10.3390/universe10010025





