Mercury’s Bow Shock and Magnetopause Variations According to MESSENGER Data
Abstract
:1. Introduction
2. Methodology for Variations Determination
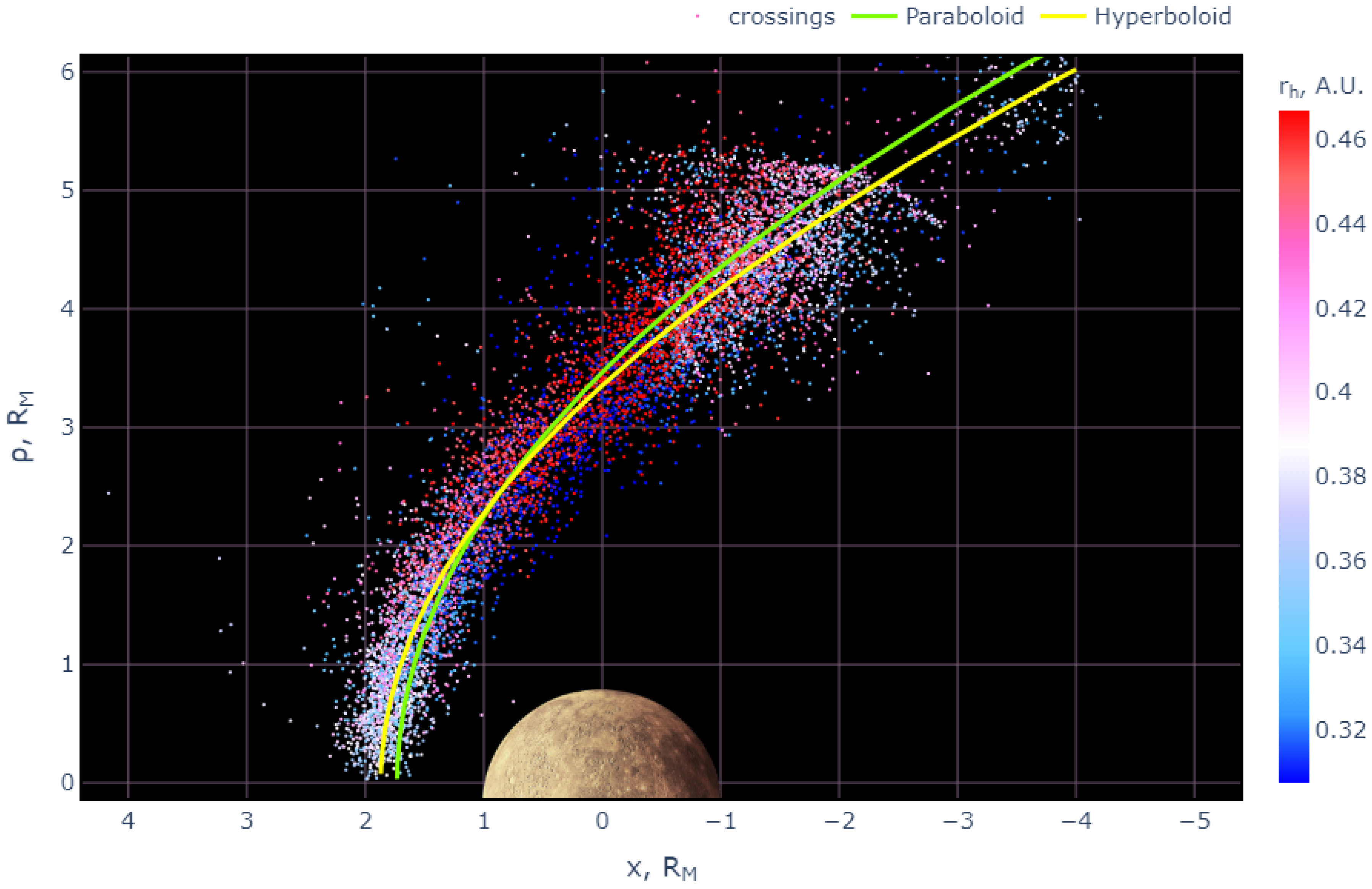
2.1. Bow Shock Surface Shape
2.2. Magnetopause Surface Shape
2.3. Magnetopause Flaring
3. Results
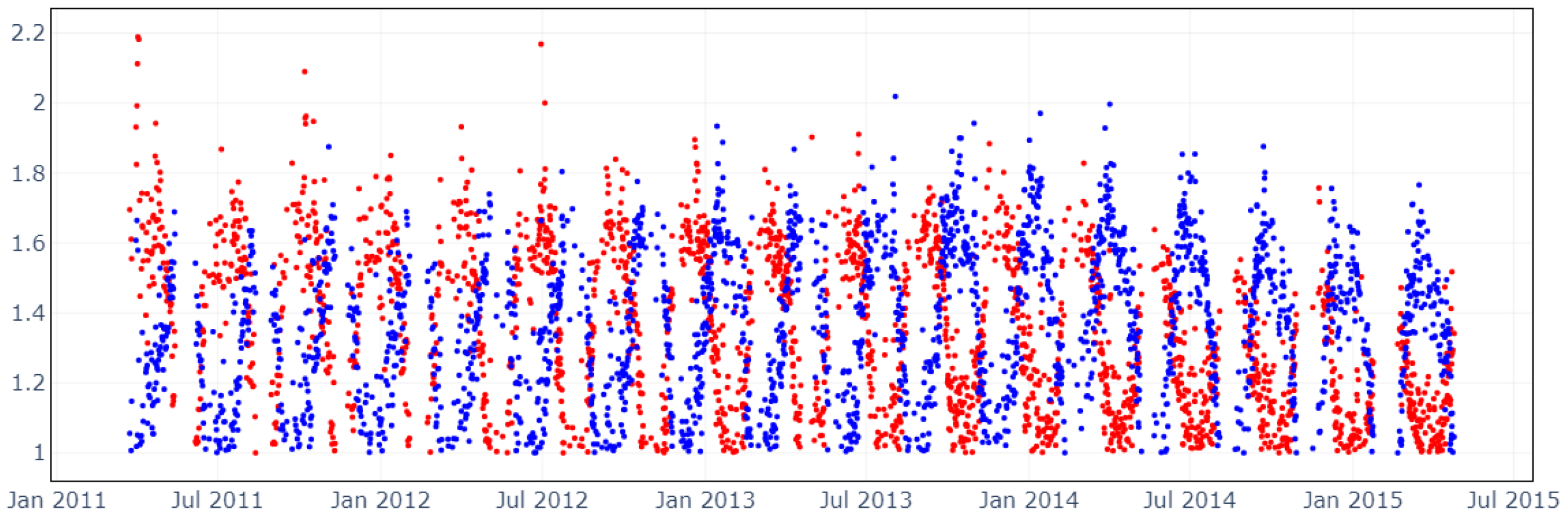
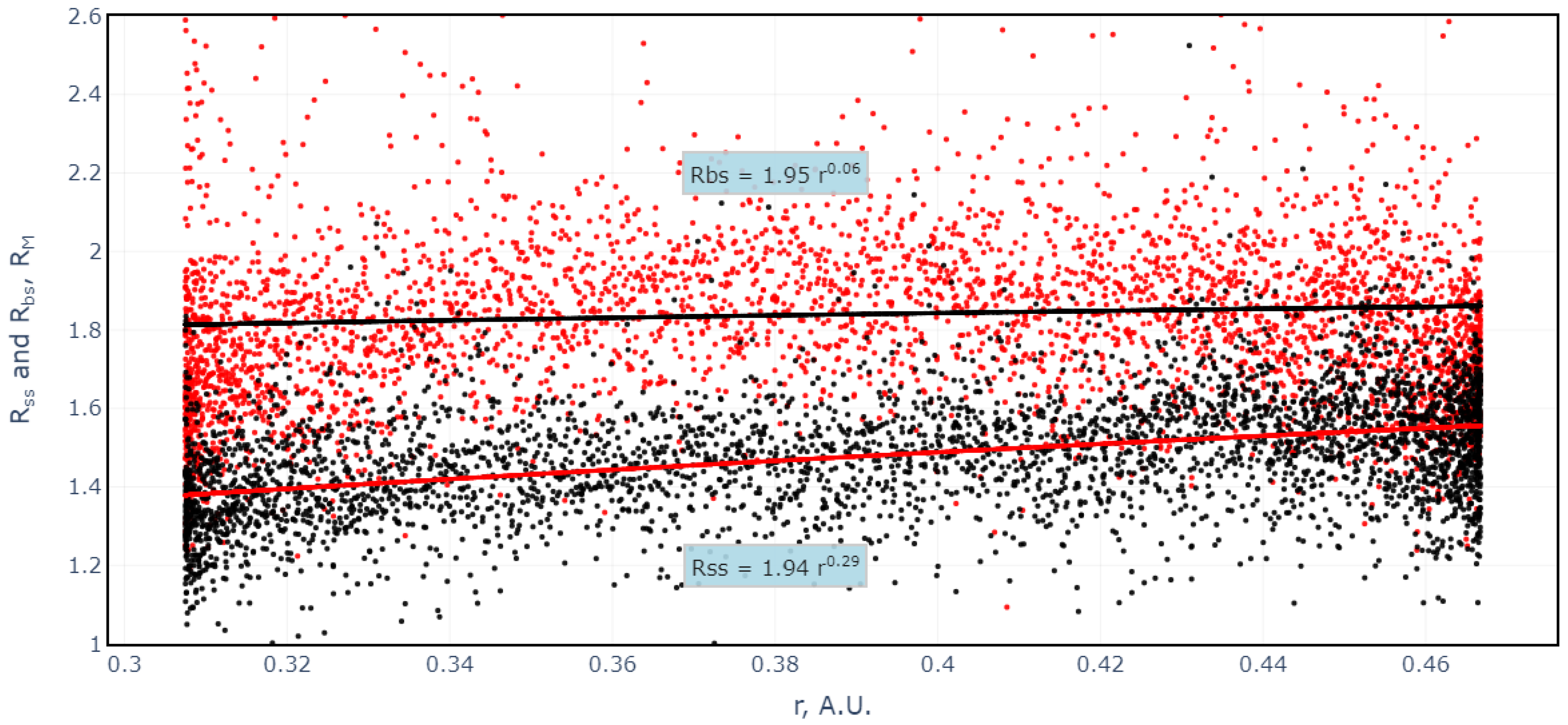
3.1. Magnetopause and Bow Shock Subsolar Distances
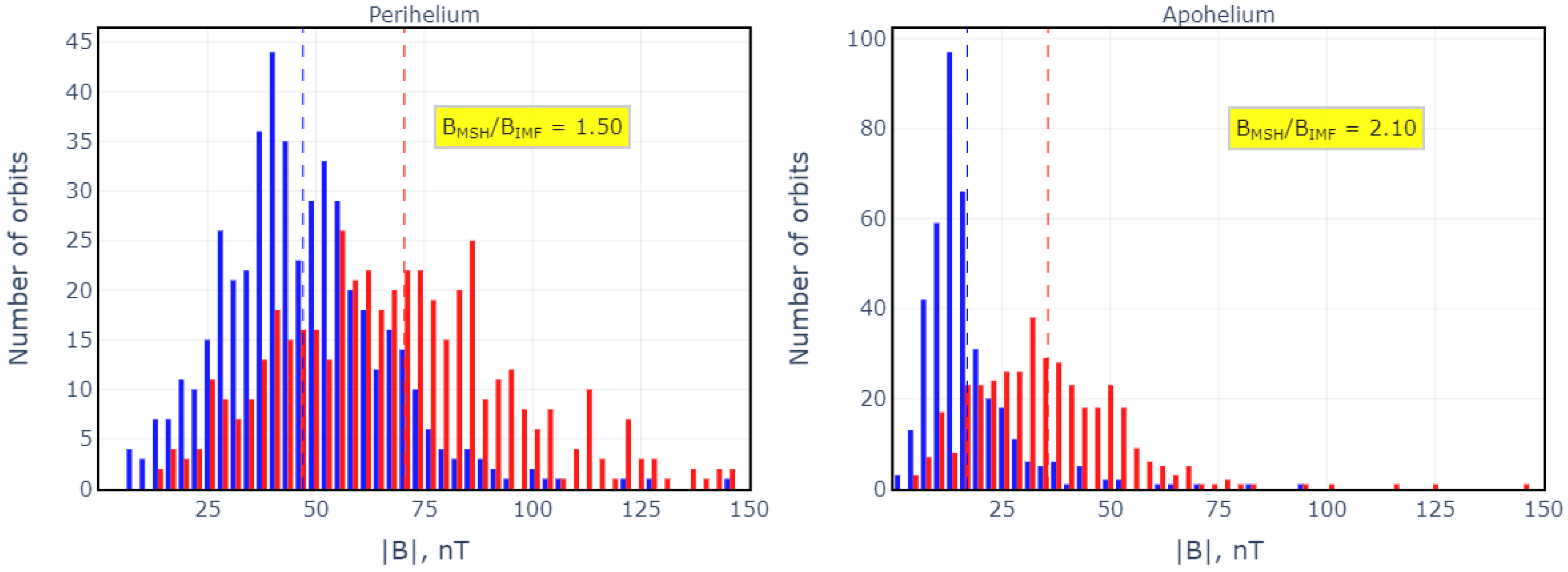
3.2. Variations of the Interplanetary Magnetic Field and the Magnetosheath Magnetic Field
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| IMF | Interplanetary Magnetic Field |
References
- Alexeev, I.I.; Belenkaya, E.S.; Bobrovnikov, S.Y.; Slavin, J.A.; Sarantos, M. Paraboloid model of Mercury’s magnetosphere. J. Geophys. Res. Space Phys. 2008, 113, A12210. [Google Scholar] [CrossRef]
- Alexeev, I.I.; Belenkaya, E.S.; Slavin, J.A.; Korth, H.; Anderson, B.J.; Baker, D.N.; Boardsen, S.A.; Johnson, C.L.; Purucker, M.E.; Sarantos, M.; et al. Mercury’s magnetospheric magnetic field after the first two MESSENGER flybys. Icarus 2010, 209, 23–39. [Google Scholar] [CrossRef]
- Anderson, B.J.; Johnson, C.L.; Korth, H.; Winslow, R.M.; Borovsky, J.E.; Purucker, M.E.; Slavin, J.A.; Solomon, S.C.; Zuber, M.T.; McNutt, R.L., Jr. Low-degree structure in Mercury’s planetary magnetic field. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef]
- Winslow, R.M.; Anderson, B.J.; Johnson, C.L.; Slavin, J.A.; Korth, H.; Purucker, M.E.; Baker, D.N.; Solomon, S.C. Mercury’s magnetopause and bow shock from MESSENGER Magnetometer observations. J. Geophys. Res. Space Phys. 2013, 118, 2213–2227. [Google Scholar] [CrossRef]
- Slavin, J.A.; DiBraccio, G.A.; Gershman, D.J.; Imber, S.M.; Poh, G.K.; Raines, J.M.; Zurbuchen, T.H.; Jia, X.; Baker, D.N.; Glassmeier, K.H.; et al. MESSENGER observations of Mercury’s dayside magnetosphere under extreme solar wind conditions. J. Geophys. Res. Space Phys. 2014, 119, 8087–8116. [Google Scholar] [CrossRef]
- Slavin, J.A.; Middleton, H.R.; Raines, J.M.; Jia, X.; Zhong, J.; Sun, W.J.; Livi, S.; Imber, S.M.; Poh, G.K.; Akhavan-Tafti, M.; et al. MESSENGER Observations of Disappearing Dayside Magnetosphere Events at Mercury. J. Geophys. Res. Space Phys. 2019, 124, 6613–6635. [Google Scholar] [CrossRef]
- Philpott, L.C.; Johnson, C.L.; Winslow, R.M.; Anderson, B.J.; Korth, H.; Purucker, M.E.; Solomon, S.C. Constraints on the secular variation of Mercury’s magnetic field from the combined analysis of MESSENGER and Mariner 10 data. Geophys. Res. Lett. 2014, 41, 6627–6634. [Google Scholar] [CrossRef]
- Siscoe, G.; Christopher, L. Variations in the solar wind stand-off distance at Mercury. Geophys. Res. Lett. 1975, 2, 158–160. [Google Scholar] [CrossRef]
- Russell, C.T. On the relative locations of the bow shocks of the terrestrial planets. Geophys. Res. Lett. 1977, 4, 387–390. [Google Scholar] [CrossRef]
- Shue, J.H.; Chao, J.K.; Fu, H.C.; Russell, C.T.; Song, P.; Khurana, K.K.; Singer, H.J. A new functional form to study the solar wind control of the magnetopause size and shape. J. Geophys. Res. Space Phys. 1997, 102, 9497–9511. [Google Scholar] [CrossRef]
- Johnson, C.L.; Philpott, L.C.; Anderson, B.J.; Korth, H.; Hauck II, S.A.; Heyner, D.; Phillips, R.J.; Winslow, R.M.; Solomon, S.C. MESSENGER observations of induced magnetic fields in Mercury’s core. Geophys. Res. Lett. 2016, 43, 2436–2444. [Google Scholar] [CrossRef]
- Philpott, L.C.; Johnson, C.L.; Anderson, B.J.; Winslow, R.M. The Shape of Mercury’s Magnetopause: The Picture From MESSENGER Magnetometer Observations and Future Prospects for BepiColombo. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027544. [Google Scholar] [CrossRef]
- Zhong, J.; Wan, W.X.; Slavin, J.A.; Wei, Y.; Lin, R.L.; Chai, L.H.; Raines, J.M.; Rong, Z.J.; Han, X.H. Mercury’s three-dimensional asymmetric magnetopause. J. Geophys. Res. Space Phys. 2015, 120, 7658–7671. [Google Scholar] [CrossRef]
- Zhong, J.; Wan, W.X.; Wei, Y.; Slavin, J.A.; Raines, J.M.; Rong, Z.J.; Chai, L.H.; Han, X.H. Compressibility of Mercury’s dayside magnetosphere. Geophys. Res. Lett. 2015, 42, 10135–10139. [Google Scholar] [CrossRef]
- Zhong, J.H.; Shue, J.H.; Wei, Y.; Slavin, J.A.; Zhang, H.; Rong, Z.J.; Chai, L.H.; Wan, W.X. Effects of Orbital Eccentricity and IMF Cone Angle on the Dimensions of Mercury’s Magnetosphere. Astrophys. J. 2020, 892, 2. [Google Scholar] [CrossRef]
- He, P.; Xu, X.; Yu, H.; Wang, X.; Wang, M.; Chang, Q.; Zhou, Z.; Luo, L.; Li, H. The Mercury’s Bow-shock Models Near Perihelion and Aphelion. Astron. J. 2022, 164, 260. [Google Scholar] [CrossRef]
- Slavin, J.A.; Holzer, R.E. The effect of erosion on the solar wind stand-off distance at Mercury. J. Geophys. Res. Space Phys. 1979, 84, 2076–2082. [Google Scholar] [CrossRef]
- Boardsen, S.A.; Sundberg, T.; Slavin, J.A.; Anderson, B.J.; Korth, H.; Solomon, S.C.; Blomberg, L.G. Observations of Kelvin-Helmholtz waves along the dusk-side boundary of Mercury’s magnetosphere during MESSENGER’s third flyby. Geophys. Res. Lett. 2010, 37, L12101. [Google Scholar] [CrossRef]
- Slavin, J.A.; Acuña, M.H.; Anderson, B.J.; Baker, D.N.; Benna, M.; Gloeckler, G.; Gold, R.E.; Ho, G.C.; Killen, R.M.; Korth, H.; et al. Mercury’s Magnetosphere After MESSENGER’s First Flyby. Science 2008, 321, 85–89. [Google Scholar] [CrossRef]
- Belenkaya, E.; Pensionerov, I. What Density of Magnetosheath Sodium Ions Can Provide the Observed Decrease in the Magnetic Field of the “Double Magnetopause” during the First MESSENGER Flyby? Symmetry 2021, 13, 1168. [Google Scholar] [CrossRef]
- DiBraccio, G.A.; Slavin, J.A.; Boardsen, S.A.; Anderson, B.J.; Korth, H.; Zurbuchen, T.H.; Raines, J.M.; Baker, D.N.; McNutt, R.L., Jr.; Solomon, S.C. MESSENGER observations of magnetopause structure and dynamics at Mercury. J. Geophys. Res. Space Phys. 2013, 118, 997–1008. [Google Scholar] [CrossRef]
- Zhong, J.; Lee, L.C.; Slavin, J.A.; Zhang, H.; Wei, Y. MESSENGER Observations of Reconnection in Mercury’s Magnetotail Under Strong IMF Forcing. J. Geophys. Res. Space Phys. 2023, 128, e2022JA031134. [Google Scholar] [CrossRef]
- Veselovsky, I.S.; Dmitriev, A.V.; Suvorova, A.V.; Tarsina, M.V. Solar wind variation with the cycle. J. Astrophys. Astron. 2000, 21, 423–429. [Google Scholar] [CrossRef]
- Chapman, J.F.; Cairns, I.H. Three-dimensional modeling of Earth’s bow shock: Shock shape as a function of Alfvén Mach number. J. Geophys. Res. Space Phys. 2003, 108, 1174. [Google Scholar] [CrossRef]
- Slavin, J.A.; Anderson, B.J.; Zurbuchen, T.H.; Baker, D.N.; Krimigis, S.M.; Acuña, M.H.; Benna, M.; Boardsen, S.A.; Gloeckler, G.; Gold, R.E.; et al. MESSENGER observations of Mercury’s magnetosphere during northward IMF. Geophys. Res. Lett. 2009, 36, L02101. [Google Scholar] [CrossRef]
- Belenkaya, E.; Bobrovnikov, S.; Alexeev, I.; Kalegaev, V.; Cowley, S. A model of Jupiter’s magnetospheric magnetic field with variable magnetopause flaring. Planet. Space Sci. 2005, 53, 863–872. [Google Scholar] [CrossRef]
- Johnson, C.L.; Purucker, M.E.; Korth, H.; Anderson, B.J.; Winslow, R.M.; Al Asad, M.M.H.; Slavin, J.A.; Alexeev, I.I.; Phillips, R.J.; Zuber, M.T.; et al. MESSENGER observations of Mercury’s magnetic field structure. J. Geophys. Res. Planets 2012, 117, E00L14. [Google Scholar] [CrossRef]
- Heyner, D.; Nabert, C.; Liebert, E.; Glassmeier, K.H. Concerning reconnection-induction balance at the magnetopause of Mercury. J. Geophys. Res. Space Phys. 2016, 121, 2935–2961. [Google Scholar] [CrossRef]
- Winslow, R.M.; Philpott, L.; Paty, C.S.; Lugaz, N.; Schwadron, N.A.; Johnson, C.L.; Korth, H. Statistical study of ICME effects on Mercury’s magnetospheric boundaries and northern cusp region from MESSENGER. J. Geophys. Res. Space Phys. 2017, 122, 4960–4975. [Google Scholar] [CrossRef]
- Kobel, E.; Flückiger, E.O. A model of the steady state magnetic field in the magnetosheath. J. Geophys. Res. Space Phys. 1994, 99, 23617–23622. [Google Scholar] [CrossRef]
- Heyner, D.; Auster, H.U.; Fornaçon, K.H.; Carr, C.; Richter, I.; Mieth, J.Z.D.; Kolhey, P.; Exner, W.; Motschmann, U.; Baumjohann, W.; et al. The BepiColombo Planetary Magnetometer MPO-MAG: What Can We Learn from the Hermean Magnetic Field? Space Sci. Rev. 2021, 217, 52. [Google Scholar] [CrossRef]
- Anderson, B.J.; Johnson, C.L.; Korth, H. A magnetic disturbance index for Mercury’s magnetic field derived from MESSENGER Magnetometer data. Geochem. Geophys. Geosystems 2013, 14, 3875–3886. [Google Scholar] [CrossRef]
- Alexeev, I.; Parunakian, D.; Dyadechkin, S.; Belenkaya, E.; Khodachenko, M.; Kallio, E.; Alho, M. Calculation of the Initial Magnetic Field for Mercury’s Magnetosphere Hybrid Model. Cosm. Res. 2018, 56, 108–114. [Google Scholar] [CrossRef]
- James, M.K.; Imber, S.M.; Bunce, E.J.; Yeoman, T.K.; Lockwood, M.; Owens, M.J.; Slavin, J.A. Interplanetary magnetic field properties and variability near Mercury’s orbit. J. Geophys. Res. Space Phys. 2017, 122, 7907–7924. [Google Scholar] [CrossRef]
- Belenkaya, E.S. Reconnection modes for near-radial interplanetary magnetic field. J. Geophys. Res. Space Phys. 1998, 103, 26487–26494. [Google Scholar] [CrossRef]
- Wardinski, I.; Langlais, B.; Thébault, E. Correlated Time-Varying Magnetic Fields and the Core Size of Mercury. J. Geophys. Res. Planets 2019, 124, 2178–2197. [Google Scholar] [CrossRef]

| Paper | Power Index | Power Index | ||||
|---|---|---|---|---|---|---|
| Siscoe 1975 [8] | 1.9 | 1.7–2.0 | - | - | - | |
| Russell 1977 [9] | 1.3 | - | - | 1.9 | - | - |
| Winslow 2013 [4] | 1.45 | 1.35–1.55 | 0.30 | 1.96 | 1.89–2.29 | - |
| Zhong 2015 [14] | 1.51 | 1.38–1.65 | 0.42 | - | - | - |
| Johnson 2016 [11] | - | - | 0.29 | - | - | - |
| Zhong 2020 [15] | - | 1.43–1.60 | 0.22 | - | - | - |
| Philpott 2020 [12] | 1.46 | 1.40–1.54 | - | - | - | - |
| He 2022 [16] | - | - | - | - | 1.92–2.10 | - |
| Current paper | 1.48 | 1.38–1.55 | 0.29 | 1.84 | 1.81–1.86 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nevsky, D.; Lavrukhin, A.; Alexeev, I. Mercury’s Bow Shock and Magnetopause Variations According to MESSENGER Data. Universe 2024, 10, 40. https://doi.org/10.3390/universe10010040
Nevsky D, Lavrukhin A, Alexeev I. Mercury’s Bow Shock and Magnetopause Variations According to MESSENGER Data. Universe. 2024; 10(1):40. https://doi.org/10.3390/universe10010040
Chicago/Turabian StyleNevsky, Dmitry, Alexander Lavrukhin, and Igor Alexeev. 2024. "Mercury’s Bow Shock and Magnetopause Variations According to MESSENGER Data" Universe 10, no. 1: 40. https://doi.org/10.3390/universe10010040
APA StyleNevsky, D., Lavrukhin, A., & Alexeev, I. (2024). Mercury’s Bow Shock and Magnetopause Variations According to MESSENGER Data. Universe, 10(1), 40. https://doi.org/10.3390/universe10010040








