Gravitational Lensing Effects from Models of Loop Quantum Gravity with Rigorous Quantum Parameters

Abstract

Many previous works have studied gravitational lensing effects from Loop Quantum Gravity. So far, gravitational lensing effects from Loop Quantum Gravity have only been studied by choosing large quantum parameters much larger than the Planck scale. However, by construction, the quantum parameters of the effective models of Loop Quantum Gravity are usually related to the Planck length and, thus, are extremely small. In this work, by strictly imposing the quantum parameters as initially constructed, we study the true quantum corrections of gravitational lensing effects by five effective black hole models of Loop Quantum Gravity. Our study reveals several interesting results, including the different scales of quantum corrections displayed by each model and the connection between the quantum correction of deflection angles and the quantum correction of the metric. Observables related to the gravitational lensing effect are also obtained for all models in the case of SgrA* and M87*.

1. Introduction

Loop Quantum Gravity (LQG) is a background-independent candidate theory of quantum gravity [1,2,3]. While the full theory of LQG is very complicated, the extraction of physically observable phenomena from full LQG is extremely difficult. There have been many works obtaining the physical effects of LQG from its symmetry-reduced models with great success. One such example is Loop Quantum Cosmology (LQC) [4], from which many exciting results have been obtained. The most important result is the resolution of big bang singularity by big bounce [5]. A similar approach to simplify the theory has also been applied to many models of spherically symmetric black holes (BHs) [6,7,8,9,10,11,12,13,14,15], also leading to the resolution of BH singularity. The latest works on LQG black holes have also produced BH models [16] maintaining general covariance [17].

One of the most critical questions is “How can such a quantum theory of gravity be tested?” From an observational point of view, the answer to such a question may reside in examining as many quantum corrections to classical phenomena as possible. A fundamental theory should be able to consistently explain all experimental observations using precisely the same rigorously imposed fundamental quantum parameters. This motivated us to test the theory in various classically observed scenarios, strictly keeping quantum parameters as introduced in the original model.

So far, many works have focused on the phenomenology of LQG, studying how the theory can impact classically observable phenomena. Examples include the quasinormal modes of the non-rotating LQG black holes [18,19], the shadow cast by a rotating polymerized black hole constructed using the revised Newman–Janis method [20], and the Hawking radiation spectra and evaporation of spherically symmetric LQG black holes [21,22,23,24].

One potential testing ground for the theory is gravitational lensing near the BH, where, theoretically, photons (or other particles) could travel multiple times around the BH before escaping, making it possible to amplify the quantum effects to a certain degree. Generally speaking, gravitational lensing effects describe a phenomenon where a photon emitted from a distant source is deflected by a massive celestial object between the source and the observer, such as galaxies or supermassive black holes generating a strong gravitation field, leading to the bending of light trajectories and deflections of the image of the source as being received by the observer. There are two main approaches to studying the gravitational lensing effect, namely the weak field limits, where the light bending occurs far away from the center of the lens, inducing light deflections around or less than a few arcseconds, and the strong field limits [25,26,27,28,29,30,31], which studies the strong gravitational lensing effect happening near the photon ring of the lens of the BH. In this work, we would like to explore the gravitational lensing effects near the photon sphere of the BH using the strong-field-limit method, since the quantum corrections are usually suppressed as the distance from the black hole becomes larger.

There are three main goals for this work. First and foremost, although gravitational lensing effects from LQG have been studied by many works [32,33,34,35], these works treat the quantum parameter as a running parameter valued in the magnitude of 1. Indeed, many interesting results can be extracted from such treatments, and one can argue that, due to the quantization ambiguity of LQG, the possibility of modifying the regulator and quantum parameters in the theory exists at a fundamental level. However, it should be noted that the quantum parameters defined in the effective models of LQG are usually related to the Planck length, which is an astonishingly small number. It is doubtful that the quantum parameter can be a quantity valued at the magnitude of 1. Therefore, the most essential purpose of this work is to treat these quantum parameters seriously and to look at the quantum corrections to the gravitational lensing effect coming from these rigorously chosen quantum operators and whether there is any remote hope of detecting such quantum effects via currently available experiments.

Second, many effective BH models of LQG, such as the Ashtekar–Olmedo–Singh (AOS) and Gambini–Olmedo-Pullin (GOP) models, have yet to be tested using the gravitational lensing effects. We would also like to explore these models in our investigation of the true quantum impact of LQG on the gravitational lensing effects using rigorously imposed quantum parameters.

Third, so far, most of the works discussing the gravitational lensing effects of LQG study LQG models individually. In this paper, however, we will investigate the gravitational lensing effect of a total of five LQG effective BH models, including the AOS model, the GOP model, two newly proposed models satisfying general covariance (MC1) and (MC2), and the quantum Oppenheimer–Schneider (qOS). We hope that by making comparisons of different models of LQG, we can achieve a better understanding of the various scales of quantum corrections in terms of the gravitational lensing effects from different effective models of LQG, their source of origin, their impacting factors in the theory, and what could make direct observations possible. We also hope that the same methodology can be applied to study other observational effects of LQG in the near future, enabling a more extensive understanding of the observational effects of the theory in regions where actual experiments are plausible.

The structure of this work is as follows: In Section 2, we briefly introduce the definitions of all five models studied, including the exact definitions and values of the quantum parameters present in each model. In the meantime, we will also provide a quick overview of how to compute the gravitational lensing effect using the strong field limit. Since this topic has been covered thoroughly by many previous works such as [27,33], we will include only the most essential steps in obtaining the deflection angle and lens observables. In Section 3, we will first compute the quantum corrections of the deflection angle in all five models, then calculate the lens observables, providing a comparison and analysis. In the final section of this paper, we will summarize the main results obtained in this work and provide additional insights into how to interpret these results.

2. Technical Background

2.1. BH Models from Effective LQG

A simple, spherically symmetric LQG BH model starts by imposing the homogeneous condition in the interior region of the Schwarzschild BH. Given the ADM decomposition $\Sigma \times R$ of the 4-dimensional manifold $\mathcal{M}$, where $\Sigma$ is the spatial 3-manifold, define $q^{ab}$ to be the metric on $\Sigma$. After performing symmetry reduction, the canonical variables of classical general relativity, namely the Ashtekar connection $A_a^i\left(x\right)$ and its conjugate densitized triad $E_i^a\left(x\right)=\sqrt{q}{e}_i^a$ with $e_i^a{e}^{bi}=q^{ab}$, are reduced to [36]:

$$\begin{array}{cc}\hfill & E_i^a{\tau }^i{\partial }_a=p_c{\tau }_{3}sin\theta {\displaystyle \frac{\partial }{\partial x}}+{\displaystyle \frac{p_b}{L_0}}{\tau }_{2}sin\theta {\displaystyle \frac{\partial }{\partial \theta }}-{\displaystyle \frac{p_b}{L_0}}{\tau }_1{\displaystyle \frac{\partial }{\partial \varphi }},\hfill \\ \hfill & A_a^i{\tau }_i\mathrm{d}{x}^a={\displaystyle \frac{c}{L_0}}{\tau }_3\mathrm{d}x+b{\tau }_2\mathrm{d}\theta -b{\tau }_{1}sin\theta \mathrm{d}\varphi +{\tau }_{3}cos\theta \mathrm{d}\varphi ,\hfill \end{array}$$

(1)

where ${\tau }_i$ is a basis of $\mathfrak{su}\left(\mathfrak{2}\right)$ Lie algebra. The non-vanishing Poisson brackets between canonical variables reads:

$$\left\{p_b,b\right\}=-G\gamma ,\left\{c,p_c\right\}=2G\gamma .$$

(2)

Under these variables, classical general relativity reduces to the Hamiltonian constrained system of the following smeared Hamiltonian constraint:

$$H:={\int }_{\mathcal{C}}NC=-{\displaystyle \frac{1}{2G\gamma }}\left(\left(b+{\displaystyle \frac{{\gamma }^2}{b}}\right)p_b+2c{p}_c\right),$$

(3)

where N is the lapse function of the ADM decomposition.

Following similar techniques in LQC, the Hamiltonian constraint can be regularized using holonomy–flux algebra to produce the effective Hamiltonian constraint, and generally [36] the holonomy corrections of the effective Hamiltonian constraint can be simplified by performing the following regularization:

$$c\to {\displaystyle \frac{sin\left({\delta }_{c}c\right)}{{\delta }_c}},b\to {\displaystyle \frac{sin\left({\delta }_{b}b\right)}{{\delta }_b}},$$

(4)

where the quantum corrections are controlled by the quantum parameters $\delta c$ and $\delta b$ due to the fundamental discreteness of LQG. Finally, the effective Hamiltonian of Loop Quantum Schwarzschild BH can be obtained as:

$$H_{\mathrm{eff}}=-{\displaystyle \frac{1}{2G\gamma }}\left[\left({\displaystyle \frac{sin\left({\delta }_{b}b\right)}{{\delta }_b}}+{\displaystyle \frac{{\gamma }^2{\delta }_b}{sin\left({\delta }_{b}b\right)}}\right)p_b+2{\displaystyle \frac{sin\left({\delta }_{c}c\right)}{{\delta }_c}}{p}_c\right].$$

(5)

the effective metric of the theory can in principle be obtained by solving the Hamiltonian evolution equations.

In this paper, we focus on the static spherically symmetric spacetimes obtained from the effective models of LQG, which in general can be described by the line element:

$$\mathrm{d}{s}^2=-A\left(r\right)\mathrm{d}{t}^2+B\left(r\right)\mathrm{d}{r}^2+C\left(r\right)\mathrm{d}{\mathsf{\Omega }}^2.$$

(6)

Specifically, we consider the region outside of the BH horizon of the following five candidate LQG black hole (BH) models:

• Ashtekar–Olmedo–Singh (AOS) model obtained by considering a quantum BH exterior extension of the BH interior quantized using polymer quantization techniques similar to LQC [37,38]:

  $$\begin{array}{cc}\hfill & A_{AOS}\left(r\right)={\left({\displaystyle \frac{r}{r_S}}\right)}^{2ϵ}{\displaystyle \frac{\left(1-{\left(\frac{r_S}{r}\right)}^{1+ϵ}\right){\left(2+ϵ+ϵ{\left(\frac{r_S}{r}\right)}^{1+ϵ}\right)}^2\left({(2+ϵ)}^2-{ϵ}^2{\left(\frac{r_S}{r}\right)}^{1+ϵ}\right)}{16\left(1+\frac{{\delta }_c^2{L}_0^2{\gamma }^2{r}_S^2}{16r^4}\right){(1+ϵ)}^4}},\hfill \\ \hfill & B_{AOS}\left(r\right)=\left(1+{\displaystyle \frac{{\delta }_c^2{L}_0^2{\gamma }^2{r}_S^2}{16r^4}}\right){\displaystyle \frac{{\left(ϵ+{\left(\frac{r}{r_S}\right)}^{1+ϵ}(2+ϵ)\right)}^2}{\left({\left(\frac{r}{r_S}\right)}^{1+ϵ}-1\right)\left({\left(\frac{r}{r_S}\right)}^{1+ϵ}{(2+ϵ)}^2-{ϵ}^2\right)}},\hfill \\ \hfill & C_{AOS}\left(r\right)=r^2\left(1+{\displaystyle \frac{{\gamma }^2{L}_0^2{\delta }_c^2{r}_S^2}{16r^4}}\right),\hfill \end{array}$$

  (7)

  for $r\in [r_S,\infty )$, $r_S=2Gm$ is the Schwarzschild radius, and

  $$L_o{\delta }_c={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\gamma {\Delta }^2}{4{\pi }^{2}m}}\right)}^{1/3},ϵ+1=\sqrt{1+{\gamma }^2{\left({\displaystyle \frac{\sqrt{\Delta }}{\sqrt{2\pi }{\gamma }^{2}m}}\right)}^{2/3}},$$

  (8)

  are quantum parameters depending on both the Imirzi parameter $\gamma$ and the area gap $\Delta =21.17l_p^2$ (when setting $\gamma =1$), namely the minimum nonzero eigenvalue of the area operator in LQG. $l_p$ is Planck length.
• The Gambini–Olmedo–Pullin (GOP) model describes the improved dynamics obtained under the more general spherically symmetric reduction in the classical phase space [8,39]:

  $$\begin{array}{cc}\hfill & A_{GOP}^{\alpha }\left(r\right)=\left(1-{\displaystyle \frac{r_S}{r+r_0}}+\alpha {\displaystyle \frac{\Delta }{4\pi }}{\displaystyle \frac{r_S^4}{{\left(r+r_0\right)}^6{\left(1+\frac{r_S}{r+r_0}\right)}^2}}\right),\hfill \\ \hfill & B_{GOP}^{\alpha }\left(r\right)={\displaystyle \frac{{\left(1+\frac{\delta x}{2\left(r+r_0\right)}\right)}^2}{\left(1-\frac{r_S}{r+r_0}+\alpha \frac{\Delta }{4\pi }\frac{r_S^4}{{\left(r+r_0\right)}^6{\left(1+\frac{r_S}{r+r_0}\right)}^2}\right)}},\hfill \\ \hfill & C_{GOP}\left(r\right)={\left(r+r_0\right)}^2,\hfill \end{array}$$

  (9)

  where

  $$r_0={\left({\displaystyle \frac{2Gm\Delta }{4\pi }}\right)}^{1/3},$$

  (10)
  $\alpha$ is a parameter with choices 0 and 1. The difference between these two choices is verified to be negligible concerning gravitational lensing effects.
• Two newly proposed LQG BH models satisfying the minimal conditions for maintaining general covariance (MC1 and MC2) are provided [16]:

  $$\begin{array}{cc}\hfill & A_{MC1}\left(r\right)=1-{\displaystyle \frac{2M}{r}}+{\zeta }_{MC}^2{\displaystyle \frac{M^2}{r^2}}{\left(1-{\displaystyle \frac{2M}{r}}\right)}^2,\hfill \\ \hfill & A_{MC2}\left(r\right)=1-{\displaystyle \frac{2M}{r}},\hfill \\ \hfill & B_{MC1}\left(r\right)=B_{MC2}\left(r\right)=A_{MC1}{\left(r\right)}^{-1},\hfill \\ \hfill & C_{MC1}=C_{MC2}=r^2,\hfill \end{array}$$

  (11)

  where ${\zeta }_{MC}={\displaystyle \frac{\sqrt{4\sqrt{3}\pi {\gamma }^3{l}_p^2}}{M}}$ is the quantum parameter for both models. The gravitational lensing effect of this model has been studied recently in [40] by treating ${\zeta }_{MC}$ as an arbitrary parameter in the order ${\zeta }_{MC}\sim 1$. In our paper, we stick strictly to the original theory, where ${\zeta }_{MC}={\displaystyle \frac{\sqrt{4\sqrt{3}\pi {\gamma }^3{l}_p^2}}{M}}$.
• The quantum Oppenheimer–Schneider (qOS) model obtained by matching the exterior effective spacetime with the interior effective LQC-like model [11]:

  $$\begin{array}{cc}\hfill & A_{qOS}\left(r\right)=1-{\displaystyle \frac{2M}{r}}+{\displaystyle \frac{{\zeta }_{qOS}{M}^2}{r^4}},\hfill \\ \hfill & B_{qOS}\left(r\right)=A_{qOS}{\left(r\right)}^{-1},\hfill \\ \hfill & C_{qOS}\left(r\right)=r^2,\hfill \end{array}$$

  (12)

  where ${\zeta }_{qOS}=16\sqrt{3}{\gamma }^3{l}_p^2$. The gravitational lensing effect of this model has also been studied previously in [41] considering ${\zeta }_{qOS}\sim 1$. In this work, we also keep the quantum parameter as ${\zeta }_{qOS}=16\sqrt{3}{\gamma }^3{l}_p^2$.

2.2. Gravitational Lensing from Strong Field Limit and Lens Observables

Since the quantum parameters of the above-mentioned BH models are valued at the order of minuscule constants, such as the Planck length $l_p$ or Planck area $l_p^2$, the quantum correction to the gravitational lensing effect is inevitably small. Consequently, the photon trajectories who have the closest distance to the lens during the trip near the photon ring have the largest impact from quantum corrections. Let the closest distance to the lens of a photon trajectory be $r_0$, and the minimum such distance is the BH photon sphere $r_m$, satisfying [42,43]:

$${\displaystyle \frac{C^{\prime }\left(r_m\right)}{C\left(r_m\right)}}={\displaystyle \frac{A^{\prime }\left(r_m\right)}{A\left(r_m\right)}}.$$

(13)

For arbitrary theories with the line element (6), given impact parameter b, the deflection angle $\alpha$ between the source and the image can be computed as [44]:

$$\begin{array}{cc}\hfill \alpha \left(r_0\right)& =I\left(r_0\right)-\pi \hfill \\ \hfill I\left(r_0\right)& =2{\int }_{r_0}^{\infty }{\displaystyle \frac{1}{C}}\sqrt{{\displaystyle \frac{AB}{1/u^2-A/C}}}dr\hfill \end{array}$$

(14)

For $r_0\to r_m$, the gravitational lensing effect can be approximated by the strong field limit. A general approach to obtain the strong field limit for BH whose line elements take the form (6) is described in [27]. As an alternative to the original proposal, we consider the variable $z=1-{\displaystyle \frac{r_0}{r}}$ introduced in [42,43], allowing for the direct conversion between z and r. The integral can then be rewritten as:

$$\begin{array}{cc}\hfill I\left(r_0\right)& ={\int }_0^{1}R\left(z,r_0\right)f\left(z,r_0\right)dz,\hfill \end{array}$$

(15)

where we have

$$\begin{array}{cc}\hfill R\left(z,r_0\right)& ={\displaystyle \frac{2r^2\sqrt{A\left(r\right)B\left(r\right)C_0}}{r_{0}C\left(r\right)}}\hfill \\ \hfill f\left(z,r_0\right)& ={\displaystyle \frac{1}{\sqrt{A_0-\frac{A\left(r\right)C_0}{C\left(r\right)}}}},\hfill \end{array}$$

(16)

where $A_0:=A\left(r_0\right)$ and $C_0:=C\left(r_0\right)$. $R(z,r_0)$ is regular for $r\ge r_0\ge r_m$, while $f(z,r_0)$ is divergent in z as $z\to 0$, i.e., $r\to r_0$. We expand the divergent term $f(z,r_0)$ up to the second order of z as follows:

$$f\left(z,r_0\right)\sim f_0\left(z,r_0\right)={\displaystyle \frac{1}{\sqrt{c_1\left(r_0\right)z+c_2\left(r_0\right)z^2}}},$$

(17)

where

$$\begin{array}{cc}\hfill & c_1\left(r_0\right)=-r_0{A}_0^{\prime }+{\displaystyle \frac{r_0{A}_0{C}_0^{\prime }}{C_0}}\hfill \\ \hfill & c_2\left(r_0\right)=r_0{\displaystyle \frac{-2r_0{A}_0{C}_0^{\prime 2}-C_0^2\left(2A_0^{\prime }+r_0{A}_0^{″}\right)+C_0\left[2r_0{A}_0^{\prime }{C}_0^{\prime }+A_0\left(2C_0^{\prime }+r_{0}2C_0^{″}\right)\right]}{2C_0^2}}\hfill \end{array}$$

(18)

which captures the dominant contribution of the divergence as $z\to 0$.

Using this expansion, the integral $I\left(r_0\right)$ can be split into a regular part $I_R\left(r_0\right)$ and a divergent part $I_D\left(r_0\right)$ as follows:

$$\begin{array}{cc}\hfill I\left(r_0\right)& =I_D\left(r_0\right)+I_R\left(r_0\right)\hfill \\ \hfill I_D\left(r_0\right)& ={\int }_0^{1}R\left(0,r_m\right)f_0\left(z,r_0\right)dz\hfill \\ \hfill I_R\left(r_0\right)& ={\int }_0^1\left[R\left(z,r_0\right)f\left(z,r_0\right)-R\left(0,r_m\right)f_0\left(z,r_0\right)\right]dz.\hfill \end{array}$$

(19)

As a result, the deflection angle can be computed in terms of the impact parameter b as follows:

$$\alpha \left(b\right)=-aln\left({\displaystyle \frac{b}{b_m}}-1\right)+u+\mathcal{O}\left[\left(b-b_m\right)ln\left(b-b_m\right)\right],$$

(20)

where:

$$\begin{array}{cc}\hfill a& \equiv {\displaystyle \frac{R\left(0,r_m\right)}{2\sqrt{c_2\left(r_m\right)}}},\hfill \\ \hfill u& \equiv aln\delta +I_R\left(r_0\right)-\pi ,\hfill \\ \hfill \delta & \equiv r_m^2\left({\displaystyle \frac{C^{″}\left(r_m\right)}{C\left(r_m\right)}}-{\displaystyle \frac{A^{″}\left(r_m\right)}{A\left(r_m\right)}}\right).\hfill \end{array}$$

(21)

Despite the dependence of the impact factor b in $\alpha \left(b\right)$, using the factors a and u, several b-independent lens observables can also be extracted [27,33,40]:

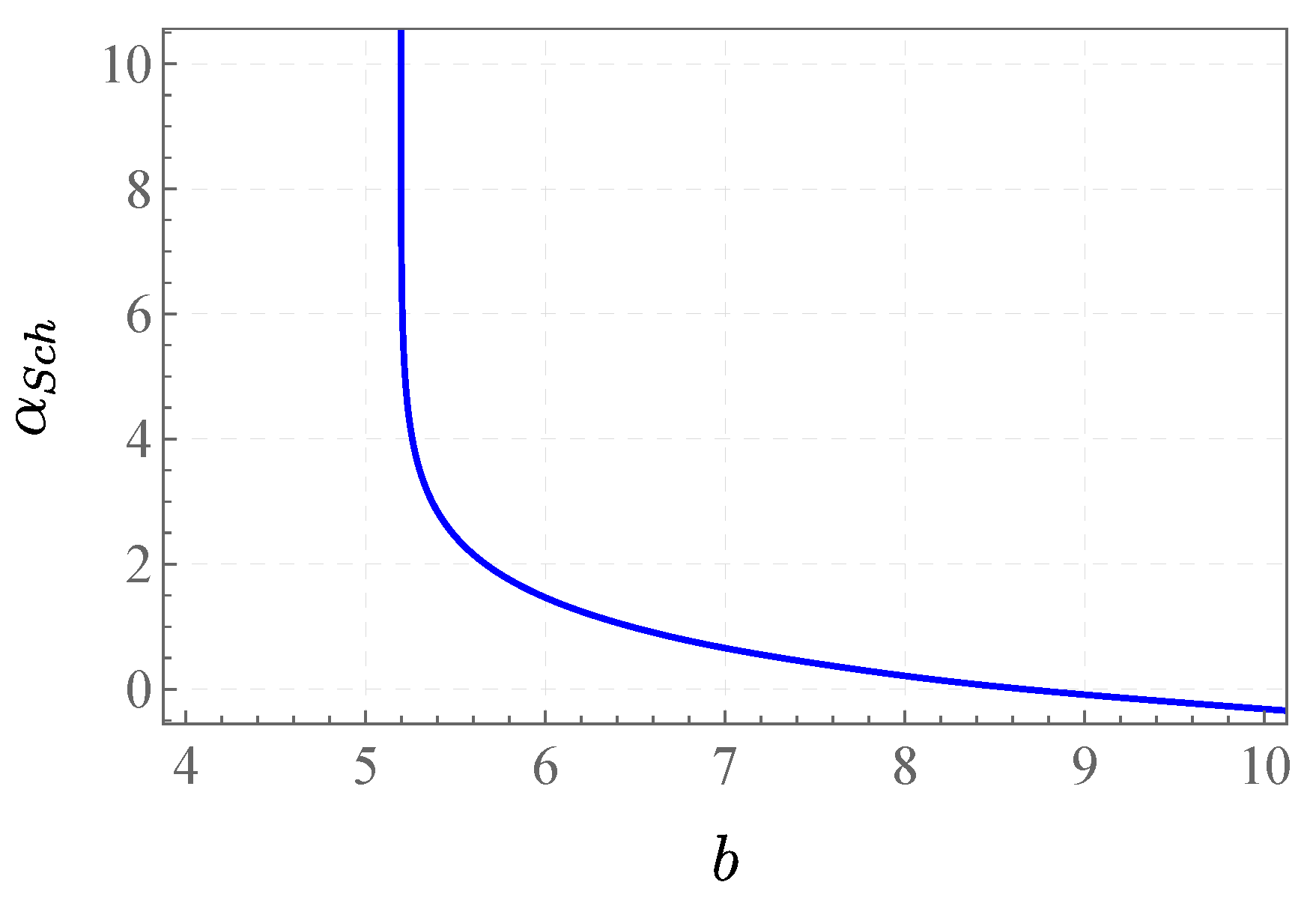
• The angle ${\theta }_{\infty }$ of the innermost image. The angle $\theta$ is defined as the observed angle between the lens BH and the image of the source as being observed after deflection via the lens. Since the photon trajectory can go around the lens multiple times before finally reaching the observer, there can be a total of n images of the source. n is not bounded, since the deflection angle is unbounded for $b\to b_m$. Therefore, a limit ${\theta }_{\infty }\approx {\displaystyle \frac{b_m}{D_{OL}}}$ can be obtained by taking $n\to \infty$, where $D_{OL}$ is the distance between the lens BH and the observer.
• The angular separation s between the outermost image and the innermost image (the lower bound of the series of images as $n\to$, since these images are unlikely to be distinguishable):

  $$s:={\theta }_1-{\theta }_{\infty }\sim {\theta }_{\infty }{\mathrm{e}}^{{\displaystyle \frac{u-2\pi }{a}}}.$$

  (22)
• The quotient $\mu$ of the flux of the outermost relativistic image to that of all other relativistic images:

  $$\mu \sim {\displaystyle \frac{\left({\mathrm{e}}^{\frac{4\pi }{a}}-1\right)\left({\mathrm{e}}^{\frac{2\pi }{a}}+{\mathrm{e}}^{\frac{u}{a}}\right)}{{\mathrm{e}}^{\frac{4\pi }{a}}+{\mathrm{e}}^{\frac{2\pi }{a}}+{\mathrm{e}}^{\frac{u}{a}}}}$$

  (23)
• The time delay $\Delta T_{n,m}$ between the n-th and m-th relativistic images. Particularly, for spherically symmetrical BH [44]:

  $${\displaystyle \frac{\Delta T_{2,1}}{{\theta }_{\infty }}}={\displaystyle \frac{D_{OL}}{c}},$$

  (24)

  where c is the speed of light.

These b-independent lens observables are only dependent on the quantum parameter of the theory, thus serving as an ideal testing ground for studying the quantum correction of the gravitational lensing effect from LQG.

2.3. Exact Values of the Quantum Parameters

In this paper, we use the values of the quantum parameter in all BH models of LQG as they were originally constructed to capture the precise impact of the quantum effects. For all of the results we obtained, we set $c=1$, $G=1$, and we also rescale the radial direction such that $M=1$, and the Schwarzschild radius of the center BH is always $R_s=2M=2$. This rescaling also impacts the quantum parameters due to their dependence on $l_p$ or $\Delta$, based on the actual mass of the center black hole, which varies for different cases. In this work, we choose SgrA* and M87* to study the quantum effects. For the case of SgrA* [45], by choosing its mass to be $m_{{\mathrm{SgrA}}^{*}}=4.3\times {10}^6 M_{\odot }$, its Schwarzschild radius in international units as $r_{s,{\mathrm{SgrA}}^{*}}=1.27034\times {10}^{10}\mathrm{m}$ and its distance to the observer to be $D_{OL}=8.35\mathrm{kpc}$, the value of the Planck length after the rescaling equals $l_{p,{\mathrm{SgrA}}^{*}}={\displaystyle \frac{2}{r_{s,{\mathrm{SgrA}}^{*}}}}\times 1.61623\times {10}^{-35}=2.54456\times {10}^{-45}$ and ${\Delta }_{{\mathrm{SgrA}}^{*}}=21.17l_{p,{\mathrm{SgrA}}^{*}}^2=1.37072\times {10}^{-88}$. For the case of M87* [46], by choosing its mass to be $m_{\mathrm{M}{87}^{*}}=6.5\times {10}^9 M_{\odot }$, its Schwarzschild radius in international units as $r_{s,\mathrm{M}{87}^{*}}=1.92028\times {10}^{13}\mathrm{m}$, and its distance to the observer to be $D_{OL}=16.8\mathrm{Mpc}$, the Planck length after the rescaling equals $l_{p,\mathrm{M}{87}^{*}}={\displaystyle \frac{2}{r_{s,\mathrm{M}{87}^{*}}}}\times 1.61623\times {10}^{-35}=1.68333\times {10}^{-48}$ and ${\Delta }_{\mathrm{M}{87}^{*}}=21.17l_{p,\mathrm{M}{87}^{*}}^2=5.99871\times {10}^{-95}$.

Here, we provide a collection of the exact values of quantum parameters we use for all five models mentioned above:

• AOS model: ${\Delta }_{{\mathrm{SgrA}}^{*}}=21.17l_{p,{\mathrm{SgrA}}^{*}}^2=1.37072\times {10}^{-88}$, ${\Delta }_{\mathrm{M}{87}^{*}}=21.17l_{p,\mathrm{M}{87}^{*}}^2=5.99871\times {10}^{-95}$.
• GOP model: ${\Delta }_{{\mathrm{SgrA}}^{*}}=21.17l_{p,{\mathrm{SgrA}}^{*}}^2=1.37072\times {10}^{-88}$, ${\Delta }_{\mathrm{M}{87}^{*}}=21.17l_{p,\mathrm{M}{87}^{*}}^2=5.99871\times {10}^{-95}$.
• MC1 and MC2 models: ${\zeta }_{MC,{\mathrm{SgrA}}^{*}}=\sqrt{4\sqrt{3}\pi {\gamma }^3{l}_{p,{\mathrm{SgrA}}^{*}}^2}=1.18713\times {10}^{-44}$, ${\zeta }_{MC,\mathrm{M}{87}^{*}}=\sqrt{4\sqrt{3}\pi {\gamma }^3{l}_{p,\mathrm{M}{87}^{*}}^2}=7.85333\times {10}^{-48}$.
• qOS model: ${\zeta }_{qOS,{\mathrm{SgrA}}^{*}}=1.79435\times {10}^{-88}$, ${\zeta }_{qOS,\mathrm{M}{87}^{*}}=7.85268\times {10}^{-95}$.

3. Main Results

3.1. Deflecting Angle $\alpha$

In this subsection, we show the quantum corrections of BH models of LQG on the gravitational lensing effect by computing the deflection angle versus the impact parameter b. Using Equation (14), the deflection angle can be computed.

Figure 1 shows the results for the deflection angle with respect to the impact factor b. Since the quantum parameters we use for all models are extremely small, all of the results for the deflection angles are very close to the Schwarzschild case:

$${\alpha }_{Sch}\approx -\mathrm{Log}[0.19245b-1]-0.40023,$$

(25)

for $M=1$. The difference can not be shown in Figure 1 as the curve for each model overlaps. To characterize the quantum effects of different models, we consider both the exact difference $D_{\alpha }$ and relative difference $R_{\alpha }$ between the deflection angle ${\alpha }_{LQG}$ of each LQG BH model and ${\alpha }_{Sch}$ of the Schwarzschild BH:

$$\begin{array}{cc}\hfill D_{\alpha }\left(b\right)& :={\alpha }_{LQG}\left(b\right)-{\alpha }_{Sch}\left(b\right),\hfill \\ \hfill R_{\alpha }\left(b\right)& :={\displaystyle \frac{{\alpha }_{LQG}\left(b\right)-{\alpha }_{Sch}\left(b\right)}{{\alpha }_{Sch}\left(b\right)}}.\hfill \end{array}$$

(26)

Moreover, for the deflecting angle, we consider the case where the impact factor is very near to the innermost possible impact factor $b_m=5.19615$ for Schwarzschild BH. A ${\mathrm{Log}}_{10}$-${\mathrm{Log}}_{10}$ graph (Figure 2) can be produced in this region by defining the relative difference $R_b$ of the impact factor as b to $b_m$:

$$R_b:={\displaystyle \frac{b-b_m}{b_m}}.$$

(27)

Figure 2 shows the exact difference $D_{\alpha }$ and relative difference $R_{\alpha }$ of the deflection angle $\alpha$ between LQG BH models and Schwarzschild BH versus the relative distance $R_b$ to Schwarzschild $b_m$. All results are obtained using input data from ${\mathrm{SgrA}}^{*}$.

Several facts can be read from this figure, as follows: First, despite the overall minor quantum corrections obtained, the five models can be split into two distinct groups using their values of $R_{\alpha }$ and $D_{\alpha }$; both AOS and GOP models are put into group I due to their relatively large quantum corrections to $\alpha$, while the other three models, namely MC1, MC2 and qOS models, all have minor quantum corrections to $\alpha$. Second, the results for the $qOS$ and $MC1$ models are very similar, making them almost indistinguishable in Figure 2. This shows that both models are closely related, at least in the region outside the photon ring.

Interestingly, the quantum correction of the deflection angles of models AOS, MC1, and qOS increases much faster than the models GOP and MC2, as $R_b\to 0$. A careful look into the theories indicates that the quantum correction of $A\left(r\right)$ of all former three models is significantly larger, as $b\to b_m$. At the same time, $A_{MC2}\left(r\right)=A_{Sch}\left(r\right)$ and $A_{GOP}\left(r\right)$ has only minimal quantum corrections compared to $B_{GOP}\left(r\right)$. Recall from (13) that the location of the photon sphere is impacted by both $A\left(r\right)$ and $C\left(r\right)$, which suggests that the patterns of these results might be related to the specific way in which the metric tensor is quantum-corrected. In particular, large changes in $A\left(r\right)$ might lead to the minimal impacting factor of the model deviating from the Schwarzschild BH. As a result, since $R_b$ is defined by computing the relative difference of b over the Schwarzschild minimal impacting factor $b_{m,Sch}$, $b\to b_m$ does not apply to both the Schwarzschild BH and the LQG model at the same time. This can further boost the difference in deflecting angle $\alpha$.

To further investigate this finding, we plot the relative difference of $A_{AOS}\left(r\right)$, $A_{MC1}\left(r\right)$ and $A_{qOS}\left(r\right)$ versus $R_b$, as well as the relative difference of $B_{GOP}$ and $B_{MC2}$ versus $R_b$ in Figure 3. Since the relative difference of the deflection angle and the relative difference of metric components both reflect on the level of quantum correction, we further define the following magnification rate Z:

$$\begin{array}{c}\hfill Z:=R_{\alpha }/R_g,\end{array}$$

(28)

where:

$$R_g:=\left\{\begin{array}{cc}{\displaystyle \frac{A\left(r\right)-A_{Sch}\left(r\right)}{A_{Sch}\left(r\right)}}\hfill & \mathrm{For}\mathrm{AOS},\mathrm{MC}1,\mathrm{qOS},\hfill \\ {\displaystyle \frac{B\left(r\right)-B_{Sch}\left(r\right)}{B_{Sch}\left(r\right)}}\hfill & \mathrm{For}\mathrm{GOP},\mathrm{MC}2.\hfill \end{array}\right.$$

(29)

Figure 3 shows the relation between the quantum corrections of metric and the quantum corrections of deflection angle $\alpha$. Figure 3a shows the relative difference in the metric for all five models. When comparing the results in Figure 3a with Figure 2d, it is straightforward to see that the relative quantum corrections of the metric are significantly smaller than the quantum corrections of the relative deflection angle $\alpha$ for the models AOS, MC1, and qOS. For the GOS and MC2 models, however, the difference is not apparent.

The same conclusion is further supported by Figure 3b,c. Figure 3b shows the magnification rate Z versus $R_b$ in the AOS model. As $R_b$ goes to 0, i.e., when $b\to b_{m,Sch}$, Z becomes increasingly larger, reaching ${10}^7$. This suggests that in this region, the relative quantum correction on the deflection angle is much higher than the relative quantum correction of the metric, significantly boosting the detectability of the theory in this region. Figure 3c shows the magnification rate Z versus $R_b$ in the GOP model. In contrast to Figure 3b, as $R_b$ goes to 0, Z becomes stable at around $Z=0.5$. This suggests that in the GOP model, the relative quantum correction on the deflection angle is not boosted when compared to the relative quantum correction of the metric.

3.2. Lensing Observables

Despite all the quantum corrections we have obtained, linking any real physical observations to these quantum effects is still challenging. This is because the deflection angle $\alpha$ is not invariant to the change in b, which can vary drastically for actual individual sources. Moreover, since the impact of quantum effects occurs only when $b\to b_{m,Sch}$, it is unlikely that any effects in this region will be straightforwardly observable.

Therefore, to detect quantum gravitational corrections from gravitational lensing effects, we turn to computing the quantum effects of lens observables. These observables are directly detectable by observations and only depend on the quantum parameter of each specific model. Therefore, these observables could offer us a direct link between the quantum effects and direct observations.

Table 1. Observables of ${\mathrm{SgrA}}^{*}$.

Type	Sch	AOS	GOP	MC1	MC2	qOS
${\theta }_{\infty }\left(\mu \mathrm{arcsec}\right)$	$26.42$	$26.42$	$26.42$	$26.42$	$26.42$	$26.42$
${\displaystyle \frac{{\theta }_{\infty }-{\theta }_{\infty ,\mathrm{Sch}}}{{\theta }_{\infty ,\mathrm{Sch}}}}$	0	$-2.0155\times {10}^{-31}$	$-1.29278\times {10}^{-91}$	$-2.60978\times {10}^{-90}$	0	$-3.32287\times {10}^{-90}$
$s\left(\mu \mathrm{arcsec}\right)$	$0.03306$	$0.03306$	$0.03306$	$0.03306$	$0.03306$	$0.03306$
${\displaystyle \frac{s-s_{,\mathrm{Sch}}}{s_{,\mathrm{Sch}}}}$	0	$4.12221\times {10}^{-30}$	$3.20814\times {10}^{-30}$	$-4.08044\times {10}^{-89}$	$-1.88176\times {10}^{-89}$	$5.31267\times {10}^{-89}$
${\mu }_m=2.5{\mathrm{Log}}_{10}\mu$	$6.82121$	$6.82121$	$6.82121$	$6.82121$	$6.82121$	$6.82121$
${\displaystyle \frac{{\mu }_m-{\mu }_{m,\mathrm{Sch}}}{{\mu }_{m,\mathrm{Sch}}}}$	0	$-3.10219\times {10}^{-31}$	$-4.6598\times {10}^{-31}$	$5.22227\times {10}^{-90}$	$2.61119\times {10}^{-90}$	$-9.97707\times {10}^{-90}$
$\Delta T_{2,1}\left(s\right)$	$691.72$	$691.72$	$691.72$	$691.72$	$691.72$	$691.72$
$\Delta T_{2,1}-\Delta T_{2,1}^{\left(\mathrm{Sch}\right)}$	0	$-1.39416\times {10}^{-28}$	$8.94242\times {10}^{-89}$	$-1.80524\times {10}^{-87}$	0	$-2.2985\times {10}^{-87}$

and

Table 2. Observables of $\mathrm{M}{87}^{*}$.

Type	Sch	AOS	GOP	MC1	MC2	qOS
${\theta }_{\infty }\left(\mu \mathrm{arcsec}\right)$	$19.8509$	$19.8509$	$19.8509$	$19.8509$	$19.8509$	$19.8509$
${\displaystyle \frac{{\theta }_{\infty }-{\theta }_{\infty ,\mathrm{Sch}}}{{\theta }_{\infty ,\mathrm{Sch}}}}$	0	$-1.53022\times {10}^{-33}$	$-5.65763\times {10}^{-98}$	$-1.14213\times {10}^{-96}$	0	$-1.4542\times {10}^{-96}$
$s\left(\mu \mathrm{arcsec}\right)$	$0.02484$	$0.02484$	$0.02484$	$0.02484$	$0.02484$	$0.02484$
${\displaystyle \frac{s-s_{,\mathrm{Sch}}}{s_{,\mathrm{Sch}}}}$	0	$3.12968\times {10}^{-32}$	$2.4357\times {10}^{-32}$	$-1.78574\times {10}^{-95}$	$-8.23521\times {10}^{-96}$	$2.325\times {10}^{-95}$
${\mu }_m=2.5{\mathrm{Log}}_{10}\mu$	$6.82121$	$6.82121$	$6.82121$	$6.82121$	$6.82121$	$6.82121$
${\displaystyle \frac{{\mu }_m-{\mu }_{m,\mathrm{Sch}}}{{\mu }_{m,\mathrm{Sch}}}}$	0	$-2.35526\times {10}^{-33}$	$-3.53783\times {10}^{-33}$	$2.28544\times {10}^{-96}$	$1.14274\times {10}^{-96}$	$-4.3663\times {10}^{-96}$
$\Delta T_{2,1}\left(s\right)$	$1.0456\times {10}^6$	$1.0456\times {10}^6$	$1.0456\times {10}^6$	$1.0456\times {10}^6$	$1.0456\times {10}^6$	$1.0456\times {10}^6$
$\Delta T_{2,1}-\Delta T_{2,1}^{\left(\mathrm{Sch}\right)}$	0	$-1.60003\times {10}^{-27}$	$-5.91575\times {10}^{-92}$	$-1.19424\times {10}^{-90}$	0	$-1.52055\times {10}^{-90}$

show the observables of ${\mathrm{SgrA}}^{*}$ and $\mathrm{M}{87}^{*}$. Each table contains three data sections, corresponding to ${\theta }_{\infty }$, s, and ${\mu }_m$, respectively. Within each section, both the exact value of observables and their relative difference to their Schwarzschild counterparts are included. “Sch” stands for Schwarzschild BH, for which all the relative differences read 0.

By comparing the data computed, it appears that the angular lens observables ${\theta }_{\infty }$ obtained from ${\mathrm{SgrA}}^{*}$ have larger quantum corrections than from $\mathrm{M}{87}^{*}$. For the AOS model where the most significant relative quantum corrections are obtained, the value from ${\mathrm{SgrA}}^{*}$ is typically around 100 times larger than from $\mathrm{M}{87}^{*}$. Also, the time delay for $\mathrm{M}{87}^{*}$ is 10 times larger than ${\mathrm{SgrA}}^{*}$ for the AOS model. This indicates that the quantum effects generated by the BH models of LQG can be very sensitive to the characteristics of the center BH.

Also, as can be seen from both Table 1 and Table 2, AOS model has the largest quantum corrections of ${\theta }_{\infty }$ and s, while the GOP model has the largest quantum correction of ${\mu }_m$. The quantum corrections generated by models MC1, MC2, and qOS are significantly smaller, making them even harder to detect. The relative difference of ${\theta }_{\infty }$ is 0 for the MC2 model, due to the fact that it shares the exact same $A\left(r\right)$ and $C\left(r\right)$ as Schwarzschild BH. Its only quantum effect comes from $B\left(r\right)$.

4. Discussion

In this work, we have studied the quantum corrections to the gravitational lensing effect induced by five different LQG black hole models, where the quantum parameter is obtained, authentic to the original theories for all cases. Using the strong-field-limit method, we successfully computed the deflection angles, as well as lens observables from these models. We have made the following three key discoveries:

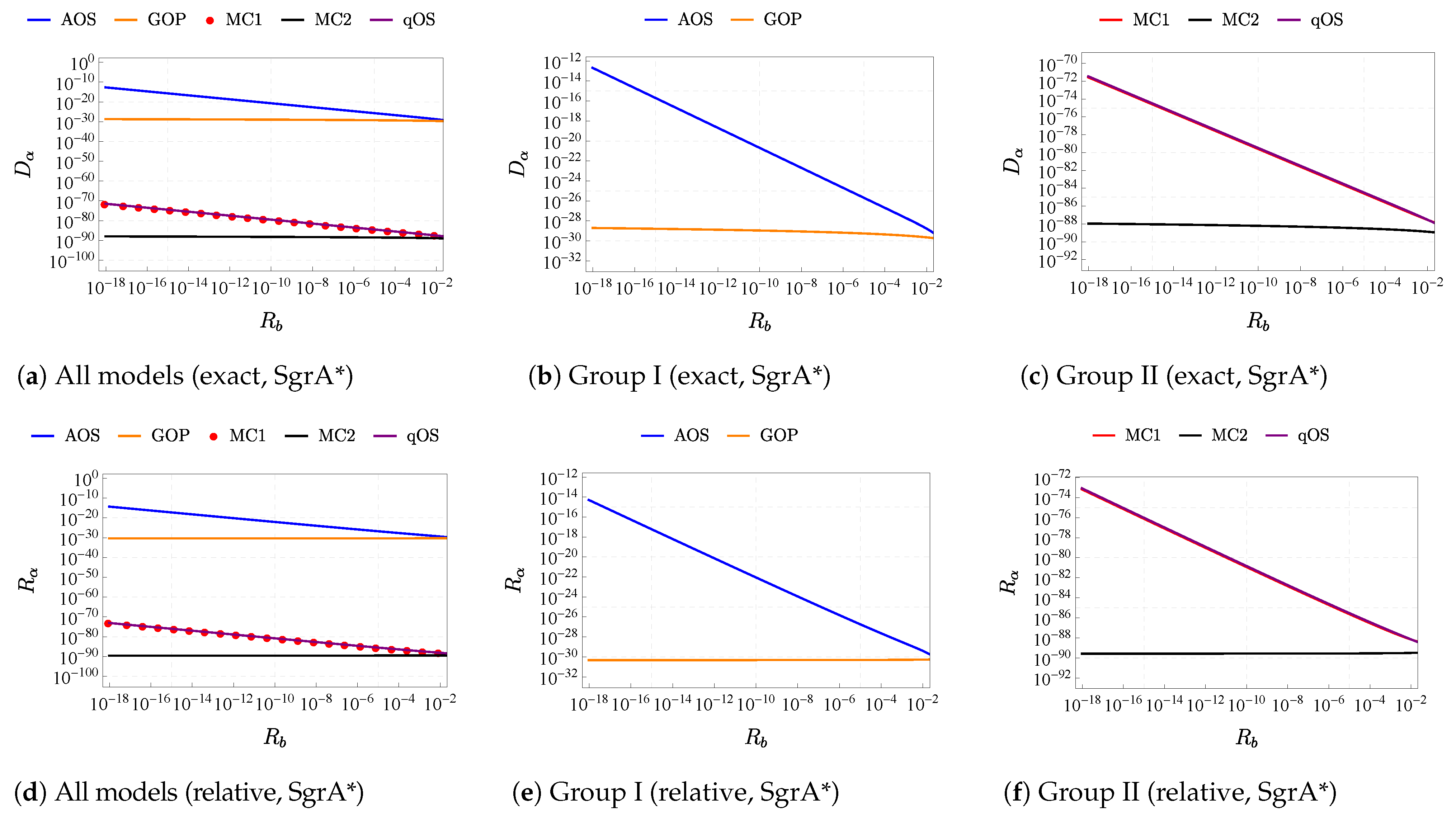
• We discovered that although the quantum effects are very small for all five models, their actual value can vary enormously; the impacts of quantum corrections of the AOS and GOP models are much higher than the impact generated by MC1, MC2, and qOS, forming two different groups of theories based the scale of quantum effects generated by each model. This might indicate the underlying connections and differences among different effective LQG models.
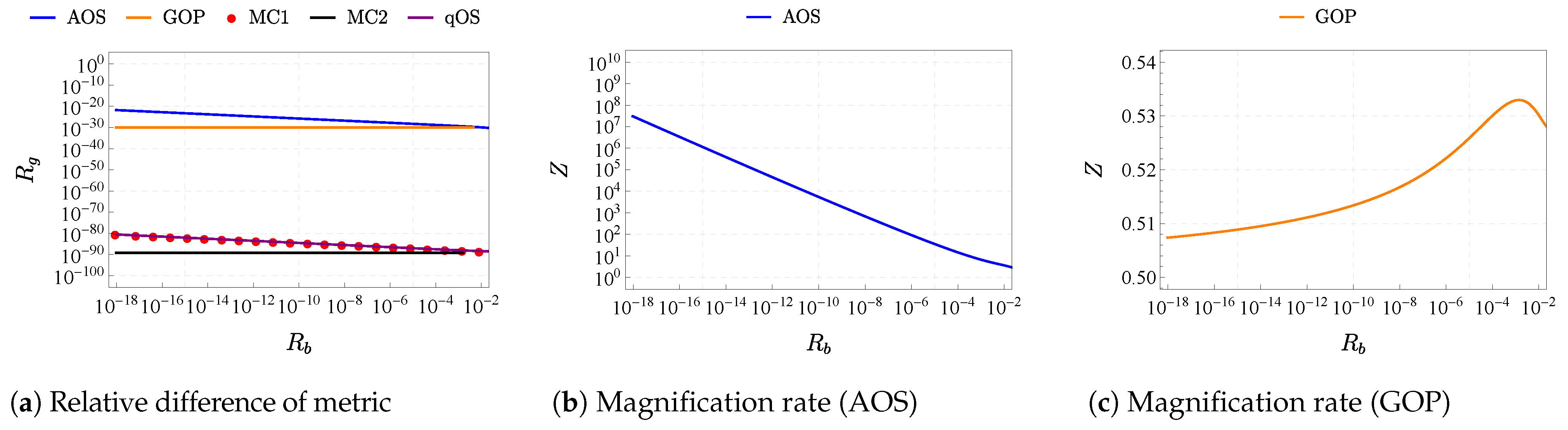
• The quantum corrections of the deflection angles are roughly in the same order as the quantum corrections of the metric tensor. Meanwhile, the ratio between the quantum corrections of the deflection angle and the quantum corrections of the metric is shown to increase drastically for the AOS, MC1, and qOS models, with the impacting parameter b being very close to the minimal impacting factor $b_m$ for Schwarzschild BH. It remains to be discovered whether such a drastic increase can have real observable effects, which can help with the detection of quantum effects from these models.
• Angular lens observables obtained from ${\mathrm{SgrA}}^{*}$ have larger quantum corrections than from $\mathrm{M}{87}^{*}$, while the time delay coming from $\mathrm{M}{87}^{*}$ is larger than ${\mathrm{SgrA}}^{*}$. For the AOS model where the most significant relative quantum corrections are observed, the value for angular observables ${\theta }_{\infty }$, s, ${\mu }_s$ from ${\mathrm{SgrA}}^{*}$ is typically around 100 times larger than that from $\mathrm{M}{87}^{*}$, while the time delay corrections from $\mathrm{M}{87}^{*}$ are 10 times larger than ${\mathrm{SgrA}}^{*}$. This indicates that the center BH with different properties can have very different quantum corrections to the gravitational lensing effects.

In this work, we have explored five different models of LQG BH and compared the quantum corrections to the gravitational lensing effect coming from these models. Using the magnitude of the produced quantum corrections as a criterion, the AOS model stands out, with all four observables being relatively large among the models we investigated. It should be noted, however, that this work aims mainly to provide a starting point towards seriously investigating the observable quantum effects of LQG BH gravitational lensing, motivating us to strictly impose the quantum parameters and study various specific LQG BH models. Since LQG remains largely a theory with many open topics, we have not attempted to determine the best candidate model in this work. The comparisons we made among different models were purely drawn to see how rigorously imposed quantum parameters can affect the behavior of these theories near the BH photon ring.

The quantum impacts we obtained in this work are extremely small due to the quantum parameters valued at the Planck scale. However, noting that the largest quantum corrections we obtained are at the order of $\sim {10}^{-30}$, possibilities still exist to amplify the quantum effects of LQG BH gravitational lensing:

• Based on our research in this work, we discovered that the characteristics of the lens object play an essential role in the gravitational lensing effect. Comparing the results obtained for SgrA* and M87*, the relative differences of the lens observables to the observables for Scharzschild BH are at least 100 times larger for SgrA* than M87*. This result suggests that by discovering new lens objects, it is possible to make the quantum effect larger on the observables, possibly even larger by orders of magnitude, making them much easier to detect.
• The remaining quantization ambiguities might also make the actual quantum effects larger. For example, during the discretization phase of LQG quantization, the minimum spacing of lattices is usually associated with the area gap, which is chosen to be the minimum nonzero eigenvalue of the area operator in Loop Quantum Gravity. This treatment provides the smallest such area gaps in the theory. However, it is not necessarily the only choice of the lattice spacing, which could contribute to larger quantum parameters of the model and thus render its quantum effects larger.
• New models from LQG. So far, the works on studying the gravitational lens effects of LQG models have only explored some effective models of the symmetry-reduced theory of LQG. In this work, we have shown that the quantum effects of different BH models of LQG can be extremely different. Thus, it is possible that some future models, such as the effective models of full canonical LQG and spin foam models which both contain additional quantum corrections, can produce different results than the effective models we studied.
• Studying the gravitational lensing effects of time-like particles, which have also become possible in recent years [47]. The behavior of the gravitational lensing of these particles can be different from photon gravitational lensing, thus providing alternatives to study the quantum effects of the theory.

In order for the quantum effects to be truly detectable, it is crucial that we discuss the current observational limits regarding BH gravitational lensing. In this work, we have mainly explored two types of lens observables, namely angular observables and time delay, for quasars specifically. The technical limits of these two types of observations are quite different. While both observations rely on the telescope to identify the lensing events, the measuring of angular observables is directly limited by the resolution of the telescope. This creates a major obstacle, due to the randomness involved in the lensing images and the resolution limit of the telescope. On the other hand, once the quasar lens event is pinpointed, the measuring of the time delay is mainly restricted by the photometric accuracy of the telescope [48], namely the ability of the telescope to track the rate at which its apparent magnitude changes; this could serve as a potential measurement of the gravitational lensing effect. Nevertheless, the technology to clearly observe the vicinity of the BH in great detail is still beyond reach, and the best current accuracy for measuring the time delay of gravitational lensing induced by galaxies can only achieve several percent. Therefore, due to the extremely small quantum corrections we obtained, it is clear that the exact quantum corrections computed in this paper are unlikely to be directly observable.

In the future, we will continue probing the possibility of testing LQG by strictly imposing the parameters and conditions as they were initially proposed and then by extensively searching its quantum corrections in the classical and semi-classical region, specifically looking for signs that indicate the quantum effect of LQG can be significantly magnified and even observed. We believe that only through the overlap of multiple such results will their actual observation eventually become possible, so that a quantum theory of gravity can truly be tested.