Particle Production in pA Collisions at Mid-Rapidity in the Color Glass Condensate
Abstract
:1. Introduction
2. Double-Inclusive Gluon Production in Dilute–Dense Scattering at Mid-Rapidity
- term: This contribution corresponds to the uncorrelated production, which is simply the square of the single inclusive spectrum.
- -first term: The first term in Equation (20) is proportional towhere the soft form factor is peaked when the momenta of the two gluons in the projectile wave function are very close to each other. Therefore, this term contributes to the Bose enhancement of the gluons in the projectile.
- -second term: The second term in Equation (20) is proportional towhere the soft form factor is peaked when the momenta of the two produced gluons are close to each other. Therefore, this term is the HBT contribution.
- -first term: The first term in Equation (21) is proportional towhere the soft form factor is peaked when the momenta of the gluons in the target that are transferred to the projectile are close to each other. Thus, this term contributes to the Bose enhancement of the gluons in the target.
- -second term: The second term in Equation (21) is proportional towhere the soft factor is peaked when the momenta of the gluons in the projectile are close to each other. Therefore, this is a contribution of the Bose enhancement of the gluons in the projectile. However, compared to the similar contribution in , these terms are suppressed by . Thus, the contribution to the Bose enhancement of the projectile gluons from the second term in can be interpreted as -corrections to the ones observed in .
3. A Specific Model for Double-Inclusive Gluon Production in Dilute–Dense Scattering
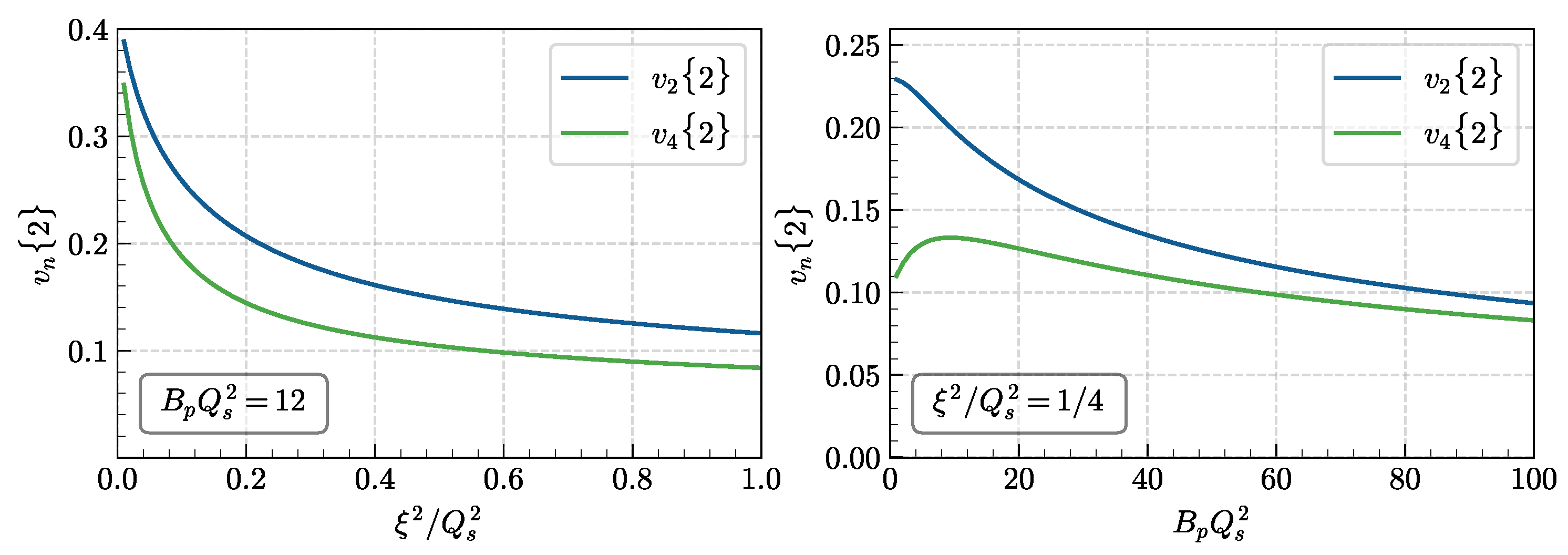
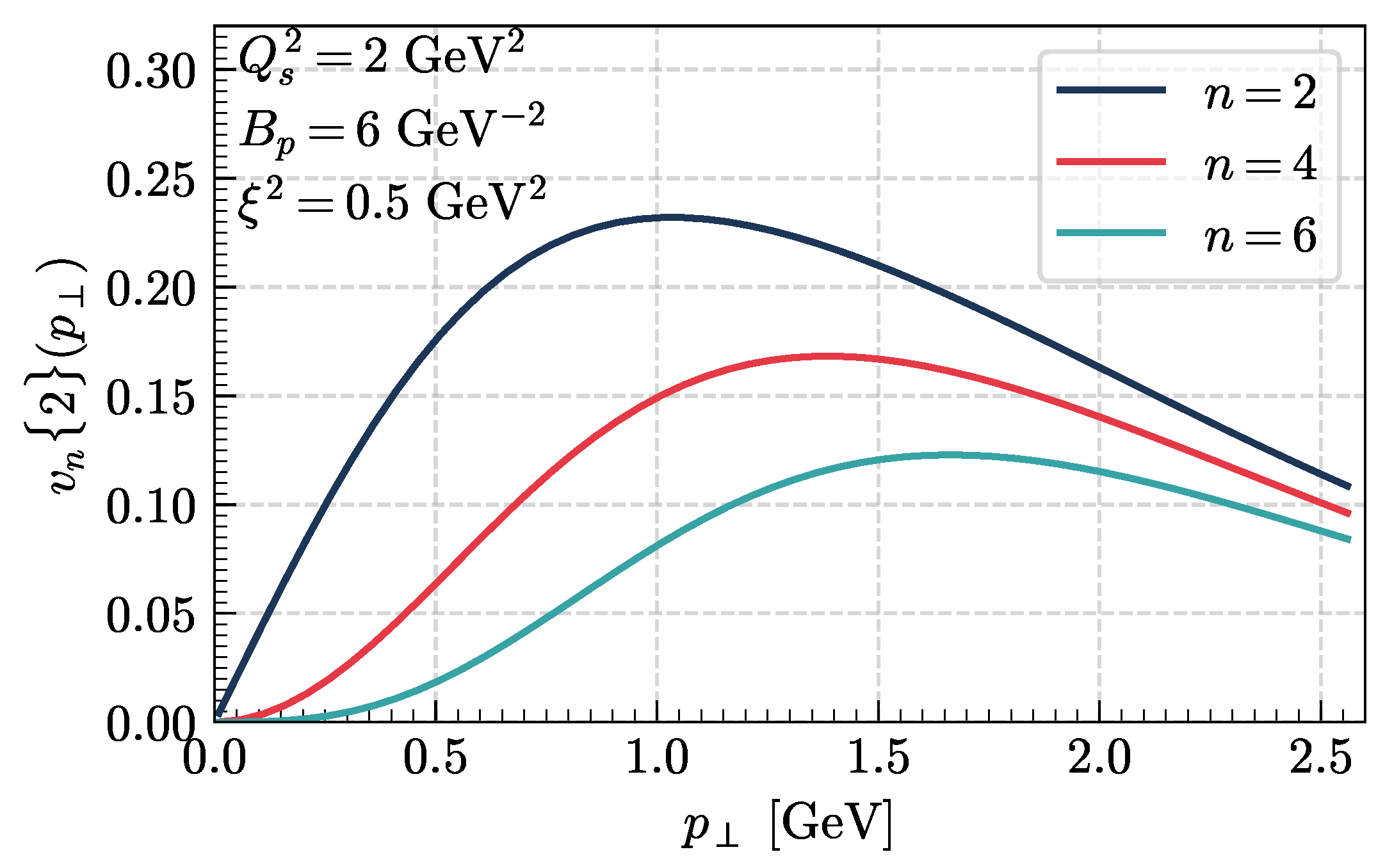
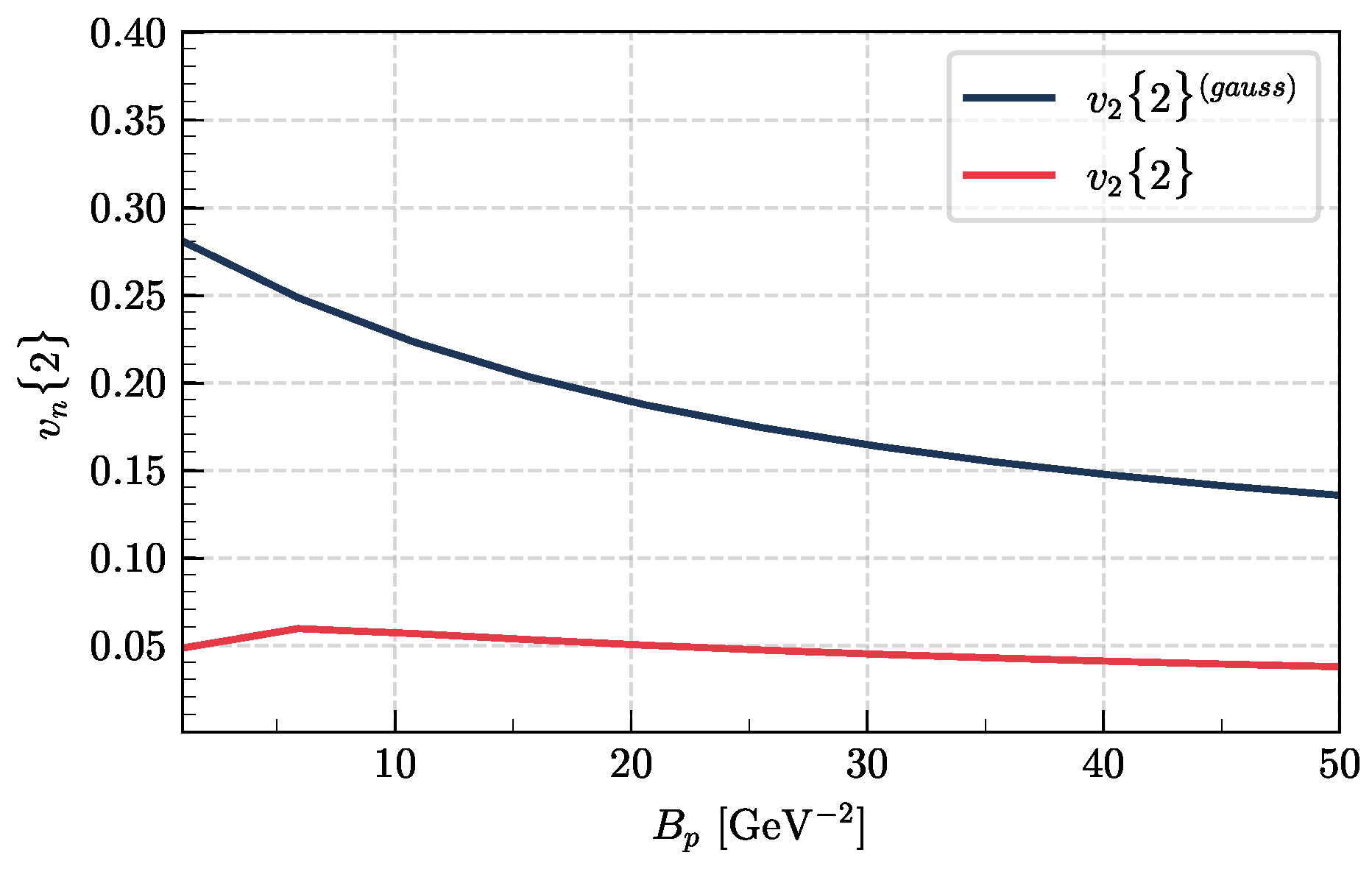
4. Two-Particle Azimuthal Harmonics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | |
| 2 | Throughout the manuscript, we use and as the shorthand notation for coordinate and momentum space integrals in the transverse direction. |
| 3 | Since we do not assume translational invariance of the projectile wave function, the function depends both on the difference and the center of mass coordinate . |
| 4 | Note that, in the eikonal approximation employed in this work, the results are independent of the energy of the collision and of the rapidity of the produced gluons. |
| 5 | The correlations that we computed are those between the final-state gluons before hadronization and neglecting any kind of final-state effects between them or with additional partons produced in the collision, or among final-state hadrons. |
| 6 | The sensitivity of azimuthal harmonics to the value of the effective mass was explored in [65] within the glasma graph approximation including non-eikonal corrections. |
References
- Khachatryan, V. et al. [CMS Collaboration] Observation of Long-Range Near-Side Angular Correlations in Proton-Proton Collisions at the LHC. J. High Energy Phys. 2010, 2010, 91. [Google Scholar] [CrossRef]
- Aaboud, M. et al. [ATLAS Collaboration] Measurements of long-range azimuthal anisotropies and associated Fourier coefficients for pp collisions at =5.02 and 13 TeV and p+Pb collisions at =5.02 TeV with the ATLAS detector. Phys. Rev. C 2017, 96, 024908. [Google Scholar] [CrossRef]
- Khachatryan, V. et al. [CMS Collaboration] Measurement of long-range near-side two-particle angular correlations in pp collisions at =13 TeV. Phys. Rev. Lett. 2016, 116, 172302. [Google Scholar] [CrossRef]
- Aguilar-Saavedra, J.A.; Amor Dos Santos, S.P.; Anjos, N.; Araque, J.P.; Cantrill, R.; Carvalho, J.; Conde Muiño, P.; Da Cunha Sargedas De Sousa, M.J.; Fiolhais, M.; Galhardo, B.; et al. Observation of Long-Range Elliptic Azimuthal Anisotropies in =13 and 2.76 TeV pp Collisions with the ATLAS Detector. Phys. Rev. Lett. 2016, 116, 172301. [Google Scholar]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Br stetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Evidence for collectivity in pp collisions at the LHC. Phys. Lett. B 2017, 765, 193–220. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of Long-Range Near-Side Angular Correlations in Proton-Lead Collisions at the LHC. Phys. Lett. B 2013, 718, 795–814. [Google Scholar] [CrossRef]
- Abelev, B. Long-range angular correlations on the near and away side in p-Pb collisions at =5.02 TeV. Phys. Lett. B 2013, 719, 29–41. [Google Scholar] [CrossRef]
- Aad, G. Observation of Associated Near-Side and Away-Side Long-Range Correlations in =5.02 TeV Proton-Lead Collisions with the ATLAS Detector. Phys. Rev. Lett. 2013, 110, 182302. [Google Scholar] [CrossRef]
- Beteta, C.A.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Measurements of long-range near-side angular correlations in =5TeV proton-lead collisions in the forward region. Phys. Lett. B 2016, 762, 473–483. [Google Scholar]
- Alver, B.; Back, B.B.; Baker, M.D.; Ballintijn, M.; Barton, D.S.; Betts, R.R.; Bickley, A.A.; Bindel, R.; Busza, W.; Carroll, A.; et al. High transverse momentum triggered correlations over a large pseudorapidity acceptance in Au+Au collisions at s(NN)**1/2 = 200 GeV. Phys. Rev. Lett. 2010, 104, 062301. [Google Scholar] [CrossRef]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Balewski, J.; Barannikova, O.; Barnby, L.S.; et al. Long range rapidity correlations and jet production in high energy nuclear collisions. Phys. Rev. C 2009, 80, 064912. [Google Scholar] [CrossRef]
- Adare, A.; Aidala, C.; Ajitan, N.N.; Akiba, Y.; Akimoto, R.; Al-Bataineh, H.; Al-Ta’ani, H.; Alexander, J.; Andrews, K.R.; Angerami, A.; et al. Measurement of long-range angular correlation and quadrupole anisotropy of pions and (anti)protons in central d+Au collisions at = 200 GeV. Phys. Rev. Lett. 2015, 114, 192301. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Aparin, A.; Arkhipkin, D.; Aschenauer, E.C.; et al. Long-range pseudorapidity dihadron correlations in d+Au collisions at =200 GeV. Phys. Lett. B 2015, 747, 265–271. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitan, N.N.; Akiba, Y.; Akimoto, R.; Al-Bataineh, H.; Alexander, J.; Alfred, M.; Al-Ta’ani, H.; et al. Measurements of elliptic and triangular flow in high-multiplicity 3He+Au collisions at =200 GeV. Phys. Rev. Lett. 2015, 115, 142301. [Google Scholar] [CrossRef]
- Jeon, S.; Heinz, U. Introduction to Hydrodynamics. Int. J. Mod. Phys. E 2015, 24, 1530010. [Google Scholar] [CrossRef]
- Romatschke, P.; Romatschke, U. Relativistic Fluid Dynamics In and Out of Equilibrium; Cambridge University Press: Cambridge, UK, 2019; ISBN 978-1-108-48368-1/978-1-108-75002-8. [Google Scholar]
- Schenke, B.; Tribedy, P.; Venugopalan, R. Fluctuating Glasma initial conditions and flow in heavy ion collisions. Phys. Rev. Lett. 2012, 108, 252301. [Google Scholar] [CrossRef] [PubMed]
- Kurkela, A.; Wiedemann, U.A.; Wu, B. Flow in AA and pA as an interplay of fluid-like and non-fluid like excitations. Eur. Phys. J. C 2019, 79, 965. [Google Scholar] [CrossRef]
- Kovchegov, Y.V.; Levin, E. Quantum Chromodynamics at High Energy; Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology (33); Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Gelis, F.; Iancu, E.; Jalilian-Marian, J.; Venugopalan, R. The Color Glass Condensate. Ann. Rev. Nucl. Part. Sci. 2010, 60, 463–489. [Google Scholar] [CrossRef]
- Altinoluk, T.; Armesto, N. Particle correlations from the initial state. Eur. Phys. J. A 2020, 56, 215. [Google Scholar] [CrossRef]
- Kovner, A.; Lublinsky, M. Angular Correlations in Gluon Production at High Energy. Phys. Rev. D 2011, 83, 034017. [Google Scholar] [CrossRef]
- Kovner, A.; Lublinsky, M. On Angular Correlations and High Energy Evolution. Phys. Rev. D 2011, 84, 094011. [Google Scholar] [CrossRef]
- Kovner, A.; Lublinsky, M. Angular and long range rapidity correlations in particle production at high energy. Int. J. Mod. Phys. E 2013, 22, 1330001. [Google Scholar] [CrossRef]
- Dumitru, A.; McLerran, L.; Skokov, V. Azimuthal asymmetries and the emergence of “collectivity” from multi-particle correlations in high-energy pA collisions. Phys. Lett. B 2015, 743, 134–137. [Google Scholar] [CrossRef]
- Dumitru, A.; Skokov, V. Anisotropy of the semiclassical gluon field of a large nucleus at high energy. Phys. Rev. D 2015, 91, 074006. [Google Scholar] [CrossRef]
- Dumitru, A.; Gelis, F.; McLerran, L.; Venugopalan, R. Glasma flux tubes and the near side ridge phenomenon at RHIC. Nucl. Phys. A 2008, 810, 91–108. [Google Scholar] [CrossRef]
- Armesto, N.; McLerran, L.; Pajares, C. Long Range Forward-Backward Correlations and the Color Glass Condensate. Nucl. Phys. A 2007, 781, 201–208. [Google Scholar] [CrossRef]
- Dumitru, A.; Dusling, K.; Gelis, F.; Jalilian-Marian, J.; Lappi, T.; Venugopalan, R. The Ridge in proton–proton collisions at the LHC. Phys. Lett. B 2011, 697, 21–25. [Google Scholar] [CrossRef]
- Dusling, K.; Venugopalan, R. Azimuthal collimation of long range rapidity correlations by strong color fields in high multiplicity hadron-hadron collisions. Phys. Rev. Lett. 2012, 108, 262001. [Google Scholar] [CrossRef] [PubMed]
- Dusling, K.; Venugopalan, R. Evidence for BFKL and saturation dynamics from dihadron spectra at the LHC. Phys. Rev. D 2013, 87, 051502. [Google Scholar] [CrossRef]
- Dusling, K.; Venugopalan, R. Explanation of systematics of CMS p+Pb high multiplicity di-hadron data at =5.02 TeV. Phys. Rev. D 2013, 87, 054014. [Google Scholar] [CrossRef]
- Dusling, K.; Venugopalan, R. Comparison of the Color Glass Condensate to dihadron correlations in proton–proton and proton–nucleus collisions. Phys. Rev. D 2013, 87, 094034. [Google Scholar] [CrossRef]
- Dusling, K.; Mace, M.; Venugopalan, R. Multiparticle collectivity from initial state correlations in high energy proton–nucleus collisions. Phys. Rev. Lett. 2018, 120, 042002. [Google Scholar] [CrossRef] [PubMed]
- Dusling, K.; Mace, M.; Venugopalan, R. Parton model description of multiparticle azimuthal correlations in pA collisions. Phys. Rev. D 2018, 97, 016014. [Google Scholar] [CrossRef]
- Altinoluk, T.; Armesto, N.; Beuf, G.; Kovner, A.; Lublinsky, M. Bose enhancement and the ridge. Phys. Lett. B 2015, 751, 448–452. [Google Scholar] [CrossRef]
- Kovchegov, Y.V.; Wertepny, D.E. Long-Range Rapidity Correlations in Heavy-Light Ion Collisions. Nucl. Phys. A 2013, 906, 50–83. [Google Scholar] [CrossRef]
- Kovchegov, Y.V.; Wertepny, D.E. Two-Gluon Correlations in Heavy-Light Ion Collisions: Energy and Geometry Dependence, IR Divergences, and kT-Factorization. Nucl. Phys. A 2014, 925, 254–295. [Google Scholar] [CrossRef]
- Altinoluk, T.; Armesto, N.; Beuf, G.; Kovner, A.; Lublinsky, M. Hanbury–Brown–Twiss measurements at large rapidity separations, or can we measure the proton radius in p-A collisions? Phys. Lett. B 2016, 752, 113–121. [Google Scholar] [CrossRef]
- Altinoluk, T.; Armesto, N.; Beuf, G.; Kovner, A.; Lublinsky, M. Quark correlations in the Color Glass Condensate: Pauli blocking and the ridge. Phys. Rev. D 2017, 95, 034025. [Google Scholar] [CrossRef]
- Altinoluk, T.; Armesto, N.; Wertepny, D.E. Correlations and the ridge in the Color Glass Condensate beyond the glasma graph approximation. J. High Energy Phys. 2018, 5, 207. [Google Scholar] [CrossRef]
- Altinoluk, T.; Armesto, N.; Kovner, A.; Lublinsky, M. Double and triple inclusive gluon production at mid rapidity: Quantum interference in p-A scattering. Eur. Phys. J. C 2018, 78, 702. [Google Scholar] [CrossRef]
- Martinez, M.; Sievert, M.D.; Wertepny, D.E. Toward Initial Conditions of Conserved Charges Part I: Spatial Correlations of Quarks and Antiquarks. J. High Energy Phys. 2018, 7, 3. [Google Scholar] [CrossRef]
- Martinez, M.; Sievert, M.D.; Wertepny, D.E. Multiparticle Production at Mid-Rapidity in the Color-Glass Condensate. J. High Energy Phys. 2019, 2, 24. [Google Scholar] [CrossRef]
- Özonder, Ş. Triple-gluon and quadruple-gluon azimuthal correlations from glasma and higher-dimensional ridges. Phys. Rev. D 2015, 91, 034005. [Google Scholar] [CrossRef]
- Özönder, Ş. Predictions on three-particle azimuthal correlations in proton–proton collisions. Turk. J. Phys. 2018, 42, 78–83. [Google Scholar] [CrossRef]
- Davy, M.K.; Marquet, C.; Shi, Y.; Xiao, B.W.; Zhang, C. Two particle azimuthal harmonics in pA collisions. Nucl. Phys. A 2019, 983, 293–309. [Google Scholar] [CrossRef]
- Zhang, C.; Marquet, C.; Qin, G.Y.; Wei, S.Y.; Xiao, B.W. Elliptic Flow of Heavy Quarkonia in pA Collisions. Phys. Rev. Lett. 2019, 122, 172302. [Google Scholar] [CrossRef]
- Zhang, C.; Marquet, C.; Qin, G.Y.; Shi, Y.; Wang, L.; Wei, S.Y.; Xiao, B.W. Collectivity of heavy mesons in proton–nucleus collisions. Phys. Rev. D 2020, 102, 034010. [Google Scholar] [CrossRef]
- Kovner, A.; Skokov, V.V. Does shape matter? v2 vs eccentricity in small x gluon production. Phys. Lett. B 2018, 785, 372–380. [Google Scholar] [CrossRef]
- Kovner, A.; Skokov, V.V. Bose enhancement, the Liouville effective action and the high multiplicity tail in p-A collisions. Phys. Rev. D 2018, 98, 014004. [Google Scholar] [CrossRef]
- Altinoluk, T.; Armesto, N.; Kovner, A.; Lublinsky, M.; Skokov, V.V. Angular correlations in pA collisions from CGC: Multiplicity and mean transverse momentum dependence of v2. Eur. Phys. J. C 2021, 81, 583. [Google Scholar] [CrossRef]
- Agostini, P.; Altinoluk, T.; Armesto, N. Multi-particle production in proton–nucleus collisions in the Color Glass Condensate. Eur. Phys. J. C 2021, 81, 760. [Google Scholar] [CrossRef]
- Jalilian-Marian, J.; Kovchegov, Y.V. Inclusive two-gluon and valence quark–gluon production in DIS and pA. Phys. Rev. D 2004, 70, 114017, Erratum in: Phys. Rev. D 2005, 71, 079901. [Google Scholar] [CrossRef]
- Kovner, A.; Lublinsky, M. One gluon, two gluon: Multigluon production via high energy evolution. J. High Energy Phys. 2006, 11, 083. [Google Scholar] [CrossRef]
- McLerran, L.D.; Venugopalan, R. Computing quark and gluon distribution functions for very large nuclei. Phys. Rev. D 1994, 49, 2233–2241. [Google Scholar] [CrossRef]
- McLerran, L.D.; Venugopalan, R. Gluon distribution functions for very large nuclei at small transverse momentum. Phys. Rev. D 1994, 49, 3352–3355. [Google Scholar] [CrossRef]
- Kovner, A.; Rezaeian, A.H. Double parton scattering in the CGC: Double quark production and effects of quantum statistics. Phys. Rev. D 2017, 96, 074018. [Google Scholar] [CrossRef]
- Kovner, A.; Rezaeian, A.H. Multiquark production in p+A collisions: Quantum interference effects. Phys. Rev. D 2018, 97, 074008. [Google Scholar] [CrossRef]
- Lappi, T.; Schenke, B.; Schlichting, S.; Venugopalan, R. Tracing the origin of azimuthal gluon correlations in the Color Glass Condensate. J. High Energy Phys. 2016, 1, 61. [Google Scholar] [CrossRef]
- Kovner, A.; Lublinsky, M.; Skokov, V. Exploring correlations in the CGC wave function: Odd azimuthal anisotropy. Phys. Rev. D 2017, 96, 016010. [Google Scholar] [CrossRef]
- Kovchegov, Y.V.; Skokov, V.V. How classical gluon fields generate odd azimuthal harmonics for the two-gluon correlation function in high-energy collisions. Phys. Rev. D 2018, 97, 094021. [Google Scholar] [CrossRef]
- Kohara, A.K.; Marquet, C.; Vila, V. Low projectile density contributions in the dilute-dense CGC framework for two-particle correlations. J. High Energy Phys. 2023, 10, 159. [Google Scholar] [CrossRef]
- Agostini, P.; Altinoluk, T.; Armesto, N. Non-eikonal corrections to multi-particle production in the Color Glass Condensate. Eur. Phys. J. C 2019, 79, 600. [Google Scholar] [CrossRef]
- Agostini, P.; Altinoluk, T.; Armesto, N. Effect of non-eikonal corrections on azimuthal asymmetries in the Color Glass Condensate. Eur. Phys. J. C 2019, 79, 790. [Google Scholar] [CrossRef]
- Agostini, P.; Altinoluk, T.; Armesto, N.; Dominguez, F.; Milhano, J.G. Multiparticle production in proton–nucleus collisions beyond eikonal accuracy. Eur. Phys. J. C 2022, 82, 1001. [Google Scholar] [CrossRef]
- Agostini, P.; Altinoluk, T.; Armesto, N. Finite width effects on the azimuthal asymmetry in proton–nucleus collisions in the Color Glass Condensate. Phys. Lett. B 2023, 840, 137892. [Google Scholar] [CrossRef]
- Golec-Biernat, K.J.; Wusthoff, M. Saturation effects in deep inelastic scattering at low Q**2 and its implications on diffraction. Phys. Rev. D 1998, 59, 014017. [Google Scholar] [CrossRef]
- Golec-Biernat, K.J.; Wusthoff, M. Saturation in diffractive deep inelastic scattering. Phys. Rev. D 1999, 60, 114023. [Google Scholar] [CrossRef]
- Dumitru, A.; Hayashigaki, A.; Jalilian-Marian, J. The Color Glass Condensate and hadron production in the forward region. Nucl. Phys. A 2006, 765, 464–482. [Google Scholar] [CrossRef]
- Altinoluk, T.; Kovner, A. Particle Production at High Energy and Large Transverse Momentum—‘The Hybrid Formalism’ Revisited. Phys. Rev. D 2011, 83, 105004. [Google Scholar] [CrossRef]
- Lappi, T. Azimuthal harmonics of color fields in a high energy nucleus. Phys. Lett. B 2015, 744, 315–319. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agostini, P.; Altinoluk, T.; Armesto, N. Particle Production in pA Collisions at Mid-Rapidity in the Color Glass Condensate. Universe 2024, 10, 58. https://doi.org/10.3390/universe10020058
Agostini P, Altinoluk T, Armesto N. Particle Production in pA Collisions at Mid-Rapidity in the Color Glass Condensate. Universe. 2024; 10(2):58. https://doi.org/10.3390/universe10020058
Chicago/Turabian StyleAgostini, Pedro, Tolga Altinoluk, and Néstor Armesto. 2024. "Particle Production in pA Collisions at Mid-Rapidity in the Color Glass Condensate" Universe 10, no. 2: 58. https://doi.org/10.3390/universe10020058
APA StyleAgostini, P., Altinoluk, T., & Armesto, N. (2024). Particle Production in pA Collisions at Mid-Rapidity in the Color Glass Condensate. Universe, 10(2), 58. https://doi.org/10.3390/universe10020058





