The Physics of Core-Collapse Supernovae: Explosion Mechanism and Explosive Nucleosynthesis
Abstract
:1. Introduction
2. The Progenitors of CCSNe: Massive Stars and Their Evolution
2.1. Pre-Supernova Evolution
2.2. Challenges and Uncertainties in Stellar Evolution
2.2.1. Mass-Loss
2.2.2. Mixing and Transport Processes
2.2.3. Magnetic Fields
2.2.4. Nuclear Reaction Rates
2.2.5. Binary Nature of Massive Stars
2.2.6. Core-Collapse Supernova Mechanism
2.2.7. Stellar Codes
3. Core-Collapse Supernova Theory
3.1. The Collapse Phase
3.2. The Bounce Phase
3.3. Neutrino Delayed Heating
3.4. Multi-Dimensional Effects
3.5. Microphysics: The Nuclear EOS and Neutrino Physics
3.6. State-of-the-Art CCSNe Codes
- FLASH [163]: a multi-physics code that, when employed for CCSNe simulations, typically uses Adaptive Mesh Refinement (AMR) for the hydrodynamics, an approximate treatment of general relativistic effects following Case A of Marek et al. [162], and a two-moment M1 scheme [156] for multidimensional neutrino transport. Most versions of the code do not include effects of nuclear burning, although a more modern version of the code, i.e., FLASH-X, is currently under development [164];
- 3DnSNeIDSA [34]: it uses an approximate treatment of general relativistic effects following Case A of Marek et al. [162], and neutrino transport is solved using a spectral method based on the isotropic source diffusion approximation (ISDA) [165], where multidimensional effects are treated using a ray-by-ray approximation. The most recent version of the code is also able to solve the magnetohydrodynamic (MHD) equations [166]. The effects of nuclear burning are usually not taken into account, although some versions of the code include small nuclear networks at low densities [167];
- PROMETHEUS-VERTEX [168,169]: it uses an approximate treatment of general relativistic effects following Case A of Marek et al. [162], and neutrino transport is solved using a variable Eddington factor closure. The multi-dimensional aspects are treated using the so-called ray-by-ray plus approximation. For regions not in nuclear statistical equilibrium a “flash-ing” approximation is used to quantify the heating due to nuclear burning;
- CHIMERA [170]: it uses an approximate treatment of general relativistic effects following Case A of Marek et al. [162], and neutrino transport is solved using a multi-group flux-limited diffusion (MGFLD) approximation following [81]. Multi-dimensional neutrino transport effects are treated using the so-called ray-by-ray approximation. Moreover, it is able to handle regions not in nuclear statistical equilibrium (NSE) using a large nuclear reaction network with up to 160 species [171];
- COCONUT-FMT [172]: it solves the general relativistic metric equations using the extended conformal flatness condition. Neutrinos are treated using a simpler, fast multigroup transport (FMT). Recently, it has been extended to solve the MHD equations [173] and Newtonian hydrodynamics. The general relativistic hydrodynamics has also been coupled with other neutrino transport codes, like VERTEX [29]. The “flash-ing” approximation from Rampp and Janka [168] is used to quantify the heating due to nuclear burning;
- Aenus-Alcar [174]: it uses an approximate treatment of general relativistic effects following Case A of Marek et al. [162]. The neutrino transport is solved using a multi-dimensional two-moment M1 scheme. For regions not in nuclear statistical equilibrium a “flash-ing” approximation is used to quantify the heating due to nuclear burning [168]. Versions of the code that include a full nuclear burning network are currently being developed [175];
- SPHYNX [176]: the only smoothed particle hydrodynamics (SPH) code (to the authors’ knowledge) employed to simulate CCSNe, capable of reaching similar resolutions to the codes mentioned above. Neutrinos are treated using the relatively simple spectral leakage scheme described in Perego et al. [177]. Nuclear burning can be incorporated to the EOS routines modularly, although no simulations including it have been tested to the author’s knowledge;
- GRMHD codes. Recently, modern GRMHD codes have been developed to perform CCSNe simulations. Kuroda et al. [157] developed a code that solves the spacetime equations using a BSSN formalism [178,179], solves the MHD equations, and uses a multi-dimensional two-moment based treatment of multidimensional neutrino transport. Other codes that follow a similar approach are currently under development, and several new multi-physics, GRMHD codes are likely to be employed for production runs of CCSNe in the next few years.
4. CCSNe in Spherical Symmetry
4.1. The Critical Luminosity Condition
4.2. The Explodability Problem
Impact of Stellar Evolution Uncertainties on the Explodability

5. Propagation of the Shock and Explosive Nucleosynthesis
5.1. Explosive Nucleosynthesis
5.2. Explosive Burning Stages
5.3. The Production of Exotic Nuclei from Neutrino Winds
5.4. The Production of p-Nuclei: The -Process in CCSNe
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weaver, T.A.; Zimmerman, G.B.; Woosley, S.E. Presupernova evolution of massive stars. Astrophys. J. 1978, 225, 1021–1029. [Google Scholar] [CrossRef]
- Woosley, S.E.; Heger, A.; Weaver, T.A. The evolution and explosion of massive stars. Rev. Mod. Phys. 2002, 74, 1015–1071. [Google Scholar] [CrossRef]
- Heger, A.; Woosley, S.E. Nucleosynthesis and Evolution of Massive Metal-Free Stars. Astrophys. J. 2010, 724, 341–373. [Google Scholar] [CrossRef]
- Ekström, S.; Meynet, G.; Chiappini, C.; Hirschi, R.; Maeder, A. Effects of rotation on the evolution of primordial stars. Astron. Astrophys. 2008, 489, 685–698. [Google Scholar] [CrossRef]
- Ekström, S.; Georgy, C.; Eggenberger, P.; Meynet, G.; Mowlavi, N.; Wyttenbach, A.; Granada, A.; Decressin, T.; Hirschi, R.; Frischknecht, U.; et al. Grids of stellar models with rotation. I. Models from 0.8 to 120 M⊙ at solar metallicity (Z = 0.014). Astron. Astrophys. 2012, 537, A146. [Google Scholar] [CrossRef]
- Chieffi, A.; Limongi, M.; Straniero, O. The evolution of a 25 M⊙ star from the main sequence up to the onset of the iron core collapse. Astrophys. J. 1998, 502, 737. [Google Scholar] [CrossRef]
- Chieffi, A.; Limongi, M. Pre-supernova Evolution of Rotating Solar Metallicity Stars in the Mass Range 13–120 M⊙ and their Explosive Yields. Astrophys. J. 2013, 764, 21. [Google Scholar] [CrossRef]
- Limongi, M.; Chieffi, A. Presupernova Evolution and Explosive Nucleosynthesis of Rotating Massive Stars in the Metallicity Range -3 ≤ [Fe/H] ≤ 0. Astrophys. J. Suppl. Ser. 2018, 237, 13. [Google Scholar] [CrossRef]
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. Ser. 2011, 192, 3. [Google Scholar] [CrossRef]
- Paxton, B.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Blinnikov, S.; Duffell, P.; Farmer, R.; Goldberg, J.A.; Marchant, P.; Sorokina, E.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Convective Boundaries, Element Diffusion, and Massive Star Explosions. Astrophys. J. Suppl. Ser. 2018, 234, 34. [Google Scholar] [CrossRef]
- Stancliffe, R.J.; Fossati, L.; Passy, J.C.; Schneider, F.R.N. Confronting uncertainties in stellar physics: Calibrating convective overshooting with eclipsing binaries. Astron. Astrophys. 2015, 575, A117. [Google Scholar] [CrossRef]
- Stancliffe, R.J.; Fossati, L.; Passy, J.C.; Schneider, F.R.N. Confronting uncertainties in stellar physics. II. Exploring differences in main-sequence stellar evolution tracks. Astron. Astrophys. 2016, 586, A119. [Google Scholar] [CrossRef]
- Rizzuti, F.; Hirschi, R.; Georgy, C.; Arnett, W.D.; Meakin, C.; Murphy, A.S. Realistic 3D hydrodynamics simulations find significant turbulent entrainment in massive stars. Mon. Not. R. Astron. Soc. 2022, 515, 4013–4019. [Google Scholar] [CrossRef]
- Rizzuti, F.; Hirschi, R.; Arnett, W.D.; Georgy, C.; Meakin, C.; Murphy, A.S.; Rauscher, T.; Varma, V. 3D stellar evolution: Hydrodynamic simulations of a complete burning phase in a massive star. Mon. Not. R. Astron. Soc. 2023, 523, 2317–2328. [Google Scholar] [CrossRef]
- Klähn, T.; Blaschke, D.; Typel, S.; van Dalen, E.N.E.; Faessler, A.; Fuchs, C.; Gaitanos, T.; Grigorian, H.; Ho, A.; Kolomeitsev, E.E.; et al. Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions. Phys. Rev. C 2006, 74, 035802. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of State and Neutron Star Properties Constrained by Nuclear Physics and Observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A.; Xu, J. Combined Constraints on the Equation of State of Dense Neutron-rich Matter from Terrestrial Nuclear Experiments and Observations of Neutron Stars. Astrophys. J. 2018, 859, 90. [Google Scholar] [CrossRef]
- Burgio, G.F.; Schulze, H.J.; Vidaña, I.; Wei, J.B. Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 2021, 120, 103879. [Google Scholar] [CrossRef]
- Raduta, A.R.; Nacu, F.; Oertel, M. Equations of state for hot neutron stars. Eur. Phys. J. A 2021, 57, 329. [Google Scholar] [CrossRef]
- Furusawa, S.; Nagakura, H. Nuclei in core-collapse supernovae engine. Prog. Part. Nucl. Phys. 2023, 129, 104018. [Google Scholar] [CrossRef]
- Nättilä, J.; Steiner, A.W.; Kajava, J.J.E.; Suleimanov, V.F.; Poutanen, J. Equation of state constraints for the cold dense matter inside neutron stars using the cooling tail method. Astron. Astrophys. 2016, 591, A25. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. 2018, 852, L29. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.; Armstrong, D.S.; Averett, T.; Ayerbe Gayoso, C.; Barcus, S.; Bellini, V.; Beminiwattha, R.S.; et al. Accurate Determination of the Neutron Skin Thickness of 208Pb through Parity-Violation in Electron Scattering. Phys. Rev. Lett. 2021, 126, 172502. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.A.; Armstrong, D.S.; Averett, T.; Ayerbe Gayoso, C.; Barcus, S.K.; Bellini, V.; Beminiwattha, R.S.; et al. Precision Determination of the Neutral Weak Form Factor of Ca 48. Phys. Rev. Lett. 2022, 129, 042501. [Google Scholar] [CrossRef] [PubMed]
- Boccioli, L.; Mathews, G.J.; O’Connor, E.P. General Relativistic Neutrino-driven Turbulence in One-dimensional Core-collapse Supernovae. Astrophys. J. 2021, 912, 29. [Google Scholar] [CrossRef]
- Mezzacappa, A.; Endeve, E.; Messer, O.E.B.; Bruenn, S.W. Physical, numerical, and computational challenges of modeling neutrino transport in core-collapse supernovae. Living Rev. Comput. Astrophys. 2020, 6, 4. [Google Scholar] [CrossRef]
- Richers, S.; Nagakura, H.; Ott, C.D.; Dolence, J.; Sumiyoshi, K.; Yamada, S. A Detailed Comparison of Multidimensional Boltzmann Neutrino Transport Methods in Core-collapse Supernovae. Astrophys. J. 2017, 847, 133. [Google Scholar] [CrossRef]
- Fischer, T.; Bastian, N.U.; Blaschke, D.; Cierniak, M.; Hempel, M.; Klähn, T.; Martínez-Pinedo, G.; Newton, W.G.; Röpke, G.; Typel, S. The State of Matter in Simulations of Core-Collapse supernovae—Reflections and Recent Developments. Publ. Astron. Soc. Aust. 2017, 34, e067. [Google Scholar] [CrossRef]
- Müller, B.; Janka, H.T.; Marek, A. A New Multi-dimensional General Relativistic Neutrino Hydrodynamics Code for Core-collapse Supernovae. II. Relativistic Explosion Models of Core-collapse Supernovae. Astrophys. J. 2012, 756, 84. [Google Scholar] [CrossRef]
- Takiwaki, T.; Kotake, K.; Suwa, Y. Three-dimensional Hydrodynamic Core-collapse Supernova Simulations for an 11.2 M⊙ Star with Spectral Neutrino Transport. Astrophys. J. 2012, 749, 98. [Google Scholar] [CrossRef]
- Lentz, E.J.; Bruenn, S.W.; Hix, W.R.; Mezzacappa, A.; Messer, O.E.B.; Endeve, E.; Blondin, J.M.; Harris, J.A.; Marronetti, P.; Yakunin, K.N. Three-dimensional Core-collapse Supernova Simulated Using a 15 M ⊙ Progenitor. Astrophys. J. 2015, 807, L31. [Google Scholar] [CrossRef]
- Janka, H.T.; Melson, T.; Summa, A. Physics of Core-Collapse Supernovae in Three Dimensions: A Sneak Preview. Annu. Rev. Nucl. Part. Sci. 2016, 66, 341–375. [Google Scholar] [CrossRef]
- Bruenn, S.W.; Lentz, E.J.; Hix, W.R.; Mezzacappa, A.; Harris, J.A.; Messer, O.E.B.; Endeve, E.; Blondin, J.M.; Chertkow, M.A.; Lingerfelt, E.J.; et al. The Development of Explosions in Axisymmetric Ab Initio Core-collapse Supernova Simulations of 12–25 M Stars. Astrophys. J. 2016, 818, 123. [Google Scholar] [CrossRef]
- Takiwaki, T.; Kotake, K.; Suwa, Y. Three-dimensional simulations of rapidly rotating core-collapse supernovae: Finding a neutrino-powered explosion aided by non-axisymmetric flows. Mon. Not. R. Astron. Soc. 2016, 461, L112–L116. [Google Scholar] [CrossRef]
- O’Connor, E.P.; Couch, S.M. Two-dimensional Core-collapse Supernova Explosions Aided by General Relativity with Multidimensional Neutrino Transport. Astrophys. J. 2018, 854, 63. [Google Scholar] [CrossRef]
- Müller, B.; Tauris, T.M.; Heger, A.; Banerjee, P.; Qian, Y.Z.; Powell, J.; Chan, C.; Gay, D.W.; Langer, N. Three-dimensional simulations of neutrino-driven core-collapse supernovae from low-mass single and binary star progenitors. Mon. Not. R. Astron. Soc. 2019, 484, 3307–3324. [Google Scholar] [CrossRef]
- Burrows, A.; Radice, D.; Vartanyan, D.; Nagakura, H.; Skinner, M.A.; Dolence, J.C. The overarching framework of core-collapse supernova explosions as revealed by 3D FORNAX simulations. Mon. Not. R. Astron. Soc. 2020, 491, 2715–2735. [Google Scholar] [CrossRef]
- Bugli, M.; Guilet, J.; Obergaulinger, M. Three-dimensional core-collapse supernovae with complex magnetic structures—I. Explosion dynamics. Mon. Not. R. Astron. Soc. 2021, 507, 443–454. [Google Scholar] [CrossRef]
- Nakamura, K.; Takiwaki, T.; Kotake, K. Three-dimensional simulation of a core-collapse supernova for a binary star progenitor of SN 1987A. Mon. Not. R. Astron. Soc. 2022, 514, 3941–3952. [Google Scholar] [CrossRef]
- Sandoval, M.A.; Hix, W.R.; Messer, O.E.B.; Lentz, E.J.; Harris, J.A. Three-dimensional Core-collapse Supernova Simulations with 160 Isotopic Species Evolved to Shock Breakout. Astrophys. J. 2021, 921, 113. [Google Scholar] [CrossRef]
- Kippenhahn, R.; Weigert, A. Stellar Structure and Evolution; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Cameron, A.G.W. On the origin of the heavy elements. Astron. J. 1957, 62, 9–10. [Google Scholar] [CrossRef]
- Clayton, D.D. Principles of Stellar Evolution and Nucleosynthesis; The University of Chicago Press: Chicago, IL, USA, 1968. [Google Scholar]
- Woosley, S.E.; Weaver, T.A. The Evolution and Explosion of Massive Stars. II. Explosive Hydrodynamics and Nucleosynthesis. Astrophys. J. Suppl. Ser. 1995, 101, 181–235. [Google Scholar] [CrossRef]
- Nomoto, K.; Kobayashi, C.; Tominaga, N. Nucleosynthesis in Stars and the Chemical Enrichment of Galaxies. Annu. Rev. Astron. Astrophys. 2013, 51, 457–509. [Google Scholar] [CrossRef]
- Roberti, L.; Limongi, M.; Chieffi, A. Zero and extremely low metallicity rotating massive stars: Evolution, explosion, and nucleosynthesis up to the heaviest nuclei. arXiv 2023, arXiv:2312.02942. [Google Scholar] [CrossRef]
- Paxton, B.; Bildsten, L.; Timmes, F.; Dotter, A.; Herwig, F. The MESA code. Astrophys. J. Suppl. Ser. 2010, 192, 3. [Google Scholar] [CrossRef]
- Paxton, B.; Marchant, P.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Cantiello, M.; Dessart, L.; Farmer, R.; Hu, H.; Langer, N.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Binaries, Pulsations, and Explosions. Astrophys. J. Suppl. Ser. 2015, 220, 15. [Google Scholar] [CrossRef]
- Ritter, C.; Herwig, F.; Jones, S.; Pignatari, M.; Fryer, C.; Hirschi, R. NuGrid stellar data set—II. Stellar yields from H to Bi for stellar models with MZAMS = 1–25 M⊙ and Z = 0.0001–0.02. Mon. Not. R. Astron. Soc. 2018, 480, 538–571. [Google Scholar] [CrossRef]
- Langer, N. Presupernova Evolution of Massive Single and Binary Stars. Annu. Rev. Astron. Astrophys. 2012, 50, 107–164. [Google Scholar] [CrossRef]
- Smith, N. Mass Loss: Its Effect on the Evolution and Fate of High-Mass Stars. Annu. Rev. Astron. Astrophys. 2014, 52, 487–528. [Google Scholar] [CrossRef]
- Chandrasekhar, S. An Introduction to the Study of Stellar Structure; University of Chicago Press: Chicago, IL, USA, 1939. [Google Scholar]
- Böhm-Vitense, E. Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen. Z. Astrophys. 1958, 46, 108. [Google Scholar]
- Arnett, W.D.; Meakin, C.; Viallet, M.; Campbell, S.W.; Lattanzio, J.C.; Mocák, M. Beyond Mixing-length Theory: A Step toward 321D. Astrophys. J. 2015, 809, 30. [Google Scholar] [CrossRef]
- Joyce, M.; Tayar, J. A Review of the Mixing Length Theory of Convection in 1D Stellar Modeling. Galaxies 2023, 11, 75. [Google Scholar] [CrossRef]
- Meynet, G.; Maeder, A. Stellar evolution with rotation. I. The computational method and the inhibiting effect of the μ-gradient. Astron. Astrophys. 1997, 321, 465–476. [Google Scholar]
- Maeder, A.; Meynet, G. The Evolution of Rotating Stars. Annu. Rev. Astron. Astrophys. 2000, 38, 143–190. [Google Scholar] [CrossRef]
- Spruit, H.C. Dynamo action by differential rotation in a stably stratified stellar interior. Astron. Astrophys. 2002, 381, 923–932. [Google Scholar] [CrossRef]
- Imbriani, G.; Straniero, O.; Terrasi, F.; Limongi, M.; Chieffi, A. Influence of the 12C(a,g)16O reaction rate on the evolution of a 15 Msun star. Nucl. Phys. A 2001, 688, 249–253. [Google Scholar] [CrossRef]
- Chieffi, A.; Roberti, L.; Limongi, M.; La Cognata, M.; Lamia, L.; Palmerini, S.; Pizzone, R.G.; Spartà, R.; Tumino, A. Impact of the New Measurement of the 12C + 12C Fusion Cross Section on the Final Compactness of Massive Stars. Astrophys. J. 2021, 916, 79. [Google Scholar] [CrossRef]
- Laplace, E.; Justham, S.; Renzo, M.; Götberg, Y.; Farmer, R.; Vartanyan, D.; de Mink, S.E. Different to the core: The pre-supernova structures of massive single and binary-stripped stars. Astron. Astrophys. 2021, 656, A58. [Google Scholar] [CrossRef]
- Brinkman, H.E.; den Hartogh, J.W.; Doherty, C.L.; Pignatari, M.; Lugaro, M. 26Aluminum from Massive Binary Stars. II. Rotating Single Stars Up to Core Collapse and Their Impact on the Early Solar System. Astrophys. J. 2021, 923, 47. [Google Scholar] [CrossRef]
- Brinkman, H.E.; Doherty, C.; Pignatari, M.; Pols, O.; Lugaro, M. Aluminium-26 from Massive Binary Stars. III. Binary Stars up to Core Collapse and Their Impact on the Early Solar System. Astrophys. J. 2023, 951, 110. [Google Scholar] [CrossRef]
- Ercolino, A.; Jin, H.; Langer, N.; Dessart, L. Interacting supernovae from wide massive binary systems. arXiv 2023, arXiv:2308.01819. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Han, Z. Binary stars in the new millennium. Prog. Part. Nucl. Phys. 2024, 134, 104083. [Google Scholar] [CrossRef]
- Jones, S.; Hirschi, R.; Pignatari, M.; Heger, A.; Georgy, C.; Nishimura, N.; Fryer, C.; Herwig, F. Code dependencies of pre-supernova evolution and nucleosynthesis in massive stars: Evolution to the end of core helium burning. Mon. Not. R. Astron. Soc. 2015, 447, 3115–3129. [Google Scholar] [CrossRef]
- Bruenn, S.W.; Sieverding, A.; Lentz, E.J.; Sukhbold, T.; Hix, W.R.; Huk, L.N.; Harris, J.A.; Messer, O.E.B.; Mezzacappa, A. Comparison of the Core-collapse Evolution of Two Nearly Equal-mass Progenitors. Astrophys. J. 2023, 947, 35. [Google Scholar] [CrossRef]
- Farmer, R.; Fields, C.E.; Petermann, I.; Dessart, L.; Cantiello, M.; Paxton, B.; Timmes, F.X. On Variations Of Pre-supernova Model Properties. Astrophys. J. Suppl. Ser. 2016, 227, 22. [Google Scholar] [CrossRef]
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Rev. Mod. Phys. 1957, 29, 547–650. [Google Scholar] [CrossRef]
- Hoyle, F.; Fowler, W.A. Nucleosynthesis in Supernovae. Astrophys. J. 1960, 132, 565. [Google Scholar] [CrossRef]
- Colgate, S.A.; White, R.H. The Hydrodynamic Behavior of Supernovae Explosions. Astrophys. J. 1966, 143, 626. [Google Scholar] [CrossRef]
- Arnett, W.D. Gravitational collapse and weak interactions. Can. J. Phys. 1966, 44, 2553–2594. [Google Scholar] [CrossRef]
- Bethe, H.A.; Wilson, J.R. Revival of a stalled supernova shock by neutrino heating. Astrophys. J. 1985, 295, 14–23. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Swesty, D.F. A generalized equation of state for hot, dense matter. Nucl. Phys. A 1991, 535, 331–376. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]
- Shen, H.; Toki, H.; Oyamatsu, K.; Sumiyoshi, K. Relativistic equation of state of nuclear matter for supernova and neutron star. Nucl. Phys. A 1998, 637, 435–450. [Google Scholar] [CrossRef]
- Hempel, M.; Schaffner-Bielich, J. A statistical model for a complete supernova equation of state. Nucl. Phys. A 2010, 837, 210–254. [Google Scholar] [CrossRef]
- Steiner, A.W.; Hempel, M.; Fischer, T. Core-collapse Supernova Equations of State Based on Neutron Star Observations. Astrophys. J. 2013, 774, 17. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Avancini, S.S.; Carlson, B.V.; Delfino, A.; Menezes, D.P.; Providência, C.; Typel, S.; Stone, J.R. Relativistic mean-field hadronic models under nuclear matter constraints. Phys. Rev. C 2014, 90, 055203. [Google Scholar] [CrossRef]
- Schneider, A.S.; Roberts, L.F.; Ott, C.D. Open-source nuclear equation of state framework based on the liquid-drop model with Skyrme interaction. Phys. Rev. C 2017, 96, 065802. [Google Scholar] [CrossRef]
- Bruenn, S.W. Stellar core collapse—Numerical model and infall epoch. Astrophys. J. Suppl. Ser. 1985, 58, 771–841. [Google Scholar] [CrossRef]
- Mezzacappa, A.; Bruenn, S.W. Type II Supernovae and Boltzmann Neutrino Transport: The Infall Phase. Astrophys. J. 1993, 405, 637. [Google Scholar] [CrossRef]
- Mezzacappa, A.; Bruenn, S.W. A Numerical Method for Solving the Neutrino Boltzmann Equation Coupled to Spherically Symmetric Stellar Core Collapse. Astrophys. J. 1993, 405, 669. [Google Scholar] [CrossRef]
- Mezzacappa, A.; Bruenn, S.W. Stellar Core Collapse: A Boltzmann Treatment of Neutrino-Electron Scattering. Astrophys. J. 1993, 410, 740. [Google Scholar] [CrossRef]
- Thompson, T.A.; Burrows, A.; Horvath, J.E. μ and τ neutrino thermalization and production in supernovae: Processes and time scales. Phys. Rev. C 2000, 62, 035802. [Google Scholar] [CrossRef]
- Horowitz, C.J. Weak magnetism for antineutrinos in supernovae. Phys. Rev. D 2002, 65, 043001. [Google Scholar] [CrossRef]
- Burrows, A.; Reddy, S.; Thompson, T.A. Neutrino opacities in nuclear matter. Nucl. Phys. A 2006, 777, 356–394. [Google Scholar] [CrossRef]
- Herwig, F.; Blöcker, T. Overshoot in giant stars. arXiv 2000, arXiv:astro-ph/9909503. [Google Scholar]
- Mezzacappa, A.; Messer, O.E.B. Neutrino transport in core collapse supernovae. J. Comput. Appl. Math. 1999, 109, 281–319. [Google Scholar] [CrossRef]
- Liebendörfer, M.; Messer, O.E.B.; Mezzacappa, A.; Bruenn, S.W.; Cardall, C.Y.; Thielemann, F.K. A Finite Difference Representation of Neutrino Radiation Hydrodynamics in Spherically Symmetric General Relativistic Spacetime. Astrophys. J. Suppl. Ser. 2004, 150, 263–316. [Google Scholar] [CrossRef]
- Glas, R.; Just, O.; Janka, H.T.; Obergaulinger, M. Three-dimensional Core-collapse Supernova Simulations with Multidimensional Neutrino Transport Compared to the Ray-by-ray-plus Approximation. Astrophys. J. 2019, 873, 45. [Google Scholar] [CrossRef]
- Pan, K.C.; Mattes, C.; O’Connor, E.P.; Couch, S.M.; Perego, A.; Arcones, A. The impact of different neutrino transport methods on multidimensional core-collapse supernova simulations. J. Phys. G Nucl. Phys. 2019, 46, 014001. [Google Scholar] [CrossRef]
- Radice, D.; Ott, C.D.; Abdikamalov, E.; Couch, S.M.; Haas, R.; Schnetter, E. Neutrino-driven Convection in Core-collapse Supernovae: High-resolution Simulations. Astrophys. J. 2016, 820, 76. [Google Scholar] [CrossRef]
- Radice, D.; Abdikamalov, E.; Ott, C.D.; Mösta, P.; Couch, S.M.; Roberts, L.F. Turbulence in core-collapse supernovae. J. Phys. G Nucl. Phys. 2018, 45, 053003. [Google Scholar] [CrossRef]
- Branch, D.; Wheeler, J.C. Supernova Explosions; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Janka, H.T. Explosion Mechanisms of Core-Collapse Supernovae. Annu. Rev. Nucl. Part Sci. 2012, 62, 407–451. [Google Scholar] [CrossRef]
- O’Connor, E.; Bollig, R.; Burrows, A.; Couch, S.; Fischer, T.; Janka, H.T.; Kotake, K.; Lentz, E.J.; Liebendörfer, M.; Messer, O.E.B.; et al. Global comparison of core-collapse supernova simulations in spherical symmetry. J. Phys. G Nucl. Phys. 2018, 45, 104001. [Google Scholar] [CrossRef]
- Melson, T.; Janka, H.T.; Marek, A. Neutrino-driven Supernova of a Low-mass Iron-core Progenitor Boosted by Three-dimensional Turbulent Convection. Astrophys. J. 2015, 801, L24. [Google Scholar] [CrossRef]
- Fischer, T. QCD phase transition drives supernova explosion of a very massive star. arXiv 2021, arXiv:2108.00196. [Google Scholar] [CrossRef]
- Epstein, R.I. Lepton-driven convection in supernovae. Mon. Not. R. Astron. Soc. 1979, 188, 305–325. [Google Scholar] [CrossRef]
- Bruenn, S.W.; Buchler, J.R.; Livio, M. Rayleigh-Taylor convective overturn in stellar collapse. Astrophys. J. 1979, 234, L183–L186. [Google Scholar] [CrossRef]
- Wilson, J.R.; Mayle, R.W. Convection in core collapse supernovae. Phys. Rep. 1988, 163, 63–77. [Google Scholar] [CrossRef]
- Bruenn, S.W.; Dineva, T. The Role of Doubly Diffusive Instabilities in the Core-Collapse Supernova Mechanism. Astrophys. J. 1996, 458, L71. [Google Scholar] [CrossRef]
- Bruenn, S.W.; Raley, E.A.; Mezzacappa, A. Fluid Stability Below the Neutrinospheres of Supernova Progenitors and the Dominant Role of Lepto-Entropy Fingers. arXiv 2004, arXiv:astro-ph/0404099. [Google Scholar] [CrossRef]
- Mezzacappa, A.; Calder, A.C.; Bruenn, S.W.; Blondin, J.M.; Guidry, M.W.; Strayer, M.R.; Umar, A.S. The Interplay between Proto–Neutron Star Convection and Neutrino Transport in Core-Collapse Supernovae. Astrophys. J. 1998, 493, 848–862. [Google Scholar] [CrossRef]
- Roberts, L.F.; Shen, G.; Cirigliano, V.; Pons, J.A.; Reddy, S.; Woosley, S.E. Protoneutron Star Cooling with Convection: The Effect of the Symmetry Energy. Phys. Rev. Lett. 2012, 108, 061103. [Google Scholar] [CrossRef] [PubMed]
- Nagakura, H.; Burrows, A.; Radice, D.; Vartanyan, D. A systematic study of proto-neutron star convection in three-dimensional core-collapse supernova simulations. Mon. Not. R. Astron. Soc. 2020, 492, 5764–5779. [Google Scholar] [CrossRef]
- Pascal, A.; Novak, J.; Oertel, M. Proto-neutron star evolution with improved charged-current neutrino-nucleon interactions. Mon. Not. R. Astron. Soc. 2022, 511, 356–370. [Google Scholar] [CrossRef]
- Akaho, R.; Harada, A.; Nagakura, H.; Iwakami, W.; Okawa, H.; Furusawa, S.; Matsufuru, H.; Sumiyoshi, K.; Yamada, S. Protoneutron Star Convection Simulated with a New General Relativistic Boltzmann Neutrino Radiation Hydrodynamics Code. Astrophys. J. 2023, 944, 60. [Google Scholar] [CrossRef]
- Wilson, J.R.; Mathews, G.J.; Dalhed, H.E. On Rapidly Rotating Magnetic Core-Collapse Supernovae. Astrophys. J. 2005, 628, 335–342. [Google Scholar] [CrossRef]
- Mösta, P.; Richers, S.; Ott, C.D.; Haas, R.; Piro, A.L.; Boydstun, K.; Abdikamalov, E.; Reisswig, C.; Schnetter, E. Magnetorotational Core-collapse Supernovae in Three Dimensions. Astrophys. J. 2014, 785, L29. [Google Scholar] [CrossRef]
- Obergaulinger, M.; Aloy, M.Á. Magnetorotational core collapse of possible GRB progenitors—I. Explosion mechanisms. Mon. Not. R. Astron. Soc. 2020, 492, 4613–4634. [Google Scholar] [CrossRef]
- Soker, N. Applying the jet feedback mechanism to core-collapse supernova explosions. Mon. Not. R. Astron. Soc. 2010, 401, 2793–2798. [Google Scholar] [CrossRef]
- Blondin, J.M.; Mezzacappa, A.; DeMarino, C. Stability of Standing Accretion Shocks, with an Eye toward Core-Collapse Supernovae. Astrophys. J. 2003, 584, 971–980. [Google Scholar] [CrossRef]
- Foglizzo, T.; Scheck, L.; Janka, H.T. Neutrino-driven Convection versus Advection in Core-Collapse Supernovae. Astrophys. J. 2006, 652, 1436–1450. [Google Scholar] [CrossRef]
- Marek, A.; Janka, H.T. Delayed Neutrino-Driven Supernova Explosions Aided by the Standing Accretion-Shock Instability. Astrophys. J. 2009, 694, 664–696. [Google Scholar] [CrossRef]
- Murphy, J.W.; Dolence, J.C.; Burrows, A. The Dominance of Neutrino-driven Convection in Core-collapse Supernovae. Astrophys. J. 2013, 771, 52. [Google Scholar] [CrossRef]
- Couch, S.M.; Ott, C.D. The Role of Turbulence in Neutrino-driven Core-collapse Supernova Explosions. Astrophys. J. 2015, 799, 5. [Google Scholar] [CrossRef]
- Müller, B. Hydrodynamics of core-collapse supernovae and their progenitors. Living Rev. Comput. Astrophys. 2020, 6, 3. [Google Scholar] [CrossRef]
- Nagakura, H.; Yamamoto, Y.; Yamada, S. A Semi-dynamical Approach to the Shock Revival in Core-collapse Supernovae. Astrophys. J. 2013, 765, 123. [Google Scholar] [CrossRef]
- Couch, S.M.; Chatzopoulos, E.; Arnett, W.D.; Timmes, F.X. The Three-dimensional Evolution to Core Collapse of a Massive Star. Astrophys. J. 2015, 808, L21. [Google Scholar] [CrossRef]
- Müller, B.; Viallet, M.; Heger, A.; Janka, H.T. The Last Minutes of Oxygen Shell Burning in a Massive Star. Astrophys. J. 2016, 833, 124. [Google Scholar] [CrossRef]
- Nagakura, H.; Takahashi, K.; Yamamoto, Y. On the importance of progenitor asymmetry to shock revival in core-collapse supernovae. Mon. Not. R. Astron. Soc. 2019, 483, 208–222. [Google Scholar] [CrossRef]
- Fields, C.E.; Couch, S.M. Three-dimensional Hydrodynamic Simulations of Convective Nuclear Burning in Massive Stars Near Iron Core Collapse. Astrophys. J. 2021, 921, 28. [Google Scholar] [CrossRef]
- O’Connor, E.; Ott, C.D. Black Hole Formation in Failing Core-Collapse Supernovae. Astrophys. J. 2011, 730, 70. [Google Scholar] [CrossRef]
- Hempel, M.; Fischer, T.; Schaffner-Bielich, J.; Liebendörfer, M. New Equations of State in Simulations of Core-collapse Supernovae. Astrophys. J. 2012, 748, 70. [Google Scholar] [CrossRef]
- Couch, S.M. The Dependence of the Neutrino Mechanism of Core-collapse Supernovae on the Equation of State. Astrophys. J. 2013, 765, 29. [Google Scholar] [CrossRef]
- Suwa, Y.; Takiwaki, T.; Kotake, K.; Fischer, T.; Liebendörfer, M.; Sato, K. On the Importance of the Equation of State for the Neutrino-driven Supernova Explosion Mechanism. Astrophys. J. 2013, 764, 99. [Google Scholar] [CrossRef]
- Fischer, T.; Hempel, M.; Sagert, I.; Suwa, Y.; Schaffner-Bielich, J. Symmetry energy impact in simulations of core-collapse supernovae. Eur. Phys. J. A 2014, 50, 46. [Google Scholar] [CrossRef]
- Char, P.; Banik, S.; Bandyopadhyay, D. A Comparative Study of Hyperon Equations of State in Supernova Simulations. Astrophys. J. 2015, 809, 116. [Google Scholar] [CrossRef]
- Olson, J.P.; Warren, M.; Meixner, M.; Mathews, G.J.; Lan, N.Q.; Dalhed, H.E. Generalized density functional equation of state for astrophysical simulations with 3-body forces and quark gluon plasma. arXiv 2016, arXiv:1612.08992. [Google Scholar]
- Furusawa, S.; Togashi, H.; Nagakura, H.; Sumiyoshi, K.; Yamada, S.; Suzuki, H.; Takano, M. A new equation of state for core-collapse supernovae based on realistic nuclear forces and including a full nuclear ensemble. J. Phys. G Nucl. Phys. 2017, 44, 094001. [Google Scholar] [CrossRef]
- Richers, S.; Ott, C.D.; Abdikamalov, E.; O’Connor, E.; Sullivan, C. Equation of state effects on gravitational waves from rotating core collapse. Phys. Rev. D 2017, 95, 063019. [Google Scholar] [CrossRef]
- Nagakura, H.; Iwakami, W.; Furusawa, S.; Okawa, H.; Harada, A.; Sumiyoshi, K.; Yamada, S.; Matsufuru, H.; Imakura, A. Simulations of Core-collapse Supernovae in Spatial Axisymmetry with Full Boltzmann Neutrino Transport. Astrophys. J. 2018, 854, 136. [Google Scholar] [CrossRef]
- Morozova, V.; Radice, D.; Burrows, A.; Vartanyan, D. The Gravitational Wave Signal from Core-collapse Supernovae. Astrophys. J. 2018, 861, 10. [Google Scholar] [CrossRef]
- Burrows, A.; Vartanyan, D.; Dolence, J.C.; Skinner, M.A.; Radice, D. Crucial Physical Dependencies of the Core-Collapse Supernova Mechanism. Space Sci. Rev. 2018, 214, 33. [Google Scholar] [CrossRef]
- Schneider, A.S.; Roberts, L.F.; Ott, C.D.; O’Connor, E. Equation of state effects in the core collapse of a 20 -M⊙ star. Phys. Rev. C 2019, 100, 055802. [Google Scholar] [CrossRef]
- Harada, A.; Nagakura, H.; Iwakami, W.; Okawa, H.; Furusawa, S.; Sumiyoshi, K.; Matsufuru, H.; Yamada, S. The Boltzmann-radiation-hydrodynamics Simulations of Core-collapse Supernovae with Different Equations of State: The Role of Nuclear Composition and the Behavior of Neutrinos. Astrophys. J. 2020, 902, 150. [Google Scholar] [CrossRef]
- Yasin, H.; Schäfer, S.; Arcones, A.; Schwenk, A. Equation of State Effects in Core-Collapse Supernovae. Phys. Rev. Lett. 2020, 124, 092701. [Google Scholar] [CrossRef]
- Boccioli, L.; Mathews, G.J.; Suh, I.S.; O’Connor, E.P. Effect of the Nuclear Equation of State on Relativistic Turbulence-induced Core-collapse Supernovae. Astrophys. J. 2022, 926, 147. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Typel, S.; Röpke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Shen, H.; Toki, H.; Oyamatsu, K.; Sumiyoshi, K. Relativistic Equation of State for Core-collapse Supernova Simulations. Astrophys. J. Suppl. Ser. 2011, 197, 20. [Google Scholar] [CrossRef]
- Togashi, H.; Nakazato, K.; Takehara, Y.; Yamamuro, S.; Suzuki, H.; Takano, M. Nuclear equation of state for core-collapse supernova simulations with realistic nuclear forces. Nucl. Phys. A 2017, 961, 78–105. [Google Scholar] [CrossRef]
- Schneider, A.S.; Constantinou, C.; Muccioli, B.; Prakash, M. Akmal-Pandharipande-Ravenhall equation of state for simulations of supernovae, neutron stars, and binary mergers. Phys. Rev. C 2019, 100, 025803. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. 2019, 887, L24. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. arXiv 2021, arXiv:2105.06979. [Google Scholar] [CrossRef]
- Sukhbold, T.; Ertl, T.; Woosley, S.E.; Brown, J.M.; Janka, H.T. Core-collapse Supernovae from 9 to 120 Solar Masses Based on Neutrino-powered Explosions. Astrophys. J. 2016, 821, 38. [Google Scholar] [CrossRef]
- Hannestad, S.; Raffelt, G. Supernova Neutrino Opacity from Nucleon-Nucleon Bremsstrahlung and Related Processes. Astrophys. J. 1998, 507, 339–352. [Google Scholar] [CrossRef]
- Buras, R.; Janka, H.T.; Keil, M.T.; Raffelt, G.G.; Rampp, M. Electron Neutrino Pair Annihilation: A New Source for Muon and Tau Neutrinos in Supernovae. Astrophys. J. 2003, 587, 320–326. [Google Scholar] [CrossRef]
- Bollig, R.; Janka, H.T.; Lohs, A.; Martínez-Pinedo, G.; Horowitz, C.J.; Melson, T. Muon Creation in Supernova Matter Facilitates Neutrino-Driven Explosions. Phys. Rev. Lett. 2017, 119, 242702. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Caballero, O.L.; Lin, Z.; O’Connor, E.; Schwenk, A. Neutrino-nucleon scattering in supernova matter from the virial expansion. Phys. Rev. C 2017, 95, 025801. [Google Scholar] [CrossRef]
- Müller, B.; Janka, H.T.; Dimmelmeier, H. A New Multi-dimensional General Relativistic Neutrino Hydrodynamic Code for Core-collapse Supernovae. I. Method and Code Tests in Spherical Symmetry. Astrophys. J. Suppl. Ser. 2010, 189, 104–133. [Google Scholar] [CrossRef]
- Shibata, M.; Kiuchi, K.; Sekiguchi, Y.; Suwa, Y. Truncated Moment Formalism for Radiation Hydrodynamics in Numerical Relativity. Prog. Theor. Phys. 2011, 125, 1255–1287. [Google Scholar] [CrossRef]
- Cardall, C.Y.; Endeve, E.; Mezzacappa, A. Conservative 3+1 general relativistic variable Eddington tensor radiation transport equations. Phys. Rev. D 2013, 87, 103004. [Google Scholar] [CrossRef]
- O’Connor, E. An Open-source Neutrino Radiation Hydrodynamics Code for Core-collapse Supernovae. Astrophys. J. Suppl. Ser. 2015, 219, 24. [Google Scholar] [CrossRef]
- Kuroda, T.; Takiwaki, T.; Kotake, K. A New Multi-energy Neutrino Radiation-Hydrodynamics Code in Full General Relativity and Its Application to the Gravitational Collapse of Massive Stars. Astrophys. J. Suppl. Ser. 2016, 222, 20. [Google Scholar] [CrossRef]
- Nagakura, H.; Iwakami, W.; Furusawa, S.; Sumiyoshi, K.; Yamada, S.; Matsufuru, H.; Imakura, A. Three-dimensional Boltzmann-Hydro Code for Core-collapse in Massive Stars. II. The Implementation of Moving-mesh for Neutron Star Kicks. Astrophys. J. Suppl. Ser. 2017, 229, 42. [Google Scholar] [CrossRef]
- Duan, H.; Fuller, G.M.; Qian, Y.Z. Collective Neutrino Oscillations. Annu. Rev. Nucl. Part. Sci. 2010, 60, 569–594. [Google Scholar] [CrossRef]
- Mirizzi, A.; Tamborra, I.; Janka, H.T.; Saviano, N.; Scholberg, K.; Bollig, R.; Hüdepohl, L.; Chakraborty, S. Supernova neutrinos: Production, oscillations and detection. Nuovo Cimento Riv. Ser. 2016, 39, 1–112. [Google Scholar] [CrossRef]
- Tamborra, I.; Shalgar, S. New Developments in Flavor Evolution of a Dense Neutrino Gas. Annu. Rev. Nucl. Part Sci. 2021, 71, 165–188. [Google Scholar] [CrossRef]
- Marek, A.; Dimmelmeier, H.; Janka, H.T.; Müller, E.; Buras, R. Exploring the relativistic regime with Newtonian hydrodynamics: An improved effective gravitational potential for supernova simulations. Astron. Astrophys. 2006, 445, 273–289. [Google Scholar] [CrossRef]
- Fryxell, B.; Olson, K.; Ricker, P.; Timmes, F.X.; Zingale, M.; Lamb, D.Q.; MacNeice, P.; Rosner, R.; Truran, J.W.; Tufo, H. FLASH: An Adaptive Mesh Hydrodynamics Code for Modeling Astrophysical Thermonuclear Flashes. Astrophys. J. Suppl. Ser. 2000, 131, 273. [Google Scholar] [CrossRef]
- Dubey, A.; Weide, K.; O’Neal, J.; Dhruv, A.; Couch, S.; Harris, J.A.; Klosterman, T.; Jain, R.; Rudi, J.; Messer, B.; et al. Flash-X: A multiphysics simulation software instrument. SoftwareX 2022, 19, 101168. [Google Scholar] [CrossRef]
- Liebendörfer, M.; Whitehouse, S.C.; Fischer, T. The Isotropic Diffusion Source Approximation for Supernova Neutrino Transport. Astrophys. J. 2009, 698, 1174–1190. [Google Scholar] [CrossRef]
- Matsumoto, J.; Takiwaki, T.; Kotake, K.; Asahina, Y.; Takahashi, H.R. 2D numerical study for magnetic field dependence of neutrino-driven core-collapse supernova models. Mon. Not. R. Astron. Soc. 2020, 499, 4174–4194. [Google Scholar] [CrossRef]
- Kotake, K.; Takiwaki, T.; Fischer, T.; Nakamura, K.; Martínez-Pinedo, G. Impact of Neutrino Opacities on Core-collapse Supernova Simulations. Astrophys. J. 2018, 853, 170. [Google Scholar] [CrossRef]
- Rampp, M.; Janka, H.T. Radiation hydrodynamics with neutrinos. Variable Eddington factor method for core-collapse supernova simulations. Astron. Astrophys. 2002, 396, 361–392. [Google Scholar] [CrossRef]
- Buras, R.; Rampp, M.; Janka, H.T.; Kifonidis, K. Two-dimensional hydrodynamic core-collapse supernova simulations with spectral neutrino transport. I. Numerical method and results for a 15 M star. Astron. Astrophys. 2006, 447, 1049–1092. [Google Scholar] [CrossRef]
- Bruenn, S.W.; Blondin, J.M.; Hix, W.R.; Lentz, E.J.; Messer, O.E.B.; Mezzacappa, A.; Endeve, E.; Harris, J.A.; Marronetti, P.; Budiardja, R.D.; et al. CHIMERA: A Massively Parallel Code for Core-collapse Supernova Simulations. Astrophys. J. Suppl. Ser. 2020, 248, 11. [Google Scholar] [CrossRef]
- Hix, W.R.; Lentz, E.J.; Bruenn, S.W.; Mezzacappa, A.; Messer, O.E.B.; Endeve, E.; Blondin, J.M.; Harris, J.A.; Marronetti, P.; Yakunin, K.N. The Multi-dimensional Character of Core-collapse Supernovae. Acta Phys. Pol. B 2016, 47, 645. [Google Scholar] [CrossRef]
- Müller, B.; Janka, H.T. Non-radial instabilities and progenitor asphericities in core-collapse supernovae. Mon. Not. R. Astron. Soc. 2015, 448, 2141–2174. [Google Scholar] [CrossRef]
- Müller, B.; Varma, V. A 3D simulation of a neutrino-driven supernova explosion aided by convection and magnetic fields. Mon. Not. R. Astron. Soc. 2020, 498, L109–L113. [Google Scholar] [CrossRef]
- Just, O.; Obergaulinger, M.; Janka, H.T. A new multidimensional, energy-dependent two-moment transport code for neutrino-hydrodynamics. Mon. Not. R. Astron. Soc. 2015, 453, 3386–3413. [Google Scholar] [CrossRef]
- Navó, G.; Reichert, M.; Obergaulinger, M.; Arcones, A. Core-collapse supernovae simulations with reduced nucleosynthesis networks. arXiv 2022, arXiv:2210.11848. [Google Scholar]
- Cabezón, R.M.; García-Senz, D.; Figueira, J. SPHYNX: An accurate density-based SPH method for astrophysical applications. Astron. Astrophys. 2017, 606, A78. [Google Scholar] [CrossRef]
- Perego, A.; Cabezón, R.M.; Käppeli, R. An Advanced Leakage Scheme for Neutrino Treatment in Astrophysical Simulations. Astrophys. J. Suppl. Ser. 2016, 223, 22. [Google Scholar] [CrossRef]
- Shibata, M.; Nakamura, T. Evolution of three-dimensional gravitational waves: Harmonic slicing case. Phys. Rev. D 1995, 52, 5428–5444. [Google Scholar] [CrossRef] [PubMed]
- Baumgarte, T.W.; Shapiro, S.L. Numerical integration of Einstein’s field equations. Phys. Rev. D 1998, 59, 024007. [Google Scholar] [CrossRef]
- Cabezón, R.M.; Pan, K.C.; Liebendörfer, M.; Kuroda, T.; Ebinger, K.; Heinimann, O.; Perego, A.; Thielemann, F.K. Core-collapse supernovae in the hall of mirrors. A three-dimensional code-comparison project. Astron. Astrophys. 2018, 619, A118. [Google Scholar] [CrossRef]
- Wang, T.; Vartanyan, D.; Burrows, A.; Coleman, M.S.B. The essential character of the neutrino mechanism of core-collapse supernova explosions. Mon. Not. R. Astron. Soc. 2022, 517, 543–559. [Google Scholar] [CrossRef]
- Vartanyan, D.; Burrows, A. Neutrino signatures of 100 2D Axisymmetric Core-Collapse Supernova Simulations. Mon. Not. R. Astron. Soc. 2023, 526, 5900–5910. [Google Scholar] [CrossRef]
- Blinnikov, S.I.; Bartunov, O.S. Non-equilibrium radiative transfer in supernova theory: Models of linear type II supernovae. Astron. Astrophys. 1993, 273, 106–122. [Google Scholar]
- Ugliano, M.; Janka, H.T.; Marek, A.; Arcones, A. Progenitor-explosion Connection and Remnant Birth Masses for Neutrino-driven Supernovae of Iron-core Progenitors. Astrophys. J. 2012, 757, 69. [Google Scholar] [CrossRef]
- Perego, A.; Hempel, M.; Fröhlich, C.; Ebinger, K.; Eichler, M.; Casanova, J.; Liebendörfer, M.; Thielemann, F.K. PUSHing Core-collapse Supernovae to Explosions in Spherical Symmetry I: The Model and the Case of SN 1987A. Astrophys. J. 2015, 806, 275. [Google Scholar] [CrossRef]
- Ertl, T.; Janka, H.T.; Woosley, S.E.; Sukhbold, T.; Ugliano, M. A Two-parameter Criterion for Classifying the Explodability of Massive Stars by the Neutrino-driven Mechanism. Astrophys. J. 2016, 818, 124. [Google Scholar] [CrossRef]
- Mabanta, Q.A.; Murphy, J.W. How Turbulence Enables Core-collapse Supernova Explosions. Astrophys. J. 2018, 856, 22. [Google Scholar] [CrossRef]
- Couch, S.M.; Warren, M.L.; O’Connor, E.P. Simulating Turbulence-aided Neutrino-driven Core-collapse Supernova Explosions in One Dimension. Astrophys. J. 2020, 890, 127. [Google Scholar] [CrossRef]
- Fryer, C.L.; Olejak, A.; Belczynski, K. The Effect of Supernova Convection On Neutron Star and Black Hole Masses. Astrophys. J. 2022, 931, 94. [Google Scholar] [CrossRef]
- Sasaki, S.; Takiwaki, T. On the treatment of phenomenological turbulent effects in one-dimensional simulations of core-collapse supernovae. Mon. Not. R. Astron. Soc. 2024, 528, 1158–1170. [Google Scholar] [CrossRef]
- Janka, H.T. Conditions for shock revival by neutrino heating in core-collapse supernovae. Astron. Astrophys. 2001, 368, 527–560. [Google Scholar] [CrossRef]
- Fryer, C.L.; Belczynski, K.; Wiktorowicz, G.; Dominik, M.; Kalogera, V.; Holz, D.E. Compact Remnant Mass Function: Dependence on the Explosion Mechanism and Metallicity. Astrophys. J. 2012, 749, 91. [Google Scholar] [CrossRef]
- Pejcha, O.; Thompson, T.A. The Physics of the Neutrino Mechanism of Core-collapse Supernovae. Astrophys. J. 2012, 746, 106. [Google Scholar] [CrossRef]
- Müller, B.; Heger, A.; Liptai, D.; Cameron, J.B. A simple approach to the supernova progenitor-explosion connection. Mon. Not. R. Astron. Soc. 2016, 460, 742–764. [Google Scholar] [CrossRef]
- Summa, A.; Hanke, F.; Janka, H.T.; Melson, T.; Marek, A.; Müller, B. Progenitor-dependent Explosion Dynamics in Self-consistent, Axisymmetric Simulations of Neutrino-driven Core-collapse Supernovae. Astrophys. J. 2016, 825, 6. [Google Scholar] [CrossRef]
- Burrows, A.; Goshy, J. A Theory of Supernova Explosions. Astrophys. J. 1993, 416, L75. [Google Scholar] [CrossRef]
- Thompson, C. Accretional Heating of Asymmetric Supernova Cores. Astrophys. J. 2000, 534, 915–933. [Google Scholar] [CrossRef]
- Fernández, R. Hydrodynamics of Core-collapse Supernovae at the Transition to Explosion. I. Spherical Symmetry. Astrophys. J. 2012, 749, 142. [Google Scholar] [CrossRef]
- Murphy, J.W.; Dolence, J.C. An Integral Condition for Core-collapse Supernova Explosions. Astrophys. J. 2017, 834, 183. [Google Scholar] [CrossRef]
- Murphy, J.W.; Burrows, A. Criteria for Core-Collapse Supernova Explosions by the Neutrino Mechanism. Astrophys. J. 2008, 688, 1159–1175. [Google Scholar] [CrossRef]
- Hanke, F.; Marek, A.; Müller, B.; Janka, H.T. Is Strong SASI Activity the Key to Successful Neutrino-driven Supernova Explosions? Astrophys. J. 2012, 755, 138. [Google Scholar] [CrossRef]
- Fernández, R. Three-dimensional simulations of SASI- and convection-dominated core-collapse supernovae. Mon. Not. R. Astron. Soc. 2015, 452, 2071–2086. [Google Scholar] [CrossRef]
- Gogilashvili, M.; Murphy, J.W. A force explosion condition for spherically symmetric core-collapse supernovae. Mon. Not. R. Astron. Soc. 2022, 515, 1610–1623. [Google Scholar] [CrossRef]
- Gogilashvili, M.; Murphy, J.W.; Miller, J.M. Including Neutrino-driven Convection into the Force Explosion Condition to Predict Explodability of Multi-dimensional Core-collapse Supernovae (FEC+). arXiv 2023, arXiv:2311.02179. [Google Scholar] [CrossRef]
- Boccioli, L.; Roberti, L.; Limongi, M.; Mathews, G.J.; Chieffi, A. Explosion Mechanism of Core-collapse Supernovae: Role of the Si/Si-O Interface. Astrophys. J. 2023, 949, 17. [Google Scholar] [CrossRef]
- Sonneborn, G.; Altner, B.; Kirshner, R.P. The Progenitor of SN 1987A: Spatially Resolved Ultraviolet Spectroscopy of the Supernova Field. Astrophys. J. 1987, 323, L35. [Google Scholar] [CrossRef]
- Bionta, R.M.; Blewitt, G.; Bratton, C.B.; Casper, D.; Ciocio, A.; Claus, R.; Cortez, B.; Crouch, M.; Dye, S.T.; Errede, S.; et al. Observation of a neutrino burst in coincidence with supernova 1987A in the Large Magellanic Cloud. Phys. Rev. Lett. 1987, 58, 1494–1496. [Google Scholar] [CrossRef]
- Hirata, K.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. Observation of a neutrino burst from the supernova SN1987A. Phys. Rev. Lett. 1987, 58, 1490–1493. [Google Scholar] [CrossRef]
- Tsang, B.T.H.; Vartanyan, D.; Burrows, A. Applications of Machine Learning to Predicting Core-collapse Supernova Explosion Outcomes. Astrophys. J. 2022, 937, L15. [Google Scholar] [CrossRef]
- Vartanyan, D.; Laplace, E.; Renzo, M.; Götberg, Y.; Burrows, A.; de Mink, S.E. Binary-stripped Stars as Core-collapse Supernovae Progenitors. Astrophys. J. 2021, 916, L5. [Google Scholar] [CrossRef]
- Chieffi, A.; Limongi, M. The Presupernova Core Mass-Radius Relation of Massive Stars: Understanding Its Formation and Evolution. Astrophys. J. 2020, 890, 43. [Google Scholar] [CrossRef]
- Rauscher, T.; Heger, A.; Hoffman, R.D.; Woosley, S.E. Nucleosynthesis in Massive Stars with Improved Nuclear and Stellar Physics. Astrophys. J. 2002, 576, 323–348. [Google Scholar] [CrossRef]
- Sieverding, A.; Martínez-Pinedo, G.; Huther, L.; Langanke, K.; Heger, A. The ν-Process in the Light of an Improved Understanding of Supernova Neutrino Spectra. Astrophys. J. 2018, 865, 143. [Google Scholar] [CrossRef]
- Curtis, S.; Ebinger, K.; Fröhlich, C.; Hempel, M.; Perego, A.; Liebendörfer, M.; Thielemann, F.K. PUSHing Core-collapse Supernovae to Explosions in Spherical Symmetry. III. Nucleosynthesis Yields. Astrophys. J. 2018, 870, 2. [Google Scholar] [CrossRef]
- Chevalier, R.A. Neutron star accretion in a supernova. Astrophys. J. 1989, 346, 847–859. [Google Scholar] [CrossRef]
- Pignatari, M.; Göbel, K.; Reifarth, R.; Travaglio, C. The production of proton-rich isotopes beyond iron: The γ-process in stars. Int. J. Mod. Phys. E 2016, 25, 1630003. [Google Scholar] [CrossRef]
- Bethe, H.A. Supernova mechanisms. Rev. Mod. Phys. 1990, 62, 801–866. [Google Scholar] [CrossRef]
- Limongi, M.; Chieffi, A. Evolution, Explosion, and Nucleosynthesis of Core-Collapse Supernovae. Astrophys. J. 2003, 592, 404–433. [Google Scholar] [CrossRef]
- Pignatari, M.; Hoppe, P.; Trappitsch, R.; Fryer, C.; Timmes, F.; Herwig, F.; Hirschi, R. The neutron capture process in the He shell in core-collapse supernovae: Presolar silicon carbide grains as a diagnostic tool for nuclear astrophysics. Geochim. Cosmochim. Acta 2018, 221, 37–46. [Google Scholar] [CrossRef]
- Limongi, M.; Chieffi, A. Hydrodynamical Modeling of the Light Curves of Core-collapse Supernovae with HYPERION. I. The Mass Range 13–25 M⊙, the Metallicities −3 ≤ [Fe/H] ≤ 0, and the Case of SN 1999em. Astrophys. J. 2020, 902, 95. [Google Scholar] [CrossRef]
- Arcones, A.; Thielemann, F.K. Neutrino-driven wind simulations and nucleosynthesis of heavy elements. J. Phys. G Nucl. Phys. 2013, 40, 013201. [Google Scholar] [CrossRef]
- Woosley, S.E.; Hoffman, R.D. The alpha-process and the r-process. Astrophys. J. 1992, 395, 202–239. [Google Scholar] [CrossRef]
- Psaltis, A.; Arcones, A.; Montes, F.; Mohr, P.; Hansen, C.J.; Jacobi, M.; Schatz, H. Constraining Nucleosynthesis in Neutrino-driven Winds: Observations, Simulations, and Nuclear Physics. Astrophys. J. 2022, 935, 27. [Google Scholar] [CrossRef]
- Wang, T.; Burrows, A. Neutrino-driven Winds in Three-dimensional Core-collapse Supernova Simulations. Astrophys. J. 2023, 954, 114. [Google Scholar] [CrossRef]
- Fröhlich, C.; Hix, W.R.; Martínez-Pinedo, G.; Liebendörfer, M.; Thielemann, F.K.; Bravo, E.; Langanke, K.; Zinner, N.T. Nucleosynthesis in neutrino-driven supernovae. New Astron. Rev. 2006, 50, 496–499. [Google Scholar] [CrossRef]
- Wanajo, S. The rp-Process in Neutrino-driven Winds. Astrophys. J. 2006, 647, 1323–1340. [Google Scholar] [CrossRef]
- Nishimura, N.; Rauscher, T.; Hirschi, R.; Cescutti, G.; Murphy, A.S.J.; Fröhlich, C. Uncertainties in νp-process nucleosynthesis from Monte Carlo variation of reaction rates. Mon. Not. R. Astron. Soc. 2019, 489, 1379–1396. [Google Scholar] [CrossRef]
- Woosley, S.E.; Howard, W.M. The p-process in supernovae. Astrophys. J. Suppl. Ser. 1978, 36, 285–304. [Google Scholar] [CrossRef]
- Prantzos, N.; Hashimoto, M.; Rayet, M.; Arnould, M. The p-process in SN 1987A. Astron. Astrophys. 1990, 238, 455–461. [Google Scholar]
- Rayet, M.; Arnould, M.; Hashimoto, M.; Prantzos, N.; Nomoto, K. The p-process in Type II supernovae. Astron. Astrophys. 1995, 298, 517. [Google Scholar]
- Arnould, M.; Goriely, S. The p-process of stellar nucleosynthesis: Astrophysics and nuclear physics status. Phys. Rep. 2003, 384, 1–84. [Google Scholar] [CrossRef]
- Pignatari, M.; Herwig, F.; Hirschi, R.; Bennett, M.; Rockefeller, G.; Fryer, C.; Timmes, F.X.; Ritter, C.; Heger, A.; Jones, S.; et al. NuGrid Stellar Data Set. I.Stellar Yields from H to Bi for Stars with Metallicities Z = 0.02 and Z = 0.01. Astrophys. J. Suppl. Ser. 2016, 225, 24. [Google Scholar] [CrossRef]
- Roberti, L.; Pignatari, M.; Psaltis, A.; Sieverding, A.; Mohr, P.; Fülöp, Z.; Lugaro, M. The cess nucleosynthesis in core-collapse supernovae—I. A novel analysis of cess yields in massive stars. Astron. Astrophys. 2023, 677, A22. [Google Scholar] [CrossRef]
- Travaglio, C.; Rauscher, T.; Heger, A.; Pignatari, M.; West, C. Role of Core-collapse Supernovae in Explaining Solar System Abundances of p Nuclides. Astrophys. J. 2018, 854, 18. [Google Scholar] [CrossRef]
- Rauscher, T.; Dauphas, N.; Dillmann, I.; Fröhlich, C.; Fülöp, Z.; Gyürky, G. Constraining the astrophysical origin of the p-nuclei through nuclear physics and meteoritic data. Rep. Prog. Phys. 2013, 76, 066201. [Google Scholar] [CrossRef]
- Kobayashi, C.; Karakas, A.I.; Lugaro, M. The Origin of Elements from Carbon to Uranium. Astrophys. J. 2020, 900, 179. [Google Scholar] [CrossRef]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef]
- Pignatari, M.; Hirschi, R.; Wiescher, M.; Gallino, R.; Bennett, M.; Beard, M.; Fryer, C.; Herwig, F.; Rockefeller, G.; Timmes, F.X. The 12C + 12C Reaction and the Impact on Nucleosynthesis in Massive Stars. Astrophys. J. 2013, 762, 31. [Google Scholar] [CrossRef]
- Cumming, J.B.; Alburger, D.E. Search for the decay of 180Tam. Phys. Rev. C 1985, 31, 1494–1498. [Google Scholar] [CrossRef] [PubMed]
- Arlandini, C.; Käppeler, F.; Wisshak, K.; Gallino, R.; Lugaro, M.; Busso, M.; Straniero, O. Neutron Capture in Low-Mass Asymptotic Giant Branch Stars: Cross Sections and Abundance Signatures. Astrophys. J. 1999, 525, 886–900. [Google Scholar] [CrossRef]
- Goriely, S.; Siess, L. Nucleosynthesis of s-elements in zero-metal AGB stars. Astron. Astrophys. 2001, 378, L25–L28. [Google Scholar] [CrossRef]
- Dillmann, I.; Käppeler, F.; Rauscher, T.; Thielemann, F.K.; Gallino, R.; Bisterzo, S. Are there only 30 p nuclides. In Proceedings of the Nuclei in the Cosmos (NIC X), Mackinac Island, MI, USA, 27 July–1 August 2008; p. 91. [Google Scholar]
- Bisterzo, S.; Gallino, R.; Straniero, O.; Cristallo, S.; Käppeler, F. The s-process in low-metallicity stars—II. Interpretation of high-resolution spectroscopic observations with asymptotic giant branch models. Mon. Not. R. Astron. Soc. 2011, 418, 284–319. [Google Scholar] [CrossRef]
- Bisterzo, S.; Gallino, R.; Käppeler, F.; Wiescher, M.; Imbriani, G.; Straniero, O.; Cristallo, S.; Görres, J.; deBoer, R.J. The branchings of the main s-process: Their sensitivity to a-induced reactions on 13C and 22Ne and to the uncertainties of the nuclear network. Mon. Not. R. Astron. Soc. 2015, 449, 506–527. [Google Scholar] [CrossRef]
- Tinsley, B.M. Evolution of the Stars and Gas in Galaxies. Fundam. Cosm. Phys. 1980, 5, 287–388. [Google Scholar] [CrossRef]
- Fragos, T.; Andrews, J.J.; Bavera, S.S.; Berry, C.P.L.; Coughlin, S.; Dotter, A.; Giri, P.; Kalogera, V.; Katsaggelos, A.; Kovlakas, K.; et al. POSYDON: A General-purpose Population Synthesis Code with Detailed Binary-evolution Simulations. Astrophys. J. Suppl. Ser. 2023, 264, 45. [Google Scholar] [CrossRef]
- Sieverding, A.; Kresse, D.; Janka, H.T. Production of 44Ti and Iron-group Nuclei in the Ejecta of 3D Neutrino-driven Supernovae. Astrophys. J. 2023, 957, L25. [Google Scholar] [CrossRef]
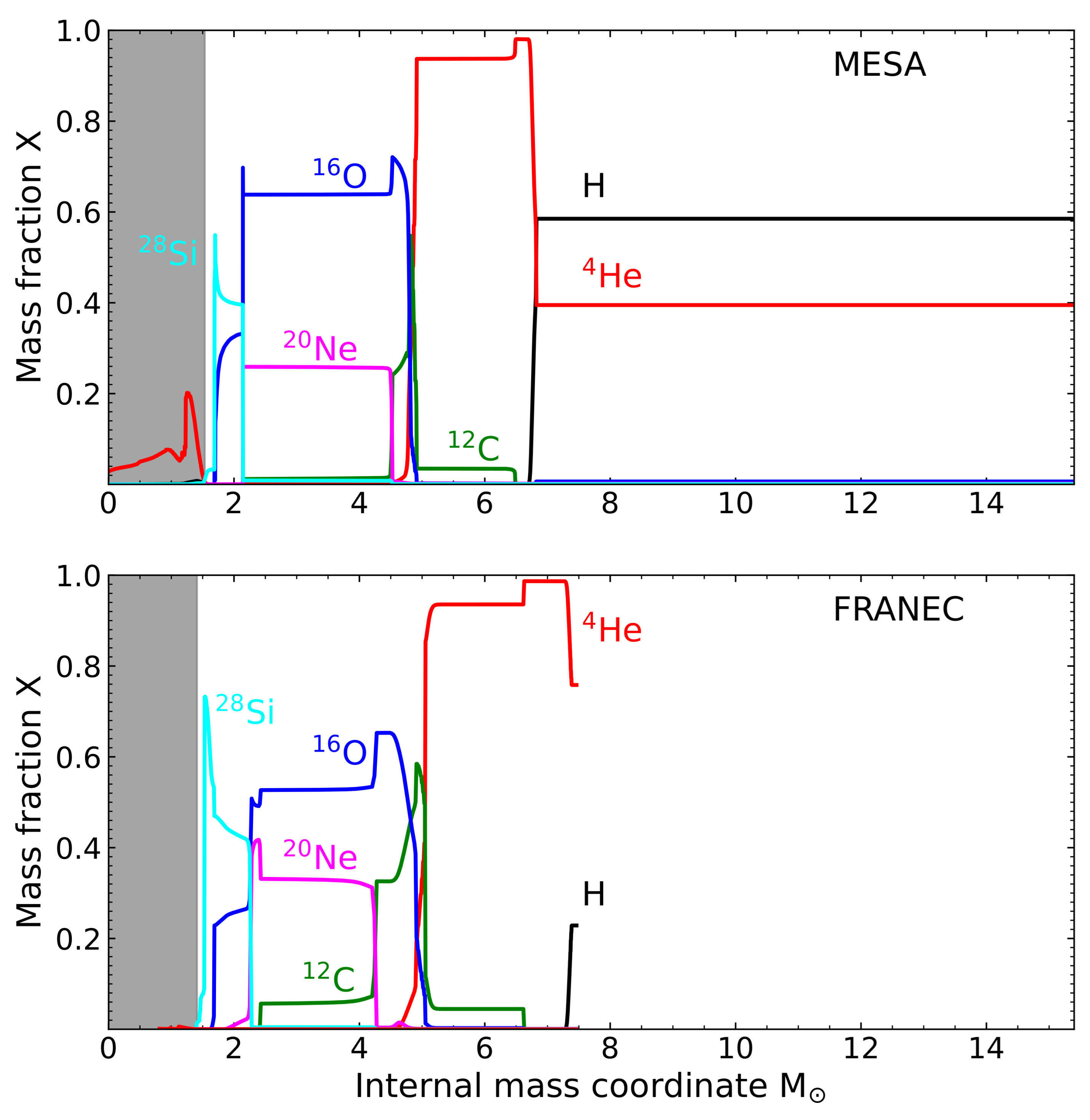
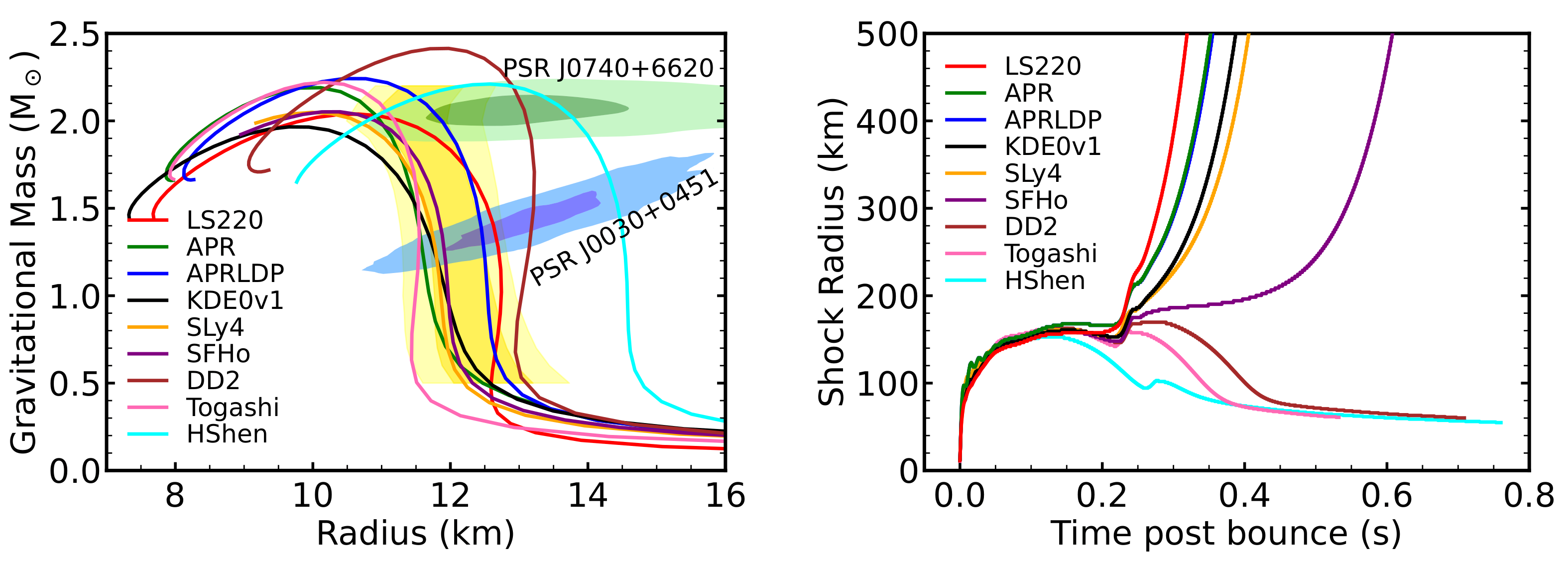

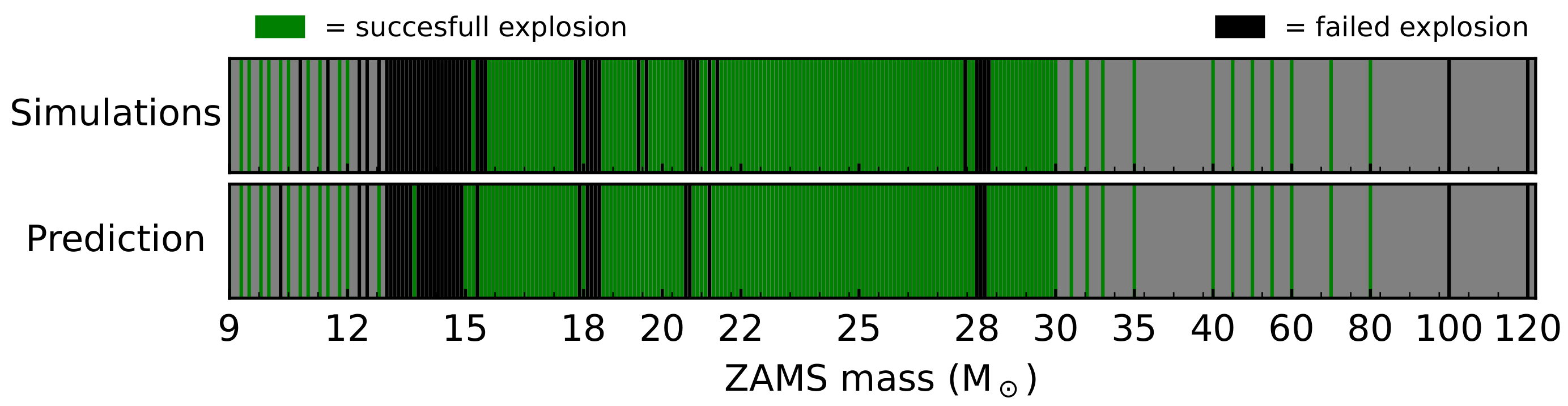

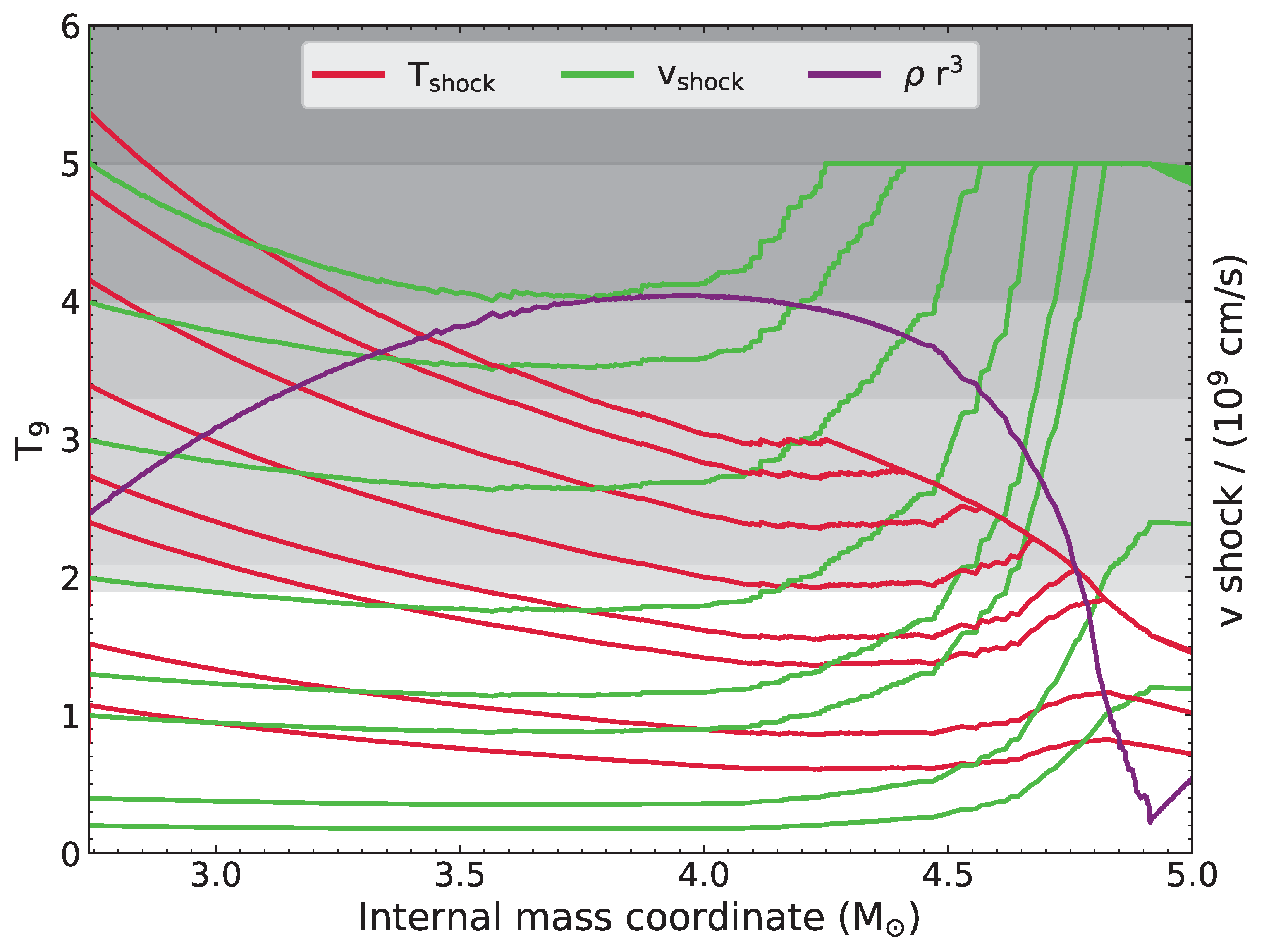
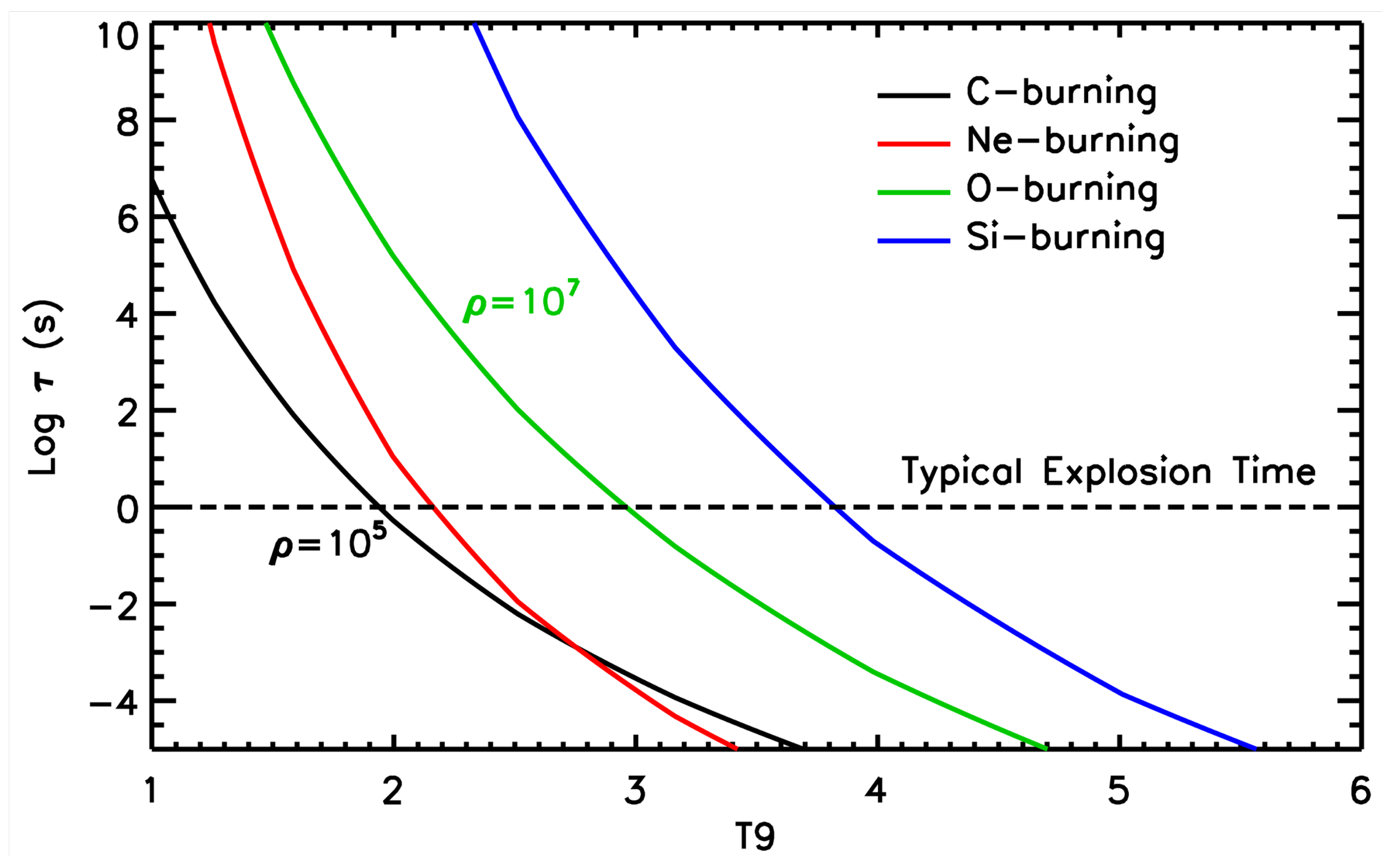
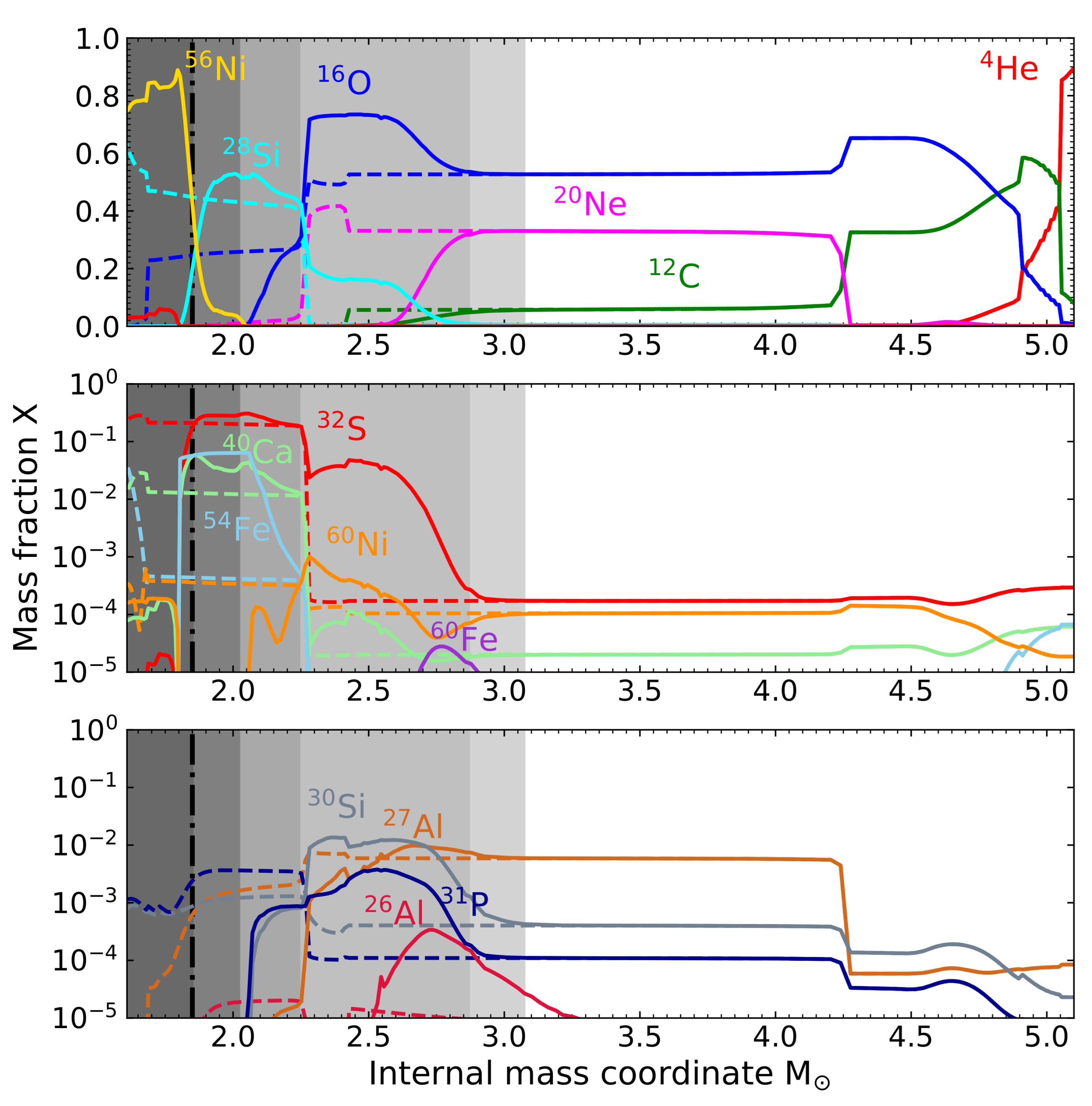
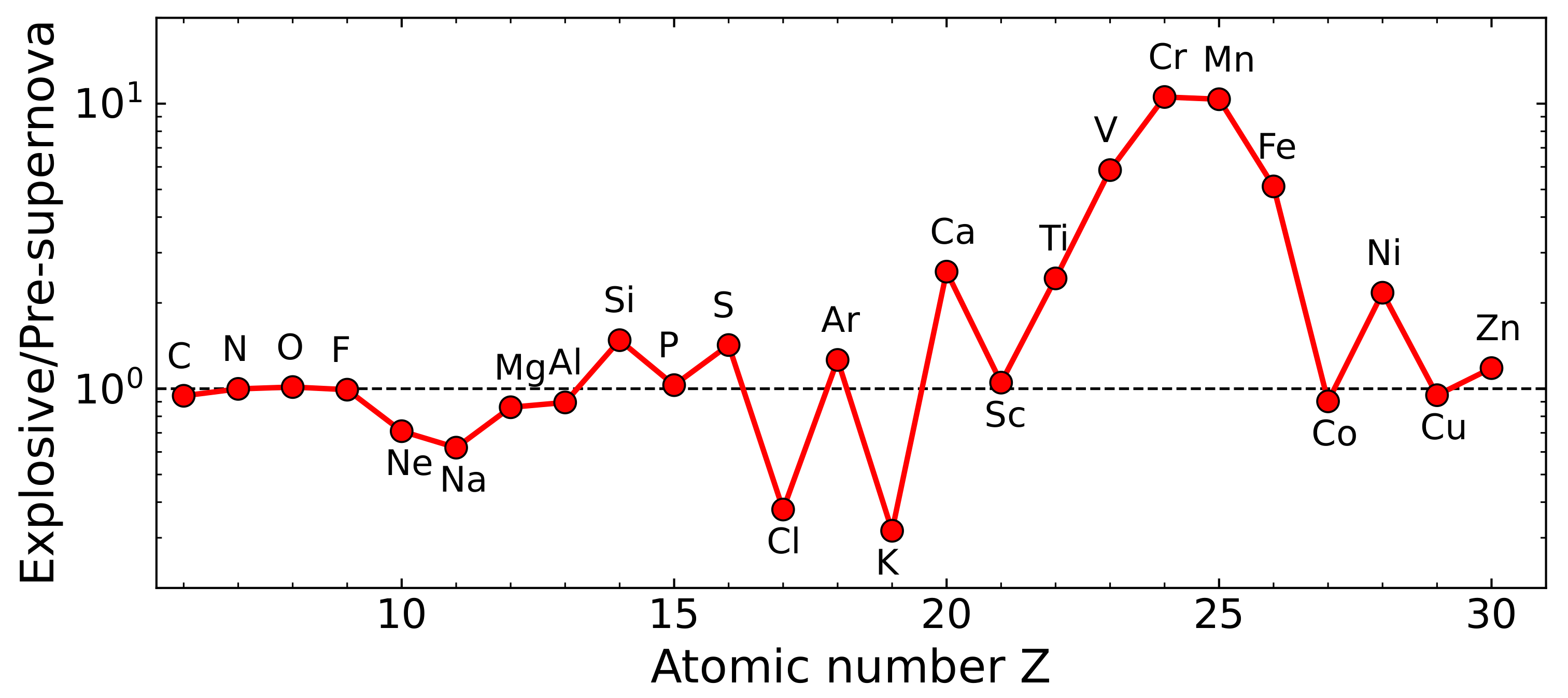

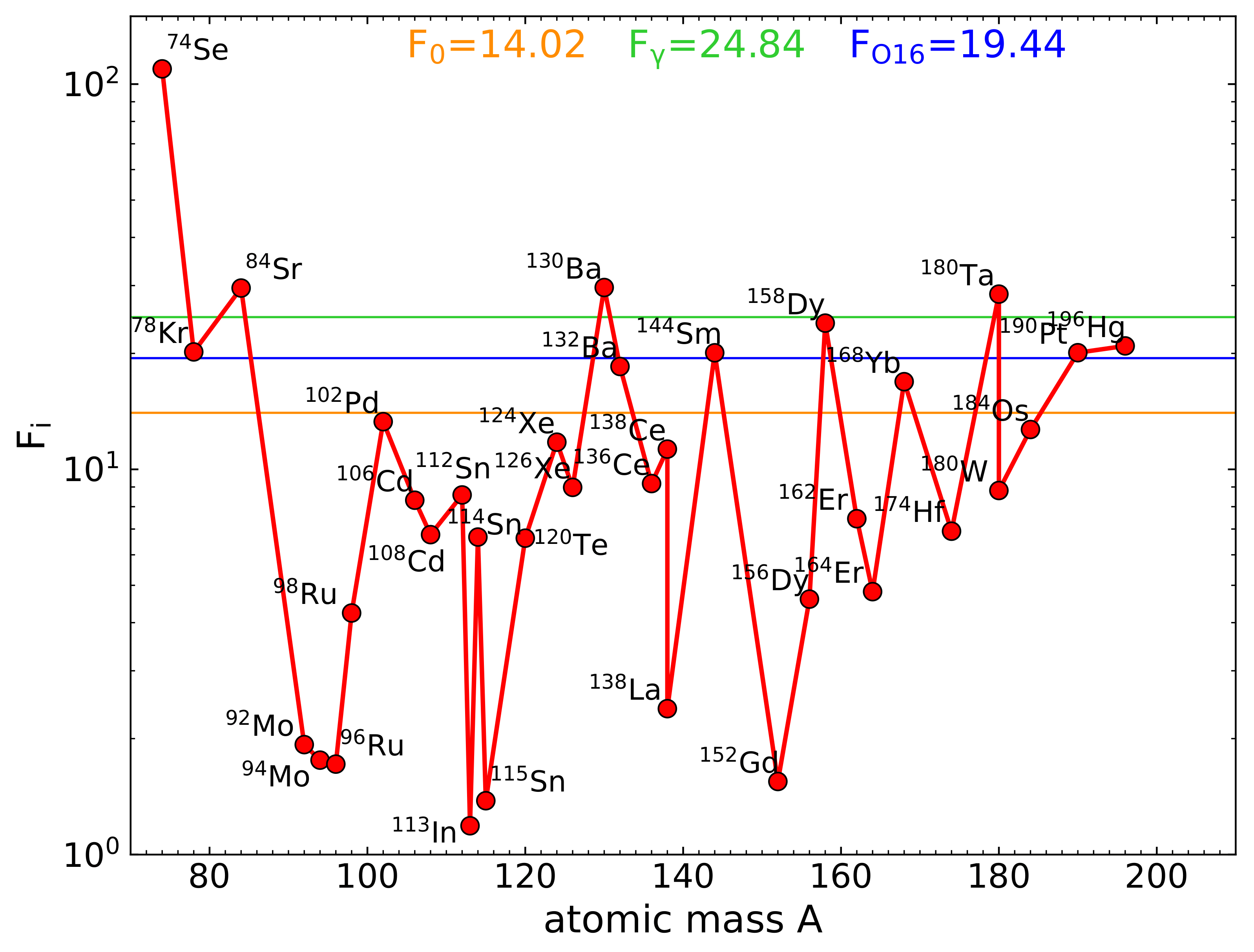
| Stage | Temperature | Mass | Radius |
|---|---|---|---|
| (GK) | () | (km) | |
| complete Si | >5 | 1.86 | 4657 |
| incomplete Si | >4 | 2.03 | 6270 |
| explosive O | >3.3 | 2.25 | 8104 |
| explosive Ne | >2.1 | 2.88 | 14,806 |
| explosive C | >1.9 | 3.07 | 16,919 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boccioli, L.; Roberti, L. The Physics of Core-Collapse Supernovae: Explosion Mechanism and Explosive Nucleosynthesis. Universe 2024, 10, 148. https://doi.org/10.3390/universe10030148
Boccioli L, Roberti L. The Physics of Core-Collapse Supernovae: Explosion Mechanism and Explosive Nucleosynthesis. Universe. 2024; 10(3):148. https://doi.org/10.3390/universe10030148
Chicago/Turabian StyleBoccioli, Luca, and Lorenzo Roberti. 2024. "The Physics of Core-Collapse Supernovae: Explosion Mechanism and Explosive Nucleosynthesis" Universe 10, no. 3: 148. https://doi.org/10.3390/universe10030148
APA StyleBoccioli, L., & Roberti, L. (2024). The Physics of Core-Collapse Supernovae: Explosion Mechanism and Explosive Nucleosynthesis. Universe, 10(3), 148. https://doi.org/10.3390/universe10030148





