High-Energy and Ultra-High-Energy Neutrino Astrophysics
Abstract
:1. Introduction
2. Neutrino Production Processes
3. The Diffuse High-Energy Neutrino Flux
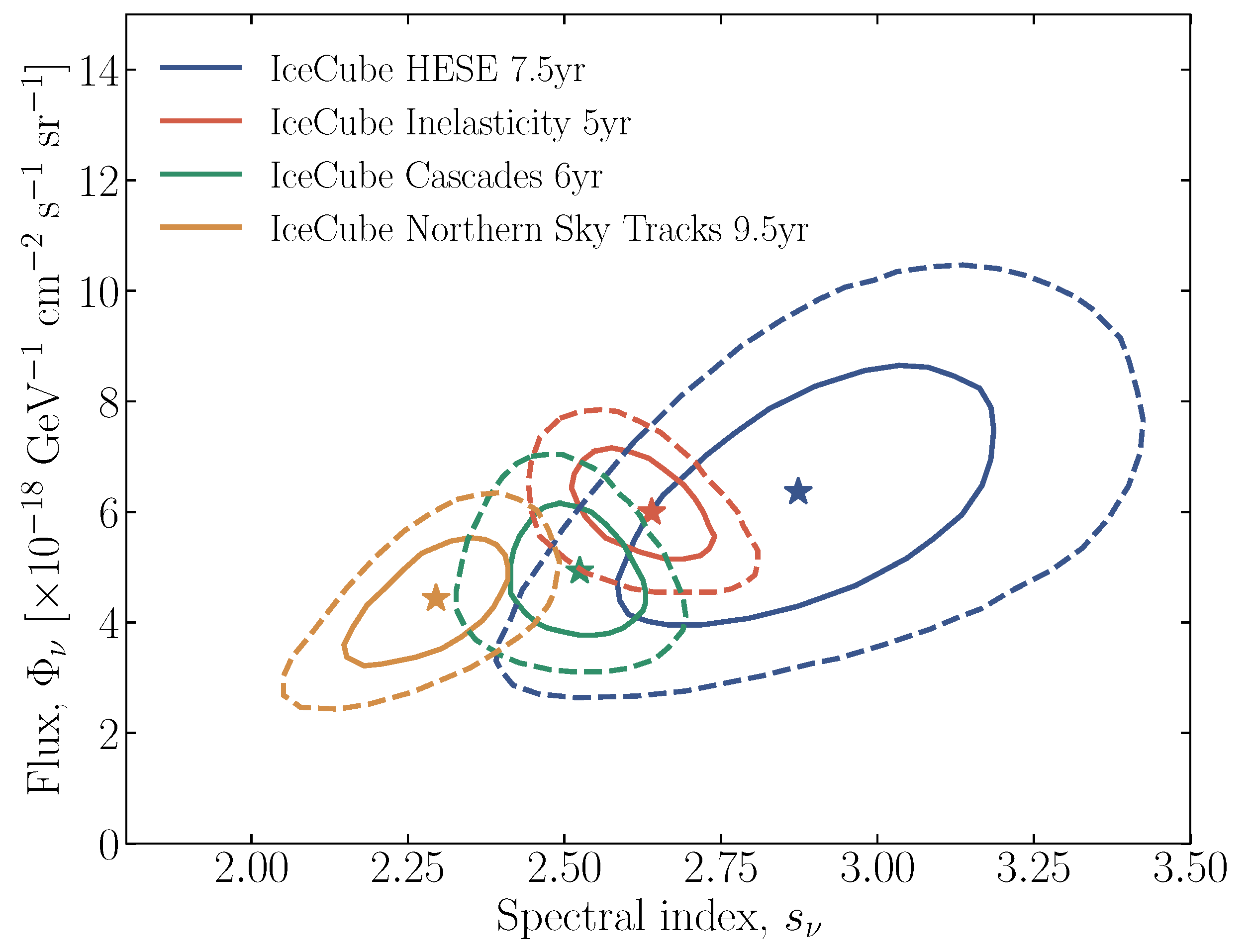
3.1. Energy Spectrum
3.2. Angular Distribution and Point Sources
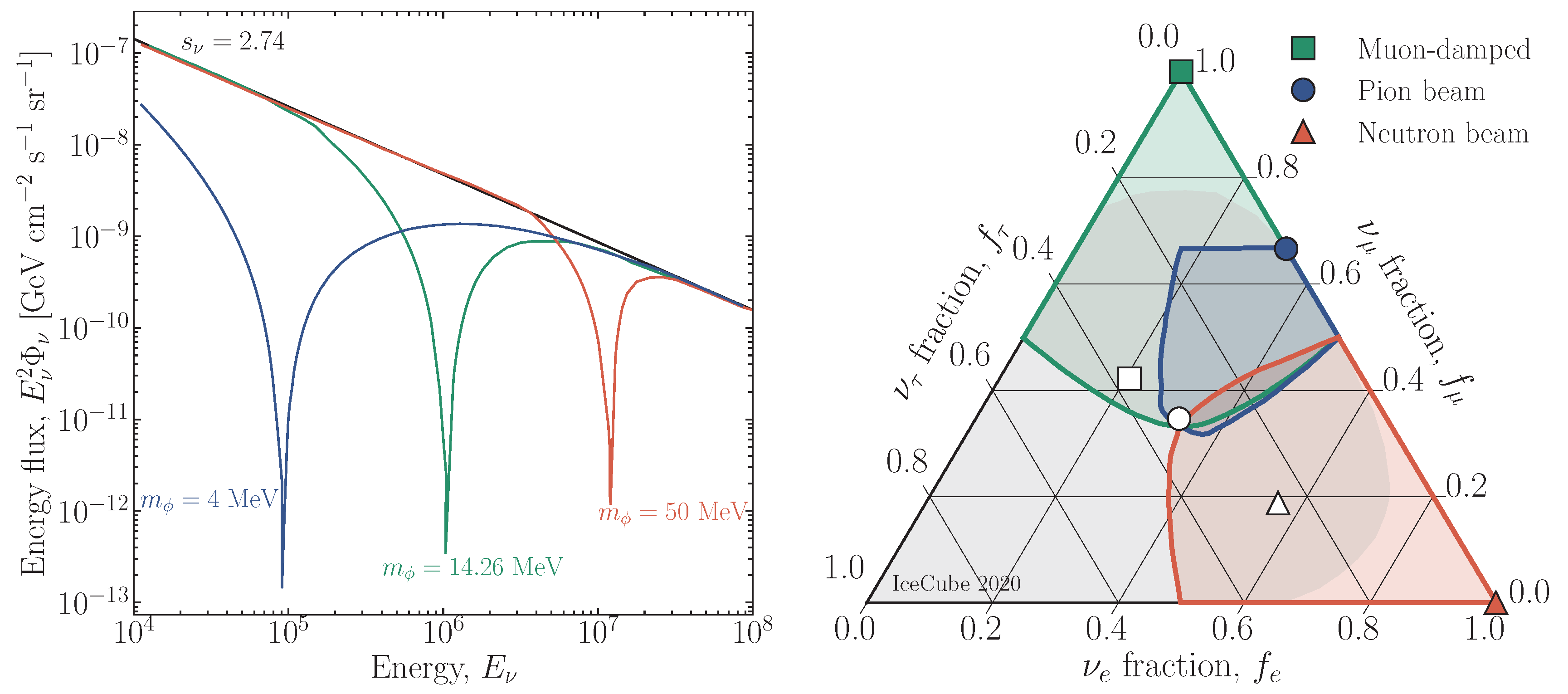
3.3. Flavor Composition
3.4. Multimessenger Connections
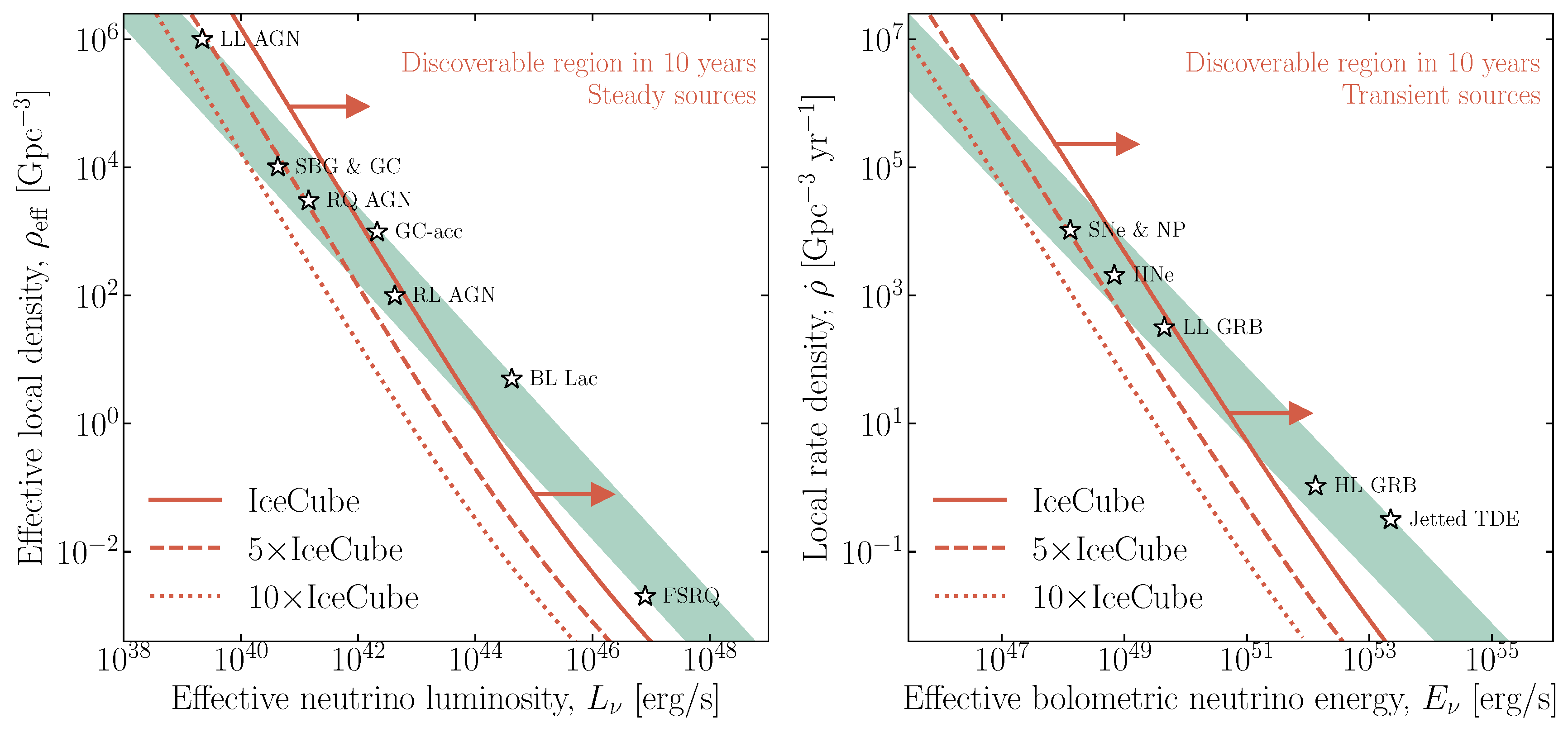
4. Astrophysical Sources of Neutrinos
4.1. Active Galactic Nuclei
4.1.1. Non-Jetted AGN
4.1.2. Blazars
4.2. Gamma-Ray Bursts
4.3. Tidal Disruption Events
4.4. Starburst Galaxies
4.5. Galaxy Clusters
4.6. Cosmogenic Neutrinos
4.7. Galactic Neutrinos
5. Neutrinos Probing beyond the Standard Model Physics
5.1. BSM Effects on Neutrino Production
5.2. BSM Effects on Neutrino Propagation
5.3. BSM Effects on Neutrino Detection
6. Summary
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HE | High-energy |
| UHE | Ultra-high-energy |
| UHECR | Ultra-high-energy cosmic rays |
| CR | Cosmic rays |
| AGN | Active galactic nucleus |
| GRB | Gamma-ray burst |
| TDE | Tidal disruption event |
| SBG | Starburst galaxy |
| GC | Galaxy cluster |
| NP | Newborn pulsar |
| SNe | Supernovae |
| HNe | Hypernovae |
| FSRQ | Flat-spectrum radio quasar |
| LL | Low-luminosity |
| HL | High-luminosity |
| BSM | Beyond the Standard Model |
References
- Aartsen, M. et al. [IceCube Collaboration] First observation of PeV-energy neutrinos with IceCube. Phys. Rev. Lett. 2013, 111, 021103. [Google Scholar] [CrossRef] [PubMed]
- Aartsen, M. et al. [IceCube Collaboration] Evidence for High-Energy Extraterrestrial Neutrinos at the IceCube Detector. Science 2013, 342, 1242856. [Google Scholar] [CrossRef] [PubMed]
- Aartsen, M. et al. [IceCube Collaboration] Observation of High-Energy Astrophysical Neutrinos in Three Years of IceCube Data. Phys. Rev. Lett. 2014, 113, 101101. [Google Scholar] [CrossRef] [PubMed]
- Aartsen, M. et al. [IceCube Collaboration] Evidence for Astrophysical Muon Neutrinos from the Northern Sky with IceCube. Phys. Rev. Lett. 2015, 115, 081102. [Google Scholar] [CrossRef] [PubMed]
- Aartsen, M. et al. [IceCube Collaboration] Characteristics of the diffuse astrophysical electron and tau neutrino flux with six years of IceCube high energy cascade data. Phys. Rev. Lett. 2020, 125, 121104. [Google Scholar] [CrossRef]
- Aartsen, M. et al. [IceCube Collaboration] Neutrino emission from the direction of the blazar TXS 0506+056 prior to the IceCube-170922A alert. Science 2018, 361, 147. [Google Scholar] [CrossRef]
- Aartsen, M. et al. [IceCube Collaboration] Multimessenger observations of a flaring blazar coincident with high-energy neutrino IceCube-170922A. Science 2018, 361, eaat1378. [Google Scholar] [CrossRef]
- Stein, R.; Velzen, S.V.; Kowalski, M.; Franckowiak, A.; Gezari, S.; Miller-Jones, J.C.; Frederick, S.; Sfaradi, I.; Bietenholz, M.F.; Horesh, A.; et al. A tidal disruption event coincident with a high-energy neutrino. Nat. Astron. 2021, 5, 510. [Google Scholar] [CrossRef]
- Aartsen, M. et al. [IceCube Collaboration] Time-Integrated Neutrino Source Searches with 10 Years of IceCube Data. Phys. Rev. Lett. 2020, 124, 051103. [Google Scholar] [CrossRef]
- Abbasi, R. et al. [IceCube Collaboration] Evidence for neutrino emission from the nearby active galaxy NGC 1068. Science 2022, 378, 538. [Google Scholar] [CrossRef]
- Meszaros, P. Astrophysical Sources of High Energy Neutrinos in the IceCube Era. Ann. Rev. Nucl. Part. Sci. 2017, 67, 45. [Google Scholar] [CrossRef]
- Vitagliano, E.; Tamborra, I.; Raffelt, G. Grand Unified Neutrino Spectrum at Earth: Sources and Spectral Components. Rev. Mod. Phys. 2020, 92, 45006. [Google Scholar] [CrossRef]
- Kurahashi, N.; Murase, K.; Santander, M. High-Energy Extragalactic Neutrino Astrophysics. Ann. Rev. Nucl. Part. Sci. 2022, 72, 365. [Google Scholar] [CrossRef]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Drury, L.O. An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rept. Prog. Phys. 1983, 46, 973. [Google Scholar] [CrossRef]
- Sjöstrand, T.; Ask, S.; Christiansen, J.R.; Corke, R.; Desai, N.; Ilten, P.; Mrenna, S.; Prestel, S.; Rasmussen, C.O.; Skands, P.Z. An introduction to PYTHIA 8.2. Comput. Phys. Commun. 2015, 191, 159. [Google Scholar] [CrossRef]
- Ostapchenko, S. Monte Carlo treatment of hadronic interactions in enhanced Pomeron scheme: I. QGSJET-II model. Phys. Rev. D 2011, 83, 014018. [Google Scholar] [CrossRef]
- Riehn, F.; Engel, R.; Fedynitch, A.; Gaisser, T.K.; Stanev, T. Hadronic interaction model Sibyll 2.3d and extensive air showers. Phys. Rev. D 2020, 102, 063002. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A.; Bugayov, V.V. Energy spectra of gamma-rays, electrons and neutrinos produced at proton-proton interactions in the very high energy regime. Phys. Rev. D 2006, 74, 034018, Erratum in Phys. Rev. 2009, 79, 039901. [Google Scholar] [CrossRef]
- Hummer, S.; Ruger, M.; Spanier, F.; Winter, W. Simplified models for photohadronic interactions in cosmic accelerators. Astrophys. J. 2010, 721, 630. [Google Scholar] [CrossRef]
- Mucke, A.; Rachen, J.P.; Engel, R.; Protheroe, R.J.; Stanev, T. On photohadronic processes in astrophysical environments. Publ. Astron. Soc. Austral. 1999, 16, 160. [Google Scholar] [CrossRef]
- Mücke, A.; Engel, R.; Rachen, J.P.; Protheroe, R.J.; Stanev, T. SOPHIA: Monte Carlo simulations of photohadronic processes in astrophysics. Comput. Phys. Commun. 2000, 124, 290. [Google Scholar] [CrossRef]
- Winter, W. Neutrinos from Cosmic Accelerators Including Magnetic Field and Flavor Effects. Adv. High Energy Phys. 2012, 2012, 586413. [Google Scholar] [CrossRef]
- Waxman, E.; Bahcall, J.N. High-energy neutrinos from cosmological gamma-ray burst fireballs. Phys. Rev. Lett. 1997, 78, 2292. [Google Scholar] [CrossRef]
- Murase, K. High energy neutrino early afterglows gamma-ray bursts revisited. Phys. Rev. D 2007, 76, 123001. [Google Scholar] [CrossRef]
- Hümmer, S.; Maltoni, M.; Winter, W.; Yaguna, C. Energy dependent neutrino flavor ratios from cosmic accelerators on the Hillas plot. Astropart. Phys. 2010, 34, 205. [Google Scholar] [CrossRef]
- Dermer, C.D.; Murase, K.; Takami, H. Variable Gamma-ray Emission Induced by Ultra-High Energy Neutral Beams: Application to 4C +21.35. Astrophys. J. 2012, 755, 147. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Vliet, A.V.; Morisi, S.; Winter, W. Unified thermal model for photohadronic neutrino production in astrophysical sources. J. Cosmol. Astropart. Phys. 2021, 2021, 028. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A. Energy spectra of gamma-rays, electrons and neutrinos produced at interactions of relativistic protons with low energy radiation. Phys. Rev. D 2008, 78, 034013, Erratum in Phys. Rev. D 2010, 82, 099901. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Bustamante, M. Bump hunting in the diffuse flux of high-energy cosmic neutrinos. Phys. Rev. D 2023, 107, 083008. [Google Scholar] [CrossRef]
- Kashti, T.; Waxman, E. Flavoring astrophysical neutrinos: Flavor ratios depend on energy. Phys. Rev. Lett. 2005, 95, 181101. [Google Scholar] [CrossRef]
- Lipari, P.; Lusignoli, M.; Meloni, D. Flavor Composition and Energy Spectrum of Astrophysical Neutrinos. Phys. Rev. D 2007, 75, 123005. [Google Scholar] [CrossRef]
- Baerwald, P.; Hümmer, S.; Winter, W. Magnetic Field and Flavor Effects on the Gamma-Ray Burst Neutrino Flux. Phys. Rev. D 2011, 83, 067303. [Google Scholar] [CrossRef]
- Baerwald, P.; Hummer, S.; Winter, W. Systematics in the Interpretation of Aggregated Neutrino Flux Limits and Flavor Ratios from Gamma-Ray Bursts. Astropart. Phys. 2012, 35, 508. [Google Scholar] [CrossRef]
- Roulet, E.; Vissani, F. On the energy of the protons producing the very high-energy astrophysical neutrinos. arXiv 2020, arXiv:2011.12769. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Observation and Characterization of a Cosmic Muon Neutrino Flux from the Northern Hemisphere using six years of IceCube data. Astrophys. J. 2016, 833, 3. [Google Scholar] [CrossRef]
- Ahlers, M.; Halzen, F. Opening a New Window onto the Universe with IceCube. Prog. Part. Nucl. Phys. 2018, 102, 73. [Google Scholar] [CrossRef]
- Abbasi, R.U. et al. [IceCube Collaboration] The IceCube high-energy starting event sample: Description and flux characterization with 7.5 years of data. Phys. Rev. D 2021, 104, 022002. [Google Scholar] [CrossRef]
- Stettner, J. et al. [IceCube Collaboration] Measurement of the Diffuse Astrophysical Muon-Neutrino Spectrum with Ten Years of IceCube Data. Proc. Sci. 2020, 358, 1017. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Measurements using the inelasticity distribution of multi-TeV neutrino interactions in IceCube. Phys. Rev. D 2019, 99, 032004. [Google Scholar] [CrossRef]
- Abbasi, R. et al. [IceCube Collaboration] Measurement of the astrophysical diffuse neutrino flux in a combined fit of IceCube’s high energy neutrino data. Proc. Sci. 2023, 444, 1064. [Google Scholar] [CrossRef]
- Palladino, A.; Winter, W. A multi-component model for observed astrophysical neutrinos. Astron. Astrophys. 2018, 615, A168. [Google Scholar] [CrossRef]
- Ambrosone, A.; Chianese, M.; Fiorillo, D.F.G.; Marinelli, A.; Miele, G.; Pisanti, O. Starburst galaxies strike back: A multi-messenger analysis with Fermi-LAT and IceCube data. Mon. Not. R. Astron. Soc. 2021, 503, 4032. [Google Scholar] [CrossRef]
- Telalovic, B.; Bustamante, M. Flavor Anisotropy in the High-Energy Astrophysical Neutrino Sky. arXiv 2023, arXiv:2310.15224. [Google Scholar]
- Fang, K.; Miller, M.C. A New Method for Finding Point Sources in High-energy Neutrino Data. Astrophys. J. 2016, 826, 102. [Google Scholar] [CrossRef]
- Feyereisen, M.R.; Tamborra, I.; Ando, S. One-point fluctuation analysis of the high-energy neutrino sky. J. Cosmol. Astropart. Phys. 2017, 2017, 057. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Search for astrophysical sources of neutrinos using cascade events in IceCube. Astrophys. J. 2017, 846, 136. [Google Scholar] [CrossRef]
- Capel, F.; Mortlock, D.J.; Finley, C. Bayesian constraints on the astrophysical neutrino source population from IceCube data. Phys. Rev. D 2020, 101, 123017, Erratum in Phys. Rev. D 2022, 105, 129904. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] An All-Sky Search for Three Flavors of Neutrinos from Gamma-Ray Bursts with the IceCube Neutrino Observatory. Astrophys. J. 2016, 824, 115. [Google Scholar] [CrossRef]
- Padovani, P.; Resconi, E.; Giommi, P.; Arsioli, B.; Chang, Y.L. Extreme blazars as counterparts of IceCube astrophysical neutrinos. Mon. Not. R. Astron. Soc. 2016, 457, 3582. [Google Scholar] [CrossRef]
- Moharana, R.; Razzaque, S. Angular correlation between IceCube high-energy starting events and starburst sources. J. Cosmol. Astropart. Phys. 2016, 2016, 021. [Google Scholar] [CrossRef]
- Resconi, E.; Coenders, S.; Padovani, P.; Giommi, P.; Caccianiga, L. Connecting blazars with ultrahigh-energy cosmic rays and astrophysical neutrinos. Mon. Not. R. Astron. Soc. 2017, 468, 597. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] The contribution of Fermi-2LAC blazars to the diffuse TeV-PeV neutrino flux. Astrophys. J. 2017, 835, 45. [Google Scholar] [CrossRef]
- Turley, C.F.; Fox, D.B.; Keivani, A.; DeLaunay, J.J.; Cowen, D.F.; Mostafa, M.; Solares, H.A.A.; Murase, K. A Coincidence Search for Cosmic Neutrino and Gamma-Ray Emitting Sources Using IceCube and Fermi LAT Public Data. Astrophys. J. 2018, 863, 64. [Google Scholar] [CrossRef]
- Lunardini, C.; Vance, G.S.; Emig, K.L.; Windhorst, R.A. Are starburst galaxies a common source of high energy neutrinos and cosmic rays? J. Cosmol. Astropart. Phys. 2019, 2019, 073. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] A Search for Neutrino Point-source Populations in 7 yr of IceCube Data with Neutrino-count Statistics. Astrophys. J. 2020, 893, 102. [Google Scholar] [CrossRef]
- Plavin, A.; Kovalev, Y.Y.; Kovalev, Y.A.; Troitsky, S. Observational Evidence for the Origin of High-energy Neutrinos in Parsec-scale Nuclei of Radio-bright Active Galaxies. Astrophys. J. 2020, 894, 101. [Google Scholar] [CrossRef]
- Buson, S.; Tramacere, A.; Pfeiffer, L.; Oswald, L.; de Menezes, R.; Azzollini, A.; Ajello, M. Beginning a Journey Across the Universe: The Discovery of Extragalactic Neutrino Factories. Astrophys. J. Lett. 2022, 933, L43, Erratum in Astrophys. J. Lett. 2022, 934, L38. [Google Scholar] [CrossRef]
- Plavin, A.V.; Kovalev, Y.Y.; Kovalev, Y.A.; Troitsky, S.V. Growing evidence for high-energy neutrinos originating in radio blazars. Mon. Not. R. Astron. Soc. 2023, 523, 1799. [Google Scholar] [CrossRef]
- Abbasi, R. et al. [IceCube Collaboration] Search for Correlations of High-energy Neutrinos Detected in IceCube with Radio-bright AGN and Gamma-Ray Emission from Blazars. Astrophys. J. 2023, 954, 75. [Google Scholar] [CrossRef]
- Buson, S.; Tramacere, A.; Oswald, L.; Barbano, E.; de Clairfontaine, G.F.; Pfeiffer, L.; Azzollini, A.; Baghmanyan, V.; Ajello, M. Extragalactic neutrino factories. arXiv 2023, arXiv:2305.11263. [Google Scholar]
- Bellenghi, C.; Padovani, P.; Resconi, E.; Giommi, P. Correlating High-energy IceCube Neutrinos with 5BZCAT Blazars and RFC Sources. Astrophys. J. Lett. 2023, 955, L32. [Google Scholar] [CrossRef]
- Moharana, R.; Razzaque, S. Angular correlation of cosmic neutrinos with ultrahigh-energy cosmic rays and implications for their sources. J. Cosmol. Astropart. Phys. 2015, 2015, 014. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube, Pierre Auger, Telescope Array Collaboration] Search for correlations between the arrival directions of IceCube neutrino events and ultrahigh-energy cosmic rays detected by the Pierre Auger Observatory and the Telescope Array. J. Cosmol. Astropart. Phys. 2016, 2016, 037. [Google Scholar] [CrossRef]
- Albert, A. et al. [IceCube, Pierre Auger, Telescope Array, Auger, ANTARES Collaboration] Search for Spatial Correlations of Neutrinos with Ultra-high-energy Cosmic Rays. Astrophys. J. 2022, 934, 164. [Google Scholar] [CrossRef]
- Aartsen M.G. et al. [IceCube Collaboration] Searches for small-scale anisotropies from neutrino point sources with three years of IceCube data. Astropart. Phys. 2015, 66, 39. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Multipole analysis of IceCube data to search for dark matter accumulated in the Galactic halo. Eur. Phys. J. C 2015, 75, 20. [Google Scholar] [CrossRef]
- Leuermann, M.; Schimp, M.; Wiebusch, C.H. Astrophysical interpretation of small-scale neutrino angular correlation searches with IceCube. Astropart. Phys. 2016, 83, 21. [Google Scholar] [CrossRef]
- Dekker, A.; Ando, S. Angular power spectrum analysis on current and future high-energy neutrino data. J. Cosmol. Astropart. Phys. 2019, 2019, 002. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Searches for Time Dependent Neutrino Sources with IceCube Data from 2008 to 2012. Astrophys. J. 2015, 807, 46. [Google Scholar] [CrossRef]
- Abbasi, R. et al. [IceCube Collaboration] A Search for Time-dependent Astrophysical Neutrino Emission with IceCube Data from 2012 to 2017. Astrophys. J. 2021, 911, 67. [Google Scholar] [CrossRef]
- Reusch, S.; Stein, R.; Kowalski, M.; Van Velzen, S.; Franckowiak, A.; Lunardini, C.; Murase, K.; Winter, W.; Miller-Jones, J.C.; Kasliwal, M.M.; et al. Candidate Tidal Disruption Event AT2019fdr Coincident with a High-Energy Neutrino. Phys. Rev. Lett. 2022, 128, 221101. [Google Scholar] [CrossRef] [PubMed]
- van Velzen, S.; Stein, R.; Gilfanov, M.; Kowalski, M.; Hayasaki, K.; Reusch, S.; Yao, Y.; Garrappa, S.; Franckowiak, A.; Gezari, S.; et al. Establishing accretion flares from massive black holes as a major source of high-energy neutrinos. arXiv 2023, arXiv:2111.09391. [Google Scholar]
- Lipari, P. Proton and Neutrino Extragalactic Astronomy. Phys. Rev. D 2008, 78, 083011. [Google Scholar] [CrossRef]
- Silvestri, A.; Barwick, S.W. Constraints on Extragalactic Point Source Flux from Diffuse Neutrino Limits. Phys. Rev. D 2010, 81, 023001. [Google Scholar] [CrossRef]
- Ahlers, M.; Halzen, F. Pinpointing Extragalactic Neutrino Sources in Light of Recent IceCube Observations. Phys. Rev. D 2014, 90, 043005. [Google Scholar] [CrossRef]
- Murase, K.; Waxman, E. Constraining High-Energy Cosmic Neutrino Sources: Implications and Prospects. Phys. Rev. D 2016, 94, 103006. [Google Scholar] [CrossRef]
- Fang, K.; Kotera, K.; Miller, M.C.; Murase, K.; Oikonomou, F. Identifying Ultrahigh-Energy Cosmic-Ray Accelerators with Future Ultrahigh-Energy Neutrino Detectors. J. Cosmol. Astropart. Phys. 2016, 2016, 017. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Bustamante, M.; Valera, V.B. Near-future discovery of point sources of ultra-high-energy neutrinos. J. Cosmol. Astropart. Phys. 2023, 2023, 026. [Google Scholar] [CrossRef]
- Bartos, I.; Veske, D.; Kowalski, M.; Marka, Z.; Marka, S. The IceCube Pie Chart: Relative Source Contributions to the Cosmic Neutrino Flux. Astrophys. J. 2021, 921, 45. [Google Scholar] [CrossRef]
- Ackermann, M.; Ahlers, M.; Anchordoqui, L.; Bustamante, M.; Connolly, A.; Deaconu, C.; Grant, D.; Gorham, P.; Halzen, F.; Karle, A. Astrophysics Uniquely Enabled by Observations of High-Energy Cosmic Neutrinos. Bull. Am. Astron. Soc. 2019, 51, 185. [Google Scholar]
- Aartsen, M.G. et al. [IceCube Collaboration] A combined maximum-likelihood analysis of the high-energy astrophysical neutrino flux measured with IceCube. Astrophys. J. 2015, 809, 98. [Google Scholar] [CrossRef]
- Mena, O.; Palomares-Ruiz, S.; Vincent, A.C. Flavor Composition of the High-Energy Neutrino Events in IceCube. Phys. Rev. Lett. 2014, 113, 091103. [Google Scholar] [CrossRef] [PubMed]
- Palomares-Ruiz, S.; Vincent, A.C.; Mena, O. Spectral analysis of the high-energy IceCube neutrinos. Phys. Rev. D 2015, 91, 103008. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Flavor Ratio of Astrophysical Neutrinos above 35 TeV in IceCube. Phys. Rev. Lett. 2015, 114, 171102. [Google Scholar] [CrossRef] [PubMed]
- Palladino, A.; Vissani, F. The natural parameterization of cosmic neutrino oscillations. Eur. Phys. J. C 2015, 75, 433. [Google Scholar] [CrossRef]
- Vincent, A.C.; Palomares-Ruiz, S.; Mena, O. Analysis of the 4-year IceCube high-energy starting events. Phys. Rev. D 2016, 94, 023009. [Google Scholar] [CrossRef]
- Abbasi, R. et al. [IceCube Collaboration] Detection of astrophysical tau neutrino candidates in IceCube. Eur. Phys. J. C 2022, 82, 1031. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Detection of a particle shower at the Glashow resonance with IceCube. Nature 2021, 591, 220, Erratum in Nature 2021, 592, E11. [Google Scholar] [CrossRef]
- Biehl, D.; Fedynitch, A.; Palladino, A.; Weiler, T.J.; Winter, W. Astrophysical Neutrino Production Diagnostics with the Glashow Resonance. J. Cosmol. Astropart. Phys. 2017, 2017, 033. [Google Scholar] [CrossRef]
- Liu, Q.; Song, N.; Vincent, A.C. Probing neutrino production in high-energy astrophysical neutrino sources with the Glashow resonance. Phys. Rev. D 2023, 108, 043022. [Google Scholar] [CrossRef]
- Pontecorvo, B. Inverse beta processes and nonconservation of lepton charge. Zh. Eksp. Teor. Fiz. 1957, 34, 247. [Google Scholar]
- Maki, Z.; Nakagawa, M.; Sakata, S. Remarks on the unified model of elementary particles. Prog. Theor. Phys. 1962, 28, 870–880. [Google Scholar] [CrossRef]
- Rachen, J.P.; Meszaros, P. Photohadronic neutrinos from transients in astrophysical sources. Phys. Rev. D 1998, 58, 123005. [Google Scholar] [CrossRef]
- Athar, H.; Jezabek, M.; Yasuda, O. Effects of neutrino mixing on high-energy cosmic neutrino flux. Phys. Rev. D 2000, 62, 103007. [Google Scholar] [CrossRef]
- Crocker, R.M.; Melia, F.; Volkas, R.R. Searching for long wavelength neutrino oscillations in the distorted neutrino spectrum of galactic supernova remnants. Astrophys. J. Suppl. 2002, 141, 147. [Google Scholar] [CrossRef]
- Barenboim, G.; Quigg, C. Neutrino observatories can characterize cosmic sources and neutrino properties. Phys. Rev. D 2003, 67, 073024. [Google Scholar] [CrossRef]
- Beacom, J.F.; Bell, N.F.; Hooper, D.; Pakvasa, S.; Weiler, T.J. Measuring flavor ratios of high-energy astrophysical neutrinos. Phys. Rev. D 2003, 68, 093005, Erratum in Phys. Rev. D 2005, 72, 019901. [Google Scholar] [CrossRef]
- Mena, O.; Mocioiu, I.; Razzaque, S. Oscillation effects on high-energy neutrino fluxes from astrophysical hidden sources. Phys. Rev. D 2007, 75, 063003. [Google Scholar] [CrossRef]
- Esmaili, A.; Farzan, Y. An Analysis of Cosmic Neutrinos: Flavor Composition at Source and Neutrino Mixing Parameters. Nucl. Phys. B 2009, 821, 197. [Google Scholar] [CrossRef]
- Choubey, S.; Rodejohann, W. Flavor Composition of UHE Neutrinos at Source and at Neutrino Telescopes. Phys. Rev. D 2009, 80, 113006. [Google Scholar] [CrossRef]
- Winter, W. Photohadronic Origin of the TeV-PeV Neutrinos Observed in IceCube. Phys. Rev. D 2013, 88, 083007. [Google Scholar] [CrossRef]
- Palladino, A.; Pagliaroli, G.; Villante, F.L.; Vissani, F. What is the Flavor of the Cosmic Neutrinos Seen by IceCube? Phys. Rev. Lett. 2015, 114, 171101. [Google Scholar] [CrossRef]
- Bustamante, M.; Tamborra, I. Using high-energy neutrinos as cosmic magnetometers. Phys. Rev. D 2020, 102, 123008. [Google Scholar] [CrossRef]
- Bustamante, M.; Ahlers, M. Inferring the flavor of high-energy astrophysical neutrinos at their sources. Phys. Rev. Lett. 2019, 122, 241101. [Google Scholar] [CrossRef]
- Song, N.; Li, S.W.; Argüelles, C.A.; Bustamante, M.; Vincent, A.C. The Future of High-Energy Astrophysical Neutrino Flavor Measurements. J. Cosmol. Astropart. Phys. 2021, 2021, 054. [Google Scholar] [CrossRef]
- Murase, K.; Fukugita, M. Energetics of High-Energy Cosmic Radiations. Phys. Rev. D 2019, 99, 063012. [Google Scholar] [CrossRef]
- Ackermann, M. et al. [Fermi-LAT Collaboration] The spectrum of isotropic diffuse gamma-ray emission between 100 MeV and 820 GeV. Astrophys. J. 2015, 799, 86. [Google Scholar] [CrossRef]
- Fenu, F. et al. [Pierre Auger Collaboration] The cosmic ray energy spectrum measured using the Pierre Auger Observatory. Proc. Sci 2017, 301, 486. [Google Scholar] [CrossRef]
- Waxman, E.; Bahcall, J.N. High-energy neutrinos from astrophysical sources: An Upper bound. Phys. Rev. D 1999, 59, 023002. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Waxman, E. High-energy astrophysical neutrinos: The Upper bound is robust. Phys. Rev. D 2001, 64, 023002. [Google Scholar] [CrossRef]
- Murase, K.; Ahlers, M.; Lacki, B.C. Testing the Hadronuclear Origin of PeV Neutrinos Observed with IceCube. Phys. Rev. D 2013, 88, 121301. [Google Scholar] [CrossRef]
- Murase, K.; Guetta, D.; Ahlers, M. Hidden Cosmic-Ray Accelerators as an Origin of TeV-PeV Cosmic Neutrinos. Phys. Rev. Lett. 2016, 116, 071101. [Google Scholar] [CrossRef] [PubMed]
- Capanema, A.; Esmaili, A.; Murase, K. New constraints on the origin of medium-energy neutrinos observed by IceCube. Phys. Rev. D 2020, 101, 103012. [Google Scholar] [CrossRef]
- Capanema, A.; Esmaili, A.; Serpico, P.D. Where do IceCube neutrinos come from? Hints from the diffuse gamma-ray flux. J. Cosmol. Astropart. Phys. 2021, 2021, 037. [Google Scholar] [CrossRef]
- Mannheim, K.; Protheroe, R.J.; Rachen, J.P. On the cosmic ray bound for models of extragalactic neutrino production. Phys. Rev. D 2001, 63, 023003. [Google Scholar] [CrossRef]
- Dermer, C.; Ramirez-Ruiz, E.; Le, T. Correlation of Photon and Neutrino Fluxes in Blazars and Gamma Ray Bursts. Astrophys. J. Lett. 2007, 664, L67. [Google Scholar] [CrossRef]
- Murase, K.; Ioka, K.; Nagataki, S.; Nakamura, T. High-energy cosmic-ray nuclei from high- and low-luminosity gamma-ray bursts and implications for multi-messenger astronomy. Phys. Rev. D 2008, 78, 023005. [Google Scholar] [CrossRef]
- Murase, K.; Ioka, K. TeV–PeV Neutrinos from Low-Power Gamma-Ray Burst Jets inside Stars. Phys. Rev. Lett. 2013, 111, 121102. [Google Scholar] [CrossRef] [PubMed]
- Senno, N.; Murase, K.; Mészáros, P. Choked Jets and Low-Luminosity Gamma-Ray Bursts as Hidden Neutrino Sources. Phys. Rev. D 2016, 93, 083003. [Google Scholar] [CrossRef]
- Kimura, S.S.; Murase, K.; Toma, K. Neutrino and Cosmic-Ray Emission and Cumulative Background from Radiatively Inefficient Accretion Flows in Low-Luminosity Active Galactic Nuclei. Astrophys. J. 2015, 806, 159. [Google Scholar] [CrossRef]
- Murase, K.; Kimura, S.S.; Meszaros, P. Hidden Cores of Active Galactic Nuclei as the Origin of Medium-Energy Neutrinos: Critical Tests with the MeV Gamma-Ray Connection. Phys. Rev. Lett. 2020, 125, 011101. [Google Scholar] [CrossRef]
- Inoue, Y.; Khangulyan, D.; Inoue, S.; Doi, A. On high-energy particles in accretion disk coronae of supermassive black holes: Implications for MeV gamma rays and high-energy neutrinos from AGN cores. arXiv 2019, arXiv:1904.00554. [Google Scholar] [CrossRef]
- Kheirandish, A.; Murase, K.; Kimura, S.S. High-energy Neutrinos from Magnetized Coronae of Active Galactic Nuclei and Prospects for Identification of Seyfert Galaxies and Quasars in Neutrino Telescopes. Astrophys. J. 2021, 922, 45. [Google Scholar] [CrossRef]
- Padovani, P.; Alexander, D.M.; Assef, R.J.; De Marco, B.; Giommi, P.; Hickox, R.C.; Richards, G.T.; Smolčić, V.; Hatziminaoglou, E.; Mainieri, V.; et al. Active galactic nuclei: What’s in a name? Astron. Astrophys. Rev. 2017, 25, 2. [Google Scholar] [CrossRef]
- Murase, K.; Stecker, F.W. High-Energy Neutrinos from Active Galactic Nuclei. In The Encyclopedia of Cosmology; World Scientific: Singapore, 2023; Chapter 10. [Google Scholar]
- Berezinsky, V.S. Extraterestrial neutrino sources and high energy neutrino astrophysics. In Proceedings of the International Conference Neutrino ’77, Baksan, Russia, 18–24 June 1977. [Google Scholar]
- Silberberg, R.; Shapiro, M.M. Neutrinos as a Probe for the Nature of and Processes in Active Galactic Nuclei. In Proceedings of the International Cosmic Ray Conference, Kyoto, Japan, 6–18 August 1979; Volume 10, p. 357. [Google Scholar]
- Eichler, D. High-energy neutrino astronomy: A probe of galactic nuclei? Astrophys. J. 1979, 232, 106. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Engels, A.A.; Baack, D.; Babić, A.; Banerjee, B.; de Almeida, U.B.; Barrio, J.A.; González, J.B.; et al. Constraints on Gamma-Ray and Neutrino Emission from NGC 1068 with the MAGIC Telescopes. Astrophys. J. 2019, 883, 135. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Ginzburg, V.L. On High Energy Neutrino Radiation of Quasars and Active Galactic Nuclei. In Proceedings of the International Cosmic Ray Conference, Paris, France, 13–25 July 1981; Volume 1, p. 238. [Google Scholar]
- Inoue, Y.; Khangulyan, D.; Doi, A. On the Origin of High-energy Neutrinos from NGC 1068: The Role of Nonthermal Coronal Activity. Astrophys. J. Lett. 2020, 891, L33. [Google Scholar] [CrossRef]
- Mbarek, R.; Philippov, A.; Chernoglazov, A.; Levinson, A.; Mushotzky, R. The Interplay between accelerated Protons, X-rays and Neutrinos in the Corona of NGC 1068: Constraints from Kinetic Plasma Simulations. arXiv 2023, arXiv:2310.15222. [Google Scholar]
- Fiorillo, D.F.G.; Petropoulou, M.; Comisso, L.; Peretti, E.; Sironi, L. TeV Neutrinos and Hard X-Rays from Relativistic Reconnection in the Corona of NGC 1068. Astrophys. J. 2024, 961, L14. [Google Scholar] [CrossRef]
- Inoue, S.; Cerruti, M.; Murase, K.; Liu, R.-Y. High-energy neutrinos and gamma rays from winds and tori in active galactic nuclei. arXiv 2022, arXiv:2207.02097. [Google Scholar] [CrossRef]
- Fang, K.; Rodriguez, E.L.; Halzen, F.; Gallagher, J.S. High-energy Neutrinos from the Inner Circumnuclear Region of NGC 1068. Astrophys. J. 2023, 956, 8. [Google Scholar] [CrossRef]
- Murase, K. Hidden Hearts of Neutrino Active Galaxies. Astrophys. J. Lett. 2022, 941, L17. [Google Scholar] [CrossRef]
- Peretti, E.; Lamastra, A.; Saturni, F.G.; Ahlers, M.; Blasi, P.; Morlino, G.; Cristofari, P. Diffusive shock acceleration at EeV and associated multimessenger flux from ultra-fast outflows driven by active galactic nuclei. Mon. Not. R. Astron. Soc. 2023, 526, 181. [Google Scholar] [CrossRef]
- Peretti, E.; Peron, G.; Tombesi, F.; Lamastra, A.; Saturni, F.G.; Cerruti, M.; Ahlers, M. Gamma-ray emission from the Seyfert galaxy NGC 4151 and multimessenger implications for ultra-fast outflows. arXiv 2023, arXiv:2303.03298. [Google Scholar]
- Mannheim, K. Neutrino signatures of the origins of cosmic rays. Nucl. Phys. B Proc. Suppl. 2014, 256–257, 264. [Google Scholar] [CrossRef]
- Aharonian, F.A. TeV gamma-rays from BL Lac objects due to synchrotron radiation of extremely high-energy protons. New Astron. 2000, 5, 377. [Google Scholar] [CrossRef]
- Mucke, A.; Protheroe, R.J. A Proton synchrotron blazar model for flaring in Markarian 501. Astropart. Phys. 2001, 15, 121. [Google Scholar] [CrossRef]
- Mannheim, K.; Biermann, P.L. Photomeson production in active galactic nuclei. Astron. Astrophys. 1989, 221, 211. [Google Scholar]
- Mannheim, K. The Proton blazar. Astron. Astrophys. 1993, 269, 67. [Google Scholar]
- Atoyan, A.M.; Dermer, C.D. High-energy neutrinos from photomeson processes in blazars. Phys. Rev. Lett. 2001, 87, 221102. [Google Scholar] [CrossRef]
- Murase, K.; Inoue, Y.; Dermer, C.D. Diffuse Neutrino Intensity from the Inner Jets of Active Galactic Nuclei: Impacts of External Photon Fields and the Blazar Sequence. Phys. Rev. D 2014, 90, 023007. [Google Scholar] [CrossRef]
- Padovani, P.; Petropoulou, M.; Giommi, P.; Resconi, E. A simplified view of blazars: The neutrino background. Mon. Not. R. Astron. Soc. 2015, 452, 1877. [Google Scholar] [CrossRef]
- Petropoulou, M.; Dimitrakoudis, S.; Padovani, P.; Mastichiadis, A.; Resconi, E. Photohadronic origin of γ-ray BL Lac emission: Implications for IceCube neutrinos. Mon. Not. R. Astron. Soc. 2015, 448, 2412. [Google Scholar] [CrossRef]
- Halzen, F.; Zas, E. Neutrino fluxes from active galaxies: A Model independent estimate. Astrophys. J. 1997, 488, 669. [Google Scholar] [CrossRef]
- Muecke, A.; Protheroe, R.J.; Engel, R.; Rachen, J.P.; Stanev, T. BL Lac Objects in the synchrotron proton blazar model. Astropart. Phys. 2003, 18, 593. [Google Scholar] [CrossRef]
- Atoyan, A.M.; Dermer, C.D. Neutral beams from blazar jets. Astrophys. J. 2003, 586, 79. [Google Scholar] [CrossRef]
- Rodrigues, X.; Heinze, J.; Palladino, A.; van Vliet, A.; Winter, W. Active Galactic Nuclei Jets as the Origin of Ultrahigh-Energy Cosmic Rays and Perspectives for the Detection of Astrophysical Source Neutrinos at EeV Energies. Phys. Rev. Lett. 2021, 126, 191101. [Google Scholar] [CrossRef] [PubMed]
- Righi, C.; Palladino, A.; Tavecchio, F.; Vissani, F. EeV astrophysical neutrinos from flat spectrum radio quasars. Astron. Astrophys. 2020, 642, A92. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Differential limit on the extremely-high-energy cosmic neutrino flux in the presence of astrophysical background from nine years of IceCube data. Phys. Rev. D 2018, 98, 062003. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] All-sky Search for Time-integrated Neutrino Emission from Astrophysical Sources with 7 yr of IceCube Data. Astrophys. J. 2017, 835, 151. [Google Scholar] [CrossRef]
- Smith, D.; Hooper, D.; Vieregg, A. Revisiting AGN as the source of IceCube’s diffuse neutrino flux. J. Cosmol. Astropart. Phys. 2021, 2021, 031. [Google Scholar] [CrossRef]
- Yuan, C.; Murase, K.; Mészáros, P. Complementarity of Stacking and Multiplet Constraints on the Blazar Contribution to the Cumulative High-Energy Neutrino Intensity. Astrophys. J. 2020, 890, 25. [Google Scholar] [CrossRef]
- Palladino, A.; Rodrigues, X.; Gao, S.; Winter, W. Interpretation of the diffuse astrophysical neutrino flux in terms of the blazar sequence. Astrophys. J. 2019, 871, 41. [Google Scholar] [CrossRef]
- Ansoldi, S. et al. [MAGIC Collaboration] The blazar TXS 0506+056 associated with a high-energy neutrino: Insights into extragalactic jets and cosmic ray acceleration. Astrophys. J. Lett. 2018, 863, L10. [Google Scholar] [CrossRef]
- Keivani, A.; Murase, K.; Petropoulou, M.; Fox, D.B.; Cenko, S.B.; Chaty, S.; Coleiro, A.; DeLaunay, J.J.; Dimitrakoudis, S.; Evans, P.A.; et al. A Multimessenger Picture of the Flaring Blazar TXS 0506+056: Implications for High-Energy Neutrino Emission and Cosmic Ray Acceleration. Astrophys. J. 2018, 864, 84. [Google Scholar] [CrossRef]
- Murase, K.; Oikonomou, F.; Petropoulou, M. Blazar Flares as an Origin of High-Energy Cosmic Neutrinos? Astrophys. J. 2018, 865, 124. [Google Scholar] [CrossRef]
- Cerruti, M.; Zech, A.; Boisson, C.; Emery, G.; Inoue, S.; Lenain, J.P. Leptohadronic single-zone models for the electromagnetic and neutrino emission of TXS 0506+056. Mon. Not. R. Astron. Soc. 2019, 483, L12, Erratum in Mon. Not. R. Astron. Soc. 2021, 502, L21–L22. [Google Scholar] [CrossRef]
- Gao, S.; Fedynitch, A.; Winter, W.; Pohl, M. Modelling the coincident observation of a high-energy neutrino and a bright blazar flare. Nat. Astron. 2019, 3, 88. [Google Scholar] [CrossRef]
- Reimer, A.; Boettcher, M.; Buson, S. Cascading Constraints from Neutrino-emitting Blazars: The Case of TXS 0506+056. Astrophys. J. 2019, 881, 46, Erratum in Astrophys. J. 2020, 899, 168. [Google Scholar] [CrossRef]
- Rodrigues, X.; Gao, S.; Fedynitch, A.; Palladino, A.; Winter, W. Leptohadronic Blazar Models Applied to the 2014–2015 Flare of TXS 0506+056. Astrophys. J. Lett. 2019, 874, L29. [Google Scholar] [CrossRef]
- Oikonomou, F.; Murase, K.; Padovani, P.; Resconi, E.; Mészáros, P. High energy neutrino flux from individual blazar flares. Mon. Not. R. Astron. Soc. 2019, 489, 4347. [Google Scholar] [CrossRef]
- Zhang, B. The Physics of Gamma-Ray Bursts; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Meszaros, P. Gamma-Ray Bursts. Rept. Prog. Phys. 2006, 69, 2259. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts & relativistic jets. Phys. Rept. 2014, 561, 1. [Google Scholar] [CrossRef]
- Vietri, M. On the acceleration of ultrahigh-energy cosmic rays in gamma-ray bursts. Astrophys. J. 1995, 453, 883. [Google Scholar] [CrossRef]
- Waxman, E. Cosmological gamma-ray bursts and the highest energy cosmic rays. Phys. Rev. Lett. 1995, 75, 386. [Google Scholar] [CrossRef]
- Baerwald, P.; Bustamante, M.; Winter, W. UHECR escape mechanisms for protons and neutrons from GRBs, and the cosmic ray-neutrino connection. Astrophys. J. 2013, 768, 186. [Google Scholar] [CrossRef]
- Globus, N.; Allard, D.; Mochkovitch, R.; Parizot, E. UHECR acceleration at GRB internal shocks. Mon. Not. R. Astron. Soc. 2015, 451, 751. [Google Scholar] [CrossRef]
- Baerwald, P.; Bustamante, M.; Winter, W. Are gamma-ray bursts the sources of ultra-high energy cosmic rays? Astropart. Phys. 2015, 62, 66. [Google Scholar] [CrossRef]
- Bustamante, M.; Baerwald, P.; Murase, K.; Winter, W. Neutrino and cosmic-ray emission from multiple internal shocks in gamma-ray bursts. Nat. Commun. 2015, 6, 6783. [Google Scholar] [CrossRef]
- Biehl, D.; Boncioli, D.; Fedynitch, A.; Winter, W. Cosmic-Ray and Neutrino Emission from Gamma-Ray Bursts with a Nuclear Cascade. Astron. Astrophys. 2018, 611, A101. [Google Scholar] [CrossRef]
- Guetta, D.; Hooper, D.; Alvarez-Muniz, J.; Halzen, F.; Reuveni, E. Neutrinos from individual gamma-ray bursts in the BATSE catalog. Astropart. Phys. 2004, 20, 429. [Google Scholar] [CrossRef]
- Li, Z. Note on the Normalization of Predicted GRB Neutrino Flux. Phys. Rev. D 2012, 85, 027301. [Google Scholar] [CrossRef]
- Hummer, S.; Baerwald, P.; Winter, W. Neutrino Emission from Gamma-Ray Burst Fireballs, Revised. Phys. Rev. Lett. 2012, 108, 231101. [Google Scholar] [CrossRef] [PubMed]
- He, H.-N.; Liu, R.-Y.; Wang, X.-Y.; Nagataki, S.; Murase, K.; Dai, Z.-G. Icecube non-detection of GRBs: Constraints on the fireball properties. Astrophys. J. 2012, 752, 29. [Google Scholar] [CrossRef]
- Tamborra, I.; Ando, S. Inspecting the supernova–gamma-ray-burst connection with high-energy neutrinos. Phys. Rev. D 2016, 93, 053010. [Google Scholar] [CrossRef]
- Tamborra, I.; Ando, S. Diffuse emission of high-energy neutrinos from gamma-ray burst fireballs. J. Cosmol. Astropart. Phys. 2015, 2015, 036. [Google Scholar] [CrossRef]
- Bustamante, M.; Murase, K.; Winter, W.; Heinze, J. Multi-messenger light curves from gamma-ray bursts in the internal shock model. Astrophys. J. 2017, 837, 33. [Google Scholar] [CrossRef]
- Liu, R.-Y.; Wang, X.-Y. Diffuse PeV neutrinos from gamma-ray bursts. Astrophys. J. 2013, 766, 73. [Google Scholar] [CrossRef]
- Pitik, T.; Tamborra, I.; Petropoulou, M. Neutrino signal dependence on gamma-ray burst emission mechanism. J. Cosmol. Astropart. Phys. 2021, 2021, 034. [Google Scholar] [CrossRef]
- Kimura, S.S. Neutrinos from Gamma-Ray Bursts. In The Encyclopedia of Cosmology; World Scientific: Singapore, 2023; Chapter 9. [Google Scholar]
- Gao, S.; Asano, K.; Meszaros, P. High Energy Neutrinos from Dissipative Photospheric Models of Gamma Ray Bursts. J. Cosmol. Astropart. Phys. 2012, 2012, 058. [Google Scholar] [CrossRef]
- Guarini, E.; Tamborra, I.; Gottlieb, O. State-of-the-art collapsar jet simulations imply undetectable subphotospheric neutrinos. Phys. Rev. D 2023, 107, 023001. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Meszaros, P. 5-GeV to 10-GeV neutrinos from gamma-ray burst fireballs. Phys. Rev. Lett. 2000, 85, 1362. [Google Scholar] [CrossRef] [PubMed]
- Meszaros, P.; Rees, M.J. Multi GeV neutrinos from internal dissipation in GRB fireballs. Astrophys. J. Lett. 2000, 541, L5. [Google Scholar] [CrossRef]
- Murase, K.; Kashiyama, K.; Mészáros, P. Subphotospheric Neutrinos from Gamma-Ray Bursts: The Role of Neutrons. Phys. Rev. Lett. 2013, 111, 131102. [Google Scholar] [CrossRef]
- Waxman, E.; Bahcall, J.N. Neutrino afterglow from gamma-ray bursts: ∼1018 eV. Astrophys. J. 2000, 541, 707. [Google Scholar] [CrossRef]
- Dai, Z.G.; Lu, T. Prompt neutrino emission from gamma-ray bursts. Astrophys. J. 2001, 551, 249. [Google Scholar] [CrossRef]
- Dermer, C.D. Neutrino, neutron, and cosmic ray production in the external shock model of gamma-ray bursts. Astrophys. J. 2002, 574, 65. [Google Scholar] [CrossRef]
- Guarini, E.; Tamborra, I.; Bégué, D.; Pitik, T.; Greiner, J. Multi-messenger detection prospects of gamma-ray burst afterglows with optical jumps. J. Cosmol. Astropart. Phys. 2022, 2022, 034. [Google Scholar] [CrossRef]
- Adrian-Martinez, S. et al. [ANTARES Collaboration] Search for muon neutrinos from gamma-ray bursts with the ANTARES neutrino telescope using 2008 to 2011 data. Astron. Astrophys. 2013, 559, A9. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Search for Prompt Neutrino Emission from Gamma-Ray Bursts with IceCube. Astrophys. J. Lett. 2015, 805, L5. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Extending the search for muon neutrinos coincident with gamma-ray bursts in IceCube data. Astrophys. J. 2017, 843, 112. [Google Scholar] [CrossRef]
- Albert, A.; André, M.; Anghinolfi, M.; Anton, G.; Ardid, M.; Aubert, J.J.; Avgitas, T.; Baret, B.; Barrios-Martí, J.; Basa, S.; et al. Search for high-energy neutrinos from bright GRBs with ANTARES. Mon. Not. R. Astron. Soc. 2017, 469, 906. [Google Scholar] [CrossRef]
- Albert, A. et al. [ANTARES Collaboration] Constraining the contribution of Gamma-Ray Bursts to the high-energy diffuse neutrino flux with 10 yr of ANTARES data. Mon. Not. R. Astron. Soc. 2020, 500, 5614. [Google Scholar] [CrossRef]
- IceCube Collaboration. GRB 221009A: Upper limits from a neutrino search with IceCube. In GRB Coordinates Network; No. 32665; NASA: Washington, DC, USA, 2022. [Google Scholar]
- Liu, R.-Y.; Zhang, H.-M.; Wang, X.-Y. Constraints on Gamma-Ray Burst Models from GRB 221009A: GeV Gamma Rays versus High-energy Neutrinos. Astrophys. J. Lett. 2023, 943, L2. [Google Scholar] [CrossRef]
- Murase, K.; Mukhopadhyay, M.; Kheirandish, A.; Kimura, S.S.; Fang, K. Neutrinos from the Brightest Gamma-Ray Burst? Astrophys. J. Lett. 2022, 941, L10. [Google Scholar] [CrossRef]
- Ai, S.; Gao, H. Model Constraints Based on the IceCube Neutrino Nondetection of GRB 221009A. Astrophys. J. 2023, 944, 115. [Google Scholar] [CrossRef]
- Murase, K.; Ioka, K.; Nagataki, S.; Nakamura, T. High Energy Neutrinos and Cosmic-Rays from Low-Luminosity Gamma-Ray Bursts? Astrophys. J. Lett. 2006, 651, L5. [Google Scholar] [CrossRef]
- Gupta, N.; Zhang, B. Neutrino Spectra from Low and High Luminosity Populations of Gamma Ray Bursts. Astropart. Phys. 2007, 27, 386. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Razzaque, S.; Mészáros, P.; Dai, Z.-G. High-energy Cosmic Rays and Neutrinos from Semi-relativistic Hypernovae. Phys. Rev. D 2007, 76, 083009. [Google Scholar] [CrossRef]
- Bloom, J.S.; Giannios, D.; Metzger, B.D.; Cenko, S.B.; Perley, D.A.; Butler, N.R.; Tanvir, N.R.; Levan, A.J.; O’Brien, P.T.; Strubbe, L.E.; et al. A relativistic jetted outburst from a massive black hole fed by a tidally disrupted star. Science 2011, 333, 203. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Liu, R.-Y. Tidal disruption jets of supermassive black holes as hidden sources of cosmic rays: Explaining the IceCube TeV-PeV neutrinos. Phys. Rev. D 2016, 93, 083005. [Google Scholar] [CrossRef]
- Senno, N.; Murase, K.; Mészáros, P. High-energy Neutrino Flares from X-Ray Bright and Dark Tidal Disruption Events. Astrophys. J. 2017, 838, 3. [Google Scholar] [CrossRef]
- Dai, L.; Fang, K. Can tidal disruption events produce the IceCube neutrinos? Mon. Not. R. Astron. Soc. 2017, 469, 1354. [Google Scholar] [CrossRef]
- Lunardini, C.; Winter, W. High Energy Neutrinos from the Tidal Disruption of Stars. Phys. Rev. D 2017, 95, 123001. [Google Scholar] [CrossRef]
- Murase, K.; Kimura, S.S.; Zhang, B.T.; Oikonomou, F.; Petropoulou, M. High-Energy Neutrino and Gamma-Ray Emission from Tidal Disruption Events. Astrophys. J. 2020, 902, 108. [Google Scholar] [CrossRef]
- Hayasaki, K. Neutrinos from tidal disruption events. arXiv 2021, arXiv:2102.11879. [Google Scholar] [CrossRef]
- Farrar, G.R.; Gruzinov, A. Giant AGN Flares and Cosmic Ray Bursts. Astrophys. J. 2009, 693, 329. [Google Scholar] [CrossRef]
- Farrar, G.R.; Piran, T. Tidal disruption jets as the source of Ultra-High Energy Cosmic Rays. arXiv 2014, arXiv:1411.0704. [Google Scholar]
- Pitik, T.; Tamborra, I.; Angus, C.R.; Auchettl, K. Is the High-energy Neutrino Event IceCube-200530A Associated with a Hydrogen-rich Superluminous Supernova? Astrophys. J. 2022, 929, 163. [Google Scholar] [CrossRef]
- Liu, R.-Y.; Xi, S.-Q.; Wang, X.-Y. Neutrino emission from an off-axis jet driven by the tidal disruption event AT2019dsg. Phys. Rev. D 2020, 102, 083028. [Google Scholar] [CrossRef]
- Winter, W.; Lunardini, C. A concordance scenario for the observed neutrino from a tidal disruption event. Nat. Astron. 2021, 5, 472. [Google Scholar] [CrossRef]
- Wu, H.-J.; Mou, G.; Wang, K.; Wang, W.; Li, Z. Could TDE outflows produce the PeV neutrino events? Mon. Not. R. Astron. Soc. 2022, 514, 4406. [Google Scholar] [CrossRef]
- Winter, W.; Lunardini, C. Interpretation of the Observed Neutrino Emission from Three Tidal Disruption Events. Astrophys. J. 2023, 948, 42. [Google Scholar] [CrossRef]
- Gao, Y.; Solomon, P.M. The Star formation rate and dense molecular gas in galaxies. Astrophys. J. 2004, 606, 271. [Google Scholar] [CrossRef]
- Thomas, T.; Pfrommer, C.; Pakmor, R. Cosmic-ray-driven galactic winds: Transport modes of cosmic rays and Alfvén-wave dark regions. Mon. Not. R. Astron. Soc. 2023, 521, 3023. [Google Scholar] [CrossRef]
- Ruszkowski, M.; Pfrommer, C. Cosmic ray feedback in galaxies and galaxy clusters: A pedagogical introduction and a topical review of the acceleration, transport, observables, and dynamical impact of cosmic rays. Astron. Astrophys. Rev. 2023, 31, 4. [Google Scholar] [CrossRef]
- Loeb, A.; Waxman, E. The Cumulative background of high energy neutrinos from starburst galaxies. J. Cosmol. Astropart. Phys. 2006, 2006, 003. [Google Scholar] [CrossRef]
- Thompson, T.A.; Quataert, E.; Waxman, E.; Loeb, A. Assessing The Starburst Contribution to the Gamma-Ray and Neutrino Backgrounds. arXiv 2006, arXiv:astro-ph/0608699. [Google Scholar]
- Tamborra, I.; Ando, S.; Murase, K. Star-forming galaxies as the origin of diffuse high-energy backgrounds: Gamma-ray and neutrino connections, and implications for starburst history. J. Cosmol. Astropart. Phys. 2014, 2014, 043. [Google Scholar] [CrossRef]
- Chang, X.-C.; Wang, X.-Y. The diffuse gamma-ray flux associated with sub-PeV/PeV neutrinos from starburst galaxies. Astrophys. J. 2014, 793, 131. [Google Scholar] [CrossRef]
- Chakraborty, S.; Izaguirre, I. Star-forming galaxies as the origin of IceCube neutrinos: Reconciliation with Fermi-LAT gamma rays. arXiv 2016, arXiv:1607.03361. [Google Scholar]
- Palladino, A.; Fedynitch, A.; Rasmussen, R.W.; Taylor, A.M. IceCube Neutrinos from Hadronically Powered Gamma-Ray Galaxies. J. Cosmol. Astropart. Phys. 2019, 2019, 004. [Google Scholar] [CrossRef]
- Peretti, E.; Blasi, P.; Aharonian, F.; Morlino, G. Cosmic ray transport and radiative processes in nuclei of starburst galaxies. Mon. Not. R. Astron. Soc. 2019, 487, 168. [Google Scholar] [CrossRef]
- Peretti, E.; Blasi, P.; Aharonian, F.; Morlino, G.; Cristofari, P. Contribution of starburst nuclei to the diffuse gamma-ray and neutrino flux. Mon. Not. R. Astron. Soc. 2020, 493, 5880. [Google Scholar] [CrossRef]
- Ha, J.-H.; Ryu, D.; Kang, H. Modeling of Cosmic-Ray Production and Transport and Estimation of Gamma-Ray and Neutrino Emissions in Starburst Galaxies. arXiv 2020, arXiv:2008.06650. [Google Scholar] [CrossRef]
- Ambrosone, A.; Chianese, M.; Fiorillo, D.F.G.; Marinelli, A.; Miele, G. Could Nearby Star-forming Galaxies Light Up the Pointlike Neutrino Sky? Astrophys. J. Lett. 2021, 919, L32. [Google Scholar] [CrossRef]
- Merckx, Y.; Correa, P.; de Vries, K.D.; Kotera, K.; Privon, G.C.; van Eijndhoven, N. Investigating starburst-driven neutrino emission from galaxies in the Great Observatories All-Sky LIRG Survey. Phys. Rev. D 2023, 108, 023015. [Google Scholar] [CrossRef]
- Voelk, H.J. The correlation between radio and far-infrared emission for disk galaxies: A calorimeter theory. Astron. Astrophys. 1989, 218, 67. [Google Scholar]
- Peretti, E.; Morlino, G.; Blasi, P.; Cristofari, P. Particle acceleration and multimessenger emission from starburst-driven galactic winds. Mon. Not. R. Astron. Soc. 2022, 511, 1336. [Google Scholar] [CrossRef]
- Bechtol, K.; Ahlers, M.; Mauro, M.D.; Ajello, M.; Vandenbroucke, J. Evidence against star-forming galaxies as the dominant source of IceCube neutrinos. Astrophys. J. 2017, 836, 47. [Google Scholar] [CrossRef]
- Krumholz, M.R.; Crocker, R.M.; Xu, S.; Lazarian, A.; Rosevear, M.; Bedwell-Wilson, J. Cosmic ray transport in starburst galaxies. Mon. Not. R. Astron. Soc. 2020, 493, 2817. [Google Scholar] [CrossRef]
- Ambrosone, A.; Chianese, M.; Fiorillo, D.F.G.; Marinelli, A.; Miele, G. Observable signatures of cosmic rays transport in Starburst Galaxies on gamma-ray and neutrino observations. Mon. Not. R. Astron. Soc. 2022, 515, 5389. [Google Scholar] [CrossRef]
- Volk, H.J.; Aharonian, F.A.; Breitschwerdt, D. The nonthermal energy content and gamma-ray emission of starburst galaxies and clusters of galaxies. Space Sci. Rev. 1996, 75, 279. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Blasi, P.; Ptuskin, V.S. Clusters of Galaxies as a Storage Room for Cosmic Rays. Astrophys. J. 1997, 487, 529. [Google Scholar] [CrossRef]
- Loeb, A.; Waxman, E. Gamma-ray background from structure formation in the intergalactic medium. Nature 2000, 405, 156. [Google Scholar] [CrossRef] [PubMed]
- Keshet, U.; Waxman, E.; Loeb, A.; Springel, V.; Hernquist, L. Gamma-rays from intergalactic shocks. Astrophys. J. 2003, 585, 128. [Google Scholar] [CrossRef]
- Kushnir, D.; Waxman, E. Nonthermal emission from clusters of galaxies. J. Cosmol. Astropart. Phys. 2009, 2009, 002. [Google Scholar] [CrossRef]
- Zandanel, F.; Tamborra, I.; Gabici, S.; Ando, S. High-energy gamma-ray and neutrino backgrounds from clusters of galaxies and radio constraints. Astron. Astrophys. 2015, 578, A32. [Google Scholar] [CrossRef]
- Fang, K.; Olinto, A.V. High-energy neutrinos from sources in clusters of galaxies. Astrophys. J. 2016, 828, 37. [Google Scholar] [CrossRef]
- Fang, K.; Murase, K. Linking High-Energy Cosmic Particles by Black Hole Jets Embedded in Large-Scale Structures. Nat. Phys. 2018, 14, 396. [Google Scholar] [CrossRef]
- Hussain, S.; Batista, R.A.; Pino, E.M.d.D.; Dolag, K. High-energy neutrino production in clusters of galaxies. Mon. Not. R. Astron. Soc. 2021, 507, 1762. [Google Scholar] [CrossRef]
- Murase, K.; Inoue, S.; Nagataki, S. Cosmic Rays Above the Second Knee from Clusters of Galaxies and Associated High-Energy Neutrino Emission. Astrophys. J. Lett. 2008, 689, L105. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Zatsepin, G.T. Cosmic rays at ultrahigh-energies (neutrino?). Phys. Lett. B 1969, 28, 423. [Google Scholar] [CrossRef]
- Heinze, J.; Boncioli, D.; Bustamante, M.; Winter, W. Cosmogenic Neutrinos Challenge the Cosmic Ray Proton Dip Model. Astrophys. J. 2016, 825, 122. [Google Scholar] [CrossRef]
- Aloisio, R.; Boncioli, D.; di Matteo, A.; Grillo, A.F.; Petrera, S.; Salamida, F. Cosmogenic neutrinos and ultra-high energy cosmic ray models. J. Cosmol. Astropart. Phys. 2015, 2015, 006. [Google Scholar] [CrossRef]
- Ahlers, M.; Halzen, F. Minimal Cosmogenic Neutrinos. Phys. Rev. D 2012, 86, 083010. [Google Scholar] [CrossRef]
- Kotera, K.; Allard, D.; Olinto, A.V. Cosmogenic Neutrinos: Parameter space and detectabilty from PeV to ZeV. J. Cosmol. Astropart. Phys. 2010, 2010, 013. [Google Scholar] [CrossRef]
- Allard, D.; Ave, M.; Busca, N.; Malkan, M.; Olinto, A.; Parizot, E.; Stecker, F.; Yamamoto, T. Cosmogenic Neutrinos from the propagation of Ultrahigh Energy Nuclei. J. Cosmol. Astropart. Phys. 2006, 2006, 005. [Google Scholar] [CrossRef]
- Greisen, K. End to the cosmic ray spectrum? Phys. Rev. Lett. 1966, 16, 748. [Google Scholar] [CrossRef]
- Zatsepin, G.T.; Kuzmin, V.A. Upper limit of the spectrum of cosmic rays. JETP Lett. 1966, 4, 78. [Google Scholar]
- Abbasi, R.U. et al. [HiRes Collaboration] First observation of the Greisen-Zatsepin-Kuzmin suppression. Phys. Rev. Lett. 2008, 100, 101101. [Google Scholar] [CrossRef]
- Athar, H.; Lin, G.-L.; Tseng, J.-J. Muon pair production by electron photon scatterings. Phys. Rev. D 2001, 64, 071302. [Google Scholar] [CrossRef]
- Li, Z.; Waxman, E. EeV neutrinos associated with UHECR sources. In Proceedings of the 32nd International Cosmic Ray Conference, Merida, Mexico, 3–11 July 2007; Volume 8, p. 262. [Google Scholar] [CrossRef]
- Wang, K.; Liu, R.-Y.; Li, Z.; Dai, Z.-G. Neutrino Production in Electromagnetic Cascades: An extra component of cosmogenic neutrino at ultrahigh energies. Phys. Rev. D 2017, 95, 063010. [Google Scholar] [CrossRef]
- Esmaeili, A.; Capanema, A.; Esmaili, A.; Serpico, P.D. Ultrahigh energy neutrinos from high-redshift electromagnetic cascades. Phys. Rev. D 2022, 106, 123016. [Google Scholar] [CrossRef]
- Aab, A. et al. [Pierre Auger Collaboration] Depth of maximum of air-shower profiles at the Pierre Auger Observatory. II. Composition implications. Phys. Rev. D 2014, 90, 122006. [Google Scholar] [CrossRef]
- Aab, A. et al. [Pierre Auger Collaboration] Evidence for a mixed mass composition at the ‘ankle’ in the cosmic-ray spectrum. Phys. Lett. B 2016, 762, 288. [Google Scholar] [CrossRef]
- Aab, A. et al. [Pierre Auger Collaboration] Combined fit of spectrum and composition data as measured by the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 2017, 2017, 038, Erratum in J. Cosmol. Astropart. Phys. 2018, 2018, E02. [Google Scholar] [CrossRef]
- Aab, A. et al. [Pierre Auger Collaboration] Inferences on mass composition and tests of hadronic interactions from 0.3 to 100 EeV using the water-Cherenkov detectors of the Pierre Auger Observatory. Phys. Rev. D 2017, 96, 122003. [Google Scholar] [CrossRef]
- Abbasi, R.U. et al. [Telescope Array Collaboration] Mass composition of ultrahigh-energy cosmic rays with the Telescope Array Surface Detector data. Phys. Rev. D 2019, 99, 022002. [Google Scholar] [CrossRef]
- Aab, A. et al. [Pierre Auger Collaboration] Probing the origin of ultra-high-energy cosmic rays with neutrinos in the EeV energy range using the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 2019, 2019, 022. [Google Scholar] [CrossRef]
- Stecker, F.W. Diffuse Fluxes of Cosmic High-Energy Neutrinos. Astrophys. J. 1979, 228, 919. [Google Scholar] [CrossRef]
- Domokos, G.; Elliott, B.; Kovesi-Domokos, S. Cosmic neutrino production in the Milky Way. J. Phys. G 1993, 19, 899. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Gaisser, T.K.; Halzen, F.; Stanev, T. Diffuse radiation from cosmic ray interactions in the galaxy. Astropart. Phys. 1993, 1, 281. [Google Scholar] [CrossRef]
- Ingelman, G.; Thunman, M. Particle production in the interstellar medium. arXiv 1996, arXiv:hep-ph/9604286. [Google Scholar]
- Evoli, C.; Grasso, D.; Maccione, L. Diffuse Neutrino and Gamma-ray Emissions of the Galaxy above the TeV. J. Cosmol. Astropart. Phys. 2007, 2007, 003. [Google Scholar] [CrossRef]
- Ahlers, M.; Murase, K. Probing the Galactic Origin of the IceCube Excess with Gamma-Rays. Phys. Rev. D 2014, 90, 023010. [Google Scholar] [CrossRef]
- Gaggero, D.; Urbano, A.; Valli, M.; Ullio, P. Gamma-ray sky points to radial gradients in cosmic-ray transport. Phys. Rev. D 2015, 91, 083012. [Google Scholar] [CrossRef]
- Ahlers, M.; Bai, Y.; Barger, V.; Lu, R. Galactic neutrinos in the TeV to PeV range. Phys. Rev. D 2016, 93, 013009. [Google Scholar] [CrossRef]
- Gaggero, D.; Grasso, D.; Marinelli, A.; Urbano, A.; Valli, M. The gamma-ray and neutrino sky: A consistent picture of Fermi-LAT, Milagro, and IceCube results. Astrophys. J. Lett. 2015, 815, L25. [Google Scholar] [CrossRef]
- Gaggero, D.; Grasso, D.; Marinelli, A.; Taoso, M.; Urbano, A. Diffuse cosmic rays shining in the Galactic center: A novel interpretation of H.E.S.S. and Fermi-LAT γ-ray data. Phys. Rev. Lett. 2017, 119, 031101. [Google Scholar] [CrossRef] [PubMed]
- Albert, A. et al. [ANTARES Collaboration] New constraints on all flavor Galactic diffuse neutrino emission with the ANTARES telescope. Phys. Rev. D 2017, 96, 062001. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Constraints on Galactic Neutrino Emission with Seven Years of IceCube Data. Astrophys. J. 2017, 849, 67. [Google Scholar] [CrossRef]
- Abbasi, R. et al. [IceCube Collaboration] Observation of high-energy neutrinos from the Galactic plane. Science 2023, 380, adc9818. [Google Scholar] [CrossRef]
- Mandelartz, M.; Tjus, J.B. Prediction of the diffuse neutrino flux from cosmic ray interactions near supernova remnants. Astropart. Phys. 2015, 65, 80. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Goldberg, H.; Paul, T.C.; da Silva, L.H.M.; Vlcek, B.J. Estimating the contribution of Galactic sources to the diffuse neutrino flux. Phys. Rev. D 2014, 90, 123010. [Google Scholar] [CrossRef]
- Fang, K.; Murase, K. Multi-messenger Implications of Sub-PeV Diffuse Galactic Gamma-Ray Emission. arXiv 2021, arXiv:2104.09491. [Google Scholar]
- Sudoh, T.; Beacom, J.F. Where are Milky Way’s hadronic PeVatrons? Phys. Rev. D 2023, 107, 043002. [Google Scholar] [CrossRef]
- Sudoh, T.; Beacom, J.F. Identifying Extended PeVatron Sources via Neutrino Shower Detection. arXiv 2023, arXiv:2305.07043. [Google Scholar] [CrossRef]
- Schwefer, G.; Mertsch, P.; Wiebusch, C. Diffuse Emission of Galactic High-energy Neutrinos from a Global Fit of Cosmic Rays. Astrophys. J. 2023, 949, 16. [Google Scholar] [CrossRef]
- Ambrosone, A.; Groth, K.M.; Peretti, E.; Ahlers, M. Galactic Diffuse Neutrino Emission from Sources beyond the Discovery Horizon. arXiv 2023, arXiv:2306.17285. [Google Scholar] [CrossRef]
- Ciafaloni, P.; Comelli, D.; Riotto, A.; Sala, F.; Strumia, A.; Urbano, A. Weak Corrections are Relevant for Dark Matter Indirect Detection. J. Cosmol. Astropart. Phys. 2011, 2011, 019. [Google Scholar] [CrossRef]
- Argüelles, C.A.; Diaz, A.; Kheirandish, A.; Olivares-Del-Campo, A.; Safa, I.; Vincent, A.C. Dark matter annihilation to neutrinos. Rev. Mod. Phys. 2021, 93, 035007. [Google Scholar] [CrossRef]
- Abbasi, R. et al. [IceCube Collaboration] Searches for Connections between Dark Matter and High-Energy Neutrinos with IceCube. arXiv, 2022; arXiv:2205.12950. [Google Scholar]
- Abbasi, R. et al. [IceCube Collaboration] Search for neutrino lines from dark matter annihilation and decay with IceCube. arXiv 2023, arXiv:2303.13663. [Google Scholar]
- Griest, K.; Kamionkowski, M. Unitarity Limits on the Mass and Radius of Dark Matter Particles. Phys. Rev. Lett. 1990, 64, 615. [Google Scholar] [CrossRef]
- Smirnov, J.; Beacom, J.F. TeV-Scale Thermal WIMPs: Unitarity and its Consequences. Phys. Rev. D 2019, 100, 043029. [Google Scholar] [CrossRef]
- Esmaili, A.; Serpico, P.D. Are IceCube neutrinos unveiling PeV-scale decaying dark matter? J. Cosmol. Astropart. Phys. 2013, 2013, 054. [Google Scholar] [CrossRef]
- Feldstein, B.; Kusenko, A.; Matsumoto, S.; Yanagida, T.T. Neutrinos at IceCube from Heavy Decaying Dark Matter. Phys. Rev. D 2013, 88, 015004. [Google Scholar] [CrossRef]
- Bai, Y.; Lu, R.; Salvadó, J. Geometric Compatibility of IceCube TeV-PeV Neutrino Excess and its Galactic Dark Matter Origin. J. High Energy Phys. 2016, 2016, 161. [Google Scholar] [CrossRef]
- Ema, Y.; Jinno, R.; Moroi, T. Cosmic-Ray Neutrinos from the Decay of Long-Lived Particle and the Recent IceCube Result. Phys. Lett. B 2014, 733, 120. [Google Scholar] [CrossRef]
- Esmaili, A.; Kang, S.K.; Serpico, P.D. IceCube events and decaying dark matter: Hints and constraints. J. Cosmol. Astropart. Phys. 2014, 2014, 054. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Reno, M.H.; Sarcevic, I. Reconciling neutrino flux from heavy dark matter decay and recent events at IceCube. J. High Energy Phys. 2014, 2014, 110. [Google Scholar] [CrossRef]
- Murase, K.; Laha, R.; Ando, S.; Ahlers, M. Testing the Dark Matter Scenario for PeV Neutrinos Observed in IceCube. Phys. Rev. Lett. 2015, 115, 071301. [Google Scholar] [CrossRef] [PubMed]
- Chianese, M.; Miele, G.; Morisi, S.; Vitagliano, E. Low energy IceCube data and a possible Dark Matter related excess. Phys. Lett. B 2016, 757, 251. [Google Scholar] [CrossRef]
- Chianese, M.; Miele, G.; Morisi, S. Dark Matter interpretation of low energy IceCube MESE excess. J. Cosmol. Astropart. Phys. 2017, 2017, 007. [Google Scholar] [CrossRef]
- Chianese, M.; Miele, G.; Morisi, S. Interpreting IceCube 6-year HESE data as an evidence for hundred TeV decaying Dark Matter. Phys. Lett. B 2017, 773, 591. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Esmaili, A.; Palomares-Ruiz, S.; Sarcevic, I. Update on decaying and annihilating heavy dark matter with the 6-year IceCube HESE data. J. Cosmol. Astropart. Phys. 2019, 2019, 051. [Google Scholar] [CrossRef]
- Chianese, M.; Fiorillo, D.F.G.; Miele, G.; Morisi, S.; Pisanti, O. Decaying dark matter at IceCube and its signature on High Energy gamma experiments. J. Cosmol. Astropart. Phys. 2019, 2019, 046. [Google Scholar] [CrossRef]
- Dekker, A.; Chianese, M.; Ando, S. Probing dark matter signals in neutrino telescopes through angular power spectrum. J. Cosmol. Astropart. Phys. 2020, 2020, 007. [Google Scholar] [CrossRef]
- Argüelles, C.A.; Delgado, D.; Friedlander, A.; Kheirandish, A.; Safa, I.; Vincent, A.C.; White, H. Dark Matter decay to neutrinos. arXiv 2022, arXiv:2210.01303. [Google Scholar] [CrossRef]
- Cohen, T.; Murase, K.; Rodd, N.L.; Safdi, B.R.; Soreq, Y. γ-ray Constraints on Decaying Dark Matter and Implications for IceCube. Phys. Rev. Lett. 2017, 119, 021102. [Google Scholar] [CrossRef] [PubMed]
- Chianese, M.; Fiorillo, D.F.G.; Hajjar, R.; Miele, G.; Saviano, N. Constraints on heavy decaying dark matter with current gamma-ray measurements. J. Cosmol. Astropart. Phys. 2021, 2021, 035. [Google Scholar] [CrossRef]
- Cao, Z. et al. [LHAASO Collaboration] Constraints on Heavy Decaying Dark Matter from 570 Days of LHAASO Observations. Phys. Rev. Lett. 2022, 129, 261103. [Google Scholar] [CrossRef] [PubMed]
- Guépin, C.; Aloisio, R.; Anchordoqui, L.A.; Cummings, A.; Krizmanic, J.F.; Olinto, A.V.; Reno, M.H.; Venters, T.M. Indirect dark matter searches at ultrahigh energy neutrino detectors. Phys. Rev. D 2021, 104, 083002. [Google Scholar] [CrossRef]
- Chianese, M.; Fiorillo, D.F.G.; Hajjar, R.; Miele, G.; Morisi, S.; Saviano, N. Heavy decaying dark matter at future neutrino radio telescopes. J. Cosmol. Astropart. Phys. 2021, 2021, 074. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Valera, V.B.; Bustamante, M.; Winter, W. Searches for dark matter decay with ultrahigh-energy neutrinos endure backgrounds. Phys. Rev. D 2023, 108, 103012. [Google Scholar] [CrossRef]
- Cappiello, C.V.; Ng, K.C.Y.; Beacom, J.F. Reverse Direct Detection: Cosmic Ray Scattering with Light Dark Matter. Phys. Rev. D 2019, 99, 063004. [Google Scholar] [CrossRef]
- Ambrosone, A.; Chianese, M.; Fiorillo, D.F.G.; Marinelli, A.; Miele, G. Starburst Galactic Nuclei as Light Dark Matter Laboratories. Phys. Rev. Lett. 2023, 131, 111003. [Google Scholar] [CrossRef]
- Herrera, G.; Murase, K. Probing Light Dark Matter through Cosmic-Ray Cooling in Active Galactic Nuclei. arXiv 2023, arXiv:2307.09460. [Google Scholar]
- Kolb, E.W.; Turner, M.S. Supernova SN 1987a and the Secret Interactions of Neutrinos. Phys. Rev. D 1987, 36, 2895. [Google Scholar] [CrossRef]
- Ioka, K.; Murase, K. IceCube PeV–EeV neutrinos and secret interactions of neutrinos. PTEP 2014, 2014, 061E01. [Google Scholar] [CrossRef]
- Ng, K.C.Y.; Beacom, J.F. Cosmic neutrino cascades from secret neutrino interactions. Phys. Rev. D 2014, 90, 065035, Erratum in Phys. Rev. D 2014, 90, 089904. [Google Scholar] [CrossRef]
- Ibe, M.; Kaneta, K. Cosmic neutrino background absorption line in the neutrino spectrum at IceCube. Phys. Rev. D 2014, 90, 053011. [Google Scholar] [CrossRef]
- Shoemaker, I.M.; Murase, K. Probing BSM Neutrino Physics with Flavor and Spectral Distortions: Prospects for Future High-Energy Neutrino Telescopes. Phys. Rev. D 2016, 93, 085004. [Google Scholar] [CrossRef]
- Kamada, A.; Yu, H.-B. Coherent Propagation of PeV Neutrinos and the Dip in the Neutrino Spectrum at IceCube. Phys. Rev. D 2015, 92, 113004. [Google Scholar] [CrossRef]
- DiFranzo, A.; Hooper, D. Searching for MeV-Scale Gauge Bosons with IceCube. Phys. Rev. D 2015, 92, 095007. [Google Scholar] [CrossRef]
- Kelly, K.J.; Machado, P.A.N. Multimessenger Astronomy and New Neutrino Physics. J. Cosmol. Astropart. Phys. 2018, 2018, 048. [Google Scholar] [CrossRef]
- Barenboim, G.; Denton, P.B.; Oldengott, I.M. Constraints on inflation with an extended neutrino sector. Phys. Rev. D 2019, 99, 083515. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Morisi, S.; Miele, G.; Saviano, N. Observable features in ultrahigh energy neutrinos due to active-sterile secret interactions. Phys. Rev. D 2020, 102, 083014. [Google Scholar] [CrossRef]
- Creque-Sarbinowski, C.; Hyde, J.; Kamionkowski, M. Resonant neutrino self-interactions. Phys. Rev. D 2021, 103, 023527. [Google Scholar] [CrossRef]
- Esteban, I.; Pandey, S.; Brdar, V.; Beacom, J.F. Probing secret interactions of astrophysical neutrinos in the high-statistics era. Phys. Rev. D 2021, 104, 123014. [Google Scholar] [CrossRef]
- Bustamante, M.; Rosenstrøm, C.; Shalgar, S.; Tamborra, I. Bounds on secret neutrino interactions from high-energy astrophysical neutrinos. Phys. Rev. D 2020, 101, 123024. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Miele, G.; Morisi, S.; Saviano, N. Cosmogenic neutrino fluxes under the effect of active-sterile secret interactions. Phys. Rev. D 2020, 101, 083024. [Google Scholar] [CrossRef]
- Murase, K.; Shoemaker, I.M. Neutrino Echoes from Multimessenger Transient Sources. Phys. Rev. Lett. 2019, 123, 241102. [Google Scholar] [CrossRef]
- Carpio, J.A.; Murase, K. Simulating neutrino echoes induced by secret neutrino interactions. J. Cosmol. Astropart. Phys. 2023, 2023, 042. [Google Scholar] [CrossRef]
- Ahlers, M.; Bustamante, M.; Mu, S. Unitarity Bounds of Astrophysical Neutrinos. Phys. Rev. D 2018, 98, 123023. [Google Scholar] [CrossRef]
- Beacom, J.F.; Bell, N.F.; Hooper, D.; Learned, J.G.; Pakvasa, S.; Weiler, T.J. PseudoDirac neutrinos: A Challenge for neutrino telescopes. Phys. Rev. Lett. 2004, 92, 011101. [Google Scholar] [CrossRef] [PubMed]
- Keranen, P.; Maalampi, J.; Myyrylainen, M.; Riittinen, J. Effects of sterile neutrinos on the ultrahigh-energy cosmic neutrino flux. Phys. Lett. B 2003, 574, 162. [Google Scholar] [CrossRef]
- Esmaili, A. Pseudo-Dirac Neutrino Scenario: Cosmic Neutrinos at Neutrino Telescopes. Phys. Rev. D 2010, 81, 013006. [Google Scholar] [CrossRef]
- Esmaili, A.; Farzan, Y. Implications of the Pseudo-Dirac Scenario for Ultra High Energy Neutrinos from GRBs. J. Cosmol. Astropart. Phys. 2012, 2012, 014. [Google Scholar] [CrossRef]
- Pakvasa, S.; Joshipura, A.; Mohanty, S. Explanation for the low flux of high energy astrophysical muon-neutrinos. Phys. Rev. Lett. 2013, 110, 171802. [Google Scholar] [CrossRef]
- Joshipura, A.S.; Mohanty, S.; Pakvasa, S. Pseudo-Dirac neutrinos via a mirror world and depletion of ultrahigh energy neutrinos. Phys. Rev. D 2014, 89, 033003. [Google Scholar] [CrossRef]
- Rasmussen, R.W.; Lechner, L.; Ackermann, M.; Kowalski, M.; Winter, W. Astrophysical neutrinos flavored with Beyond the Standard Model physics. Phys. Rev. D 2017, 96, 083018. [Google Scholar] [CrossRef]
- Brdar, V.; Hansen, R.S.L. IceCube Flavor Ratios with Identified Astrophysical Sources: Towards Improving New Physics Testability. J. Cosmol. Astropart. Phys. 2019, 2019, 023. [Google Scholar] [CrossRef]
- Rink, T.; Sen, M. Constraints on pseudo-Dirac neutrinos using high-energy neutrinos from NGC 1068. arXiv 2022, arXiv:2211.16520. [Google Scholar] [CrossRef]
- Carloni, K.; Arguelles, C.A.; Martinez-Soler, I.; Babu, K.S.; Dev, P.S.B. Probing Pseudo-Dirac Neutrinos with Astrophysical Sources at IceCube. arXiv 2022, arXiv:2212.00737. [Google Scholar]
- Beacom, J.F.; Bell, N.F.; Hooper, D.; Pakvasa, S.; Weiler, T.J. Decay of High-Energy Astrophysical Neutrinos. Phys. Rev. Lett. 2003, 90, 181301. [Google Scholar] [CrossRef] [PubMed]
- Meloni, D.; Ohlsson, T. Neutrino flux ratios at neutrino telescopes: The Role of uncertainties of neutrino mixing parameters and applications to neutrino decay. Phys. Rev. D 2007, 75, 125017. [Google Scholar] [CrossRef]
- Maltoni, M.; Winter, W. Testing neutrino oscillations plus decay with neutrino telescopes. J. High Energy Phys. 2008, 2008, 064. [Google Scholar] [CrossRef]
- Bustamante, M.; Gago, A.M.; Pena-Garay, C.P. Energy-Independent New Physics in the Flavour Ratios of High-Energy Astrophysical Neutrinos. J. High Energy Phys. 2010, 2010, 066. [Google Scholar] [CrossRef]
- Baerwald, P.; Bustamante, M.; Winter, W. Neutrino Decays over Cosmological Distances and the Implications for Neutrino Telescopes. J. Cosmol. Astropart. Phys. 2012, 2012, 020. [Google Scholar] [CrossRef]
- Dorame, L.; Miranda, O.G.; Valle, J.W.F. Invisible decays of ultra-high energy neutrinos. Front. Phys. 2013, 1, 25. [Google Scholar] [CrossRef]
- Bustamante, M.; Beacom, J.F.; Winter, W. Theoretically palatable flavor combinations of astrophysical neutrinos. Phys. Rev. Lett. 2015, 115, 161302. [Google Scholar] [CrossRef]
- Huang, Y.; Ma, B.-Q. Neutrino properties from ultra-high energy cosmic neutrinos. Universe 2015, 3, 15–21. [Google Scholar]
- Bustamante, M.; Beacom, J.F.; Murase, K. Testing decay of astrophysical neutrinos with incomplete information. Phys. Rev. D 2017, 95, 063013. [Google Scholar] [CrossRef]
- Argüelles, C.A.; Katori, T.; Salvadó, J. New Physics in Astrophysical Neutrino Flavor. Phys. Rev. Lett. 2015, 115, 161303. [Google Scholar] [CrossRef] [PubMed]
- Aartsen, M.G. et al. [IceCube Collaboration] Neutrino Interferometry for High-Precision Tests of Lorentz Symmetry with IceCube. Nat. Phys. 2018, 14, 961. [Google Scholar] [CrossRef]
- Abbasi, R. et al. [IceCube Collaboration] Search for quantum gravity using astrophysical neutrino flavour with IceCube. Nat. Phys. 2022, 18, 1287. [Google Scholar] [CrossRef]
- Testagrossa, F.; Fiorillo, D.F.G.; Bustamante, M. Two-detector flavor sensitivity to ultra-high-energy cosmic neutrinos. arXiv 2023, arXiv:2310.12215. [Google Scholar]
- Gasperini, M. Experimental Constraints on a Minimal and Nonminimal Violation of the Equivalence Principle in the Oscillations of Massive Neutrinos. Phys. Rev. D 1989, 39, 3606. [Google Scholar] [CrossRef]
- Sabbata, V.D.; Gasperini, M. Neutrino Oscillations in the Presence of Torsion. Nuovo C. A 1981, 65, 479. [Google Scholar] [CrossRef]
- Glashow, S.L.; Halprin, A.; Krastev, P.I.; Leung, C.N.; Pantaleone, J.T. Comments on neutrino tests of special relativity. Phys. Rev. D 1997, 56, 2433. [Google Scholar] [CrossRef]
- Minakata, H.; Smirnov, A.Y. High-energy cosmic neutrinos and the equivalence principle. Phys. Rev. D 1996, 54, 3698. [Google Scholar] [CrossRef] [PubMed]
- Fiorillo, D.F.G.; Mangano, G.; Morisi, S.; Pisanti, O. IceCube constraints on violation of equivalence principle. J. Cosmol. Astropart. Phys. 2021, 2021, 079. [Google Scholar] [CrossRef]
- Xu, X.-J.; He, H.-J.; Rodejohann, W. Constraining Astrophysical Neutrino Flavor Composition from Leptonic Unitarity. J. Cosmol. Astropart. Phys. 2014, 2014, 039. [Google Scholar] [CrossRef]
- Fu, L.; Ho, C.M.; Weiler, T.J. Aspects of the Flavor Triangle for Cosmic Neutrino Propagation. Phys. Rev. D 2015, 91, 053001. [Google Scholar] [CrossRef]
- Ahlers, M.; Bustamante, M.; Willesen, N.G.N. Flavors of astrophysical neutrinos with active-sterile mixing. J. Cosmol. Astropart. Phys. 2021, 2021, 029. [Google Scholar] [CrossRef]
- Hooper, D. Measuring high-energy neutrino nucleon cross-sections with future neutrino telescopes. Phys. Rev. D 2002, 65, 097303. [Google Scholar] [CrossRef]
- Hussain, S.; Marfatia, D.; McKay, D.W.; Seckel, D. Cross section dependence of event rates at neutrino telescopes. Phys. Rev. Lett. 2006, 97, 161101. [Google Scholar] [CrossRef]
- Borriello, E.; Cuoco, A.; Mangano, G.; Miele, G.; Pastor, S.; Pisanti, O.; Serpico, P.D. Disentangling neutrino-nucleon cross section and high energy neutrino flux with a km3 neutrino telescope. Phys. Rev. D 2008, 77, 045019. [Google Scholar] [CrossRef]
- Hussain, S.; Marfatia, D.; McKay, D.W. Upward shower rates at neutrino telescopes directly determine the neutrino flux. Phys. Rev. D 2008, 77, 107304. [Google Scholar] [CrossRef]
- Connolly, A.; Thorne, R.S.; Waters, D. Calculation of High Energy Neutrino-Nucleon Cross Sections and Uncertainties Using the MSTW Parton Distribution Functions and Implications for Future Experiments. Phys. Rev. D 2011, 83, 113009. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Measurement of the multi-TeV neutrino cross section with IceCube using Earth absorption. Nature 2017, 551, 596. [Google Scholar] [CrossRef]
- Bustamante, M.; Connolly, A. Extracting the Energy-Dependent Neutrino-Nucleon Cross Section above 10 TeV Using IceCube Showers. Phys. Rev. Lett. 2019, 122, 041101. [Google Scholar] [CrossRef] [PubMed]
- Marfatia, D.; McKay, D.W.; Weiler, T.J. New physics with ultra-high-energy neutrinos. Phys. Lett. B 2015, 748, 113. [Google Scholar] [CrossRef]
- Valera, V.B.; Bustamante, M.; Glaser, C. The ultra-high-energy neutrino-nucleon cross section: Measurement forecasts for an era of cosmic EeV-neutrino discovery. J. High Energy Phys. 2022, 2022, 105. [Google Scholar] [CrossRef]
- Esteban, I.; Prohira, S.; Beacom, J.F. Detector requirements for model-independent measurements of ultrahigh energy neutrino cross sections. Phys. Rev. D 2022, 106, 023021. [Google Scholar] [CrossRef]
- Valera, V.B.; Bustamante, M.; Mena, O. Joint measurement of the ultra-high-energy neutrino spectrum and cross section. arXiv 2023, arXiv:2308.07709. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiorillo, D.F.G. High-Energy and Ultra-High-Energy Neutrino Astrophysics. Universe 2024, 10, 149. https://doi.org/10.3390/universe10030149
Fiorillo DFG. High-Energy and Ultra-High-Energy Neutrino Astrophysics. Universe. 2024; 10(3):149. https://doi.org/10.3390/universe10030149
Chicago/Turabian StyleFiorillo, Damiano F. G. 2024. "High-Energy and Ultra-High-Energy Neutrino Astrophysics" Universe 10, no. 3: 149. https://doi.org/10.3390/universe10030149
APA StyleFiorillo, D. F. G. (2024). High-Energy and Ultra-High-Energy Neutrino Astrophysics. Universe, 10(3), 149. https://doi.org/10.3390/universe10030149





