Mechanisms for Producing Primordial Black Holes from Inflationary Models beyond Fine-Tuning
Abstract
1. Introduction
2. Fine-Tuning
3. Single-Field Models
3.1. Inflection Point
3.1.1. Description of the Mechanism
3.1.2. The Issue of Fine-Tuning
3.2. Step-like Potential
3.2.1. An Alternative Single-Field Mechanism
3.2.2. Studying the Fine-Tuning
4. Multi-Field Models
4.1. Two Field Model with a Non-Canonical Kinetic Term
4.2. Hybrid Model
5. Spectator Field
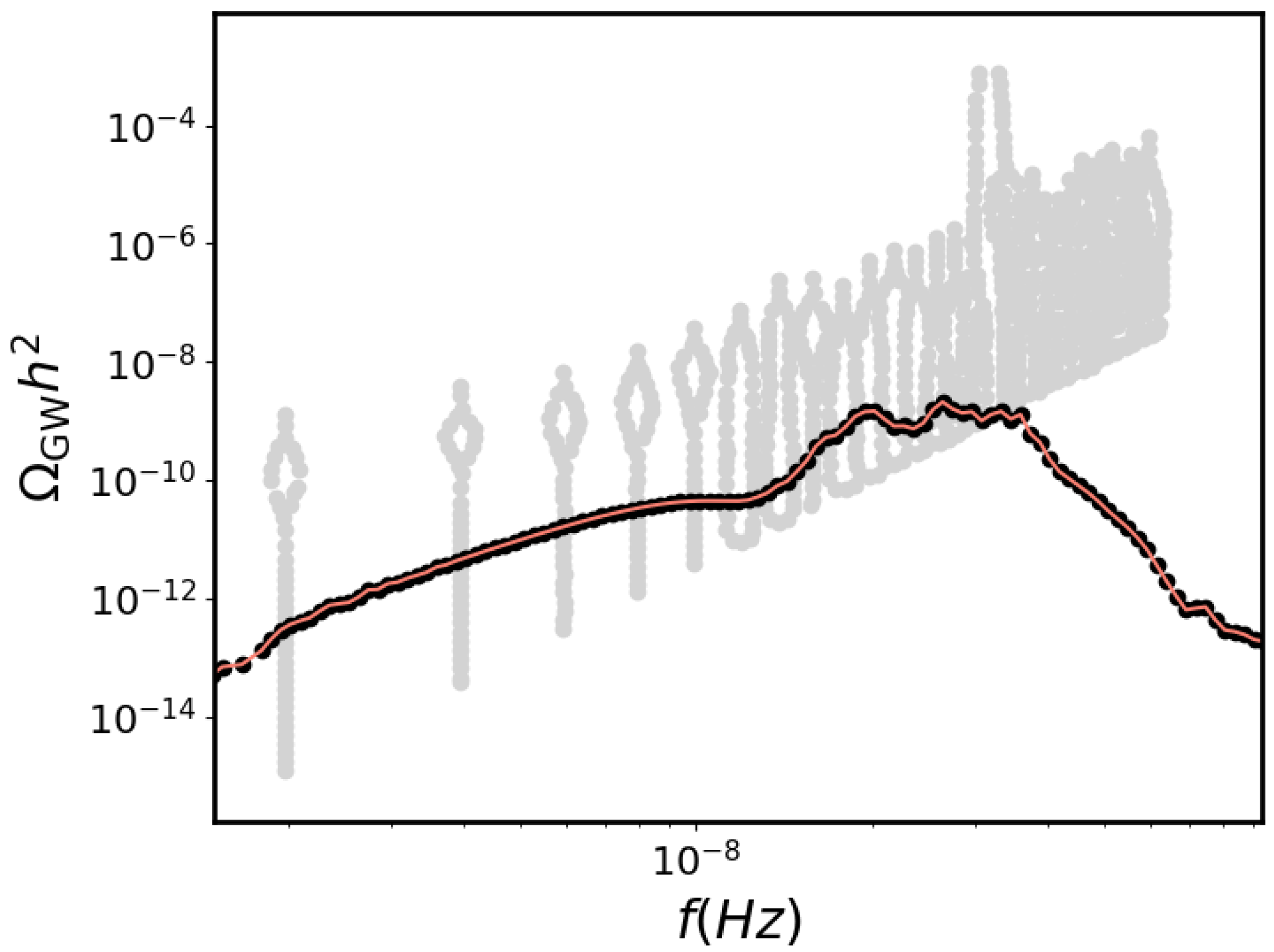
6. Step-Features Potential over Inflection-Point: An Additional Advantage in Implementation of Gws
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
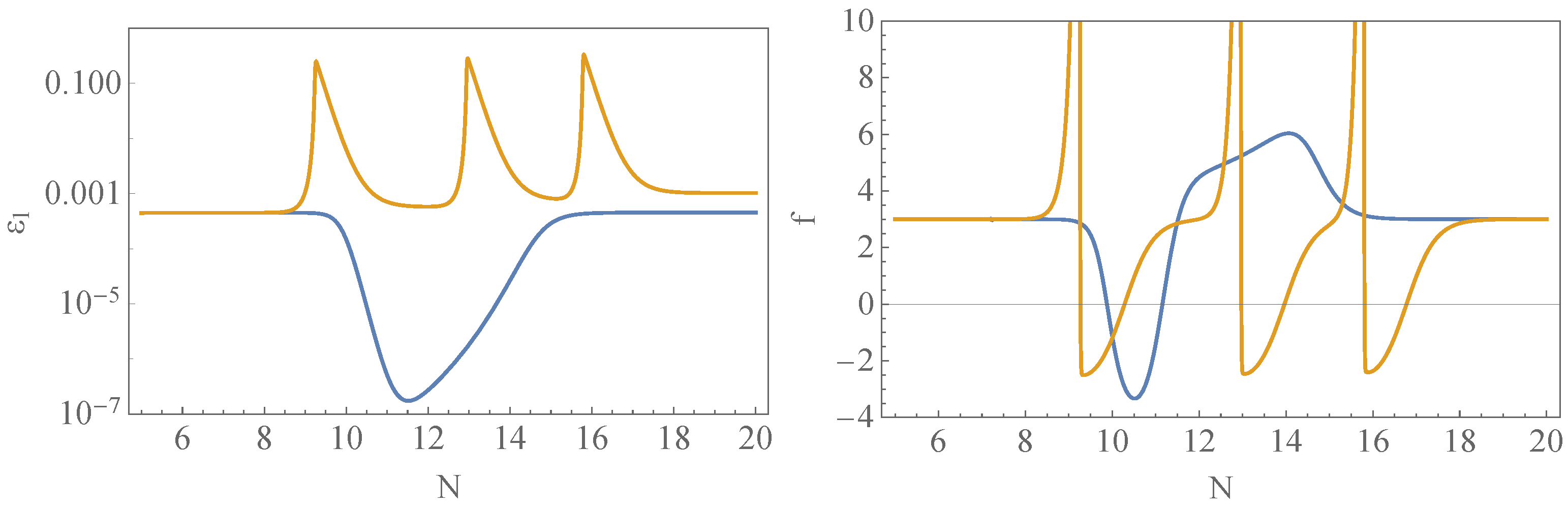
Appendix B
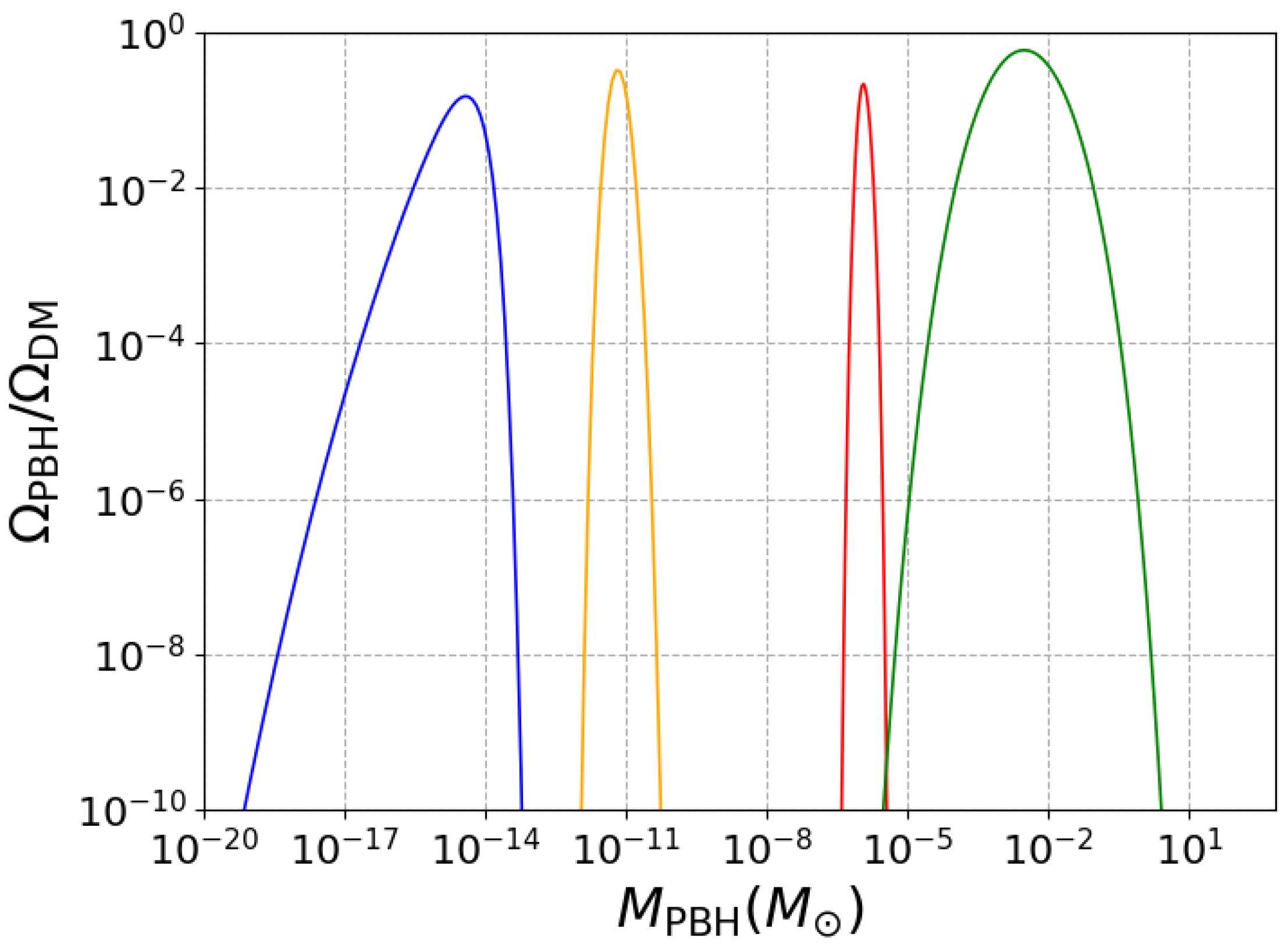
Appendix C
References
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101, Erratum in Phys. Rev. Lett. 2018, 121, 129901. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence. Astrophys. J. Lett. 2017, 851, L35. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef]
- Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Bécsy, B.; Blecha, L.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; et al. The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background. Astrophys. J. Lett. 2023, 951, L8. [Google Scholar] [CrossRef]
- Agazie, G.; Alam, M.F.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Blecha, L.; Bonidie, V.; Brazier, A.; Brook, P.R.; et al. The NANOGrav 15 yr Data Set: Observations and Timing of 68 Millisecond Pulsars. Astrophys. J. Lett. 2023, 951, L9. [Google Scholar] [CrossRef]
- Afzal, A.; Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Bécsy, B.; Blanco-Pillado, J.J.; Blecha, L.; Boddy, K.K.; et al. The NANOGrav 15 yr Data Set: Search for Signals from New Physics. Astrophys. J. Lett. 2023, 951, L11. [Google Scholar] [CrossRef]
- Antoniadis, J.; Arumugam, P.; Arumugam, S.; Babak, S.; Bagchi, M.; Nielsen, A.S.B.; Bassa, C.G.; Bathula, A.; Berthereau, A.; Bonetti, M.; et al. The second data release from the European Pulsar Timing Array - III. Search for gravitational wave signals. Astron. Astrophys. 2023, 678, A50. [Google Scholar] [CrossRef]
- Antoniadis, J.; Babak, S.; Nielsen, A.S.B.; Bassa, C.G.; Berthereau, A.; Bonetti, M.; Bortolas, E.; Brook, P.R.; Burgay, M.A.R.T.A.; Caballero, R.N.; et al. The second data release from the European Pulsar Timing Array-I. The dataset and timing analysis. Astron. Astrophys. 2023, 678, A48. [Google Scholar] [CrossRef]
- Antoniadis, J.; Arumugam, P.; Arumugam, S.; Babak, S.; Bagchi, M.; Nielsen, A.S.B.; Bassa, C.G.; Bathula, A.; Berthereau, A.; Bonetti, M.; et al. The second data release from the European Pulsar Timing Array-II. Customised pulsar noise models for spatially correlated gravitational waves. Astron. Astrophys. 2023, 678, A49. [Google Scholar] [CrossRef]
- Antoniadis, J.; Theureau, G.; Truant, R.J.; Postnov, K.; Burgay, M.; Gupta, Y.; Nielsen, A.S.B.; Verbiest, J.P.W.; Mickaliger, M.B.; Arumugam, S.; et al. The second data release from the European Pulsar Timing Array: V. Implications for massive black holes, dark matter and the early Universe. arXiv 2023, arXiv:2306.16227. [Google Scholar]
- Özsoy, O.; Tasinato, G. Inflation and Primordial Black Holes. Universe 2023, 9, 203. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial black holes—Perspectives in gravitational wave astronomy. Class. Quant. Grav. 2018, 35, 063001. [Google Scholar] [CrossRef]
- Carr, B.; Clesse, S.; Garcia-Bellido, J.; Hawkins, M.; Kuhnel, F. Observational evidence for primordial black holes: A positivist perspective. Phys. Rept. 2024, 1054, 1–68. [Google Scholar] [CrossRef]
- Khlopov, M.Y. Primordial Black Holes. Res. Astron. Astrophys. 2010, 10, 495–528. [Google Scholar] [CrossRef]
- Kuhnel, F.; Stamou, I. Reconstructing Primordial Black Hole Power Spectra from Gravitational Waves. arXiv 2024, arXiv:2404.06547. [Google Scholar]
- Ellis, J.; Fairbairn, M.; Franciolini, G.; Hütsi, G.; Iovino, A.; Lewicki, M.; Raidal, M.; Urrutia, J.; Vaskonen, V.; Veermäe, H. What is the source of the PTA GW signal? Phys. Rev. D 2024, 109, 023522. [Google Scholar] [CrossRef]
- Vaskonen, V.; Veermäe, H. Did NANOGrav see a signal from primordial black hole formation? Phys. Rev. Lett. 2021, 126, 051303. [Google Scholar] [CrossRef] [PubMed]
- Escrivà, A.; Kuhnel, F.; Tada, Y. Primordial Black Holes. arXiv 2022, arXiv:2211.05767. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Ruiz Morales, E. Primordial black holes from single field models of inflation. Phys. Dark Univ. 2017, 18, 47–54. [Google Scholar] [CrossRef]
- Hertzberg, M.P.; Yamada, M. Primordial Black Holes from Polynomial Potentials in Single Field Inflation. Phys. Rev. D 2018, 97, 083509. [Google Scholar] [CrossRef]
- Ballesteros, G.; Taoso, M. Primordial black hole dark matter from single field inflation. Phys. Rev. D 2018, 97, 023501. [Google Scholar] [CrossRef]
- Ballesteros, G.; Rey, J.; Rompineve, F. Detuning primordial black hole dark matter with early matter domination and axion monodromy. JCAP 2020, 06, 014. [Google Scholar] [CrossRef]
- Cicoli, M.; Diaz, V.A.; Pedro, F.G. Primordial Black Holes from String Inflation. JCAP 2018, 06, 034. [Google Scholar] [CrossRef]
- Stamou, I.D. Mechanisms of producing primordial black holes by breaking the SU(2, 1)/SU(2) × U(1) symmetry. Phys. Rev. D 2021, 103, 083512. [Google Scholar] [CrossRef]
- Spanos, V.C.; Stamou, I.D. Gravitational waves from no-scale supergravity. Eur. Phys. J. C 2023, 83, 4. [Google Scholar] [CrossRef]
- Dalianis, I.; Kehagias, A.; Tringas, G. Primordial black holes from α-attractors. JCAP 2019, 1, 037. [Google Scholar] [CrossRef]
- Germani, C.; Prokopec, T. On primordial black holes from an inflection point. Phys. Dark Univ. 2017, 18, 6–10. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; Garcia-Bellido, J.; Ruiz Morales, E. Primordial Black Hole production in Critical Higgs Inflation. Phys. Lett. B 2018, 776, 345–349. [Google Scholar] [CrossRef]
- Özsoy, O.; Parameswaran, S.; Tasinato, G.; Zavala, I. Mechanisms for Primordial Black Hole Production in String Theory. JCAP 2018, 7, 005. [Google Scholar] [CrossRef]
- Özsoy, O.; Lalak, Z. Primordial black holes as dark matter and gravitational waves from bumpy axion inflation. JCAP 2021, 1, 040. [Google Scholar] [CrossRef]
- Karam, A.; Koivunen, N.; Tomberg, E.; Vaskonen, V.; Veermäe, H. Anatomy of single-field inflationary models for primordial black holes. JCAP 2023, 3, 013. [Google Scholar] [CrossRef]
- Aldabergenov, Y.; Ketov, S.V. Primordial Black Holes from Volkov–Akulov–Starobinsky Supergravity. Fortsch. Phys. 2023, 71, 2300039. [Google Scholar] [CrossRef]
- Kannike, K.; Marzola, L.; Raidal, M.; Veermäe, H. Single Field Double Inflation and Primordial Black Holes. JCAP 2017, 9, 020. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kusenko, A.; Tada, Y.; Yanagida, T.T. Primordial black holes as dark matter in supergravity inflation models. Phys. Rev. D 2016, 94, 083523. [Google Scholar] [CrossRef]
- Choudhury, S.; Mazumdar, A. Primordial blackholes and gravitational waves for an inflection-point model of inflation. Phys. Lett. B 2014, 733, 270–275. [Google Scholar] [CrossRef]
- Cole, P.S.; Gow, A.D.; Byrnes, C.T.; Patil, S.P. Primordial black holes from single-field inflation: A fine-tuning audit. JCAP 2023, 08, 031. [Google Scholar] [CrossRef]
- Inomata, K.; McDonough, E.; Hu, W. Amplification of primordial perturbations from the rise or fall of the inflaton. JCAP 2022, 02, 031. [Google Scholar] [CrossRef]
- Cotner, E.; Kusenko, A. Primordial black holes from scalar field evolution in the early universe. Phys. Rev. D 2017, 96, 103002. [Google Scholar] [CrossRef]
- Kefala, K.; Kodaxis, G.P.; Stamou, I.D.; Tetradis, N. Features of the inflaton potential and the power spectrum of cosmological perturbations. Phys. Rev. D 2021, 104, 023506. [Google Scholar] [CrossRef]
- Dalianis, I.; Kodaxis, G.P.; Stamou, I.D.; Tetradis, N.; Tsigkas-Kouvelis, A. Spectrum oscillations from features in the potential of single-field inflation. Phys. Rev. D 2021, 104, 103510. [Google Scholar] [CrossRef]
- Cai, Y.F.; Ma, X.H.; Sasaki, M.; Wang, D.G.; Zhou, Z. One small step for an inflaton, one giant leap for inflation: A novel non-Gaussian tail and primordial black holes. Phys. Lett. B 2022, 834, 137461. [Google Scholar] [CrossRef]
- Choudhury, S.; Panda, S.; Sami, M. PBH formation in EFT of single field inflation with sharp transition. Phys. Lett. B 2023, 845, 138123. [Google Scholar] [CrossRef]
- Choudhury, S.; Karde, A.; Padiyar, P.; Sami, M. Primordial Black Holes from Effective Field Theory of Stochastic Single Field Inflation at NNNLO. arXiv 2024, arXiv:2403.13484. [Google Scholar]
- Gu, B.M.; Shu, F.W.; Yang, K. Inflation with shallow dip and primordial black holes. arXiv 2023, arXiv:2307.00510. [Google Scholar]
- Drees, M.; Erfani, E. Running Spectral Index and Formation of Primordial Black Hole in Single Field Inflation Models. JCAP 2012, 01, 035. [Google Scholar] [CrossRef]
- Domènech, G.; Vargas, G.; Vargas, T. An exact model for enhancing/suppressing primordial fluctuations. JCAP 2024, 3, 002. [Google Scholar] [CrossRef]
- Caravano, A.; Inomata, K.; Renaux-Petel, S. The Inflationary Butterfly Effect: Non-Perturbative Dynamics From Small-Scale Features. arXiv 2024, arXiv:2403.12811. [Google Scholar]
- Sharma, M.K.; Sami, M.; Mota, D.F. Generic Predictions for Primordial Perturbations and their implications. arXiv 2024, arXiv:2401.11142. [Google Scholar]
- Dimastrogiovanni, E.; Fasiello, M.; Papageorgiou, A. A novel PBH production mechanism from non-Abelian gauge fields during inflation. arXiv 2024, arXiv:2403.13581. [Google Scholar]
- Karam, A.; Koivunen, N.; Tomberg, E.; Racioppi, A.; Veermäe, H. Primordial black holes and inflation from double-well potentials. JCAP 2023, 9, 002. [Google Scholar] [CrossRef]
- Fumagalli, J.; Renaux-Petel, S.; Witkowski, L.T. Oscillations in the stochastic gravitational wave background from sharp features and particle production during inflation. JCAP 2021, 8, 030. [Google Scholar] [CrossRef]
- Palma, G.A.; Sypsas, S.; Zenteno, C. Seeding primordial black holes in multifield inflation. Phys. Rev. Lett. 2020, 125, 121301. [Google Scholar] [CrossRef] [PubMed]
- Anguelova, L. On Primordial Black Holes from Rapid Turns in Two-field Models. JCAP 2021, 6, 004. [Google Scholar] [CrossRef]
- Iacconi, L.; Mulryne, D.J. Multi-field inflation with large scalar fluctuations: Non-Gaussianity and perturbativity. JCAP 2023, 9, 033. [Google Scholar] [CrossRef]
- Zhou, Z.; Jiang, J.; Cai, Y.F.; Sasaki, M.; Pi, S. Primordial black holes and gravitational waves from resonant amplification during inflation. Phys. Rev. D 2020, 102, 103527. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Spanos, V.C.; Stamou, I.D. Primordial black holes and gravitational waves in multiaxion-Chern-Simons inflation. Phys. Rev. D 2022, 106, 063532. [Google Scholar] [CrossRef]
- Kawai, S.; Kim, J. Primordial black holes and gravitational waves from nonminimally coupled supergravity inflation. Phys. Rev. D 2023, 107, 043523. [Google Scholar] [CrossRef]
- Aldabergenov, Y.; Addazi, A.; Ketov, S.V. Inflation, SUSY breaking, and primordial black holes in modified supergravity coupled to chiral matter. Eur. Phys. J. C 2022, 82, 681. [Google Scholar] [CrossRef]
- Braglia, M.; Hazra, D.K.; Finelli, F.; Smoot, G.F.; Sriramkumar, L.; Starobinsky, A.A. Generating PBHs and small-scale GWs in two-field models of inflation. JCAP 2020, 8, 001. [Google Scholar] [CrossRef]
- Pi, S.; Sasaki, M. Primordial black hole formation in nonminimal curvaton scenarios. Phys. Rev. D 2023, 108, L101301. [Google Scholar] [CrossRef]
- Gundhi, A.; Ketov, S.V.; Steinwachs, C.F. Primordial black hole dark matter in dilaton-extended two-field Starobinsky inflation. Phys. Rev. D 2021, 103, 083518. [Google Scholar] [CrossRef]
- Geller, S.R.; Qin, W.; McDonough, E.; Kaiser, D.I. Primordial black holes from multifield inflation with nonminimal couplings. Phys. Rev. D 2022, 106, 063535. [Google Scholar] [CrossRef]
- Chen, C.; Ghoshal, A.; Lalak, Z.; Luo, Y.; Naskar, A. Growth of curvature perturbations for PBH formation & detectable GWs in non-minimal curvaton scenario revisited. JCAP 2023, 8, 041. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.l.; Sasaki, M. Enhanced Curvature Perturbation and Primordial Black Hole Formation in Two-stage Inflation with a break. arXiv 2024, arXiv:2404.02492. [Google Scholar]
- Heydari, S.; Karami, K. Primordial black holes in nonminimal derivative coupling inflation with quartic potential and reheating consideration. Eur. Phys. J. C 2022, 82, 83. [Google Scholar] [CrossRef]
- Pi, S.; Zhang, Y.l.; Huang, Q.G.; Sasaki, M. Scalaron from R2-gravity as a heavy field. JCAP 2018, 5, 042. [Google Scholar] [CrossRef]
- Afzal, A.; Ghoshal, A. Primordial Black Holes and Scalar-induced Gravitational Waves in Radiative Hybrid Inflation. arXiv 2024, arXiv:2402.06613. [Google Scholar]
- Spanos, V.C.; Stamou, I.D. Gravitational waves and primordial black holes from supersymmetric hybrid inflation. Phys. Rev. D 2021, 104, 123537. [Google Scholar] [CrossRef]
- Braglia, M.; Linde, A.; Kallosh, R.; Finelli, F. Hybrid α-attractors, primordial black holes and gravitational wave backgrounds. JCAP 2023, 4, 033. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J. Massive Primordial Black Holes from Hybrid Inflation as Dark Matter and the seeds of Galaxies. Phys. Rev. D 2015, 92, 023524. [Google Scholar] [CrossRef]
- Tada, Y.; Yamada, M. Stochastic dynamics of multi-waterfall hybrid inflation and formation of primordial black holes. JCAP 2023, 11, 089. [Google Scholar] [CrossRef]
- Dimopoulos, K. Waterfall stiff period can generate observable primordial gravitational waves. JCAP 2022, 10, 027. [Google Scholar] [CrossRef]
- Carr, B.; Tenkanen, T.; Vaskonen, V. Primordial black holes from inflaton and spectator field perturbations in a matter-dominated era. Phys. Rev. D 2017, 96, 063507. [Google Scholar] [CrossRef]
- Kohri, K.; Lin, C.M.; Matsuda, T. Primordial black holes from the inflating curvaton. Phys. Rev. D 2013, 87, 103527. [Google Scholar] [CrossRef]
- Stamou, I.; Clesse, S. Primordial black holes without fine-tuning from a light stochastic spectator field. Phys. Rev. D 2024, 109, 043522. [Google Scholar] [CrossRef]
- Stamou, I.; Clesse, S. Can Primordial Black Holes form in the Standard Model? arXiv 2023, arXiv:2312.06873. [Google Scholar]
- Stamou, I.D. Large curvature fluctuations from no-scale supergravity with a spectator field. arXiv 2024, arXiv:2404.02295. [Google Scholar]
- Cai, R.G.; Chen, C.; Fu, C. Primordial black holes and stochastic gravitational wave background from inflation with a noncanonical spectator field. Phys. Rev. D 2021, 104, 083537. [Google Scholar] [CrossRef]
- Gow, A.D.; Miranda, T.; Nurmi, S. Primordial black holes from a curvaton scenario with strongly non-Gaussian perturbations. JCAP 2023, 11, 006. [Google Scholar] [CrossRef]
- Hooper, D.; Ireland, A.; Krnjaic, G.; Stebbins, A. Supermassive primordial black holes from inflation. JCAP 2024, 4, 021. [Google Scholar] [CrossRef]
- Barbieri, R.; Giudice, G. Upper Bounds on Supersymmetric Particle Masses. Nucl. Phys. B 1988, 306, 63–76. [Google Scholar] [CrossRef]
- Mishra, S.S.; Sahni, V. Primordial Black Holes from a tiny bump/dip in the Inflaton potential. JCAP 2020, 4, 007. [Google Scholar] [CrossRef]
- Fu, C.; Chen, C. Sudden braking and turning with a two-field potential bump: Primordial black hole formation. JCAP 2023, 05, 005. [Google Scholar] [CrossRef]
- Dalianis, I. Features in the Inflaton Potential and the Spectrum of Cosmological Perturbations. arXiv 2023, arXiv:2310.11581. [Google Scholar]
- Kristiano, J.; Yokoyama, J. Ruling Out Primordial Black Hole Formation From Single-Field Inflation. arXiv 2022, arXiv:2211.03395. [Google Scholar]
- Fumagalli, J.; Bhattacharya, S.; Peloso, M.; Renaux-Petel, S.; Witkowski, L.T. One-loop infrared rescattering by enhanced scalar fluctuations during inflation. arXiv 2023, arXiv:2307.08358. [Google Scholar] [CrossRef]
- Choudhury, S.; Gangopadhyay, M.R.; Sami, M. No-go for the formation of heavy mass Primordial Black Holes in Single Field Inflation. arXiv 2023, arXiv:2301.10000. [Google Scholar]
- Choudhury, S.; Panda, S.; Sami, M. Galileon inflation evades the no-go for PBH formation in the single-field framework. arXiv 2023, arXiv:2304.04065. [Google Scholar] [CrossRef]
- Choudhury, S. Large fluctuations in the Sky. arXiv 2024, arXiv:2403.07343. [Google Scholar]
- Firouzjahi, H. One-loop corrections in power spectrum in single field inflation. JCAP 2023, 10, 006. [Google Scholar] [CrossRef]
- Inomata, K.; Braglia, M.; Chen, X.; Renaux-Petel, S. Questions on calculation of primordial power spectrum with large spikes: The resonance model case. JCAP 2023, 04, 011, Erratum in JCAP 2023, 9, E01. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A. Dilaton-axion inflation with PBHs and GWs. JCAP 2022, 8, 037. [Google Scholar] [CrossRef]
- Copeland, E.J.; Liddle, A.R.; Lyth, D.H.; Stewart, E.D.; Wands, D. False vacuum inflation with Einstein gravity. Phys. Rev. D 1994, 49, 6410–6433. [Google Scholar] [CrossRef]
- Dvali, G.R.; Shafi, Q.; Schaefer, R.K. Large scale structure and supersymmetric inflation without fine tuning. Phys. Rev. Lett. 1994, 73, 1886–1889. [Google Scholar] [CrossRef] [PubMed]
- The LVK Collaboration. Search for subsolar-mass black hole binaries in the second part of Advanced LIGO’s and Advanced Virgo’s third observing run. Mon. Not. Roy. Astron. Soc. 2023, 524, 5984–5992, Erratum in Mon. Not. Roy. Astron. Soc. 2023, 526, 6234. [Google Scholar] [CrossRef]
- Phukon, K.S.; Baltus, G.; Caudill, S.; Clesse, S.; Depasse, A.; Fays, M.; Fong, H.; Kapadia, S.J.; Magee, R.; Tanasijczuk, A.J. The hunt for sub-solar primordial black holes in low mass ratio binaries is open. arXiv 2021, arXiv:2105.11449. [Google Scholar]
- Dwyer, S.; Sigg, D.; Ballmer, S.W.; Barsotti, L.; Mavalvala, N.; Evans, M. Gravitational wave detector with cosmological reach. Phys. Rev. 2015, 91, 082001. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser interferometer space antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of direct measurement of the acceleration of the universe using 0.1-Hz band laser interferometer gravitational wave antenna in space. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef]
- Maggiore, M.; Van Den Broeck, C.; Bartolo, N.; Belgacem, E.; Bertacca, D.; Bizouard, M.A.; Branchesi, M.; Clesse, S.; Foffa, S.; García-Bellido, J.; et al. Science Case for the Einstein Telescope. JCAP 2020, 3, 050. [Google Scholar] [CrossRef]
- Domènech, G. Scalar Induced Gravitational Waves Review. Universe 2021, 7, 398. [Google Scholar] [CrossRef]
- Cai, R.g.; Pi, S.; Sasaki, M. Gravitational Waves Induced by non-Gaussian Scalar Perturbations. Phys. Rev. Lett. 2019, 122, 201101. [Google Scholar] [CrossRef]
- Perna, G.; Testini, C.; Ricciardone, A.; Matarrese, S. Fully non-Gaussian Scalar-Induced Gravitational Waves. arXiv 2024, arXiv:2403.06962. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Z.C.; Huang, Q.G. Implications for the non-Gaussianity of curvature perturbation from pulsar timing arrays. Phys. Rev. D 2024, 109, L061301. [Google Scholar] [CrossRef]
- Namjoo, M.H.; Firouzjahi, H.; Sasaki, M. Violation of non-Gaussianity consistency relation in a single field inflationary model. EPL 2013, 101, 39001. [Google Scholar] [CrossRef]
- Carr, B.J. The Primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1–19. [Google Scholar] [CrossRef]
- Press, W.H.; Schechter, P. Formation of Galaxies and Clusters of Galaxies by Self-Similar Gravitational Condensation. Astrophys. J. 1974, 187, 425. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Bond, J.; Kaiser, N.; Szalay, A. The Statistics of Peaks of Gaussian Random Fields. Astrophys. J. 1986, 304, 15–61. [Google Scholar] [CrossRef]
- Capela, F.; Pshirkov, M.; Tinyakov, P. Constraints on primordial black holes as dark matter candidates from capture by neutron stars. Phys. Rev. D 2013, 87, 123524. [Google Scholar] [CrossRef]
- Niikura, H.; Takada, M.; Yasuda, N.; Lupton, R.H.; Sumi, T.; More, S.; Kurita, T.; Sugiyama, S.; More, A.; Oguri, M.; et al. Microlensing constraints on primordial black holes with Subaru/HSC Andromeda observations. Nat. Astron. 2019, 3, 524–534. [Google Scholar] [CrossRef]
- Musco, I.; De Luca, V.; Franciolini, G.; Riotto, A. Threshold for primordial black holes. II. A simple analytic prescription. Phys. Rev. D 2021, 103, 063538. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Analytical thresholds for black hole formation in general cosmological backgrounds. JCAP 2021, 1, 030. [Google Scholar] [CrossRef]
- Stamou, I.D. Exploring critical overdensity thresholds in inflationary models of primordial black holes formation. Phys. Rev. D 2023, 108, 063515. [Google Scholar] [CrossRef]
- Kalaja, A.; Bellomo, N.; Bartolo, N.; Bertacca, D.; Matarrese, S.; Musco, I.; Raccanelli, A.; Verde, L. From Primordial Black Holes Abundance to Primordial Curvature Power Spectrum (and back). JCAP 2019, 10, 031. [Google Scholar] [CrossRef]
- Young, S. The primordial black hole formation criterion re-examined: Parametrisation, timing and the choice of window function. Int. J. Mod. Phys. D 2019, 29, 2030002. [Google Scholar] [CrossRef]
- Tokeshi, K.; Inomata, K.; Yokoyama, J. Window function dependence of the novel mass function of primordial black holes. JCAP 2020, 12, 038. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Racco, D.; Riotto, A. A Cosmological Signature of the SM Higgs Instability: Gravitational Waves. JCAP 2018, 9, 012. [Google Scholar] [CrossRef]
- Kohri, K.; Terada, T. Semianalytic calculation of gravitational wave spectrum nonlinearly induced from primordial curvature perturbations. Phys. Rev. D 2018, 97, 123532. [Google Scholar] [CrossRef]
- Mollerach, S.; Harari, D.; Matarrese, S. CMB polarization from secondary vector and tensor modes. Phys. Rev. D 2004, 69, 063002. [Google Scholar] [CrossRef]
- Maggiore, M. Gravitational wave experiments and early universe cosmology. Phys. Rept. 2000, 331, 283–367. [Google Scholar] [CrossRef]
- Baumann, D.; Steinhardt, P.J.; Takahashi, K.; Ichiki, K. Gravitational Wave Spectrum Induced by Primordial Scalar Perturbations. Phys. Rev. D 2007, 76, 084019. [Google Scholar] [CrossRef]

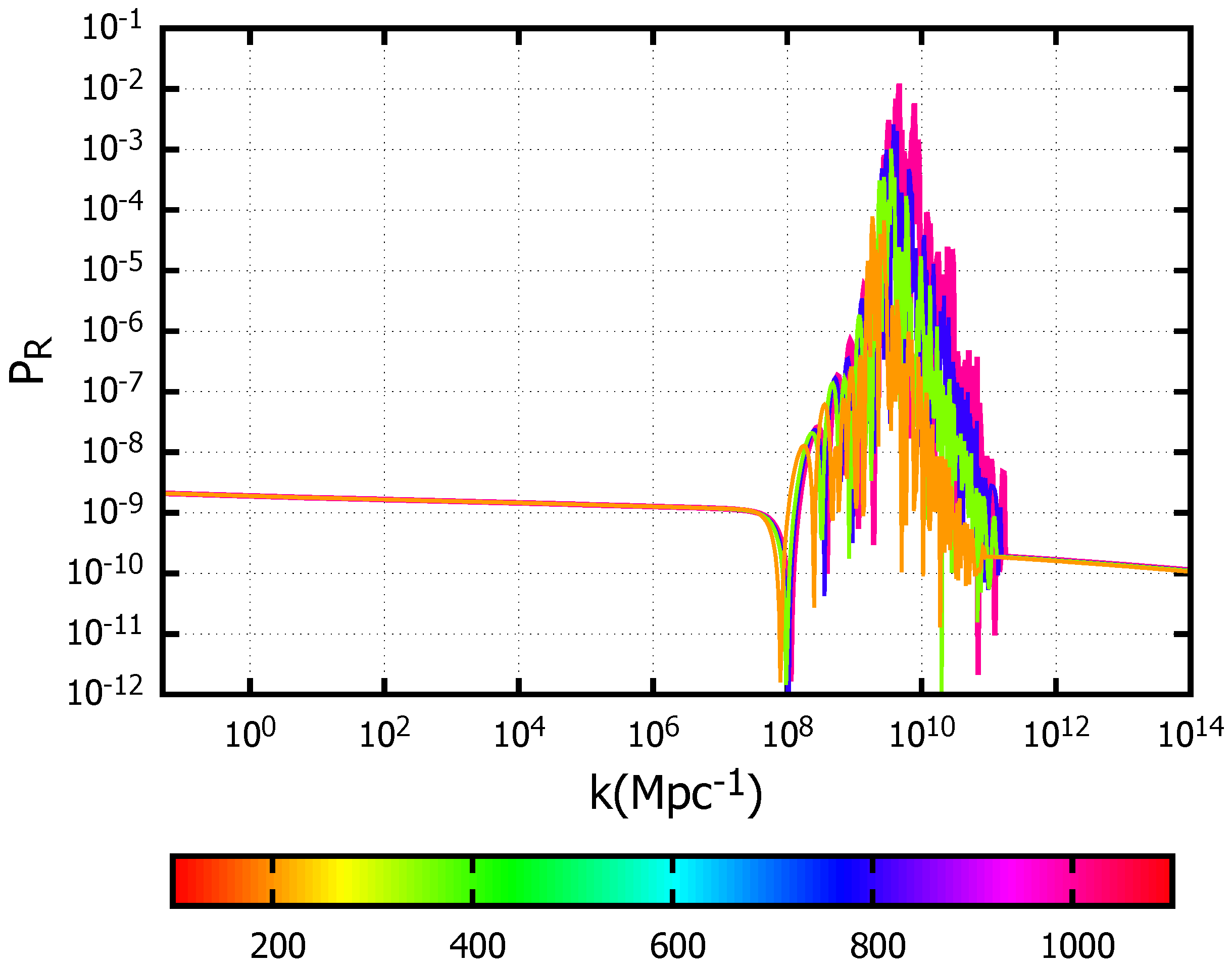


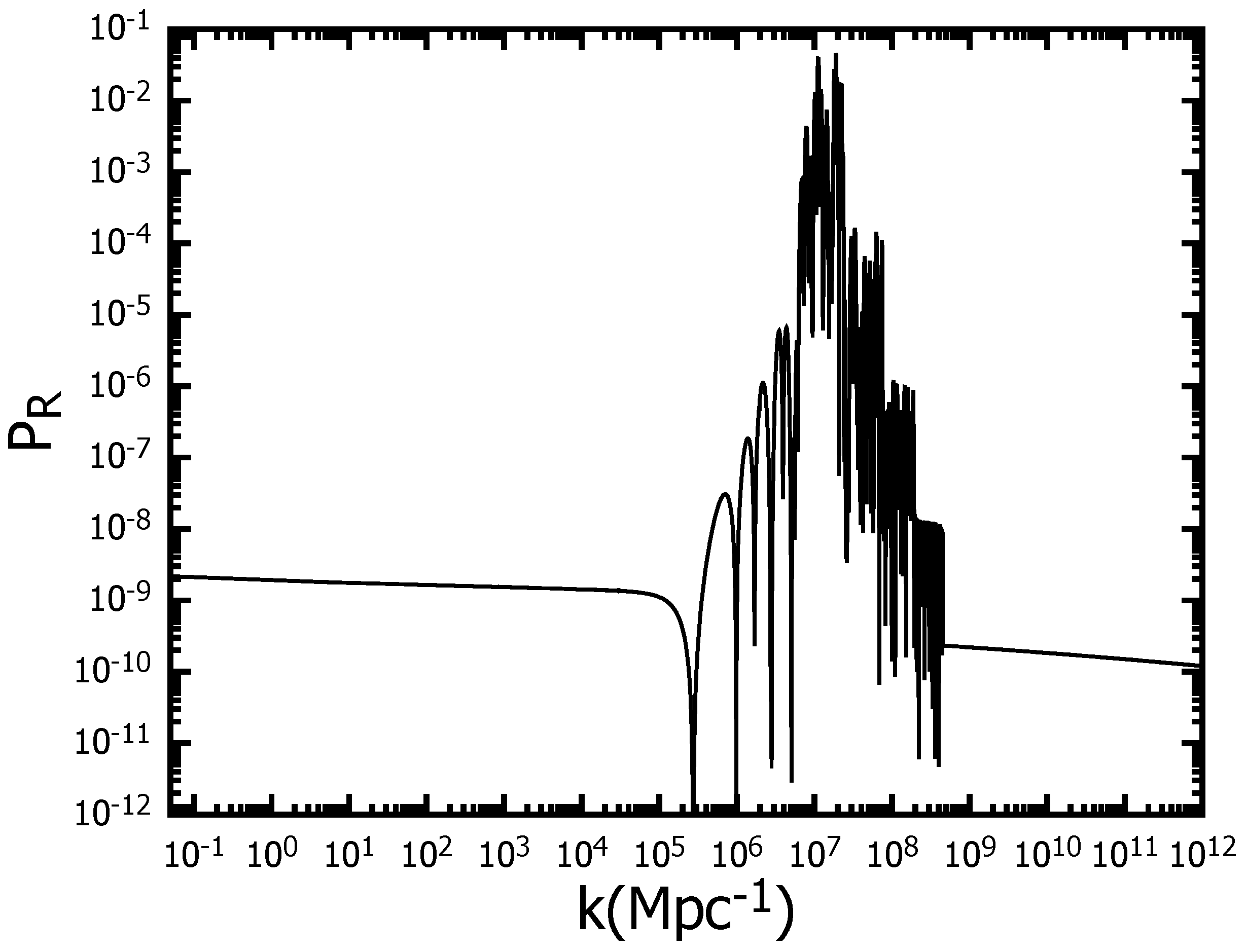
| Parameter | |
|---|---|
| a | |
| b |
| Parameter | |
|---|---|
| 18.2 | |
| c | 3.10 |
| d | 53.5 |
| Parameter | |
|---|---|
| 1.72 | |
| 71.7 | |
| 3.02 |
| Parameter | |
|---|---|
| m | 5.2 |
| g | 0.6 |
| d | 1.9 |
| 9.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamou, I. Mechanisms for Producing Primordial Black Holes from Inflationary Models beyond Fine-Tuning. Universe 2024, 10, 241. https://doi.org/10.3390/universe10060241
Stamou I. Mechanisms for Producing Primordial Black Holes from Inflationary Models beyond Fine-Tuning. Universe. 2024; 10(6):241. https://doi.org/10.3390/universe10060241
Chicago/Turabian StyleStamou, Ioanna. 2024. "Mechanisms for Producing Primordial Black Holes from Inflationary Models beyond Fine-Tuning" Universe 10, no. 6: 241. https://doi.org/10.3390/universe10060241
APA StyleStamou, I. (2024). Mechanisms for Producing Primordial Black Holes from Inflationary Models beyond Fine-Tuning. Universe, 10(6), 241. https://doi.org/10.3390/universe10060241






