Constraints on the Primordial Curvature Power Spectrum and Reheating Temperature from the NANOGrav 15-Year Dataset
Abstract
:1. Introduction
2. Scalar-Induced Gravitational Waves
3. Methodology and Results
4. Conclusions and Discussion
Funding
Data Availability Statement
Conflicts of Interest
References
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration] GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Abbott, R. et al. [LIGO Scientific Collaboration and Virgo Collaboration] GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run. Phys. Rev. X 2021, 11, 021053. [Google Scholar] [CrossRef]
- Abbott, R. et al. [LIGO Scientific Collaboration, Virgo Collaboration, and KAGRA Collaboration] GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo during the Second Part of the Third Observing Run. Phys. Rev. X 2023, 13, 041039. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and the Virgo Collaboration] Binary Black Hole Population Properties Inferred from the First and Second Observing Runs of Advanced LIGO and Advanced Virgo. Astrophys. J. Lett. 2019, 882, L24. [Google Scholar] [CrossRef]
- Chen, Z.C.; Huang, F.; Huang, Q.G. Stochastic Gravitational-wave Background from Binary Black Holes and Binary Neutron Stars and Implications for LISA. Astrophys. J. 2019, 871, 97. [Google Scholar] [CrossRef]
- Luo, H.M.; Lin, W.; Chen, Z.C.; Huang, Q.G. Extraction of gravitational wave signals with optimized convolutional neural network. Front. Phys. 2020, 15, 14601. [Google Scholar] [CrossRef]
- Chen, Z.C.; Huang, Q.G. Distinguishing Primordial Black Holes from Astrophysical Black Holes by Einstein Telescope and Cosmic Explorer. JCAP 2020, 08, 039. [Google Scholar] [CrossRef]
- Abbott, R. et al. [LIGO Scientific Collaboration and the Virgo Collaboration] Population Properties of Compact Objects from the Second LIGO-Virgo Gravitational-Wave Transient Catalog. Astrophys. J. Lett. 2021, 913, L7. [Google Scholar] [CrossRef]
- Chen, Z.C.; Yuan, C.; Huang, Q.G. Confronting the primordial black hole scenario with the gravitational-wave events detected by LIGO-Virgo. Phys. Lett. B 2022, 829, 137040. [Google Scholar] [CrossRef]
- Abbott, R. et al. [LIGO Scientific Collaboration, Virgo Collaboration, and KAGRA Collaboration] Population of Merging Compact Binaries Inferred Using Gravitational Waves through GWTC-3. Phys. Rev. X 2023, 13, 011048. [Google Scholar] [CrossRef]
- Chen, Z.C.; Du, S.S.; Huang, Q.G.; You, Z.Q. Constraints on primordial-black-hole population and cosmic expansion history from GWTC-3. JCAP 2023, 03, 024. [Google Scholar] [CrossRef]
- Liu, L.; You, Z.Q.; Wu, Y.; Chen, Z.C. Constraining the merger history of primordial-black-hole binaries from GWTC-3. Phys. Rev. D 2023, 107, 063035. [Google Scholar] [CrossRef]
- Zheng, L.M.; Li, Z.; Chen, Z.C.; Zhou, H.; Zhu, Z.H. Towards a reliable reconstruction of the power spectrum of primordial curvature perturbation on small scales from GWTC-3. Phys. Lett. B 2023, 838, 137720. [Google Scholar] [CrossRef]
- You, Z.Q.; Chen, Z.C.; Liu, L.; Yi, Z.; Liu, X.J.; Wu, Y.; Gong, Y. Constraints on peculiar velocity distribution of binary black holes using gravitational waves with GWTC-3. JCAP 2024, 05, 031. [Google Scholar] [CrossRef]
- Chen, Z.C.; Liu, L. Constraining the nonstandard propagating gravitational waves in the cosmological background with GWTC-3. arXiv 2024, arXiv:2405.10031. [Google Scholar]
- Liu, X.J.; You, Z.Q.; Chen, Z.C.; Du, S.S.; Li, A.; Zhu, X.J. On the Spin Period Distribution of Millisecond Pulsars. Astrophys. J. 2024, 962, 80. [Google Scholar] [CrossRef]
- Du, S.S.; Liu, X.J.; Chen, Z.C.; You, Z.Q.; Zhu, X.J.; Zhu, Z.H. On the initial spin period distribution of neutron stars. arXiv 2024, arXiv:2402.14030. [Google Scholar]
- Wei, H.; Chen, Z.C.; Liu, J. Cosmological Constraints on Variable Warm Dark Matter. Phys. Lett. B 2013, 720, 271–276. [Google Scholar] [CrossRef]
- Wei, H.; Liu, J.; Chen, Z.C.; Yan, X.P. Indistinguishability of Warm Dark Matter, Modified Gravity, and Coupled Cold Dark Matter. Phys. Rev. D 2013, 88, 043510. [Google Scholar] [CrossRef]
- Du, S.S.; Wei, J.J.; You, Z.Q.; Chen, Z.C.; Zhu, Z.H.; Liang, E.W. Model-independent determination of H0 and ΩK, 0 using time-delay galaxy lenses and gamma-ray bursts. Mon. Not. R. Astron. Soc. 2023, 521, 4963–4975. [Google Scholar] [CrossRef]
- Chen, Z.C.; Wu, Y.; Wei, H. Post–Newtonian Approximation of Teleparallel Gravity Coupled with a Scalar Field. Nucl. Phys. B 2015, 894, 422–438. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, Z.C.; Wang, J.; Wei, H. f(T) non-linear massive gravity and the cosmic acceleration. Commun. Theor. Phys. 2015, 63, 701–708. [Google Scholar] [CrossRef]
- Huang, Y.; Gong, Y.; Liang, D.; Yi, Z. Thermodynamics of scalar–tensor theory with non-minimally derivative coupling. Eur. Phys. J. C 2015, 75, 351. [Google Scholar] [CrossRef]
- Zhu, Y.; Gong, Y. PPN parameters in gravitational theory with nonminimally derivative coupling. Int. J. Mod. Phys. D 2016, 26, 1750005. [Google Scholar] [CrossRef]
- Gong, Y.; Papantonopoulos, E.; Yi, Z. Constraints on scalar–tensor theory of gravity by the recent observational results on gravitational waves. Eur. Phys. J. C 2018, 78, 738. [Google Scholar] [CrossRef]
- Fanizza, G.; Franchini, G.; Gasperini, M.; Tedesco, L. Comparing the luminosity distance for gravitational waves and electromagnetic signals in a simple model of quadratic gravity. Gen. Rel. Grav. 2020, 52, 111. [Google Scholar] [CrossRef]
- Agazie, G. et al. [The NANOGrav Collaboration] The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background. Astrophys. J. Lett. 2023, 951, L8. [Google Scholar] [CrossRef]
- Agazie, G. et al. [The NANOGrav Collaboration] The NANOGrav 15 yr Data Set: Observations and Timing of 68 Millisecond Pulsars. Astrophys. J. Lett. 2023, 951, L9. [Google Scholar] [CrossRef]
- Zic, A. et al. [The PPTA Collaboration] The Parkes Pulsar Timing Array third data release. Publ. Astron. Soc. Austral. 2023, 40, e049. [Google Scholar] [CrossRef]
- Reardon, D.J. et al. [The PPTA Collaboration] Search for an Isotropic Gravitational-wave Background with the Parkes Pulsar Timing Array. Astrophys. J. Lett. 2023, 951, L6. [Google Scholar] [CrossRef]
- Antoniadis, J. et al. [EPTA Collaboration] The second data release from the European Pulsar Timing Array—I. The dataset and timing analysis. Astron. Astrophys. 2023, 678, A48. [Google Scholar] [CrossRef]
- Antoniadis, J. et al. [EPTA Collaboration and InPTA Collaboration] The second data release from the European Pulsar Timing Array - III. Search for gravitational wave signals. Astron. Astrophys. 2023, 678, A50. [Google Scholar] [CrossRef]
- Xu, H.; Chen, S.; Guo, Y.; Jiang, J.; Wang, B.; Xu, J.; Xue, Z.; Caballero, R.N.; Yuan, J.; Xu, Y.; et al. Searching for the Nano-Hertz Stochastic Gravitational Wave Background with the Chinese Pulsar Timing Array Data Release I. Res. Astron. Astrophys. 2023, 23, 075024. [Google Scholar] [CrossRef]
- Afzal, A. et al. [The NANOGrav Collaboration] The NANOGrav 15 yr Data Set: Search for Signals from New Physics. Astrophys. J. Lett. 2023, 951, L11. [Google Scholar] [CrossRef]
- Agazie, G. et al. [The NANOGrav Collaboration] The NANOGrav 15 yr Data Set: Constraints on Supermassive Black Hole Binaries from the Gravitational-wave Background. Astrophys. J. Lett. 2023, 952, L37. [Google Scholar] [CrossRef]
- Antoniadis, J. et al. [EPTA Collaboration] The second data release from the European Pulsar Timing Array: IV. Implications for massive black holes, dark matter and the early Universe. arXiv 2023, arXiv:2306.16227. [Google Scholar]
- Yi, Z.; Gao, Q.; Gong, Y.; Wang, Y.; Zhang, F. Scalar induced gravitational waves in light of Pulsar Timing Array data. Sci. China Phys. Mech. Astron. 2023, 66, 120404. [Google Scholar] [CrossRef]
- Franciolini, G.; Iovino, A., Jr.; Vaskonen, V.; Veermae, H. Recent Gravitational Wave Observation by Pulsar Timing Arrays and Primordial Black Holes: The Importance of Non–Gaussianities. Phys. Rev. Lett. 2023, 131, 201401. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Z.C.; Huang, Q.G. Implications for the non-Gaussianity of curvature perturbation from pulsar timing arrays. Phys. Rev. D 2024, 109, L061301. [Google Scholar] [CrossRef]
- Vagnozzi, S. Inflationary interpretation of the stochastic gravitational wave background signal detected by pulsar timing array experiments. JHEAp 2023, 39, 81–98. [Google Scholar] [CrossRef]
- Cai, Y.F.; He, X.C.; Ma, X.H.; Yan, S.F.; Yuan, G.W. Limits on scalar-induced gravitational waves from the stochastic background by pulsar timing array observations. Sci. Bull. 2023, 68, 2929–2935. [Google Scholar] [CrossRef] [PubMed]
- Bi, Y.C.; Wu, Y.M.; Chen, Z.C.; Huang, Q.G. Implications for the supermassive black hole binaries from the NANOGrav 15-year data set. Sci. China Phys. Mech. Astron. 2023, 66, 120402. [Google Scholar] [CrossRef]
- Wu, Y.M.; Chen, Z.C.; Huang, Q.G. Cosmological interpretation for the stochastic signal in pulsar timing arrays. Sci. China Phys. Mech. Astron. 2024, 67, 240412. [Google Scholar] [CrossRef]
- Franciolini, G.; Racco, D.; Rompineve, F. Footprints of the QCD Crossover on Cosmological Gravitational Waves at Pulsar Timing Arrays. Phys. Rev. Lett. 2024, 132, 081001. [Google Scholar] [CrossRef] [PubMed]
- You, Z.Q.; Yi, Z.; Wu, Y. Constraints on primordial curvature power spectrum with pulsar timing arrays. JCAP 2023, 11, 065. [Google Scholar] [CrossRef]
- Jin, J.H.; Chen, Z.C.; Yi, Z.; You, Z.Q.; Liu, L.; Wu, Y. Confronting sound speed resonance with pulsar timing arrays. JCAP 2023, 09, 016. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Z.C.; Huang, Q.G. Probing the equation of state of the early Universe with pulsar timing arrays. JCAP 2023, 11, 071. [Google Scholar] [CrossRef]
- An, H.; Su, B.; Tai, H.; Wang, L.T.; Yang, C. Phase transition during inflation and the gravitational wave signal at pulsar timing arrays. arXiv 2023, arXiv:2308.00070. [Google Scholar]
- Zhang, Z.; Cai, C.; Su, Y.H.; Wang, S.; Yu, Z.H.; Zhang, H.H. Nano-Hertz gravitational waves from collapsing domain walls associated with freeze-in dark matter in light of pulsar timing array observations. Phys. Rev. D 2023, 108, 095037. [Google Scholar] [CrossRef]
- Das, B.; Jaman, N.; Sami, M. Gravitational wave background from quintessential inflation and NANOGrav data. Phys. Rev. D 2023, 108, 103510. [Google Scholar] [CrossRef]
- Balaji, S.; Domènech, G.; Franciolini, G. Scalar-induced gravitational wave interpretation of PTA data: The role of scalar fluctuation propagation speed. JCAP 2023, 10, 041. [Google Scholar] [CrossRef]
- Du, X.K.; Huang, M.X.; Wang, F.; Zhang, Y.K. Did the nHZ Gravitational Waves Signatures Observed By NANOGrav Indicate Multiple Sector SUSY Breaking? arXiv 2023, arXiv:2307.02938. [Google Scholar]
- Oikonomou, V.K. Flat energy spectrum of primordial gravitational waves versus peaks and the NANOGrav 2023 observation. Phys. Rev. D 2023, 108, 043516. [Google Scholar] [CrossRef]
- Yi, Z.; You, Z.Q.; Wu, Y.; Chen, Z.C.; Liu, L. Exploring the NANOGrav Signal and Planet-mass Primordial Black Holes through Higgs Inflation. arXiv 2023, arXiv:2308.14688. [Google Scholar]
- Yi, Z.; You, Z.Q.; Wu, Y. Model-independent reconstruction of the primordial curvature power spectrum from PTA data. JCAP 2024, 01, 066. [Google Scholar] [CrossRef]
- Chen, Z.C.; Huang, Q.G.; Liu, C.; Liu, L.; Liu, X.J.; Wu, Y.; Wu, Y.M.; Yi, Z.; You, Z.Q. Prospects for Taiji to detect a gravitational-wave background from cosmic strings. JCAP 2024, 03, 022. [Google Scholar] [CrossRef]
- Wu, Y.M.; Chen, Z.C.; Bi, Y.C.; Huang, Q.G. Constraining the graviton mass with the NANOGrav 15 year data set. Class. Quant. Grav. 2024, 41, 075002. [Google Scholar] [CrossRef]
- Bi, Y.C.; Wu, Y.M.; Chen, Z.C.; Huang, Q.G. Constraints on the velocity of gravitational waves from the NANOGrav 15-year data set. Phys. Rev. D 2024, 109, L061101. [Google Scholar] [CrossRef]
- Chen, Z.C.; Wu, Y.M.; Bi, Y.C.; Huang, Q.G. Search for nontensorial gravitational-wave backgrounds in the NANOGrav 15-year dataset. Phys. Rev. D 2024, 109, 084045. [Google Scholar] [CrossRef]
- Liu, L.; Wu, Y.; Chen, Z.C. Simultaneously probing the sound speed and equation of state of the early Universe with pulsar timing arrays. JCAP 2024, 04, 011. [Google Scholar] [CrossRef]
- Fei, Q. Constraints on the primordial curvature power spectrum by pulsar timing array data: A polynomial parameterization approach. Commun. Theor. Phys. 2024, 76, 015404. [Google Scholar] [CrossRef]
- Chen, Z.C.; Li, S.L.; Wu, P.; Yu, H. NANOGrav hints for first-order confinement-deconfinement phase transition in different QCD-matter scenarios. Phys. Rev. D 2024, 109, 043022. [Google Scholar] [CrossRef]
- Wang, Z.; Lei, L.; Jiao, H.; Feng, L.; Fan, Y.Z. The nanohertz stochastic gravitational wave background from cosmic string loops and the abundant high redshift massive galaxies. Sci. China Phys. Mech. Astron. 2023, 66, 120403. [Google Scholar] [CrossRef]
- Chen, Z.C.; Liu, L. Is PSR J0514-4002E in a PBH-NS binary? arXiv 2024, arXiv:2401.12889. [Google Scholar]
- Chen, Z.C.; Liu, L. Can we distinguish the adiabatic fluctuations and isocurvature fluctuations with pulsar timing arrays? arXiv 2024, arXiv:2402.16781. [Google Scholar]
- Chen, Z.C.; Li, J.; Liu, L.; Yi, Z. Probing the speed of scalar-induced gravitational waves with pulsar timing arrays. Phys. Rev. D 2024, 109, L101302. [Google Scholar] [CrossRef]
- Chen, Z.C.; Liu, L. Detecting a Gravitational-Wave Background from Null Energy Condition Violation: Prospects for Taiji. arXiv 2024, arXiv:2404.08375. [Google Scholar]
- Chen, Z.C.; Liu, L. Constraints on Inflation with Null Energy Condition Violation from Advanced LIGO and Advanced Virgo’s First Three Observing Runs. arXiv 2024, arXiv:2404.07075. [Google Scholar]
- Geller, M.; Ghosh, S.; Lu, S.; Tsai, Y. Challenges in interpreting the NANOGrav 15-year dataset as early Universe gravitational waves produced by an ALP induced instability. Phys. Rev. D 2024, 109, 063537. [Google Scholar] [CrossRef]
- Zhu, X.J.; Cui, W.; Thrane, E. The minimum and maximum gravitational-wave background from supermassive binary black holes. Mon. Not. R. Astron. Soc. 2019, 482, 2588–2596. [Google Scholar] [CrossRef]
- Li, J.; Chen, Z.C.; Huang, Q.G. Measuring the tilt of primordial gravitational-wave power spectrum from observations. Sci. China Phys. Mech. Astron. 2019, 62, 110421, Erratum in Sci. China Phys. Mech. Astron. 2021, 64, 250451. [Google Scholar] [CrossRef]
- Chen, Z.C.; Yuan, C.; Huang, Q.G. Non-tensorial gravitational wave background in NANOGrav 12.5-year data set. Sci. China Phys. Mech. Astron. 2021, 64, 120412. [Google Scholar] [CrossRef]
- Wu, Y.M.; Chen, Z.C.; Huang, Q.G. Constraining the Polarization of Gravitational Waves with the Parkes Pulsar Timing Array Second Data Release. Astrophys. J. 2022, 925, 37. [Google Scholar] [CrossRef]
- Chen, Z.C.; Wu, Y.M.; Huang, Q.G. Searching for isotropic stochastic gravitational-wave background in the international pulsar timing array second data release. Commun. Theor. Phys. 2022, 74, 105402. [Google Scholar] [CrossRef]
- Chen, Z.C.; Wu, Y.M.; Huang, Q.G. Search for the Gravitational-wave Background from Cosmic Strings with the Parkes Pulsar Timing Array Second Data Release. Astrophys. J. 2022, 936, 20. [Google Scholar] [CrossRef]
- Wu, Y.M.; Chen, Z.C.; Huang, Q.G.; Zhu, X.; Bhat, N.D.R.; Feng, Y.; Hobbs, G.; Manchester, R.N.; Russell, C.J.; Shannon, R.M. Constraining ultralight vector dark matter with the Parkes Pulsar Timing Array second data release. Phys. Rev. D 2022, 106, L081101. [Google Scholar] [CrossRef]
- Falxa, M. et al. [IPTA Collaboration] Searching for continuous Gravitational Waves in the second data release of the International Pulsar Timing Array. Mon. Not. R. Astron. Soc. 2023, 521, 5077–5086. [Google Scholar] [CrossRef]
- Wu, Y.M.; Chen, Z.C.; Huang, Q.G. Search for stochastic gravitational-wave background from massive gravity in the NANOGrav 12.5-year dataset. Phys. Rev. D 2023, 107, 042003. [Google Scholar] [CrossRef]
- Wu, Y.M.; Chen, Z.C.; Huang, Q.G. Pulsar timing residual induced by ultralight tensor dark matter. JCAP 2023, 09, 021. [Google Scholar] [CrossRef]
- Agazie, G. et al. [The International Pulsar Timing Array Collaboration] Comparing Recent Pulsar Timing Array Results on the Nanohertz Stochastic Gravitational-wave Background. Astrophys. J. 2024, 966, 105. [Google Scholar] [CrossRef]
- Hawking, S. Gravitationally collapsed objects of very low mass. Mon. Not. R. Astron. Soc. 1971, 152, 75. [Google Scholar] [CrossRef]
- Carr, B.J.; Hawking, S.W. Black holes in the early Universe. Mon. Not. R. Astron. Soc. 1974, 168, 399–415. [Google Scholar] [CrossRef]
- Ananda, K.N.; Clarkson, C.; Wands, D. The Cosmological gravitational wave background from primordial density perturbations. Phys. Rev. D 2007, 75, 123518. [Google Scholar] [CrossRef]
- Baumann, D.; Steinhardt, P.J.; Takahashi, K.; Ichiki, K. Gravitational Wave Spectrum Induced by Primordial Scalar Perturbations. Phys. Rev. D 2007, 76, 084019. [Google Scholar] [CrossRef]
- Saito, R.; Yokoyama, J. Gravitational wave background as a probe of the primordial black hole abundance. Phys. Rev. Lett. 2009, 102, 161101, Erratum in Phys. Rev. Lett. 2011, 107, 069901. [Google Scholar] [CrossRef] [PubMed]
- Domènech, G. Scalar Induced Gravitational Waves Review. Universe 2021, 7, 398. [Google Scholar] [CrossRef]
- Alabidi, L.; Kohri, K.; Sasaki, M.; Sendouda, Y. Observable Spectra of Induced Gravitational Waves from Inflation. JCAP 2012, 09, 017. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial black holes—Perspectives in gravitational wave astronomy. Class. Quant. Grav. 2018, 35, 063001. [Google Scholar] [CrossRef]
- Nakama, T.; Silk, J.; Kamionkowski, M. Stochastic gravitational waves associated with the formation of primordial black holes. Phys. Rev. D 2017, 95, 043511. [Google Scholar] [CrossRef]
- Kohri, K.; Terada, T. Semianalytic calculation of gravitational wave spectrum nonlinearly induced from primordial curvature perturbations. Phys. Rev. D 2018, 97, 123532. [Google Scholar] [CrossRef]
- Di, H.; Gong, Y. Primordial black holes and second order gravitational waves from ultra-slow-roll inflation. JCAP 2018, 07, 007. [Google Scholar] [CrossRef]
- Cheng, S.L.; Lee, W.; Ng, K.W. Primordial black holes and associated gravitational waves in axion monodromy inflation. JCAP 2018, 07, 001. [Google Scholar] [CrossRef]
- Lu, Y.; Gong, Y.; Yi, Z.; Zhang, F. Constraints on primordial curvature perturbations from primordial black hole dark matter and secondary gravitational waves. JCAP 2019, 12, 031. [Google Scholar] [CrossRef]
- Cai, R.G.; Pi, S.; Wang, S.J.; Yang, X.Y. Resonant multiple peaks in the induced gravitational waves. JCAP 2019, 05, 013. [Google Scholar] [CrossRef]
- Cai, R.g.; Pi, S.; Sasaki, M. Gravitational Waves Induced by non-Gaussian Scalar Perturbations. Phys. Rev. Lett. 2019, 122, 201101. [Google Scholar] [CrossRef] [PubMed]
- Cai, R.G.; Pi, S.; Wang, S.J.; Yang, X.Y. Pulsar Timing Array Constraints on the Induced Gravitational Waves. JCAP 2019, 10, 059. [Google Scholar] [CrossRef]
- Cai, R.G.; Guo, Z.K.; Liu, J.; Liu, L.; Yang, X.Y. Primordial black holes and gravitational waves from parametric amplification of curvature perturbations. JCAP 2020, 06, 013. [Google Scholar] [CrossRef]
- Wu, Y. Merger history of primordial black-hole binaries. Phys. Rev. D 2020, 101, 083008. [Google Scholar] [CrossRef]
- Cai, R.G.; Ding, Y.C.; Yang, X.Y.; Zhou, Y.F. Constraints on a mixed model of dark matter particles and primordial black holes from the galactic 511 keV line. JCAP 2021, 03, 057. [Google Scholar] [CrossRef]
- Pi, S.; Sasaki, M. Gravitational Waves Induced by Scalar Perturbations with a Lognormal Peak. JCAP 2020, 09, 037. [Google Scholar] [CrossRef]
- Domènech, G.; Pi, S.; Sasaki, M. Induced gravitational waves as a probe of thermal history of the universe. JCAP 2020, 08, 017. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Z.K.; Cai, R.G. Effects of the surrounding primordial black holes on the merger rate of primordial black hole binaries. Phys. Rev. D 2019, 99, 063523. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Z.K.; Cai, R.G. Effects of the merger history on the merger rate density of primordial black hole binaries. Eur. Phys. J. C 2019, 79, 717. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Z.K.; Cai, R.G.; Kim, S.P. Merger rate distribution of primordial black hole binaries with electric charges. Phys. Rev. D 2020, 102, 043508. [Google Scholar] [CrossRef]
- Liu, L.; Yang, X.Y.; Guo, Z.K.; Cai, R.G. Testing primordial black hole and measuring the Hubble constant with multiband gravitational-wave observations. JCAP 2023, 01, 006. [Google Scholar] [CrossRef]
- Chen, Z.C.; Yuan, C.; Huang, Q.G. Pulsar Timing Array Constraints on Primordial Black Holes with NANOGrav 11-Year Dataset. Phys. Rev. Lett. 2020, 124, 251101. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C.; Chen, Z.C.; Huang, Q.G. Scalar induced gravitational waves in different gauges. Phys. Rev. D 2020, 101, 063018. [Google Scholar] [CrossRef]
- Yuan, C.; Chen, Z.C.; Huang, Q.G. Log-dependent slope of scalar induced gravitational waves in the infrared regions. Phys. Rev. D 2020, 101, 043019. [Google Scholar] [CrossRef]
- Yuan, C.; Chen, Z.C.; Huang, Q.G. Probing primordial–black-hole dark matter with scalar induced gravitational waves. Phys. Rev. D 2019, 100, 081301. [Google Scholar] [CrossRef]
- Carr, B.; Kohri, K.; Sendouda, Y.; Yokoyama, J. Constraints on primordial black holes. Rept. Prog. Phys. 2021, 84, 116902. [Google Scholar] [CrossRef]
- Liu, L.; Christiansen, O.; Guo, Z.K.; Cai, R.G.; Kim, S.P. Gravitational and electromagnetic radiation from binary black holes with electric and magnetic charges: Circular orbits on a cone. Phys. Rev. D 2020, 102, 103520. [Google Scholar] [CrossRef]
- Liu, L.; Christiansen, O.; Ruan, W.H.; Guo, Z.K.; Cai, R.G.; Kim, S.P. Gravitational and electromagnetic radiation from binary black holes with electric and magnetic charges: Elliptical orbits on a cone. Eur. Phys. J. C 2021, 81, 1048. [Google Scholar] [CrossRef]
- Yi, Z.; Fei, Q. Constraints on primordial curvature spectrum from primordial black holes and scalar-induced gravitational waves. Eur. Phys. J. C 2023, 83, 82. [Google Scholar] [CrossRef]
- Papanikolaou, T.; Tzerefos, C.; Basilakos, S.; Saridakis, E.N. Scalar induced gravitational waves from primordial black hole Poisson fluctuations in f(R) gravity. JCAP 2022, 10, 013. [Google Scholar] [CrossRef]
- Papanikolaou, T.; Tzerefos, C.; Basilakos, S.; Saridakis, E.N. No constraints for f(T) gravity from gravitational waves induced from primordial black hole fluctuations. Eur. Phys. J. C 2023, 83, 31. [Google Scholar] [CrossRef]
- Chakraborty, A.; Chanda, P.K.; Pandey, K.L.; Das, S. Formation and Abundance of Late-forming Primordial Black Holes as Dark Matter. Astrophys. J. 2022, 932, 119. [Google Scholar] [CrossRef]
- Liu, L.; Kim, S.P. Gravitational and electromagnetic radiations from binary black holes with electric and magnetic charges. arXiv 2022, arXiv:2201.01138. [Google Scholar]
- Chen, Z.C.; Huang, Q.G. Merger Rate Distribution of Primordial-Black-Hole Binaries. Astrophys. J. 2018, 864, 61. [Google Scholar] [CrossRef]
- Liu, L.; Kim, S.P. Merger rate of charged black holes from the two-body dynamical capture. JCAP 2022, 03, 059. [Google Scholar] [CrossRef]
- Chen, Z.C.; Kim, S.P.; Liu, L. Gravitational and electromagnetic radiation from binary black holes with electric and magnetic charges: Hyperbolic orbits on a cone. Commun. Theor. Phys. 2023, 75, 065401. [Google Scholar] [CrossRef]
- Meng, D.S.; Yuan, C.; Huang, Q.G. Primordial black holes generated by the non-minimal spectator field. Sci. China Phys. Mech. Astron. 2023, 66, 280411. [Google Scholar] [CrossRef]
- Garcia-Saenz, S.; Lu, Y.; Shuai, Z. Scalar-induced gravitational waves from ghost inflation and parity violation. Phys. Rev. D 2023, 108, 123507. [Google Scholar] [CrossRef]
- Huang, Q.G.; Yuan, C.; Chen, Z.C.; Liu, L. GW230529_181500: A Potential Primordial Binary Black Hole Merger in the Mass Gap. arXiv 2024, arXiv:2404.05691. [Google Scholar]
- Chen, Z.C.; Hall, A. Confronting primordial black holes with LIGO-Virgo-KAGRA and the Einstein Telescope. arXiv 2024, arXiv:2402.03934. [Google Scholar]
- Martin, J.; Motohashi, H.; Suyama, T. Ultra Slow-Roll Inflation and the non-Gaussianity Consistency Relation. Phys. Rev. D 2013, 87, 023514. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A.; Yokoyama, J. Inflation with a constant rate of roll. JCAP 2015, 09, 018. [Google Scholar] [CrossRef]
- Yi, Z.; Gong, Y. On the constant-roll inflation. JCAP 2018, 03, 052. [Google Scholar] [CrossRef]
- Yi, Z.; Gong, Y. Nonminimal coupling and inflationary attractors. Phys. Rev. D 2016, 94, 103527. [Google Scholar] [CrossRef]
- Fei, Q.; Gong, Y.; Lin, J.; Yi, Z. The reconstruction of tachyon inflationary potentials. JCAP 2017, 08, 018. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Ruiz Morales, E. Primordial black holes from single field models of inflation. Phys. Dark Univ. 2017, 18, 47–54. [Google Scholar] [CrossRef]
- Germani, C.; Prokopec, T. On primordial black holes from an inflection point. Phys. Dark Univ. 2017, 18, 6–10. [Google Scholar] [CrossRef]
- Motohashi, H.; Hu, W. Primordial Black Holes and Slow-Roll Violation. Phys. Rev. D 2017, 96, 063503. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; Garcia-Bellido, J.; Ruiz Morales, E. Primordial Black Hole production in Critical Higgs Inflation. Phys. Lett. B 2018, 776, 345–349. [Google Scholar] [CrossRef]
- Yi, Z.; Gong, Y. Gauss–Bonnet Inflation and the String Swampland. Universe 2019, 5, 200. [Google Scholar] [CrossRef]
- Yi, Z.; Gong, Y.; Sabir, M. Inflation with Gauss–Bonnet coupling. Phys. Rev. D 2018, 98, 083521. [Google Scholar] [CrossRef]
- Ballesteros, G.; Beltran Jimenez, J.; Pieroni, M. Black hole formation from a general quadratic action for inflationary primordial fluctuations. JCAP 2019, 06, 016. [Google Scholar] [CrossRef]
- Dalianis, I.; Kehagias, A.; Tringas, G. Primordial black holes from α-attractors. JCAP 2019, 01, 037. [Google Scholar] [CrossRef]
- Bezrukov, F.; Pauly, M.; Rubio, J. On the robustness of the primordial power spectrum in renormalized Higgs inflation. JCAP 2018, 02, 040. [Google Scholar] [CrossRef]
- Kannike, K.; Marzola, L.; Raidal, M.; Veermäe, H. Single Field Double Inflation and Primordial Black Holes. JCAP 2017, 09, 020. [Google Scholar] [CrossRef]
- Fei, Q.; Yi, Z.; Yang, Y. The Reconstruction of Non-Minimal Derivative Coupling Inflationary Potentials. Universe 2020, 6, 213. [Google Scholar] [CrossRef]
- Lin, J.; Gao, Q.; Gong, Y.; Lu, Y.; Zhang, C.; Zhang, F. Primordial black holes and secondary gravitational waves from k and G inflation. Phys. Rev. D 2020, 101, 103515. [Google Scholar] [CrossRef]
- Lin, J.; Gao, S.; Gong, Y.; Lu, Y.; Wang, Z.; Zhang, F. Primordial black holes and scalar induced gravitational waves from Higgs inflation with noncanonical kinetic term. Phys. Rev. D 2023, 107, 043517. [Google Scholar] [CrossRef]
- Yi, Z.; Zhu, Z.H. Inflationary attractors from a non-canonical kinetic term. arXiv 2021, arXiv:2106.10303. [Google Scholar]
- Gao, Q.; Gong, Y.; Yi, Z. Primordial black holes and secondary gravitational waves from natural inflation. Nucl. Phys. B 2021, 969, 115480. [Google Scholar] [CrossRef]
- Gao, Q.; Gong, Y.; Yi, Z. On the constant-roll inflation with large and small ηH. Universe 2019, 5, 215. [Google Scholar] [CrossRef]
- Gao, Q. Primordial black holes and secondary gravitational waves from chaotic inflation. Sci. China Phys. Mech. Astron. 2021, 64, 280411. [Google Scholar] [CrossRef]
- Yi, Z.; Gong, Y.; Wang, B.; Zhu, Z.h. Primordial black holes and secondary gravitational waves from the Higgs field. Phys. Rev. D 2021, 103, 063535. [Google Scholar] [CrossRef]
- Yi, Z.; Gao, Q.; Gong, Y.; Zhu, Z.h. Primordial black holes and scalar-induced secondary gravitational waves from inflationary models with a noncanonical kinetic term. Phys. Rev. D 2021, 103, 063534. [Google Scholar] [CrossRef]
- Yi, Z.; Zhu, Z.H. NANOGrav signal and LIGO-Virgo primordial black holes from the Higgs field. JCAP 2022, 05, 046. [Google Scholar] [CrossRef]
- Yi, Z. Primordial black holes and scalar-induced gravitational waves from the generalized Brans-Dicke theory. JCAP 2023, 03, 048. [Google Scholar] [CrossRef]
- Zhang, F.; Gong, Y.; Lin, J.; Lu, Y.; Yi, Z. Primordial non-Gaussianity from G-inflation. JCAP 2021, 04, 045. [Google Scholar] [CrossRef]
- Pi, S.; Zhang, Y.l.; Huang, Q.G.; Sasaki, M. Scalaron from R2-gravity as a heavy field. JCAP 2018, 05, 042. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Tronconi, A.; Vardanyan, T.; Venturi, G. Non-Canonical Inflation and Primordial Black Holes Production. Phys. Lett. B 2019, 791, 201–205. [Google Scholar] [CrossRef]
- Fu, C.; Wu, P.; Yu, H. Primordial Black Holes from Inflation with Nonminimal Derivative Coupling. Phys. Rev. D 2019, 100, 063532. [Google Scholar] [CrossRef]
- Fu, C.; Wu, P.; Yu, H. Scalar induced gravitational waves in inflation with gravitationally enhanced friction. Phys. Rev. D 2020, 101, 023529. [Google Scholar] [CrossRef]
- Dalianis, I.; Karydas, S.; Papantonopoulos, E. Generalized Non-Minimal Derivative Coupling: Application to Inflation and Primordial Black Hole Production. JCAP 2020, 06, 040. [Google Scholar] [CrossRef]
- Gundhi, A.; Steinwachs, C.F. Scalaron–Higgs inflation reloaded: Higgs-dependent scalaron mass and primordial black hole dark matter. Eur. Phys. J. C 2021, 81, 460. [Google Scholar] [CrossRef]
- Cheong, D.Y.; Lee, S.M.; Park, S.C. Primordial black holes in Higgs-R2 inflation as the whole of dark matter. JCAP 2021, 01, 032. [Google Scholar] [CrossRef]
- Zhang, F. Primordial black holes and scalar induced gravitational waves from the E model with a Gauss–Bonnet term. Phys. Rev. D 2022, 105, 063539. [Google Scholar] [CrossRef]
- Zhang, F.; Lin, J.; Lu, Y. Double-peaked inflation model: Scalar induced gravitational waves and primordial-black-hole suppression from primordial non-Gaussianity. Phys. Rev. D 2021, 104, 063515, Erratum in Phys. Rev. D 2021, 104, 129902. [Google Scholar] [CrossRef]
- Kawai, S.; Kim, J. Primordial black holes from Gauss–Bonnet-corrected single field inflation. Phys. Rev. D 2021, 104, 083545. [Google Scholar] [CrossRef]
- Cai, R.G.; Chen, C.; Fu, C. Primordial black holes and stochastic gravitational wave background from inflation with a noncanonical spectator field. Phys. Rev. D 2021, 104, 083537. [Google Scholar] [CrossRef]
- Chen, P.; Koh, S.; Tumurtushaa, G. Primordial black holes and induced gravitational waves from inflation in the Horndeski theory of gravity. arXiv 2021, arXiv:2107.08638. [Google Scholar]
- Karam, A.; Koivunen, N.; Tomberg, E.; Vaskonen, V.; Veermäe, H. Anatomy of single-field inflationary models for primordial black holes. JCAP 2023, 03, 013. [Google Scholar] [CrossRef]
- Ashoorioon, A.; Rostami, A.; Firouzjaee, J.T. EFT compatible PBHs: Effective spawning of the seeds for primordial black holes during inflation. JHEP 2021, 07, 087. [Google Scholar] [CrossRef]
- Liu, J.; Gong, Y.; Yi, Z. Constant-roll inflation with non-minimally derivative coupling. arXiv 2024, arXiv:2404.04978. [Google Scholar] [CrossRef]
- Dandoy, V.; Domcke, V.; Rompineve, F. Search for scalar induced gravitational waves in the international pulsar timing array data release 2 and NANOgrav 12.5 years datasets. SciPost Phys. Core 2023, 6, 060. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220–1223. [Google Scholar] [CrossRef]
- Harigaya, K.; Inomata, K.; Terada, T. Induced gravitational waves with kination era for recent pulsar timing array signals. Phys. Rev. D 2023, 108, 123538. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kohri, K.; Sugiyama, N. Cosmological constraints on late time entropy production. Phys. Rev. Lett. 1999, 82, 4168. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kohri, K.; Sugiyama, N. MeV scale reheating temperature and thermalization of neutrino background. Phys. Rev. D 2000, 62, 023506. [Google Scholar] [CrossRef]
- Hannestad, S. What is the lowest possible reheating temperature? Phys. Rev. D 2004, 70, 043506. [Google Scholar] [CrossRef]
- Hasegawa, T.; Hiroshima, N.; Kohri, K.; Hansen, R.S.L.; Tram, T.; Hannestad, S. MeV-scale reheating temperature and thermalization of oscillating neutrinos by radiative and hadronic decays of massive particles. JCAP 2019, 12, 012. [Google Scholar] [CrossRef]
- Ashton, G.; Hübner, M.; Lasky, P.D.; Talbot, C.; Ackley, K.; Biscoveanu, S.; Chu, Q.; Divakarla, A.; Easter, P.J.; Goncharov, B.; et al. BILBY: A user-friendly Bayesian inference library for gravitational-wave astronomy. Astrophys. J. Suppl. 2019, 241, 27. [Google Scholar] [CrossRef]
- Skilling, J. Nested Sampling. AIP Conf. Proc. 2004, 735, 395–405. [Google Scholar] [CrossRef]
- Moore, C.J.; Vecchio, A. Ultra-low-frequency gravitational waves from cosmological and astrophysical processes. Nat. Astron. 2021, 5, 1268–1274. [Google Scholar] [CrossRef]
- Lamb, W.G.; Taylor, S.R.; van Haasteren, R. Rapid refitting techniques for Bayesian spectral characterization of the gravitational wave background using pulsar timing arrays. Phys. Rev. D 2023, 108, 103019. [Google Scholar] [CrossRef]
- Johnson, M.C.; Kamionkowski, M. Dynamical and Gravitational Instability of Oscillating-Field Dark Energy and Dark Matter. Phys. Rev. D 2008, 78, 063010. [Google Scholar] [CrossRef]
- Turner, M.S. Coherent Scalar Field Oscillations in an Expanding Universe. Phys. Rev. D 1983, 28, 1243. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. Essentials of k essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Silverstein, E.; Tong, D. Scalar speed limits and cosmology: Acceleration from D-cceleration. Phys. Rev. D 2004, 70, 103505. [Google Scholar] [CrossRef]
- Liddle, A.R.; Leach, S.M. How long before the end of inflation were observable perturbations produced? Phys. Rev. D 2003, 68, 103503. [Google Scholar] [CrossRef]
- Allahverdi, R.; Brandenberger, R.; Cyr-Racine, F.Y.; Mazumdar, A. Reheating in Inflationary Cosmology: Theory and Applications. Ann. Rev. Nucl. Part. Sci. 2010, 60, 27–51. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Reheating after inflation. Phys. Rev. Lett. 1994, 73, 3195–3198. [Google Scholar] [CrossRef] [PubMed]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Towards the theory of reheating after inflation. Phys. Rev. D 1997, 56, 3258–3295. [Google Scholar] [CrossRef]
- Domènech, G. Induced gravitational waves in a general cosmological background. Int. J. Mod. Phys. D 2020, 29, 2050028. [Google Scholar] [CrossRef]
- Dufaux, J.F.; Bergman, A.; Felder, G.N.; Kofman, L.; Uzan, J.P. Theory and Numerics of Gravitational Waves from Preheating after Inflation. Phys. Rev. D 2007, 76, 123517. [Google Scholar] [CrossRef]
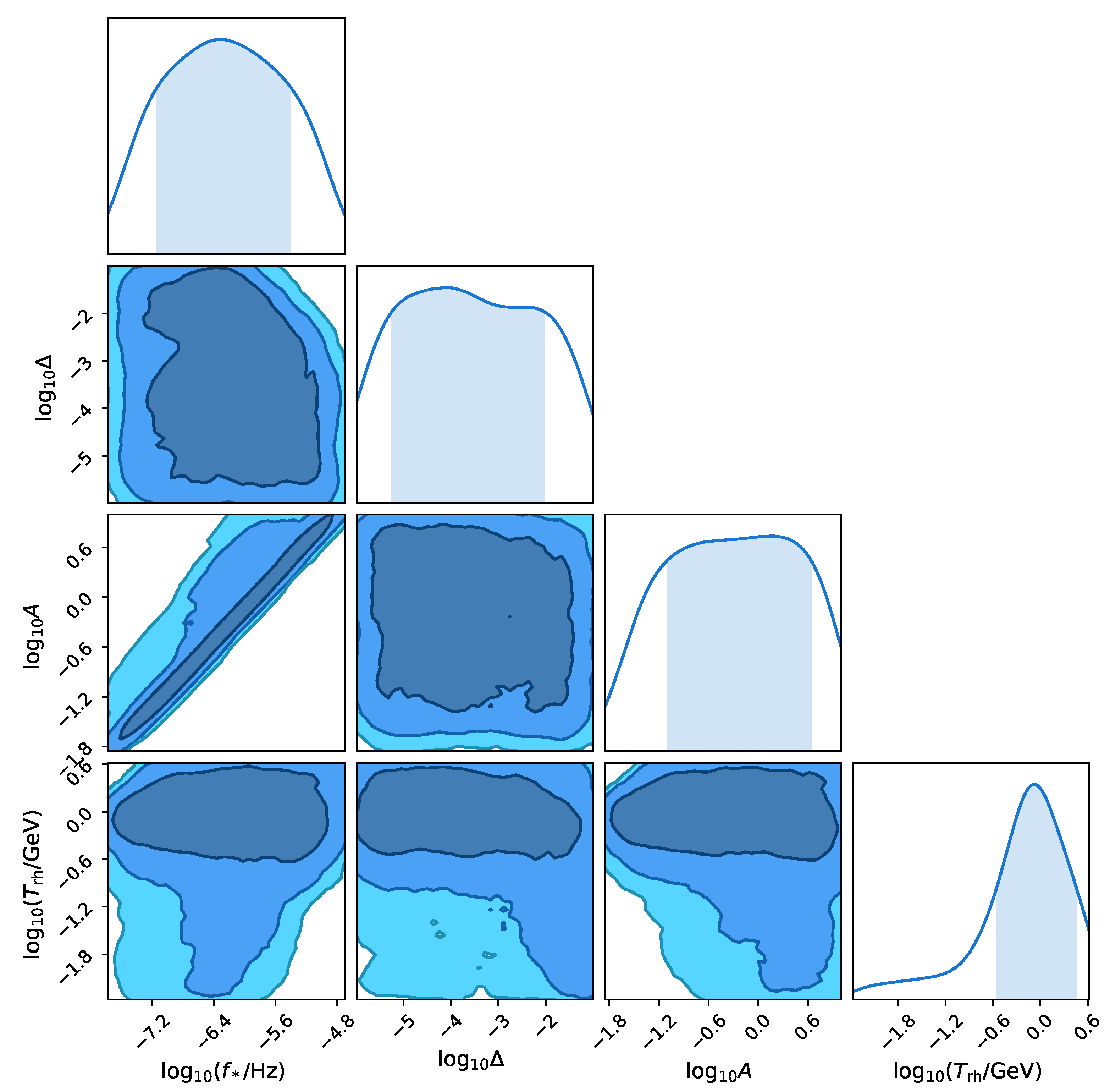

| Parameter | ||||
|---|---|---|---|---|
| prior | ||||
| posterior |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, Q. Constraints on the Primordial Curvature Power Spectrum and Reheating Temperature from the NANOGrav 15-Year Dataset. Universe 2024, 10, 251. https://doi.org/10.3390/universe10060251
Fei Q. Constraints on the Primordial Curvature Power Spectrum and Reheating Temperature from the NANOGrav 15-Year Dataset. Universe. 2024; 10(6):251. https://doi.org/10.3390/universe10060251
Chicago/Turabian StyleFei, Qin. 2024. "Constraints on the Primordial Curvature Power Spectrum and Reheating Temperature from the NANOGrav 15-Year Dataset" Universe 10, no. 6: 251. https://doi.org/10.3390/universe10060251
APA StyleFei, Q. (2024). Constraints on the Primordial Curvature Power Spectrum and Reheating Temperature from the NANOGrav 15-Year Dataset. Universe, 10(6), 251. https://doi.org/10.3390/universe10060251





