The cos 2ϕh Asymmetry in K± Mesons and the Λ-Hyperon-Produced SIDIS Process at Electron Ion Colliders
Abstract
:1. Introduction
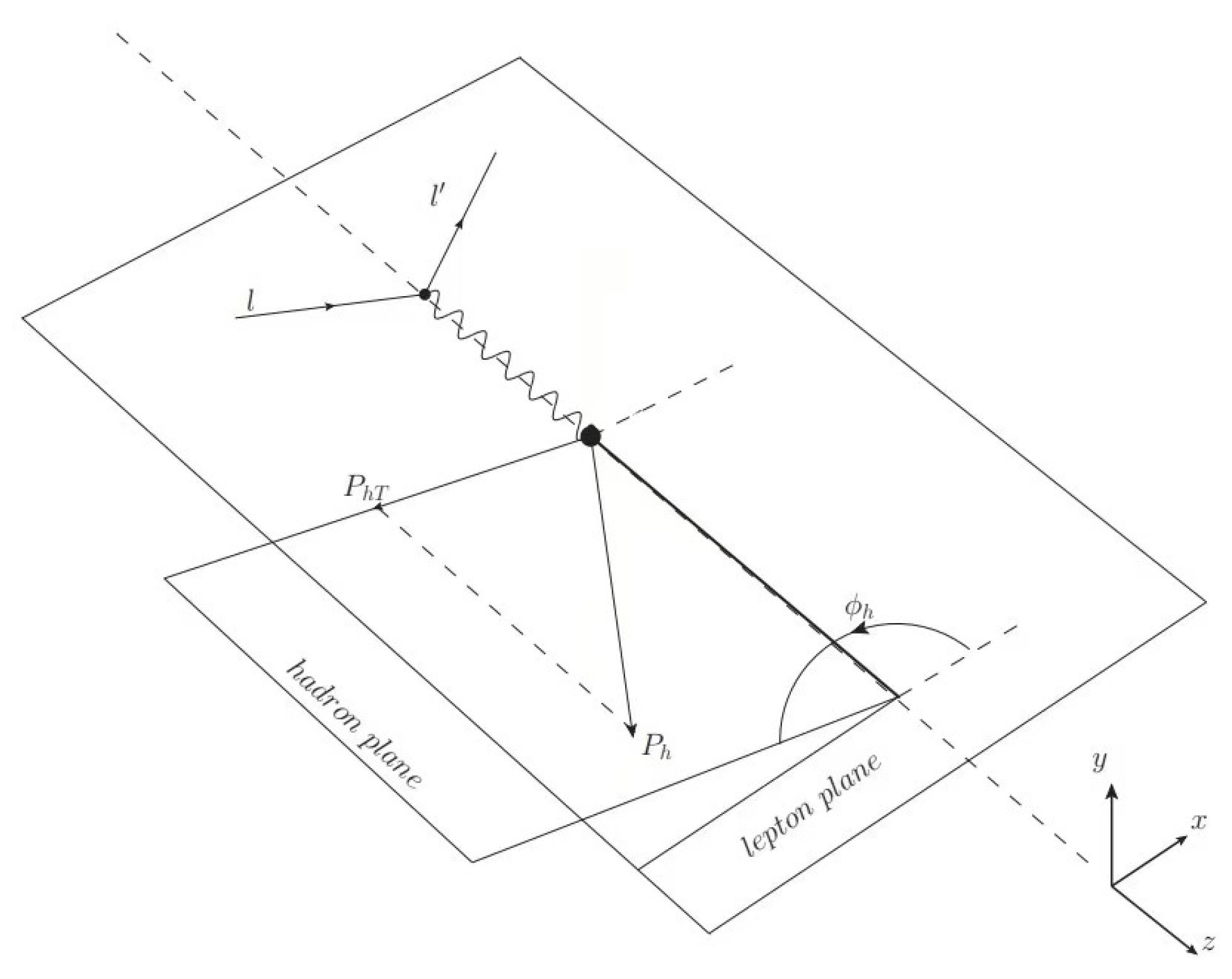
2. Formalism of the Asymmetry in the SIDIS Process
2.1. TMD Evolution Effects
2.2. The Structure Functions
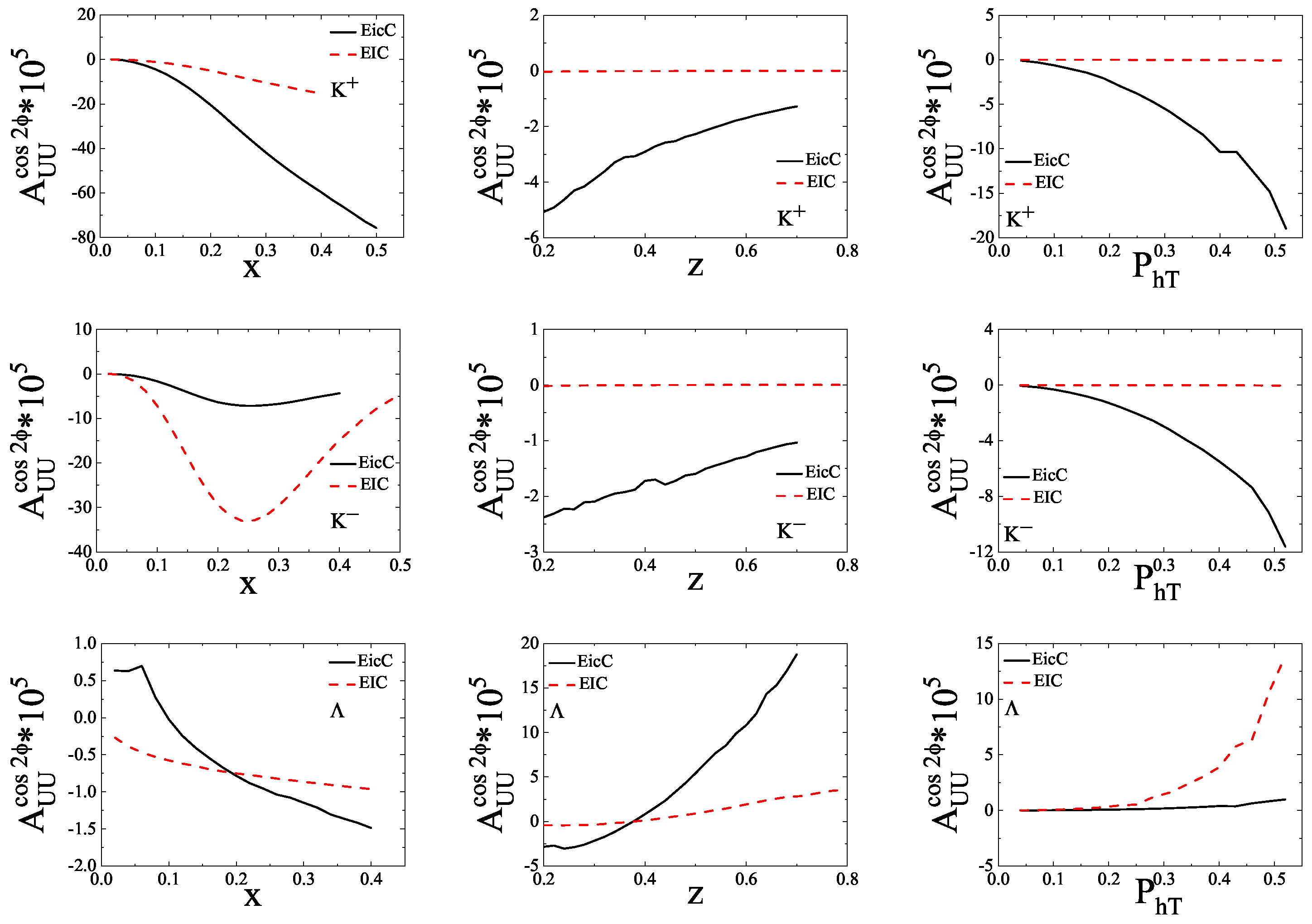
3. Numerical Estimate
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boer, D. Investigating the origins of transverse spin asymmetries at RHIC. Phys. Rev. D 1999, 60, 014012. [Google Scholar] [CrossRef]
- Boer, D.; Mulders, P.J. Time reversal odd distribution functions in leptoproduction. Phys. Rev. D 1998, 57, 5780–5786. [Google Scholar] [CrossRef]
- Meissner, S.; Metz, A.; Schlegel, M.; Goeke, K. Generalized parton correlation functions for a spin-0 hadron. J. High Energy Phys. 2008, 8, 038. [Google Scholar] [CrossRef]
- Meissner, S.; Metz, A.; Goeke, K. Relations between generalized and transverse momentum dependent parton distributions. Phys. Rev. D 2007, 76, 034002. [Google Scholar] [CrossRef]
- Tangerman, R.D.; Mulders, P.J. Intrinsic transverse momentum and the polarized Drell-Yan process. Phys. Rev. D 1995, 51, 3357–3372. [Google Scholar] [CrossRef]
- Meissner, S.; Metz, A.; Schlegel, M. Generalized parton correlation functions for a spin-1/2 hadron. J. High Energy Phys. 2009, 8, 056. [Google Scholar] [CrossRef]
- Kotzinian, A. New quark distributions and semiinclusive electroproduction on the polarized nucleons. Nucl. Phys. B 1995, 441, 234–248. [Google Scholar] [CrossRef]
- Collins, J.C. Fragmentation of transversely polarized quarks probed in transverse momentum distributions. Nucl. Phys. B 1993, 396, 161–182. [Google Scholar] [CrossRef]
- Collins, J.C. Leading twist single transverse-spin asymmetries: Drell-Yan and deep inelastic scattering. Phys. Lett. B 2002, 536, 43–48. [Google Scholar] [CrossRef]
- Ji, X.D.; Yuan, F. Parton distributions in light cone gauge: Where are the final state interactions? Phys. Lett. B 2002, 543, 66–72. [Google Scholar] [CrossRef]
- Belitsky, A.V.; Ji, X.; Yuan, F. Final state interactions and gauge invariant parton distributions. Nucl. Phys. B 2003, 656, 165–198. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Hwang, D.S.; Schmidt, I. Initial state interactions and single spin asymmetries in Drell-Yan processes. Nucl. Phys. B 2002, 642, 344–356. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Hwang, D.S.; Schmidt, I. Final state interactions and single spin asymmetries in semiinclusive deep inelastic scattering. Phys. Lett. B 2002, 530, 99–107. [Google Scholar] [CrossRef]
- Boer, D.; Brodsky, S.J.; Hwang, D.S. Initial state interactions in the unpolarized Drell-Yan process. Phys. Rev. D 2003, 67, 054003. [Google Scholar] [CrossRef]
- Bacchetta, A.; Schaefer, A.; Yang, J.J. Sivers function in a spectator model with axial vector diquarks. Phys. Lett. B 2004, 578, 109–118. [Google Scholar] [CrossRef]
- Maji, T.; Chakrabarti, D.; Mukherjee, A. Sivers and cos2ϕ asymmetries in semi-inclusive deep inelastic scattering in light-front holographic model. Phys. Rev. D 2018, 97, 014016. [Google Scholar] [CrossRef]
- Pasquini, B.; Schweitzer, P. Pion transverse momentum dependent parton distributions in a light-front constituent approach, and the Boer-Mulders effect in the pion-induced Drell-Yan process. Phys. Rev. D 2014, 90, 014050. [Google Scholar] [CrossRef]
- Lu, Z.; Ma, B.Q.; Zhu, J. Boer-Mulders function of the pion in the MIT bag model. Phys. Rev. D 2012, 86, 094023. [Google Scholar] [CrossRef]
- Ceccopieri, F.A.; Courtoy, A.; Noguera, S.; Scopetta, S. Pion nucleus Drell–Yan process and parton transverse momentum in the pion. Eur. Phys. J. C 2018, 78, 644. [Google Scholar] [CrossRef]
- Noguera, S.; Scopetta, S. Pion transverse momentum dependent parton distributions in the Nambu and Jona-Lasinio model. J. High Energy Phys. 2015, 11, 102. [Google Scholar] [CrossRef]
- Khalek, R.A.; Accardi, A.; Adam, J.; Adamiak, D.; Akers, W.; Albaladejo, M.; Al-bataineh, A.; Alexeev, M.G.; Ameli, F.; Antonioli, P.; et al. Science Requirements and Detector Concepts for the Electron-Ion Collider: EIC Yellow Report. Nucl. Phys. A 2022, 1026, 122447. [Google Scholar] [CrossRef]
- Aschenauer, E.C.; Balitsky, I.; Bland, L.; Brodsky, S.J.; Burkardt, M.; Burkert, V.; Chen, J.P.; Deshpande, A.; Diehl, M.; Gamberg, L.; et al. Pre-Town Meeting on Spin Physics at an Electron-Ion Collider. Eur. Phys. J. A 2017, 53, 71. [Google Scholar] [CrossRef]
- Zeng, C.; Liu, T.; Sun, P.; Zhao, Y. Toward three-dimensional nucleon structures at the Electron-Ion Collider in China: A study of the Sivers function. Phys. Rev. D 2022, 106, 094039. [Google Scholar] [CrossRef]
- Ji, X.D.; Ma, J.P.; Yuan, F. QCD factorization for spin-dependent cross sections in DIS and Drell-Yan processes at low transverse momentum. Phys. Lett. B 2004, 597, 299–308. [Google Scholar] [CrossRef]
- Pitonyak, D.; Schlegel, M.; Metz, A. Polarized hadron pair production from electron-positron annihilation. Phys. Rev. D 2014, 89, 054032. [Google Scholar] [CrossRef]
- Boer, D. Angular dependences in inclusive two-hadron production at BELLE. Nucl. Phys. B 2009, 806, 23–67. [Google Scholar] [CrossRef]
- Seidl, R.A.; Hasuko, K.; Abe, K.; Adachi, I.; Aihara, H.; Anipko, D.; Asano, Y.; Aushev, T.; Bakich, A.M.; Balagura, V.; et al. Measurement of azimuthal asymmetries in inclusive production of hadron pairs in e+e− annihilation at Belle. Phys. Rev. Lett. 2006, 96, 232002. [Google Scholar] [CrossRef] [PubMed]
- Jaffe, R.L.; Ji, X.D. Chiral odd parton distributions and Drell-Yan processes. Nucl. Phys. B 1992, 375, 527–560. [Google Scholar] [CrossRef]
- Lambertsen, M.; Vogelsang, W. Drell-Yan lepton angular distributions in perturbative QCD. Phys. Rev. D 2016, 93, 114013. [Google Scholar] [CrossRef]
- Collins, J.C.; Soper, D.E.; Sterman, G.F. Transverse Momentum Distribution in Drell-Yan Pair and W and Z Boson Production. Nucl. Phys. B 1985, 250, 199–224. [Google Scholar] [CrossRef]
- Idilbi, A.; Ji, X.D.; Ma, J.P.; Yuan, F. Collins-Soper equation for the energy evolution of transverse-momentum and spin dependent parton distributions. Phys. Rev. D 2004, 70, 074021. [Google Scholar] [CrossRef]
- Gurjar, B.; Mondal, C. Predicting sin(2ϕ-ϕs) azimuthal asymmetry in pion-proton induced Drell-Yan process using holographic light-front QCD. Phys. Rev. D 2024, 109, 014038. [Google Scholar] [CrossRef]
- Collins, J.C.; Hautmann, F. Infrared divergences and nonlightlike eikonal lines in Sudakov processes. Phys. Lett. B 2000, 472, 129–134. [Google Scholar] [CrossRef]
- Aybat, S.M.; Rogers, T.C. TMD Parton Distribution and Fragmentation Functions with QCD Evolution. Phys. Rev. D 2011, 83, 114042. [Google Scholar] [CrossRef]
- Bacchetta, A.; D’Alesio, U.; Diehl, M.; Miller, C.A. Single-spin asymmetries: The Trento conventions. Phys. Rev. D 2004, 70, 117504. [Google Scholar] [CrossRef]
- Bacchetta, A.; Diehl, M.; Goeke, K.; Metz, A.; Mulders, P.J.; Schlegel, M. Semi-inclusive deep inelastic scattering at small transverse momentum. J. High Energy Phys. 2007, 2, 093. [Google Scholar] [CrossRef]
- Cahn, R.N. Critique of Parton Model Calculations of Azimuthal Dependence in Leptoproduction. Phys. Rev. D 1989, 40, 3107–3110. [Google Scholar] [CrossRef] [PubMed]
- Chang, W.C.; McClellan, R.E.; Peng, J.C.; Teryaev, O. Lepton Angular Distributions of Fixed-target Drell-Yan Experiments in Perturbative QCD and a Geometric Approach. Phys. Rev. D 2019, 99, 014032. [Google Scholar] [CrossRef]
- Wan, J.; Tan, C.; Lu, Z. The cos2ϕ azimuthal asymmetry in e+e− → π+π− X process. Phys. Lett. B 2020, 811, 135884. [Google Scholar] [CrossRef]
- Collins, J. Foundations of Perturbative QCD. Camb. Monogr. Part. Phys. Nucl. Phys. Cosmol. 2011, 32, 1–624. [Google Scholar]
- Yang, S.; Song, J.; Wang, X.; Li, D.M.; Lu, Z. The Sivers asymmetry in charged Kaon and Λ hyperon produced SIDIS process at electron ion colliders. Eur. Phys. J. C 2023, 83, 1148. [Google Scholar] [CrossRef]
- Kang, Z.B.; Xiao, B.W.; Yuan, F. QCD Resummation for Single Spin Asymmetries. Phys. Rev. Lett. 2011, 107, 152002. [Google Scholar] [CrossRef] [PubMed]
- Echevarria, M.G.; Idilbi, A.; Scimemi, I. Unified treatment of the QCD evolution of all (un-)polarized transverse momentum dependent functions: Collins function as a study case. Phys. Rev. D 2014, 90, 014003. [Google Scholar] [CrossRef]
- Echevarria, M.G.; Idilbi, A.; Schäfer, A.; Scimemi, I. Model-Independent Evolution of Transverse Momentum Dependent Distribution Functions (TMDs) at NNLL. Eur. Phys. J. C 2013, 73, 2636. [Google Scholar] [CrossRef]
- Echevarria, M.G.; Idilbi, A.; Kang, Z.B.; Vitev, I. QCD Evolution of the Sivers Asymmetry. Phys. Rev. D 2014, 89, 074013. [Google Scholar] [CrossRef]
- Landry, F.; Brock, R.; Nadolsky, P.M.; Yuan, C.P. Tevatron Run-1 Z boson data and Collins-Soper-Sterman resummation formalism. Phys. Rev. D 2003, 67, 073016. [Google Scholar] [CrossRef]
- Qiu, J.W.; Zhang, X.F. QCD prediction for heavy boson transverse momentum distributions. Phys. Rev. Lett. 2001, 86, 2724–2727. [Google Scholar] [CrossRef] [PubMed]
- Konychev, A.V.; Nadolsky, P.M. Universality of the Collins-Soper-Sterman nonperturbative function in gauge boson production. Phys. Lett. B 2006, 633, 710–714. [Google Scholar] [CrossRef]
- Ellis, R.K.; Ross, D.A.; Veseli, S. Vector boson production in hadronic collisions. Nucl. Phys. B 1997, 503, 309–338. [Google Scholar] [CrossRef]
- Kang, Z.B.; Prokudin, A.; Sun, P.; Yuan, F. Extraction of Quark Transversity Distribution and Collins Fragmentation Functions with QCD Evolution. Phys. Rev. D 2016, 93, 014009. [Google Scholar] [CrossRef]
- Lai, H.L.; Guzzi, M.; Huston, J.; Li, Z.; Nadolsky, P.M.; Pumplin, J.; Yuan, C.P. New parton distributions for collider physics. Phys. Rev. D 2010, 82, 074024. [Google Scholar] [CrossRef]
- Florian, D.D.; Sassot, R.; Stratmann, M. Global analysis of fragmentation functions for pions and kaons and their uncertainties. Phys. Rev. D 2007, 75, 114010. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, Z.; Schmidt, I. Transverse polarization of the Λ hyperon from unpolarized quark fragmentation in the diquark model. Phys. Rev. D 2017, 96, 034010. [Google Scholar] [CrossRef]
- Botje, M. QCDNUM: Fast QCD Evolution and Convolution. Comput. Phys. Commun. 2011, 182, 490–532. [Google Scholar] [CrossRef]
- Lu, Z.; Schmidt, I. Updating Boer-Mulders functions from unpolarized pd and pp Drell-Yan data. Phys. Rev. D 2010, 81, 034023. [Google Scholar] [CrossRef]
- Airapetian, A.; Akopov, N.; Akopov, Z.; Amarian, M.; Andrus, A.; Aschenauer, E.C.; Augustyniak, W.; Avakian, R.; Avetissian, A.; Avetissian, E.; et al. Single-spin asymmetries in semi-inclusive deep-inelastic scattering on a transversely polarized hydrogen target. Phys. Rev. Lett. 2005, 94, 012002. [Google Scholar] [CrossRef]
- Airapetian, A.; Akopov, N.; Akopov, Z.; Aschenauerf, E.C.; Augustyniak, W.; Avakian, R.; Avetissian, A.; Avetisyan, E.; Bacchetta, A.; Belostotski, S.; et al. Effects of transversity in deep-inelastic scattering by polarized protons. Phys. Lett. B 2010, 693, 11–16. [Google Scholar] [CrossRef]
- Ageev, E.S.; Alexakhin, V.Y.; Alexandrov, Y.; Alexeev, G.D.; Alexeev, M.; Amoroso, A.; Badełek, B.; Balestra, F.; Ball, J.; Barth, J.; et al. A New measurement of the Collins and Sivers asymmetries on a transversely polarised deuteron target. Nucl. Phys. B 2007, 765, 31–70. [Google Scholar] [CrossRef]
- Adolph, C.; Alekseev, M.G.; Alexakhin, V.Y.; Alexandrov, Y.; Alexeev, G.D.; Amoroso, A.; Antonov, A.A.; Austregesilo, A.; Badelek, B.; Balestra, F.; et al. Experimental investigation of transverse spin asymmetries in muon-p SIDIS processes: Collins asymmetries. Phys. Lett. B 2012, 717, 376–382. [Google Scholar] [CrossRef]
- Anselmino, M.; Boglione, M.; D’Alesio, U.; Hernandez, J.O.G.; Melis, S.; Murgia, F.; Prokudin, A. Extracting the Kaon Collins function from e+e− hadron pair production data. Phys. Rev. D 2016, 93, 034025. [Google Scholar] [CrossRef]
- Yang, S.; Xu, Q.; Zhang, Y.; Wang, X. The Collins Asymmetry in Λ Hyperon Produced SIDIS Process at Electron–Ion Colliders. Symmetry 2023, 15, 841. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Li, Y.; Xue, S.-C.; Li, H.; Wang, X. The cos 2ϕh Asymmetry in K± Mesons and the Λ-Hyperon-Produced SIDIS Process at Electron Ion Colliders. Universe 2024, 10, 280. https://doi.org/10.3390/universe10070280
Song J, Li Y, Xue S-C, Li H, Wang X. The cos 2ϕh Asymmetry in K± Mesons and the Λ-Hyperon-Produced SIDIS Process at Electron Ion Colliders. Universe. 2024; 10(7):280. https://doi.org/10.3390/universe10070280
Chicago/Turabian StyleSong, Jianxi, Yanli Li, Shi-Chen Xue, Hui Li, and Xiaoyu Wang. 2024. "The cos 2ϕh Asymmetry in K± Mesons and the Λ-Hyperon-Produced SIDIS Process at Electron Ion Colliders" Universe 10, no. 7: 280. https://doi.org/10.3390/universe10070280
APA StyleSong, J., Li, Y., Xue, S. -C., Li, H., & Wang, X. (2024). The cos 2ϕh Asymmetry in K± Mesons and the Λ-Hyperon-Produced SIDIS Process at Electron Ion Colliders. Universe, 10(7), 280. https://doi.org/10.3390/universe10070280






