Isospin QCD as a Laboratory for Dense QCD
Abstract
:1. Introduction
2. A Quark–Meson Model at Finite Density: Outline
3. A Quark–Meson Model: Mean Field Treatments
4. Purely Hadronic Descriptions: Tree Level Analyses
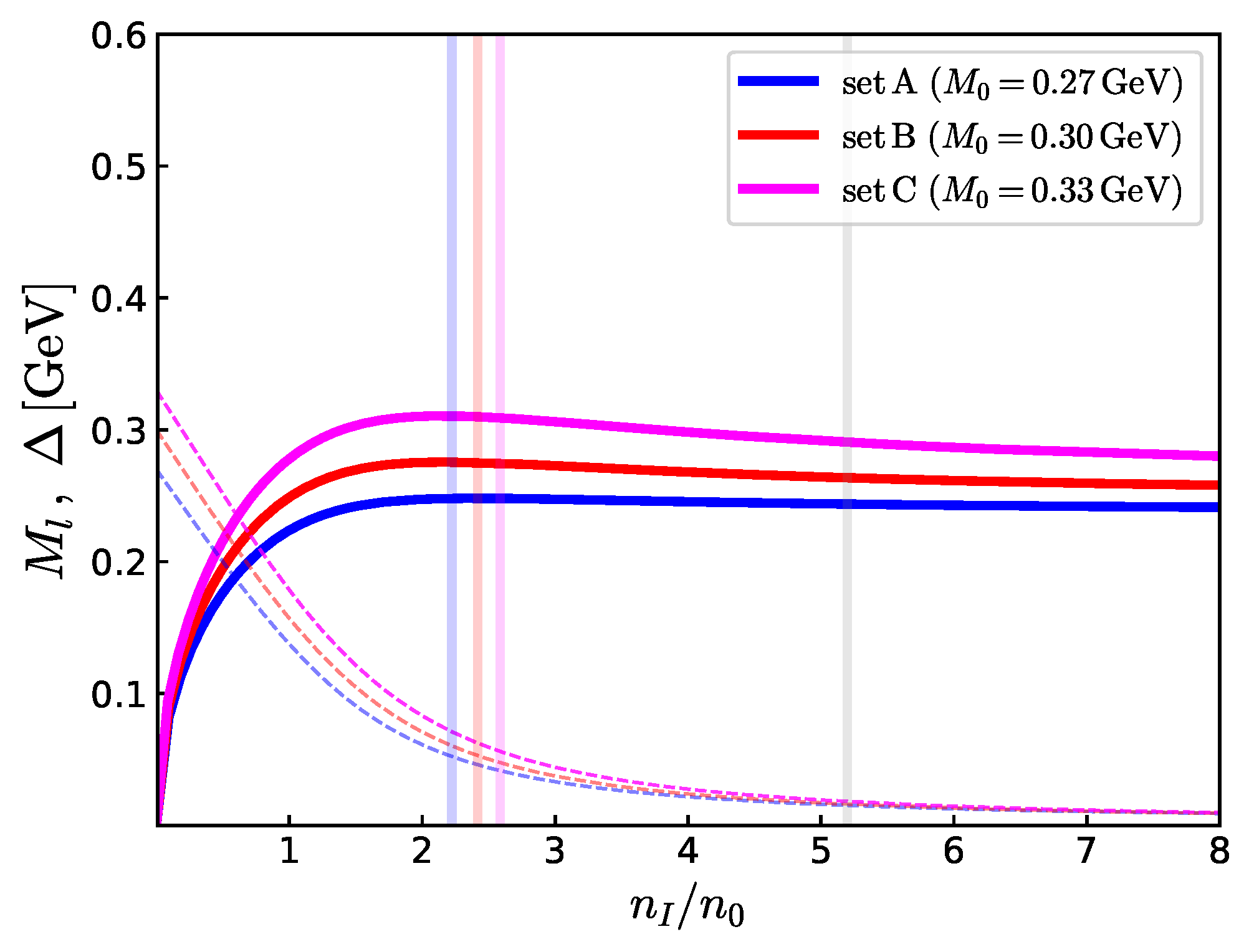
4.1. Gap Equations at Tree Level
4.2. Meson Kinetic and Mass Matrices at Tree Level
4.2.1. The Spectra of , , and
4.2.2. The Spectra of
5. Quark Descriptions
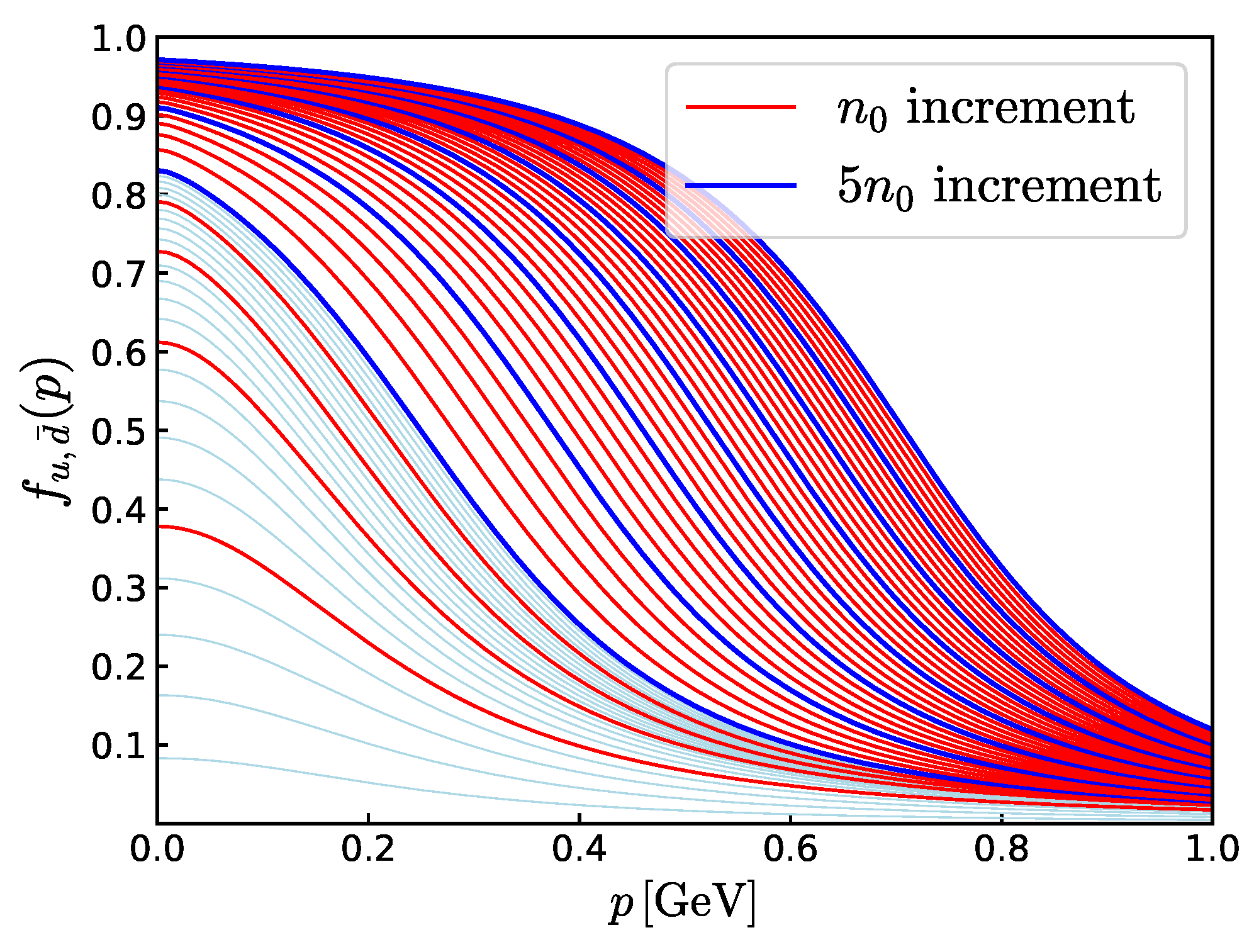
5.1. The Structure of the Effective Potential
5.2. The Structure of the Gap Equations
6. Meson Poles at One-Loop: Parameter Fixing
6.1. Meson Poles
6.2. Parameter Fixing
7. Equations of State at Zero Temperature
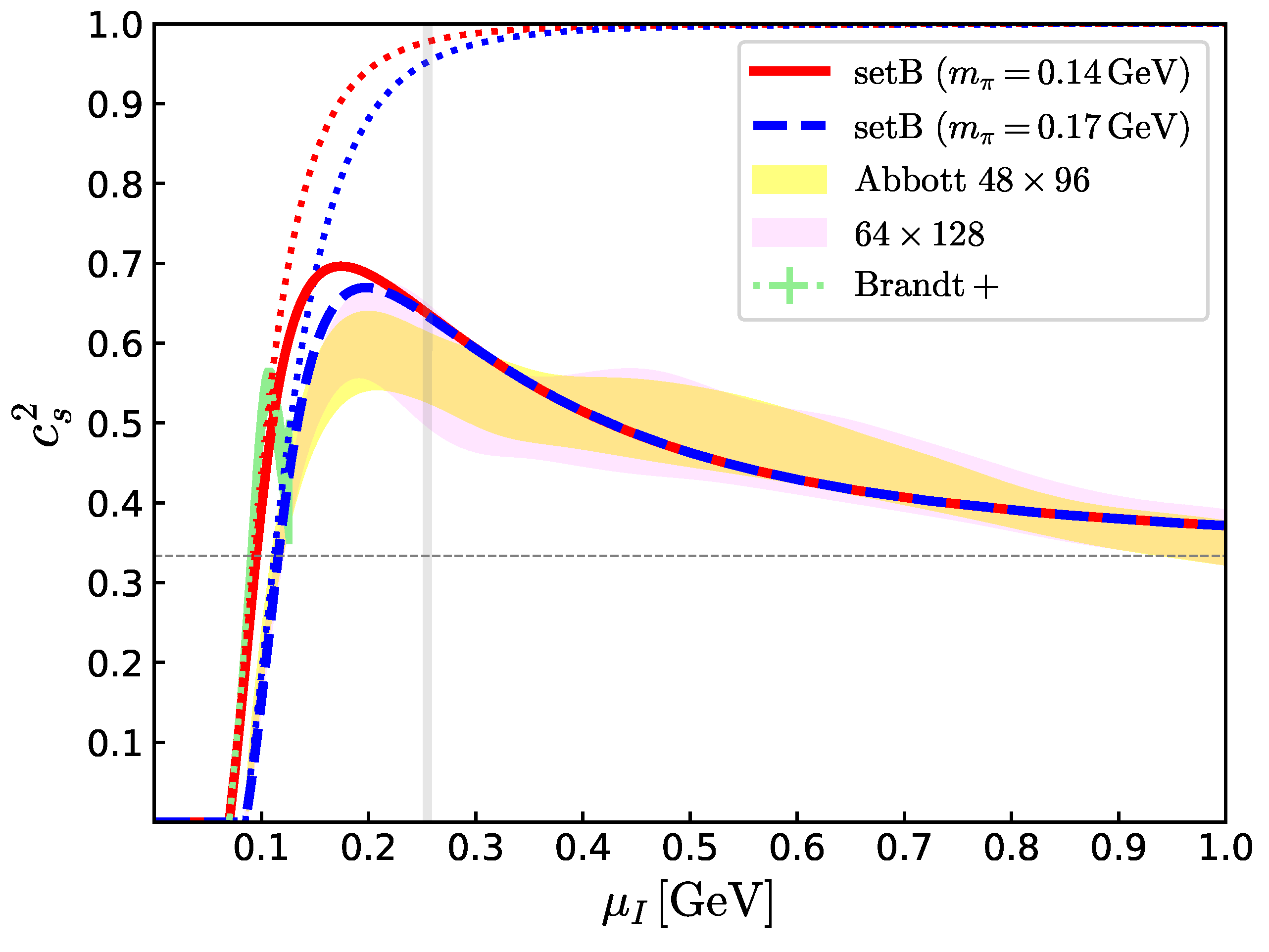
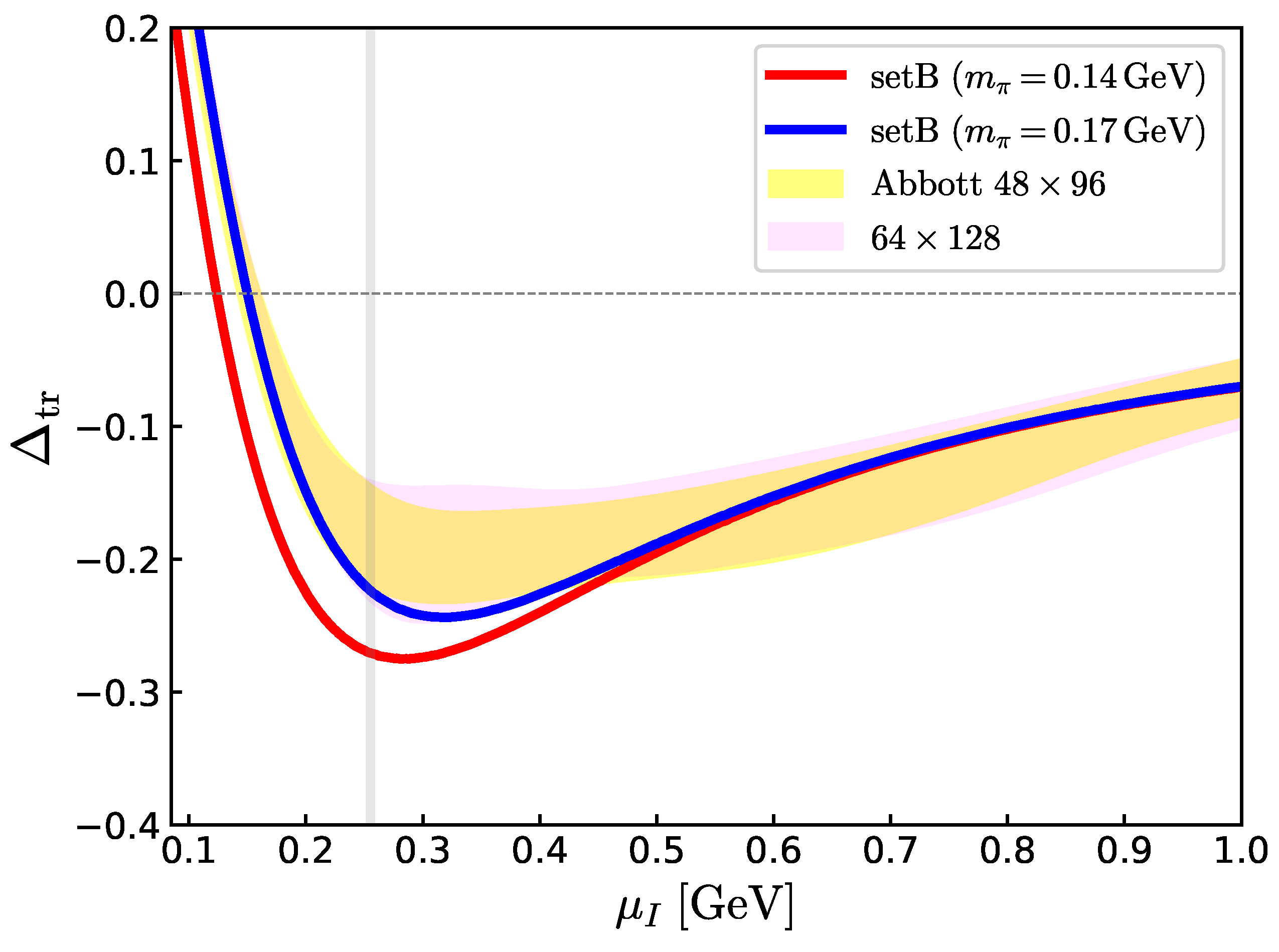
7.1. High-Density Regime: Conformal Behaviors
7.2. High-Density Regime: Perturbative and Power Corrections
7.3. Quark Saturation
8. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QC2D | two-color quantum chromodynamics |
| QCDI | isospin QCD |
| EOS | equations of state |
| –300 MeV | non-perturbative scale in QCD |
| nuclear saturation density | |
| ChPT | Chiral perturbation theory |
References
- Kogut, J.B.; Stephanov, M.A.; Toublan, D. On two color QCD with baryon chemical potential. Phys. Lett. B 1999, 464, 183–191. [Google Scholar] [CrossRef]
- Kogut, J.B.; Stephanov, M.A.; Toublan, D.; Verbaarschot, J.J.M.; Zhitnitsky, A. QCD-like theories at finite baryon density. Nucl. Phys. B 2000, 582, 477–513. [Google Scholar] [CrossRef]
- Iida, K.; Itou, E.; Murakami, K.; Suenaga, D. Lattice study on finite density QC2D towards zero temperature. arXiv 2024, arXiv:2405.20566. [Google Scholar]
- Iida, K.; Itou, E.; Lee, T.G. Two-colour QCD phases and the topology at low temperature and high density. J. High Energy Phys. 2020, 1, 181. [Google Scholar] [CrossRef]
- Iida, K.; Itou, E.; Lee, T.G. Relative scale setting for two-color QCD with Nf = 2 Wilson fermions. Prog. Theor. Exp. Phys. 2021, 2021, 013B05. [Google Scholar] [CrossRef]
- Boz, T.; Giudice, P.; Hands, S.; Skullerud, J.I. Dense two-color QCD towards continuum and chiral limits. Phys. Rev. D 2020, 101, 074506. [Google Scholar] [CrossRef]
- Boz, T.; Cotter, S.; Fister, L.; Mehta, D.; Skullerud, J.I. Phase transitions and gluodynamics in 2-colour matter at high density. Eur. Phys. J. A 2013, 49, 87. [Google Scholar] [CrossRef]
- Cotter, S.; Giudice, P.; Hands, S.; Skullerud, J.I. Towards the phase diagram of dense two-color matter. Phys. Rev. D 2013, 87, 034507. [Google Scholar] [CrossRef]
- Hands, S.; Kenny, P.; Kim, S.; Skullerud, J.I. Lattice Study of Dense Matter with Two Colors and Four Flavors. Eur. Phys. J. A 2011, 47, 60. [Google Scholar] [CrossRef]
- Astrakhantsev, N.; Braguta, V.; Ilgenfritz, E.; Kotov, A.; Nikolaev, A. Lattice study of thermodynamic properties of dense QC2D. Phys. Rev. D 2020, 102, 074507. [Google Scholar] [CrossRef]
- Bornyakov, V.G.; Braguta, V.V.; Nikolaev, A.A.; Rogalyov, R.N. Effects of Dense Quark Matter on Gluon Propagators in Lattice QC2D. Phys. Rev. D 2020, 102, 114511. [Google Scholar] [CrossRef]
- Muroya, S.; Nakamura, A.; Nonaka, C. Behavior of hadrons at finite density: Lattice study of color SU(2) QCD. Phys. Lett. B 2003, 551, 305–310. [Google Scholar] [CrossRef]
- Suenaga, D.; Murakami, K.; Itou, E.; Iida, K. Probing the hadron mass spectrum in dense two-color QCD with the linear sigma model. Phys. Rev. D 2023, 107, 054001. [Google Scholar] [CrossRef]
- Suenaga, D.; Murakami, K.; Itou, E.; Iida, K. Mass spectrum of spin-one hadrons in dense two-color QCD: Novel predictions by extended linear sigma model. arXiv 2023, arXiv:2312.17017. [Google Scholar] [CrossRef]
- Kawaguchi, M.; Suenaga, D. Sound velocity peak induced by the chiral partner in dense two-color QCD. arXiv 2024, arXiv:2402.00430. [Google Scholar] [CrossRef]
- Sun, G.f.; He, L.; Zhuang, P. BEC-BCS crossover in the Nambu-Jona-Lasinio model of QCD. Phys. Rev. D 2007, 75, 096004. [Google Scholar] [CrossRef]
- Brauner, T.; Fukushima, K.; Hidaka, Y. Two-color quark matter: U(1)(A) restoration, superfluidity, and quarkyonic phase. Phys. Rev. D 2009, 80, 074035, Erratum in Phys. Rev. D 2010, 81, 119904. [Google Scholar] [CrossRef]
- Strodthoff, N.; von Smekal, L. Polyakov-Quark-Meson-Diquark Model for two-color QCD. Phys. Lett. B 2014, 731, 350–357. [Google Scholar] [CrossRef]
- Strodthoff, N.; Schaefer, B.J.; von Smekal, L. Quark-meson-diquark model for two-color QCD. Phys. Rev. D 2012, 85, 074007. [Google Scholar] [CrossRef]
- Abbott, R.; Detmold, W.; Illa, M.; Parreño, A.; Perry, R.J.; Romero-López, F.; Shanahan, P.E.; Wagman, M.L. QCD constraints on isospin-dense matter and the nuclear equation of state. arXiv 2024, arXiv:2406.09273. [Google Scholar]
- Abbott, R.; Detmold, W.; Romero-López, F.; Davoudi, Z.; Illa, M.; Parreño, A.; Perry, R.J.; Shanahan, P.E.; Wagman, M.L. Lattice quantum chromodynamics at large isospin density: 6144 pions in a box. arXiv 2023, arXiv:2307.15014. [Google Scholar]
- Brandt, B.B.; Cuteri, F.; Endrodi, G. Equation of state and speed of sound of isospin-asymmetric QCD on the lattice. J. High Energy Phys. 2023, 7, 55. [Google Scholar] [CrossRef]
- Son, D.T.; Stephanov, M.A. QCD at finite isospin density. Phys. Rev. Lett. 2001, 86, 592–595. [Google Scholar] [CrossRef]
- Son, D.T.; Stephanov, M.A. QCD at finite isospin density: From pion to quark-antiquark condensation. Phys. Atom. Nucl. 2001, 64, 834–842. [Google Scholar] [CrossRef]
- Splittorff, K.; Son, D.T.; Stephanov, M.A. QCD-like theories at finite baryon and isospin density. Phys. Rev. D 2001, 64, 016003. [Google Scholar] [CrossRef]
- Gómez Nicola, A.; Vioque-Rodríguez, A. Effective Lagrangian at nonzero isospin chemical potential. Phys. Rev. D 2022, 106, 114017. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Xia, C.J.; Ruggieri, M. Thermodynamics and susceptibilities of isospin imbalanced QCD matter. Eur. Phys. J. C 2020, 80, 46. [Google Scholar] [CrossRef]
- Fraga, E.S.; Palhares, L.F.; Villavicencio, C. Quark mass and isospin dependence of the deconfining critical temperature. Phys. Rev. D 2009, 79, 014021. [Google Scholar] [CrossRef]
- Stiele, R.; Fraga, E.S.; Schaffner-Bielich, J. Thermodynamics of (2+1)-flavor strongly interacting matter at nonzero isospin. Phys. Lett. B 2014, 729, 72–78. [Google Scholar] [CrossRef]
- Graf, T.; Schaffner-Bielich, J.; Fraga, E.S. Perturbative thermodynamics at nonzero isospin density for cold QCD. Phys. Rev. D 2016, 93, 085030. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G.; Fraga, E.S.; Hippert, M.; Schaffner-Bielich, J.; Schmalzbauer, S. New class of compact stars: Pion stars. Phys. Rev. D 2018, 98, 094510. [Google Scholar] [CrossRef]
- Fukushima, K.; Hatsuda, T. The phase diagram of dense QCD. Rep. Prog. Phys. 2011, 74, 014001. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Kojo, T. QCD equations of state and speed of sound in neutron stars. AAPPS Bull. 2021, 31, 11. [Google Scholar] [CrossRef]
- Vuorinen, A. Particle-theory Input for Neutron-star Physics. Acta Phys. Polon. B 2024, 55, 4-A4. [Google Scholar] [CrossRef]
- Drischler, C.; Han, S.; Lattimer, J.M.; Prakash, M.; Reddy, S.; Zhao, T. Limiting masses and radii of neutron stars and their implications. Phys. Rev. C 2021, 103, 045808. [Google Scholar] [CrossRef]
- Han, M.Z.; Huang, Y.J.; Tang, S.P.; Fan, Y.Z. Plausible presence of new state in neutron stars with masses above 0.98MTOV. Sci. Bull. 2023, 68, 913–919. [Google Scholar] [CrossRef]
- Kojo, T.; Baym, G.; Hatsuda, T. Implications of NICER for Neutron Star Matter: The QHC21 Equation of State. Astrophys. J. 2022, 934, 46. [Google Scholar] [CrossRef]
- Huang, Y.J.; Baiotti, L.; Kojo, T.; Takami, K.; Sotani, H.; Togashi, H.; Hatsuda, T.; Nagataki, S.; Fan, Y.Z. Merger and Postmerger of Binary Neutron Stars with a Quark-Hadron Crossover Equation of State. Phys. Rev. Lett. 2022, 129, 181101. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, Y.; Fukushima, K.; Hotokezaka, K.; Kyutoku, K. Gravitational Wave Signal for Quark Matter with Realistic Phase Transition. Phys. Rev. Lett. 2023, 130, 091404. [Google Scholar] [CrossRef] [PubMed]
- Kedia, A.; Kim, H.I.; Suh, I.S.; Mathews, G.J. Binary neutron star mergers as a probe of quark-hadron crossover equations of state. Phys. Rev. D 2022, 106, 103027. [Google Scholar] [CrossRef]
- Bauswein, A.; Bastian, N.U.F.; Blaschke, D.B.; Chatziioannou, K.; Clark, J.A.; Fischer, T.; Oertel, M. Identifying a first-order phase transition in neutron star mergers through gravitational waves. Phys. Rev. Lett. 2019, 122, 061102. [Google Scholar] [CrossRef] [PubMed]
- McLerran, L.; Reddy, S. Quarkyonic Matter and Neutron Stars. Phys. Rev. Lett. 2019, 122, 122701. [Google Scholar] [CrossRef] [PubMed]
- Jeong, K.S.; McLerran, L.; Sen, S. Dynamically generated momentum space shell structure of quarkyonic matter via an excluded volume model. Phys. Rev. C 2020, 101, 035201. [Google Scholar] [CrossRef]
- Kojo, T. Stiffening of matter in quark-hadron continuity. Phys. Rev. D 2021, 104, 074005. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Kojo, T.; McLerran, L.D. Momentum Shell in Quarkyonic Matter from Explicit Duality: A Dual Model for Cold, Dense QCD. Phys. Rev. Lett. 2024, 132, 112701. [Google Scholar] [CrossRef]
- Hayata, T.; Hidaka, Y.; Nishimura, K. Dense QCD2 with matrix product states. arXiv 2023, arXiv:2311.11643. [Google Scholar] [CrossRef]
- Mannarelli, M. Meson condensation. Particles 2019, 2, 411–443. [Google Scholar] [CrossRef]
- Chiba, R.; Kojo, T. Sound velocity peak and conformality in isospin QCD. Phys. Rev. D 2024, 109, 076006. [Google Scholar] [CrossRef]
- Chiba, R.; Kojo, T.; Suenaga, D. Thermal effects on sound velocity peak and conformality in isospin QCD. arXiv 2024, arXiv:2403.02538. [Google Scholar]
- Fujimoto, Y. Enhanced contribution of the pairing gap to the QCD equation of state at large isospin chemical potential. Phys. Rev. D 2024, 109, 054035. [Google Scholar] [CrossRef]
- Cohen, T.D. QCD inequalities for the nucleon mass and the free energy of baryonic matter. Phys. Rev. Lett. 2003, 91, 032002. [Google Scholar] [CrossRef]
- Navarrete, P.; Paatelainen, R.; Seppänen, K. Perturbative QCD meets phase quenching: The pressure of cold Quark Matter. arXiv 2024, arXiv:2403.02180. [Google Scholar]
- Fujimoto, Y.; Reddy, S. Bounds on the equation of state from QCD inequalities and lattice QCD. Phys. Rev. D 2024, 109, 014020. [Google Scholar] [CrossRef]
- Moore, G.D.; Gorda, T. Bounding the QCD Equation of State with the Lattice. J. High Energy Phys. 2023, 12, 133. [Google Scholar] [CrossRef]
- Adhikari, P.; Andersen, J.O.; Kneschke, P. On-shell parameter fixing in the quark-meson model. Phys. Rev. D 2017, 95, 036017. [Google Scholar] [CrossRef]
- Ayala, A.; Bandyopadhyay, A.; Farias, R.L.S.; Hernández, L.A.; Hernández, J.L. QCD equation of state at finite isospin density from the linear sigma model with quarks: The cold case. arXiv 2023, arXiv:2301.13633. [Google Scholar] [CrossRef]
- Gao, B.; Minamikawa, T.; Kojo, T.; Harada, M. Impacts of the U(1)A anomaly on nuclear and neutron star equation of state based on a parity doublet model. Phys. Rev. C 2022, 106, 065205. [Google Scholar] [CrossRef]
- Minamikawa, T.; Gao, B.; Kojo, T.; Harada, M. Chiral restoration of nucleons in neutron star matter: Studies based on a parity doublet model. arXiv 2023, arXiv:2302.00825. [Google Scholar]
- Hatsuda, T.; Tachibana, M.; Yamamoto, N.; Baym, G. New critical point induced by the axial anomaly in dense QCD. Phys. Rev. Lett. 2006, 97, 122001. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, N.; Tachibana, M.; Hatsuda, T.; Baym, G. Phase structure, collective modes, and the axial anomaly in dense QCD. Phys. Rev. D 2007, 76, 074001. [Google Scholar] [CrossRef]
- Hatsuda, T.; Tachibana, M.; Yamamoto, N. Spectral Continuity in Dense QCD. Phys. Rev. D 2008, 78, 011501. [Google Scholar] [CrossRef]
- Zhang, Z.; Fukushima, K.; Kunihiro, T. Number of the QCD critical points with neutral color superconductivity. Phys. Rev. D 2009, 79, 014004. [Google Scholar] [CrossRef]
- Schäfer, T.; Wilczek, F. Continuity of quark and hadron matter. Phys. Rev. Lett. 1999, 82, 3956–3959. [Google Scholar] [CrossRef]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hadron-Quark Crossover and Massive Hybrid Stars with Strangeness. Astrophys. J. 2013, 764, 12. [Google Scholar] [CrossRef]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hadron–quark crossover and massive hybrid stars. Prog. Theor. Exp. Phys. 2013, 2013, 073D01. [Google Scholar] [CrossRef]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hyperon Puzzle, Hadron-Quark Crossover and Massive Neutron Stars. Eur. Phys. J. A 2016, 52, 65. [Google Scholar] [CrossRef]
- Tajima, H.; Tsutsui, S.; Doi, T.M.; Iida, K. Density-Induced Hadron–Quark Crossover via the Formation of Cooper Triples. Symmetry 2023, 15, 333. [Google Scholar] [CrossRef]
- Ma, Y.L.; Rho, M. Towards the hadron–quark continuity via a topology change in compact stars. Prog. Part. Nucl. Phys. 2020, 113, 103791. [Google Scholar] [CrossRef]
- ’t Hooft, G. A Planar Diagram Theory for Strong Interactions. Nucl. Phys. B 1974, 72, 461. [Google Scholar] [CrossRef]
- Witten, E. Baryons in the 1/n Expansion. Nucl. Phys. B 1979, 160, 57–115. [Google Scholar] [CrossRef]
- Nishimura, T.; Kitazawa, M.; Kunihiro, T. Anomalous enhancement of dilepton production as a precursor of color superconductivity. Prog. Theor. Exp. Phys. 2022, 2022, 093D02. [Google Scholar] [CrossRef]
- Kitazawa, M.; Koide, T.; Kunihiro, T.; Nemoto, Y. Pre-critical phenomena of two-flavor color superconductivity in heated quark matter: Diquark-pair fluctuations and non-Fermi liquid behavior. Prog. Theor. Phys. 2005, 114, 117–155. [Google Scholar] [CrossRef]
- Kitazawa, M.; Koide, T.; Kunihiro, T.; Nemoto, Y. Precursor of color superconductivity in hot quark matter. Phys. Rev. D 2002, 65, 091504. [Google Scholar] [CrossRef]
- Blaschke, D.; Buballa, M.; Dubinin, A.; Roepke, G.; Zablocki, D. Generalized Beth–Uhlenbeck approach to mesons and diquarks in hot, dense quark matter. Ann. Phys. 2014, 348, 228–255. [Google Scholar] [CrossRef]
- Boz, T.; Hajizadeh, O.; Maas, A.; Skullerud, J.I. Finite-density gauge correlation functions in QC2D. Phys. Rev. D 2019, 99, 074514. [Google Scholar] [CrossRef]
- Kojo, T.; Baym, G. Color screening in cold quark matter. Phys. Rev. D 2014, 89, 125008. [Google Scholar] [CrossRef]
- Suenaga, D.; Kojo, T. Gluon propagator in two-color dense QCD: Massive Yang-Mills approach at one-loop. Phys. Rev. D 2019, 100, 076017. [Google Scholar] [CrossRef]
- Kojo, T.; Suenaga, D. Thermal quarks and gluon propagators in two-color dense QCD. Phys. Rev. D 2021, 103, 094008. [Google Scholar] [CrossRef]
- Contant, R.; Huber, M.Q. Dense two-color QCD from Dyson-Schwinger equations. Phys. Rev. D 2020, 101, 014016. [Google Scholar] [CrossRef]
- Kojo, T.; Hidaka, Y.; McLerran, L.; Pisarski, R.D. Quarkyonic Chiral Spirals. Nucl. Phys. A 2010, 843, 37–58. [Google Scholar] [CrossRef]
- Kojo, T.; Pisarski, R.D.; Tsvelik, A.M. Covering the Fermi Surface with Patches of Quarkyonic Chiral Spirals. Phys. Rev. D 2010, 82, 074015. [Google Scholar] [CrossRef]
- Kojo, T.; Hidaka, Y.; Fukushima, K.; McLerran, L.D.; Pisarski, R.D. Interweaving Chiral Spirals. Nucl. Phys. A 2012, 875, 94–138. [Google Scholar] [CrossRef]
- Kojo, T.; Su, N. The quark mass gap in a magnetic field. Phys. Lett. B 2013, 720, 192–197. [Google Scholar] [CrossRef]
- Kojo, T.; Su, N. The quark mass gap in strong magnetic fields. Nucl. Phys. A 2014, 931, 763–768. [Google Scholar] [CrossRef]
- Hattori, K.; Kojo, T.; Su, N. Mesons in strong magnetic fields: (I) General analyses. Nucl. Phys. A 2016, 951, 1–30. [Google Scholar] [CrossRef]
- Novikov, V.A.; Okun, L.B.; Shifman, M.A.; Vainshtein, A.I.; Voloshin, M.B.; Zakharov, V.I. Charmonium and Gluons: Basic Experimental Facts and Theoretical Introduction. Phys. Rep. 1978, 41, 1–133. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD and Resonance Physics. Theoretical Foundations. Nucl. Phys. B 1979, 147, 385–447. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD and Resonance Physics: Applications. Nucl. Phys. B 1979, 147, 448–518. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Charge Conjugation, a New Quantum Number G, and Selection Rules Concerning a Nucleon Anti-nucleon System. Nuovo Cim. 1956, 10, 749–753. [Google Scholar] [CrossRef]
- Andersen, J.O.; Adhikari, P.; Kneschke, P. Pion condensation and QCD phase diagram at finite isospin density. Proc. Sci. 2019, 336, 197. [Google Scholar] [CrossRef]
- Coleman, S.R.; Weinberg, E.J. Radiative Corrections as the Origin of Spontaneous Symmetry Breaking. Phys. Rev. D 1973, 7, 1888–1910. [Google Scholar] [CrossRef]
- Duarte, D.C.; Hernandez-Ortiz, S.; Jeong, K.S.; McLerran, L.D. Quarkyonic effective field theory, quark-nucleon duality, and ghosts. Phys. Rev. D 2021, 104, L091901. [Google Scholar] [CrossRef]
- Hatsuda, T.; Kunihiro, T. QCD phenomenology based on a chiral effective Lagrangian. Phys. Rep. 1994, 247, 221–367. [Google Scholar] [CrossRef]
- Tanabashi, M. et al. [Particle Data Group] Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Ananthanarayan, B.; Caprini, I.; Das, D. Electromagnetic charge radius of the pion at high precision. Phys. Rev. Lett. 2017, 119, 132002. [Google Scholar] [CrossRef]
- Koponen, J.; Bursa, F.; Davies, C.T.H.; Dowdall, R.J.; Lepage, G.P. Size of the pion from full lattice QCD with physical u, d, s and c quarks. Phys. Rev. D 2016, 93, 054503. [Google Scholar] [CrossRef]
- Wang, G.; Liang, J.; Draper, T.; Liu, K.F.; Yang, Y.B. Lattice Calculation of Pion Form Factor with Overlap Fermions. Phys. Rev. D 2021, 104, 074502. [Google Scholar] [CrossRef]
- Polyakov, M.V. Generalized parton distributions and strong forces inside nucleons and nuclei. Phys. Lett. B 2003, 555, 57–62. [Google Scholar] [CrossRef]
- Kharzeev, D.E. Mass radius of the proton. Phys. Rev. D 2021, 104, 054015. [Google Scholar] [CrossRef]
- Kaiser, N.; Weise, W. Sizes of the Nucleon. arXiv 2024, arXiv:2404.11292. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Fukushima, K.; McLerran, L.D.; Praszalowicz, M. Trace Anomaly as Signature of Conformality in Neutron Stars. Phys. Rev. Lett. 2022, 129, 252702. [Google Scholar] [CrossRef]
- Marczenko, M.; McLerran, L.; Redlich, K.; Sasaki, C. Reaching percolation and conformal limits in neutron stars. arXiv 2022, arXiv:2207.13059. [Google Scholar] [CrossRef]
- Tajima, H.; Iida, K.; Liang, H. Nonrelativistic trace anomaly and equation of state in dense fermionic matter. Phys. Rev. C 2024, 109, 055203. [Google Scholar] [CrossRef]
- Kojo, T.; Powell, P.D.; Song, Y.; Baym, G. Phenomenological QCD equation of state for massive neutron stars. Phys. Rev. D 2015, 91, 045003. [Google Scholar] [CrossRef]
- Kojo, T.; Suenaga, D. Peaks of sound velocity in two color dense QCD: Quark saturation effects and semishort range correlations. Phys. Rev. D 2022, 105, 076001. [Google Scholar] [CrossRef]
- Geißel, A.; Gorda, T.; Braun, J. Pressure and speed of sound in two-flavor color-superconducting quark matter at next-to-leading order. arXiv 2024, arXiv:2403.18010. [Google Scholar]
- Braun, J.; Geißel, A.; Schallmo, B. Speed of sound in dense strong-interaction matter. SciPost Phys. Core 2024, 7, 015. [Google Scholar] [CrossRef]
- Leonhardt, M.; Pospiech, M.; Schallmo, B.; Braun, J.; Drischler, C.; Hebeler, K.; Schwenk, A. Symmetric nuclear matter from the strong interaction. Phys. Rev. Lett. 2020, 125, 142502. [Google Scholar] [CrossRef]
- Fukushima, K.; Kojo, T.; Weise, W. Hard-core deconfinement and soft-surface delocalization from nuclear to quark matter. Phys. Rev. D 2020, 102, 096017. [Google Scholar] [CrossRef]
- Saito, K.; Tsushima, K.; Thomas, A.W. Nucleon and hadron structure changes in the nuclear medium and impact on observables. Prog. Part. Nucl. Phys. 2007, 58, 1–167. [Google Scholar] [CrossRef]
- Geesaman, D.F.; Saito, K.; Thomas, A.W. The nuclear EMC effect. Ann. Rev. Nucl. Part. Sci. 1995, 45, 337–390. [Google Scholar] [CrossRef]
- Koch, V.; McLerran, L.; Miller, G.A.; Vovchenko, V. Might Normal Nuclear Matter be Quarkyonic? arXiv 2024, arXiv:2403.15375. [Google Scholar]
- McLerran, L.; Miller, G.A. The Quark Pauli Principle and the Transmutation of Nuclear Matter. arXiv 2024, arXiv:2405.11074. [Google Scholar]
- McLerran, L.; Pisarski, R.D. Phases of cold, dense quarks at large N(c). Nucl. Phys. A 2007, 796, 83–100. [Google Scholar] [CrossRef]
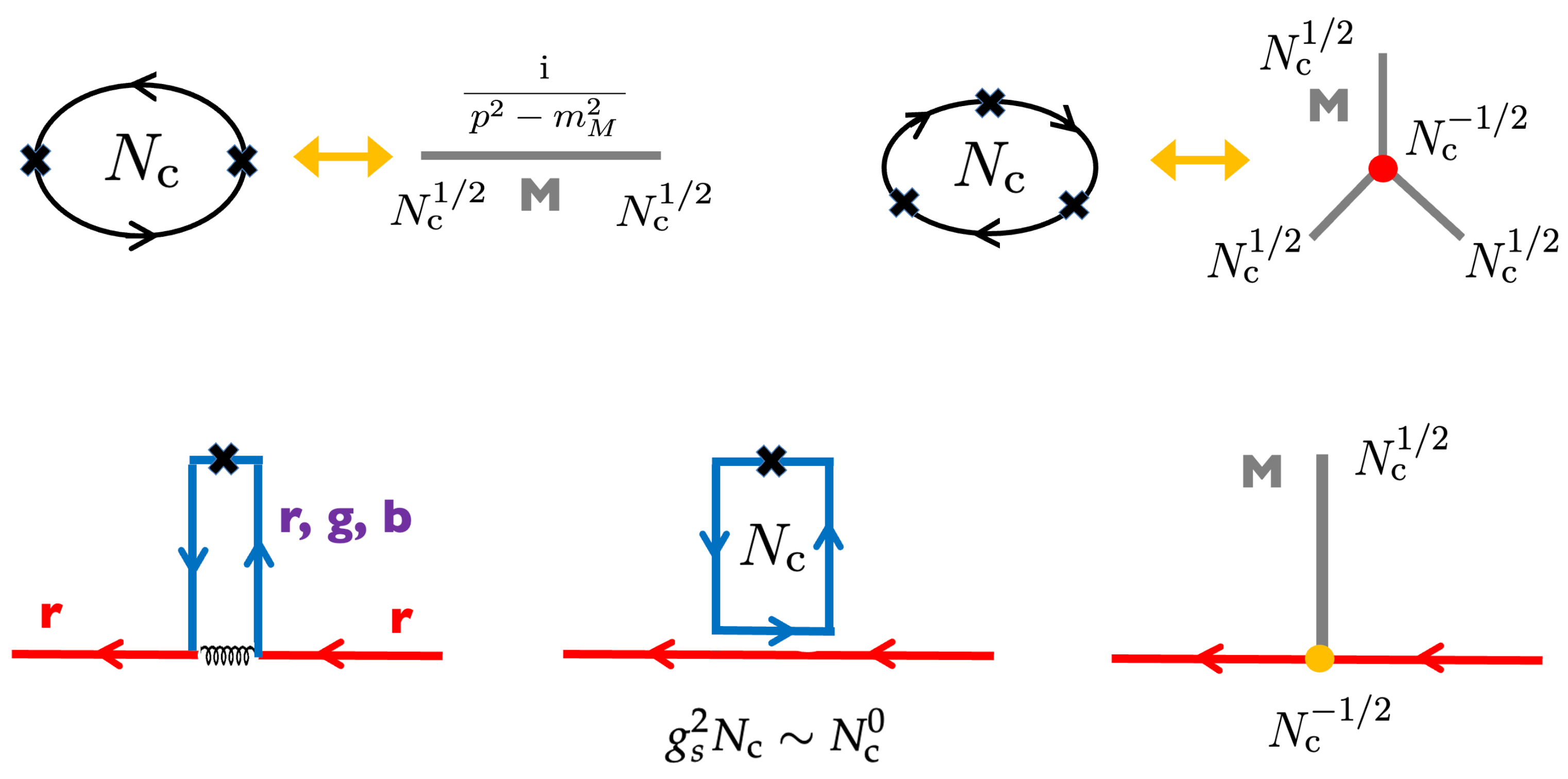
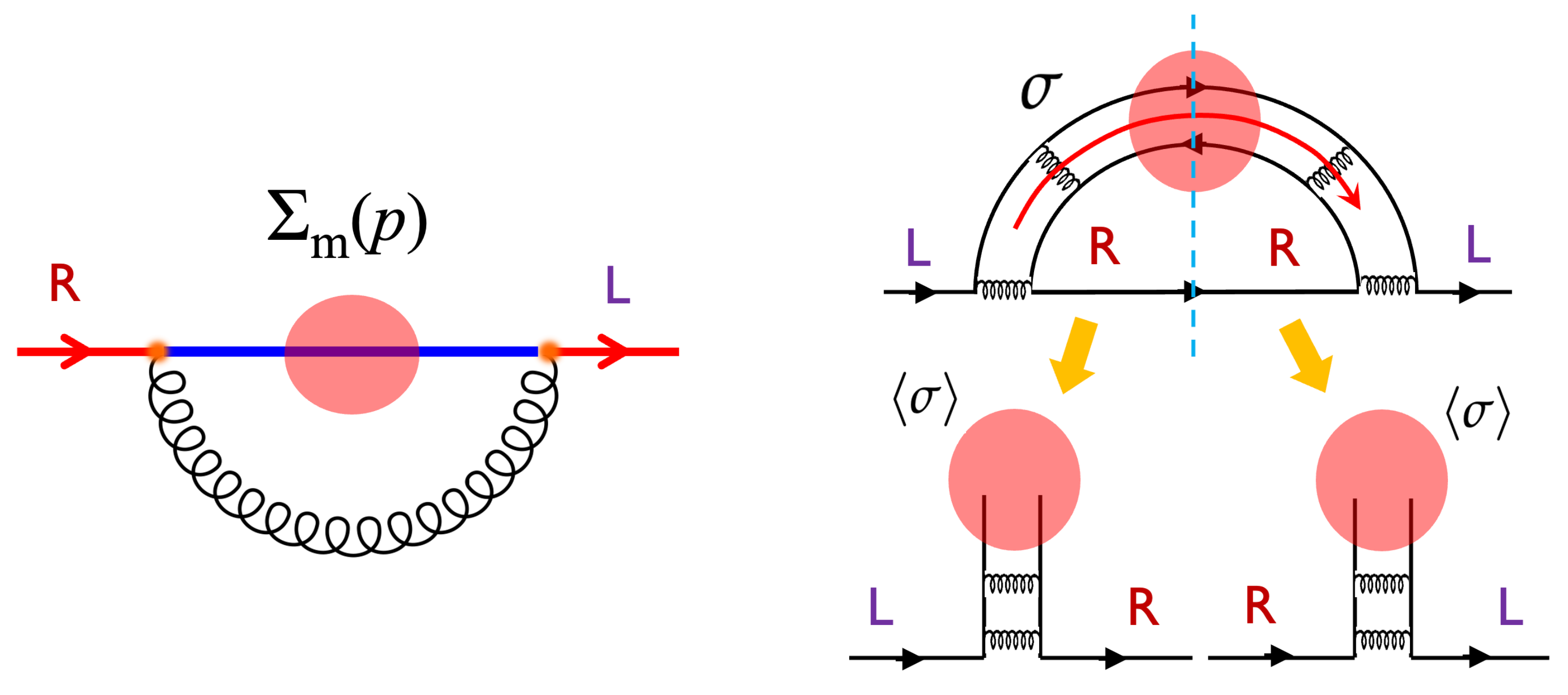
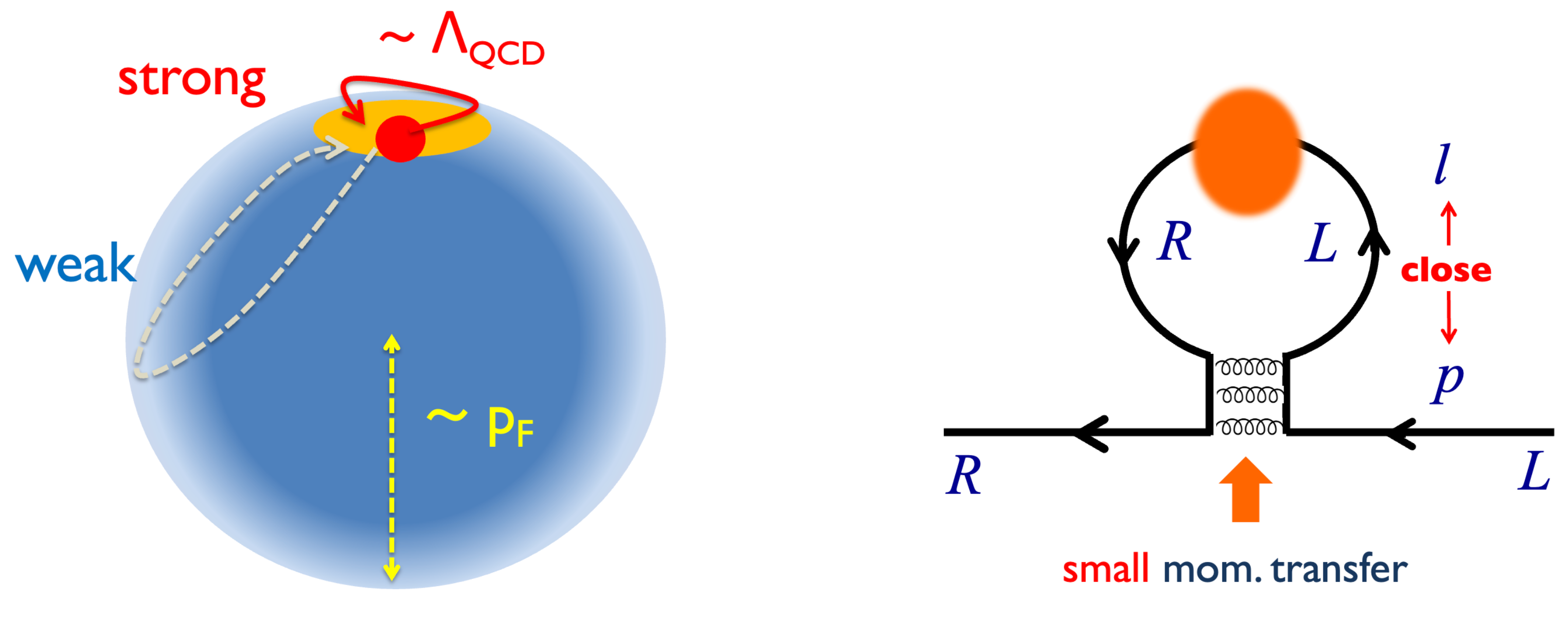
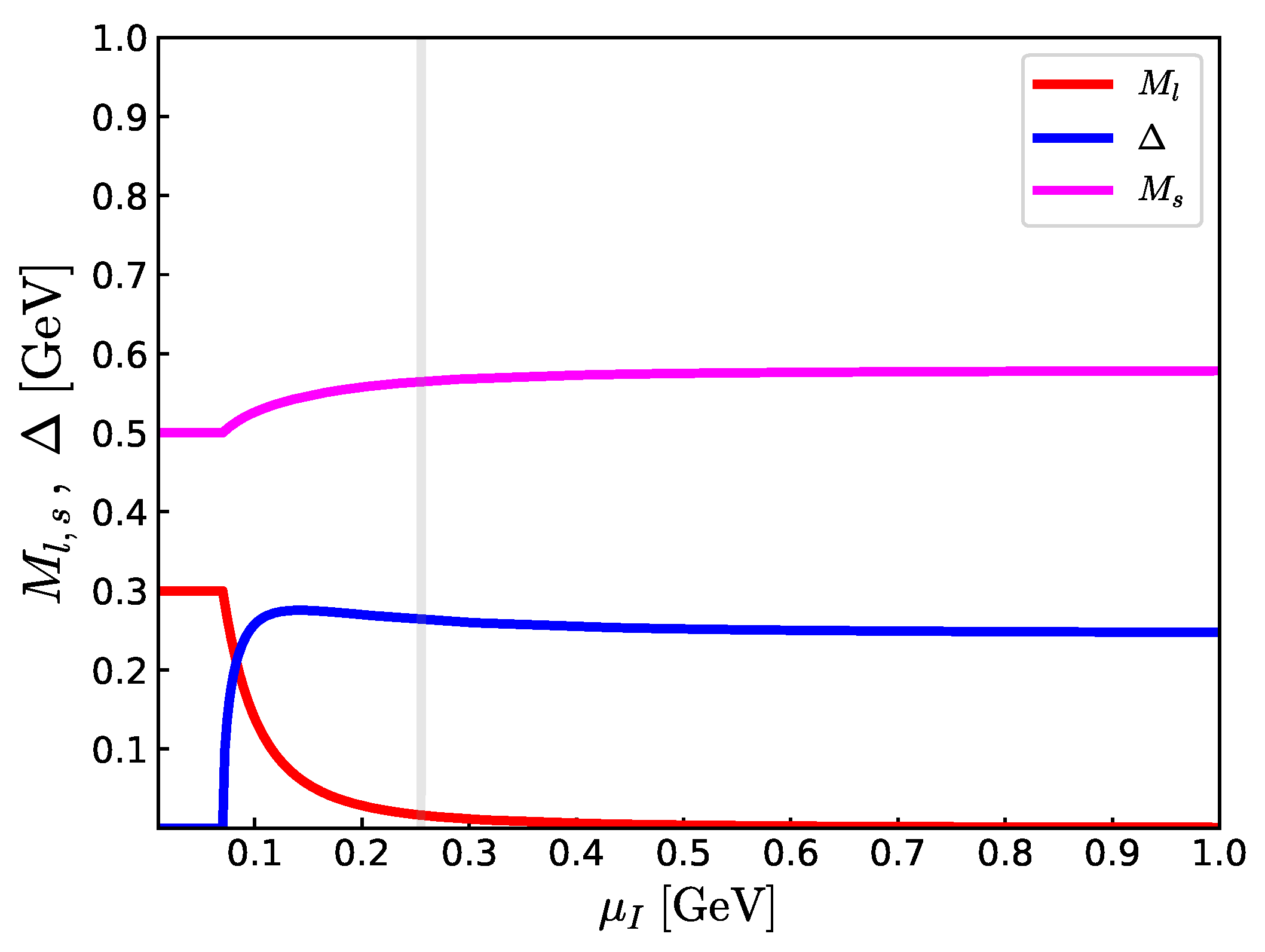



| Set | g | |||||||
|---|---|---|---|---|---|---|---|---|
| A | 0.27 | 0.50 | 3.0 | 38.1 | 1.2 | |||
| B | 0.30 | 0.50 | 3.3 | 42.4 | 1.6 | |||
| C | 0.33 | 0.50 | 3.6 | 60.0 | 2.0 |
| Set | |||||||
|---|---|---|---|---|---|---|---|
| A | 0.14 | 0.50 | 0.52 | 0.97 | 0.51 | 0.67 | 0.75 |
| B | 0.14 | 0.50 | 0.54 | 0.97 | 0.54 | 0.73 | 0.80 |
| C | 0.14 | 0.50 | 0.55 | 0.95 | 0.64 | 0.81 | 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kojo, T.; Suenaga, D.; Chiba, R. Isospin QCD as a Laboratory for Dense QCD. Universe 2024, 10, 293. https://doi.org/10.3390/universe10070293
Kojo T, Suenaga D, Chiba R. Isospin QCD as a Laboratory for Dense QCD. Universe. 2024; 10(7):293. https://doi.org/10.3390/universe10070293
Chicago/Turabian StyleKojo, Toru, Daiki Suenaga, and Ryuji Chiba. 2024. "Isospin QCD as a Laboratory for Dense QCD" Universe 10, no. 7: 293. https://doi.org/10.3390/universe10070293
APA StyleKojo, T., Suenaga, D., & Chiba, R. (2024). Isospin QCD as a Laboratory for Dense QCD. Universe, 10(7), 293. https://doi.org/10.3390/universe10070293






