Screened Scalar Fields in the Laboratory and the Solar System
Abstract
:1. Introduction
2. Theoretical Background
3. Constraint Calculation
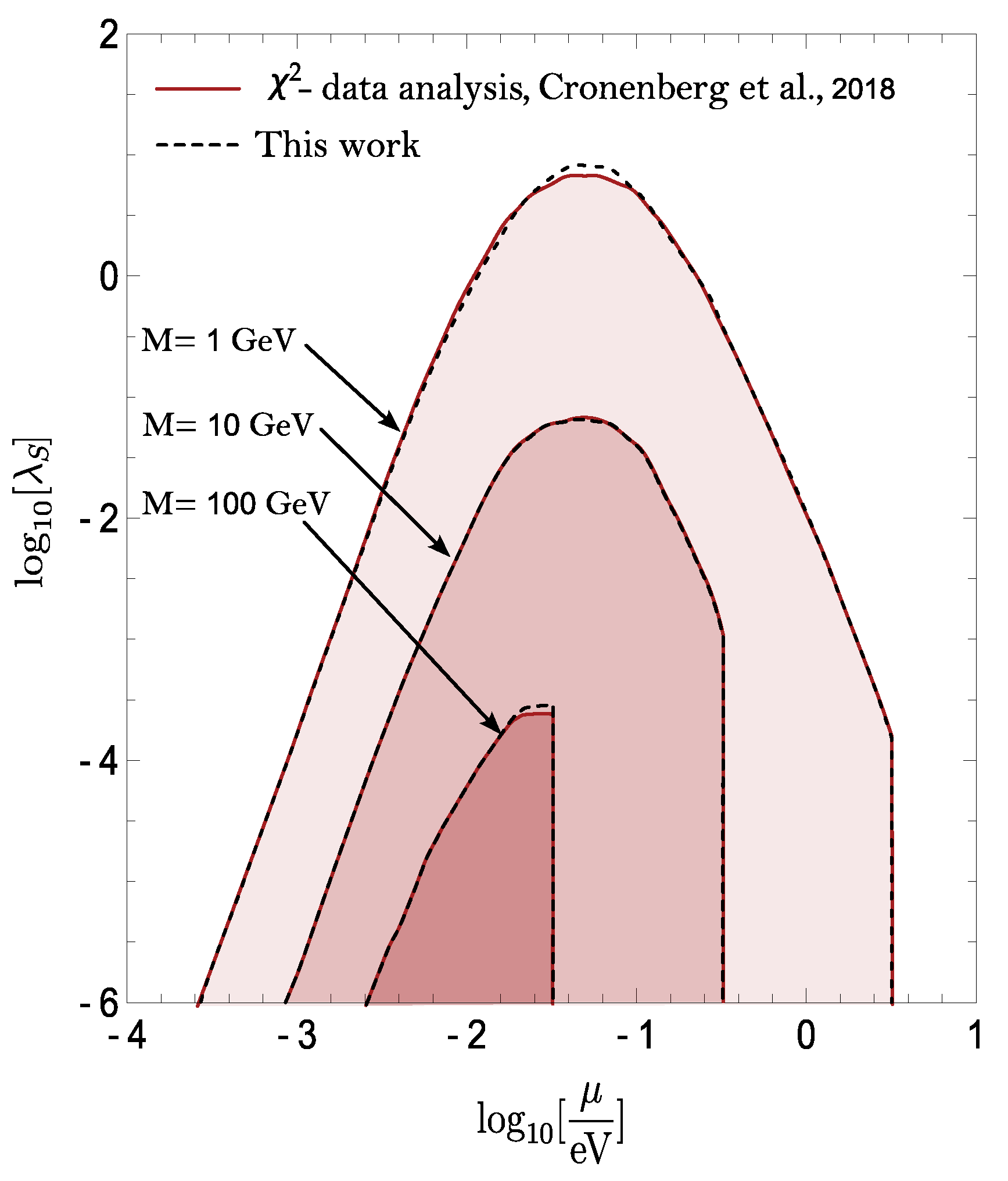
3.1. qBounce Constraints
3.2. Neutron Interferometry Constraints
- 1.
- Profile modeIn this mode, the following phase shiftis evaluated for both chambers, with the vacuum chamber having its pressure at mbar, which corresponds to the lowest pressure measured in the experiment. The experiment actually measuredThis quantity is negative, since the potential is more suppressed close to the chamber walls and due to . The experiment constrainsas will be further detailed in Appendix B.1.
- 2.
- Pressure modeIn this mode, the following quantity is measured insteadwith a vacuum pressure of mbar and a reference pressure of mbar. Scalar field parameters are constrained ifas is detailed in Appendix B.2.
3.3. Computing Observables for Lunar Laser Ranging
3.4. Computing the Pressure in the Cannex Experiment
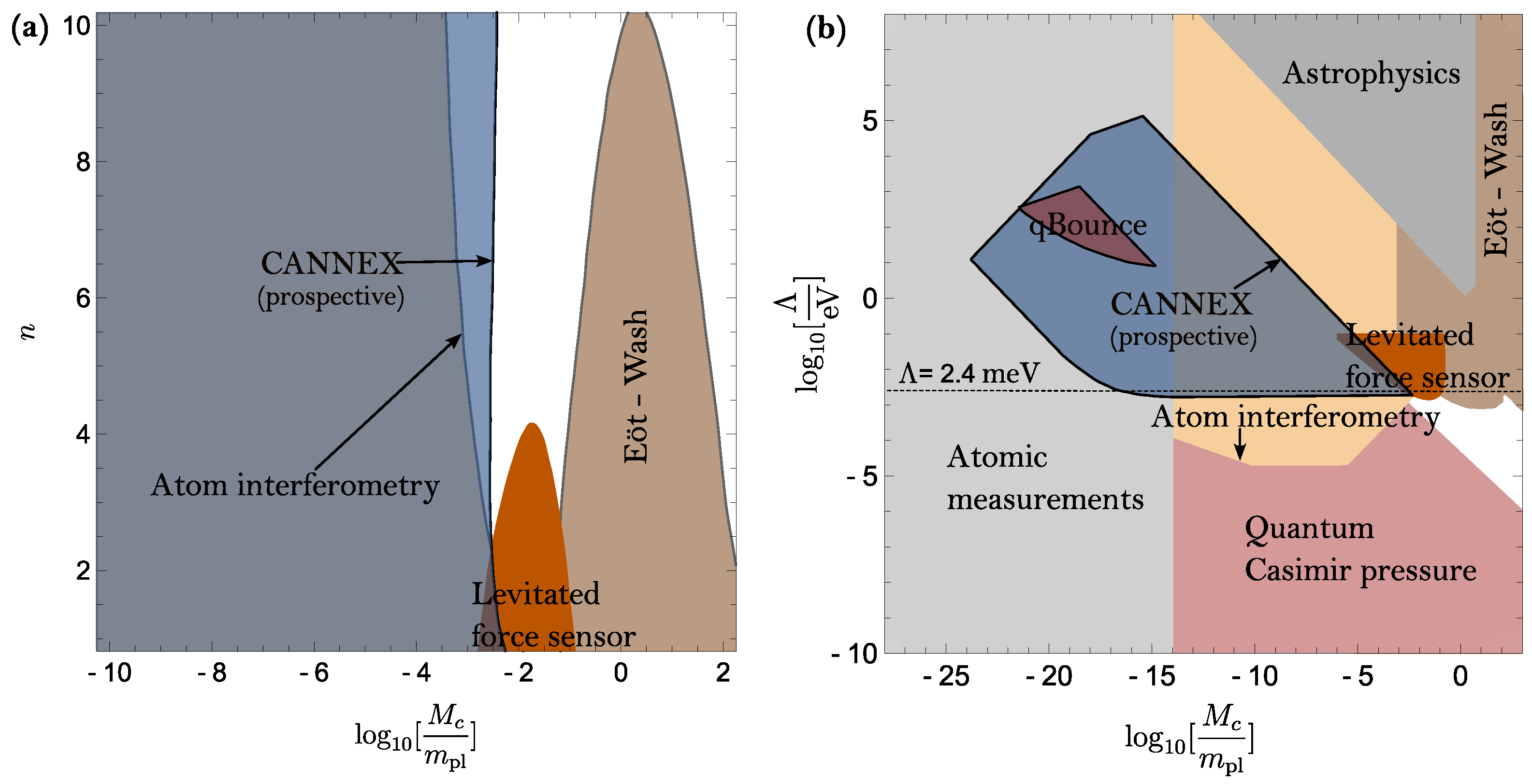
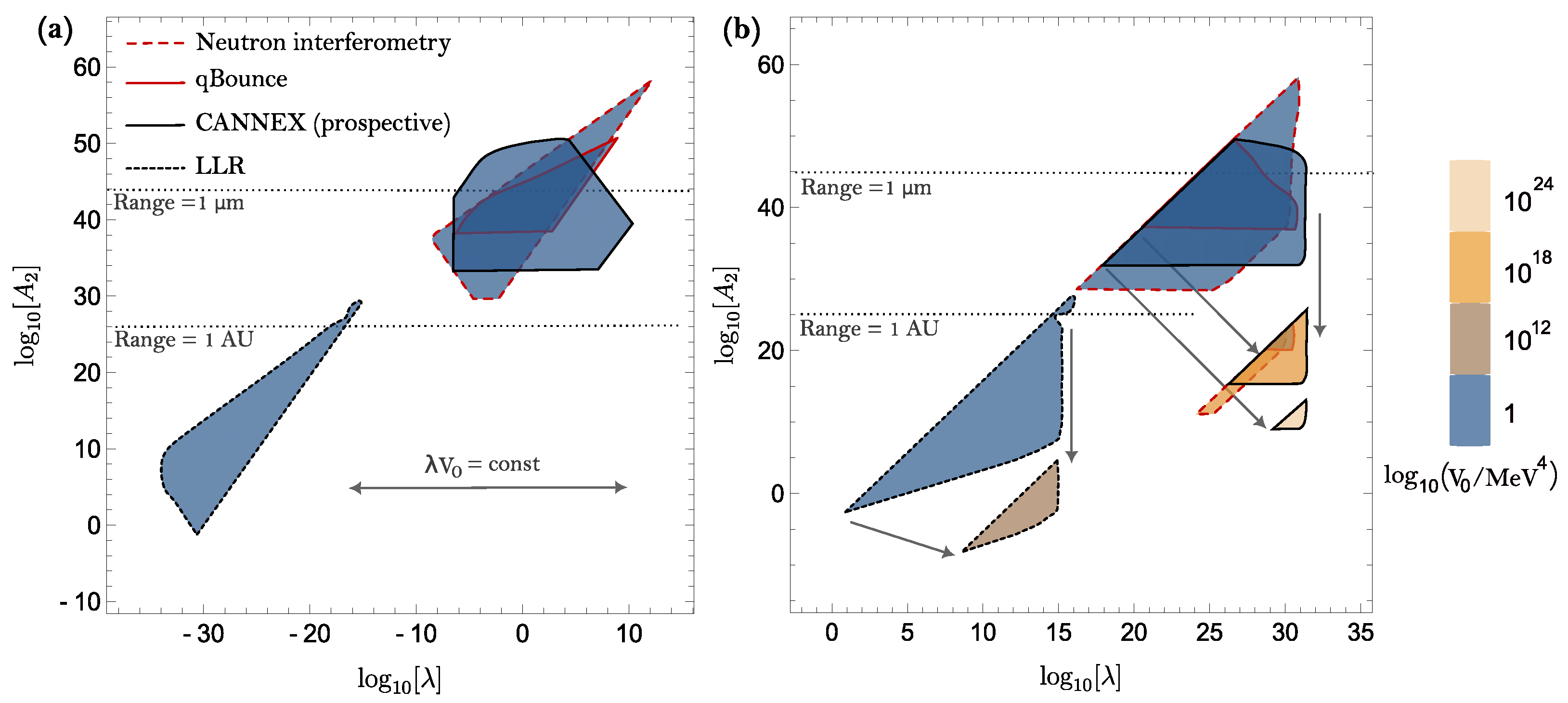
4. Results
4.1. Chameleon Constraints
4.2. Symmetron Constraints
4.3. Dilaton Constraints
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Additional Information on qBounce Constraints
Appendix A.1. Comparison of Previous and New qBounce Analysis
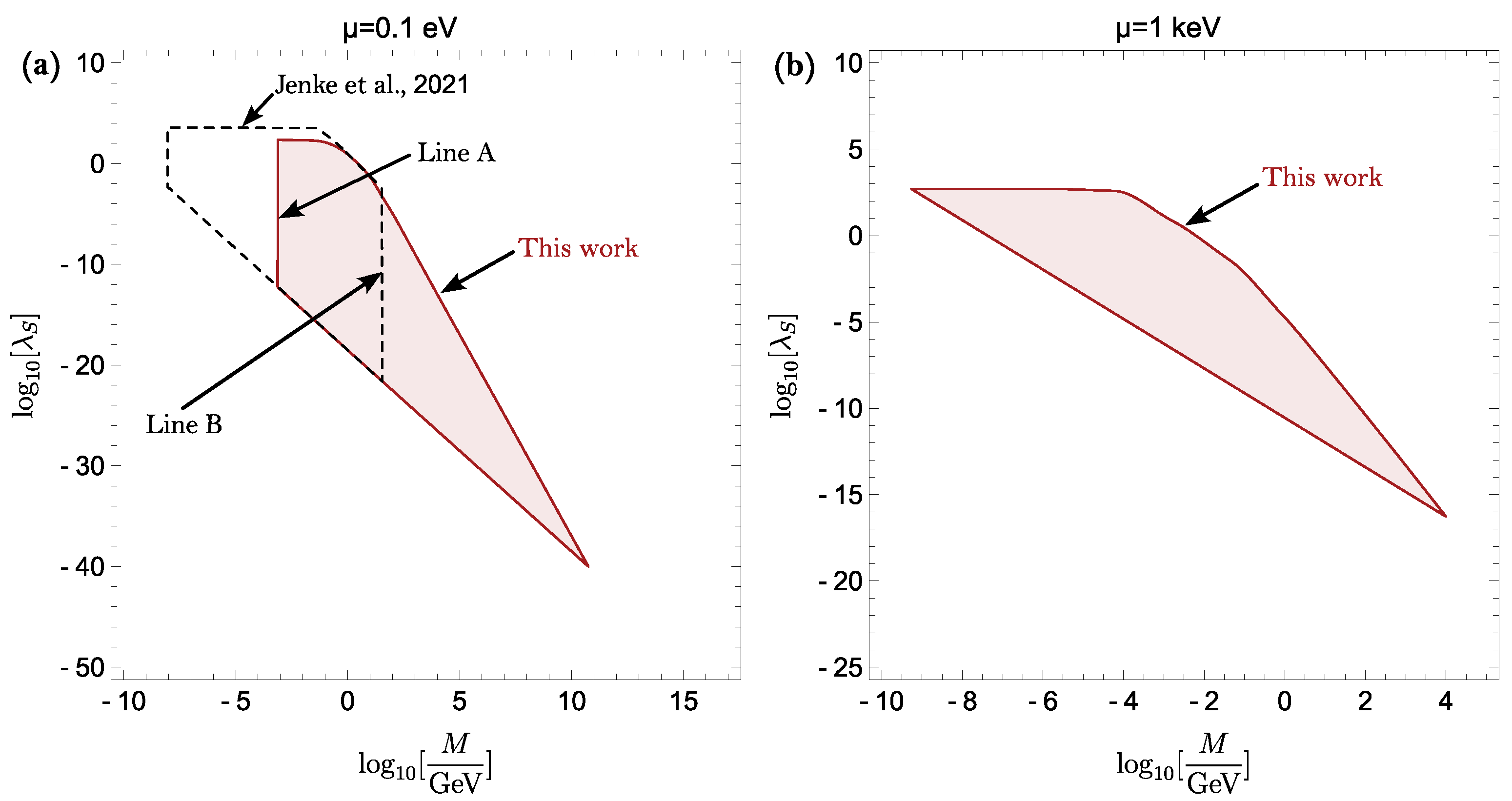
Appendix A.2. Constraint Criteria for qBounce
Appendix B. Constraint Criteria for Neutron Interferometry
Appendix B.1. Profile Mode
Appendix B.2. Pressure Mode
Appendix C. Screening Charge
References
- Fujii, Y.; Maeda, K.-i. The Scalar-Tensor Theory of Gravitation; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Joyce, A.; Jain, B.; Khoury, J.; Trodden, M. Beyond the Cosmological Standard Model. Phys. Rept. 2015, 568, 1–98. [Google Scholar] [CrossRef]
- Dickey, J.O.; Bender, P.L.; Faller, J.E.; Newhall, X.X.; Ricklefs, R.L.; Ries, J.G.; Shelus, P.J.; Veillet, C.; Whipple, A.L.; Wiant, J.R.; et al. Lunar Laser Ranging: A Continuing Legacy of the Apollo Program. Science 1994, 265, 482–490. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Heckel, B.R.; Nelson, A.E. Tests of the gravitational inverse square law. Ann. Rev. Nucl. Part. Sci. 2003, 53, 77–121. [Google Scholar] [CrossRef]
- Kapner, D.J.; Cook, T.S.; Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoyle, C.D.; Swanson, H.E. Tests of the Gravitational Inverse-Square Law below the Dark-Energy Length Scale. Phys. Rev. Lett. 2007, 98, 021101. [Google Scholar] [CrossRef]
- Burrage, C.; Copeland, E.J.; Millington, P. Radial acceleration relation from symmetron fifth forces. Phys. Rev. D 2017, 95, 064050, Erratum in Phys. Rev. D 2017, 95, 129902. [Google Scholar] [CrossRef]
- O’Hare, C.A.J.; Burrage, C. Stellar kinematics from the symmetron fifth force in the Milky Way disk. Phys. Rev. D 2018, 98, 064019. [Google Scholar] [CrossRef]
- Burrage, C.; Copeland, E.J.; Käding, C.; Millington, P. Symmetron scalar fields: Modified gravity, dark matter, or both? Phys. Rev. D 2019, 99, 043539. [Google Scholar] [CrossRef]
- Käding, C. Lensing with Generalized Symmetrons. Astronomy 2023, 2, 128–140. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon fields: Awaiting surprises for tests of gravity in space. Phys. Rev. Lett. 2004, 93, 171104. [Google Scholar] [CrossRef] [PubMed]
- Dehnen, H.; Frommert, H.; Ghaboussi, F. Higgs field and a new scalar—Tensor theory of gravity. Int. J. Theor. Phys. 1992, 31, 109–114. [Google Scholar] [CrossRef]
- Gessner, E. A new scalar tensor theory for gravity and the flat rotation curves of spiral galaxies. Astrophys. Space Sci. 1992, 196, 29–43. [Google Scholar] [CrossRef]
- Damour, T.; Polyakov, A.M. The String dilaton and a least coupling principle. Nucl. Phys. B 1994, 423, 532–558. [Google Scholar] [CrossRef]
- Pietroni, M. Dark energy condensation. Phys. Rev. D 2005, 72, 043535. [Google Scholar] [CrossRef]
- Olive, K.A.; Pospelov, M. Environmental dependence of masses and coupling constants. Phys. Rev. D 2008, 77, 043524. [Google Scholar] [CrossRef]
- Brax, P.; van de Bruck, C.; Davis, A.C.; Shaw, D. The Dilaton and Modified Gravity. Phys. Rev. D 2010, 82, 063519. [Google Scholar] [CrossRef]
- Hinterbichler, K.; Khoury, J. Symmetron Fields: Screening Long-Range Forces Through Local Symmetry Restoration. Phys. Rev. Lett. 2010, 104, 231301. [Google Scholar] [CrossRef] [PubMed]
- Hinterbichler, K.; Khoury, J.; Levy, A.; Matas, A. Symmetron Cosmology. Phys. Rev. D 2011, 84, 103521. [Google Scholar] [CrossRef]
- Gasperini, M.; Piazza, F.; Veneziano, G. Quintessence as a runaway dilaton. Phys. Rev. D 2002, 65, 023508. [Google Scholar] [CrossRef]
- Damour, T.; Piazza, F.; Veneziano, G. Violations of the equivalence principle in a dilaton runaway scenario. Phys. Rev. D 2002, 66, 046007. [Google Scholar] [CrossRef]
- Damour, T.; Piazza, F.; Veneziano, G. Runaway dilaton and equivalence principle violations. Phys. Rev. Lett. 2002, 89, 081601. [Google Scholar] [CrossRef] [PubMed]
- Brax, P.; van de Bruck, C.; Davis, A.C.; Li, B.; Shaw, D.J. Nonlinear Structure Formation with the Environmentally Dependent Dilaton. Phys. Rev. D 2011, 83, 104026. [Google Scholar] [CrossRef]
- Brax, P.; Fischer, H.; Käding, C.; Pitschmann, M. The environment dependent dilaton in the laboratory and the solar system. Eur. Phys. J. C 2022, 82, 934. [Google Scholar] [CrossRef] [PubMed]
- Dvali, G.R.; Gabadadze, G.; Porrati, M. 4-D gravity on a brane in 5-D Minkowski space. Phys. Lett. B 2000, 485, 208–214. [Google Scholar] [CrossRef]
- Nicolis, A.; Rattazzi, R.; Trincherini, E. The Galileon as a local modification of gravity. Phys. Rev. D 2009, 79, 064036. [Google Scholar] [CrossRef]
- Ali, A.; Gannouji, R.; Hossain, M.W.; Sami, M. Light mass galileons: Cosmological dynamics, mass screening and observational constraints. Phys. Lett. B 2012, 718, 5–14. [Google Scholar] [CrossRef]
- Burrage, C.; Sakstein, J. A Compendium of Chameleon Constraints. J. Cosmol. Astropart. Phys. 2016, 11, 045. [Google Scholar] [CrossRef]
- Burrage, C.; Sakstein, J. Tests of Chameleon Gravity. Living Rev. Rel. 2018, 21, 1. [Google Scholar] [CrossRef]
- Pokotilovski, Y.N. Strongly coupled chameleon fields: Possible test with a neutron Lloyd’s mirror interferometer. Phys. Lett. B 2013, 719, 341–345. [Google Scholar] [CrossRef]
- Pokotilovski, Y.N. Potential of the neutron Lloyd’s mirror interferometer for the search for new interactions. J. Exp. Theor. Phys. 2013, 116, 609–619. [Google Scholar] [CrossRef]
- Jenke, T.; Cronenberg, G.; Burgdörfer, J.; Chizhova, L.A.; Geltenbort, P.; Ivanov, A.N.; Lauer, T.; Lins, T.; Rotter, S.; Saul, H.; et al. Gravity Resonance Spectroscopy Constrains Dark Energy and Dark Matter Scenarios. Phys. Rev. Lett. 2014, 112, 151105. [Google Scholar] [CrossRef]
- Baum, S.; Cantatore, G.; Hoffmann, D.H.H.; Karuza, M.; Semertzidis, Y.K.; Upadhye, A.; Zioutas, K. Detecting solar chameleons through radiation pressure. Phys. Lett. B 2014, 739, 167–173. [Google Scholar] [CrossRef]
- Burrage, C.; Copeland, E.J.; Hinds, E.A. Probing Dark Energy with Atom Interferometry. J. Cosmol. Astropart. Phys. 2015, 03, 042. [Google Scholar] [CrossRef]
- Hamilton, P.; Jaffe, M.; Haslinger, P.; Simmons, Q.; Müller, H.; Khoury, J. Atom-interferometry constraints on dark energy. Science 2015, 349, 849–851. [Google Scholar] [CrossRef]
- Lemmel, H.; Brax, P.; Ivanov, A.N.; Jenke, T.; Pignol, G.; Pitschmann, M.; Potocar, T.; Wellenzohn, M.; Zawisky, M.; Abele, H. Neutron Interferometry constrains dark energy chameleon fields. Phys. Lett. B 2015, 743, 310–314. [Google Scholar] [CrossRef]
- Burrage, C.; Copeland, E.J. Using Atom Interferometry to Detect Dark Energy. Contemp. Phys. 2016, 57, 164–176. [Google Scholar] [CrossRef]
- Elder, B.; Khoury, J.; Haslinger, P.; Jaffe, M.; Müller, H.; Hamilton, P. Chameleon Dark Energy and Atom Interferometry. Phys. Rev. D 2016, 94, 044051. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Cronenberg, G.; Höllwieser, R.; Pitschmann, M.; Jenke, T.; Wellenzohn, M.; Abele, H. Exact solution for chameleon field, self-coupled through the Ratra-Peebles potential with n=1 and confined between two parallel plates. Phys. Rev. D 2016, 94, 085005. [Google Scholar] [CrossRef]
- Burrage, C.; Kuribayashi-Coleman, A.; Stevenson, J.; Thrussell, B. Constraining symmetron fields with atom interferometry. J. Cosmol. Astropart. Phys. 2016, 12, 041. [Google Scholar] [CrossRef]
- Jaffe, M.; Haslinger, P.; Xu, V.; Hamilton, P.; Upadhye, A.; Elder, B.; Khoury, J.; Müller, H. Author Correction: Testing sub-gravitational forces on atoms from a miniature in-vacuum source mass. Nat. Phys. 2017, 13, 938. [Google Scholar] [CrossRef]
- Brax, P.; Pitschmann, M. Exact solutions to nonlinear symmetron theory: One- and two-mirror systems. Phys. Rev. D 2018, 97, 064015. [Google Scholar] [CrossRef]
- Sabulsky, D.O.; Dutta, I.; Hinds, E.A.; Elder, B.; Burrage, C.; Copeland, E.J. Experiment to detect dark energy forces using atom interferometry. Phys. Rev. Lett. 2019, 123, 061102. [Google Scholar] [CrossRef] [PubMed]
- Brax, P.; Burrage, C.; Davis, A.C. Laboratory constraints. Int. J. Mod. Phys. D 2018, 27, 1848009. [Google Scholar] [CrossRef]
- Cronenberg, G.; Brax, P.; Filter, H.; Geltenbort, P.; Jenke, T.; Pignol, G.; Pitschmann, M.; Thalhammer, M.; Abele, H. Acoustic Rabi oscillations between gravitational quantum states and impact on symmetron dark energy. Nat. Phys. 2018, 14, 1022–1026. [Google Scholar] [CrossRef]
- Zhang, X.; Niu, R.; Zhao, W. Constraining the scalar-tensor gravity theories with and without screening mechanisms by combined observations. Phys. Rev. D 2019, 100, 024038. [Google Scholar] [CrossRef]
- Cuendis, S.A.; Baier, J.; Barth, K.; Baum, S.; Bayirli, A.; Belov, A.; Bräuninger, H.; Cantatore, G.; Carmona, J.M.; Castel, J.F.; et al. First Results on the Search for Chameleons with the KWISP Detector at CAST. Phys. Dark Univ. 2019, 26, 100367. [Google Scholar] [CrossRef]
- Jenke, T.; Bosina, J.; Micko, J.; Pitschmann, M.; Sedmik, R.; Abele, H. Gravity resonance spectroscopy and dark energy symmetron fields: qBOUNCE experiments performed with Rabi and Ramsey spectroscopy. Eur. Phys. J. ST 2021, 230, 1131–1136. [Google Scholar] [CrossRef]
- Pitschmann, M. Exact solutions to nonlinear symmetron theory: One- and two-mirror systems. II. Phys. Rev. D 2021, 103, 084013. [Google Scholar] [CrossRef]
- Brax, P.; Casas, S.; Desmond, H.; Elder, B. Testing Screened Modified Gravity. Universe 2021, 8, 11. [Google Scholar] [CrossRef]
- Qvarfort, S.; Rätzel, D.; Stopyra, S. Constraining modified gravity with quantum optomechanics. New J. Phys. 2022, 24, 033009. [Google Scholar] [CrossRef]
- Yin, P.; Li, R.; Yin, C.; Xu, X.; Bian, X.; Xie, H.; Duan, C.K.; Huang, P.; He, J.H.; Du, J. Experiments with levitated force sensor challenge theories of dark energy. Nat. Phys. 2022, 18, 1181–1185. [Google Scholar] [CrossRef]
- Betz, J.; Manley, J.; Wright, E.M.; Grin, D.; Singh, S. Searching for Chameleon Dark Energy with Mechanical Systems. Phys. Rev. Lett. 2022, 129, 131302. [Google Scholar] [CrossRef] [PubMed]
- Brax, P.; Davis, A.C.; Elder, B. Screened scalar fields in hydrogen and muonium. Phys. Rev. D 2023, 107, 044008. [Google Scholar] [CrossRef]
- Hartley, D.; Käding, C.; Howl, R.; Fuentes, I. Quantum-enhanced screened dark energy detection. Eur. Phys. J. C 2024, 84, 49. [Google Scholar] [CrossRef] [PubMed]
- Fischer, H.; Käding, C.; Sedmik, R.I.P.; Abele, H.; Brax, P.; Pitschmann, M. Search for environment-dependent dilatons. Phys. Dark Univ. 2024, 43, 101419. [Google Scholar] [CrossRef]
- Fischer, H.; Käding, C.; Lemmel, H.; Sponar, S.; Pitschmann, M. Search for dark energy with neutron interferometry. Prog. Theor. Exp. Phys. 2024, 2024, 023E02. [Google Scholar] [CrossRef]
- Fischer, H.; Sedmik, R.I.P. Numerical Methods for Scalar Field Dark Energy in Table-top Experiments and Lunar Laser Ranging. arXiv 2024, arXiv:2401.16179. [Google Scholar]
- Klimchitskaya, G.L.; Mostepanenko, V.M. The Nature of Dark Energy and Constraints on Its Hypothetical Constituents from Force Measurements. Universe 2024, 10, 119. [Google Scholar] [CrossRef]
- Haghmoradi, H.; Fischer, H.; Bertolini, A.; Galić, I.; Intravaia, F.; Pitschmann, M.; Schimpl, R.; Sedmik, R.I.P. Force metrology with plane parallel plates: Final design review and outlook. Physics 2024, 6, 690–741. [Google Scholar] [CrossRef]
- Brax, P.; Fichet, S. Quantum Chameleons. Phys. Rev. D 2019, 99, 104049. [Google Scholar] [CrossRef]
- Burrage, C.; Käding, C.; Millington, P.; Minář, J. Open quantum dynamics induced by light scalar fields. Phys. Rev. D 2019, 100, 076003. [Google Scholar] [CrossRef]
- Burrage, C.; Käding, C.; Millington, P.; Minář, J. Influence functionals, decoherence and conformally coupled scalars. J. Phys. Conf. Ser. 2019, 1275, 012041. [Google Scholar] [CrossRef]
- Käding, C.; Pitschmann, M.; Voith, C. Dilaton-induced open quantum dynamics. Eur. Phys. J. C 2023, 83, 767. [Google Scholar] [CrossRef] [PubMed]
- Báez-Camargo, A.L.; Hartley, D.; Käding, C.; Fuentes-Guridi, I. Dynamical Casimir effect with screened scalar fields. arXiv 2024, arXiv:2404.02630. [Google Scholar]
- Hartley, D.; Käding, C.; Howl, R.; Fuentes, I. Quantum simulation of dark energy candidates. Phys. Rev. D 2019, 99, 105002. [Google Scholar] [CrossRef]
- Sedmik, R.I.P.; Pitschmann, M. Next Generation Design and Prospects for Cannex. Universe 2021, 7, 234. [Google Scholar] [CrossRef]
- Brax, P.; Pignol, G.; Roulier, D. Probing Strongly Coupled Chameleons with Slow Neutrons. Phys. Rev. D 2013, 88, 083004. [Google Scholar] [CrossRef]
- Vainshtein, A. To the problem of nonvanishing gravitation mass. Phys. Lett. B 1972, 39, 393–394. [Google Scholar] [CrossRef]
- Abele, H.; Jenke, T.; Leeb, H.; Schmiedmayer, J. Ramsey’s method of separated oscillating fields and its application to gravitationally induced quantum phase shifts. Phys. Rev. D 2010, 81, 065019. [Google Scholar] [CrossRef]
- Jenke, T.; Geltenbort, P.; Lemmel, H.; Abele, H. Realization of a gravity-resonance-spectroscopy technique. Nat. Phys. 2011, 7, 468–472. [Google Scholar] [CrossRef]
- Sponar, S.; Sedmik, R.I.P.; Pitschmann, M.; Abele, H.; Hasegawa, Y. Tests of fundamental quantum mechanics and dark interactions with low-energy neutrons. Nat. Rev. Phys. 2021, 3, 309–327. [Google Scholar] [CrossRef]
- Rauch, H.; Treimer, W.; Bonse, U. Test of a single crystal neutron interferometer. Phys. Lett. 1974, 47A, 369–371. [Google Scholar] [CrossRef]
- Rauch, H.; Werner, S.A. Neutron Interferometry; Clarendon Press: Oxford, UK, 2000. [Google Scholar]
- Müller, J.; Murphy, T.W.; Schreiber, U.; Shelus, P.J.; Torre, J.M.; Williams, J.G.; Boggs, D.H.; Bouquillon, S.; Bourgoin, A.; Hofmann, F. Lunar Laser Ranging: A tool for general relativity, lunar geophysics and Earth science. J. Geodesy 2019, 93, 2195–2210. [Google Scholar] [CrossRef]
- Sakstein, J. Tests of Gravity with Future Space-Based Experiments. Phys. Rev. D 2018, 97, 064028. [Google Scholar] [CrossRef]
- Kraiselburd, L.; Landau, S.J.; Salgado, M.; Sudarsky, D.; Vucetich, H. Equivalence Principle in Chameleon Models. Phys. Rev. D 2018, 97, 104044. [Google Scholar] [CrossRef]
- Hofmann, F.; Müller, J. Relativistic tests with lunar laser ranging. Class. Quant. Grav. 2018, 35, 035015. [Google Scholar] [CrossRef]
- Pitschmann, M. The High Precision Frontier: Search for New Physics with “Tabletop Experiments” & Beyond. Habilitation Thesis, TU Wien, 2023. Available online: https://iopscience.iop.org/article/10.1088/1361-6382/aa8f7a/meta#skip-to-content-link-target (accessed on 7 July 2024).
- Panda, C.D.; Tao, M.J.; Ceja, M.; Khoury, J.; Tino, G.M.; Müller, H. Measuring gravitational attraction with a lattice atom interferometer. Nature 2024, 1, 1–6. [Google Scholar] [CrossRef]
- Upadhye, A. Symmetron dark energy in laboratory experiments. Phys. Rev. Lett. 2013, 110, 031301. [Google Scholar] [CrossRef]

| Scalar Field | ||
| Chameleon | ||
| Symmetron | ||
| Dilaton |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, H.; Käding, C.; Pitschmann, M. Screened Scalar Fields in the Laboratory and the Solar System. Universe 2024, 10, 297. https://doi.org/10.3390/universe10070297
Fischer H, Käding C, Pitschmann M. Screened Scalar Fields in the Laboratory and the Solar System. Universe. 2024; 10(7):297. https://doi.org/10.3390/universe10070297
Chicago/Turabian StyleFischer, Hauke, Christian Käding, and Mario Pitschmann. 2024. "Screened Scalar Fields in the Laboratory and the Solar System" Universe 10, no. 7: 297. https://doi.org/10.3390/universe10070297





