Precision Higgs Constraints in U(1) Extensions of the Standard Model with a Light Z′-Boson
Abstract
1. Introduction
2. Scalar Sector of the SWSM
Scalar Couplings
- Scalar–fermion couplings:
- Scalar–vector boson couplings: whereandwhere is the ratio of the VeVs. In the SWSM region of the parameter space, the neutral boson mixing angle is smaller than [14]; hence, we consider the leading contributions to the vertex factors in the limit ().
- Scalar–scalar couplings:
3. Production of Scalar Particles in the LHC
4. Decays of Scalars
4.1. Total Width of the Higgs Boson
4.2. Decay Channels
5. Implementation
6. Signal Strengths
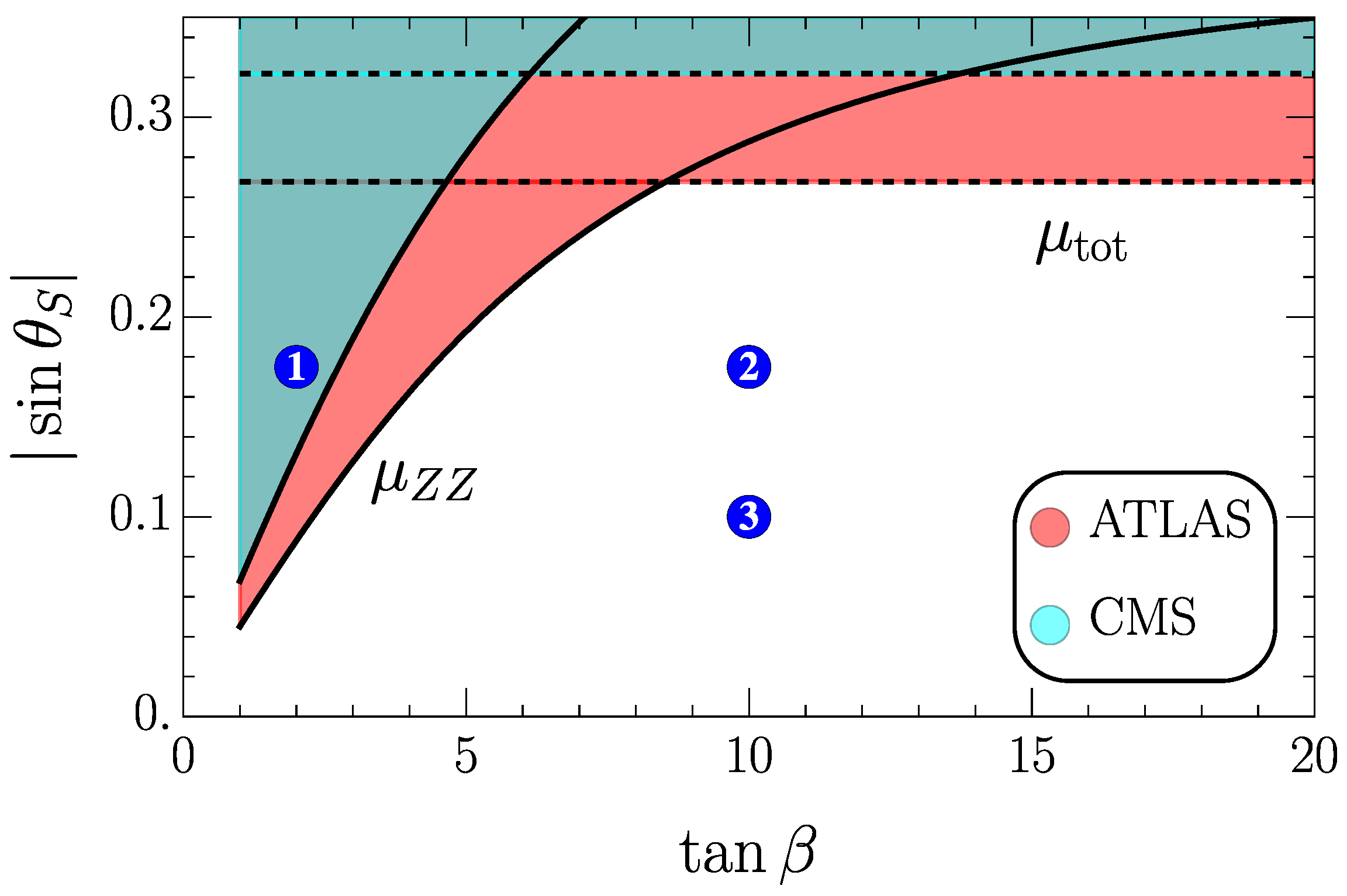
7. Benchmarks and Exclusion Bounds
8. Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SM | standard model |
| LHC | Large Hadron Collider |
| BSM | beyond the standard model |
| SWSM | superweak extension of the standard model |
| VEV | vacuum expectation value |
| HNL | heavy neutral lepton |
| BEH | Brout–Englert–Higgs |
| ggF | gluon–gluon fusion |
| VS | production of the scalar with a vector boson |
| VBF | vector boson fusion |
| ttS | production of the scalar with a pair |
| LO | leading order |
| NLO | next-to-leading order |
| NNLO | next-to-next-to-leading order |
| parton density function | |
| C.L. | confidence level |
| BP | benchmark point |
References
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. 2012, B716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. 2012, B716, 30–61. [Google Scholar] [CrossRef]
- Navas, S.; Amsler, C.; Gutsche, T.; Hanhart, C.; Hernández-Rey, J.J.; Lourenço, C.; Masoni, A.; Mikhasenko, M.; Mitchell, R.E.; Patrignani, C.; et al. Review of Particle Physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Hayrapetyan, A.; Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Damanakis, K.; Dragicevic, M.; Hussain, P.S.; Jeitler, M.; et al. Searches for Higgs boson production through decays of heavy resonances. arXiv 2024, arXiv:2403.16926. [Google Scholar]
- Appelquist, T.; Dobrescu, B.A.; Hopper, A.R. Nonexotic Neutral Gauge Bosons. Phys. Rev. D 2003, 68, 035012. [Google Scholar] [CrossRef]
- Langacker, P. The Physics of Heavy Z′ Gauge Bosons. Rev. Mod. Phys. 2009, 81, 1199–1228. [Google Scholar] [CrossRef]
- Robens, T. Constraining extended scalar sectors at current and future colliders—An update. In Proceedings of the 8th Workshop on Theory, Phenomenology and Experiments in Flavour Physics, Capri, Italy, 11–13 June 2022; Springer: Berlin/Heidelberg, Germany, 2023; Volume 292, pp. 141–152. [Google Scholar]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abdinov, O.; Abed Abud, A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; et al. Search for high-mass dilepton resonances using 139 fb−1 of pp collision data collected at = 13 TeV with the ATLAS detector. Phys. Lett. B 2019, 796, 68–87. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Dragicevic, M.; Escalante Del Valle, A.; Frühwirth, R.; Jeitler, M.; et al. Search for resonant and nonresonant new phenomena in high-mass dilepton final states at = 13 TeV. JHEP 2021, 7, 208. [Google Scholar]
- Banerjee, D.; Burtsev, V.E.; Chumakov, A.G.; Cooke, D.; Crivelli, P.; Depero, E.; Dermenev, A.V.; Donskov, S.V.; Dusaev, R.R.; Enik, T.; et al. Dark matter search in missing energy events with NA64. Phys. Rev. Lett. 2019, 123, 121801. [Google Scholar] [CrossRef] [PubMed]
- Trócsányi, Z. Super-weak force and neutrino masses. Symmetry 2020, 12, 107. [Google Scholar] [CrossRef]
- Ilten, P.; Soreq, Y.; Williams, M.; Xue, W. Serendipity in dark photon searches. JHEP 2018, 6, 4. [Google Scholar] [CrossRef]
- Curtin, D.; Essig, R.; Gori, S.; Shelton, J. Illuminating Dark Photons with High-Energy Colliders. JHEP 2015, 2, 157. [Google Scholar] [CrossRef]
- Péli, Z.; Trócsányi, Z. Exclusion bounds for neutral gauge bosons. Phys. Rev. D 2024, 110, 015027. [Google Scholar] [CrossRef]
- Djouadi, A. The Anatomy of Electro-Weak Symmetry Breaking. I: The Higgs boson in the Standard Model. Phys. Rept. 2008, 457, 1–216. [Google Scholar] [CrossRef]
- ATLAS Wiki. Available online: https://twiki.cern.ch/twiki/bin/view/AtlasPublic/HiggsTheoryPlots (accessed on 18 December 2025).
- Aad, G.; Abbott, B.; Abeling, K.; Abidi, S.H.; Aboulhorma, A.; Abramowicz, H.; Abreu, H.; Abulaiti, Y.; Abusleme Hoffman, A.C.; Acharya, B.S.; et al. Evidence of off-shell Higgs boson production from ZZ leptonic decay channels and constraints on its total width with the ATLAS detector. Phys. Lett. B 2023, 846, 138223. [Google Scholar] [CrossRef]
- Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Damanakis, K.; Dragicevic, M.; Escalante Del Valle, A.; Frühwirth, R.; Jeitler, M.; et al. Measurement of the Higgs boson width and evidence of its off-shell contributions to ZZ production. Nat. Phys. 2022, 18, 1329–1334. [Google Scholar]
- Péli, Z.; Trócsányi, Z. Precise prediction for the mass of the W boson in gauged U(1) extensions of the standard model. Phys. Rev. D 2023, 108, L031704. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abeling, K.; Abidi, S.H.; Aboulhorma, A.; Abramowicz, H.; Abreu, H.; Abulaiti, Y.; Abusleme Hoffman, A.C.; et al. A detailed map of Higgs boson interactions by the ATLAS experiment ten years after the discovery. Nature 2022, 607, 52–59, Erratum in Nature 2022, 612, E24. [Google Scholar]
- Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Damanakis, K.; Dragicevic, M.; Escalante Del Valle, A.; Hussain, P.S.; Jeitler, M.; et al. A portrait of the Higgs boson by the CMS experiment ten years after the discovery. Nature 2022, 607, 60–68, Erratum in Nature 2023, 623, E4. [Google Scholar]
- Iwamoto, S.; Seller, K.; Trócsányi, Z. Sterile neutrino dark matter in a U(1) extension of the standard model. JCAP 2022, 1, 35. [Google Scholar] [CrossRef]
| h | s | |||||
|---|---|---|---|---|---|---|
| – | BP1 | BP2 | BP3 | BP1 | BP2 | BP3 |
| [pb] | 53 | 53 | 54 | |||
| [] | ||||||
| – | – | – | ||||
| ine | ||||||
| < | < | < | ||||
| – | – | – | ||||
| – | – | – | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Péli, Z.; Trócsányi, Z. Precision Higgs Constraints in U(1) Extensions of the Standard Model with a Light Z′-Boson. Universe 2025, 11, 12. https://doi.org/10.3390/universe11010012
Péli Z, Trócsányi Z. Precision Higgs Constraints in U(1) Extensions of the Standard Model with a Light Z′-Boson. Universe. 2025; 11(1):12. https://doi.org/10.3390/universe11010012
Chicago/Turabian StylePéli, Zoltán, and Zoltán Trócsányi. 2025. "Precision Higgs Constraints in U(1) Extensions of the Standard Model with a Light Z′-Boson" Universe 11, no. 1: 12. https://doi.org/10.3390/universe11010012
APA StylePéli, Z., & Trócsányi, Z. (2025). Precision Higgs Constraints in U(1) Extensions of the Standard Model with a Light Z′-Boson. Universe, 11(1), 12. https://doi.org/10.3390/universe11010012







