Probing the Sources of Ultra-High-Energy Cosmic Rays—Constraints from Cosmic-Ray Measurements
Abstract
1. Introduction
2. Characteristics of UHECR Sources—Constraints from the Measured Spectrum and Composition
- A not-too-strong source evolution: The redshift evolution of the source population is often parameterized as , where z is the redshift and m a free model parameter. It has been shown that a strong source evolution with , where the sources are predominantly far away, leads to an overproduction of low-energy secondaries and hence an overshoot of the spectrum below the ankle [48,49,74]. Additionally, strong source evolution can lead to an overproduction of -rays not compatible with current limits [48,75], and they can also overshoot the limits on cosmogenic neutrinos in the case of a secondary proton-producing population [76,77]. A source evolution with is associated with intermediate-luminosity AGNs and even stronger evolutions with high-luminosity AGNs [78], thus disfavoring both as the sole sources of UHECRs.
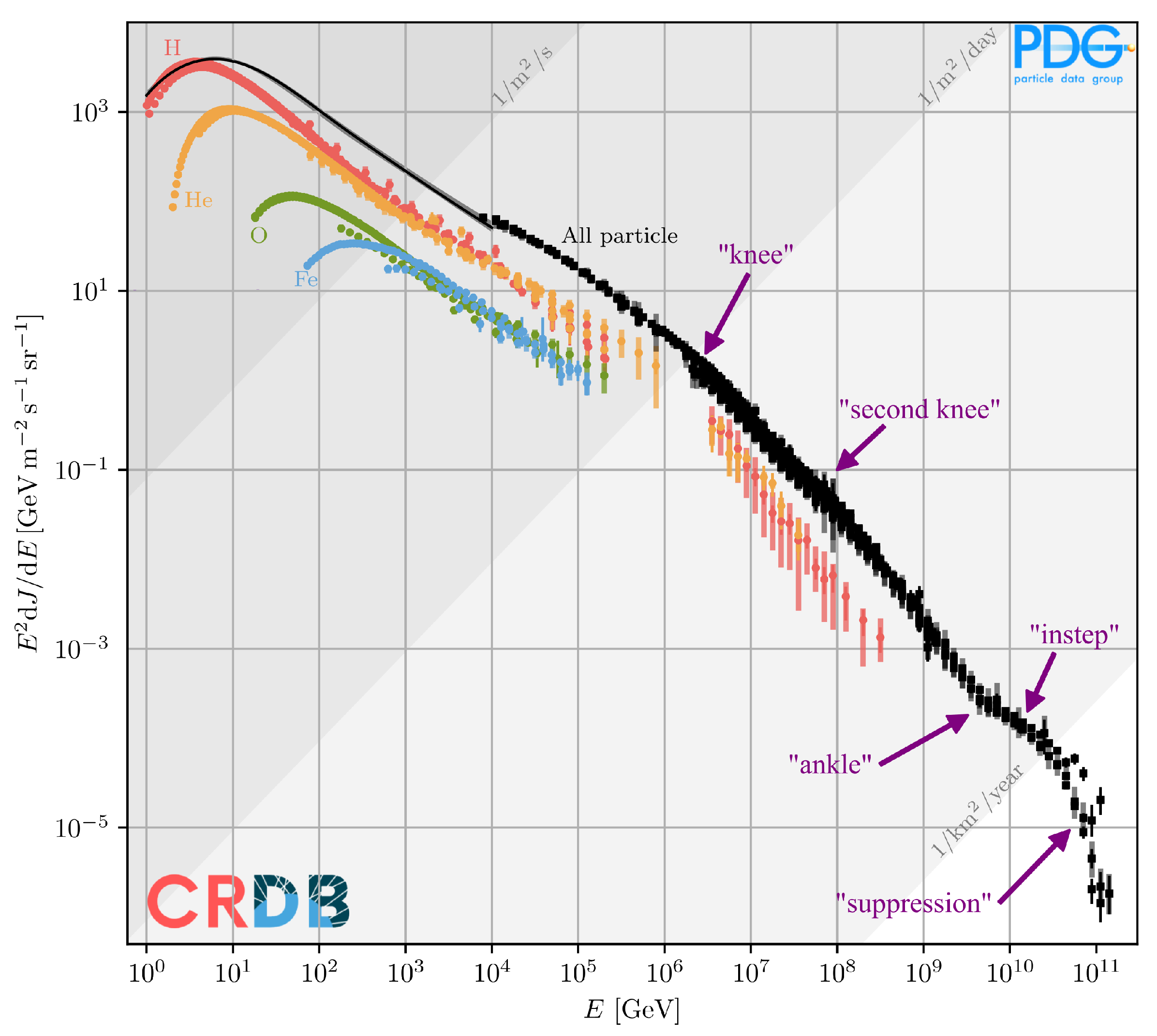
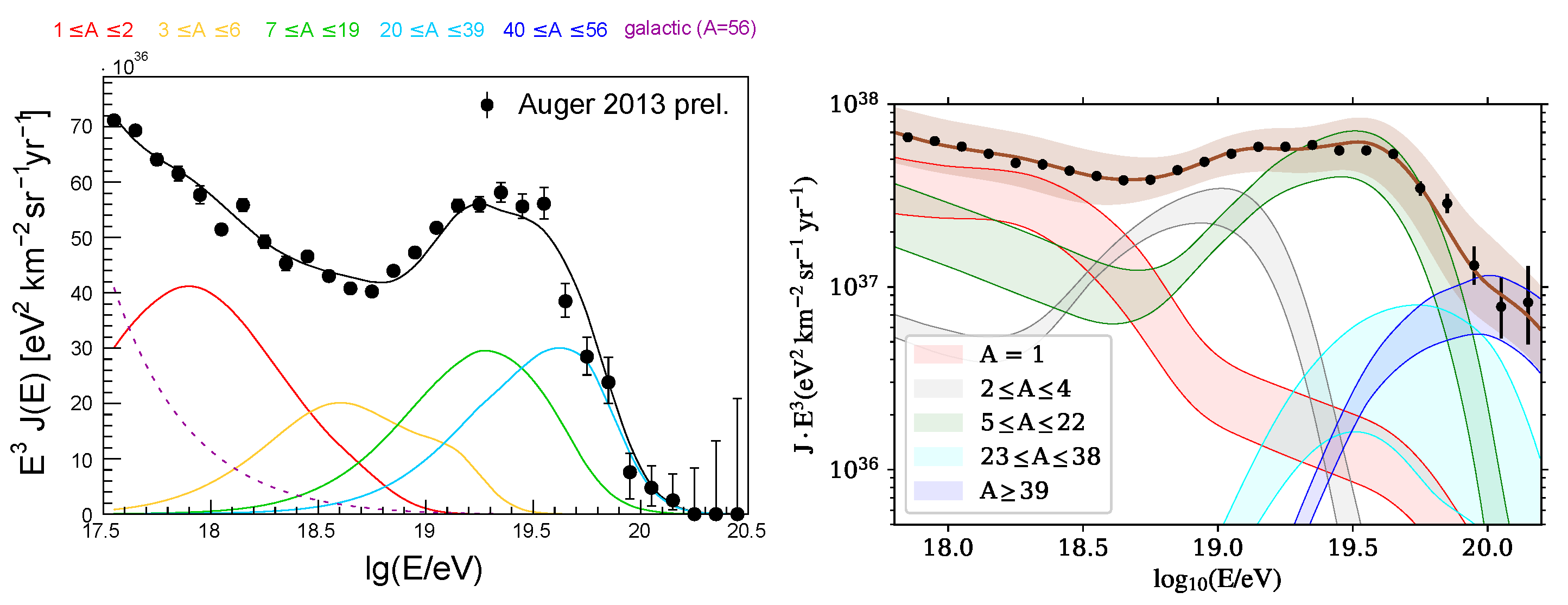
- A hard emission spectrum in combination with a mixed (often nitrogen-dominated) composition: This is necessary in order to describe the pronounced features of the spectrum and the progressively heavier composition above the ankle, in combination with the small mixing between elements indicated by the distributions [12]. As shown in Figure 2, each nuclear component only contributes to a small energy range. In those models, the instep is explained by the transition from helium to nitrogen, and no additional flux contribution, e.g., from a local source, is necessary. Note that a scenario where the instep is generated by a few foreground sources is also disfavored by the fact that the spectrum feature is consistently observed over the whole declination range covered by Auger [79]. The major point of criticism about these models is that values for the spectral index are unexpected from shock acceleration. Note, however, that the spectrum given in Equation (1) relates to the emission leaving the source environment, so the true acceleration spectrum may differ due to magnetic confinement and interactions in the source environment [44]. Also, the inferred value of is strongly influenced by the shape of the cutoff function [50], systematic uncertainties [49], and the assumed source evolution (anti-correlation between m and [74]). Additionally, the flux suppression of low-energy particles in the EGMF can have a substantial effect on [46,50], although extremely strong magnetic fields between the Milky Way and the first sources of around 10–200 nG have to be assumed to obtain in accordance with shock acceleration. A consequence of the hard Peters cycle source emission is that the predicted rigidity of UHECRs above the ankle stays relatively constant, with only a small spread at [80].
- Almost-identical maximum source rigidities: In [81], the extent to which it is justified to approximate all sources as the same is examined, while even within one source class, variations between source luminosity, size, magnetic field, etc., are expected. The authors of [81] built a model where the maximum source rigidity varies between candidates in the population . It was found that values are preferred, meaning that the population variance is surprisingly low within a factor of a few, and that UHECR sources are essentially “standard candles”. This is necessary to explain the sharp features in the energy spectrum along with the small allowed mixing of the mass composition. In [82], the small allowed variance of the maximum rigidity was confirmed, while they found that the spectral index allows for a larger variation. Explaining the unexpectedly narrow maximum rigidity range is currently one of the pressing questions about UHECR sources. One proposed explanation is that BNS mergers are the sources of UHECRs, for which the small variance in NS masses driving the dynamo gravitationally could explain the similarity between maximum rigidities [83].
3. Constraints from Cosmic-Ray Arrival Directions
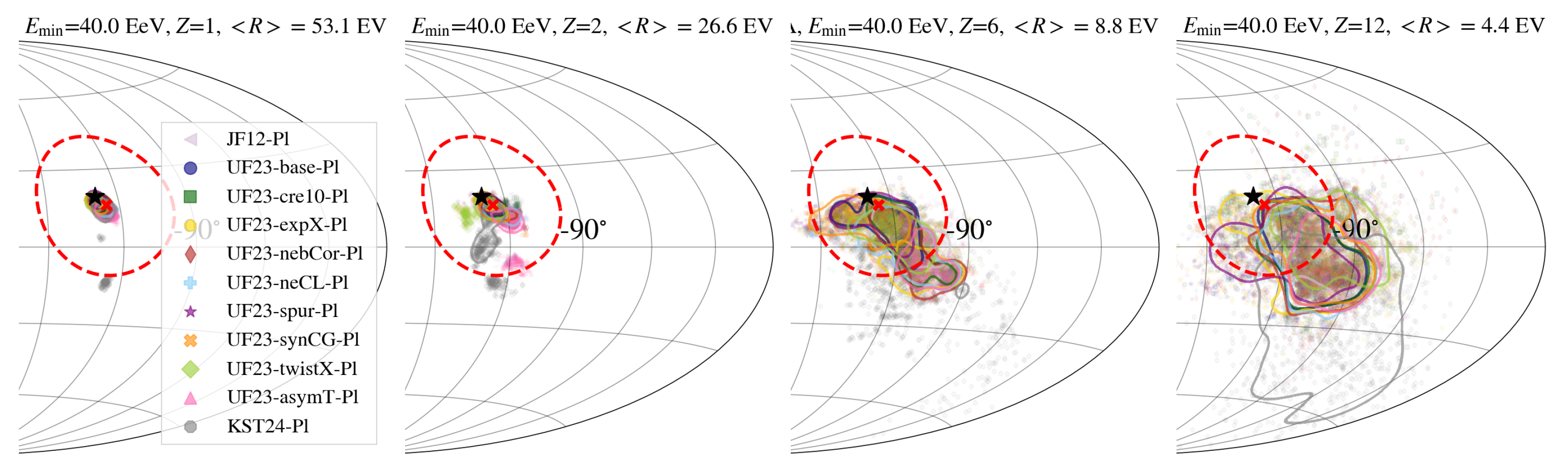
3.1. Influence of the Galactic Magnetic Field
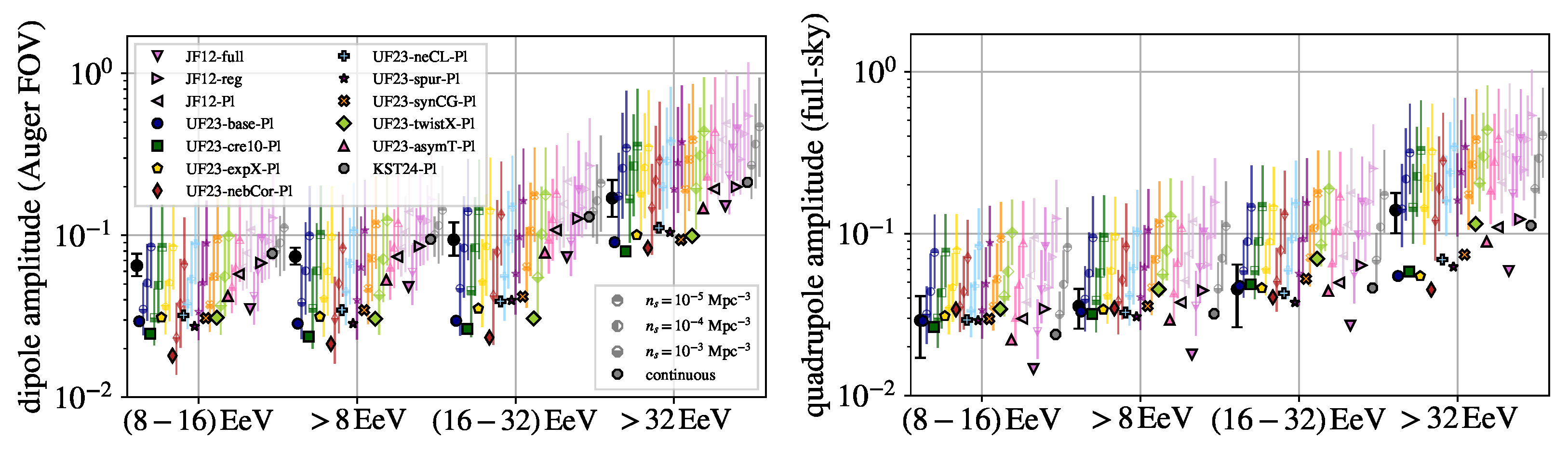
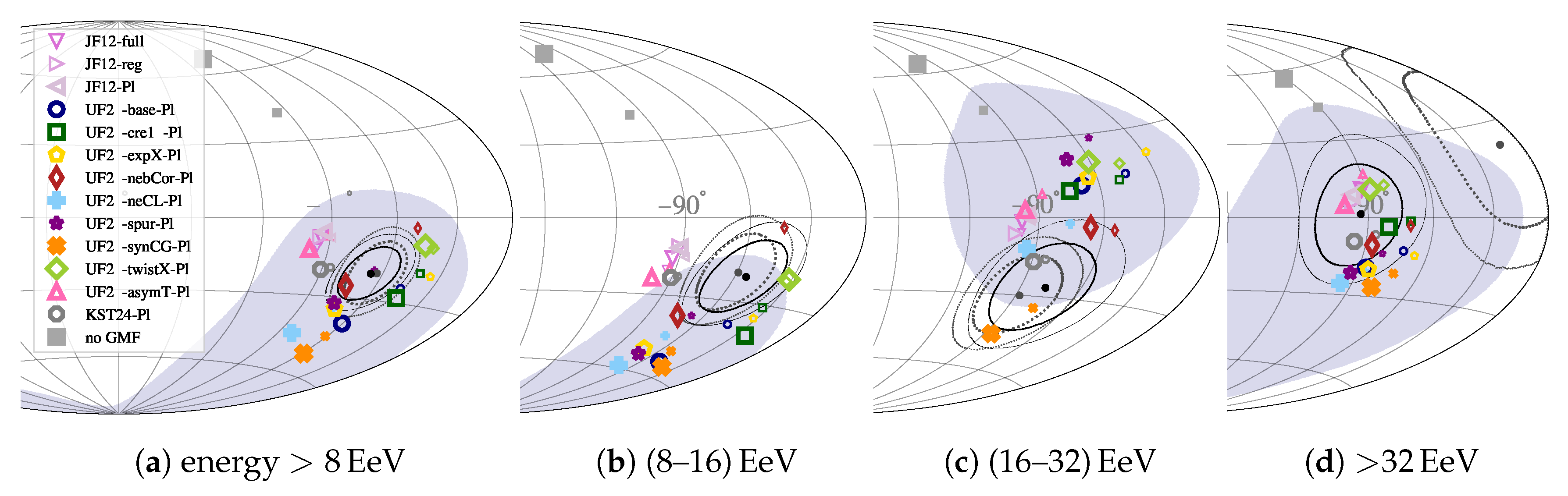
3.2. Constraints from Large-Scale Anisotropies
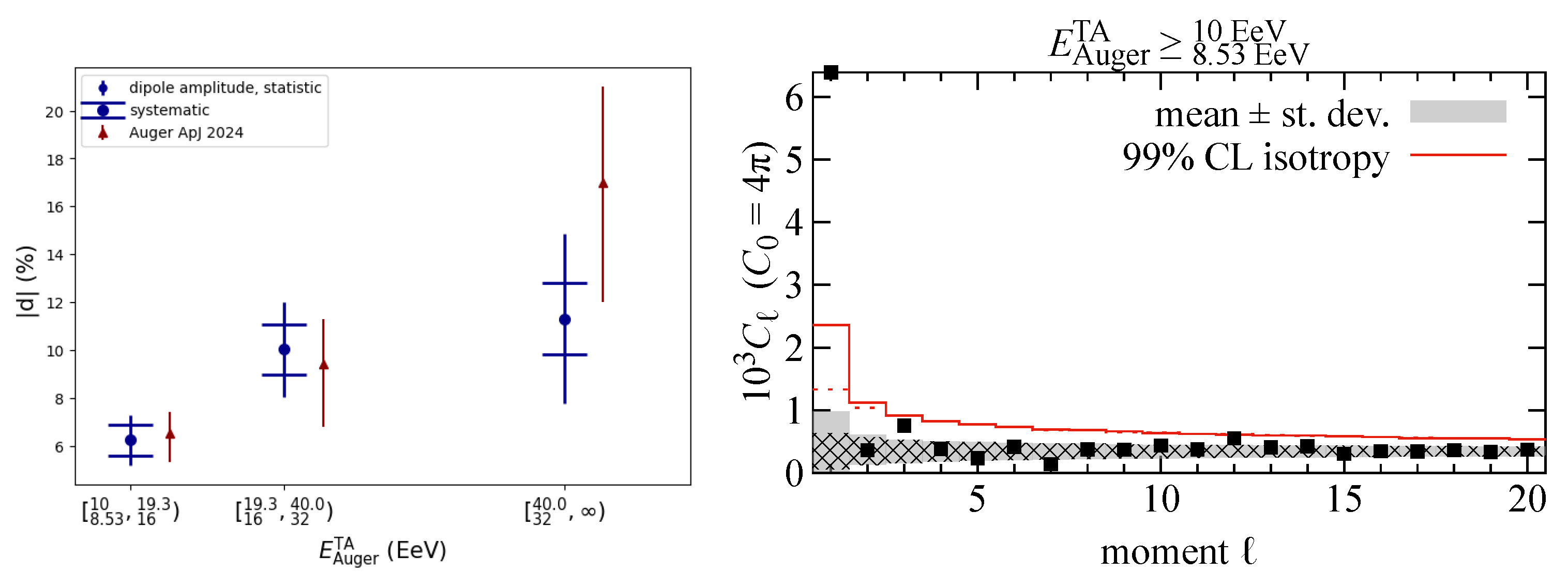
- A few sources dominate the UHECR flux EeV and generate the dipole. This scenario is explored in, for example [66,67], where a model based on a few nearby radio galaxies in combination with a diffuse background from farther-away unresolved radio galaxies is used to explain spectrum, composition, and large-scale anisotropies. In most cases discussed in [67], the EGMF has to be rather strong, with around for coherence length in order not to produce too-strong anisotropies, and the flux is dominated by Virgo A (situated in the Virgo cluster) and Fornax A (see also [104]). With only a few dominant sources, reproducing the subdominant quadrupole and the dipole direction energy evolution requires fine-tuning. Additionally, it is difficult to explain the smoothness of the UHECR energy spectrum (without any bumps hinting at contributions by individual sources) and the fact that the spectrum exhibits the same features in every direction [24,79].
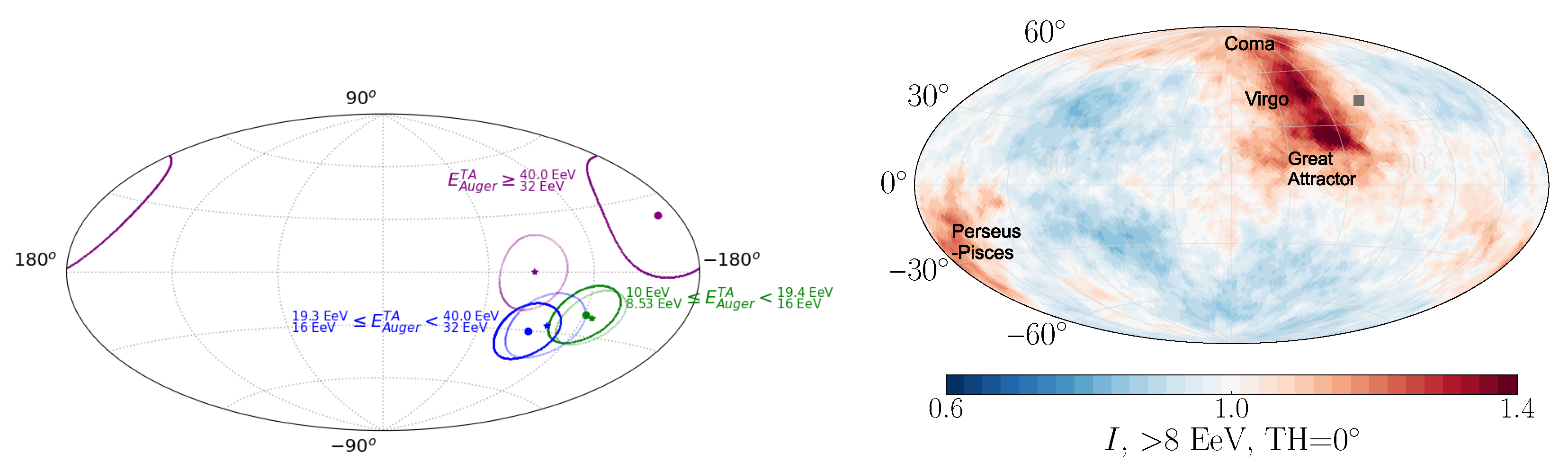
- An even more extreme case would be that only one source is responsible for the dipole, a scenario that was explored long before high-statistics UHECR measurements and models of the GMF were available; see, e.g., [105,106]. This is an especially compelling hypothesis because the dominance of a single source would naturally explain the observed similarity of the sources described in Section 2 as well as the directional uniformity of the spectral features. Using the newest measurements of the spectrum and composition, in [107], a model with the nearest radio galaxy Cen A (at around distance) supplying the flux above the ankle is tuned to the data. Qualitatively, the model reproduces the large-scale anisotropy for a very strong EGMF field strength of around 5–15 that has to be present between Cen A and Earth. When requiring that the model also reproduces the intermediate-scale cosmic-ray excess in the Centaurus region properly (see Section 3.3), an even stronger EGMF of 20–35 is necessary [108]. Note, however, that the dipole direction is not reproduced well with Cen A as the only source without at least minor contributions from other sources [108].
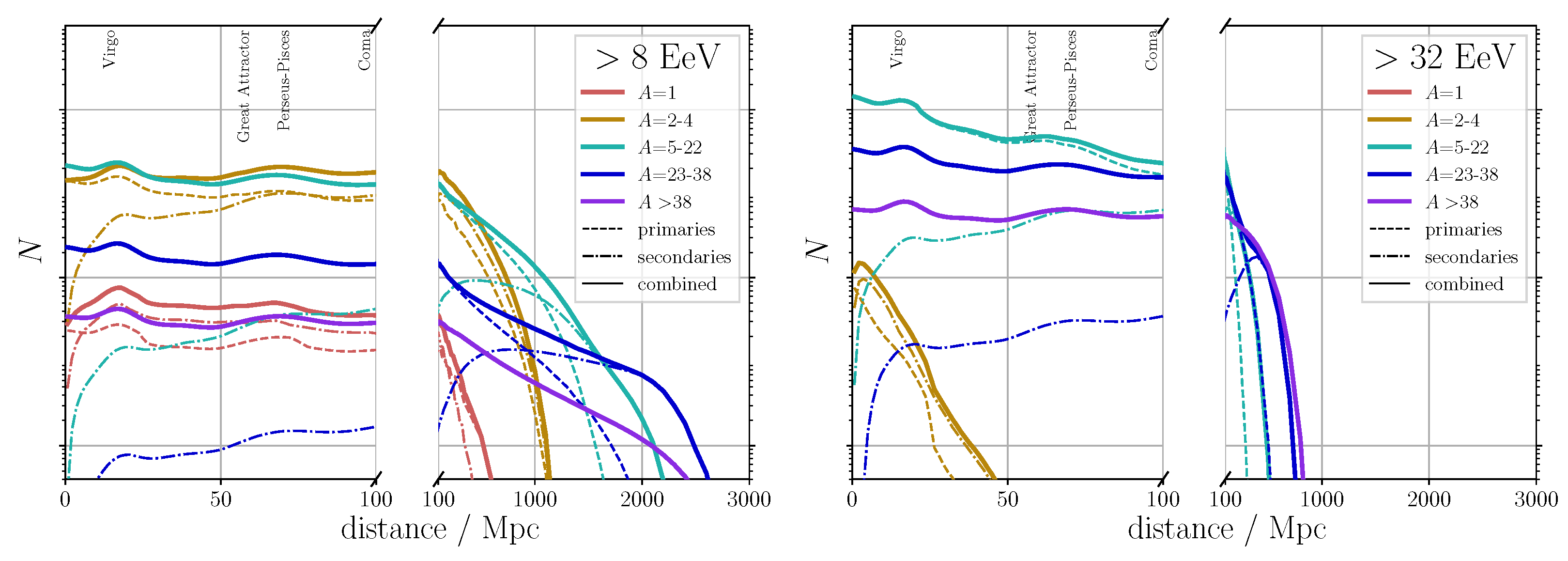
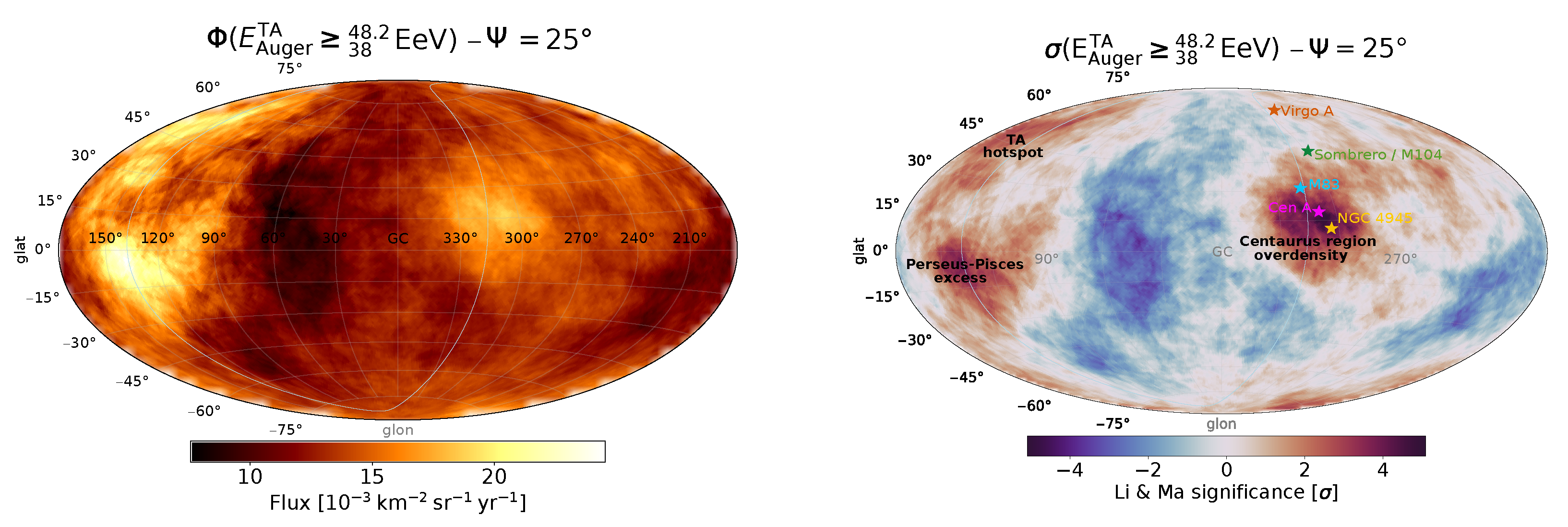
- UHECR sources are numerous and at least roughly follow the large-scale structure (LSS), as explored in [80,88,98,99,109,110,111,112,113,114,115,116,117,118]. These sources could be, for example, compact objects tracing the matter distribution or transient events occurring more often in matter-dense regions, or the acceleration of UHECRs could happen in accretion shocks present around galaxy clusters and filaments [119]. In this scenario, the cosmic-ray flux is dominated by galaxy clusters, most importantly Virgo, Great Attractor, and Coma (all in the Galactic north), as well as Perseus-Pisces. This is visible in Figure 5 (right) showing the flux at the edge of the Galaxy expected from such a model. Note that in such models, the cosmic-ray dipole is mostly generated by (sources in) the galaxy clusters in the Galactic north, whose flux is then coherently deflected southward to reproduce the observed dipole direction (see Figure 5 (left)). The absence of a flux excess in the Virgo direction that is sometimes regarded as peculiar (e.g., [120]) is hence naturally explained by GMF deflections. It was demonstrated in [80] that the (dark) matter distribution can be used as a bias-free estimator of the UHECR source distribution, meaning that neither an increased amount of sources in overdense nor in underdense regions is preferred (see also [109]). Especially if Virgo, as an overdense cluster region, is not emitting UHECRs (e.g., due to magnetic confinement [121]), the dipole cannot be reproduced well with that model. The case of multiple sources following the LSS is a natural assumption that is frequently discussed in the literature, and predictions about anisotropies and constraints on quantities such as source density and distribution have been drawn using the newest models of the GMF; therefore, the following part of this subsection will concentrate on that scenario.
3.3. Constraints from Intermediate-Scale Anisotropies
3.3.1. Correlation with Cen A
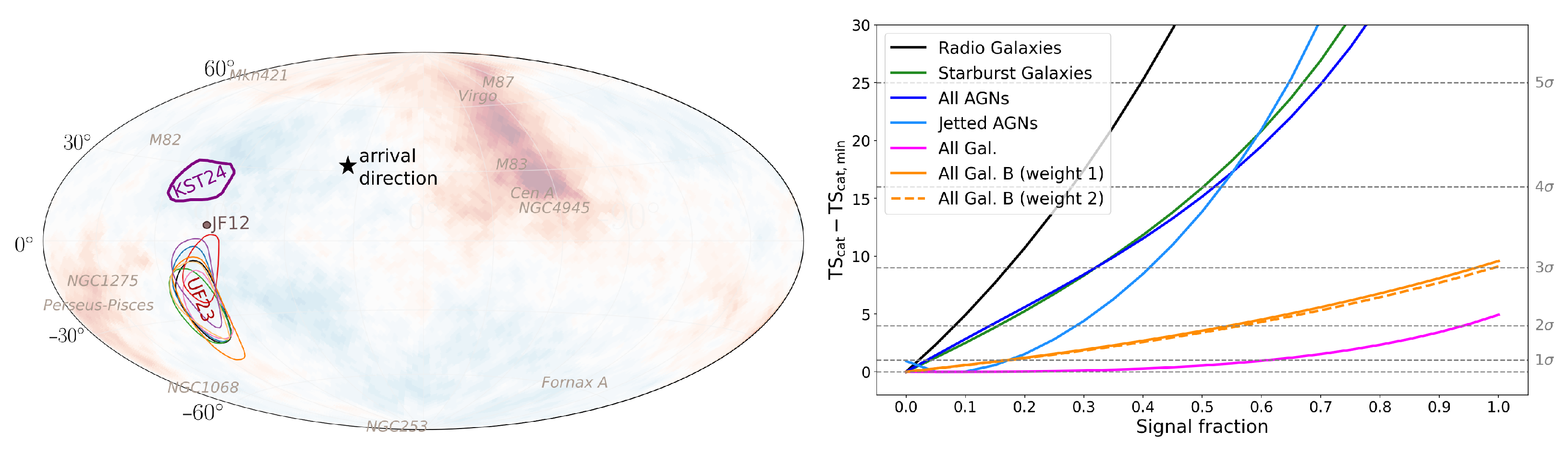
3.3.2. Correlation with Active Galactic Nuclei
3.3.3. Correlation with Starburst Galaxies
3.3.4. Deflection Patterns and Multiplets
3.4. Constraints from the Highest-Energy Events
4. Conclusions and Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CR | Cosmic Ray |
| UHECR | Ultra-high-energy Cosmic Ray |
| TA | Telescope Array |
| GZK | Greisen, Zatsepin, Kuzmin |
| LSS | Large-scale Structure |
| GMF | Galactic Magnetic Field |
| EGMF | Extragalactic Magnetic Field |
| FOV | Field of View |
| CNO | Carbon, Nitrogen, Oxygen |
References
- Hillas, A.M. The Origin of Ultra-High-Energy Cosmic Rays. Annu. Rev. Astron. Astrophys. 1984, 22, 425–444. [Google Scholar] [CrossRef]
- Lovelace, R.V.E. Dynamo model of double radio sources. Nature 1976, 262, 649–652. [Google Scholar] [CrossRef]
- Waxman, E. Cosmological Gamma-Ray Bursts and the Highest Energy Cosmic Rays. Phys. Rev. Lett. 1995, 75, 386–389. [Google Scholar] [CrossRef]
- Blandford, R.D. Acceleration of Ultra High Energy Cosmic Rays. Phys. Scr. 2000, T85, 191. [Google Scholar] [CrossRef]
- Anchordoqui, L.A. Ultra-High-Energy Cosmic Rays. Phys. Rep. 2019, 801, 1–93. [Google Scholar] [CrossRef]
- Alves Batista, R.; Biteau, J.; Bustamante, M.; Dolag, K.; Engel, R.; Fang, K.; Kampert, K.H.; Kostunin, D.; Mostafa, M.; Murase, K.; et al. Open Questions in Cosmic-Ray Research at Ultrahigh Energies. Front. Astron. Space Sci. 2019, 6, 23. [Google Scholar] [CrossRef]
- Matthews, J.H.; Bell, A.R.; Blundell, K.M. Particle acceleration in astrophysical jets. New Astron. Rev. 2020, 89, 101543. [Google Scholar] [CrossRef]
- Globus, N.; Blandford, R. Ultra High Energy Cosmic Rays. arXiv 2025, arXiv:2505.21846. [Google Scholar] [CrossRef]
- Zhang, B.T. Source Models of UHECRs. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 001. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. The Pierre Auger Cosmic Ray Observatory. Nucl. Instrum. Methods Phys. Res. A 2015, 798, 172–213. [Google Scholar] [CrossRef]
- Kawai, H.; Yoshida, S.; Yoshii, H.; Tanaka, K.; Cohen, F.; Fukushima, M.; Hayashida, N.; Hiyama, K.; Ikeda, D.; Kido, E.; et al. Telescope Array Experiment. Nucl. Phys. Proc. Suppl. 2008, 175–176, 221–226. [Google Scholar] [CrossRef]
- Fitoussi, T.; for the Pierre Auger Collaboration. Mass composition of ultra-high-energy cosmic rays at the Pierre Auger Observatory. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 041. [Google Scholar] [CrossRef]
- Stadelmaier, M.; for the Pierre Auger Collaboration. Reconstructing Air-Shower Observables using a Universality-Based Model at the Pierre Auger Observatory. In Proceedings of the 39th International Cosmic Ray Conference (ICRC 2025), Geneva, Switzerland, 15–24 July 2025; Volume 501, p. 426. [Google Scholar] [CrossRef]
- Unger, M.; Farrar, G.R. The Coherent Magnetic Field of the Milky Way. Astrophys. J. 2024, 970, 95. [Google Scholar] [CrossRef]
- Korochkin, A.; Semikoz, D.; Tinyakov, P. The coherent magnetic field of the Milky Way halo, Local Bubble and Fan Region. Astron. Astrophys. 2025, 693, A284. [Google Scholar] [CrossRef]
- Durrer, R.; Neronov, A. Cosmological Magnetic Fields: Their Generation, Evolution and Observation. Astron. Astrophys. Rev. 2013, 21, 62. [Google Scholar] [CrossRef]
- Blunier, J.; Neronov, A.; Semikoz, D. Revision of conservative lower bound on intergalactic magnetic field from Fermi and Cherenkov telescope observations of extreme blazars. arXiv 2025, arXiv:2506.22285. [Google Scholar] [CrossRef]
- Acciari, V.A.; Agudo, I.; Aniello, T.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Artero, M.; Asano, K.; Baack, D.; Babić, A.; et al. A lower bound on intergalactic magnetic fields from time variability of 1ES 0229+200 from MAGIC andFermi/LAT observations. Astron. Astrophys. 2023, 670, A145. [Google Scholar] [CrossRef]
- The Plack Collaboration. Planck 2015 results—XIX. Constraints on primordial magnetic fields. Astron. Astrophys. 2016, 594, A19. [Google Scholar] [CrossRef]
- Pshirkov, M.S.; Tinyakov, P.G.; Urban, F.R. New limits on extragalactic magnetic fields from rotation measures. Phys. Rev. Lett. 2016, 116, 191302. [Google Scholar] [CrossRef] [PubMed]
- Vazza, F.; Locatelli, N.; Rajpurohit, K.; Banfi, S.; Domínguez-Fernández, P.; Wittor, D.; Angelinelli, M.; Inchingolo, G.; Brienza, M.; Hackstein, S.; et al. Magnetogenesis and the Cosmic Web: A Joint Challenge for Radio Observations and Numerical Simulations. Galaxies 2021, 9, 109. [Google Scholar] [CrossRef]
- Bister, T. Probing UHECR sources—Constraints from cosmic-ray measurements. In Proceedings of the 39th International Cosmic Ray Conference (ICRC 2025), Geneva, Switzerland, 15–24 July 2025; Volume 501, p. 1387. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration Features of the Energy Spectrum of Cosmic Rays above 2.5 × 1018 eV using the Pierre Auger Observatory. Phys. Rev. Lett. 2020, 125, 121106. [CrossRef]
- Kim, J.; for the Telescope Array Collaboration. Energy Spectrum Measured by the Telescope Array Surface Detectors. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Malargüe, Argentina, 17–21 November 2024; Volume 484, p. 037. [Google Scholar] [CrossRef]
- Tsunesada, Y.; for the Pierre Auger Collaboration and the Telescope Array Collaboration. Measurement of UHECR energy spectrum with the Pierre Auger Observatory and the Telescope Array. In Proceedings of the 38th International Cosmic Ray Conference (ICRC2023), Nagoya, Japan, 26 July–3 August 2023; Volume 444, p. 406. [Google Scholar] [CrossRef]
- Navas, S.; Amsler, C.; Gutsche, T.; Hanhart, C.; Hernández-Rey, J.J.; Lourenço, C.; Masoni, A.; Mikhasenko, M.; Mitchell, R.E.; Patrignani, C.; et al. Review of particle physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Maurin, D.; Ahlers, M.; Dembinski, H.; Haungs, A.; Mangeard, P.S.; Melot, F.; Mertsch, P.; Wochele, D.; Wochele, J. A cosmic-ray database update: CRDB v4.1. Eur. Phys. J. C 2023, 83, 971. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Depth of maximum of air-shower profiles at the Pierre Auger Observatory. II. Composition implications. Phys. Rev. D 2014, 90, 122006. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Inference of the Mass Composition of Cosmic Rays with Energies from 1018.5 to 1020 eV Using the Pierre Auger Observatory and Deep Learning. Phys. Rev. Lett. 2025, 134, 021001. [Google Scholar] [CrossRef] [PubMed]
- The Pierre Auger Collaboration. Testing hadronic-model predictions of depth of maximum of air-shower profiles and ground-particle signals using hybrid data of the Pierre Auger Observatory. Phys. Rev. D 2024, 109, 102001. [Google Scholar] [CrossRef]
- Kim, J.; Bergman, D.; Telescope Array Collaboration. The fractional analysis of mass composition measured by the Telescope Array FADC fluorescence detectors in hybrid mode. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 098. [Google Scholar] [CrossRef]
- Yushkov, A.; for the Pierre Auger Collaboration and the Telescope Array Collaboration. Depth of maximum of air-shower profiles: Testing the compatibility of the measurements at the Pierre Auger Observatory and the Telescope Array. In Proceedings of the 38th International Cosmic Ray Conference (ICRC2023), Nagoya, Japan, 26 July–3 August 2023; Volume 444, p. 249. [Google Scholar] [CrossRef]
- The Telescope Array Collaboration. Isotropy of Cosmic Rays beyond 1020 eV Favors Their Heavy Mass Composition. Phys. Rev. Lett. 2024, 133, 041001. [Google Scholar] [CrossRef]
- Prosekin, A.; for the Telescope Array Collaboration. Evaluation of the Telescope Array surface detector’s energy reconstruction performance using a deep neural network and hybrid data. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 040. [Google Scholar] [CrossRef]
- Gaisser, T.K.; Stanev, T.; Tilav, S. Cosmic Ray Energy Spectrum from Measurements of Air Showers. arXiv 2013, arXiv:1303.3565. [Google Scholar] [CrossRef]
- Aloisio, R.; Berezinsky, V.; Gazizov, A. Transition from galactic to extragalactic cosmic rays. Astropart. Phys. 2012, 39–40, 129–143. [Google Scholar] [CrossRef]
- Allard, D. Extragalactic propagation of ultrahigh energy cosmic-rays. Astropart. Phys. 2012, 39–40, 33–43. [Google Scholar] [CrossRef]
- Greisen, K. End to the Cosmic-Ray Spectrum? Phys. Rev. Lett. 1966, 16, 748–750. [Google Scholar] [CrossRef]
- Zatsepin, G.; Kuzmin, V. Upper limit of the spectrum of cosmic rays. JETP Lett. 1966, 4, 78–80. [Google Scholar]
- The Pierre Auger Collaboration. Combined fit of spectrum and composition data as measured by the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 2017, 2017, 038. [Google Scholar] [CrossRef]
- Berezinsky, V.; Gazizov, A.; Grigorieva, S. On astrophysical solution to ultrahigh energy cosmic rays. Phys. Rev. D 2006, 74, 043005. [Google Scholar] [CrossRef]
- Hooper, D.; Taylor, A.M. On the heavy chemical composition of the ultra-high energy cosmic rays. Astropart. Phys. 2010, 33, 151–159. [Google Scholar] [CrossRef]
- Taylor, A.M.; Ahlers, M.; Hooper, D. Indications of negative evolution for the sources of the highest energy cosmic rays. Phys. Rev. D 2015, 92, 063011. [Google Scholar] [CrossRef]
- Unger, M.; Farrar, G.R.; Anchordoqui, L.A. Origin of the ankle in the ultra-high energy cosmic ray spectrum and of the extragalactic protons below it. Phys. Rev. D 2015, 92, 123001. [Google Scholar] [CrossRef]
- Heinze, J.; Fedynitch, A.; Boncioli, D.; Winter, W. A New View on Auger Data and Cosmogenic Neutrinos in Light of Different Nuclear Disintegration and Air-shower Models. Astrophys. J. 2019, 873, 88. [Google Scholar] [CrossRef]
- Mollerach, S.; Roulet, E. Extragalactic cosmic rays diffusing from two populations of sources. Phys. Rev. D 2020, 101, 103024. [Google Scholar] [CrossRef]
- Bergmann, D.; for the Telescope Array Collaboration. Telescope Array Combined Fit to Cosmic Ray Spectrum and Composition. In Proceedings of the 37th International Cosmic Ray Conference (ICRC 2021), Berlin, Germany, 15–22 July 2021; Volume 395, p. 338. [Google Scholar] [CrossRef]
- Pierre Auger Collaboration. Constraining the sources of ultra-high-energy cosmic rays across and above the ankle with the spectrum and composition data measured at the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 2023, 05, 024. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Constraining models for the origin of ultra-high-energy cosmic rays with a novel combined analysis of arrival directions, spectrum, and composition data measured at the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 2024, 01, 022. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Impact of the magnetic horizon on the interpretation of the Pierre Auger Observatory spectrum and composition data. J. Cosmol. Astropart. Phys. 2024, 2024, 094. [Google Scholar] [CrossRef]
- Peters, B. Primary cosmic radiation and extensive air showers. Il Nuovo Cimento (1955–1965) 1961, 22, 800–819. [Google Scholar] [CrossRef]
- Comisso, L.; Farrar, G.R.; Muzio, M.S. Ultra-High-Energy Cosmic Rays Accelerated by Magnetically Dominated Turbulence. Astrophys. J. Lett. 2024, 977, L18. [Google Scholar] [CrossRef]
- Muzio, M.S.; Anchordoqui, L.A.; Unger, M. Peters cycle at the end of the cosmic ray spectrum? Phys. Rev. D 2024, 109, 023006. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Constraints on the origin of cosmic rays above 1018 eV from large-scale anisotropy searches in data of the Pierre Auger Observatory. Astrophys. J. Lett. 2012, 762, L13. [Google Scholar] [CrossRef]
- Aloisio, R.; Berezinsky, V.; Blasi, P. Ultra high energy cosmic rays: Implications of Auger data for source spectra and chemical composition. J. Cosmol. Astropart. Phys. 2014, 2014, 020. [Google Scholar] [CrossRef]
- Muzio, M.S.; Farrar, G.R.; Unger, M. Probing the environments surrounding ultrahigh energy cosmic ray accelerators and their implications for astrophysical neutrinos. Phys. Rev. D 2022, 105, 023002. [Google Scholar] [CrossRef]
- Luce, Q.; Marafico, S.; Biteau, J.; Condorelli, A.; Deligny, O. Observational Constraints on Cosmic-Ray Escape from Ultrahigh-energy Accelerators. Astrophys. J. 2022, 936, 62. [Google Scholar] [CrossRef]
- Baerwald, P.; Bustamante, M.; Winter, W. UHECR escape mechanisms for protons and neutrons from GRBs, and the cosmic ray-neutrino connection. Astrophys. J. 2013, 768, 186. [Google Scholar] [CrossRef]
- Globus, N.; Allard, D.; Parizot, E. A complete model of the CR spectrum and composition across the Galactic to Extragalactic transition. Phys. Rev. D 2015, 92, 021302. [Google Scholar] [CrossRef]
- Globus, N.; Allard, D.; Mochkovitch, R.; Parizot, E. UHECR acceleration at GRB internal shocks. Mon. Not. R. Astron. Soc. 2015, 451, 751–790. [Google Scholar] [CrossRef]
- Biehl, D.; Boncioli, D.; Fedynitch, A.; Winter, W. Cosmic ray and neutrino emission from gamma-ray bursts with a nuclear cascade. Astron. Astrophys. 2018, 611, A101. [Google Scholar] [CrossRef]
- Zhang, B.T.; Murase, K.; Kimura, S.S.; Horiuchi, S.; Mészáros, P. Low-luminosity gamma-ray bursts as the sources of ultrahigh-energy cosmic ray nuclei. Phys. Rev. D 2018, 97, 083010. [Google Scholar] [CrossRef]
- Heinze, J.; Biehl, D.; Fedynitch, A.; Boncioli, D.; Rudolph, A.; Winter, W. Systematic parameter space study for the UHECR origin from GRBs in models with multiple internal shocks. Mon. Not. R. Astron. Soc. 2020, 498, 5990–6004. [Google Scholar] [CrossRef]
- Rodrigues, X.; Heinze, J.; Palladino, A.; van Vliet, A.; Winter, W. Active Galactic Nuclei Jets as the Origin of Ultrahigh-Energy Cosmic Rays and Perspectives for the Detection of Astrophysical Source Neutrinos at EeV Energies. Phys. Rev. Lett. 2021, 126, 191101. [Google Scholar] [CrossRef] [PubMed]
- Supanitsky, A.; Cobos, A.; Etchegoyen, A. Origin of the light cosmic ray component below the ankle. Phys. Rev. D 2018, 98, 103016. [Google Scholar] [CrossRef]
- Eichmann, B.; Rachen, J.P.; Merten, L.; van Vliet, A.; Becker Tjus, J. Ultra-high-energy cosmic rays from radio galaxies. J. Cosmol. Astropart. Phys. 2018, 2018, 036. [Google Scholar] [CrossRef]
- Eichmann, B.; Kachelrieß, M.; Oikonomou, F. Explaining the UHECR spectrum, composition and large-scale anisotropies with radio galaxies. J. Cosmol. Astropart. Phys. 2022, 07, 006. [Google Scholar] [CrossRef]
- Guépin, C.; Kotera, K.; Barausse, E.; Fang, K.; Murase, K. Ultra-high-energy cosmic rays and neutrinos from tidal disruptions by massive black holes. Astron. Astrophys. 2018, 616, A179. [Google Scholar] [CrossRef]
- Biehl, D.; Boncioli, D.; Lunardini, C.; Winter, W. Tidally disrupted stars as a possible origin of both cosmic rays and neutrinos at the highest energies. Sci. Rep. 2018, 8, 10828. [Google Scholar] [CrossRef]
- Plotko, P.; Winter, W.; Lunardini, C.; Yuan, C. Ultra-High-Energy Cosmic Rays from Neutrino-Emitting Tidal Disruption Events. arXiv 2024, arXiv:2410.19047. [Google Scholar] [CrossRef]
- Condorelli, A.; Boncioli, D.; Peretti, E.; Petrera, S. Testing hadronic and photo-hadronic interactions as responsible for UHECR and neutrino fluxes from Starburst Galaxies. Phys. Rev. D 2023, 107, 083009. [Google Scholar] [CrossRef]
- Fang, K.; Murase, K. Linking high-energy cosmic particles by black-hole jets embedded in large-scale structures. Nat. Phys. 2018, 14, 396–398. [Google Scholar] [CrossRef]
- Rossoni, S.; Boncioli, D.; Sigl, G. Investigating binary-neutron-star mergers as production sites of high-energy neutrinos. arXiv 2024, arXiv:2407.19957. [Google Scholar] [CrossRef]
- Alves Batista, R.; de Almeida, R.M.; Lago, B.; Kotera, K. Cosmogenic photon and neutrino fluxes in the Auger era. J. Cosmol. Astropart. Phys. 2019, 2019, 002. [Google Scholar] [CrossRef]
- Globus, N.; Allard, D.; Parizot, E.; Piran, T. Probing the Extragalactic Cosmic-Ray Origin with Gamma-Ray and Neutrino Backgrounds. Astrophys. J. Lett. 2017, 839, L22. [Google Scholar] [CrossRef]
- Ehlert, D.; van Vliet, A.; Oikonomou, F.; Winter, W. Constraints on the proton fraction of cosmic rays at the highest energies and the consequences for cosmogenic neutrinos and photons. J. Cosmol. Astropart. Phys. 2024, 02, 022. [Google Scholar] [CrossRef]
- Muzio, M.S.; Unger, M.; Wissel, S. Prospects for joint cosmic ray and neutrino constraints on the evolution of trans-Greisen-Zatsepin-Kuzmin proton sources. Phys. Rev. D 2023, 107, 103030. [Google Scholar] [CrossRef]
- Hasinger, G.; Miyaji, T.; Schmidt, M. Luminosity-dependent evolution of soft X-ray selected AGN: New Chandra and XMM-Newton surveys. Astron. Astrophys. 2005, 441, 417–434. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. The Energy Spectrum of Ultra-High Energy Cosmic Rays across Declinations −90° to +44.8° as measured at the Pierre Auger Observatory. arXiv 2025, arXiv:2506.11688. [Google Scholar] [CrossRef]
- Bister, T.; Farrar, G.R. Constraints on UHECR Sources and Extragalactic Magnetic Fields from Directional Anisotropies. Astrophys. J. 2024, 966, 71. [Google Scholar] [CrossRef]
- Ehlert, D.; Oikonomou, F.; Unger, M. Curious case of the maximum rigidity distribution of cosmic-ray accelerators. Phys. Rev. D 2023, 107, 103045. [Google Scholar] [CrossRef]
- Luce, Q.; Biteau, J.; Deligny, O.; Condorelli, A. Indication of population effect in UHECR sources. In Proceedings of the 39th International Cosmic Ray Conference (ICRC 2025), Geneva, Switzerland, 14–24 July 2025; Volume 501, p. 322. [Google Scholar]
- Farrar, G.R. Binary Neutron Star Mergers as the Source of the Highest Energy Cosmic Rays. Phys. Rev. Lett. 2025, 134, 081003. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.T.; Murase, K.; Ekanger, N.; Bhattacharya, M.; Horiuchi, S. Ultraheavy Ultrahigh-Energy Cosmic Rays. arXiv 2024, arXiv:2405.17409. [Google Scholar] [CrossRef]
- Lundquist, J.P.; Vorobiov, S.; Merten, L.; Reimer, A.; Boughelilba, M.; Da Vela, P.; Tavecchio, F.; Bonnoli, G.; Righi, C. Combined Fit of Spectrum and Composition for FR0 Radio-galaxy-emitted Ultra–high energy Cosmic Rays with Resulting Secondary Photons and Neutrinos. Astrophys. J. 2025, 978, 20. [Google Scholar] [CrossRef]
- Farrar, G.R.; Sutherland, M.S. Deflections of UHECRs in the Galactic magnetic field. J. Cosmol. Astropart. Phys. 2019, 2019, 004. [Google Scholar] [CrossRef]
- Eichmann, B.; Winchen, T. Galactic magnetic field bias on inferences from UHECR data. J. Cosmol. Astropart. Phys. 2020, 2020, 047. [Google Scholar] [CrossRef]
- Bister, T.; Farrar, G.R.; Unger, M. The Large-scale Anisotropy and Flux (de)magnification of Ultrahigh-energy Cosmic Rays in the Galactic Magnetic Field. Astrophys. J. Lett. 2024, 975, L21. [Google Scholar] [CrossRef]
- Liouville, J. Nouvelle démonstration d’un théorème sur les irrationnelles algébriques. C. R. Acad. Sci. Paris 1844, 18, 910–911. [Google Scholar]
- Korochkin, A.; Semikoz, D.; Tinyakov, P. UHECR deflections in the Galactic magnetic field. arXiv 2025, arXiv:2501.16158. [Google Scholar] [CrossRef]
- Unger, M.; Farrar, G.R. The Galactic Magnetic Field and UHECR Deflections. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 003. [Google Scholar] [CrossRef]
- Jaffe, T.R. Practical Modeling of Large-Scale Galactic Magnetic Fields: Status and Prospects. Galaxies 2019, 7, 52. [Google Scholar] [CrossRef]
- Jansson, R.; Farrar, G.R. The Galactic Magnetic Field. Astrophys. J. 2012, 761, L11. [Google Scholar] [CrossRef]
- Jansson, R.; Farrar, G.R. A New Model of the Galactic Magnetic Field. Astrophys. J. 2012, 757, 14. [Google Scholar] [CrossRef]
- The Planck collaboration. Planck intermediate results—XLII. Large-scale Galactic magnetic fields. Astron. Astrophys. 2016, 596, A103. [Google Scholar] [CrossRef]
- Pelgrims, V.; Ferrière, K.; Boulanger, F.; Lallement, R.; Montier, L. Modeling the magnetized Local Bubble from dust data. Astron. Astrophys. 2020, 636, A17. [Google Scholar] [CrossRef]
- Pelgims, V.; Maris, I.; Unger, M. The Effect of Our Cosmic Neighborhood’s Magnetic Field on UHECR Propagation. In Proceedings of the 39th International Cosmic Ray Conference (ICRC 2025), Geneva, Switzerland, 14–24 July 2025; Volume 501, p. 357. [Google Scholar]
- The Pierre Auger Collaboration. Observation of a Large-scale Anisotropy in the Arrival Directions of Cosmic Rays above 8×1018 eV. Science 2017, 357, 1266–1270. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Large-scale Cosmic-ray Anisotropies with 19 yr of Data from the Pierre Auger Observatory. Astrophys. J. 2024, 976, 48. [Google Scholar] [CrossRef]
- Rubtsov, G.; for the Pierre Auger Collaboration and the Telescope Array Collaboration. Update on full-sky searches for large- and medium-scale anisotropies in the UHECR flux using the Pierre Auger Observatory and the Telescope Array. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 009. [Google Scholar] [CrossRef]
- L. Caccianiga for the Pierre Auger Collaboration. Update on the searches for anisotropies in UHECR arrival directions with the Pierre Auger Observatory and the Telescope Array. In Proceedings of the 38th International Cosmic Ray Conference (ICRC2023), Nagoya, Japan, 26 July–3 August 2023; Volume 444, p. 521. [Google Scholar] [CrossRef]
- The Telescope Array Collaboration. Search for Large-scale Anisotropy on Arrival Directions of Ultra-high-energy Cosmic Rays Observed with the Telescope Array Experiment. Astrophys. J. Lett. 2020, 898, L28. [Google Scholar] [CrossRef]
- The Telescope Array Collaboration. Indications of Intermediate-Scale Anisotropy of Cosmic Rays with Energy Greater Than 57 EeV in the Northern Sky Measured with the Surface Detector of the Telescope Array Experiment. Astrophys. J. 2014, 790, L21. [Google Scholar] [CrossRef]
- Seo, J.; Ryu, D.; Kang, H. Energy Spectrum and Mass Composition of Ultra-High-Energy Cosmic Rays Originating from Relativistic Jets of Nearby Radio Galaxies. arXiv 2025, arXiv:2506.15110. [Google Scholar] [CrossRef]
- Berezinskii, V.S.; Grigor’eva, S.I.; Dogiel, V.A. Predicted spectrum and anisotropy of the ultra-high energy cosmic rays in a single-source model. Astron. Astrophys. 1990, 232, 582–588. [Google Scholar]
- Isola, C.; Lemoine, M.; Sigl, G. Centaurus A as the Source of ultra-high energy cosmic rays? Phys. Rev. D 2001, 65, 023004. [Google Scholar] [CrossRef]
- Mollerach, S.; Roulet, E. Case for Centaurus A as the main source of ultrahigh-energy cosmic rays. Phys. Rev. D 2024, 110, 063030. [Google Scholar] [CrossRef]
- Bister, T. The source of the cosmic-ray excess in the Centaurus region—Constraints on possible candidates, mass composition and cosmic magnetic fields. arXiv 2025, arXiv:2509.06594. [Google Scholar] [CrossRef]
- Waxman, E.; Fisher, K.B.; Piran, T. The Signature of a Correlation between Cosmic-ray Sources above 1019 eV and Large-Scale Structure. Astrophys. J. 1997, 483, 1–7. [Google Scholar] [CrossRef]
- Cuoco, A.; D’Abrusco, R.; Longo, G.; Miele, G.; Serpico, P.D. The footprint of large scale cosmic structure on the ultrahigh energy cosmic ray distribution. J. Cosmol. Astropart. Phys. 2006, 2006, 009. [Google Scholar] [CrossRef]
- Harari, D.; Mollerach, S.; Roulet, E. Anisotropies of ultrahigh energy cosmic ray nuclei diffusing from extragalactic sources. Phys. Rev. D 2015, 92, 063014. [Google Scholar] [CrossRef]
- Tinyakov, P.G.; Urban, F.R. Full sky harmonic analysis hints at large ultra-high energy cosmic ray deflections. JETP 2015, 120, 533–540. [Google Scholar] [CrossRef]
- Globus, N.; Piran, T. The Extragalactic Ultra-high-energy Cosmic-Ray Dipole. Astrophys. J. Lett. 2017, 850, L25. [Google Scholar] [CrossRef]
- di Matteo, A.; Tinyakov, P. How isotropic can the UHECR flux be? Mon. Not. R. Astron. Soc. 2018, 476, 715–723. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Large-scale cosmic-ray anisotropies above 4 EeV measured by the Pierre Auger Observatory. Astrophys. J. 2018, 868, 4. [Google Scholar] [CrossRef]
- Globus, N.; Piran, T.; Hoffman, Y.; Carlesi, E.; Pomarède, D. Cosmic ray anisotropy from large-scale structure and the effect of magnetic horizons. Mon. Not. R. Astron. Soc. 2019, 484, 4167–4173. [Google Scholar] [CrossRef]
- Ding, C.; Globus, N.; Farrar, G.R. The Imprint of Large-scale Structure on the Ultrahigh-energy Cosmic-Ray Sky. Astrophys. J. Lett. 2021, 913, L13. [Google Scholar] [CrossRef]
- Allard, D.; Aublin, J.; Baret, B.; Parizot, E. What can be learnt from UHECR anisotropies observations—I. Large-scale anisotropies and composition features. Astron. Astrophys. 2022, 664, A120. [Google Scholar] [CrossRef]
- Simeon, P.; Globus, N.; Barrow, K.S.S.; Blandford, R. A Hierarchical Shock Model of Ultra-High-Energy Cosmic Rays. arXiv 2025, arXiv:2503.10795. [Google Scholar] [CrossRef]
- Fargion, D.; De Sanctis Lucentini, P.G.; Khlopov, M.Y. UHECR Clustering: Lightest Nuclei from Local Sheet Galaxies. Universe 2024, 10, 323. [Google Scholar] [CrossRef]
- Condorelli, A.; Biteau, J.; Adam, R. Impact of Galaxy Clusters on the Propagation of Ultrahigh-energy Cosmic Rays. Astrophys. J. 2023, 957, 80. [Google Scholar] [CrossRef]
- Hoffman, Y.; Carlesi, E.; Pomarède, D.; Tully, R.B.; Courtois, H.M.; Gottlöber, S.; Libeskind, N.I.; Sorce, J.G.; Yepes, G. The quasi-linear nearby Universe. Nat. Astron. 2018, 2, 680–687. [Google Scholar] [CrossRef]
- Alves Batista, R. The Quest for the Origins of Ultra-High-Energy Cosmic Rays. arXiv 2025, arXiv:2412.17201. [Google Scholar] [CrossRef]
- Allard, D.; Aublin, J.; Baret, B.; Parizot, E. What can be learnt from UHECR anisotropies observations Paper II: Intermediate-scale anisotropies. Astron. Astrophys. 2024, 686, A292. [Google Scholar] [CrossRef]
- Ajello, M.; Romani, R.W.; Gasparrini, D.; Shaw, M.S.; Bolmer, J.; Cotter, G.; Finke, J.; Greiner, J.; Healey, S.E.; King, O.; et al. The cosmic evolution of Fermi BL Lacertae objects. Astrophys. J. 2013, 780, 73. [Google Scholar] [CrossRef]
- Gruppioni, C.; Pozzi, F.; Rodighiero, G.; Delvecchio, I.; Berta, S.; Pozzetti, L.; Zamorani, G.; Andreani, P.; Cimatti, A.; Ilbert, O.; et al. The Herschel PEP/HerMES luminosity function—I. Probing the evolution of PACS selected Galaxies to z≃4. Mon. Not. R. Astron. Soc. 2013, 432, 23–52. [Google Scholar] [CrossRef]
- Farrar, G.R.; Gruzinov, A. Giant AGN flares and cosmic ray bursts. Astrophys. J. 2009, 693, 329–332. [Google Scholar] [CrossRef]
- He, H.N.; Kusenko, A.; Nagataki, S.; Zhang, B.B.; Yang, R.Z.; Fan, Y.Z. Monte Carlo Bayesian search for the plausible source of the Telescope Array hotspot. Phys. Rev. D 2016, 93, 043011. [Google Scholar] [CrossRef]
- Hackstein, S.; Vazza, F.; Brüggen, M.; Sorce, J.G.; Gottlöber, S. Simulations of ultra-high energy cosmic rays in the local Universe and the origin of cosmic magnetic fields. Mon. Not. R. Astron. Soc. 2018, 475, 2519–2529. [Google Scholar] [CrossRef]
- Valade, A.; Libeskind, N.I.; Pomarede, D.; Tully, R.B.; Hoffmann, Y.; Pfeifer, S.; Kourkchi, E. Identification of Basins of Attraction in the Local Universe. Nat. Astron. 2024, 8, 1610–1616. [Google Scholar] [CrossRef]
- Lang, R.G.; Taylor, A.M.; de Souza, V. Ultrahigh-energy cosmic rays dipole and beyond. Phys. Rev. D 2021, 103, 063005. [Google Scholar] [CrossRef]
- Vícha, J.; Bakalová, A.; Müller, A.L.; Tkachenko, O.; Stadelmaier, M.K. A Heavy-metal Scenario of Ultra-high-energy Cosmic Rays. Astrophys. J. Lett. 2025, 986, L34. [Google Scholar] [CrossRef]
- Martins, E.E.; for the Pierre Auger Collaboration. Prospects of a composition-enhanced search for large-scale anisotropy with the Pierre Auger Observatory. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 102. [Google Scholar] [CrossRef]
- Golup, G.; for the Pierre Auger Collaboration. An update on the arrival direction studies made with data from the Pierre Auger Observatory. In Proceedings of the 38th International Cosmic Ray Conference (ICRC2023), Nagoya, Japan, 26 July–3 August 2023; Volume 444, p. 252. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Arrival Directions of Cosmic Rays above 32 EeV from Phase One of the Pierre Auger Observatory. Astrophys. J. 2022, 935, 170. [Google Scholar] [CrossRef]
- Kim, J.; for the Telescope Array Collaboration. Telescope Array Surface Detector Medium-scale Anisotropy Analyses. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 097. [Google Scholar] [CrossRef]
- Kim, J.; Ryu, D.; Kang, H.; Kim, S.; Rey, S.C. Filaments of galaxies as a clue to the origin of ultrahigh-energy cosmic rays. Science Advances 2019, 5, eaau8227. [Google Scholar] [CrossRef] [PubMed]
- The Pierre Auger Collaboration. The flux of ultra-high-energy cosmic rays along the supergalactic plane measured at the Pierre Auger Observatory. Astrophys. J. 2025, 984, 123. [Google Scholar] [CrossRef]
- The Telescope Array Collaboration. Observation of Declination Dependence in the Cosmic Ray Energy Spectrum. arXiv 2024, arXiv:2406.08612. [Google Scholar] [CrossRef]
- Globus, N.; Allard, D.; Parizot, E.; Lachaud, C.; Piran, T. Can We Reconcile the TA Excess and Hotspot with Auger Observations? Astrophys. J. 2017, 836, 163. [Google Scholar] [CrossRef]
- Plotko, P.; Vliet, A.V.; Rodrigues, X.; Winter, W. Differences Between the Pierre Auger Observatory and Telescope Array Spectra: Systematic Effects or Indication of a Local Source of Ultra-High-Energy Cosmic Rays? Astrophys. J. 2023, 953, 129. [Google Scholar] [CrossRef]
- Cavallo, G. On the sources of ultra-high energy cosmic rays. Astron. Astrophys. 1978, 65, 415–419. [Google Scholar]
- Romero, G.E.; Combi, J.A.; Perez Bergliaffa, S.E.; Anchordoqui, L.A. Centaurus A as a source of extragalactic cosmic rays with arrival energies well beyond the GZK cutoff. Astropart. Phys. 1996, 5, 279–283. [Google Scholar] [CrossRef]
- Farrar, G.R.; Piran, T. Deducing the Source of Ultrahigh Energy Cosmic Rays. arXiv 2000, arXiv:astro-ph/0010370. [Google Scholar] [CrossRef]
- Gorbunov, D.; Tinyakov, P.; Tkachev, I.; Troitsky, S. Comment on “Correlation of the Highest-Energy Cosmic Rays with Nearby Extragalactic Objects”. JETP Lett. 2007, 87, 461–463. [Google Scholar] [CrossRef]
- Wykes, S.; Croston, J.H.; Hardcastle, M.J.; Eilek, J.A.; Biermann, P.L.; Achterberg, A.; Bray, J.D.; Lazarian, A.; Haverkorn, M.; Protheroe, R.J.; et al. Mass entrainment and turbulence-driven acceleration of ultra-high energy cosmic rays in Centaurus A. Astron. Astrophys. 2013, 558, A19. [Google Scholar] [CrossRef]
- Wang, J.; Reville, B.; Rieger, F.M.; Aharonian, F.A. Acceleration of ultra-high-energy cosmic rays in the kiloparsec-scale jets of nearby radio galaxies. arXiv 2024, arXiv:2411.16674. [Google Scholar] [CrossRef]
- Lemoine, M.; Waxman, E. Anisotropy vs chemical composition at ultra-high energies. J. Cosmol. Astropart. Phys. 2009, 2009, 009. [Google Scholar] [CrossRef]
- Achterberg, A.; Gallant, Y.A.; Kirk, J.G.; Guthmann, A.W. Particle acceleration by ultrarelativistic shocks: Theory and simulations. Mon. Not. R. Astron. Soc. 2001, 328, 393–408. [Google Scholar] [CrossRef]
- Rieger, F.M. Active Galactic Nuclei as Potential Sources of Ultra-High Energy Cosmic Rays. Universe 2022, 8, 607. [Google Scholar] [CrossRef]
- Caprioli, D. “Espresso” acceleration of ultra-high-energy cosmic rays. Astrophys. J. 2015, 811, L38. [Google Scholar] [CrossRef]
- Murase, K.; Stecker, F.W. High-Energy Neutrinos from Active Galactic Nuclei. In The Encyclopedia of Cosmology; World Scientific Publishing: London, UK, 2023; pp. 483–540. [Google Scholar] [CrossRef]
- Kimura, S.S.; Murase, K.; Zhang, B.T. Ultrahigh-energy cosmic-ray nuclei from black hole jets: Recycling galactic cosmic rays through shear acceleration. Phys. Rev. D 2018, 97, 023026. [Google Scholar] [CrossRef]
- Matthews, J.H.; Bell, A.R.; Blundell, K.M.; Araudo, A.T. Ultrahigh energy cosmic rays from shocks in the lobes of powerful radio galaxies. Mon. Not. R. Astron. Soc. 2019, 482, 4303–4321. [Google Scholar] [CrossRef]
- Ehlert, D.; Oikonomou, F.; Peretti, E. Ultra-high-energy cosmic rays from ultra-fast outflows of active galactic nuclei. arXiv 2025, arXiv:2411.05667. [Google Scholar] [CrossRef]
- Resconi, E.; Coenders, S.; Padovani, P.; Giommi, P.; Caccianiga, L. Connecting blazars with ultrahigh-energy cosmic rays and astrophysical neutrinos. Mon. Not. R. Astron. Soc. 2017, 468, 597–606. [Google Scholar] [CrossRef]
- Mbarek, R.; Caprioli, D. Revisiting Propagation Delays of Ultra-High-Energy Cosmic Rays from Long-lived Sources. arXiv 2025, arXiv:2502.01022. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Correlation of the Highest-Energy Cosmic Rays with Nearby Extragalactic Objects. Science 2007, 318, 938–943. [Google Scholar] [CrossRef] [PubMed]
- Galvez Ureña, A.; for the Pierre Auger Collaboration and the Telescope Array Collaboration. New full-sky studies of the distribution of ultra-high-energy cosmic-ray arrival directions. In Proceedings of the 39th International Cosmic Ray Conference (ICRC 2025), Geneva, Switzerland, 14–24 July 2025; Volume 501, p. 282. [Google Scholar]
- de Oliveira, C.; Lang, R.G.; Batista, P. On Gamma Rays as Predictors of Ultra-high-energy Cosmic-Ray Flux in Active Galactic Nuclei. Astrophys. J. 2025, 981, 123. [Google Scholar] [CrossRef]
- Partenheimer, A.; Fang, K.; Alves Batista, R.; Almeida, R.M.d. Ultra-high-energy Cosmic Ray Sources can be Gamma-ray Dim. Astrophys. J. Lett. 2024, 967, L15. [Google Scholar] [CrossRef]
- Merten, L.; Boughelilba, M.; Reimer, A.; Vela, P.D.; Vorobiov, S.; Tavecchio, F.; Bonnoli, G.; Lundquist, J.P.; Righi, C. Scrutinizing FR 0 Radio Galaxies as Ultra-High-Energy Cosmic Ray Source Candidates. Astropart. Phys. 2021, 128, 102564. [Google Scholar] [CrossRef]
- Anjos, R.C.; Coimbra-Araujo, C.H. Central accumulation of magnetic flux in massive Seyfert galaxies as a possible engine to trigger ultrahigh energy cosmic rays. Phys. Rev. D 2017, 96, 023008. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. An Indication of anisotropy in arrival directions of ultra-high-energy cosmic rays through comparison to the flux pattern of extragalactic gamma-ray sources. Astrophys. J. Lett. 2018, 853, L29. [Google Scholar] [CrossRef]
- Kuznetsov, M.; for the Pierre Auger Collaboration and the Telescope Array Collaboration. Possible interpretations of the joint observations of UHECR arrival directions using data recorded at the Telescope Array and the Pierre Auger Observatory. In Proceedings of the 38th International Cosmic Ray Conference (ICRC2023), Nagoya, Japan, 26 July–3 August 2023; Volume 444, p. 528. [Google Scholar] [CrossRef]
- Higuchi, R.; Sako, T.; Fujii, T.; Kawata, K.; Kido, E. Effects of the Galactic Magnetic Field on the UHECR Correlation Studies with Starburst Galaxies. Astrophys. J. 2023, 949, 107. [Google Scholar] [CrossRef]
- Deval, L.; Engel, R.; Fitoussi, T.; Roulet, E.; Unger, M. Impact of the Galactic magnetic field modelling on studies of the UHECRs arrival direction. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 080. [Google Scholar] [CrossRef]
- Lunardini, C.; Vance, G.S.; Emig, K.L.; Windhorst, R.A. Are starburst galaxies a common source of high energy neutrinos and cosmic rays? J. Cosmol. Astropart. Phys. 2019, 2019, 073. [Google Scholar] [CrossRef]
- van Vliet, A.; Palladino, A.; Taylor, A.; Winter, W. Extragalactic magnetic field constraints from ultrahigh-energy cosmic rays from local galaxies. Mon. Not. R. Astron. Soc. 2022, 510, 1289–1297. [Google Scholar] [CrossRef]
- de Oliveira, C.; de Souza, V. Nearby active galactic nuclei and starburst galaxies as sources of the measured UHECRs anisotropy signal. J. Cosmol. Astropart. Phys. 2023, 2023, 058. [Google Scholar] [CrossRef]
- Anchordoqui, L.A. Acceleration of ultrahigh-energy cosmic rays in starburst superwinds. Phys. Rev. D 2018, 97, 063010. [Google Scholar] [CrossRef]
- Romero, G.E.; Müller, A.L.; Roth, M. Particle acceleration in the superwinds of starburst galaxies. Astron. Astrophys. 2018, 616, A57. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Torres, D.F. Exploring the superwind mechanism for generating ultrahigh-energy cosmic rays using large-scale modeling of starbursts. Phys. Rev. D 2020, 102, 023034. [Google Scholar] [CrossRef]
- Peretti, E.; Morlino, G.; Blasi, P.; Cristofari, P.; Ahlers, M. Exploring galactic wind superbubbles by multimessenger observations. In Proceedings of the 37th International Cosmic Ray Conference (ICRC 2021), Berlin, Germany, 15–22 July 2021; Volume 395, p. 995. [Google Scholar] [CrossRef]
- Kachelriess, M. Extragalactic cosmic rays. In Proceedings of the 37th International Cosmic Ray Conference (ICRC 2021), Berlin, Germany, 15–22 July 2021; Volume 395, p. 018. [Google Scholar] [CrossRef]
- Marafico, S.; Biteau, J.; Condorelli, A.; Deligny, O.; Bregeon, J. Closing the Net on Transient Sources of Ultrahigh-energy Cosmic Rays. Astrophys. J. 2024, 972, 4. [Google Scholar] [CrossRef]
- Bister, T.; Biteau, J. Prospects for constraining transient sources of UHECRs with arrival-direction data. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 070. [Google Scholar] [CrossRef]
- Bell, A.R.; Matthews, J.H. Echoes of the past: Ultra-high-energy cosmic rays accelerated by radio galaxies, scattered by starburst galaxies. Mon. Not. R. Astron. Soc. 2022, 511, 448–456. [Google Scholar] [CrossRef]
- Taylor, A.M.; Matthews, J.H.; Bell, A.R. UHECR echoes from the Council of Giants. Mon. Not. R. Astron. Soc. 2023, 524, 631–642. [Google Scholar] [CrossRef]
- Dolgikh, K.; Korochkin, A.; Rubtsov, G.; Semikoz, D.; Tkachev, I. Cen A hotspot in Ultra-High-Energy Cosmic Rays illuminated by M83 or Cen A? arXiv 2025, arXiv:2505.14344. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Search for magnetically-induced signatures in the arrival directions of ultra-high-energy cosmic rays measured at the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 2020, 06, 017. [Google Scholar] [CrossRef]
- Apollonio, L.; for the Pierre Auger Collaboration. Update on the intermediate arrival-direction analyses of the Pierre Auger Observatory. In Proceedings of the 39th International Cosmic Ray Conference (ICRC 2025), Geneva, Switzerland, 14–24 July 2025; Volume 501, p. 172. [Google Scholar]
- The Telescope Array Collaboration. Evidence for a Supergalactic Structure of Magnetic Deflection Multiplets of Ultra-high-energy Cosmic Rays. Astrophys. J. 2020, 899, 86. [Google Scholar] [CrossRef]
- He, H.N.; Kido, E.; Duan, K.K.; Yang, Y.; Higuchi, R.; Fan, Y.Z.; Wang, T.; Jiang, L.Y.; Li, R.L.; Zhu, B.Y.; et al. Evidence for the Sombrero Galaxy as an Accelerator of the Highest-Energy Cosmic Rays. arXiv 2024, arXiv:2412.11966. [Google Scholar] [CrossRef]
- Golup, G.; Harari, D.; Mollerach, S.; Roulet, E. Source position reconstruction and constraints on the galactic magnetic field from ultra-high energy cosmic rays. Astropart. Phys. 2009, 32, 269–277. [Google Scholar] [CrossRef]
- Wirtz, M.; Bister, T.; Erdmann, M. Towards extracting cosmic magnetic field structures from cosmic-ray arrival directions. EPJC 2021, 81, 794. [Google Scholar] [CrossRef]
- Schulte, J.; Bister, T.; Erdmann, M. An all-sky search method for coherent magnetic field deflections of ultra-high-energy cosmic rays based on Deep Learning. In Proceedings of the 38th International Cosmic Ray Conference (ICRC2023), Nagoya, Japan, 26 July–3 August 2023; Volume 444, p. 198. [Google Scholar] [CrossRef]
- Takeda, M.; Hayashida, N.; Honda, K.; Inoue, N.; Kadota, K.; Kakimoto, F.; Kamata, K.; Kawaguchi, S.; Kawasaki, Y.; Kawasumi, N.; et al. Small-scale anisotropy of cosmic rays above 1019 eV observed with the Akeno Giant Air Shower Array. Astrophys. J. 1999, 522, 225–237. [Google Scholar] [CrossRef]
- Uchihori, Y.; Nagano, M.; Takeda, M.; Teshima, M.; Lloyd-Evans, J.; Watson, A.A. Cluster Analysis of Extremely High Energy Cosmic Rays in the Northern Sky. Astropart. Phys. 2000, 13, 151–160. [Google Scholar] [CrossRef]
- Sigl, G.; Lemoine, M.; Olinto, A.V. Maximum likelihood analysis of clusters of ultrahigh energy cosmic rays. Phys. Rev. D 1997, 56, 4470–4479. [Google Scholar] [CrossRef]
- Dubovsky, S.L.; Tinyakov, P.G.; Tkachev, I.I. Statistics of Clustering of Ultrahigh Energy Cosmic Rays and the Number of Their Sources. Phys. Rev. Lett. 2000, 85, 1154–1157. [Google Scholar] [CrossRef]
- Sigl, G.; Miniati, F.; Ensslin, T. Ultra-High Energy Cosmic Ray Probes of Large Scale Structure and Magnetic Fields. Phys. Rev. D 2004, 70, 043007. [Google Scholar] [CrossRef]
- Singh, S.; Ma, C.P.; Arons, J. Gamma-Ray Bursts and Magnetars as Possible Sources of Ultra High Energy Cosmic Rays: Correlation of Cosmic Ray Event Positions with IRAS Galaxies. Phys. Rev. D 2004, 69, 063003. [Google Scholar] [CrossRef]
- Kachelriess, M.; Semikoz, D. Ultra-high energy cosmic rays from a finite number of point sources. Astropart. Phys. 2005, 23, 486–492. [Google Scholar] [CrossRef]
- The Telescope Array Collaboration. An extremely energetic cosmic ray observed by a surface detector array. Science 2023, 382, 903–907. [Google Scholar] [CrossRef] [PubMed]
- Unger, M.; Farrar, G.R. Where Did the Amaterasu Particle Come From? Astrophys. J. Lett. 2024, 962, L5. [Google Scholar] [CrossRef]
- Bourriche, N.; Capel, F. Beyond the Local Void: A comprehensive view on the origins of the Amaterasu particle. arXiv 2024, arXiv:2406.16483. [Google Scholar] [CrossRef]
- Kuznetsov, M.Y. A nearby source of ultra-high energy cosmic rays. J. Cosmol. Astropart. Phys. 2024, 2024, 042. [Google Scholar] [CrossRef]
- Bianciotto, M.; for the Pierre Auger Collaboration. Constraining the origin of the highest-energy cosmic-ray events detected by the Pierre Auger Observatory: A three-dimensional approach. In Proceedings of the 39th International Cosmic Ray Conference (ICRC 2025), Geneva, Switzerland, 14–24 July 2025; Volume 501, p. 195. [Google Scholar] [CrossRef]
- Lang, R.G. New physics as a possible explanation for the Amaterasu particle. J. Cosmol. Astropart. Phys. 2024, 2024, 023. [Google Scholar] [CrossRef]
- Sarmah, P.; Das, N.; Borah, D.; Chakraborty, S.; Mehta, P. The Amaterasu particle: Constraining the superheavy dark matter origin of UHECRs. arXiv 2024, arXiv:2406.03174. [Google Scholar] [CrossRef]
- Frampton, P.H.; Kephart, T.W. The Amaterasu cosmic ray as a magnetic monopole and implications for extensions of the standard model. PLB 2024, 855, 138777. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Castillo, K.P. Sombrero Galaxy as an Accelerator of Ultrahigh Energy Cosmic Ray Nuclei. arXiv 2025, arXiv:2503.13315. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Dova, M.T.; McCauley, T.P.; Reucroft, S.; Swain, J.D. Unmasking the tail of the cosmic ray spectrum. PLB 2000, 482, 343–348. [Google Scholar] [CrossRef]
- Guo, G.; Qian, Y.Z.; Wu, M.R. Binary Neutron Star Mergers as Potential Sources for Ultra-High-Energy Cosmic Rays and High-Energy Neutrinos. arXiv 2025, arXiv:2506.17581. [Google Scholar] [CrossRef]
- Andrade Dourado, L.; Boncioli, D.; di Matteo, A.; Evoli, C.; Petrera, S.; Salamida, F. Towards the implementation of the photodisintegration interaction in SimProp Sirente. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 067. [Google Scholar] [CrossRef]
- Apollonio, L.; for the Pierre Auger Collaboration. Amplifying UHECR arrival direction information using mass estimators at the Pierre Auger Observatory. In Proceedings of the 7th International Symposium on Ultra High Energy Cosmic Rays (UHECR2024), Mendoza, Argentina, 17–21 November 2024; Volume 484, p. 068. [Google Scholar] [CrossRef]
- The IceCube Collaboration. Evidence for neutrino emission from the nearby active galaxy NGC 1068. Science 2022, 378, 538–543. [Google Scholar] [CrossRef] [PubMed]
- Stein, R.; Velzen, S.v.; Kowalski, M.; Franckowiak, A.; Gezari, S.; Miller-Jones, J.C.A.; Frederick, S.; Sfaradi, I.; Bietenholz, M.F.; Horesh, A.; et al. A tidal disruption event coincident with a high-energy neutrino. Nat. Astron. 2021, 5, 510–518. [Google Scholar] [CrossRef]
- The IceCube Collaboration. Searches for Neutrinos from Gamma-Ray Bursts Using the IceCube Neutrino Observatory. Astrophys. J. 2022, 939, 116. [Google Scholar] [CrossRef]
- Ahlers, M.; Allekotte, I.; Alvarez-Muniz, J.; Anastasi, G.A.; Anchordoqui, L.; de Cassia Dos Anjos, R.; Balakrishnan, H.H.; Alves Batista, R.; Bellido, J.; Bertaina, M.; et al. Ideas and Requirements for the Global Cosmic-Ray Observatory (GCOS). arXiv 2025, arXiv:2502.05657. [Google Scholar] [CrossRef]
- The POEMMA Collaboration. The POEMMA (Probe of Extreme Multi-Messenger Astrophysics) observatory. J. Cosmol. Astropart. Phys. 2021, 2021, 007. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bister, T. Probing the Sources of Ultra-High-Energy Cosmic Rays—Constraints from Cosmic-Ray Measurements. Universe 2025, 11, 331. https://doi.org/10.3390/universe11100331
Bister T. Probing the Sources of Ultra-High-Energy Cosmic Rays—Constraints from Cosmic-Ray Measurements. Universe. 2025; 11(10):331. https://doi.org/10.3390/universe11100331
Chicago/Turabian StyleBister, Teresa. 2025. "Probing the Sources of Ultra-High-Energy Cosmic Rays—Constraints from Cosmic-Ray Measurements" Universe 11, no. 10: 331. https://doi.org/10.3390/universe11100331
APA StyleBister, T. (2025). Probing the Sources of Ultra-High-Energy Cosmic Rays—Constraints from Cosmic-Ray Measurements. Universe, 11(10), 331. https://doi.org/10.3390/universe11100331





