The Mass Profile of NGC 3268 from Its Stellar Kinematics
Abstract
1. Introduction
2. Materials and Methods
2.1. Photometric Data
Surface Brightness and Colour Profiles
2.2. Spectroscopic Data
2.2.1. Sky Subtraction
2.2.2. Definite Extraction and Kinematics Measurement
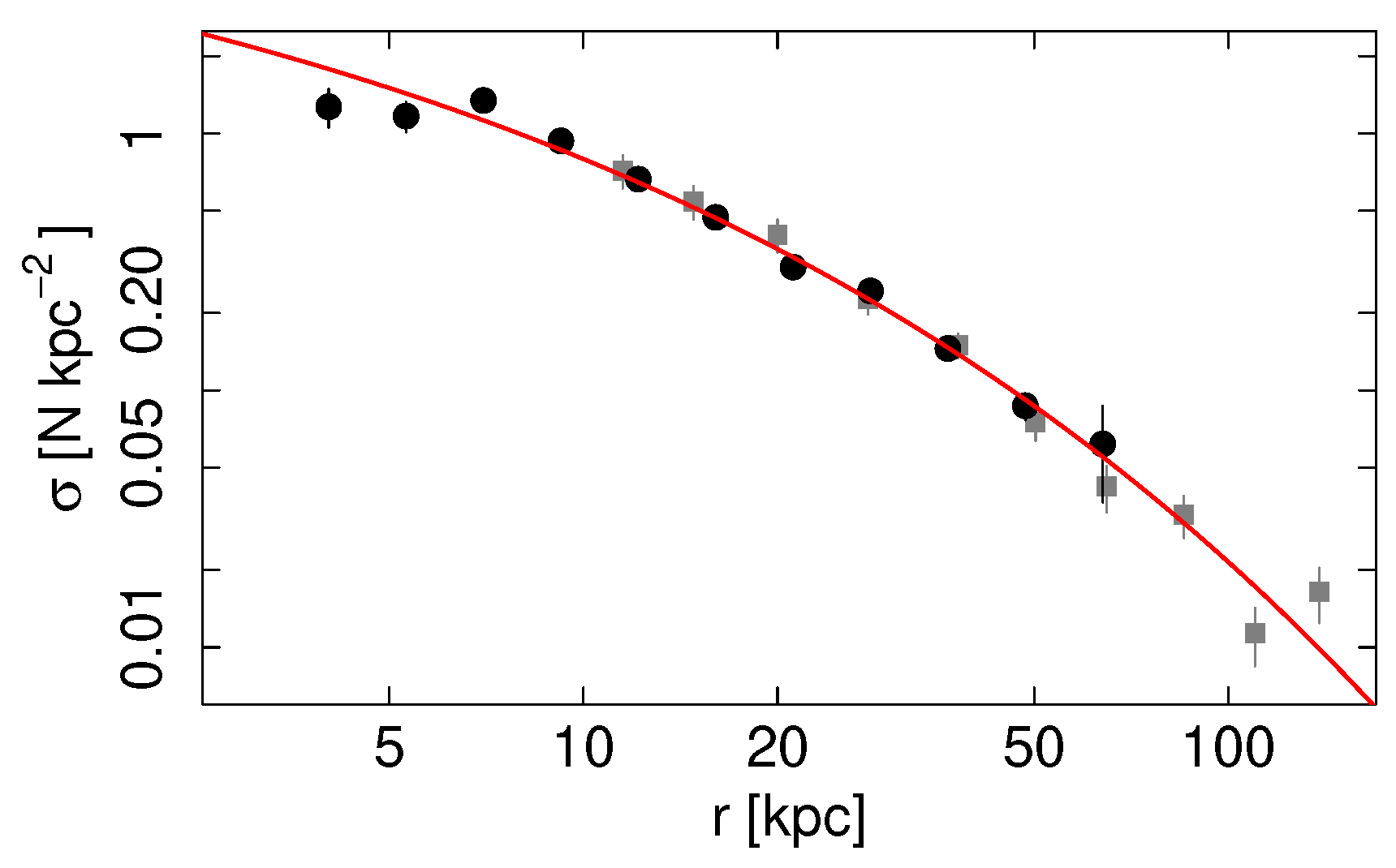
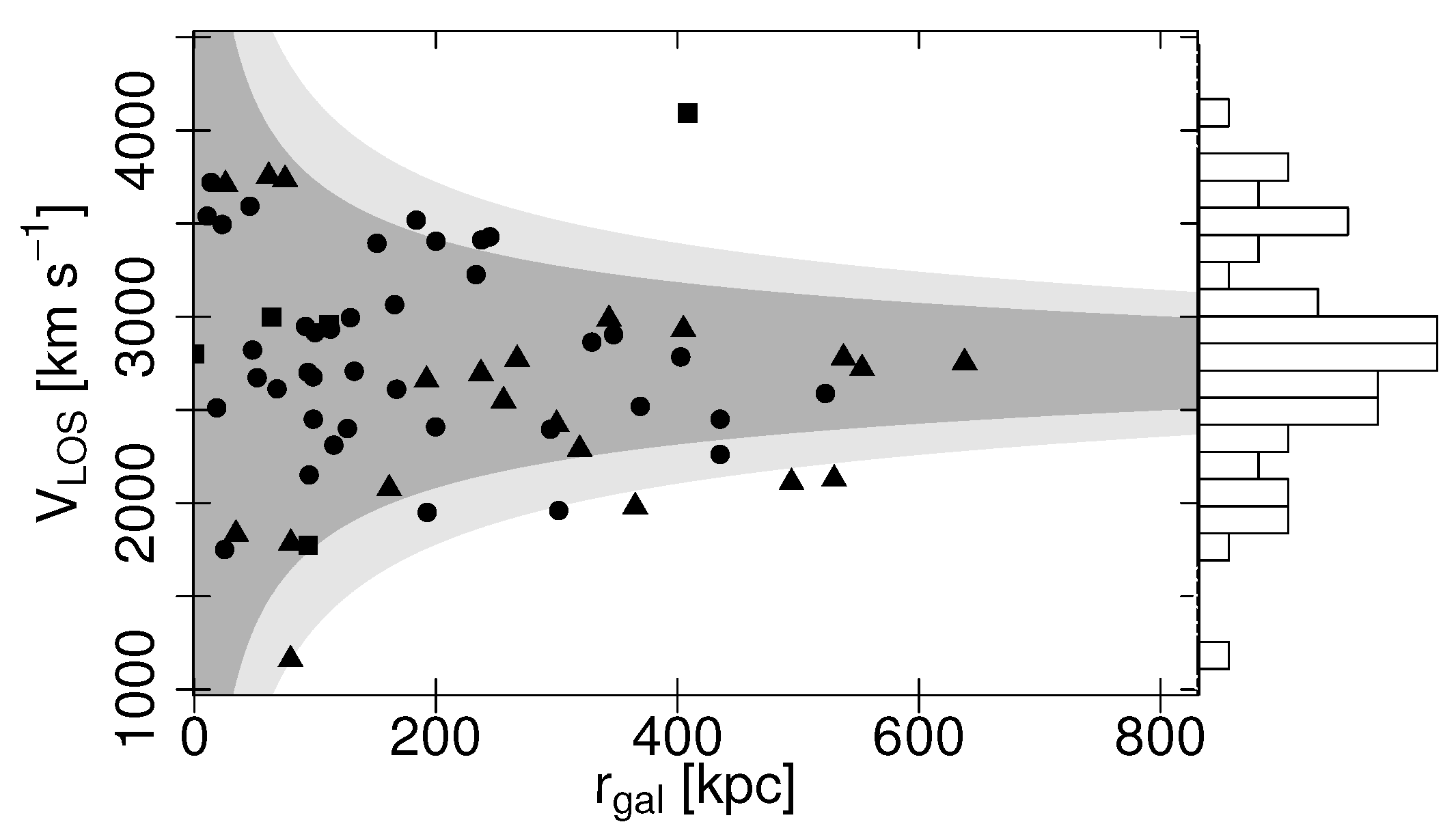
2.3. Other Kinematical Sources
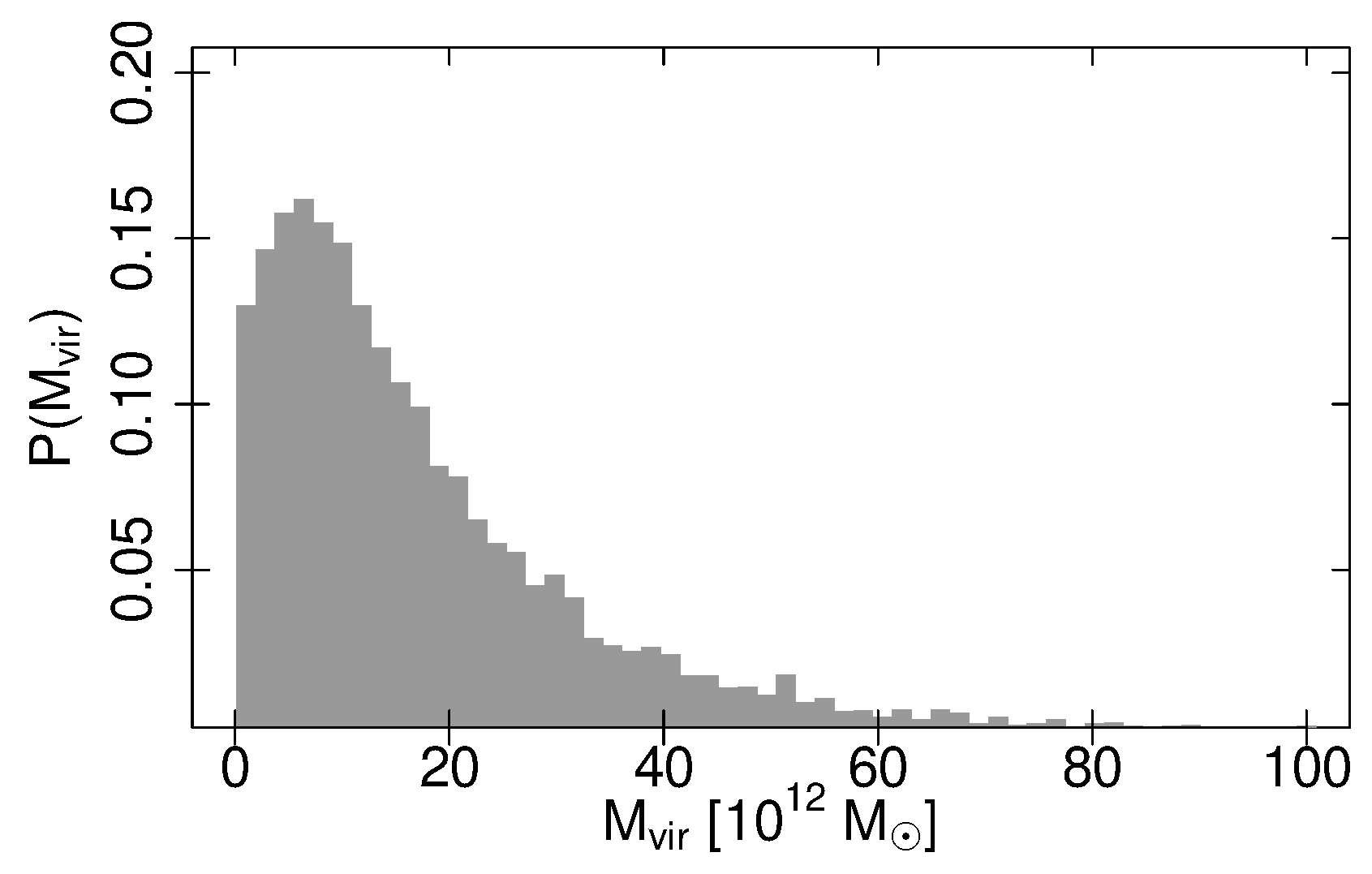
2.4. Dark Matter Haloes from a Numerical Simulation
2.5. Dynamic Modelling
2.5.1. Spherical Jeans Analysis
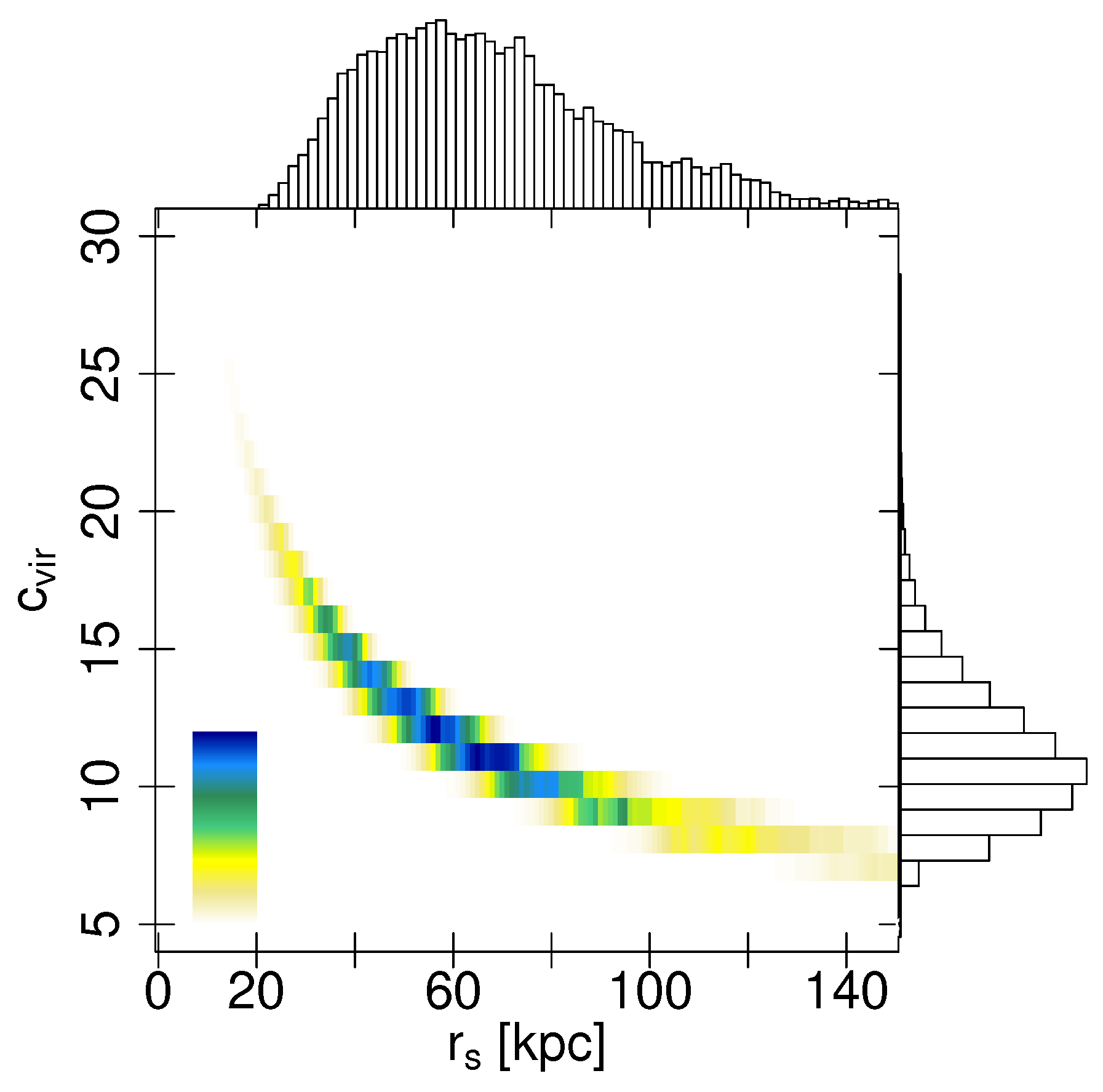
2.5.2. Bayesian Treatment and Prior Distribution
3. Results
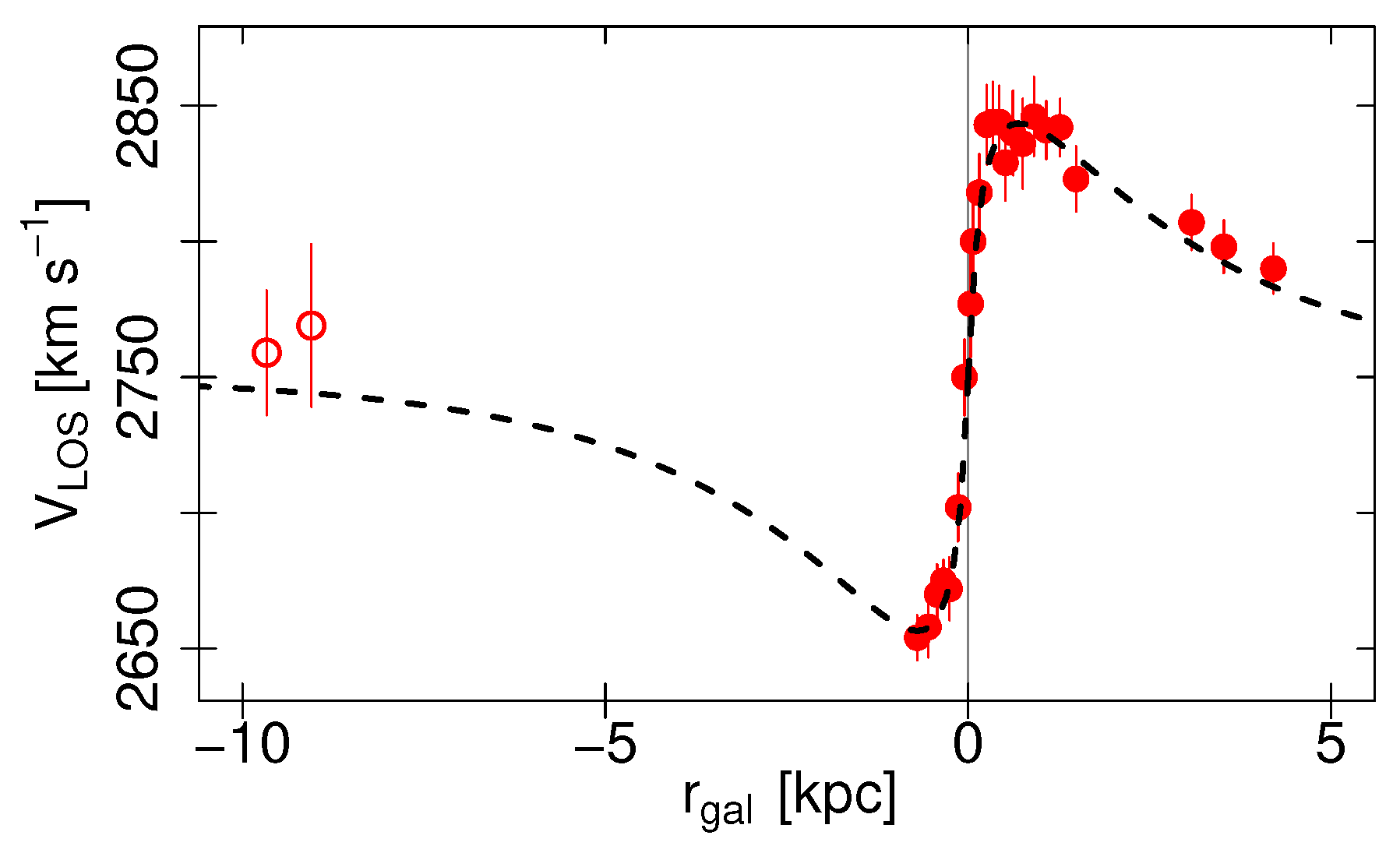
3.1. Kinematics of the Stellar Population in NGC 3268
3.2. Stellar Population Synthesis
3.3. Kinematical Fitting of the Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Surface Brightness Profile of NGC 3268
| PA | |||
|---|---|---|---|
| (arcsec) | (mag arcsec−2) | (deg) | |
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − | ||
| − | − |
References
- Bond, J.R.; Kofman, L.; Pogosyan, D. How filaments of galaxies are woven into the cosmic web. Nature 1996, 380, 603–606. [Google Scholar] [CrossRef]
- Oser, L.; Ostriker, J.P.; Naab, T.; Johansson, P.H.; Burkert, A. The Two Phases of Galaxy Formation. Astrophys. J. 2010, 725, 2312–2323. [Google Scholar] [CrossRef]
- Forbes, D.A.; Spitler, L.R.; Strader, J.; Romanowsky, A.J.; Brodie, J.P.; Foster, C. Evidence for two phases of galaxy formation from radial trends in the globular cluster system of NGC 1407. Mon. Not. R. Astron. Soc. 2011, 413, 2943–2949. [Google Scholar] [CrossRef]
- Nanayakkara, T.; Glazebrook, K.; Schreiber, C.; Chittenden, H.; Brammer, G.; Esdaile, J.; Jacobs, C.; Kacprzak, G.G.; Kawinwanichakij, L.; Kimmig, L.C.; et al. The Formation Histories of Massive and Quiescent Galaxies in the 3 < z < 4.5 Universe. Astrophys. J. 2025, 981, 78. [Google Scholar] [CrossRef]
- Damjanov, I.; McCarthy, P.J.; Abraham, R.G.; Glazebrook, K.; Yan, H.; Mentuch, E.; Le Borgne, D.; Savaglio, S.; Crampton, D.; Murowinski, R.; et al. Red Nuggets at z ~1.5: Compact Passive Galaxies and the Formation of the Kormendy Relation. Astrophys. J. 2009, 695, 101–115. [Google Scholar] [CrossRef]
- van Dokkum, P.G.; Whitaker, K.E.; Brammer, G.; Franx, M.; Kriek, M.; Labbé, I.; Marchesini, D.; Quadri, R.; Bezanson, R.; Illingworth, G.D.; et al. The Growth of Massive Galaxies Since z = 2. Astrophys. J. 2010, 709, 1018–1041. [Google Scholar] [CrossRef]
- Schawinski, K.; Urry, C.M.; Simmons, B.D.; Fortson, L.; Kaviraj, S.; Keel, W.C.; Lintott, C.J.; Masters, K.L.; Nichol, R.C.; Sarzi, M.; et al. The green valley is a red herring: Galaxy Zoo reveals two evolutionary pathways towards quenching of star formation in early- and late-type galaxies. Mon. Not. R. Astron. Soc. 2014, 440, 889–907. [Google Scholar] [CrossRef]
- Pulsoni, C.; Gerhard, O.; Arnaboldi, M.; Pillepich, A.; Rodriguez-Gomez, V.; Nelson, D.; Hernquist, L.; Springel, V. The stellar halos of ETGs in the IllustrisTNG simulations. II. Accretion, merger history, and dark halo connection. Astron. Astrophys. 2021, 647, A95. [Google Scholar] [CrossRef]
- Baldry, I.K.; Balogh, M.L.; Bower, R.G.; Glazebrook, K.; Nichol, R.C.; Bamford, S.P.; Budavari, T. Galaxy bimodality versus stellar mass and environment. Mon. Not. R. Astron. Soc. 2006, 373, 469–483. [Google Scholar] [CrossRef]
- Bahé, Y.M.; McCarthy, I.G.; Balogh, M.L.; Font, A.S. Why does the environmental influence on group and cluster galaxies extend beyond the virial radius? Mon. Not. R. Astron. Soc. 2013, 430, 3017–3031. [Google Scholar] [CrossRef]
- Lacerna, I.; Rodriguez, F.; Montero-Dorta, A.D.; O’Mill, A.L.; Cora, S.A.; Artale, M.C.; Ruiz, A.N.; Hough, T.; Vega-Martínez, C.A. On the environmental influence of groups and clusters of galaxies beyond the virial radius: Galactic conformity at few Mpc scales. Mon. Not. R. Astron. Soc. 2022, 513, 2271–2284. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics - Implications for galaxies. Astrophys. J. 1983, 270, 371–383. [Google Scholar] [CrossRef]
- Hodson, A.O.; Zhao, H. Generalizing MOND to explain the missing mass in galaxy clusters. Astron. Astrophys. 2017, 598, A127. [Google Scholar] [CrossRef]
- Moffat, J.W.; Rahvar, S. The MOG weak field approximation and observational test of galaxy rotation curves. Mon. Not. R. Astron. Soc. 2013, 436, 1439–1451. [Google Scholar] [CrossRef]
- Napolitano, N.R.; Romanowsky, A.J.; Capaccioli, M.; Douglas, N.G.; Arnaboldi, M.; Coccato, L.; Gerhard, O.; Kuijken, K.; Merrifield, M.R.; Bamford, S.P.; et al. The PN.S Elliptical Galaxy Survey: A standard ΛCDM halo around NGC 4374? Mon. Not. R. Astron. Soc. 2011, 411, 2035–2053. [Google Scholar] [CrossRef]
- Schuberth, Y.; Richtler, T.; Hilker, M.; Salinas, R.; Dirsch, B.; Larsen, S.S. Dynamics of the NGC 4636 globular cluster system. II. Improved constraints from a large sample of globular cluster velocities. Astron. Astrophys. 2012, 544, A115. [Google Scholar] [CrossRef]
- Longobardi, A.; Peng, E.W.; Côté, P.; Mihos, J.C.; Ferrarese, L.; Puzia, T.H.; Lançon, A.; Zhang, H.X.; Muñoz, R.P.; Blakeslee, J.P.; et al. The Next Generation Virgo Cluster Survey (NGVS). XXXI. The Kinematics of Intracluster Globular Clusters in the Core of the Virgo Cluster. Astrophys. J. 2018, 864, 36. [Google Scholar] [CrossRef]
- Hilker, M.; Richtler, T.; Barbosa, C.E.; Arnaboldi, M.; Coccato, L.; Mendes de Oliveira, C. The Hydra I cluster core. II. Kinematic complexity in a rising velocity dispersion profile around the cD galaxy NGC 3311. Astron. Astrophys. 2018, 619, A70. [Google Scholar] [CrossRef]
- Harris, W.E.; Harris, G.L.; Hudson, M.J. Dark Matter Halos in Galaxies and Globular Cluster Populations. II. Metallicity and Morphology. Astrophys. J. 2015, 806, 36. [Google Scholar] [CrossRef]
- Tully, R.B.; Courtois, H.M.; Dolphin, A.E.; Fisher, J.R.; Héraudeau, P.; Jacobs, B.A.; Karachentsev, I.D.; Makarov, D.; Makarova, L.; Mitronova, S.; et al. Cosmicflows-2: The Data. Astron. J. 2013, 146, 86. [Google Scholar] [CrossRef]
- Wong, K.W.; Irwin, J.A.; Wik, D.R.; Sun, M.; Sarazin, C.L.; Fujita, Y.; Reiprich, T.H. Suzaku X-ray Observations of the Nearest Non-Cool Core Cluster, Antlia: Dynamically Young but with Remarkably Relaxed Outskirts. Astron. J. 2016, 829, 49. [Google Scholar] [CrossRef]
- Gargiulo, I.D.; García, F.; Combi, J.A.; Caso, J.P.; Bassino, L.P. XMM-Newton observations of NGC 3268 in the Antlia Galaxy Cluster: Characterization of a hidden group of galaxies at z ≈ 0.41. Mon. Not. R. Astron. Soc. 2018, 479, 240–250. [Google Scholar] [CrossRef]
- Hopp, U.; Materne, J. The Antlia cluster of galaxies and its environment: The Hydra I-Centaurus supercluster. Astron. Astrophys. Suppl. Ser. 1985, 61, 93–106. [Google Scholar]
- Ferguson, H.C.; Sandage, A. Population Studies in Groups and Clusters of Galaxies. III. A Catalog of Galaxies in Five Nearby Galaxies. Astron. J. 1990, 100, 1–31. [Google Scholar] [CrossRef]
- Smith Castelli, A.V.; Bassino, L.P.; Richtler, T.; Cellone, S.A.; Aruta, C.; Infante, L. Galaxy populations in the Antlia cluster—I. Photometric properties of early-type galaxies. Mon. Not. R. Astron. Soc. 2008, 386, 2311–2322. [Google Scholar] [CrossRef]
- Smith Castelli, A.V.; Cellone, S.A.; Faifer, F.R.; Bassino, L.P.; Richtler, T.; Romero, G.A.; Calderón, J.P.; Caso, J.P. Galaxy populations in the Antlia cluster—III. Properties of faint early-type galaxies. Mon. Not. R. Astron. Soc. 2012, 419, 2472–2488. [Google Scholar] [CrossRef]
- Calderón, J.P.; Bassino, L.P.; Cellone, S.A.; Richtler, T.; Caso, J.P.; Gómez, M. Early-type galaxies in the Antlia Cluster: A deep look into scaling relations. Mon. Not. R. Astron. Soc. 2015, 451, 791–803. [Google Scholar] [CrossRef]
- Calderón, J.P.; Bassino, L.P.; Cellone, S.A.; Gómez, M. Early-type galaxies in the Antlia cluster: Catalogue and isophotal analysis. Mon. Not. R. Astron. Soc. 2018, 477, 1760–1771. [Google Scholar] [CrossRef]
- Calderón, J.P.; Bassino, L.P.; Cellone, S.A.; Gómez, M.; Caso, J.P. Early-type galaxies in the Antlia cluster: Global properties. Mon. Not. R. Astron. Soc. 2020, 497, 1791–1806. [Google Scholar] [CrossRef]
- Smith Castelli, A.V.; Faifer, F.R.; Richtler, T.; Bassino, L.P. Galaxy populations in the Antlia cluster—II. Compact elliptical galaxy candidates. Mon. Not. R. Astron. Soc. 2008, 391, 685–699. [Google Scholar] [CrossRef]
- Caso, J.P.; Vega Neme, L.; De Bórtoli, B.J.; Bassino, L.P.; Richtler, T.; Smith Castelli, A. Compact ellipticals in the Antlia cluster of galaxies. Astron. Astrophys. 2024, 691, A307. [Google Scholar] [CrossRef]
- Dirsch, B.; Richtler, T.; Bassino, L.P. The globular cluster systems of NGC 3258 and NGC 3268 in the Antlia cluster. Astron. Astrophys. 2003, 408, 929–939. [Google Scholar] [CrossRef]
- Bassino, L.P.; Richtler, T.; Dirsch, B. VLT photometry in the Antlia cluster: The giant ellipticals NGC3258 and NGC3268 and their globular cluster systems. Mon. Not. R. Astron. Soc. 2008, 386, 1145–1156. [Google Scholar] [CrossRef]
- Caso, J.P.; Bassino, L.P.; Gómez, M. Globular cluster systems as tracers of the evolutionary history in NGC 3258 and NGC 3268. Mon. Not. R. Astron. Soc. 2017, 470, 3227–3238. [Google Scholar] [CrossRef]
- Schlafly, E.F.; Finkbeiner, D.P. Measuring Reddening with Sloan Digital Sky Survey Stellar Spectra and Recalibrating SFD. Astrophys. J. 2011, 737, 103. [Google Scholar] [CrossRef]
- Huang, S.; Ho, L.C.; Peng, C.Y.; Li, Z.Y.; Barth, A.J. The Carnegie-Irvine Galaxy Survey. III. The Three-component Structure of Nearby Elliptical Galaxies. Astrophys. J. 2013, 766, 47. [Google Scholar] [CrossRef]
- Caso, J.P.; Bassino, L.P.; Richtler, T.; Smith Castelli, A.V.; Faifer, F.R. Ultracompact dwarfs around NGC 3258 in the Antlia cluster. Mon. Not. R. Astron. Soc. 2013, 430, 1088–1101. [Google Scholar] [CrossRef]
- Caso, J.P.; Bassino, L.P.; Richtler, T.; Calderón, J.P.; Smith Castelli, A.V. Ultracompact dwarfs around NGC 3268. Mon. Not. R. Astron. Soc. 2014, 442, 891–899. [Google Scholar] [CrossRef]
- Norris, M.A.; Sharples, R.M.; Bridges, T.; Gebhardt, K.; Forbes, D.A.; Proctor, R.; Faifer, F.R.; Forte, J.C.; Beasley, M.A.; Zepf, S.E.; et al. Gemini/GMOS spectroscopy of the spheroid and globular cluster system of NGC 3923. Mon. Not. R. Astron. Soc. 2008, 385, 40–52. [Google Scholar] [CrossRef]
- Lane, R.R.; Salinas, R.; Richtler, T. Dark matter deprivation in the field elliptical galaxy NGC 7507. Astrophys. J. 2015, 574, A93. [Google Scholar] [CrossRef]
- Cappellari, M.; Emsellem, E. Parametric Recovery of Line-of-Sight Velocity Distributions from Absorption-Line Spectra of Galaxies via Penalized Likelihood. Publ. Astron. Soc. Pac. 2004, 116, 138–147. [Google Scholar] [CrossRef]
- Cappellari, M. Improving the full spectrum fitting method: Accurate convolution with Gauss-Hermite functions. Mon. Not. R. Astron. Soc. 2017, 466, 798–811. [Google Scholar] [CrossRef]
- Cappellari, M. Full spectrum fitting with photometry in PPXF: Stellar population versus dynamical masses, non-parametric star formation history and metallicity for 3200 LEGA-C galaxies at redshift z ≈ 0.8. Mon. Not. R. Astron. Soc. 2023, 526, 3273–3300. [Google Scholar] [CrossRef]
- Vazdekis, A.; Sánchez-Blázquez, P.; Falcón-Barroso, J.; Cenarro, A.J.; Beasley, M.A.; Cardiel, N.; Gorgas, J.; Peletier, R.F. Evolutionary stellar population synthesis with MILES - I. The base models and a new line index system. Mon. Not. R. Astron. Soc. 2010, 404, 1639–1671. [Google Scholar] [CrossRef]
- Vazdekis, A.; Koleva, M.; Ricciardelli, E.; Röck, B.; Falcón-Barroso, J. UV-extended E-MILES stellar population models: Young components in massive early-type galaxies. Mon. Not. R. Astron. Soc. 2016, 463, 3409–3436. [Google Scholar] [CrossRef]
- Joanes, D.N.; Gill, C.A. Comparing measures of sample skewness and kurtosis. J. R. Stat. Soc. Ser. D (The Stat.) 1998, 47, 183–189. [Google Scholar] [CrossRef]
- Lim, S.; Peng, E.W.; Côté, P.; Ferrarese, L.; Roediger, J.C.; Liu, C.; Spengler, C.; Sola, E.; Duc, P.A.; Sales, L.V.; et al. The Next Generation Virgo Cluster Survey (NGVS). XXVII. The Size and Structure of Globular Cluster Systems and Their Connection to Dark Matter Halos. Astrophys. J. 2024, 966, 168. [Google Scholar] [CrossRef]
- Klypin, A.; Yepes, G.; Gottlöber, S.; Prada, F.; Heß, S. MultiDark simulations: The story of dark matter halo concentrations and density profiles. Mon. Not. R. Astron. Soc. 2016, 457, 4340–4359. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [Planck Collaboration] Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar] [CrossRef]
- Behroozi, P.S.; Wechsler, R.H.; Wu, H.Y. The ROCKSTAR Phase-space Temporal Halo Finder and the Velocity Offsets of Cluster Cores. Astrophys. J. 2013, 762, 109. [Google Scholar] [CrossRef]
- Vale, A.; Ostriker, J.P. The non-parametric model for linking galaxy luminosity with halo/subhalo mass. Mon. Not. R. Astron. Soc. 2006, 371, 1173–1187. [Google Scholar] [CrossRef]
- Conroy, C.; Wechsler, R.H.; Kravtsov, A.V. Modeling Luminosity-dependent Galaxy Clustering through Cosmic Time. Astrophys. J. 2006, 647, 201–214. [Google Scholar] [CrossRef]
- Caso, J.P. The mass profile of NGC 3377 from a Bayesian approach. Mon. Not. R. Astron. Soc. 2022, 511, 5314–5327. [Google Scholar] [CrossRef]
- Lan, T.W.; Ménard, B.; Mo, H. The galaxy luminosity function in groups and clusters: The faint-end upturn and the connection to the field luminosity function. Mon. Not. R. Astron. Soc. 2016, 459, 3998–4019. [Google Scholar] [CrossRef]
- Girelli, G.; Pozzetti, L.; Bolzonella, M.; Giocoli, C.; Marulli, F.; Baldi, M. The stellar-to-halo mass relation over the past 12 Gyr. I. Standard ΛCDM model. Astron. Astrophys. 2020, 634, A135. [Google Scholar] [CrossRef]
- McNaught-Roberts, T.; Norberg, P.; Baugh, C.; Lacey, C.; Loveday, J.; Peacock, J.; Baldry, I.; Bland-Hawthorn, J.; Brough, S.; Driver, S.P.; et al. Galaxy And Mass Assembly (GAMA): The dependence of the galaxy luminosity function on environment, redshift and colour. Mon. Not. R. Astron. Soc. 2014, 445, 2125–2145. [Google Scholar] [CrossRef]
- Łokas, E.L. Dark matter distribution in dwarf spheroidal galaxies. Mon. Not. R. Astron. Soc. 2002, 333, 697–708. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Richardson, T.; Fairbairn, M. Analytical solutions to the mass-anisotropy degeneracy with higher order Jeans analysis: A general method. Mon. Not. R. Astron. Soc. 2013, 432, 3361–3380. [Google Scholar] [CrossRef]
- Mamon, G.A.; Łokas, E.L. Dark matter in elliptical galaxies—II. Estimating the mass within the virial radius. Mon. Not. R. Astron. Soc. 2005, 363, 705–722. [Google Scholar] [CrossRef]
- van der Marel, R.P.; Franx, M. A New Method for the Identification of Non-Gaussian Line Profiles in Elliptical Galaxies. Astrophys. J. 1993, 407, 525. [Google Scholar] [CrossRef]
- Emsellem, E.; Cappellari, M.; Krajnović, D.; van de Ven, G.; Bacon, R.; Bureau, M.; Davies, R.L.; de Zeeuw, P.T.; Falcón-Barroso, J.; Kuntschner, H.; et al. The SAURON project—IX. A kinematic classification for early-type galaxies. Mon. Not. R. Astron. Soc. 2007, 379, 401–417. [Google Scholar] [CrossRef]
- Coccato, L.; Gerhard, O.; Arnaboldi, M.; Das, P.; Douglas, N.G.; Kuijken, K.; Merrifield, M.R.; Napolitano, N.R.; Noordermeer, E.; Romanowsky, A.J.; et al. Kinematic properties of early-type galaxy haloes using planetary nebulae*. Mon. Not. R. Astron. Soc. 2009, 394, 1249–1283. [Google Scholar] [CrossRef]
- Salinas, R.; Richtler, T.; Bassino, L.P.; Romanowsky, A.J.; Schuberth, Y. Kinematic properties of the field elliptical NGC 7507. Astron. Astrophys. 2012, 538, A87. [Google Scholar] [CrossRef]
- Shetty, S.; Cappellari, M. Salpeter Normalization of the Stellar Initial Mass Function for Massive Galaxies at z ~1. Astrophys. J. Lett. 2014, 786, L10. [Google Scholar] [CrossRef]
- Li, H.; Ge, J.; Mao, S.; Cappellari, M.; Long, R.J.; Li, R.; Emsellem, E.; Dutton, A.A.; Li, C.; Bundy, K.; et al. SDSS-IV MaNGA: Variation of the Stellar Initial Mass Function in Spiral and Early-type Galaxies. Astrophys. J. 2017, 838, 77. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Dumont, A.; Seth, A.C.; Strader, J.; Sand, D.J.; Voggel, K.; Hughes, A.K.; Crnojević, D.; Forbes, D.A.; Mateo, M.; Pearson, S. Investigating the dark matter halo of NGC 5128 using a discrete dynamical model. Astron. Astrophys. 2024, 685, A132. [Google Scholar] [CrossRef]
- Grillo, C. On the Average Density Profile of Dark-matter Halos in the Inner Regions of Massive Early-type Galaxies. Astrophys. J. Lett. 2012, 747, L15. [Google Scholar] [CrossRef]
- Veršič, T.; Thater, S.; van de Ven, G.; Watkins, L.L.; Jethwa, P.; Leaman, R.; Zocchi, A. Total mass slopes and enclosed mass constrained by globular cluster system dynamics. Astron. Astrophys. 2024, 681, A46. [Google Scholar] [CrossRef]
- Bullock, J.S.; Kolatt, T.S.; Sigad, Y.; Somerville, R.S.; Kravtsov, A.V.; Klypin, A.A.; Primack, J.R.; Dekel, A. Profiles of dark haloes: Evolution, scatter and environment. Mon. Not. R. Astron. Soc. 2001, 321, 559–575. [Google Scholar] [CrossRef]
- Bryan, G.L.; Norman, M.L. Statistical Properties of X-Ray Clusters: Analytic and Numerical Comparisons. Astrophys. J. 1998, 495, 80–99. [Google Scholar] [CrossRef]
- Cappellari, M.; Emsellem, E.; Bacon, R.; Bureau, M.; Davies, R.L.; De Zeeuw, P.T.; Falcón-Barroso, J.; Krajnović, D.; Kuntschner, H.; McDermid, R.M.; et al. The SAURON project—X. The orbital anisotropy of elliptical and lenticular galaxies: Revisiting the (V/σ, ε) diagram with integral-field stellar kinematics. Mon. Not. R. Astron. Soc. 2007, 379, 418–444. [Google Scholar] [CrossRef]
- Caso, J.P.; Richtler, T. Deconstructing the Antlia cluster core. Astron. Astrophys. 2015, 584, A125. [Google Scholar] [CrossRef]
- Praton, E.A.; Schneider, S.E. Infall-related Observational Effects around Clusters: Large-Scale Structure, Transverse Motions, and Redshift-Space Artifacts. Astrophys. J. 1994, 422, 46. [Google Scholar] [CrossRef]
- Ramos-Almendares, F.; Sales, L.V.; Abadi, M.G.; Doppel, J.E.; Muriel, H.; Peng, E.W. Simulating the spatial distribution and kinematics of globular clusters within galaxy clusters in illustris. Mon. Not. R. Astron. Soc. 2020, 493, 5357–5368. [Google Scholar] [CrossRef]
- Forbes, D.A.; Alabi, A.; Romanowsky, A.J.; Brodie, J.P.; Strader, J.; Usher, C.; Pota, V. The SLUGGS survey: Globular clusters and the dark matter content of early-type galaxies. Mon. Not. R. Astron. Soc. 2016, 458, L44–L48. [Google Scholar] [CrossRef]
- Hudson, M.J.; Harris, G.L.; Harris, W.E. Dark Matter Halos in Galaxies and Globular Cluster Populations. Astrophys. J. 2014, 787, L5. [Google Scholar] [CrossRef]
- Harris, W.E.; Blakeslee, J.P.; Harris, G.L.H. Galactic Dark Matter Halos and Globular Cluster Populations. III. Extension to Extreme Environments. Astrophys. J. 2017, 836, 67. [Google Scholar] [CrossRef]
- Harris, W.E.; Morningstar, W.; Gnedin, O.Y.; O’Halloran, H.; Blakeslee, J.P.; Whitmore, B.C.; Côté, P.; Geisler, D.; Peng, E.W.; Bailin, J.; et al. Globular Cluster Systems in Brightest Cluster Galaxies: A Near-universal Luminosity Function? Astrophys. J. 2014, 797, 128. [Google Scholar] [CrossRef]
- Nakazawa, K.; Makishima, K.; Fukazawa, Y.; Tamura, T. ASCA Observations of a Near-by Cluster in Antlia. Publ. Astron. Soc. Jpn. 2000, 52, 623–630. [Google Scholar] [CrossRef]
- Sun, M.; Voit, G.M.; Donahue, M.; Jones, C.; Forman, W.; Vikhlinin, A. Chandra Studies of the X-Ray Gas Properties of Galaxy Groups. Astrophys. J. 2009, 693, 1142–1172. [Google Scholar] [CrossRef]
- Lacerna, I.; Hernández-Toledo, H.M.; Avila-Reese, V.; Abonza-Sane, J.; del Olmo, A. Isolated elliptical galaxies in the local Universe. Astron. Astrophys. 2016, 588, A79. [Google Scholar] [CrossRef]
- Kinyumu, M.K.; Kimani, N.; Nyenge, R.; Obonyo, W. Properties of isolated galaxies in the Digital Survey Isolated Galaxies (DSIG) catalogue within a redshift range (0.005 < z < 0.080). Mon. Not. R. Astron. Soc. 2024, 527, 1368–1380. [Google Scholar] [CrossRef]
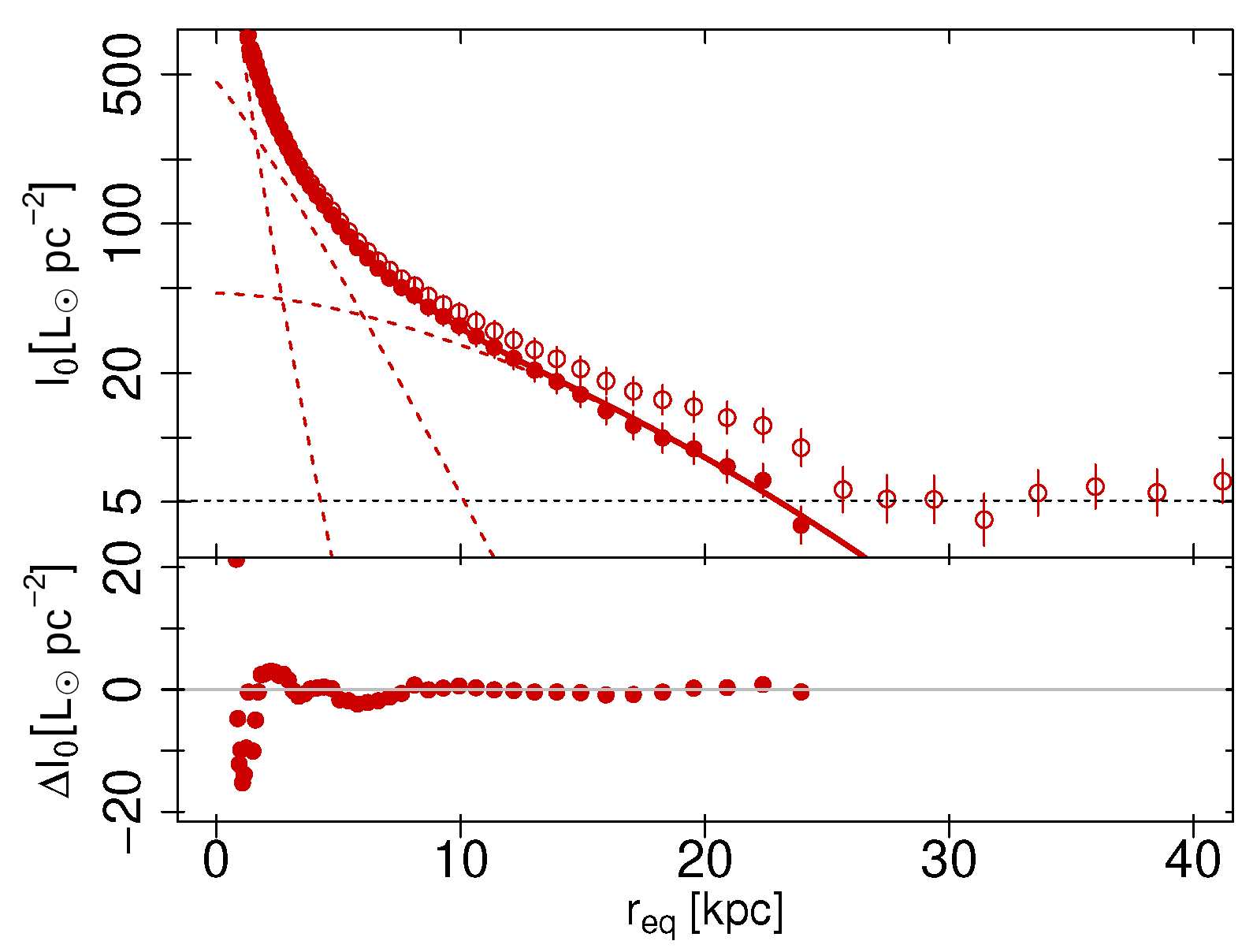
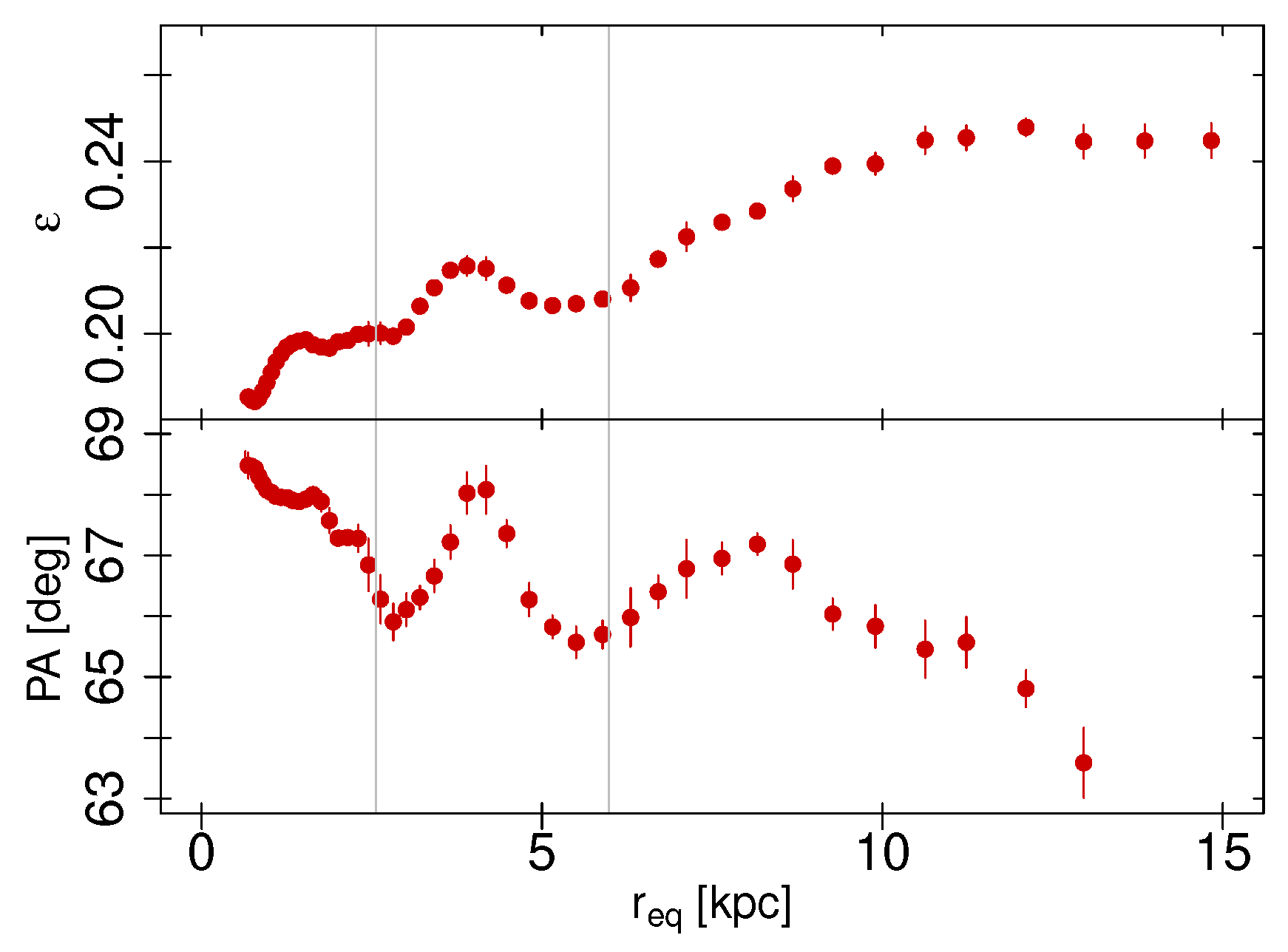



| n | |||
|---|---|---|---|
| Inner component | 60,200 ± 13,000 | ||
| Intermediate component | |||
| Outer component | 10,600 ± 1500 |
| (arcsec) | (arcsec) | (km s−1) | (km s−1) |
|---|---|---|---|
| −4.1 | 0.7 | ||
| −3.2 | 0.7 | ||
| −2.5 | 0.5 | ||
| −2.0 | 0.5 | ||
| −1.5 | 0.5 | ||
| −0.8 | 0.5 | ||
| −0.3 | 0.5 | ||
| 0.2 | 0.5 | ||
| 0.9 | 0.5 | ||
| 1.5 | 0.5 | ||
| 2.0 | 0.5 | ||
| 2.5 | 0.5 | ||
| 3.0 | 0.5 | ||
| 3.6 | 0.6 | ||
| 4.4 | 0.9 | ||
| 5.3 | 1.0 | ||
| 6.3 | 1.0 | ||
| 7.4 | 1.1 | ||
| 8.7 | 1.2 | ||
| 18.0 | 2.0 | ||
| 20.0 | 2.0 | ||
| 24.6 | 2.3 | ||
| 39.0 | 6.0 | ||
| 47.5 | 4.5 | ||
| 80.0 | 5.0 | ||
| 37.0 | 6.0 | ||
| 41.0 | 5.0 | ||
| 61.0 | 5.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caso, J.P.; De Bórtoli, B.J.; Richtler, T. The Mass Profile of NGC 3268 from Its Stellar Kinematics. Universe 2025, 11, 344. https://doi.org/10.3390/universe11100344
Caso JP, De Bórtoli BJ, Richtler T. The Mass Profile of NGC 3268 from Its Stellar Kinematics. Universe. 2025; 11(10):344. https://doi.org/10.3390/universe11100344
Chicago/Turabian StyleCaso, Juan Pablo, Bruno Javier De Bórtoli, and Tom Richtler. 2025. "The Mass Profile of NGC 3268 from Its Stellar Kinematics" Universe 11, no. 10: 344. https://doi.org/10.3390/universe11100344
APA StyleCaso, J. P., De Bórtoli, B. J., & Richtler, T. (2025). The Mass Profile of NGC 3268 from Its Stellar Kinematics. Universe, 11(10), 344. https://doi.org/10.3390/universe11100344






