Linking Planetary Ephemeris Reference Frames to ICRF via Millisecond Pulsars
Abstract
1. Introduction
2. Data and Methods
2.1. Timing Data
2.2. VLBI Data
2.3. All Datasets
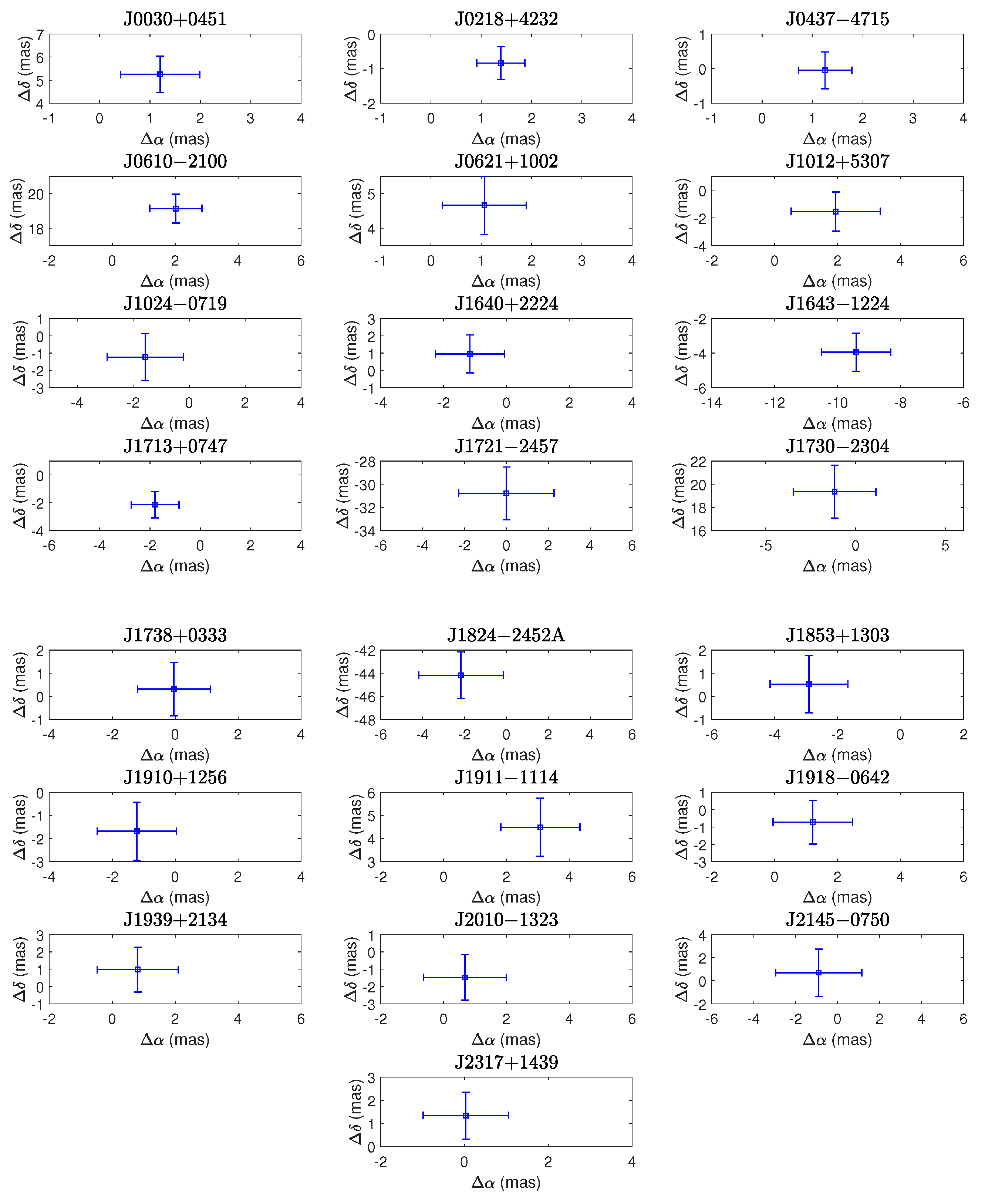
2.4. Method of the Frame-Tie Rotation
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Abbreviations
| BIPM | Bureau International des Poids et Mesures |
| CPTA | Chinese Pulsar Timing Array |
| CRF | Celestial Reference Frame |
| CRS | Celestial Reference System |
| DE | Development Ephemeris |
| DM | Dispersion measure |
| DR | data release |
| EOP | Earth Orientation Parameter |
| EPTA | European Pulsar Timing Array |
| EVN | European VLBI Network |
| FAST | Five-hundred-meter Aperture Spherical radio Telescope |
| GPS | Global Positioning System |
| GWs | gravitational waves |
| ICRF | International Celestial Reference Frame |
| IPTA | International Pulsar Timing Array |
| JPL | Jet Propulsion Laboratory |
| LBA | Long Baseline Array |
| mas | milliarcsecond |
| MJD | Modified Julian Date |
| MPTA | MeerKAT Pulsar Timing Array |
| MSP | Millisecond pulsar |
| NANOGrav | North American Nanohertz Observatory for Gravitational Waves |
| PPTA | Parkes Pulsar Timing Array |
| PTA | Pulsar Timing Array |
| SLR | Satellite Laser Ranging |
| SSB | solar system barycenter |
| TCB | barycentric coordinate time |
| TDB | barycentric dynamic time |
| ToAs | Pulse times of arrival |
| TT | Terrestrial Time |
| VLBA | Very Long Baseline Array |
| VLBI | Very Long Baseline Interferometry |
References
- Malkin, Z. Towards a robust estimation of orientation parameters between ICRF and Gaia celestial reference frames. Mon. Not. R. Astron. Soc. 2021, 506, 5540–5547. [Google Scholar] [CrossRef]
- Ma, C.; Feissel, M. Definition and Realization of the International Celestial Reference System by VLBI Astrometry of Extragalactic Objects. Astron. J. 1998, 116, 516. [Google Scholar] [CrossRef]
- Fey, A.L.; Gordon, D.; Jacobs, C.S.; Ma, C.; Gaume, R.A.; Arias, E.F.; Bianco, G.; Boboltz, D.A.; Böckmann, S.; Bolotin, S.; et al. The Second Realization of the International Celestial Reference Frame by Very Long Baseline Interferometry. Astron. J. 2015, 150, 58. [Google Scholar] [CrossRef]
- Charlot, P.; Jacobs, C.S.; Gordon, D.; Lambert, S.; de Witt, A.; Boehm, J.; Fey, A.L.; Heinkelmann, R.; Skurikhina, E.; Titov, O.; et al. The third realization of the International Celestial Reference Frame by very long baseline interferometry. Astron. Astrophys. 2020, 644, A159. [Google Scholar] [CrossRef]
- Folkner, W.M.; Charlot, P.; Finger, M.H.; Williams, J.G.; Sovers, O.J.; Newhall, X.; Standish, E.M., Jr. Determination of the extragalactic-planetary frame tie from joint analysis of radio interferometric and lunar laser ranging measurements. Astron. Astrophys. 1994, 287, 279–289. [Google Scholar]
- Folkner, W.M. Relativistic aspects of the JPL Planetary Ephemeris. Proc. Int. Astron. Union 2010, 261, 155–158. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H.; Park, R.S.; Kuchynka, P. The Planetary and Lunar Ephemerides DE430 and DE431. Interplanet. Netw. Prog. Rep. 2014, 42, 196. [Google Scholar]
- Park, R.S.; Folkner, W.M.; Williams, J.G.; Boggs, D.H. The JPL Planetary and Lunar Ephemerides DE440 and DE441. Astron. J. 2021, 161, 105. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H. The Planetary and Lunar Ephemeris DE 421. Interplanet. Netw. Prog. Rep. 2009, 42, 178. [Google Scholar]
- Pitjeva, E.; Pavlov, D.; Aksim, D.; Kan, M. Planetary and lunar ephemeris EPM2021 and its significance for Solar system research. Proc. Int. Astron. Union 2022, 364, 220–225. [Google Scholar] [CrossRef]
- Fienga, A.; Bigot, L.; Mary, D.; Deram, P.; Di Ruscio, A.; Bernus, L.; Gastineau, M.; Laskar, J. Evolution of INPOP planetary ephemerides and Bepi-Colombo simulations. Proc. Int. Astron. Union 2022, 364, 31–51. [Google Scholar] [CrossRef]
- Tomsick, J.A.; Coughenour, B.M.; Hare, J.; Krivonos, R.; Bodaghee, A.; Chaty, S.; Clavel, M.; Fornasini, F.M.; Rodriguez, J.; Shaw, A.W. Using Chandra Localizations and Gaia Distances and Proper Motions to Classify Hard X-Ray Sources Discovered by INTEGRAL. Astron. J. 2021, 914, 48. [Google Scholar] [CrossRef]
- Li, L. Preliminary Study on the Construction of Pulsar-Based Space-Time Reference Frame. Ph.D. Dissertation, University of Chinese Academy of Sciences, Beijing, China, 2016. [Google Scholar]
- Yang, P.; Huang, Y.; Li, P.J.; Wang, H.; Fan, M.; Liu, S.Y.; Shan, Q.; Qin, S.H.; Liu, Q.H. Orbit determination of China’s first mars probe Tianwen-1 during interplanetary cruise. Adv. Space Res. 2022, 69, 1060–1071. [Google Scholar] [CrossRef]
- Lindegren, L. The Gaia reference frame for bright sources examined using VLBI observations of radio stars. Astron. Astrophys. 2020, 633, A1. [Google Scholar] [CrossRef]
- Chatterjee, S.; Brisken, W.F.; Vlemmings, W.H.T.; Goss, W.M.; Lazio, T.J.W.; Cordes, J.M.; Thorsett, S.E.; Fomalont, E.B.; Lyne, A.G.; Kramer, M. Precision Astrometry with the Very Long Baseline Array: Parallaxes and Proper Motions for 14 Pulsars. Astron. J. 2009, 698, 250–265. [Google Scholar] [CrossRef]
- Ding, H.; Deller, A.T.; Stappers, B.W.; Lazio, T.J.W.; Kaplan, D.; Chatterjee, S.; Brisken, W.; Cordes, J.; Freire, P.C.C.; Fonseca, E.; et al. The MSPSRπ catalogue: VLBA astrometry of 18 millisecond pulsars. Mon. Not. R. Astron. Soc. 2023, 519, 4982–5007. [Google Scholar] [CrossRef]
- Edwards, R.T.; Hobbs, G.B.; Manchester, R.N. TEMPO2, a new pulsar timing package–II. The timing model and precision estimates. Mon. Not. R. Astron. Soc. 2006, 372, 1549–1574. [Google Scholar] [CrossRef]
- Hobbs, G.B.; Edwards, R.T.; Manchester, R.N. TEMPO2, a new pulsar-timing package–I. An overview. Mon. Not. R. Astron. Soc. 2006, 369, 655–672. [Google Scholar] [CrossRef]
- Wang, J.B.; Coles, W.A.; Hobbs, G.; Shannon, R.M.; Manchester, R.N.; Kerr, M.; Yuan, J.P.; Wang, N.; Bailes, M.; Bhat, N.D.R.; et al. Comparison of pulsar positions from timing and very long baseline astrometry. Mon. Not. R. Astron. Soc. 2017, 469, 425–434. [Google Scholar] [CrossRef]
- Liu, N.; Zhu, Z.; Antoniadis, J.; Liu, J.C.; Zhang, H.; Jiang, N. Comparison of dynamical and kinematic reference frames via pulsar positions from timing, Gaia, and interferometric astrometry. Astron. Astrophys. 2023, 670, A173. [Google Scholar] [CrossRef]
- Verbiest, J.P.W.; Lentati, L.; Hobbs, G.; van Haasteren, R.; Demorest, P.B.; Janssen, G.H.; Wang, J.B.; Desvignes, G.; Caballero, R.N.; Keith, M.J.; et al. The International Pulsar Timing Array: First data release. Mon. Not. R. Astron. Soc. 2016, 458, 1267–1288. [Google Scholar] [CrossRef]
- Perera, B.B.P.; DeCesar, M.E.; Demorest, P.B.; Kerr, M.; Lentati, L.; Nice, D.J.; Osłowski, S.; Ransom, S.M.; Keith, M.J.; Arzoumanian, Z.; et al. The International Pulsar Timing Array: Second data release. Mon. Not. R. Astron. Soc. 2019, 490, 4666–4687. [Google Scholar] [CrossRef]
- Miles, M.T.; Shannon, R.M.; Bailes, M.; Reardon, D.J.; Keith, M.J.; Cameron, A.D.; Parthasarathy, A.; Shamohammadi, M.; Spiewak, R.; van Straten, W.; et al. The MeerKAT Pulsar Timing Array: First data release. Mon. Not. R. Astron. Soc. 2023, 519, 3976–3991. [Google Scholar] [CrossRef]
- Shamohammadi, M.; Bailes, M.; Flynn, C.; Reardon, D.J.; Shannon, R.M.; Buchner, S.; Cameron, A.D.; Camilo, F.; Corongiu, A.; Geyer, M.; et al. MeerKAT Pulsar Timing Array parallaxes and proper motions. Mon. Not. R. Astron. Soc. 2024, 530, 287–306. [Google Scholar] [CrossRef]
- Deller, A.T.; Verbiest, J.P.W.; Tingay, S.J.; Balies, M. Extremely High Precision VLBI Astrometry of PSR J0437-4715 and Implications for Theories of Gravity. Astron. J. 2008, 685, L67–L70. [Google Scholar] [CrossRef]
- Deller, A.T.; Archibald, A.M.; Brisken, W.F.; Chatterjee, S.; Janssen, G.H.; Kaspi, V.M.; Lorimer, D.; Lyne, A.G.; McLaughlin, M.A.; Ransom, S.; et al. A Parallax Distance and Mass Estimate for the Transitional Millisecond Pulsar System J1023+0038. Astrophys. J. Lett. 2012, 756, L25. [Google Scholar] [CrossRef]
- Deller, A.T.; Vigeland, S.J.; Kaplan, D.L.; Goss, W.M.; Brisken, W.F.; Chatterjee, S.; Cordes, J.M.; Janssen, G.H.; Lazio, T.J.W.; Petrov, L.; et al. Microarcsecond VLBI Pulsar Astrometry with PSRπ. Two Binary Millisecond Pulsars with White Dwarf Companions. Astron. J. 2016, 828, 8. [Google Scholar] [CrossRef]
- Deller, A.T.; Goss, W.M.; Brisken, W.F.; Chatterjee, S.; Cordes, J.M.; Janssen, G.H.; Kovalev, Y.Y.; Lazio, T.J.W.; Petrov, L.; Stappers, B.W.; et al. Microarcsecond VLBI Pulsar Astrometry with PSRπ. Parallax Distances for 57 Pulsars. Astron. J. 2019, 875, 100. [Google Scholar] [CrossRef]
- Xu, H.; Chen, S.; Guo, Y.; Jiang, J.; Wang, B.; Xu, J.; Xue, Z.; Nicolas, C.R.; Yuan, J.; Xu, Y.; et al. Searching for the Nano-Hertz Stochastic Gravitational Wave Background with the Chinese Pulsar Timing Array Data Release I. Res. Astron. Astrophys. 2023, 23, 075024. [Google Scholar] [CrossRef]
- Bailes, M.; Barr, E.; Bhat, N.D.R.; Brink, J.; Buchner, S.; Burgay, M.; Camilo, F.; Champion, D.; Hessels, J.; Jameson, A.; et al. MeerTime—The MeerKAT Key Science Program on Pulsar Timing. In Proceedings of the MeerKAT Science: On the Pathway to the, SKA, Stellenbosch, South Africa, 25–27 May 2016; Volume 277, p. 11. [Google Scholar] [CrossRef]
- Dewdney, P.E.; Hall, P.J.; Schilizzi, R.T.; Lazio, T.J.W. The Square Kilometre Array. Proc. IEEE 2009, 97, 1482–1496. [Google Scholar] [CrossRef]
- Yan, Z.; Shen, Z.Q.; Yuan, J.P.; Wang, N.; Rottmann, H.; Alef, W. VLBI astrometry of two millisecond pulsars. Proc. Int. Astron. Union 2013, 291, 562–564. [Google Scholar] [CrossRef]
- Lorimer, D.R. Binary and Millisecond Pulsars. Living Rev. Relativ. 2008, 11, 8. [Google Scholar] [CrossRef] [PubMed]
- Champion, D.J.; Hobbs, G.B.; Manchester, R.N.; Edwards, R.T.; Backer, D.C.; Bailes, M.; Bhat, N.D.; Burke-Spolaor, S.; Coles, W.; Demorest, P.B.; et al. Measuring the Mass of Solar System Planets Using Pulsar Timing. Astrophys. J. Lett. 2010, 720, L201–L205. [Google Scholar] [CrossRef]
- Dai, J.P.; Han, W.; Wang, N. The Influence of Different Solar System Planetary Ephemerides on Pulsar Timing. Res. Astron. Astrophys. 2024, 24, 085008. [Google Scholar] [CrossRef]
- Chen, S.; Caballero, R.N.; Guo, Y.J.; Chalumeau, A.; Liu, K.; Shaifullah, G.; Lee, K.J.; Babak, S.; Desvignes, G.; Parthasarathy, A.; et al. Common-red-signal analysis with 24-yr high-precision timing of the European Pulsar Timing Array: Inferences in the stochastic gravitational-wave background search. Mon. Not. R. Astron. Soc. 2021, 508, 4970–4993. [Google Scholar] [CrossRef]
- Liu, N.; Zhu, Z.; Antoniadis, J.; Liu, J.C.; Zhang, H. Systematics of planetary ephemeris reference frames inferred from pulsar timing astrometry. Astron. Astrophys. 2023, 674, A187. [Google Scholar] [CrossRef]
- Du, Y.J.; Yang, J.; Campbell, R.M.; Janssen, G.; Stappers, B.; Chen, D. Very Long Baseline Interferometry Measured Proper Motion and Parallax of the γ-Ray Millisecond Pulsar PSR J0218+4232. Astrophys. J. Lett. 2014, 782, L38. [Google Scholar] [CrossRef]
- Ma, C.; Arias, E.F.; Bianco, G.; Boboltz, D.A.; Bolotin, S.L.; Charlot, P.; Engelhardt, G.; Fey, A.L.; Gaume, R.A.; Gontier, A.M.; et al. The Second Realization of the International Celestial Reference Frame by Very Long Baseline Interferometry. IERS Tech. Notes 2009, 35, 47. [Google Scholar]
- Kaplan, D.L.; Kupfer, T.; Nice, D.J.; Irrgang, A.; Heber, U.; Arzoumanian, Z.; Beklen, E.; Crowter, K.; DeCesar, M.E.; Demorest, P.B.; et al. PSR J1024-0719: A Millisecond Pulsar in an Unusual Long-period Orbit. Astron. J. 2016, 826, 86. [Google Scholar] [CrossRef]
- Zhou, D.K.; Wang, P.; Li, D.; Fang, J.H.; Miao, C.C.; Freire, P.C.C.; Zhang, L.; Zhang, D.D.; Chen, H.X.; Feng, Y.; et al. A discovery of two slow pulsars with FAST: “Ronin” from the globular cluster M15. Sci. China Phys. Mech. Astron. 2024, 67, 269512. [Google Scholar] [CrossRef]
- Reid, M.J.; Brunthaler, A.; Menten, K.M.; Sanna, A.; Xu, Y.; Li, J.J.; Wu, Y.; Hu, B.; Zheng, X.W.; Zhang, B.; et al. Techniques for Accurate Parallax Measurements for 6.7 GHz Methanol Masers. Astron. J. 2017, 154, 63. [Google Scholar] [CrossRef]
- Standish, E.M.; Fienga, A. Accuracy limit of modern ephemerides imposed by the uncertainties in asteroid masses. Astron. Astrophys. 2002, 384, 322–328. [Google Scholar] [CrossRef]
- Hobbs, G.; Guo, L.; Caballero, R.N.; Coles, W.; Lee, K.J.; Manchester, R.N.; Reardon, D.J.; Matsakis, D.; Tong, M.L.; Arzoumanian, Z.; et al. A pulsar-based time-scale from the International Pulsar Timing Array. Mon. Not. R. Astron. Soc. 2020, 491, 5951–5965. [Google Scholar] [CrossRef]
- Ding, H.; Deller, A.T.; Freire, P.C.; Petrov, L. A millisecond pulsar position determined to 0.2 mas precision with VLBI. Astron. Astrophys. 2024, 691, A47. [Google Scholar] [CrossRef]
- Rodin, A.; Sekido, M. Pulsar VLBI Observations. In Proceedings of the 6th EVN Sysposium, Bonn, Germany, 25–28 June 2002; p. 247. [Google Scholar]
- Rioja, M.J.; Dodson, R.; Orosz, G.; Imai, H.; Frey, S. MultiView High Precision VLBI Astrometry at Low Frequencies. Astron. J. 2017, 153, 105. [Google Scholar] [CrossRef]
- Yan, Z.; Shen, Z.Q.; Wu, Y.J.; Zhao, R.B.; Liu, J.; Huang, Z.P.; Wang, R.; Wang, X.W.; Liu, Q.H.; Li, B.; et al. Shanghai Tianma Radio Telescope and Its Role in Pulsar Astronomy. Universe 2024, 10, 195. [Google Scholar] [CrossRef]
- Yan, Z.; Shen, Z.Q.; Jiang, P.; Zhang, B.; Zhang, H.Y.; Cui, L.; Luo, J.T.; Chen, R.R.; Jiang, W.; Zhang, H.; et al. Pathfinding Pulsar Observations with the CVN Incorporating the FAST. Chin. Phys. Lett. 2024, 41, 117501. [Google Scholar] [CrossRef]
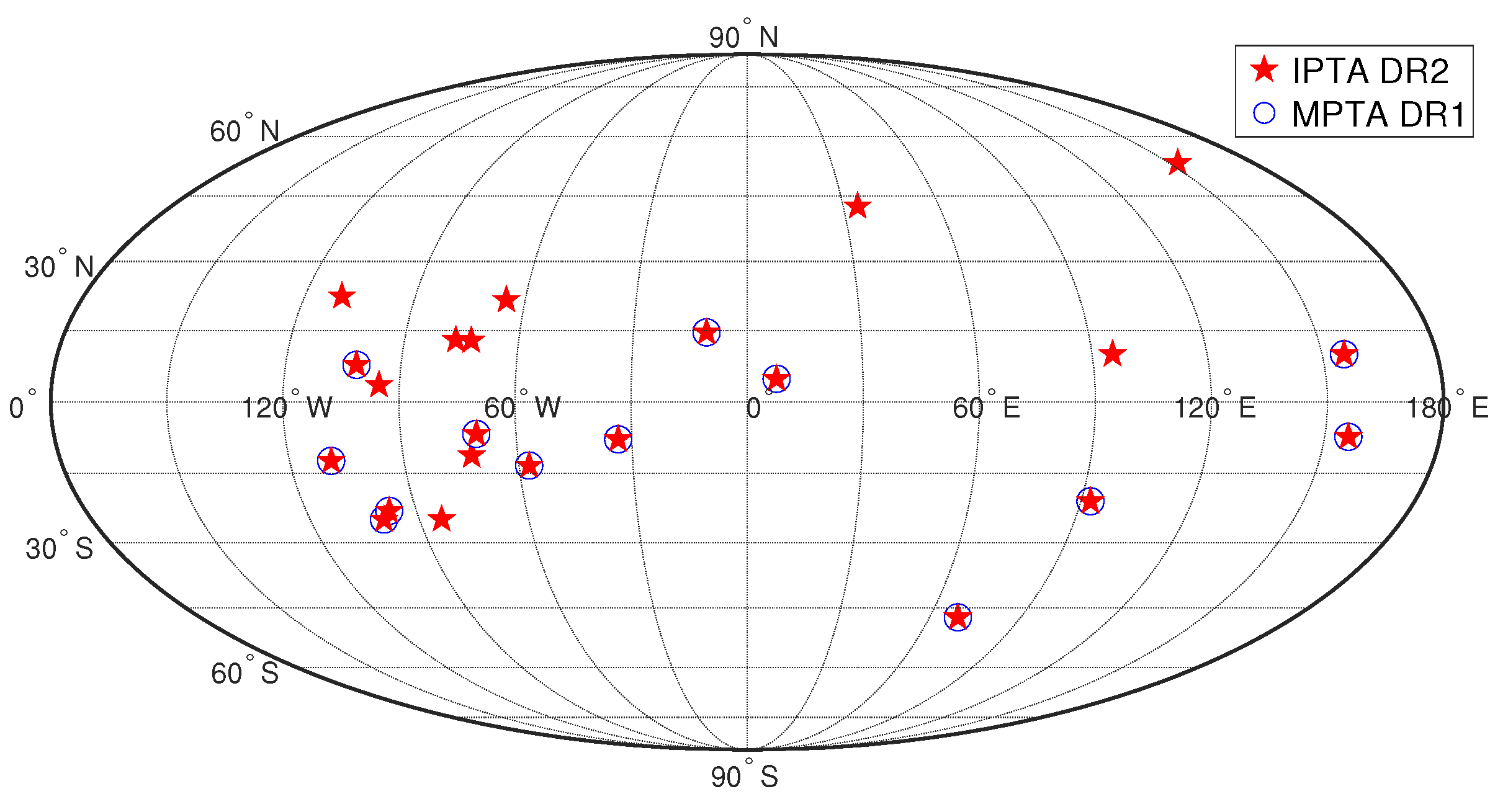
| PSR Name | |||||
|---|---|---|---|---|---|
| hh:mm:ss | dd:mm:ss | Mas yr−1 | Mas yr−1 | Mas | |
| J0030+0451 | 00:30:27.42832(5) | 04:51:39.70915(2) | −5.87(28) | −0.33(66) | 2.84(16) |
| J0218+4232 | 02:18:06.35739(5) | 42:32:17.3822(5) | 5.32(8) | −3.12(14) | 1.00(10) |
| J0437-4715 | 04:37:15.912533(5) | −47:15:09.20860(5) | 121.443(14) | −71.474(1) | 6.415(7) |
| J0610-2100 | 06:10:13.59549(2) | −21:00:27.93139(2) | 9.04(6) | 16.72(8) | - |
| J0621+1002 | 06:21:22.11435(20) | 10:02:38.7317(1) | 3.40(9) | −0.05(35) | - |
| J1012+5307 | 10:12:33.43752(4) | 53:07:02.30017(4) | 2.613(7) | −25.498(10) | 0.54(18) |
| J1024-0719 | 10:24:38.67548(8) | −07:19:19.43142(25) | −35.55(3) | −49.10(7) | 0.63(21) |
| J1640+2224 | 16:40:16.74485(2) | 22:24:08.84107(5) | 2.10(1) | −11.35(1) | 0.27(31) |
| J1643-1224 | 16:43:38.16155(3) | −12:24:58.67328(2) | 6.13(2) | 4.31(8) | 1.44(10) |
| J1713+0737 | 17:13:49.533196(3) | 07:47:37.49258(1) | 4.924(1) | −3.917(2) | 0.87(2) |
| J1721-2457 | 17:21:05.49794(16) | −24:57:06.1755(3) | 2.49(96) | −13.39(13) | - |
| J1730-2304 | 17:30:21.66840(12) | −23:04:31.1572(32) | 20.36(32) | 2.06(6.2) | 1.00(29) |
| J1738+0333 | 17:38:53.9664(1) | 03:33:10.8722(4) | 7.12(5) | 5.16(16) | - |
| J1824-2452A | 18:24:32.0079(2) | −24:52:10.837(5) | −0.18(11) | −0.95(242) | 0.45(36) |
| J1853+1303 | 18:53:57.31880(6) | 13:03:44.0687(2) | −1.65(4) | −2.78(8) | 0.40(36) |
| J1910+1256 | 19:10:09.70147(5) | 12:56:25.4868(2) | 0.12(2) | −7.03(4) | −1.31 |
| J1911-1114 | 19:11:49.28235(2) | −11:14:22.4811(2) | −13.71(15) | −9.27(88) | 1.12(133) |
| J1918-0642 | 19:18:48.03314(4) | −06:42:34.8894(2) | −7.14(2) | −5.97(7) | 1.00(17) |
| J1939+2134 | 19:39:38.56125(2) | 21:34:59.12593(3) | 0.074(1) | −0.4099(26) | 0.485(137) |
| J2010-1323 | 20:10:45.92064(5) | −13:23:56.06566(6) | 2.579(56) | −5.95(24) | 0.49(14) |
| J2145-0750 | 21:45:50.46059(5) | −07:50:18.4869(3) | −9.57(3) | −8.92(7) | 1.84(10) |
| J2317+1439 | 23:17:09.23664(6) | 14:39:31.2560(18) | −1.32(3) | 3.47(5) | 0.135(100) |
| PSR Name | Epoch | |||||
|---|---|---|---|---|---|---|
| MJD | hh:mm:ss | dd:mm:ss | Mas yr−1 | Mas yr−1 | Mas | |
| J0030+0451 [17] | 57849 | 00:30:27.42502(6) | 04:51:39.7159(2) | −6.13(7) | 0.34(31) | 3.02(7) |
| J0218+4232 [39] | 55849 | 02:18:06.358569(2) | 42:32:17.37515(8) | 5.35(5) | −3.74(12) | 0.16(9) |
| J0437-4715 [26] | 54100 | 04:37:15.88325(3) | −47:15:09.031863(4) | 121.679(5) | −71.820(9) | 6.396(5) |
| J0610-2100 [17] | 57757 | 06:10:13.60053(8) | −21:00:27.7923(2) | 9.1(1) | 15.96(49) | 0.73(10) |
| J0621+1002 [17] | 57685 | 06:21:22.11617(12) | 10:02:38.7261(3) | 3.5(2) | −1.37(35) | 0.86(15) |
| J1012+5307 [17] | 57700 | 10:12:33.43991(4) | 53:07:02.1110(1) | 2.67(5) | −25.39(29) | 1.17(9) |
| J1024-0719 [17] | 57797 | 10:24:38.65725(6) | −07:19:19.8014(2) | −35.32(7) | −48.1(2) | 0.94(6) |
| J1640+2224 [17] | 57500 | 16:40:16.74587(7) | 22:24:08.7642(1) | 2.19(9) | −11.30(29) | 0.68(8) |
| J1643-1224 [17] | 57700 | 16:43:38.16407(1) | −12:24:58.6531(4) | 6.2(2) | 3.3(6) | 1.31(35) |
| J1713+0747 [16] | 52275 | 17:13:49.5306(1) | 07:47:37.519(2) | 4.75(1) | −3.67(2) | 0.95(5) |
| J1721-2457 [17] | 57820 | 17:21:05.49936(2) | −24:57:06.2210(6) | 2.5(3) | −1.9(9) | 0.0(2) |
| J1730-2304 [17] | 57821 | 17:30:21.67969(2) | −23:04:31.1749(5) | 20.3(2) | −4.8(5) | 1.57(18) |
| J1738+0333 [17] | 57829 | 17:38:53.97001(6) | 03:33:10.9124(1) | 6.98(8) | 5.18(16) | 0.50(6) |
| J1824-2452A [17] | 57836 | 18:24:32.00791(4) | −24:52:10.912(1) | 0.3(6) | −3.9(25) | 0.1(5) |
| J1853+1303 [17] | 57846 | 18:53:57.31785(6) | 13:03:44.0471(1) | −1.4(1) | −2.8(2) | 0.49(7) |
| J1910+1256 [17] | 57847 | 19:10:09.70165(3) | 12:56:25.4316(6) | 0.50(4) | −6.85(9) | 0.254(35) |
| J1911-1114 [17] | 57768 | 19:11:49.27544(1) | −11:14:22.5547(3) | −13.8(2) | −10.3(4) | 0.38(27) |
| J1918-0642 [17] | 57768 | 19:18:48.02959(1) | −06:42:34.9335(2) | −7.1(1) | −5.7(3) | 0.60(12) |
| J1939+2134 [17] | 57850 | 19:39:38.56134(7) | 21:34:59.1233(2) | 0.08(7) | −0.43(11) | 0.384(94) |
| J2010-1323 [29] | 56000 | 20:10:45.9211(1) | −13:23:56.083(4) | 2.36(23) | −5.61(28) | 0.48(14) |
| J2145-0750 [28] | 54100 | 21:45:50.4588(1) | −07:50:18.513(2) | −9.46(5) | −9.08(6) | 1.63(4) |
| J2317+1439 [29] | 56000 | 23:17:09.2364(1) | 14:39:31.265(1) | −1.48(2) | 3.81(1) | 0.60(100) |
| PSR Name | |||||||
|---|---|---|---|---|---|---|---|
| Mas | Mas | Mas yr−1 | Mas yr−1 | Mas yr−1 | Mas yr−1 | Mas yr−1 | |
| J0030+0451 | 1.20 | 5.25 | −6.13 | 0.34 | −5.87 | −0.33 | −0.67 |
| J0218+4232 | 1.39 | −0.84 | 5.35 | −3.74 | 5.32 | −3.12 | 0.62 |
| J0437-4715 | 1.25 | −0.05 | 121.68 | −71.82 | 121.44 | −71.47 | 0.35 |
| J0610-2100 | 2.02 | 19.13 | 9.10 | 15.96 | 9.04 | 16.72 | 0.76 |
| J0621+1002 | 1.06 | 4.66 | 3.50 | −1.37 | 3.40 | −0.05 | 1.32 |
| J1012+5307 | 1.94 | −1.55 | 2.67 | −25.39 | 2.61 | −25.49 | −0.10 |
| J1024-0719 | −1.57 | −1.23 | −35.32 | −48.10 | −35.55 | −49.10 | −1.00 |
| J1640+2224 | −1.16 | 0.95 | 2.19 | −11.30 | 2.10 | −11.35 | −0.05 |
| J1643-1224 | −9.41 | −3.95 | 6.20 | 3.30 | 6.13 | 4.314 | 1.01 |
| J1713+0747 | −1.8 | −2.15 | 4.75 | −3.67 | 4.92 | −3.92 | −0.25 |
| J1721-2457 | 0 | −30.79 | 2.50 | −1.90 | 2.49 | −13.39 | −11.49 |
| J1730-2304 | −1.17 | 19.35 | 20.30 | −4.80 | 20.36 | 2.06 | 6.86 |
| J1738+0333 | −0.04 | 0.31 | 6.98 | 5.18 | 7.12 | 5.16 | −0.02 |
| J1824-2452A | −2.17 | −44.18 | 0.30 | −3.90 | −0.18 | −0.95 | 2.95 |
| J1853+1303 | −2.91 | 0.52 | −1.40 | −2.80 | −1.65 | −2.78 | 0.02 |
| J1910+1256 | −1.22 | −1.68 | 0.50 | −6.85 | 0.12 | −7.03 | −0.18 |
| J1911-1114 | 3.08 | 4.49 | −13.80 | −10.30 | −13.71 | −9.27 | 1.03 |
| J1918-0642 | 1.21 | −0.72 | −7.10 | −5.70 | −7.14 | −5.97 | −0.27 |
| J1939+2134 | 0.81 | 0.98 | 0.08 | −0.43 | 0.08 | −0.35 | 0.08 |
| J2010-1323 | 0.68 | −1.47 | 2.36 | −5.61 | 2.58 | −5.95 | −0.34 |
| J2145-0750 | −0.9 | 0.7 | −9.57 | −8.92 | −9.57 | −8.92 | 0.00 |
| J2317+1439 | 0.03 | 1.34 | −1.48 | 3.81 | −1.32 | 3.47 | −0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Song, Y.; Yan, Z.; Li, L.; Wang, G. Linking Planetary Ephemeris Reference Frames to ICRF via Millisecond Pulsars. Universe 2025, 11, 54. https://doi.org/10.3390/universe11020054
Guo L, Song Y, Yan Z, Li L, Wang G. Linking Planetary Ephemeris Reference Frames to ICRF via Millisecond Pulsars. Universe. 2025; 11(2):54. https://doi.org/10.3390/universe11020054
Chicago/Turabian StyleGuo, Li, Yueqi Song, Zhen Yan, Liang Li, and Guangli Wang. 2025. "Linking Planetary Ephemeris Reference Frames to ICRF via Millisecond Pulsars" Universe 11, no. 2: 54. https://doi.org/10.3390/universe11020054
APA StyleGuo, L., Song, Y., Yan, Z., Li, L., & Wang, G. (2025). Linking Planetary Ephemeris Reference Frames to ICRF via Millisecond Pulsars. Universe, 11(2), 54. https://doi.org/10.3390/universe11020054






