Intermediate Coupling Regime in Dilatonic f(R,T) Inflationary Universe
Abstract
1. Introduction
2. Cosmology in Dilatonic Gravity
3. Inflation in Dilatonic Gravity
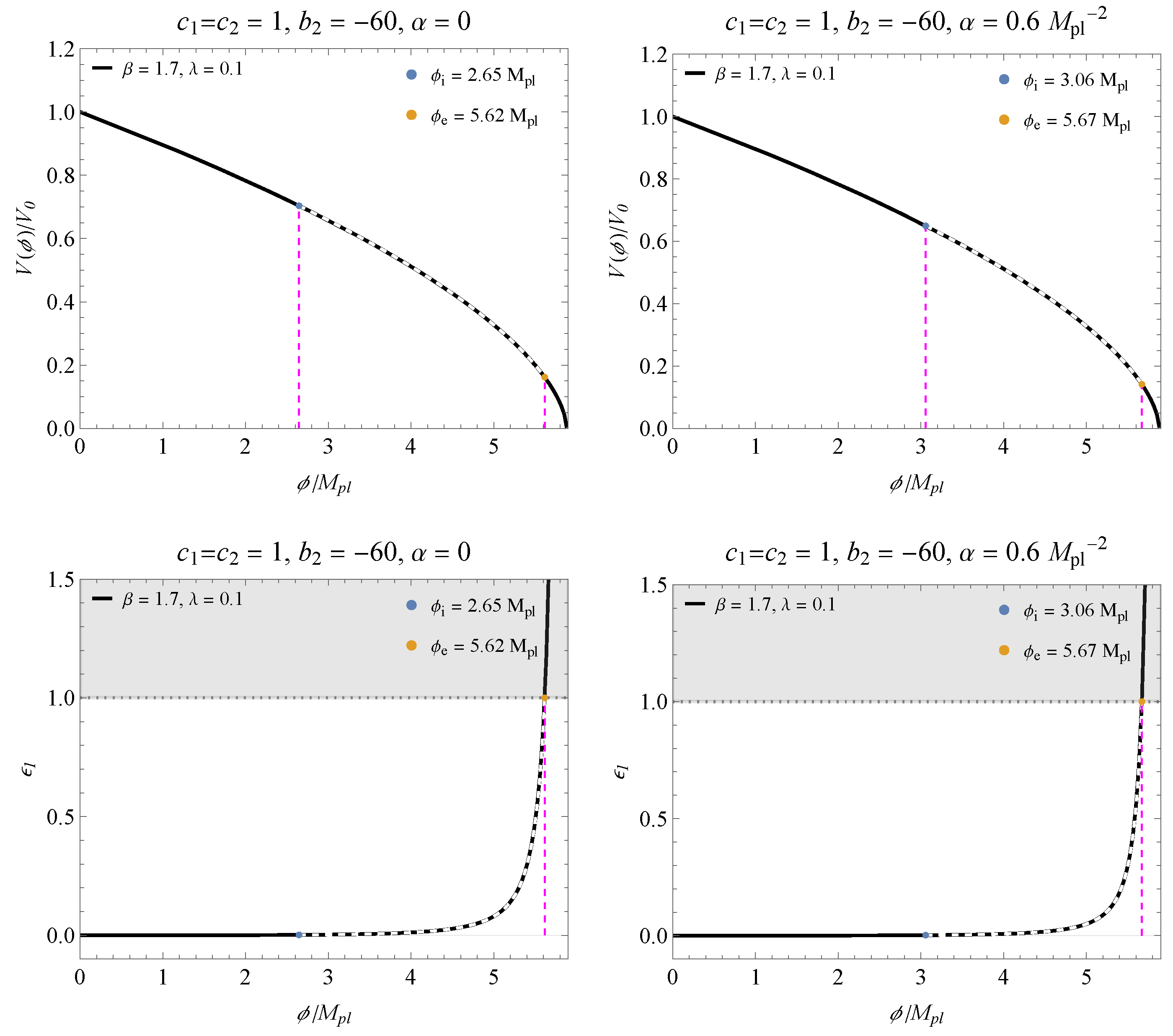
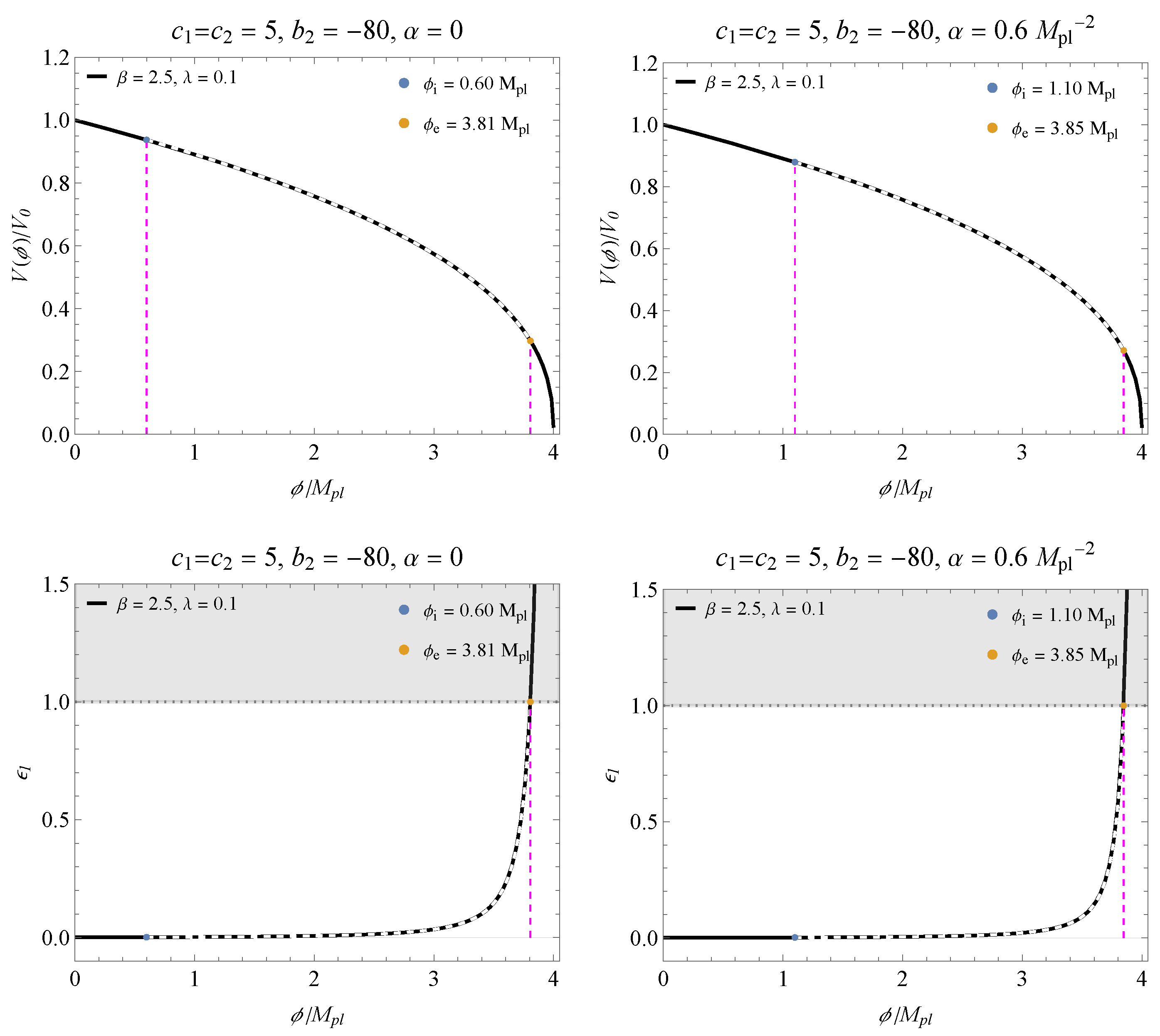
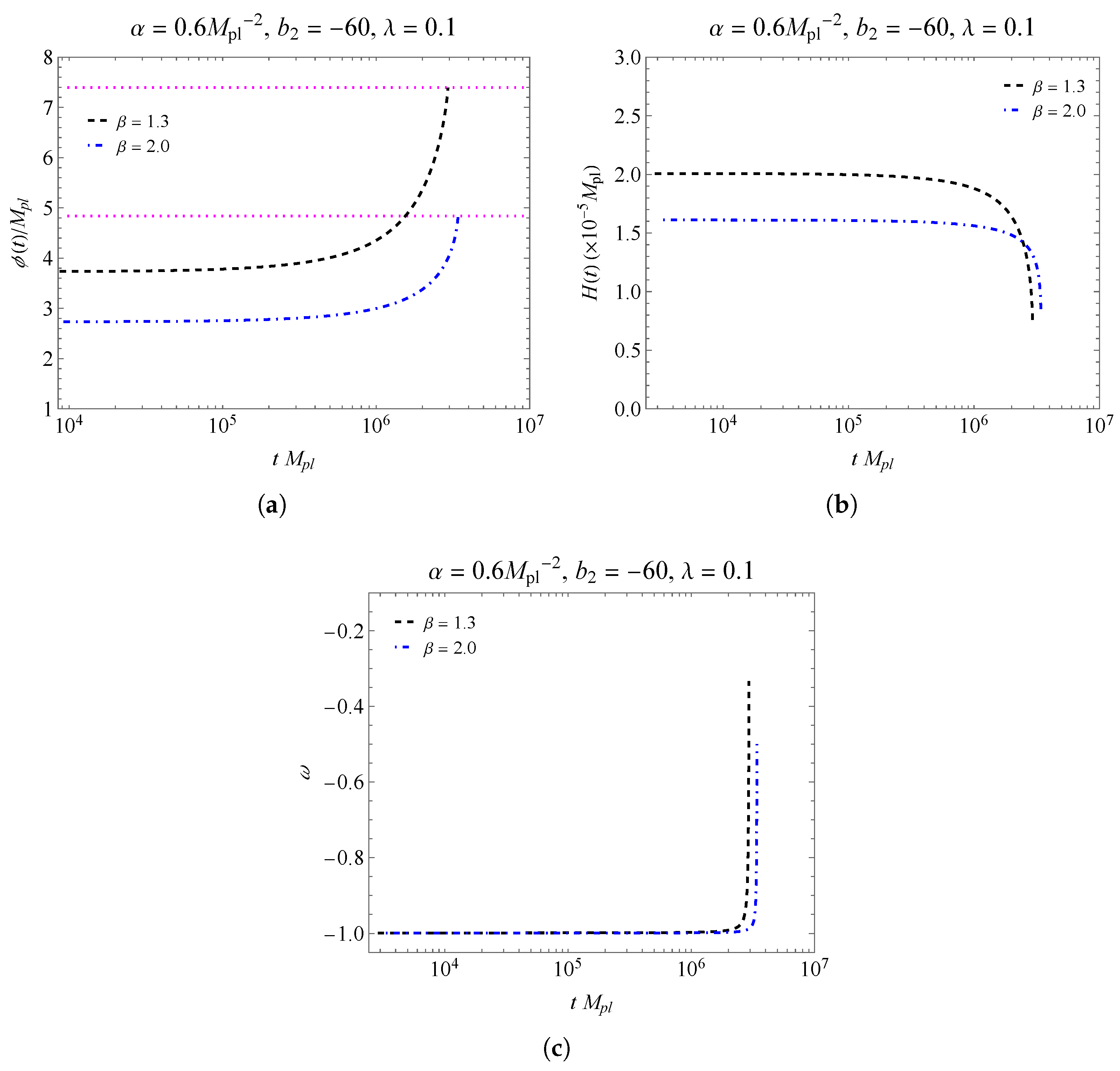
4. Inflationary Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for grand unified theories with radiatively induced symmetry breaking. Phys. Rev. Lett. 1982, 48, 1220. [Google Scholar] [CrossRef]
- Linde, A.D. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Chibisov, G. Quantum fluctuations and a nonsingular universe. ZhETF Pisma Redaktsiiu 1981, 33, 549–553. [Google Scholar]
- Guth, A.H.; Pi, S.-Y. Fluctuations in the new inflationary universe. Phys. Rev. Lett. 1982, 49, 1110. [Google Scholar] [CrossRef]
- Hawking, S.W. The development of irregularities in a single bubble inflationary universe. Phys. Lett. B 1982, 115, 295–297. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Dynamics of phase transition in the new inflationary universe scenario and generation of perturbations. Phys. Lett. B 1982, 117, 175–178. [Google Scholar] [CrossRef]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Class of quintessential inflation models with parameter space consistent with bicep2. Phys. Rev. D 2014, 89, 123513. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Trotta, R.; Vennin, V. The best inflationary models after planck. J. Cosmol. Astropart. Phys. 2014, 2014, 039. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopædia inflationaris. Phys. Dark Universe 2014, 5, 75–235. [Google Scholar] [CrossRef]
- Geng, C.-Q.; Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Quintessential inflation with canonical and noncanonical scalar fields and planck 2015 results. Phys. Rev. D 2015, 92, 023522. [Google Scholar] [CrossRef]
- Huang, Q.-G.; Wang, K.; Wang, S. Inflation model constraints from data released in 2015. Phys. Rev. D 2016, 93, 103516. [Google Scholar] [CrossRef]
- Linde, A. Particle physics and inflationary cosmology. arXiv 2005, arXiv:hep-th/0503203. [Google Scholar]
- Dolgov, A.; Linde, A.D. Baryon asymmetry in the inflationary universe. Phys. Lett. B 1982, 116, 329–334. [Google Scholar] [CrossRef]
- Abbott, L.F.; Farhi, E.; Wise, M.B. Particle production in the new inflationary cosmology. Phys. Lett. B 1982, 117, 29–33. [Google Scholar] [CrossRef]
- Starobinsky, A. Nonsingular model of the universe with the quantum-gravitational de sitter stage and its observational consequences. In Quantum Gravity; Springer: Berlin/Heidelberg, Germany, 1984; pp. 103–128. [Google Scholar]
- Dolgov, A.; Hansen, S. Equation of motion of a classical scalar field with back reaction of produced particles. Nucl. Phys. B 1999, 548, 408–426. [Google Scholar] [CrossRef]
- Traschen, J.H.; Brandenberger, R.H. Particle production during out-of-equilibrium phase transitions. Phys. Rev. D 1990, 42, 2491. [Google Scholar] [CrossRef]
- Odintsov, S.; Oikonomou, V. f (r) gravity inflation with string-corrected axion dark matter. Phys. Rev. D 2019, 99, 064049. [Google Scholar] [CrossRef]
- Oikonomou, V. Exponential inflation with f (r) gravity. Phys. Rev. D 2018, 97, 064001. [Google Scholar] [CrossRef]
- Kleidis, K.; Oikonomou, V. Scalar field assisted f (r) gravity inflation. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850137. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.; Oikonomou, V. Constant-roll inflation in f (r) gravity. Class. Quantum Gravity 2017, 34, 245012. [Google Scholar] [CrossRef]
- Zhong, Y.; Sáez-Chillón Gómez, D. Inflation in mimetic f (g) gravity. Symmetry 2018, 10, 170. [Google Scholar] [CrossRef]
- Rezazadeh, K.; Abdolmaleki, A.; Karami, K. Logamediate inflation in f (t) teleparallel gravity. Astrophys. J. 2017, 836, 228. [Google Scholar] [CrossRef]
- Shabani, H.; Farhoudi, M. Cosmological and solar system consequences of f (r, t) gravity models. Phys. Rev. D 2014, 90, 044031. [Google Scholar] [CrossRef]
- Moraes, P.; Sahoo, P. Modeling wormholes in f (r, t) gravity. Phys. Rev. D 2017, 96, 044038. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Santos, J.; Moraes, P.; Sahoo, P. Inflation in f (r, t) gravity. Eur. Phys. J. Plus 2020, 135, 576. [Google Scholar] [CrossRef]
- Santos, J.R.L.; da Costa, S.S.; Santos, R.S. Cosmological models for f(r,t) − Λ (ϕ) gravity. Phys. Dark Univ. 2023, 42, 101356. [Google Scholar] [CrossRef]
- Witten, E. Some properties of o (32) superstrings. Phys. Lett. B 1984, 149, 351–356. [Google Scholar] [CrossRef]
- Witten, E. String theory dynamics in various dimensions. Nucl. Phys. B 1995, 443, 85–126. [Google Scholar] [CrossRef]
- Gasperini, M. Dilatonic interpretation of quintessence? Phys. Rev. D 2001, 64, 043510. [Google Scholar] [CrossRef]
- Gasperini, M.; Piazza, F.; Veneziano, G. Quintessence as a runaway dilaton. Phys. Rev. D 2001, 65, 023508. [Google Scholar] [CrossRef]
- Brito, F.A.; Borges, C.H.; Campos, J.A.; Costa, F.G. Weak coupling regime in dilatonic f (r, t) cosmology. Universe 2024, 10, 134. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.; Nojiri, S.; Odintsov, S.D. f (r, t) gravity. Phys. Rev. D-Part. Fields Gravit. Cosmol. 2011, 84, 024020. [Google Scholar] [CrossRef]
- Damour, T.; Polyakov, A.M. The string dilation and a least coupling principle. Nucl. Phys. B 1994, 423, 532–558. [Google Scholar] [CrossRef]
- Alvarenga, F.G.; Cruz-Dombriz, A.d.; Houndjo, M.J.S.; Rodrigues, M.E. Sáez-Gómez Dynamics of scalar perturbations f(R,T) gravity. Phys. Rev. D 2013, 87, 103526, Erratum in Phys. Rev. D 2013, 87, 129905. [Google Scholar] [CrossRef]
- Fisher, S.B.; Carlson, E.D. Reexamining f(R,T) gravity. Phys. Rev. D 2019, 100, 064059. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Lobato, R.V.; Moraes, P.H.R.S.; Arbail, J.D.V.; Marinho, R.M., Jr.; Otoniel, E.; Malheiro, M. Stellar equilibrium configurations of white dwarfs in the f(R, T) gravity. Eur. Phys. J. C 2017, 77, 871. [Google Scholar] [CrossRef]
- Ordines, T.M.; Carlson, E.D. Limits on f(R, T) gravity from Earth’s atmosphere. Phys. Rev. D 2019, 99, 104052. [Google Scholar] [CrossRef]
- Fazlollahi, H.R. Holographic dark energy in non-conserved gravity theory. Commun. Theor. Phys. 2024, 76, 4. [Google Scholar] [CrossRef]
- Fazlollahi, H.R. Non-conserved modified gravity theory. Eur. Phys. J. C 2023, 83, 923. [Google Scholar] [CrossRef]
- Bertini, N.R.; Velten, H. Fully conservative f(R,T) gravity and Solar System constraints. Phys. Rev. D 2023, 107, 124005. [Google Scholar] [CrossRef]
- Pretel, J.M.Z.; Jorás, S.E.; Reis, R.R.R.; Arbañil, J.D.V. Neutron stars in f (R, T) gravity with conserved energy-momentum tensor: Hydrostatic equilibrium and asteroseismology. J. Cosmol. Astropart. Phys. 2021, 8, 055. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Santos, S.I.D.; Moraes, P.H.R.S.; Malheiro, M. Strange stars in energy–momentum-conserved f(R, T) gravity. Int. J. Mod. Phys. D 2020, 29, 2050075. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Kara, A.H.; Gadjagboui, B. On symmetries and conservation laws of some spacetimes in f(R,T) gravity. Mod. Phys. Lett. A 2019, 34, 1975003. [Google Scholar] [CrossRef]
- Singh, V.; Beesham, A. The f(R, Tϕ) gravity models with conservation of energy–momentum tensor. Eur. Phys. J. C 2018, 78, 564. [Google Scholar]
- Lobato, R.V.; Carvalho, G.A.; Martins, A.G.; Moraes, P.H.R.S. Energy nonconservation as a link between f(R, T) gravity and noncommutative quantum theory. Eur. Phys. J. Plus 2019, 134, 132. [Google Scholar] [CrossRef]
- Santos, S.I.D.; Carvalho, G.A.; Moraes, P.H.R.S.; Lenzi, C.H.; Malheiro, M. A conservative energy-momentum tensor in the f(R, T) gravity and its implications for the phenomenology of neutron stars. Eur. Phys. J. Plus. 2019, 134, 398. [Google Scholar] [CrossRef]
- Shabani, H.; Ziaie, A.H. Interpretation of f(R,T) gravity in terms of a conserved effective fluid. Int. J. Mod. Phys. A 2018, 33, 1850050. [Google Scholar] [CrossRef]
- Shabani, H.; Ziaie, A.H. Consequences of energy conservation violation: Late time solutions of Λ(T)CDM subclass of f(R,T) gravity using dynamical system approach. Eur. Phys. J. C 2017, 77, 282. [Google Scholar] [CrossRef]
- Gasperini, M.; Veneziano, G. The pre-big bang scenario in string cosmology. Phys. Rep. 2003, 373, 1–212. [Google Scholar] [CrossRef]
- Gasperini, M. Dilaton cosmology and phenomenology. In String Theory and Fundamental Interactions: Gabriele Veneziano and Theoretical Physics: Historical and Contemporary Perspectives; Springer: Berlin/Heidelberg, Germany, 2008; pp. 787–844. [Google Scholar]
- Linde, A.D. Chaotic inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Coleman, S.; Weinberg, E. Radiative corrections as the origin of spontaneous symmetry breaking. Phys. Rev. D 1973, 7, 1888. [Google Scholar] [CrossRef]
- Belinsky, V.; Khalatnikov, I.; Grishchuk, L.; Zeldovich, Y.B. Inflationary Stages in Cosmological Models with a Scalar Field. Tech. Rep., International Centre for Theoretical Physics. 1985. Available online: https://inis.iaea.org/records/gxtfj-ses31 (accessed on 4 February 2025).
- Peebles, P.; Ratra, B. Cosmology with a time-variable cosmological’constant’. Astrophys. J. 1988, 325, L17–L20. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P.J. Cosmological consequences of a rolling homogeneous scalar field. Phys. Rev. D 1988, 37, 3406. [Google Scholar] [CrossRef] [PubMed]
- Wetterich, C. The cosmon model for an asymptotically vanishing time-dependent cosmological“constant”. arXiv 1994, arXiv:hep-th/9408025. [Google Scholar]
- Ferreira, P.G.; Joyce, M. Cosmology with a primordial scaling field. Phys. Rev. D 1998, 58, 023503. [Google Scholar] [CrossRef]
- Lucchin, F.; Matarrese, S. Power-law inflation. Phys. Rev. D 1985, 32, 1316. [Google Scholar] [CrossRef] [PubMed]
- Halliwell, J.J. Scalar fields in cosmology with an exponential potential. Phys. Lett. B 1987, 185, 341–344. [Google Scholar] [CrossRef]
- Wetterich, C. Kaluza-klein cosmology and the inflationary universe. Nucl. Phys. B 1985, 252, 309–320. [Google Scholar] [CrossRef]
- Shafi, Q.; Wetterich, C. Inflation with higher dimensional gravity. Phys. Lett. B 1985, 152, 51–55. [Google Scholar] [CrossRef]
- Alcaniz, J.S.; Carvalho, F. β-exponential inflation. Europhys. Lett. 2007, 79, 39001. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1968; Volume 55. [Google Scholar]
- Lima, J.; Silva, R.; Plastino, A. Nonextensive thermostatistics and the h theorem. Phys. Rev. Lett. 2001, 86, 2938. [Google Scholar] [CrossRef] [PubMed]
- Benisty, D.; Guendelman, E.I.; Saridakis, E.N. The scale factor potential approach to inflation. Eur. Phys. J. C 2020, 80, 480. [Google Scholar] [CrossRef]
- Liddle, A.R.; Lyth, D.H. Cosmological Inflation and Large-Scale Structure; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Lyth, D.H.; Riotto, A. Particle physics models of inflation and the cosmological density perturbation. Phys. Rep. 1999, 314, 1–146. [Google Scholar] [CrossRef]
- Santos, M.; Benetti, M.; Alcaniz, J.; Brito, F.; Silva, R. Cmb constraints on β-exponential inflationary models. J. Cosmol. Astropart. Phys. 2018, 2018, 023. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.; Bartolo, N.; Basak, S.; et al. Planck 2018 results-x. constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar]
- Ade, P.A.; Ahmed, Z.; Amiri, M.; Barkats, D.; Thakur, R.B.; Bischoff, C.; Beck, D.; Bock, J.; Boenish, H.; Bullock, E.; et al. Improved constraints on primordial gravitational waves using planck, wmap, and bicep/keck observations through the 2018 observing season. Phys. Rev. Lett. 2021, 127, 151301. [Google Scholar] [CrossRef] [PubMed]
- Tristram, M.; Banday, A.J.; Górski, K.M.; Keskitalo, R.; Lawrence, C.R.; Andersen, K.J.; Barreiro, R.B.; Borrill, J.; Colombo, L.P.L.; Eriksen, H.K.; et al. Improved limits on the tensor-to-scalar ratio using BICEP and Planck data. Phys. Rev. D 2022, 105, 083524. [Google Scholar] [CrossRef]
- Santos, F.B.M.D.; da Costa, S.S.; Silva, R.; Benetti, M.; Alcaniz, J. Constraining non-minimally coupled β-exponential inflation with CMB data. J. Cosmol. Astropart. Phys. 2022, 2022, 001. [Google Scholar] [CrossRef]
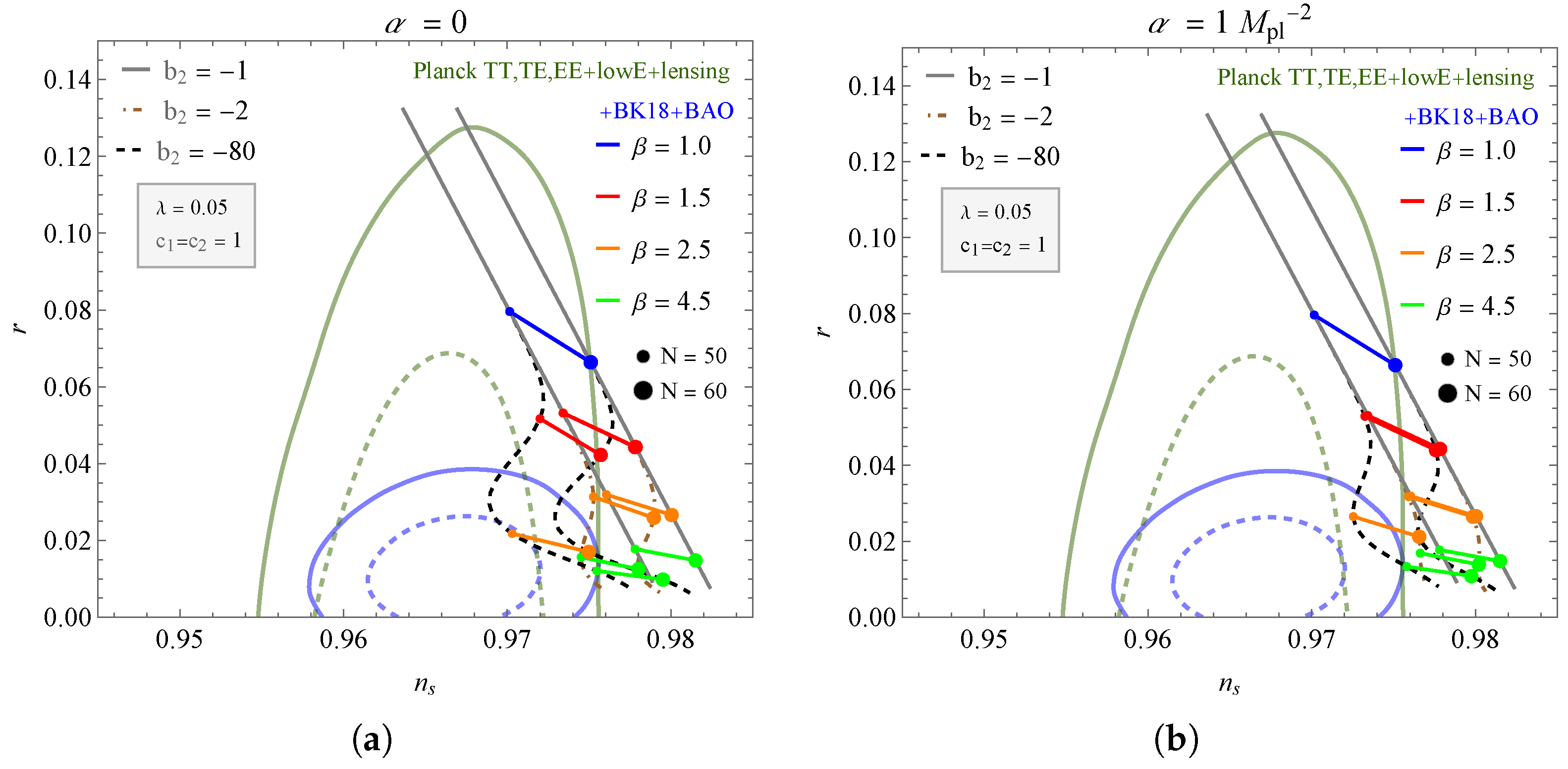
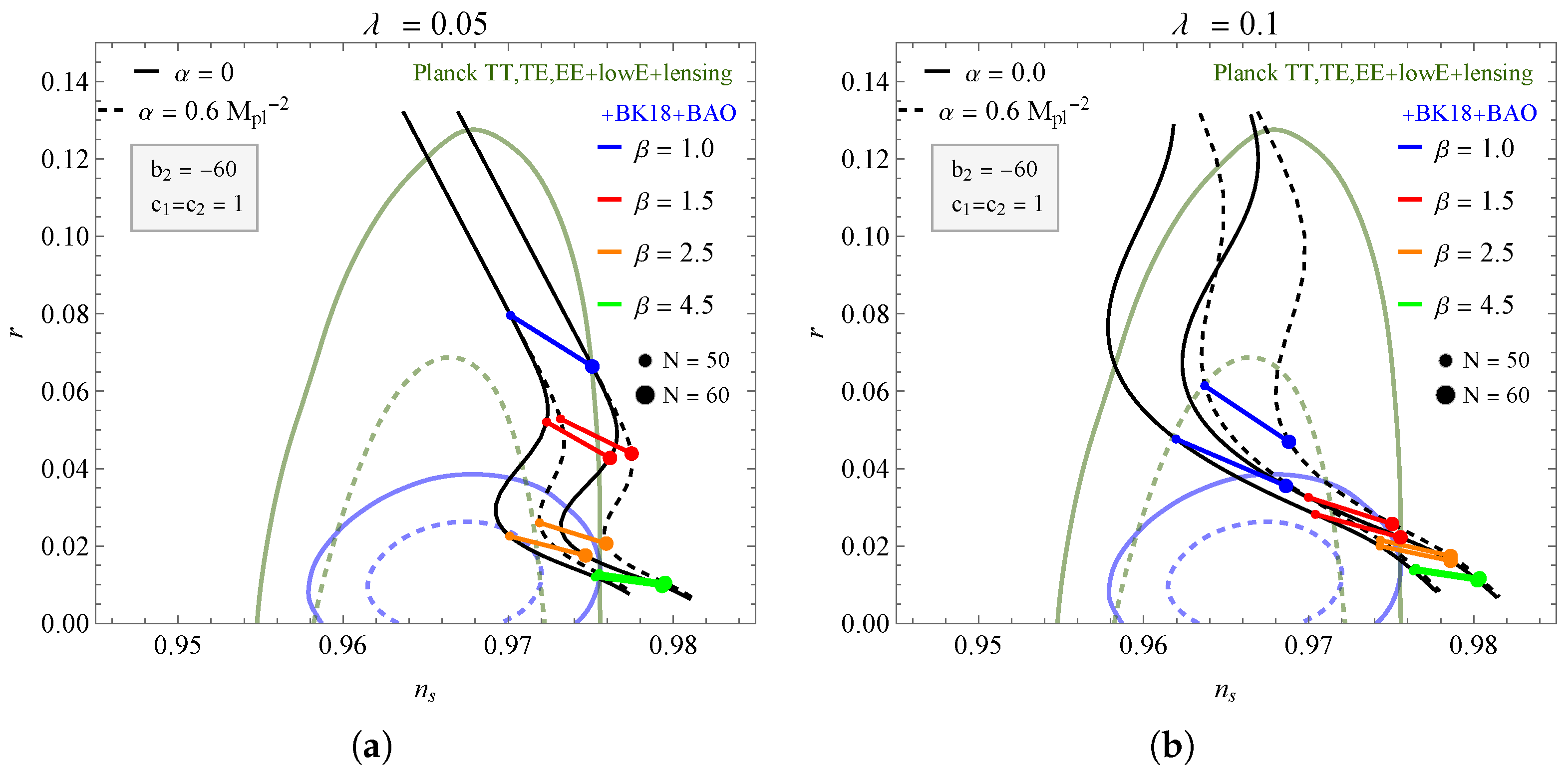
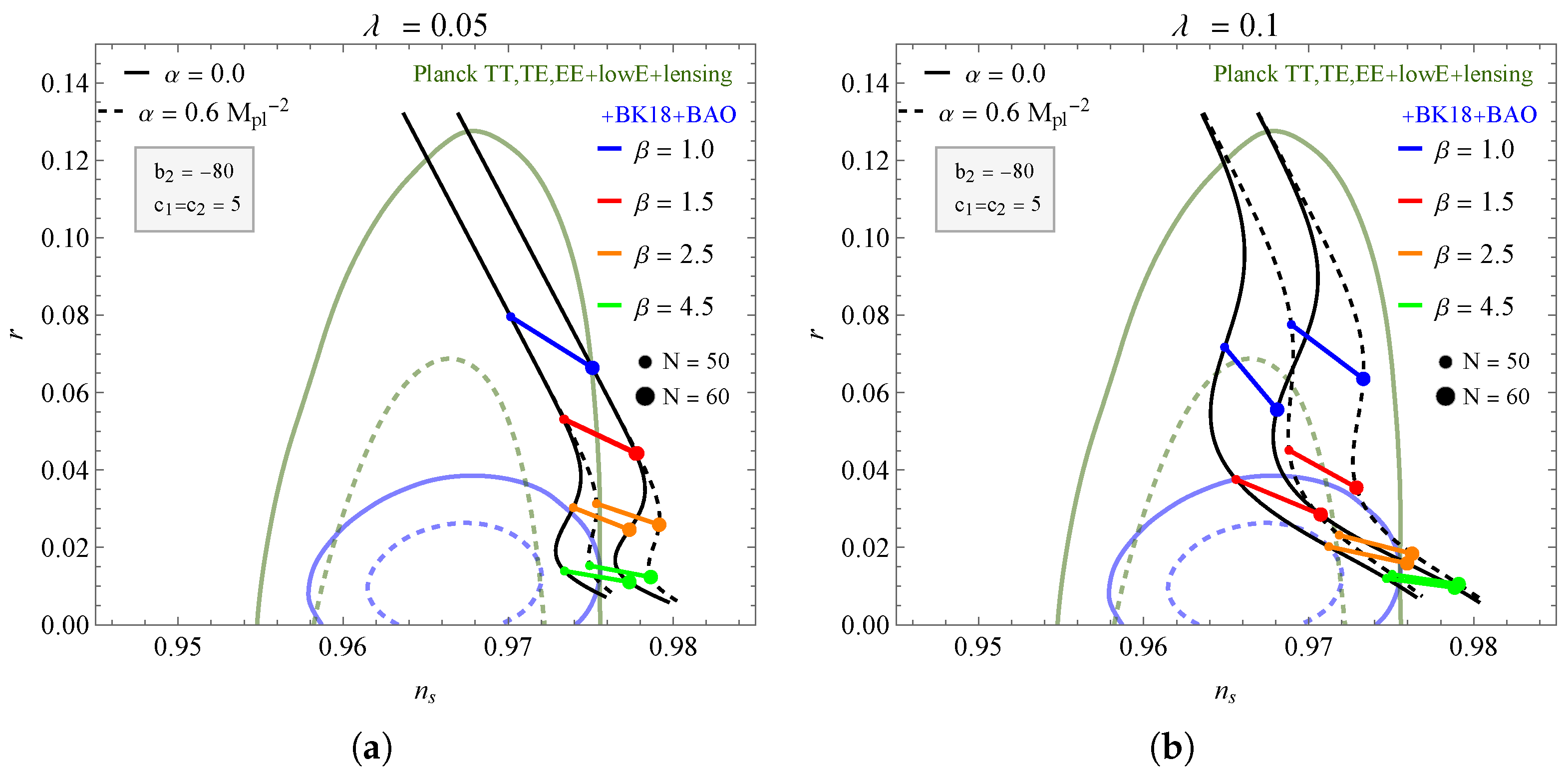
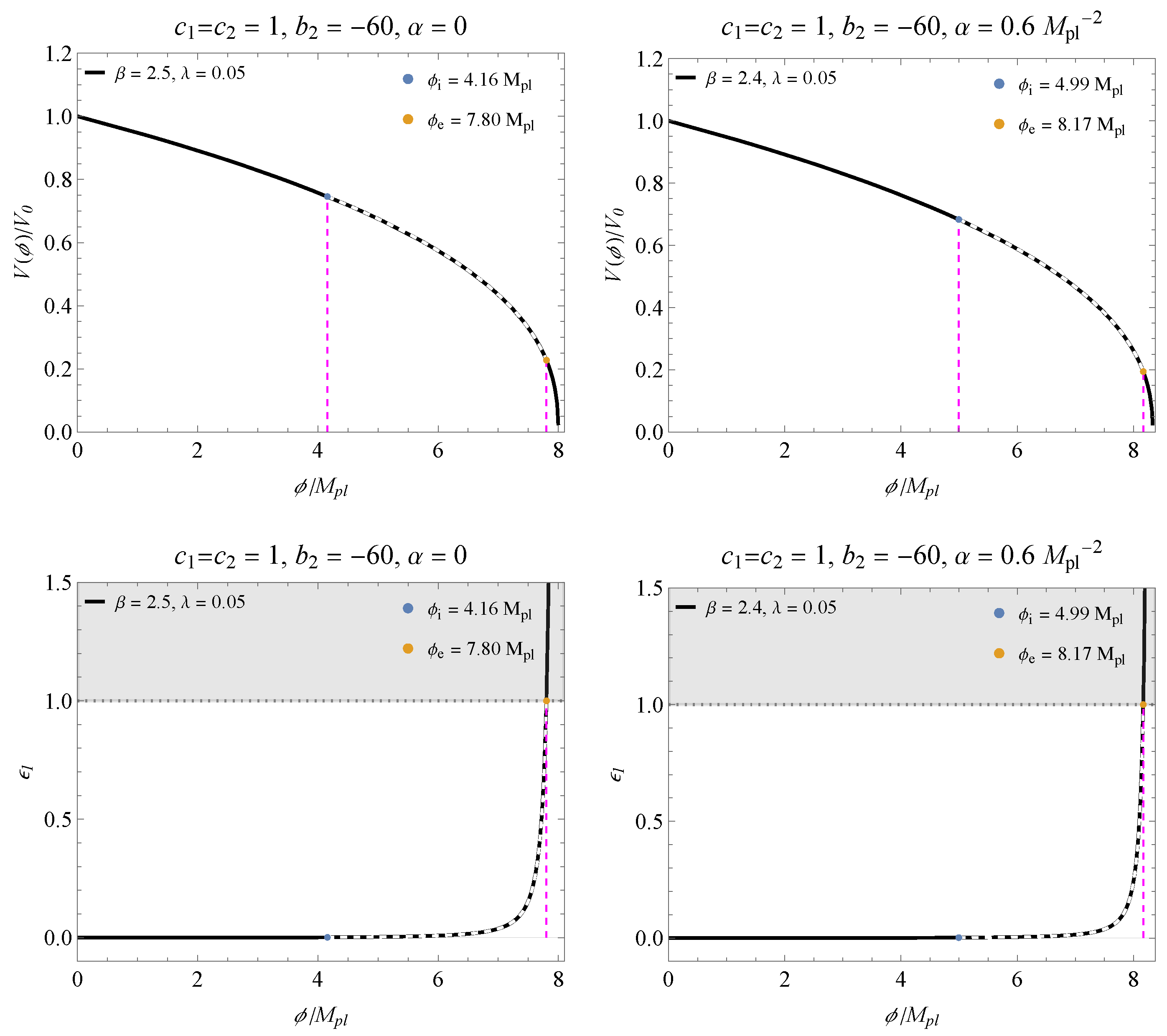

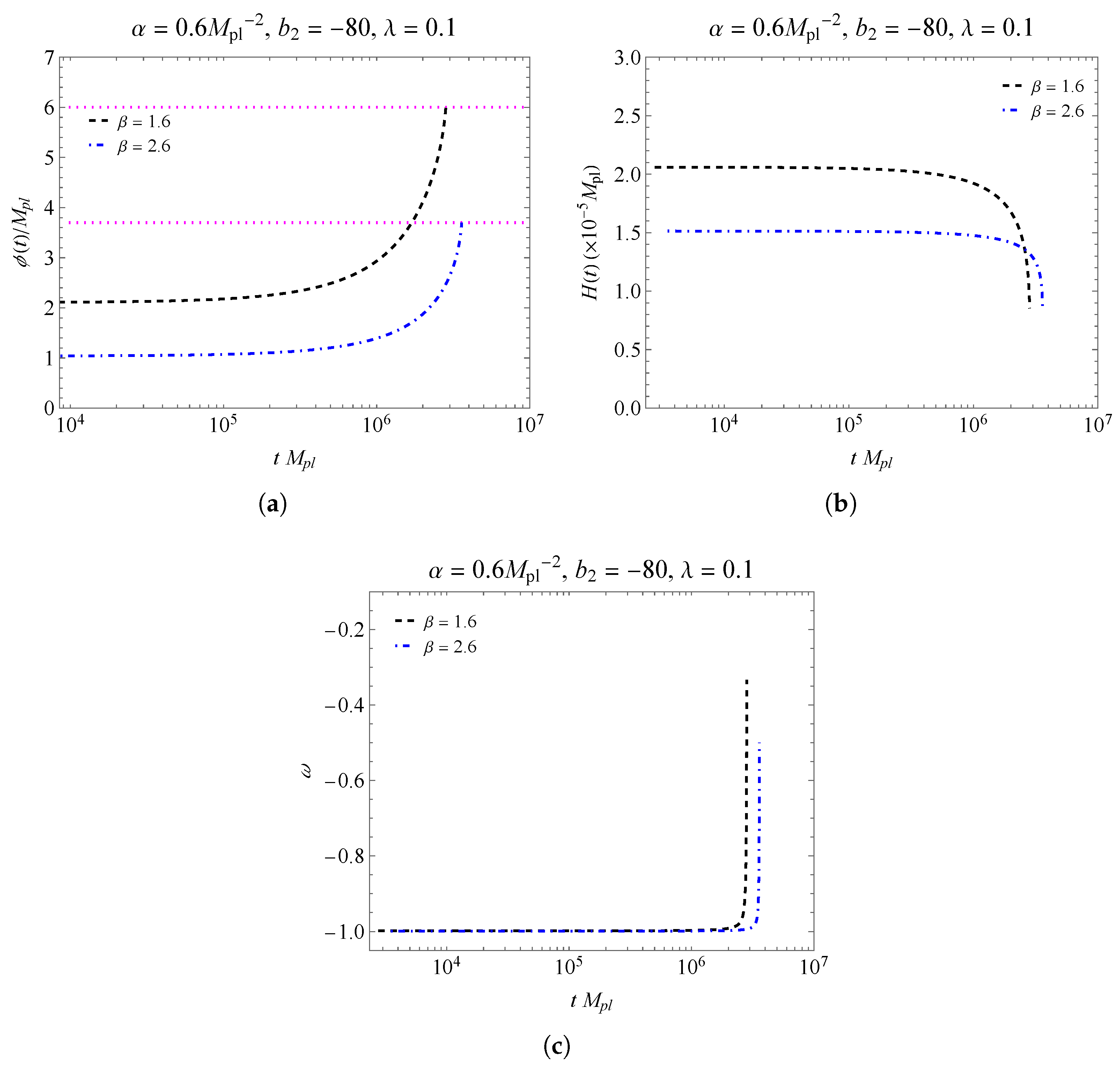
| and | and | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.97551 | 0.036281 | 0.96907 | 0.027086 | 0.97551 | 0.036281 | 0.97277 | 0.032546 | |
| 0.97634 | 0.029575 | 0.97123 | 0.019479 | 0.97634 | 0.029575 | 0.97275 | 0.023523 | |
| 0.97671 | 0.026622 | 0.97247 | 0.017087 | 0.97671 | 0.026622 | 0.97335 | 0.020223 | |
| 0.97725 | 0.022191 | 0.97414 | 0.014311 | 0.97725 | 0.022191 | 0.97459 | 0.016314 | |
| 0.97759 | 0.019488 | 0.97499 | 0.012928 | 0.97759 | 0.019488 | 0.97535 | 0.014426 | |
| 0.96950 | 0.033537 | 0.97274 | 0.037130 | 0.97440 | 0.039341 | 0.97489 | 0.039717 | |
| 0.97009 | 0.022558 | 0.97189 | 0.026011 | 0.97395 | 0.030277 | 0.97535 | 0.031291 | |
| 0.97212 | 0.017431 | 0.97282 | 0.019737 | 0.97317 | 0.023815 | 0.97522 | 0.025328 | |
| 0.97527 | 0.012000 | 0.97551 | 0.012902 | 0.97341 | 0.013908 | 0.97494 | 0.015281 | |
| r | r | r | r | |||||
| 0.96657 | 0.035820 | 0.96629 | 0.044100 | 0.96406 | 0.053499 | 0.96896 | 0.061721 | |
| 0.97449 | 0.019523 | 0.97454 | 0.020953 | 0.97155 | 0.019428 | 0.97213 | 0.022190 | |
| 0.97529 | 0.017192 | 0.97539 | 0.018228 | 0.97303 | 0.016015 | 0.97345 | 0.017890 | |
| 0.97600 | 0.014816 | 0.97615 | 0.015552 | 0.97421 | 0.013200 | 0.97458 | 0.014474 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brito, F.A.; Borges, C.H.A.B.; Campos, J.A.V.; Costa, F.G. Intermediate Coupling Regime in Dilatonic f(R,T) Inflationary Universe. Universe 2025, 11, 65. https://doi.org/10.3390/universe11020065
Brito FA, Borges CHAB, Campos JAV, Costa FG. Intermediate Coupling Regime in Dilatonic f(R,T) Inflationary Universe. Universe. 2025; 11(2):65. https://doi.org/10.3390/universe11020065
Chicago/Turabian StyleBrito, Francisco A., Carlos H. A. B. Borges, Jose A. V. Campos, and Francisco G. Costa. 2025. "Intermediate Coupling Regime in Dilatonic f(R,T) Inflationary Universe" Universe 11, no. 2: 65. https://doi.org/10.3390/universe11020065
APA StyleBrito, F. A., Borges, C. H. A. B., Campos, J. A. V., & Costa, F. G. (2025). Intermediate Coupling Regime in Dilatonic f(R,T) Inflationary Universe. Universe, 11(2), 65. https://doi.org/10.3390/universe11020065






