Time Scales of Slow-Roll Inflation in Asymptotically Safe Cosmology
Abstract
:1. Introduction
- The Big Bang singularity is followed by the Reuter FP-driven era (RFPE). This covers the Planck era ending at for QIM1, while it ends at for QIM2. (Here stands for the Planck second, in the units ).
- For QIM2, there occurs the crossover era (COE1) lasting from to , during which the dimensionless gravitational couplings keep their FP values, but the dimensionless inflaton mass changes from its constant FP value to its IR behavior. The duration of COE1 is rather short, so it ends at .
- The crossover era (COE2) with constant dimensionful inflaton mass, but the crossover scaling behaviors of the gravitational couplings show up in both QIM1 and QIM2 and are followed numerically from to the end of the slow-roll inflation at settled by the value of the slow-roll parameter. COE2 starts with a preinflationary era followed by the era of slow-roll inflation, which sets on at . As it is shown below, during most of the preinflationary era, the kinetic energy density of the scalar field dominates over the field-dependent piece of its potential energy density, and the latter takes over when the slow-roll inflation sets on, preceded by the equality .
- The discussion of the evolution in terms of the dimensionless quantities [1,56,57] reveals that even the preinflationary era, both in QIM1 and QIM2, is divided into two suberas due to the scale dependence of the dark energy density, i.e., due to quantum effects. Those suberas are separated by the equality of the dark energy density to the potential energy density , i.e., .
2. Model
3. Neglection of the RG Flow of the Inflaton Mass: QIM1
3.1. Evolution in Terms of the Dimensionful Quantities
3.2. Numerical Results
- For the wide range of the inflaton mass, there occurs the slow-roll inflation for preceded by the preinflationary era for , subdividing COE2 into three suberas. The last one, the postinflationary era for has not been followed by us numerically since our model does not incorporate the physics yielding the graceful exit from the slow-roll inflation. In particular, the desirable slow-roll inflation has been achieved for the choice , and it is characterized by the time scalesthe parametersand the spectral observablesThe formulas used here (and below in connection with QIM2) for the evaluation of the spectral parameters of the fluctuations are just the same as those used for GRM. Although quantum improvement modifies the cosmological background and the Mukhanov–Sasaki equation is modified, too, we have shown in Appendix B that when the slow roll sets on, the quantum effects are already dead. This justifies evaluating the spectral parameters by the usage of the same formulas for the models GRM, QIM1, and QIM2. The inflaton mass providing the desirable inflation turned out to be four orders of magnitude smaller than in the corresponding classical model. Except for the tensor fraction, the results given in Equation (30) are in disagreement with the recent Planck2018 data [61,62]; the amplitude of the scalar perturbations turns out to be eight orders of magnitude smaller than its value deduced from the observations. Due to the time delay in the onset of the slow roll, the value of the Hubble parameter is, by cca, four orders of magnitude less in QIM1 than in the corresponding GRM. The time delay occurs due to the four orders of magnitude smaller inflaton mass. The rough estimate given in Equation (A28) also shows that the amplitude should be underestimated in QIM1 by the ratio .
- The evolution in RFPE, i.e., for , is rather close to the one described by the analytic estimates given in Appendix A. For example, for , the relative discrepancy between the numerically determined endpoint and its analytic estimate given by Equation (A6) remains less than 0.3 percent when the time is varied from to , justifying that we have chosen sufficiently early time in order to settle the initial conditions via the analytic formulas given in Appendix A. Furthermore, one can conclude that the piece of the phase trajectory belonging to RFPE is essentially independent of the inflaton mass and the inverse proportionality of the Hubble parameter and the RG scale k with the cosmological time t, given by Equations (A4) and (A3), is a rather good approximation. Therefore, the time does not depend on the inflaton mass.
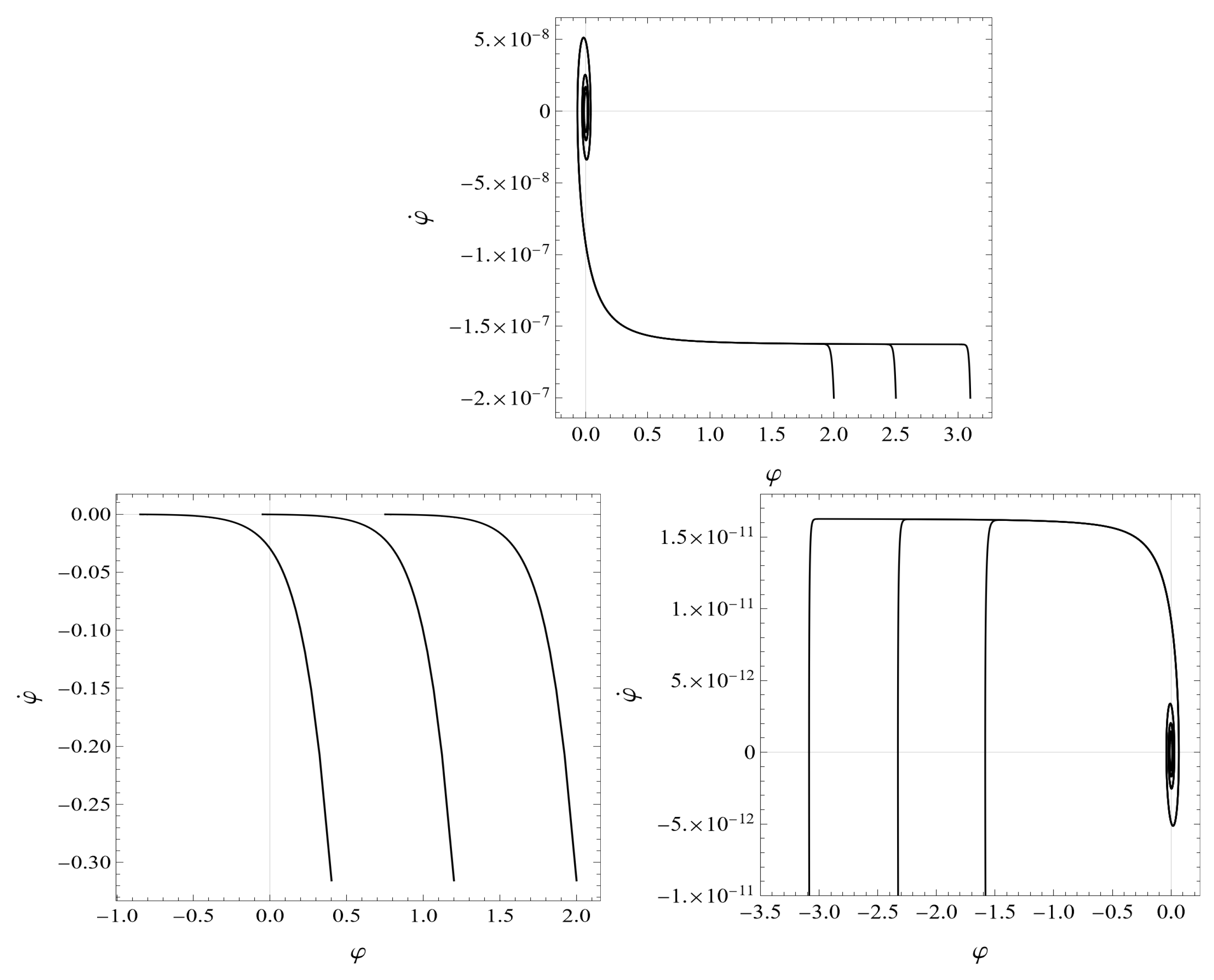
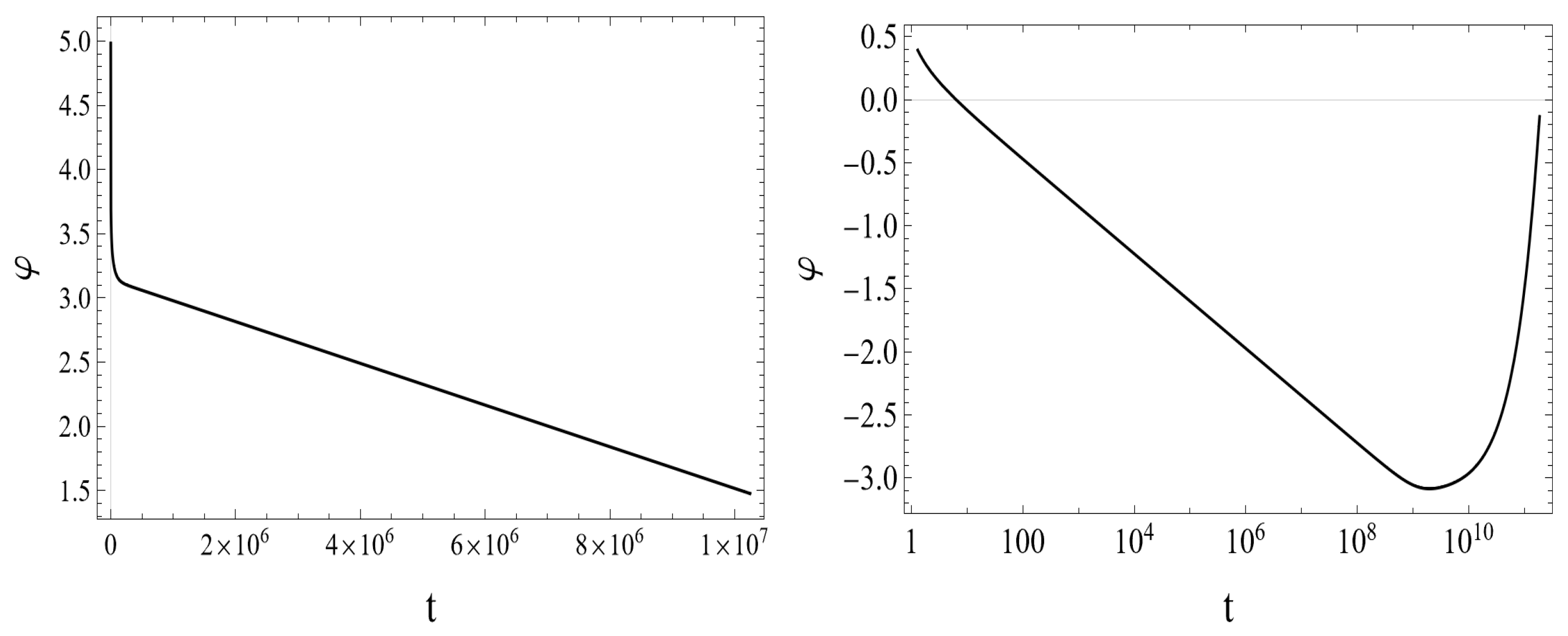
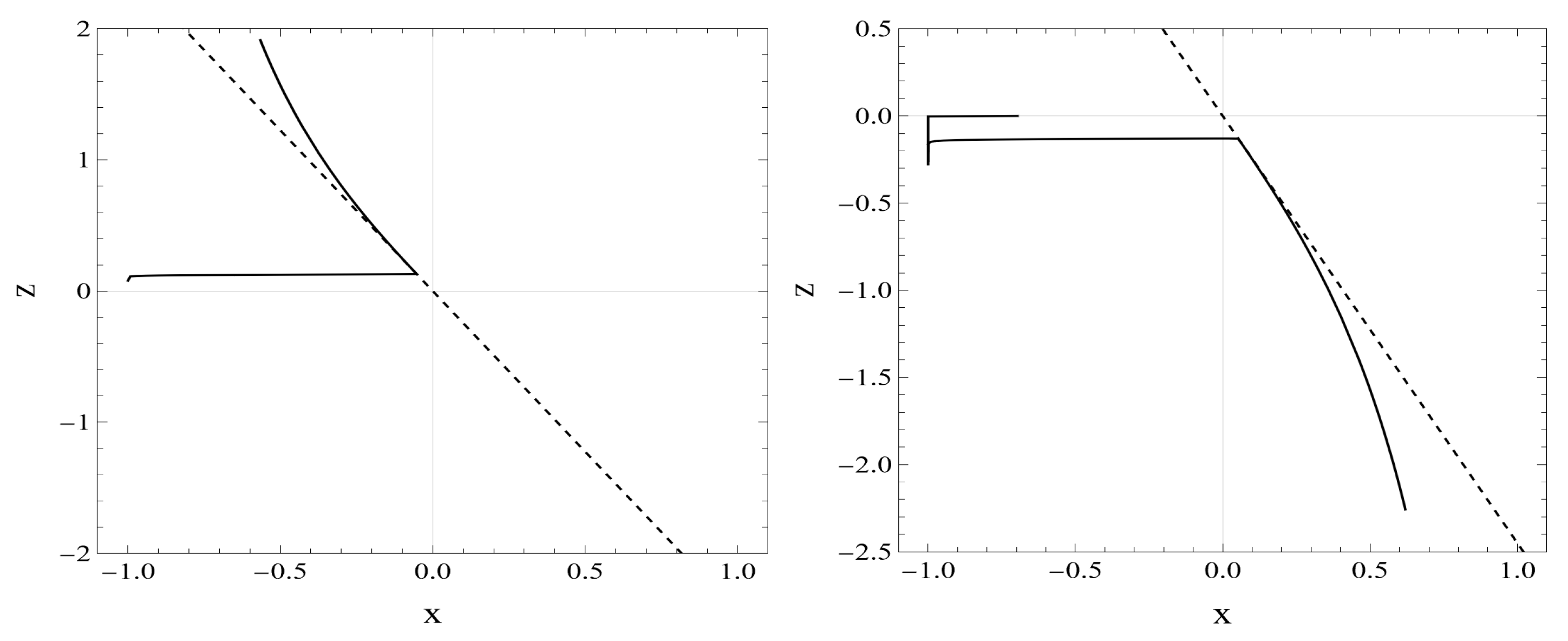
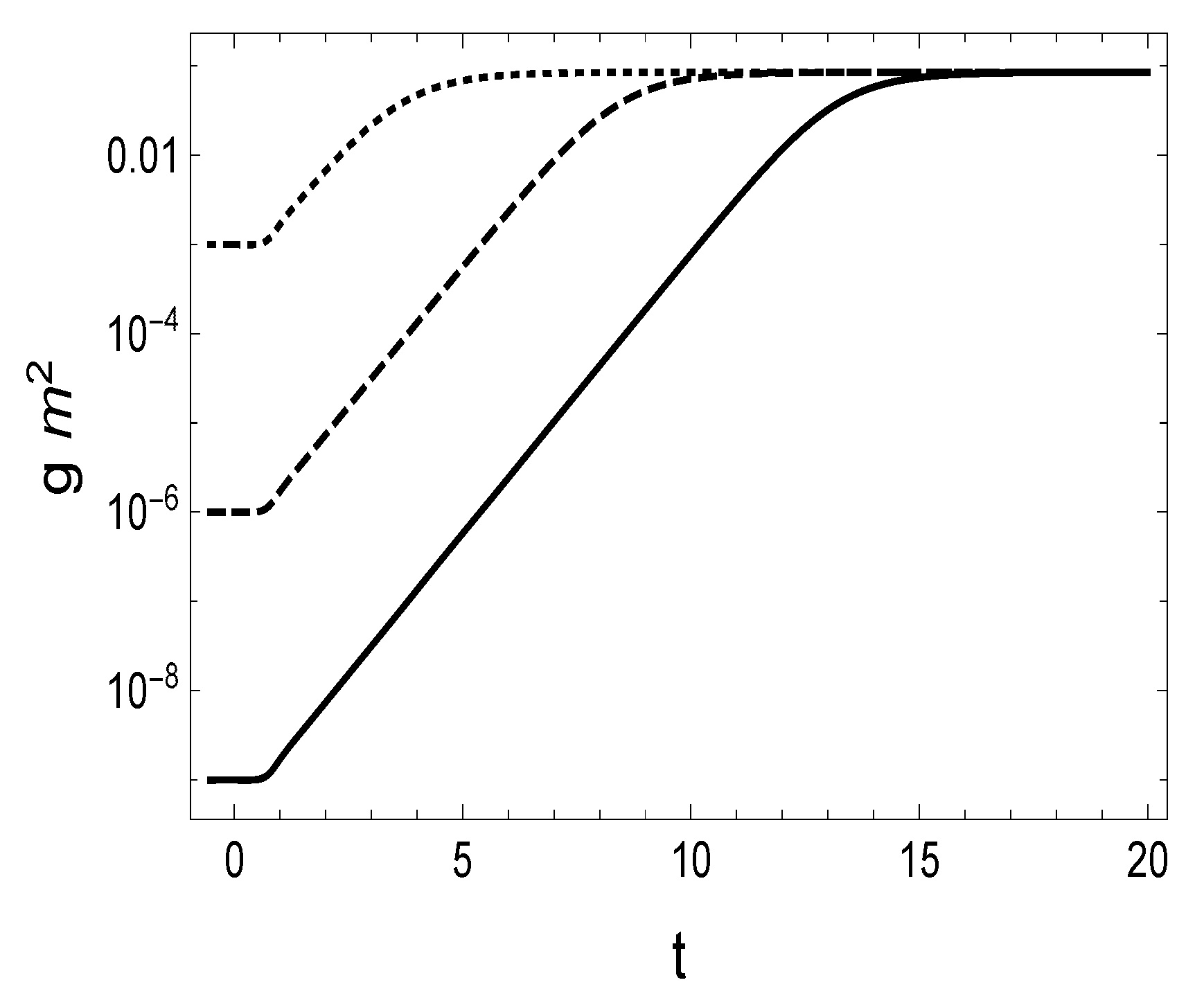
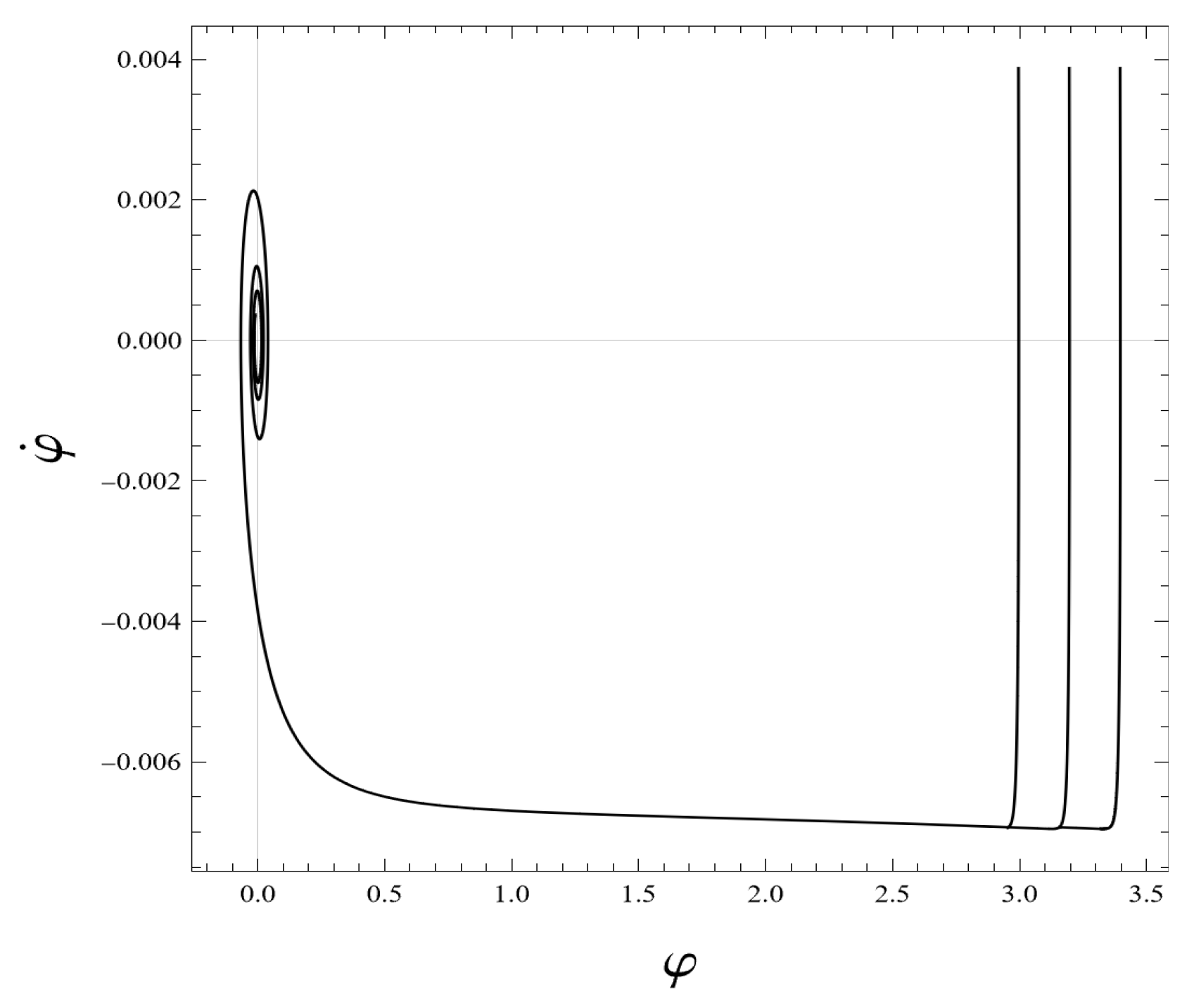
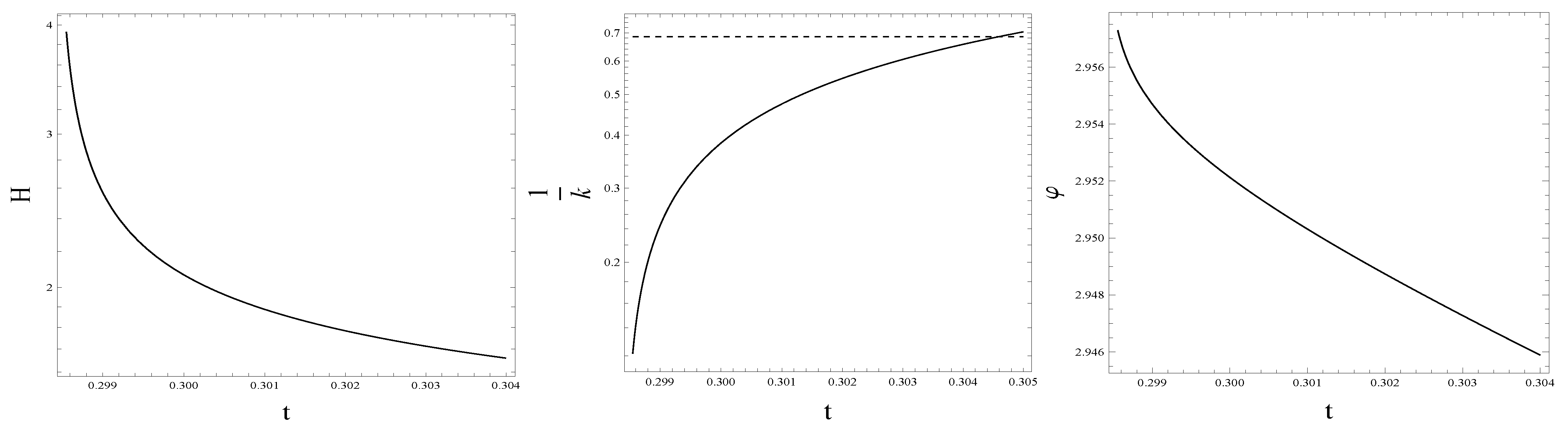
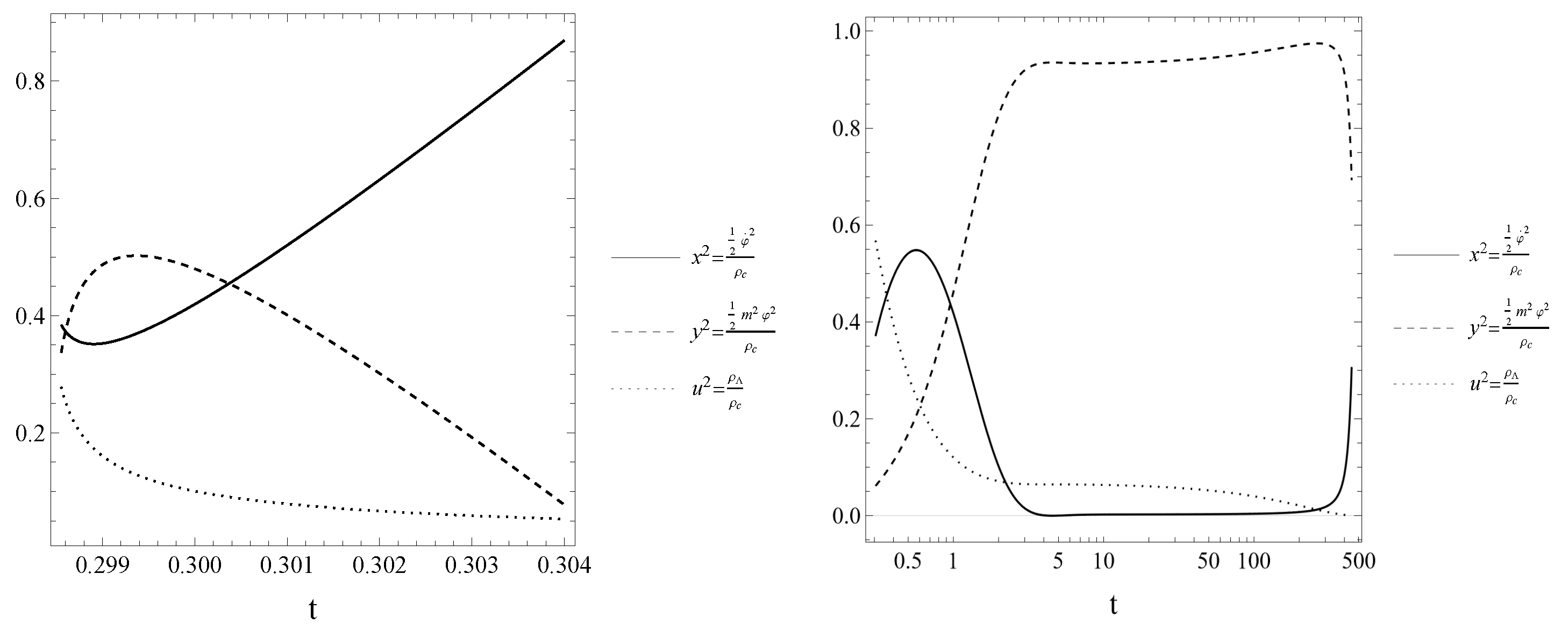
- As shown in Figure 1 (the bottom plot to the right), the phase trajectories run onto the universal attractor (with for ) even in the quantum-improved case. In QIM1, the desirable slow-roll inflation sets on at the scale . Therefore, as we argued in Appendix B, the quantum-improved attractor given by Equation (A14) is practically the same as the classical attractor given by Equation (A20), except for the big difference in the numerical values of the inflaton masses in QIM1 and GRM. Nevertheless, there is a difference in the evolution of the system in the classical GRM and in QIM1 that can be explained by the time dependence of the field in both cases, shown in Figure 2. Along the classical trajectory, the magnitude of the inflaton field decreases strictly monotonically up to the end of the slow-roll era and starts to oscillate around zero afterward for . On the plot to the left in Figure 2, it is well distinguishable the preinflationary era with a rather steep fall off of followed by the slow-roll era, with an almost linear decrease of with increasing time t (c.f. Equation (A20)), both well known [58]. The plot to the right in Figure 2 shows the time dependence of in QIM1. In RFPE (with ) for the evolution of the system can be estimated as given in Appendix A; the gravitational couplings evolve according to the scaling laws dictated by the Reuter FP, and the scalar field exhibits an ultrahard EoS. Just after the end of RFPE, crosses zero at ( on the plot). With the start of COE2, the scaling laws of the gravitational couplings alter: according to Equations (3) and (4), raises slightly, keeping its order of magnitude, while falls off proportionally with . This implies that the yet huge kinetic energy density of the scalar field increases further at the cost of the dark energy density falling off proportionally to (see the plot to the left on Figure 3). Therefore, the field continues to decrease through negative values and runs up the potential on the other side, where it reaches the turning point at at the time , where takes its maximum value and the inflaton field loses its kinetic energy density, terminating the preinflationary era. Reaching the turning point of is preceded by getting equal the fraction of the kinetic energy density and that of the potential energy density to the critical energy density (the point of the equality lies at on the plot to the left in Figure 3). Rather soon after the turning point, the slow roll sets on, i.e., . Then an almost linear decrease of takes place (c.f. Equation (A20)), followed by the damped oscillations of the field for , like in the classical case.
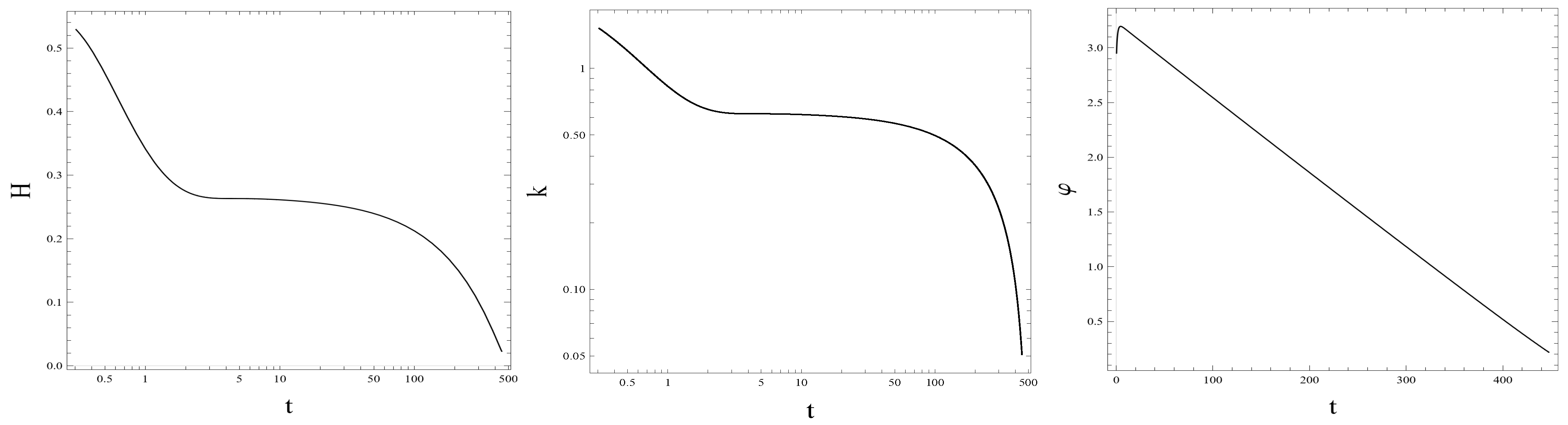
- The plots on the top of Figure 4 show that the Hubble parameter H and the energy scale k exhibit quite similar time dependences: both of them suffer a fall off of roughly eight orders of magnitude during the preinflationary era followed by a rather slow (less than an order of magnitude) decrease during the slow roll era. In the preinflationary era, except for its very beginning and very end, the potential energy density and the dark energy density are negligible as compared with the kinetic energy density (see the plot to the left in Figure 3), and it holds . Therefore, the Friedmann equations reduce to the onesproviding the ODE with the solutionwhere . This estimate fits the numerical results with better than a relative accuracy of . Then one obtainsandwhich states that the field amplitude decreases roughly proportionally with the logarithm of the time the system spent in the preinflationary era (as shown on the plot to the right in Figure 2). Approaching the end of the preinflationary era, the increasing fraction of the potential energy density becomes equal to the decreasing fraction of the kinetic energy density of the inflaton field at times , and this precedes the onset of the slow roll energetically with some delay at (see the plot to the left in Figure 3).It is argued in Appendix D that in the slow-roll inflationary era, the Hubble parameter should show a rather slight linear decrease with increasing cosmological time t. It has been found that the numerically evaluated value of the Hubble parameter H is in a few percentage agreement with the value obtained from the analytical Formula (A21), except at the very end of the slow-roll era.As it is shown on the plot on the bottom of Figure 4, the ratio is constant for except for the rather short time interval lasting from the beginning of the preinflationary era to the zero-crossing time of . Except for the latter time interval, it holds the relation (shown by the dashed line on the plot) with good accuracy. Let us insert the expression of given by the reduced consistency condition (22) and as given in Equation (9) into the first Friedmann Equation (7), make the approximation , and neglect the term in Equation (4); then we find thatwhich yields the estimate for with good accuracy, in agreement with the result of numerics. The ratio is somewhat smaller in RFPE than its value in the preinflationary and inflationary eras; its increase happens during the short time interval .
- The various time dependences (see Equation (A4) in Appendix A), (see Equation (32)), and (see Equation (A21) in Appendix D) of the Hubble parameter in RFPE, the preinflationary, and slow-roll inflationary eras, respectively, inform one on the time dependence of the scale factor,and on that of the deceleration parameterThus, one finds that the quantum gravitational effects, being strong in the Reuter FP driven and the preinflationary eras, do not result in the accelerating expansion of the universe; the latter occurs due to the presence of the inflaton field in the slow-roll era, with the characteristic value of the deceleration parameter , which corresponds to an almost exponential increase of the scale factor . It is worthwhile mentioning that in RFPE the scalar field behaves like dust so far as the time dependence of the scale factor is considered, which is the consequence of the interplay between the ultrahard EoS and the Reuter FP governed scaling laws of the gravitational couplings (see Appendix A).
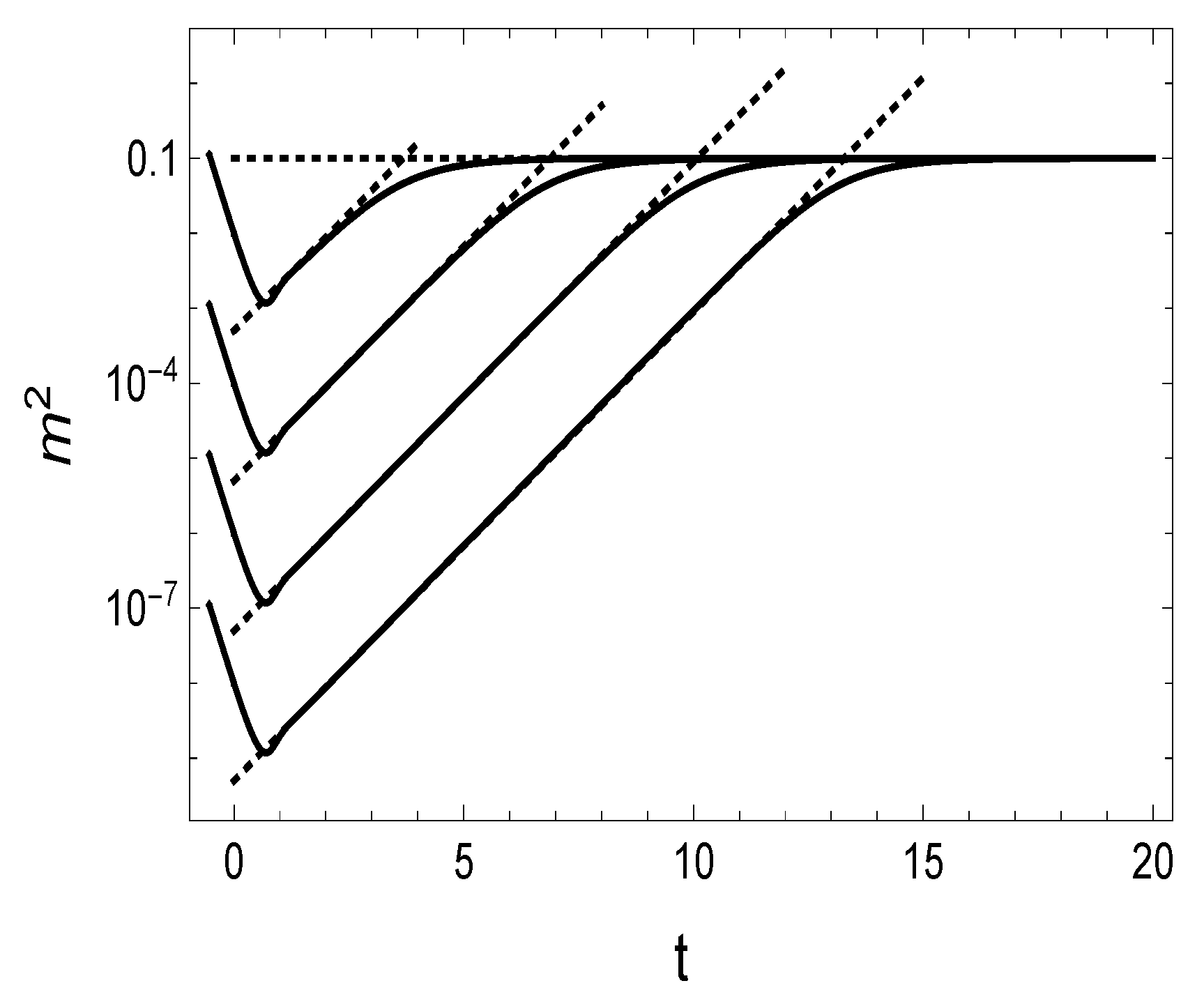
- It has been shown that the slow-roll inflationary era occurs inside COE2 for a wide range of the inflaton mass m. In Table 1, one can see that the onset time of the slow roll is shifted to later times, and the duration of the slow-roll era becomes longer by a few orders of magnitude when the inflaton mass decreases from to while the number of e-foldings rises within an order of magnitude.
- Comparing the time scales of the desirable slow-roll inflation given in Equation (28) for QIM1 with those for the classical model, GRM, given in Equation (25), one sees that there are (i) four orders of magnitude time delay in the start and (ii) also four orders of magnitude increase of the duration of the desirable slow-roll inflation due to the quantum gravitational effects. At around the scale (at the time ), the running Newton coupling rather suddenly reaches its classical value , while the running cosmological constant is yet huge (of the order of ) at that scale and decreases only slowly with decreasing scale k. This circumstance hinders the inflaton field from losing its kinetic energy density as fast as in the classical case. Furthermore, as it is seen in the plots in Figure 2, the desirable slow roll starts roughly at the same value of in the classical and the quantum-improved cases, but the corresponding potential energy density in the quantum-improved case is eight orders of magnitude less than in the classical case due to the change in the required value of . This is another reason that much more time is needed for the potential energy density to take over the kinetic energy density of the inflaton field in the quantum-improved case. In spite of the different timing of the slow roll in GRM and QIM1, the main qualitative features of the slow-roll inflation are negligibly affected by the quantum effects, except for the amplitude for the scalar perturbations, as discussed in Appendix D on the level of analytic estimates. A comparison of our numerical results, obtained for the desirable slow roll, given in Equations (26) and (27) for GRM and in Equations (29) and (30) for QIM1, completely supports the expectation that only the amplitude of the scalar perturbations is affected significantly by the quantum improvement. The reason is the rather small inflaton mass required to achieve the desirable number of e-foldings. Maybe accidentally, GRM yields better, an order-of-magnitude agreement of with the observational data given in Refs. [61,62], than QIM1. Therefore, one has to conclude that the simple inflaton potential with scale-independent inflaton mass works much worse in the quantum-improved case than in the classical one.
3.3. Evolution in Terms of the Dimensionless Quantities
3.3.1. General Considerations
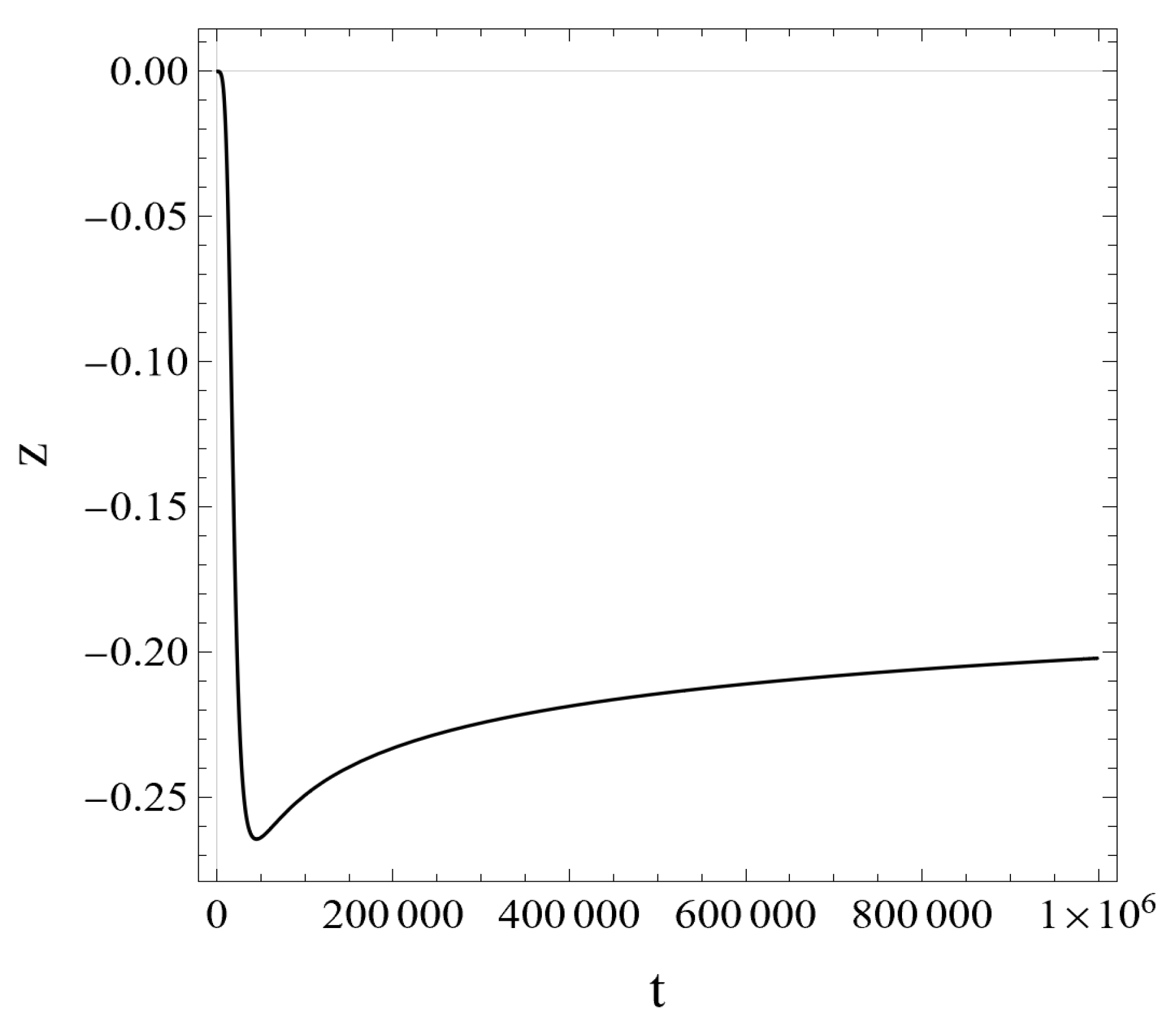
- The variable keeps strictly one of the constant valuesin RFPE. Since (see Appendix A), it holdsimplying that in RFPE. (Here, we made use of eq. (27) in Ref. [1] applied to our case.) This means that in the limit , i.e., in the limit (). Therefore, the CFP corresponding to the Big Bang continues to evolve with the scale factor a.
- In RFPE, is negligible as compared with , , so that one findsThe variable z shows up time dependence (N-dependence) in RFPE, but it tends to zero in the limit .
3.3.2. Numerical Results
4. Scale-Dependent Inflaton Mass
4.1. Interpolation Formula for the Running Inflaton Mass
4.2. Cosmological Evolution in QIM2
4.2.1. Evolution Equations
4.2.2. Numerical Results
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Analytic Estimate of the Evolution in RFPE for QIM1
Appendix B. Quantum-Improved Universal Attractor
Appendix C. Slow-Roll Inflation in GRM
Appendix D. Influence of the Inflaton Mass on the Observable Features of the Slow-Roll Inflation
Appendix E. Analytic Solution of the Evolution Equations in RFPE for QIM2
Appendix F. Evolution in COE1 for QIM2
References
- Hindmarsh, M.; Litim, D.; Rahmede, C. Asymptotically Safe Cosmology. J. Cosmol. Astropart. Phys. 2011, 7, 19. [Google Scholar] [CrossRef]
- Bonanno, A.; Saueressig, F. Asymptotically safe cosmology—A status report. C. R. Phys. 2017, 18, 254. [Google Scholar] [CrossRef]
- Mandal, R.; Gangopadhyay, S.; Lahir, A. Cosmology with modified continuity equation in asymptotically safe gravity. Eur. Phys. J. Plus 2022, 137, 1110. [Google Scholar] [CrossRef]
- Tye, S.-H.H.; Xu, J. Comment on Asymptotically Safe Inflation. Phys. Rev. D 2010, 82, 127302. [Google Scholar] [CrossRef]
- Weinberg, S. Asymptotically Safe Inflation. Phys. Rev. D 2010, 81, 083535. [Google Scholar] [CrossRef]
- Biemans, J.; Platania, A.; Saueressig, F. Quantum gravity on foliated spacetime–asymptotically safe and sound. Phys. Rev. D 2017, 95, 086013. [Google Scholar] [CrossRef]
- Bonanno, A.; Gionti, G.; Platania, A. Bouncing and emergent cosmologies from ADM RG flows. arXiv 2017, arXiv:1710.06317. [Google Scholar]
- Anagnostopoulos, F.K.; Basilakos, S.; Kofinas, G.; Zarikas, V. Constraining the Asymptotically Safe Cosmology: Cosmic acceleration without dark energy. J. Cosmol. Astropart. Phys. 2019, 2, 053. [Google Scholar] [CrossRef]
- Pawlowski, J.M.; Reichert, M.; Wetterich, C.; Yamada, M. Higgs scalar potential in asymptotically safe quantum gravity. Phys. Rev. D 2019, 99, 086010. [Google Scholar] [CrossRef]
- Wetterich, C. Effective scalar potential in asymptotically safe quantum gravity. Universe 2021, 7, 45. [Google Scholar] [CrossRef]
- Platania, A. From renormalization group flows to cosmology. Front. Phys. 2020, 8, 188. [Google Scholar] [CrossRef]
- Eichhorn, A.; Pauly, M. Constraining power of asymptotic safety for scalar fields. Phys. Rev. D 2021, 103, 026006. [Google Scholar] [CrossRef]
- Hoshina, H. Asymptotically free and safe quantum gravity scenarios consistent with Hubble, laboratory, and inflation scale physics. Phys. Rev. D 2022, 106, 086024. [Google Scholar] [CrossRef]
- Weinberg, S. Understanding of Fundamental Constituents of Matter; Zichichi, A., Ed.; Plenum Press: New York, NY, USA, 1977. [Google Scholar]
- Reuter, M.; Saueressig, F. Quantum Einstein Gravity. New J. Phys. 2012, 14, 055022. [Google Scholar] [CrossRef]
- Reuter, M.; Saueressig, F. Quantum Gravity and the Functional Renormalization Group: The Road towards Asymptotic Safety; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Bonanno, A.; Eichhorn, A.; Gies, H.; Pawlowski, J.M.; Percacci, R.; Reuter, M.; Saueressig, F.; Vacca, G.P. Critical reflections on asymptotically safe gravity. Front. Phys. 2020, 8, 269. [Google Scholar] [CrossRef]
- Reuter, M. Nonperturbative Evolution Equation for Quantum Gravity. Phys. Rev. D 1998, 57, 971. [Google Scholar] [CrossRef]
- Lauscher, O.; Reuter, M. Ultraviolet Fixed Point and Generalized Flow Equation of Quantum Gravity. Phys. Rev. D 2001, 65, 025013. [Google Scholar] [CrossRef]
- Lauscher, O.; Reuter, M. Is Quantum Einstein Gravity Nonperturbatively Renormalizable? Class. Quantum Grav. 2002, 19, 483. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Proper time flow equation for gravity. J. High Energy Phys. 2005, 2005, 35. [Google Scholar] [CrossRef]
- Litim, D.F. Fixed points of quantum gravity. Phys. Rev. Lett. 2004, 92, 201301. [Google Scholar] [CrossRef]
- Reuter, M.; Saueressig, F. Functional Renormalization Group Equations, Asymptotic Safety, and Quantum Einstein Gravity. arXiv 2007, arXiv:0708.1317. [Google Scholar]
- Codello, A.; Percacci, R.; Rahmede, C. Investigating the Ultraviolet Properties of Gravity with a Wilsonian Renormalization Group Equation. Ann. Phys. 2009, 324, 414. [Google Scholar] [CrossRef]
- Christiansen, N.; Litim, D.F.; Pawlowski, J.M.; Rodigast, A. Fixed points and infrared completion of quantum gravity. Phys. Lett. B 2014, 728, 114. [Google Scholar] [CrossRef]
- Donà, P.; Eichhorn, A.; Percacci, R. Matter matters in asymptotically safe quantum gravity. Phys. Rev. D 2014, 89, 084035. [Google Scholar] [CrossRef]
- Dupuis, N.; Canet, L.; Eichhorn, A.; Metzner, W.; Pawlowski, J.M.; Tissier, M.; Wschebor, N. The nonperturbative functional renormalization group and its applications. Phys. Rept. 2021, 910, 1–114. [Google Scholar]
- Eichhorn, A.; Schiffer, M. Asymptotic safety of gravity with matter. In Handbook of Quantum Gravity; Bambi, C., Modesto, L., Shapiro, I.L., Eds.; Springer: Berlin, Germany, 2023; p. 89. [Google Scholar]
- Biemans, J.; Platania, A.; Saueressig, F. Renormalization group fixed points of foliated gravity-matter systems. J. High Energy Phys. 2017, 2017, 93. [Google Scholar] [CrossRef]
- Eichhorn, A. Asymptotically safe gravity. arXiv 2020, arXiv:2003.00044. [Google Scholar]
- Percacci, R.; Perini, D. Contraints on Matter from Asymptotic Safety. Phys. Rev. D 2003, 67, 081503. [Google Scholar] [CrossRef]
- Wetterich, C. Quantum gravity and scale symmetry in cosmology. arXiv 2022, arXiv:2211.03596. [Google Scholar]
- Sen, S.; Wetterich, C.; Yamada, M. Scaling solutions for asymptotically free quantum gravity. J. High Energy Phys. 2023, 2023, 54. [Google Scholar] [CrossRef]
- Meibohm, J.; Pawlowski, J.M.; Reichert, M. Asymptotic safety of gravity-matter systems. Phys. Rev. D 2016, 93, 084035. [Google Scholar] [CrossRef]
- Pastor-Gutiérrez, Á.; Pawlowski, J.M.; Reichert, M. The Asymptotically Safe Standard Model: From quantum gravity to dynamical chiral symmetry breaking. SciPost Phys. 2023, 15, 105. [Google Scholar] [CrossRef]
- Laporte, C.; Pereira, A.D.; Saueressig, F.; Wang, J. Scalar-Tensor theories within Asymptotic Safety. J. High Energy Phys. 2021, 2021, 1. [Google Scholar] [CrossRef]
- Gubitosi, G.; Ripken, C.; Saueressig, F. Scales and hierachies in asymptotically safe quantum gravity: A review. Found. Phys. 2019, 49, 972. [Google Scholar] [CrossRef]
- Manrique, E.; Rechenberger, S.; Saueressig, F. Asymptotically Safe Lorentzian Gravity. Phys. Rev. Lett. 2011, 106, 251302. [Google Scholar] [CrossRef] [PubMed]
- Pawlowski, J.M.; Strodthoff, N. Real time correlation functions and the functional renormalization group. Phys. Rev. D 2015, 92, 094009. [Google Scholar] [CrossRef]
- Nagy, S.; Sailer, K.; Steib, I. Renormalization of Lorentzian conformally reduced gravity. Class. Quantum Gravity 2019, 36, 155004. [Google Scholar] [CrossRef]
- Knorr, B.; Schiffer, M. Non-Perturbative Propagators in Quantum Gravity. Universe 2021, 7, 216. [Google Scholar] [CrossRef]
- Platania, A. Causality, unitarity and stability in quantum gravity: A non-perturbative perspective. arXiv 2022, arXiv:2206.04072. [Google Scholar] [CrossRef]
- Nagy, S.; Sailer, K. Interpolation formulas for asymptotically safe cosmology. Universe 2023, 9, 184. [Google Scholar] [CrossRef]
- Donoghue, J.F. Do ΛCC and G run? Acta Phys. Pol. B 2024, 55, 12-A1.1–12-A1.17. [Google Scholar]
- Basile, I.; Buoninfante, L.; Di Filippo, F.; Knorr, B.; Platania, A.; Tokareva, A. Lectures in Quantum Gravity, Lecture notes PhD school “Towards Quantum Gravity”, Nordita Scientific Program “Quantum Gravity: From gravitational EFTs to UV complete approaches”. arXiv 2004, arXiv:2412.08690. [Google Scholar]
- Saueressig, F. The Functional Renormalization Group in Quantum Gravity. In Handbook of Quantum Gravity; Bambi, C., Modesto, L., Shapiro, I.L., Eds.; Springer: Singapore, 2024. [Google Scholar]
- Bonanno, A.; Denz, T.; Pawlowski, J.M.; Reichert, M. Reconstructing the graviton. SciPost Phys. 2022, 12, 001. [Google Scholar] [CrossRef]
- Wetterich, C. Average Action and the Renormalization Group Equations. Nucl. Phys. B 1991, 352, 529. [Google Scholar] [CrossRef]
- Griguolo, L.; Percacci, R. The beta functions of a scalar theory coupled to gravity. Phys. Rev. D 1995, 52, 5787. [Google Scholar] [CrossRef]
- Narain, G.; Percacci, R. Renormalization Group Flow in Scalar-Tensor Theories. I. Class. Quantum Gravity 2009, 27, 075001. [Google Scholar] [CrossRef]
- Narain, G.; Rahmede, C. Renormalization Group Flow in Scalar-Tensor Theories. II. Class. Quantum Gravity 2010, 27, 075002. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Bonanno, A.; Reuter, M. Cosmology of the Planck Era from a Renormalization Group for Quantum Gravity. Phys. Rev. D 2002, 65, 043508. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Cosmology with selfadjusting vacuum energy density from a renormalization group fixed point. Phys. Lett. B 2002, 527, 9. [Google Scholar] [CrossRef]
- Babić, A.; Guberina, B.; Horvat, R.; Stefancić, H. Renormalization-group running cosmologies—A scale-setting procedure. Phys. Rev. D 2005, 71, 124041. [Google Scholar] [CrossRef]
- Copeland, E.J.; Liddle, A.R.; Wands, D. Exponential potentials and cosmological scaling solutions. Phys. Rev. D 1998, 57, 4686. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753. [Google Scholar] [CrossRef]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Ashtekar, A.; Sloan, D. Probability of Inflation in Loop Quantum Cosmology. Gen. Rel. Grav. 2011, 43, 3619. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith K., M.; Dunkley, J.; Bennett C., L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta M., R.; Page, L.; et al. Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Forconi, M.; Giarè, W.; Valentino, E.D.; Melchiorri, A. Cosmological constraints on slow roll inflation: An update. Phys. Rev. D 2021, 104, 103528. [Google Scholar] [CrossRef]
- Planck Akrami, Y. et al. [Planck Collaboration]. Planck 2018 results-X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Litim, D.F. Optimisation of the exact renormalisation group. Phys. Lett. B 2000, 486, 92. [Google Scholar] [CrossRef]
- Litim, D.F. Optimised Renormalisation Group Flows. Phys. Rev. D 2001, 64, 105007. [Google Scholar] [CrossRef]
- Wetterich, C. Exact evolution equation for the effective potential. Phys. Lett. B 1993, 301, 90. [Google Scholar] [CrossRef]
- Silva, A. Emergence of inflaton potential from asymptotically safe gravity. Phys. Lett. B 2025, 860, 139154. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [BICEP/Keck Collaboration]. Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season. Phys. Rev. Lett. 2021, 127, 151301. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S.S. Cosmic Inflation: Background dynamics, Quantum fluctuations and Reheating. arXiv 2024, arXiv:2403.10606. [Google Scholar]

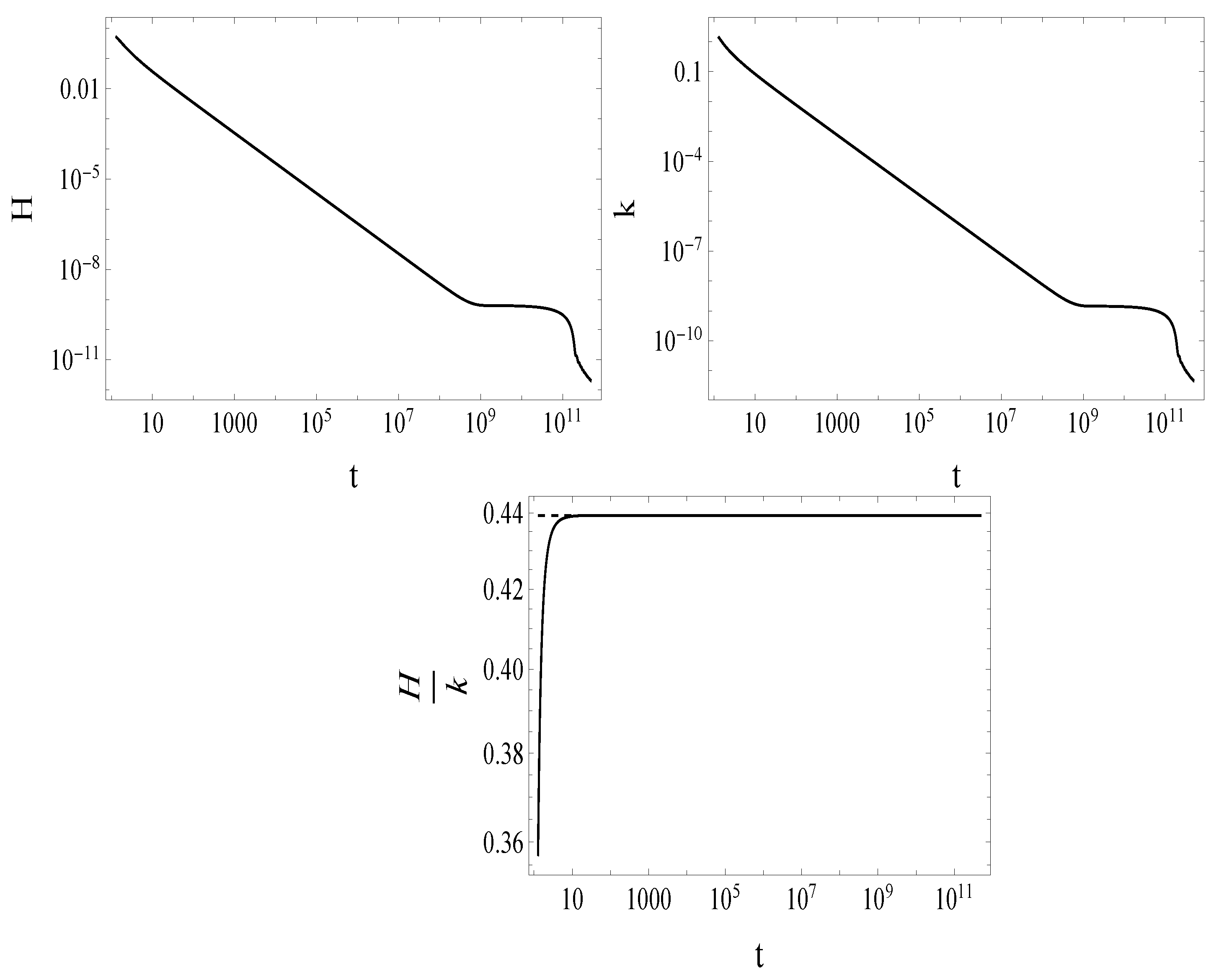

| 110 | |||
| 92 | |||
| 75 | |||
| 60 | |||
| 47 | |||
| 36 | |||
| 26 | |||
| 18 |
| NGFP1 | 0.2 | ||||
| NGFP2 | 0 |
| 960 | ||||||
| 820 | ||||||
| 714 | ||||||
| 622 | ||||||
| 551 | ||||||
| 488 | ||||||
| 436 | ||||||
| 391 | ||||||
| 353 | ||||||
| 320 | ||||||
| 290 |
| Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| QIM1 | ||||||||
| QIM2 | 448 |
| GRM | QIM1 | QIM2 | |
|---|---|---|---|
| GRM | QIM1 | QIM2 | |
|---|---|---|---|
| ∼t−1 | ∼t−2 | ∼t−2 | |
| H | ∼t−1 | ∼t−1 | ∼t−1 |
| k | ― | ∼t−1 | ∼t−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagy, J.; Nagy, S.; Sailer, K. Time Scales of Slow-Roll Inflation in Asymptotically Safe Cosmology. Universe 2025, 11, 77. https://doi.org/10.3390/universe11030077
Nagy J, Nagy S, Sailer K. Time Scales of Slow-Roll Inflation in Asymptotically Safe Cosmology. Universe. 2025; 11(3):77. https://doi.org/10.3390/universe11030077
Chicago/Turabian StyleNagy, József, Sándor Nagy, and Kornél Sailer. 2025. "Time Scales of Slow-Roll Inflation in Asymptotically Safe Cosmology" Universe 11, no. 3: 77. https://doi.org/10.3390/universe11030077
APA StyleNagy, J., Nagy, S., & Sailer, K. (2025). Time Scales of Slow-Roll Inflation in Asymptotically Safe Cosmology. Universe, 11(3), 77. https://doi.org/10.3390/universe11030077







