Abstract
We consider the thermodynamic and stability problem of Kerr black holes arising from the nonextensive/nonadditive nature of the Bekenstein–Hawking entropy formula. Nonadditive thermodynamics is often criticized by asserting that the zeroth law cannot be compatible with nonadditive composition rules, so in this work we follow the so-called formal logarithm method to derive an additive entropy function for Kerr black holes also satisfying the zeroth law’s requirement. Starting from the most general, equilibrium compatible, nonadditive entropy composition rule of Abe, we consider the simplest non-parametric approach that is generated by the explicit nonadditive form of the Bekenstein–Hawking formula. This analysis extends our previous results on the Schwarzschild case, and shows that the zeroth law-compatible temperature function in the model is independent of the mass–energy parameter of the black hole. By applying the Poincaré turning point method, we also study the thermodynamic stability problem in the system.
1. Introduction
After the finding of the Kerr solution [1], the mathematical and physical properties of the corresponding black hole spacetimes have been widely investigated. As a culmination of the work done in the first decade, the four laws of black hole mechanics were formulated by Bardeen, Carter, and Hawking [2]. These four laws show a striking similarity to the laws of thermodynamics and can be summarized as the following:
- The zeroth law of black hole mechanics states that the surface gravity κ of a stationary black hole is constant over the horizon, which is essentially the requirement of transitivity of the equilibrium state.
- The first law manifests a relation between variations in the mass M, horizon area A, and angular momentum J if the black hole is perturbed,where is the angular velocity of the horizon.
- The second law of black hole mechanics is Hawking’s area theorem, which states that the surface area of the event horizon never decreases with time,
- The third law is formulated by stating that it is impossible to achieve in a finite series of physical processes.
The close analogy between the four laws of black hole mechanics and the laws of ordinary thermodynamics is intriguing. In this analogy, the mass of the black hole mathematically corresponds to the energy of a thermodynamic system, the area of the horizon to the entropy, and the surface gravity to the temperature. While the correspondence between mass and energy is a physical identity, the other two correspondences are only analogy in classical general relativity. Classical black holes have zero temperature, and the area of the horizon has a dimension of length squared. With the physical penetration of the black hole entropy by Bekenstein [3] and the semi-classical derivation of black hole radiation by Hawking [4], we can treat black holes as thermodynamic systems with the Bekenstein–Hawking entropy
at the Hawking temperature
Investigations in gravitating systems have pointed out that entropy functions with nonextensive nature tend to appear in systems with long-range interactions like gravity (e.g., [5] and references therein). The Bekenstein–Hawking black hole entropy also seems to be nonextensive because it is proportional to the area of the horizon instead of being proportional to the black hole volume (although the problem of how to compute the volume of a general black hole and how it is related to the horizon area is also a nontrivial question [6]). The nonextensive nature of black hole thermodynamics has been studied with many approaches and various methods [7,8,9,10,11,12,13,14,15,16], and in the present paper we also consider a simple model to the Kerr problem that we have already investigated in the Schwarzschild case [17]. The main idea behind this approach is to study the system in equilibrium while also requiring to satisfy the zeroth law of thermodynamics.
1.1. Equilibrium Compatibility
As a fundamental formula, we start with the most general functional form of nonadditive entropy composition rules (derived by Abe [18]), requiring only the existence of equilibrium in the system. Assuming that the total entropy is given by the entropies of the subsystems and as where f is a class symmetric function, Abe derived the most general pseudoadditivity rule for the entropy,
where is a differential function of S and is a constant parameter. By setting to zero with the physical requirement of zero joint entropy for zero subsystem entropies, Abe’s equation becomes
Obviously, for standard additive thermodynamic systems, is the identity function and the λ parameter is zero. In more general cases, however, equilibrium compatibility requires the nonadditive entropy composition rules to satisfy Equation (2) for any thermodynamic system.
Perhaps the most well-known example for a nonstandard case was proposed by Tsallis in 1988 [19], where he introduced an entropic function
by generalizing the Boltzmann–Gibbs formula . Based on this entropy approach, Tsallis has also generalized the standard Boltzmann–Gibbs theory to nonextensive statistical mechanics [20]. It is easy to see that the Tsallis entropy recovers the Boltzmann–Gibbs entropy for , and when one considers two independent systems A and B, the Tsallis entropy of the composed system satisfies
1.2. Zeroth Law Compatibility
One of the crucial criticisms of nonextensive thermodynamics is that the transitivity property of thermal equilibrium and the definition of an empirical temperature (i.e., the zeroth law of thermodynamics) do not seem to be compatible with nonadditive entropy composition rules. In standard thermodynamics, the empirical temperature is defined as
This definition is derived from total energy conservation and maximum entropy postulate in the system with the assumption of additivity of these two thermodynamic variables. In a recent paper [21], Biró and Ván generalized this derivation to the case of nonadditive composition laws of the entropy and the energy functions as well. In their analysis—by keeping the maximum entropy principle and the total energy conservation—they found that a new zeroth law-compatible temperature can be obtained from the more general definition
where L and are the so-called formal logarithm functions of the nonadditive thermal variables, which map the original (nonadditive) composition laws to additive ones; i.e.,
It can be shown [21] that the formal logarithm of the Tsallis entropy (3)
is another well-known parametric generalization of the Boltzmann–Gibbs formula; namely, the Rényi entropy function
which was introduced by the Hungarian mathematician, Alfréd Rényi in the middle of the last century [22,23]. According to the properties of the formal logarithm mapping, and as opposed to the Tsallis formula, the Rényi entropy is additive for factorizing probabilities, so the corresponding temperature function (obtained by assuming energy additivity in the system)
is a well-defined empirical temperature that is compatible with all laws of thermodynamics, including the zeroth’s law as well.
1.3. A Parametric Approach
Recently, based on the above formal logarithm approach to the nonextensive problem of black hole thermodynamics, we investigated the thermodynamic [24] and stability [25] properties of the Schwarzschild solution. In the analysis of [24], we regarded the Bekenstein–Hawking entropy of black hole event horizons as a nonextensive Tsallis entropy, which for small energies and for small parameter values () was assumed to follow the nonadditive Tsallis composition law (4). As a result, the corresponding zeroth law-compatible entropy function became the Rényi entropy, and the resulting temperature exhibited some interesting features. Most notably, we observed that the relation between the temperature and the mass–energy parameter of the black hole had the same form as the one obtained from a black hole in AdS space by using the original Boltzmann–Gibbs entropy formula. The temperature has a minimum in both cases, and from the temperature–mass–energy relation, we could derive a correspondence between the nonextensitivity parameter (λ) of the Schwarzschild-Rényi model and the AdS curvature parameter.
In [25], we also investigated the thermodynamic stability of the problem. In the standard Boltzmann picture, Schwarzschild black holes seem to be thermodynamically unstable in the canonical treatment because their heat capacity is always negative. The standard stability analysis of extensive systems however is not generally applicable to black holes, since it strongly depends on the additivity of the entropy function [26], which is clearly not true for the Bekenstein–Hawking entropy of black holes. To avoid the inapplicability of the classical Hessian analysis to nonadditive systems, Kaburaki et al. [27] proposed the Poincaré turning point method [28] to investigate the thermodynamic stability of black holes. This method is a topological approach that does not depend on the additivity of the entropy function, and it has been widely applied to problems in astrophysical and gravitating systems [26,27,29,30,31] where—as we have already mentioned—entropy functions with nonextensive nature tend to appear frequently due to the long-range interaction property of the gravitational field.
We could apply both the standard Hessian and the Poincaré stability methods in our Schwarzschild–Rényi problem, since the entropy function given by the formal logarithm approach is an additive function. In [25], we first investigated the question of a pure, isolated black hole in the microcanonical ensemble. We showed that these configurations are stable against spherically symmetric perturbations, just like in the classical picture. Next, we also investigated the problem of a black hole surrounded by a bath of thermal radiation in the canonical treatment. We found that in contrast to the standard picture, Schwarzschild black holes can be in stable equilibrium with thermal radiation at a fixed temperature in the Rényi approach. We observed that a stability change occurs at a certain value of the mass–energy parameter which belongs to the minimum temperature solution. Smaller mass black holes are unstable, while larger mass black holes become stable in this model. These results are similar to the ones obtained by Hawking and Page in AdS space within the standard Boltzmann entropy approach [32]. Motivated by this similarity, we also investigated the question of a possible phase transition in the canonical picture and found that a Hawking–Page-like black hole phase transition occurs in a very similar manner as in AdS space. The corresponding critical temperature depends only on the Rényi entropy parameter.
To extend the above studies on the Schwarzschild–Rényi model, we have also examined the thermodynamic and stability properties of Kerr black holes within the Tsallis–Rényi approach [33]. We analyzed the thermodynamic stability of the problem in both the microcanonical and canonical ensembles, and found a stability change in the latter case. We showed that a Hawking–Page-like phase transition and a first-order small black hole/large black hole transition occur in this system, analogous to the ones of rotating black holes in AdS space [34,35,36]. By this we also confirmed the similarity between the Rényi–asymptotically flat and Boltzmann–AdS approaches to black hole thermodynamics in the rotating case.
1.4. A Nonparametric Approach
Abe’s general equilibrium-compatible entropy composition Formula (2) and the formal logarithm approach is not restricted to the Tsallis–Rényi model. In [21], Biró and Ván derived the formal logarithm map to all of those nonadditive entropy functions which satisfy Abe’s composition law, and showed that the most general form of equilibrium and zeroth law compatible entropy functions reads as
The Tsallis–Rényi model in this framework is a very interesting parametric approach to the nonextensive problem of black hole thermodynamics; however, there is another relevant nonadditive composition rule which one should also consider in connection with the problem—namely, the original nonadditive composition rule arising from the Bekenstein–Hawking entropy expression. Indeed, we started with the question of the nonextensivity/nonadditivity of the standard black hole entropy function, but we have not yet discussed whether it can satisfy the equilibrium compatibility condition of Abe’s formula. In a recent paper [17], we investigated the thermodynamic and stability problem of a Schwarzschild black hole by considering the nonadditive entropy composition rule that is emerging from the Bekenstein–Hawking description. We showed that in this case the entropy composition rule of the Schwarzschild problem takes the form
which—as it can be easily verified—corresponds to the case of and in Abe’s Formula (2). Starting from (13) and also applying the formal logarithm method of Biró and Ván, we investigated the thermodynamics and stability of the problem. The new additive entropy function for the black hole was obtained as
by mapping the composition law (13) to its formal logarithm. Assuming additivity of the energy function in the system, we obtained the new zeroth law-compatible entropy formula for Schwarzschild black holes as
which is a linear function of the mass–energy parameter. From definition (6), one obtains the corresponding zeroth law-compatible temperature of the black hole as
which is an energy-independent constant. Therefore, in this model, all black holes have the same temperature, which is independent of their size or mass. For this case, the heat capacity of the hole diverges, and the Hessian method cannot provide a definite result for the thermodynamic stability of the problem. On the other hand, the Poincaré turning point method can still be applied, and we could show that pure isolated black holes are thermodynamically stable against spherically symmetric perturbations within the approach.
In the present paper, we extend this non-parametric zeroth law-compatible approach to black hole thermodynamics by considering the problem of rotating black holes. We study the function arising from the Bekenstein–Hawking formula in the the Kerr case without any parameter but satisfying Abe’s composition rule . By regarding this as the new additive entropy function of the Kerr black holes via the formal logarithm approach, we investigate the thermodynamic and stability properties of the rotating problem.
2. Results
2.1. Kerr Black Holes
The spacetime metric of a rotating black hole is given by the Kerr solution
where
Here, M is the mass–energy of the black hole and a is its rotational parameter. The thermodynamic variables of the black hole can be expressed by the horizon radius and the rotational parameter a. The mass–energy parameter can be written as
the angular momentum of the black hole is
and the angular velocity of the horizon is
The Bekenstein–Hawking entropy is
while the Hawking temperature of the black hole horizon is
The heat capacity at constant Ω is given by
and the heat capacity at constant J is
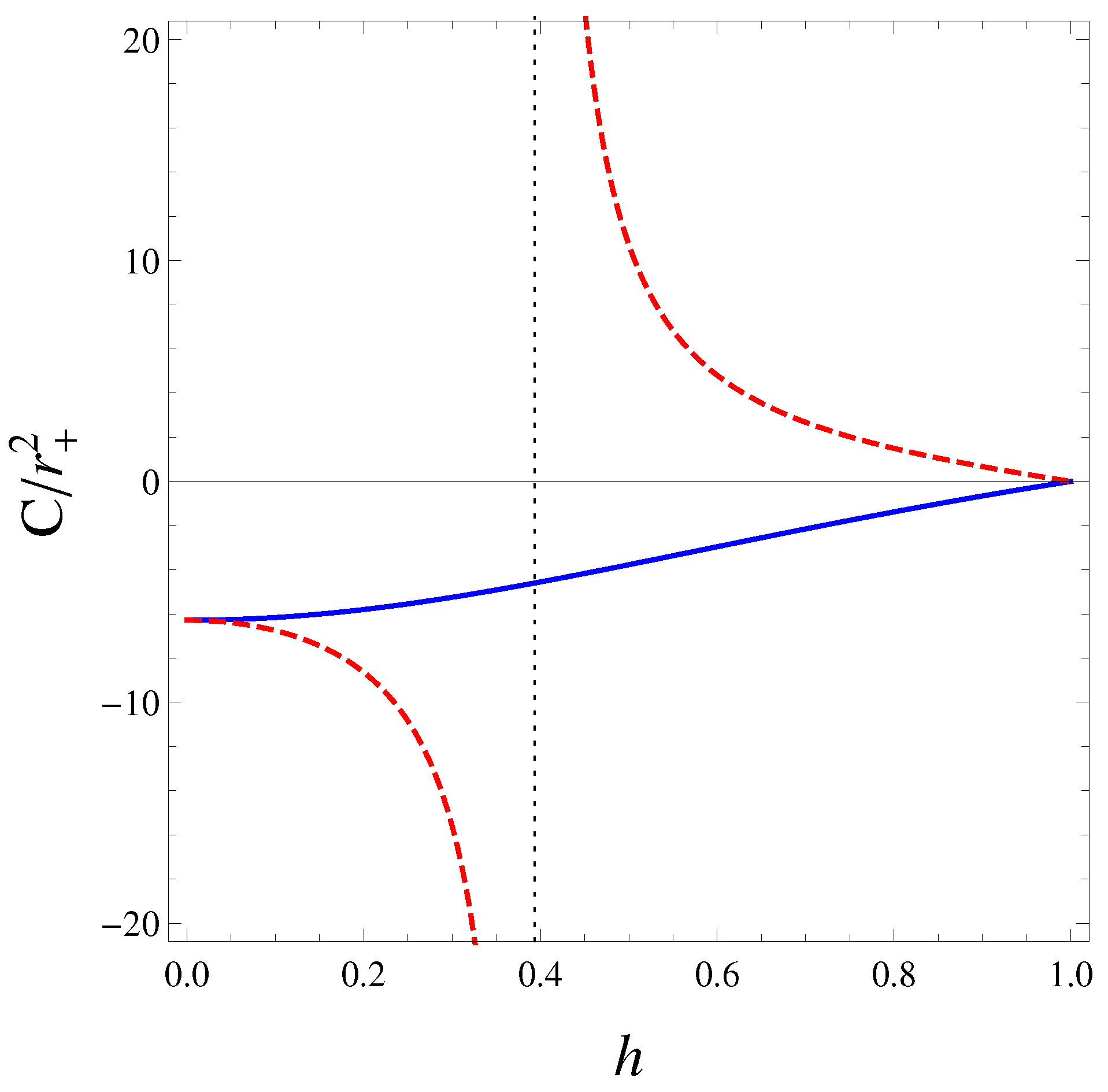
We plotted the heat capacities and as functions of in Figure 1. is negative for all h, and diverges at . is negative for and positive for . Kaburaki et al. [27] considered the thermodynamic stability of standard Kerr black holes by using the Poincaré turning point method. They concluded that isolated Kerr black holes are thermodynamically stable with respect to axisymmetric perturbations. They also found that faster rotating black holes () are more stable than slower rotating ones () in a heat bath.
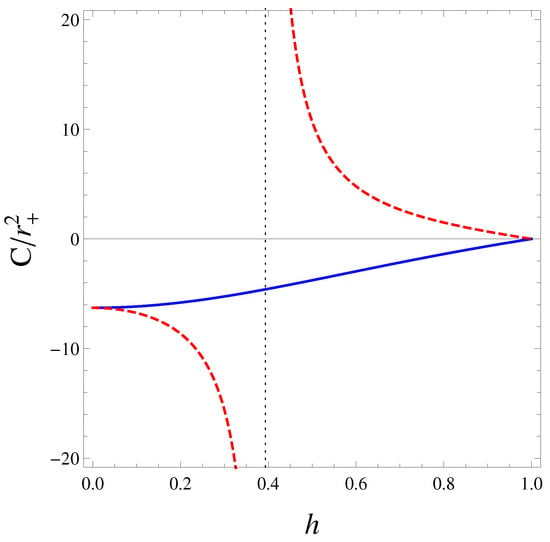
Figure 1.
Plots of heat capacities (blue solid) and (red dashed) as functions of h. diverges at . is negative for and positive for . The heat capacities coincide at the limit values (Schwarzschild holes) and (extreme Kerr holes).
2.2. The Formal Logarithm Approach
In order to extend the non-parametric results of the Schwarzschild problem obtained by the formal logarithm approach, the following non-trivial equation has to be solved for Kerr black holes,
where, and from now on, we omit the λ index of H for obvious reasons, and is the Bekenstein–Hawking entropy of Kerr black holes. Clearly, the simple Schwarzschild solution is not working in the rotating case, but after some effort, one can show that
can describe the Kerr solution, where we have fixed the overall factor of S to reproduce the Schwarzschild result (14) in the limit. Comparing this result with the mass–energy parameter of the black hole (19), we can conclude that the new equilibrium- and zeroth law-compatible entropy function of Kerr black holes obtained by the formal logarithm method based on the nonadditive and non-parametric approach arising from the Bekenstein–Hawking model is the same linear function of the energy,
as in the Schwarzschild problem. By assuming energy additivity in the system as before, the corresponding zeroth law-compatible temperature function from (6) becomes
which is again the same energy-independent constant that we obtained in the Schwarzschild case. Furthermore, both heat capacities— and —diverge, and the entropy and temperature functions versus the energy of the hole are plotted in Figure 2 and Figure 3, respectively.
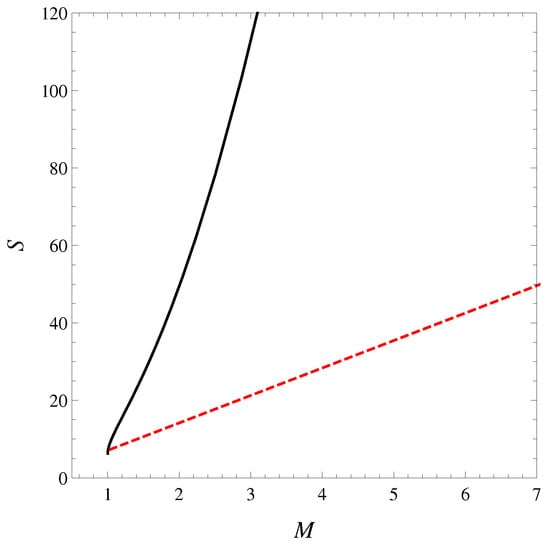
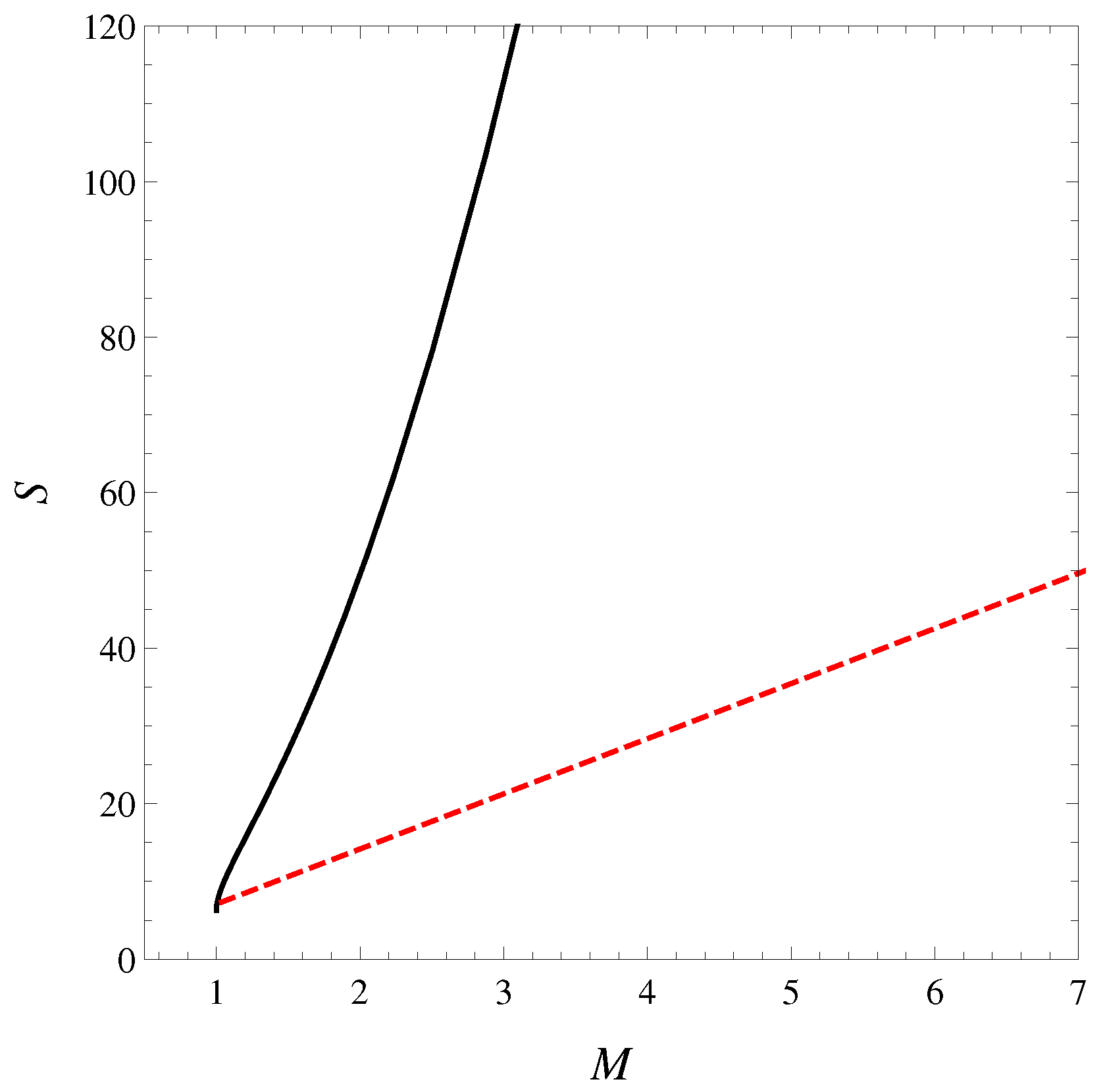
Figure 2.
Plots of entropy S as a function of the mass–energy parameter M at fixed J, standard (black solid) and formal logarithm (red dashed) approaches. The standard entropy is asymptotically convex (being proportional to in the large M limit). The new entropy is a straight line because the entropy is proportional to the mass–energy.
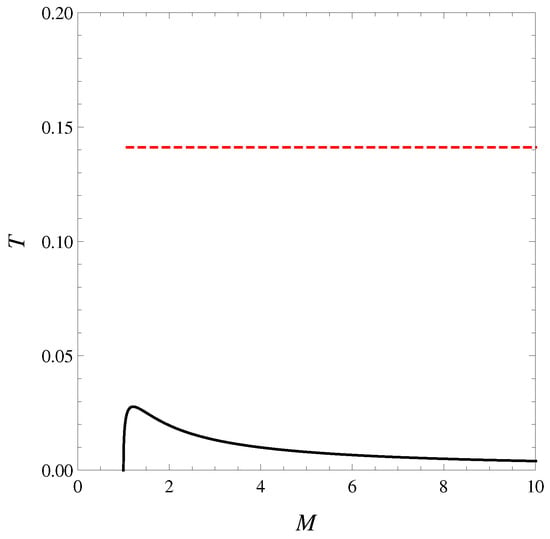
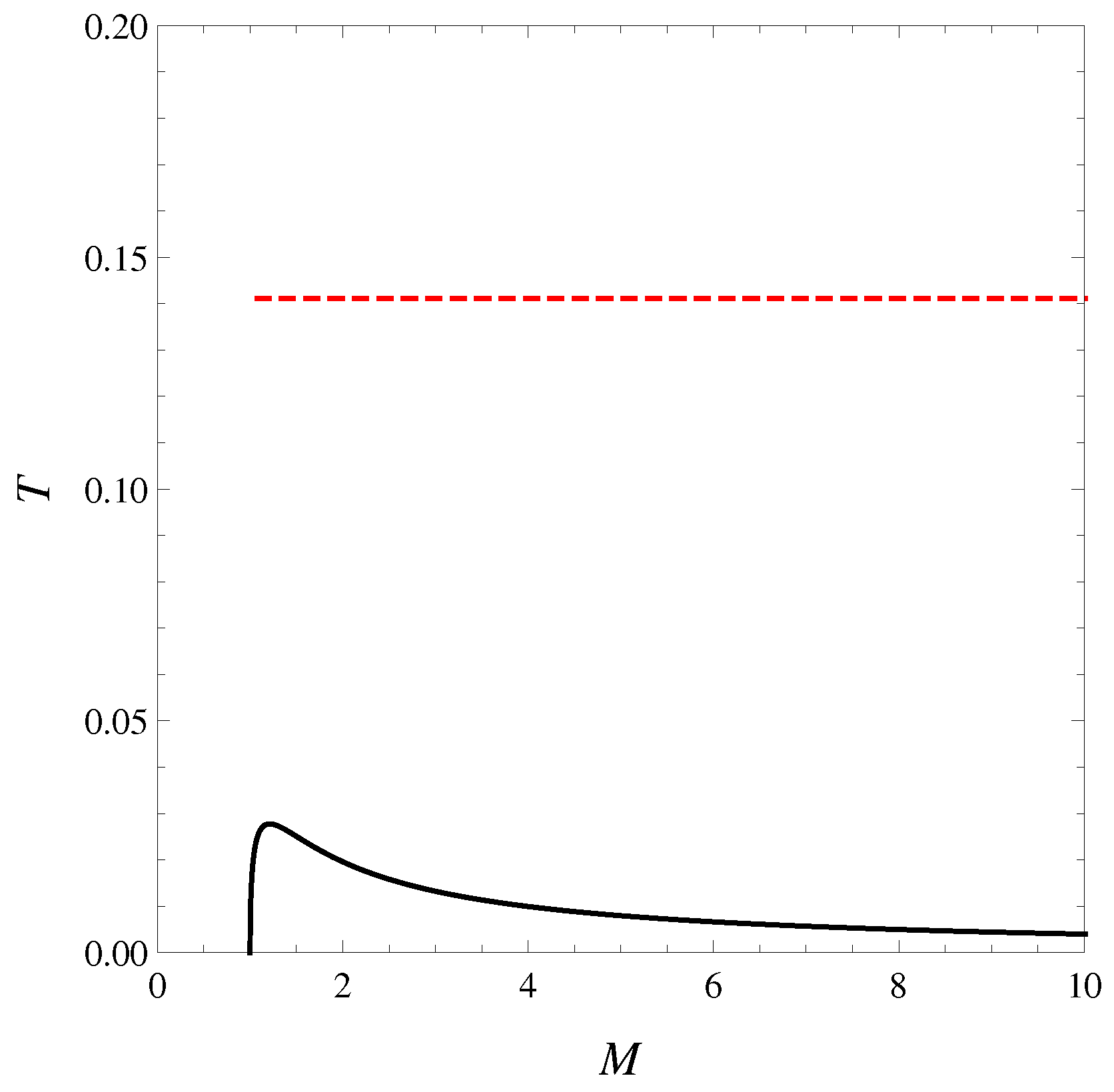
Figure 3.
Plots of temperature T as a function of the mass–energy parameter M at fixed J— standard (black solid) and formal logarithm (red dashed) approaches. The standard temperature has a local maximum. The smaller mass branch corresponds with , and the larger mass with . The new temperature is a horizontal line because it is an energy-independent constant.
2.3. Stability Analysis
Although the new formal logarithmic entropy function (27) of Kerr black holes is additive for composition, the Hessian method for stability analysis cannot be used, because (like in the Schwarzschild problem) the heat capacities are divergent. Nevertheless, the Poincaré method can still provide information about the stability of the system. Here we briefly summarize the essence of this method, as we will use it in the following analysis. For more details, please consult with the original references.
By applying the Poincaré approach, one can easily separate stable and unstable configurations for cases of a one-parameter series of equilibria. Suppose is a distribution function whose extrema define stable equilibrium configurations if the extremal value of Z is a maximum. Consider now the equilibrium value , where is a solution of . If the derivative function plotted versus y has the topology of a continuous and differentiable curve, it can be shown that stability changes will occur only at points where the tangents of the curve are vertical. The distribution function Z is called Massieu function, y is called control parameter, and the points with vertical tangents are called turning points. The branch with negative slope near the turning point is always unstable, while the branch with positive slope near the turning point is more stable.
In cases when the black holes are isolated from their surroundings, the thermodynamic problem can be described in the microcanonical ensemble. Here the Massieu function of the system is the entropy function, and the corresponding control parameters are the mass–energy, M, and the angular momentum, J. The derivative functions are and , and we plotted the stability curves at constant J and the stability curves at constant M on Figure 4 and Figure 5, respectively. One can see on the plots that there are no turning points on the curves in the standard thermodynamic treatment; therefore, Kaburaki et al. [27] concluded that isolated Kerr black holes are stable against axisymmetric perturbations.
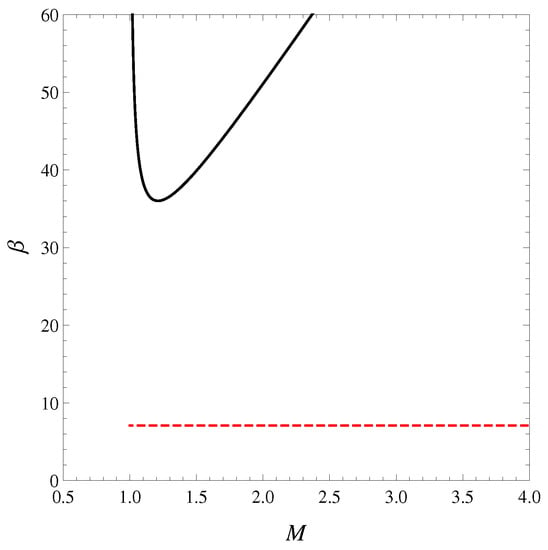
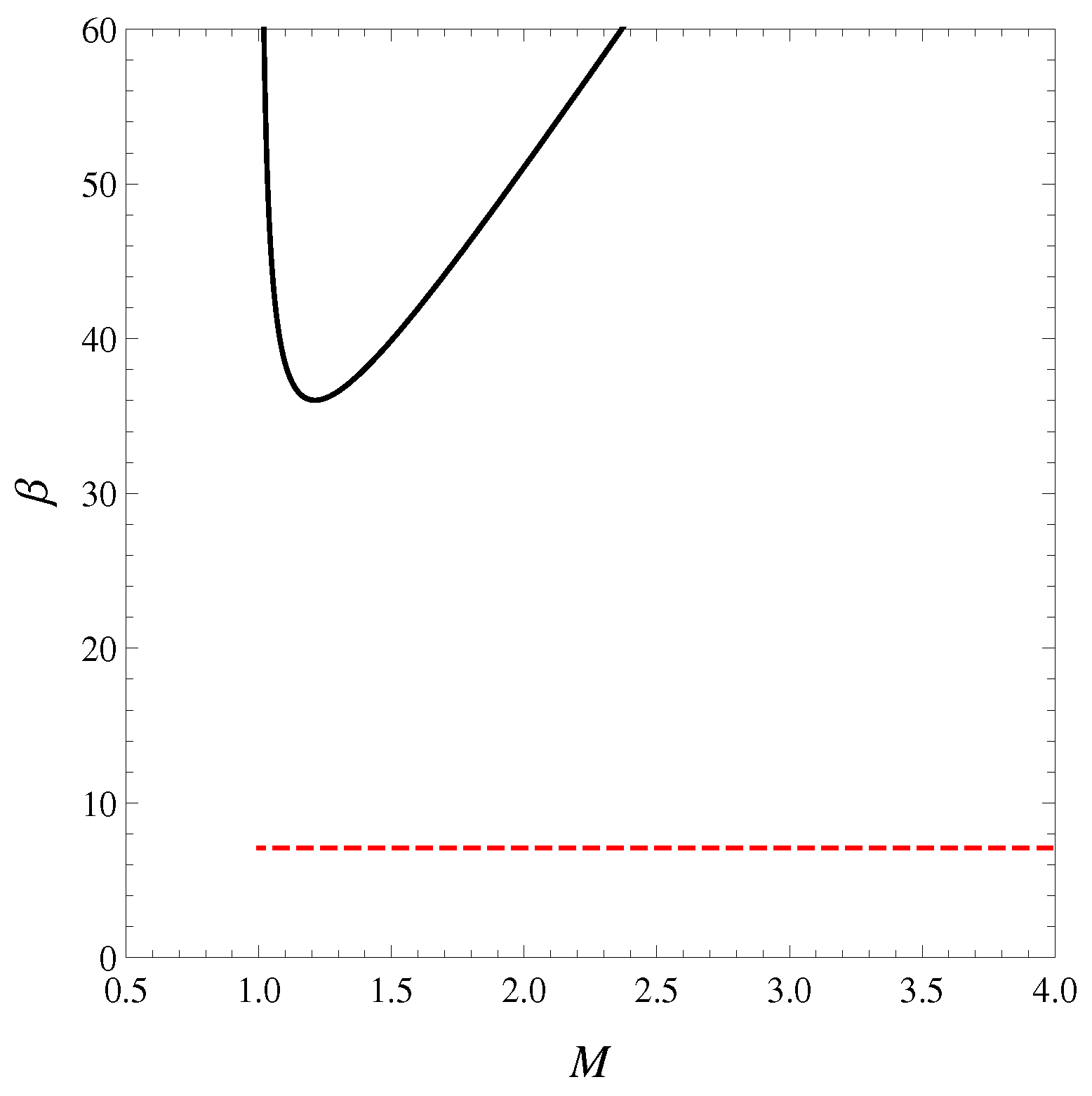
Figure 4.
Plots of stability curves at fixed J of standard (black solid) and formal logarithm (red dashed) approaches in the microcanonical treatment. No vertical tangent occurs in either cases. By rotating the figure clockwise with , the stability curves of the canonical treatment can be obtained; i.e., at fixed J. There is a vertical tangent on the stability curve of standard case. The smaller mass branch () is more stable than the larger mass branch (). No turning point appears on the stability curve of the formal logarithm approach.
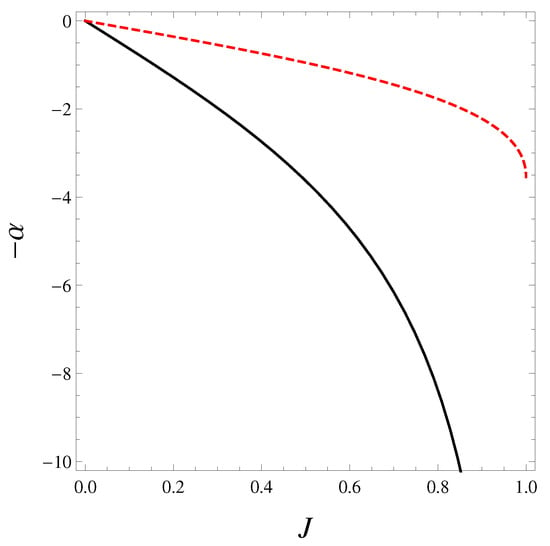
Figure 5.
Plots of stability curves at fixed M of standard (black solid) and formal logarithm (red dashed) approaches in the microcanonical treatment. No turning point appears on either stability curve.
In the case of the formal logarithm approach, the stability curve is simply a horizontal line, while is a monotonically decreasing convex curve. There are no turning points (i.e., points with vertical tangents) on these curves either, so based on these results, we can conclude that isolated Kerr black holes are also thermodynamically stable against axisymmetric perturbations in the formal logarithm approach.
The canonical ensemble depicts the system of a black hole in equilibrium with an infinite reservoir of thermal radiation at constant temperature. The Massieu function in this case is , and the control parameters are β and J. The pair of conjugate variables are the functions at fixed J and at fixed β. The stability curve at constant J for the standard case can be obtained by clockwise rotating Figure 4 with . The stability curve at fixed β in the standard treatment is plotted in Figure 6. In this case, the stability curve exhibits a turning point where a stability change occurs in the system. Based on these observations, Kaburaki et al. [27] concluded that fast rotation can stabilize black holes in a heat bath.
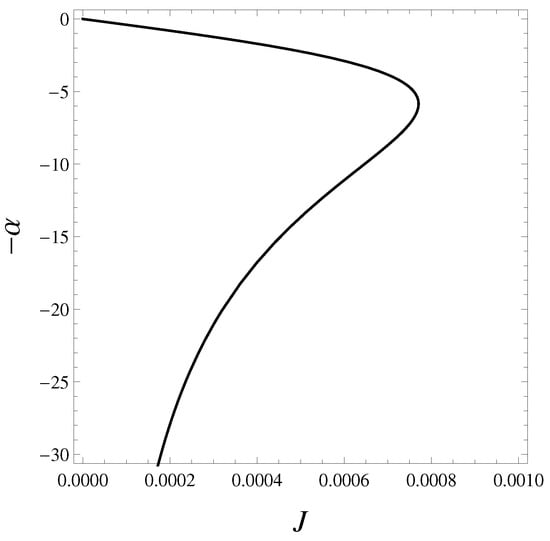
Figure 6.
Stability curve at fixed β of the standard case in the canonical treatment. There is a vertical tangent. The more stable positive slope branch corresponds to fast rotation (). The less stable negative slope branch corresponds to slow rotation ().
For the formal logarithm approach, the Massieu function Ψ turns out to be identically zero in the canonical case, so we can conclude that all black hole configurations are equally probable or improbable in this model.
3. Discussion
In this paper, we considered an equilibrium and zeroth law-compatible approach to the thermodynamic and stability problem of rotating black holes in standard four dimensions. The model we adopted was based on the nonadditive entropy composition law of Kerr black holes arising from the standard Bekenstein–Hawking entropy function. By solving Abe’s Formula (2) for with zero λ parameter and applying the formal logarithm method of Biró and Ván [21], we derived the following zeroth law-compatible entropy function for Kerr black holes
We showed that the above entropy expression is a linear function of the black hole’s energy, and also that the corresponding temperature function must be a constant; i.e., independent of the mass–energy parameter of the black hole. These results are consistent with what we had previously found in studying the Schwarzschild solution by using the same approach [17].
In the analysis of the thermodynamic stability problem, we have found some strange and presumably unphysical results. These are, for example, diverging heat capacities, a horizontal stability curve, and a Massieu function which is always zero. Indeed, after some careful analysis of the present model, one can show that the function of the Bekenstein–Hawking entropy in the system is always the mass–energy parameter of the black hole up to some constant factor, so the new entropy function can only result a constant temperature, no matter what complicated black hole spacetime is considered. Comparing these findings with our previous results on the problem by using the parametric Tsallis–Rényi approach [24,25,33], we conclude that the present non-parametric approach to black hole thermodynamics based on the Bekenstein–Hawking entropy nonadditivity is most likely an unrealistic one. Based on this conclusion, it is more reasonable to further study the parametric case, where the zeroth law-compatible temperature function of the system is not independent of the black hole mass.
Non-zero parameter values may arise in different physical situations; for example, from the long-range interaction property of the gravitational field [13] or from finite size reservoir corrections in the canonical approach [37,38]. Other parametric corrections to the Bekenstein–Hawking formula also appear from quantum considerations stemming either from string theory, loop quantum gravity, or other semi-classical theories (e.g., [39] and references therein). In these models, the parameter corrections are small, and by connecting them to λ in Abe’s Formula (2), it can be expected that the Tsallis rule (4) is obtained quite generally in the leading order. Furthermore, from the zeroth law requirement in thermal equilibrium, the Rényi entropy arises quite naturally via the formal logarithm method [21]. Based on these lines, the approach seems to be quite generic for parametric corrections to the Bekenstein–Hawking model in the small parameter and small energy limit. In [24], we also considered a semi-classical estimate for the horizon radius at the minimum temperature for micro black holes which led to a Bekenstein bound [40] on the λ parameter value that could be directly connected to the corresponding AdS curvature in the model.
On the other hand, in the Tsallis–Rényi approach, the formal logarithm entropy function satisfies both the triviality condition and the leading order additivity requirement. These conditions are discussed in more detail by Biró and Ván in [21]. In the black hole problem, however, the leading order additivity condition does not seem to be a natural choice when one considers the classical, large (i.e., far from quantum size) black hole region. In this limit, it looks more physical not to require this condition, and by doing so, we are led to a different parametric description of black hole thermodynamics that is still equilibrium- and zeroth law-compatible. We intend to study this direction in our future investigations.
Acknowledgments
Viktor G. Czinner thanks to Fundação para a Ciência e Tecnologia (FCT) Portugal, for financial support through Grant No. UID/FIS/00099/2013.
Author Contributions
Both authors contributed equally to the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kerr, R.P. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 1963, 11, 237–238. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The Four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Padmanabhan, T. Statistical Mechanics of Gravitating Systems. Phys. Rep. 1990, 188, 285–362. [Google Scholar] [CrossRef]
- Ong, Y.C. Never judge a black hole by its area. J. Cosmol. Astropart. Phys. 2015, 2015, 3. [Google Scholar] [CrossRef] [PubMed]
- Landsberg, P.T.; Tranah, D. Entropies need not to be concave. Phys. Lett. A 1980, 78, 219–220. [Google Scholar] [CrossRef]
- Bishop, N.; Landsberg, P. The thermodynamics of a system containing two black holes and black-body radiation. Gen. Relat. Gravit. 1987, 19, 1083–1090. [Google Scholar] [CrossRef]
- Landsberg, P. Is equilibrium always an entropy maximum? J. Stat. Phys. 1984, 35, 159–169. [Google Scholar] [CrossRef]
- Pavón, D.; Rubí, J. On some properties of the entropy of a system containing a black hole. Gen. Relat. Gravit. 1986, 18, 1245–1250. [Google Scholar] [CrossRef]
- Maddox, J. When entropy does not seem extensive. Nature 1993, 365, 103. [Google Scholar]
- Gour, G. Entropy bounds for charged and rotating systems. Class. Quantum Gravity 2003, 20, 3403–3412. [Google Scholar] [CrossRef]
- Oppenheim, J. Thermodynamics with long-range interactions: From Ising models to black holes. Phys. Rev. E 2003, 68, 016108. [Google Scholar] [CrossRef] [PubMed]
- Pesci, A. Entropy of gravitating systems: Scaling laws versus radial profiles. Class. Quantum Gravity 2007, 24, 2283–2300. [Google Scholar] [CrossRef]
- Aranha, R.F.; de Oliveira, H.P.; Damiao Soares, I.; Tonini, E.V. The Efficiency of Gravitational Bremsstrahlung Production in the Collision of Two Schwarzschild Black Holes. Int. J. Mod. Phys. D 2008, 17, 2049–2064. [Google Scholar] [CrossRef]
- Tsallis, C.; Cirto, L.J.L. Black hole thermodynamical entropy. Eur. Phys. J. C 2013, 73, 2487. [Google Scholar] [CrossRef]
- Czinner, V.G. Black hole entropy and the zeroth law of thermodynamics. Int. J. Mod. Phys. D 2015, 24, 1542015. [Google Scholar] [CrossRef]
- Abe, S. General pseudoadditivity of composable entropy prescribed by the existence of equilibrium. Phys. Rev. E 2001, 63, 061105. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Non-Extensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin, Germany, 2009. [Google Scholar]
- Biró, T.S.; Ván, P. Zeroth law compatibility of nonadditive thermodynamics. Phys. Rev. E 2011, 83, 061147. [Google Scholar] [CrossRef] [PubMed]
- Rényi, A. On the dimension and entropy of probability distributions. Acta Math. Acad. Sci. Hung. 1959, 10, 193–215. [Google Scholar] [CrossRef]
- Renyi, A. Probability Theory; Elsevier: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Biró, T.S.; Czinner, V.G. A q-parameter bound for particle spectra based on black hole thermodynamics with Rényi entropy. Phys. Lett. B 2013, 726, 861–865. [Google Scholar] [CrossRef]
- Czinner, V.G.; Iguchi, H. Rényi entropy and the thermodynamic stability of black holes. Phys. Lett. B 2016, 752, 306–310. [Google Scholar] [CrossRef]
- Arcioni, G.; Lozano-Tellechea, E. Stability and critical phenomena of black holes and black rings. Phys. Rev. D 2005, 72, 104021. [Google Scholar] [CrossRef]
- Kaburaki, O.; Okamoto, I.; Katz, J. Thermodynamic Stability of Kerr Black holes. Phys. Rev. D 1993, 47, 2234–2241. [Google Scholar] [CrossRef]
- Poincaré, H. Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation. Acta Math. 1885, 7, 259–380. [Google Scholar] [CrossRef]
- Katz, J.; Okamoto, I.; Kaburaki, O. Thermodynamic stability of pure black holes. Class. Quantum Gravity 1993, 10, 1323–1339. [Google Scholar] [CrossRef]
- Kaburaki, O. Critical behavior of extremal Kerr-Newman black holes. Gen. Relat. Gravit. 1996, 28, 843–854. [Google Scholar] [CrossRef]
- Azreg-Aïnou, M.; Rodrigues, M.E. Thermodynamical, geometrical and Poincaré methods for charged black holes in presence of quintessence. J. High Energy Phys. 2013, 2013, 146. [Google Scholar] [CrossRef]
- Hawking, S.W.; Page, D.N. Thermodynamics of Black Holes in anti-De Sitter Space. Commun. Math. Phys. 1983, 87, 577–588. [Google Scholar] [CrossRef]
- Czinner, V.G.; Iguchi, H. Thermodynamics, stability and Hawking–Page transition of Kerr black holes from Rényi statistics. 2017; in preparation. [Google Scholar]
- Caldarelli, M.M.; Cognola, G.; Klemm, D. Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories. Class. Quantum Gravity 2000, 17, 399–420. [Google Scholar] [CrossRef]
- Tsai, Y.D.; Wu, X.N.; Yang, Y. Phase Structure of Kerr-AdS Black Hole. Phys. Rev. D 2012, 85, 044005. [Google Scholar] [CrossRef]
- Altamirano, N.; Kubiznak, D.; Mann, R.B.; Sherkatghanad, Z. Thermodynamics of rotating black holes and black rings: Phase transitions and thermodynamic volume. Galaxies 2014, 2, 89–159. [Google Scholar] [CrossRef]
- Biró, T.S. Ideal gas provides q-entropy. Physica A 2013, 392, 3132–3139. [Google Scholar] [CrossRef]
- Biró, T.S.; Barnaföldi, G.G.; Ván, P. Quark-gluon plasma connected to finite heat bath. Eur. Phys. J. A 2013, 49, 110. [Google Scholar] [CrossRef]
- Carlip, S. Black Hole Thermodynamics. Int. J. Mod. Phys. D 2014, 23, 1430023. [Google Scholar] [CrossRef]
- Bekenstein, J.D. A Universal Upper Bound on the Entropy to Energy Ratio for Bounded Systems. Phys. Rev. D 1981, 23, 287–298. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).