Scaling Properties of the Mean Multiplicity and Pseudorapidity Density in e−+e+, e±+p, p(
p
¯
)+p, p+A and A+A(B) Collisions
Abstract
:1. Introduction
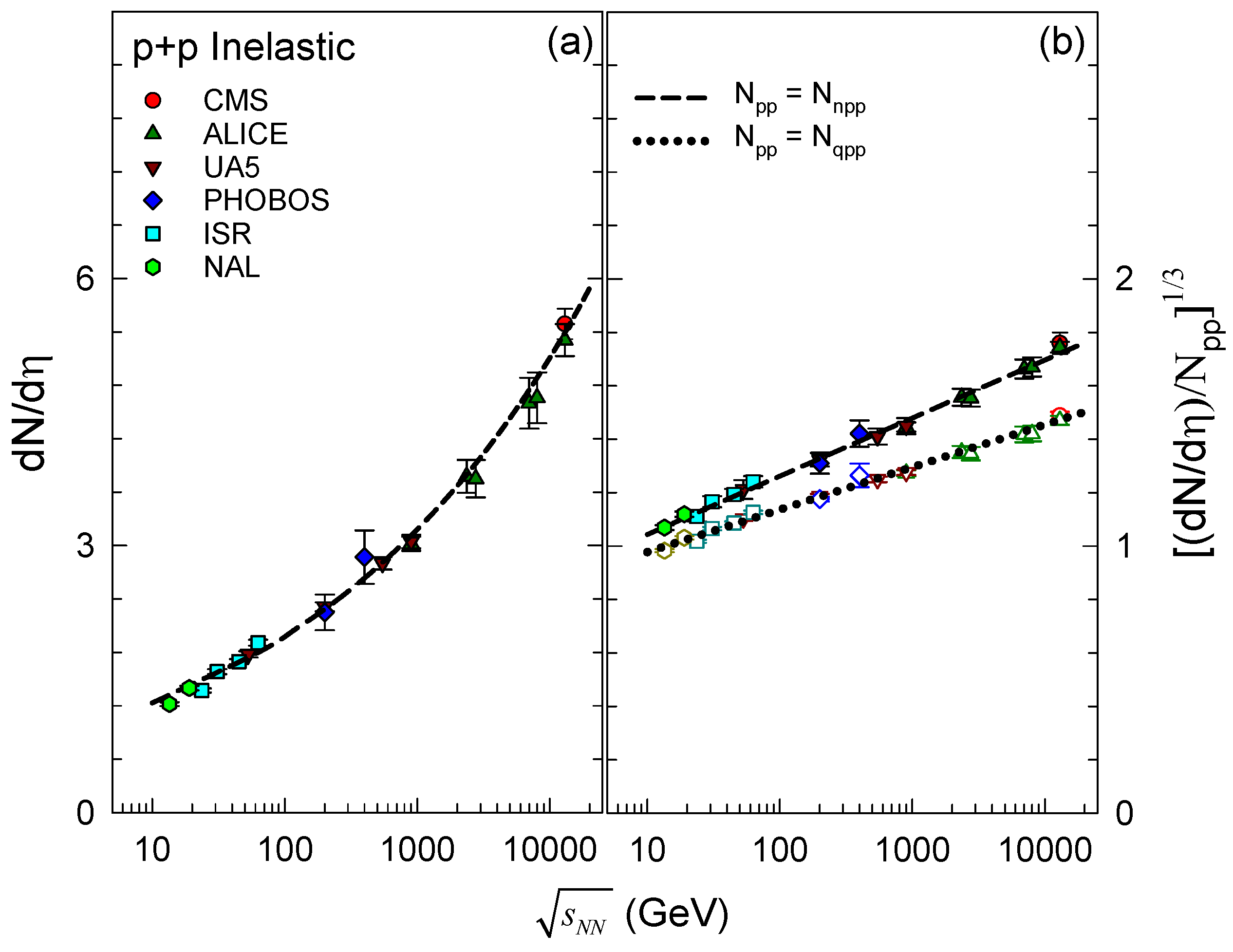
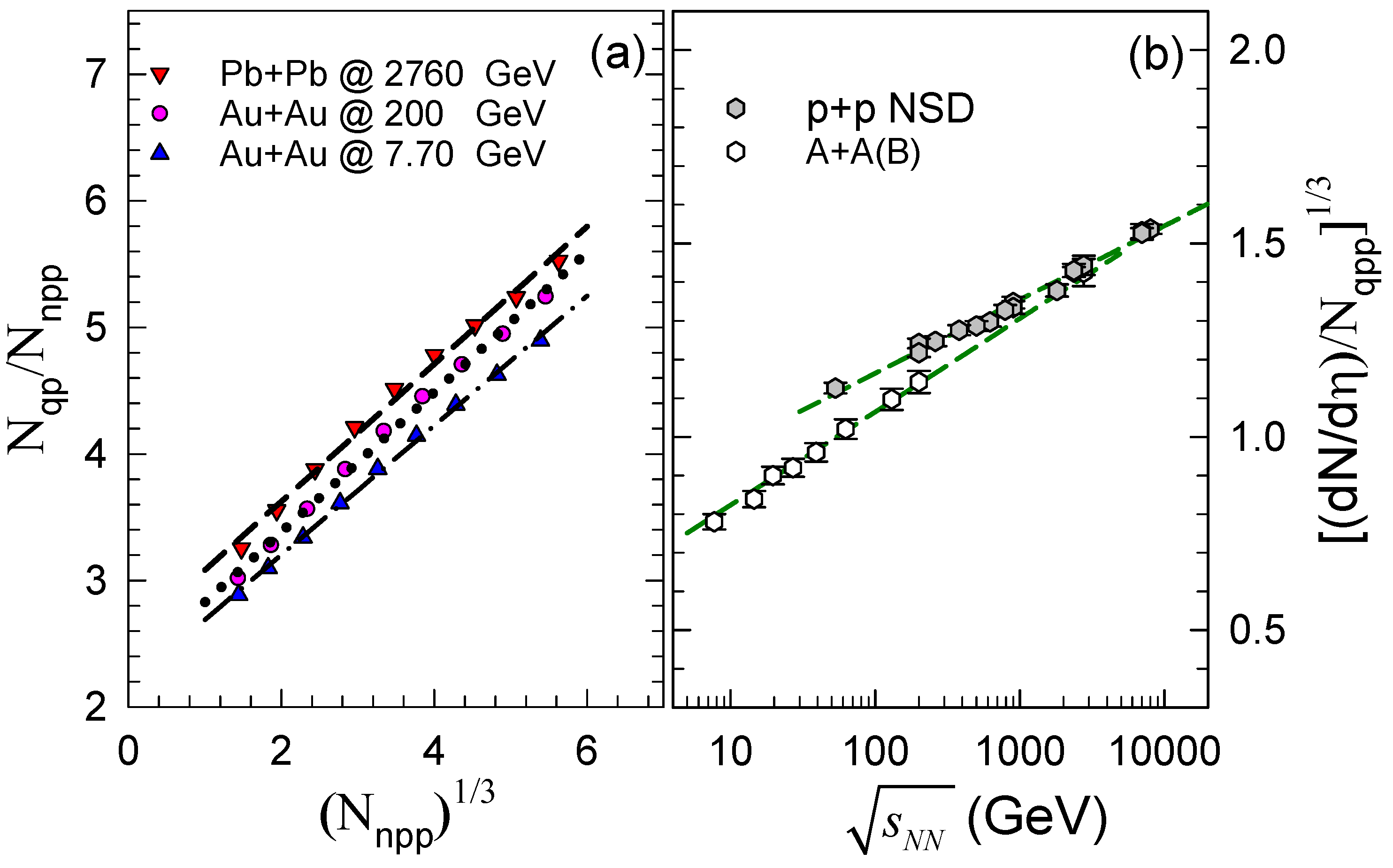
2. Analysis
3. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kittel, W.; De Wolf, E.A. Soft Multihadron Dynamics; World Scientific: Hackensack, NJ, USA, 2005. [Google Scholar]
- Armesto, N.; Borghini, N.; Jeon, S.; Wiedemann, U.A.; Abreu, S.; Akkelin, V.; Alam, J.; Albacete, J.L.; Andronic, A.; Antonov, D.; et al. Heavy Ion Collisions at the LHC—Last Call for Predictions. J. Phys. 2008, 35, 054001. [Google Scholar] [CrossRef]
- Grosse-Oetringhaus, J.F.; Reygers, K. Charged-Particle Multiplicity in Proton-Proton Collisions. J. Phys. 2010, 37, 083001. [Google Scholar] [CrossRef]
- Alver, B.; Back, B.B.; Baker, M.D.; Ballintijn, M.; Barton, D.S.; Betts, R.R.; Bickley, A.A.; Bindel, R.; Budzanowski, A.; Busza, W.; et al. Phobos results on charged particle multiplicity and pseudorapidity distributions in Au+Au, Cu+Cu, d+Au, and p+p collisions at ultra-relativistic energies. Phys. Rev. 2011, 83, 024913. [Google Scholar]
- Aamodt, K. Centrality dependence of the charged-particle multiplicity density at mid-rapidity in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. Lett. 2011, 106, 032301. [Google Scholar] [CrossRef] [PubMed]
- Chatrchyan, S. Dependence on pseudorapidity and centrality of charged hadron production in PbPb collisions at a nucleon-nucleon centre-of-mass energy of 2.76 TeV. J. High Energy Phys. 2011, 08, 141. [Google Scholar] [CrossRef]
- Aad, G. Measurement of the centrality dependence of the charged particle pseudorapidity distribution in lead-lead collisions at = 2.76 TeV with the ATLAS detector. Phys. Lett. 2012, B710, 363–382. [Google Scholar] [CrossRef] [Green Version]
- Adamczyk, L. Inclusive charged hadron elliptic flow in Au + Au collisions at = 7.7–39 GeV. Phys. Rev. 2012, 86, 054908. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Akimoto, R.; Al-Bataineh, H.; Alexander, J.; Alfred, M.; Al-Jamel, A.; et al. Transverse energy production and charged-particle multiplicity at midrapidity in various systems from = 7.7 to 200 GeV. Phys. Rev. 2016, 93, 024901. [Google Scholar]
- Kharzeev, D.; Levin, E.; Nardi, M. Color glass condensate at the LHC: Hadron multiplicities in pp, pA and AA collisions. Nucl. Phys. 2005, 747, 609–629. [Google Scholar] [CrossRef]
- Armesto, N.; Salgado, C.A.; Wiedemann, U.A. Relating high-energy lepton-hadron, proton-nucleus and nucleus-nucleus collisions through geometric scaling. Phys. Rev. Lett. 2005, 94, 022002. [Google Scholar] [CrossRef] [PubMed]
- Albrow, M.G.; Begel, M.; Bourilkov, D.; Campanelli, M.; Chlebana, F.; De Roeck, A.; Dittmann, J.R.; Ellis, S.D.; Field, B.; Field, R.; et al. Tevatron-for-LHC Report of the QCD Working Group. arXiv, 2006; arXiv:hep-ph/0610012. [Google Scholar]
- Werner, K. The hadronic interaction model EPOS. Nucl. Phys. Proc. Suppl. 2008, 175–176, 81–87. [Google Scholar] [CrossRef]
- Dusling, K.; Venugopalan, R. Explanation of systematics of CMS p+Pb high multiplicity di-hadron data at = 5.02 TeV. Phys. Rev. 2013, D87, 054014. [Google Scholar]
- Khachatryan, V. Observation of Long-Range Near-Side Angular Correlations in Proton-Proton Collisions at the LHC. J. High Energy Phys. 2010, 1009, 091. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Admove, D.; Anare, A.M.; Aggarwal, M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Long-range angular correlations on the near and away side in p-Pb collisions at = 5.02 TeV. Phys. Lett. 2013, B719, 29–41. [Google Scholar] [CrossRef] [Green Version]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Observation of Associated Near-Side and Away-Side Long-Range Correlations in = 5.02 TeV Proton-Lead Collisions with the ATLAS Detector. Phys. Rev. Lett. 2013, 110, 182302. [Google Scholar] [CrossRef] [PubMed]
- Chatrchyan, S.; Khachatyan, V.; Sirunyan, A.M.; Tumasyan, A. Observation of long-range near-side angular correlations in proton-lead collisions at the LHC. Phys. Lett. 2013, B718, 795–814. [Google Scholar] [CrossRef]
- Adare, A.; Aidala, C.; Ajitanand, N.N.; Zhou, S. Measurement of long-range angular correlation and quadrupole anisotropy of pions and (anti)protons in central d+Au collisions at = 200 GeV. Phys. Rev. Lett. 2015, 114, 192301. [Google Scholar] [CrossRef] [PubMed]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Akimoto, R.; Al-Bataineh, H.; Alexander, J.; Alfred, M.; Al-Ta’ani, H.; et al. Measurements of elliptic and triangular flow in high-multiplicity 3He+Au collisions at = 200 GeV. Phys. Rev. Lett. 2015, 115, 142301. [Google Scholar] [CrossRef] [PubMed]
- Bozek, P. Collective flow in p-Pb and d-Pd collisions at TeV energies. Phys. Rev. 2012, C85, 014911. [Google Scholar]
- Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Alexander, J.; Amirikas, R.; Aphecetche, L.; Aronson, S.H.; Averbeck, R.; et al. Bose-Einstein correlations of charged pion pairs in Au + Au collisions at = 200 GeV. Phys. Rev. Lett. 2004, 93, 152302. [Google Scholar] [CrossRef]
- Miller, M.L.; Reygers, K.; Sanders, S.J.; Steinberg, P. Glauber modeling in high energy nuclear collisions. Ann. Rev. Nucl. Part. Sci. 2007, 57, 205–243. [Google Scholar] [CrossRef]
- Lacey, R.A.; Wei, R.; Ajitanand, N.N.; Taranenko, A. Initial eccentricity fluctuations and their relation to higher-order flow harmonics. Phys. Rev. 2011, C83, 044902. [Google Scholar] [CrossRef]
- Eremin, S.; Voloshin, S. Nucleon participants or quark participants? Phys. Rev. 2003, C67, 064905. [Google Scholar] [CrossRef]
- Bialas, A.; Bzdak, A. Wounded quarks and diquarks in heavy ion collisions. Phys. Lett. 2007, B649, 263–268. [Google Scholar] [CrossRef]
- Nouicer, R. Charged particle multiplicities in A+A and p+p collisions in the constituent quarks framework. Eur. Phys. J. 2007, C49, 281–286. [Google Scholar] [CrossRef]
- Adler, S.S. Transverse-energy distributions at midrapidity in p+p , d+Au , and Au+Au collisions at = 62.4–200 GeV and implications for particle-production models. Phys. Rev. 2014, C89, 044905. [Google Scholar]
- Fagundes, D.A.; Menon, M.J.; Silva, P.V.R.G. On the rise of the proton-proton cross-sections at high energies. J. Phys. 2013, G40, 065005. [Google Scholar] [CrossRef]
- Feinberg, E.L. Multiple production of hadrons at cosmic ray energies (experimental results and theoretical concepts). Phys. Rept. 1972, 5, 237–350. [Google Scholar] [CrossRef]
- Albini, E.; Capiluppi, P.; Giacomelli, G.; Rossi, A.M. Mean Charged Hadron Multiplicities in High-Energy Collisions. Nuovo Cim. 1976, A32, 101. [Google Scholar] [CrossRef]
- Basile, M. Evidence of the Same Multiparticle Production Mechanism in p-p Collisions as in e+ e− Annihilation. Phys. Lett. 1980, 92B, 367. [Google Scholar] [CrossRef]
- Basile, M. A Detailed Study of Average Charged Particle Multiplicity Versus Available Energy and Invariant Mass at Different in pp Interactions. Nuovo Cim. 1982, A67, 244. [Google Scholar] [CrossRef]
- Back, B.B. Comparison of the total charged particle multiplicity in high-energy heavy ion collisions with e+ e− and p p/anti-p p data. arXiv, 2003; arXiv:nucl-ex/0301017. [Google Scholar]
- Nyiri, J. Quark structure of hadrons and high-energy collisions. Int. J. Mod. Phys. 2003, A18, 2403–2458. [Google Scholar] [CrossRef]
- Sarkisyan, E.K.G.; Sakharov, A.S. On similarities of bulk observables in nuclear and particle collisions. arXiv, 2004; arXiv:hep-ph/0410324. [Google Scholar]
- Nakamura, K.; Particle Data Group. Review of particle physics. J. Phys. 2010, G37, 075021. [Google Scholar] [CrossRef]
- Benecke, J.; Blobel, V.; Breitenlohner, P.; Fesefeldt, H.; Heilmann, H.G.; Idschok, U. Rapidity Gap Separation and Study of Single Diffraction Dissociation in p p Collisions at 12-GeV/c and 24-GeV/c. Nucl. Phys. 1974, B76, 29–47. [Google Scholar] [CrossRef]
- Morse, W.M.; Barnes, V.E.; Carmony, D.D.; Christian, R.S.; Garfinkel, A.F.; Rangan, L.K.; Erwin, A.R.; Harvey, E.H.; Loveless, R.J.; Thompson, M.A. π+p, K+p and pp Topological Cross-Sections and Inclusive Interactions at 100-GeV Using a Hybrid Bubble Chamber-Spark Chamber System and a Tagged Beam. Phys. Rev. 1977, D15, 66. [Google Scholar]
- Breakstone, A. Charged Multiplicity Distribution in p p Interactions at ISR Energies. Phys. Rev. 1984, D30, 528. [Google Scholar]
- Alner, G.J. Scaling Violations in Multiplicity Distributions at 200-GeV and 900-GeV. Phys. Lett. 1986, 167B, 476–480. [Google Scholar] [CrossRef]
- Ansorge, R.E. Charged Particle Multiplicity Distributions at 200-GeV and 900-GeV Center-Of-Mass Energy. Z. Phys. 1989, C43, 357. [Google Scholar]
- Adloff, C. Evolution of e p fragmentation and multiplicity distributions in the Breit frame. Nucl. Phys. 1997, B504, 3–23. [Google Scholar] [CrossRef]
- Breitweg, J. Measurement of multiplicity and momentum spectra in the current and target regions of the Breit frame in deep inelastic scattering at HERA. Eur. Phys. J. 1999, C11, 251–270. [Google Scholar] [CrossRef]
- Chekanov, S. Multiplicity moments in deep inelastic scattering at HERA. Phys. Lett. 2001, B510, 36–54. [Google Scholar] [CrossRef]
- Khachatryan, V. Pseudorapidity distribution of charged hadrons in proton-proton collisions at = 13 TeV. Phys. Lett. 2015, B751, 143–163. [Google Scholar] [CrossRef] [Green Version]
- Adam, J. Pseudorapidity and transverse-momentum distributions of charged particles in proton-proton collisions at = 13 TeV. Phys. Lett. 2016, B753, 319–329. [Google Scholar] [CrossRef]
- Aamodt, K. Charged-particle multiplicity measurement in proton-proton collisions at = 0.9 and 2.36 TeV with ALICE at LHC. Eur. Phys. J. 2010, C68, 89–108. [Google Scholar] [CrossRef] [Green Version]
- Adam, J. Charged-particle multiplicities in proton–proton collisions at = 0.9 to 8 TeV. Eur. Phys. J. 2017, C77, 33. [Google Scholar] [CrossRef]
- Alner, G.J. Scaling of Pseudorapidity Distributions at c.m. Energies Up to 0.9-TeV. Z. Phys. 1986, C33, 1–6. [Google Scholar]
- Nouicer, R. Pseudorapidity distributions of charged particles in d + Au and p + p collisions at s(NN)**(1/2) = 200-GeV. J. Phys. 2004, G30, S1133–S1138. [Google Scholar] [CrossRef]
- Whitmore, J. Experimental Results on Strong Interactions in the NAL Hydrogen Bubble Chamber. Phys. Rept. 1974, 10, 273–373. [Google Scholar] [CrossRef]
- Khachatryan, V. Transverse-momentum and pseudorapidity distributions of charged hadrons in pp collisions at = 7 TeV. Phys. Rev. Lett. 2010, 105, 022002. [Google Scholar] [CrossRef] [PubMed]
- Abe, F. Pseudorapidity distributions of charged particles produced in interactions at = 630 GeV and 1800 GeV. Phys. Rev. 1990, D41, 2330. [Google Scholar]
- Albajar, C. A Study of the General Characteristics of Collisions at = 0.2-TeV to 0.9-TeV. Nucl. Phys. 1990, B335, 261–287. [Google Scholar] [CrossRef]
- Aad, G. Measurement of the centrality dependence of the charged-particle pseudorapidity distribution in proton-lead collisions at = 5.02 TeV with the ATLAS detector. Eur. Phys. J. 2016, 76, 199. [Google Scholar] [CrossRef] [PubMed]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lacey, R.A.; Liu, P.; Magdy, N.; Csanád, M.; Schweid, B.; Ajitanand, N.N.; Alexander, J.; Pak, R.
Scaling Properties of the Mean Multiplicity and Pseudorapidity Density in e−+e+, e±+p, p(
Lacey RA, Liu P, Magdy N, Csanád M, Schweid B, Ajitanand NN, Alexander J, Pak R.
Scaling Properties of the Mean Multiplicity and Pseudorapidity Density in e−+e+, e±+p, p(
Lacey, Roy A., Peifeng Liu, Niseem Magdy, Máté Csanád, Benjamin Schweid, Nuggehalli N. Ajitanand, John Alexander, and Robert Pak.
2018. "Scaling Properties of the Mean Multiplicity and Pseudorapidity Density in e−+e+, e±+p, p(
Lacey, R. A., Liu, P., Magdy, N., Csanád, M., Schweid, B., Ajitanand, N. N., Alexander, J., & Pak, R.
(2018). Scaling Properties of the Mean Multiplicity and Pseudorapidity Density in e−+e+, e±+p, p(





