A Note on Rectangular Partially Massless Fields
Abstract
:Contents
| 1 | Introduction | 2 |
| 2 | Notation and Conventions | 4 |
| 3 | Higher-Order Higher-Spin Singletons | 6 |
| 3.1 Unitary Higher-Spin Singletons . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 6 | |
| 3.2 Non-Unitary, Higher-Order Extension . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 12 | |
| 3.3 Candidates for Higher-Spin Higher-Order Singletons . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 15 | |
| 4 | Flato-Frønsdal Theorem | 20 |
| 5 | Conclusions | 22 |
| A | Branching Rules and Tensor Products of | 22 |
| A.1 Branching Rules for . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 22 | |
| A.2 Computing Tensor Products . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 23 | |
| B | Technical Proofs | 24 |
| B.1 Proof of the Branching Rule for Unitary HS Singletons . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 24 | |
| B.2 Proof of the Branching Rule for Rectangular Partially Massless Fields . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 27 | |
| References | 32 | |
1. Introduction
- They are unitary and irreducible representations (UIRs) of that remain irreducible when restricted to UIRs of , or in other words they correspond to the class of elementary particles in d-dimensional anti-de Sitter space which are conformal. This property is the very definition of a conformally massless UIR, and it turns out that the singletons are precisely the UIRs to which conformally massless UIRs can be lifted.
- The tensor product of two singletons contains all conformally massless fields in AdS [7]. In any dimensions however, the representations appearing in the decomposition of the tensor product of two singletons (of spin 0 or ) are no longer conformally massless but make up, by definition, all of the composite massless UIRs of [6,8,9,10]. In other words, composite massless UIRs are those modules which appear in the decomposition of the tensor product of two singletons.
2. Notation and Conventions
- A (generalised Verma) module is characterised by the lowest weight , where is the weight (in general a real number, and more often in this paper, a positive integer) corresponding to the minimal energy of the AdS field described by this representation and ℓ is a dominant integral weight corresponding to the spin of the representation. If irreducible, those modules will be denoted , whereas if reducible (or indecomposable), they will be denoted .
- The spin , with (and where is the integer part of x), is a integral dominant weight. The property that the weight ℓ is integral means that its components are either all integers or all half-integers. The fact that ℓ is dominant means that the components are ordered in decreasing order, and all positive except for the component when . More precisely,and
- In order to deal more efficiently with weight having several identical components, we will use the notation:in other words the number h of components with the same value ℓ appears as the exponent of the latter. For the special cases where all components of the highest weight are equal either to 0 or to , we will use bold symbols (and forget about the brackets), i.e.,We will also write only the non-vanishing components of the various weight encountered in this paper, i.e.,
- If the spin is given by an irrep of an even dimensional orthogonal algebra, i.e., for , the last component of this highest weight (if non-vanishing) can either be positive or negative. Whenever the statements involving such a weight does not depend on this sign, we will write with the understanding that can be replaced by . However, if the sign of the component matters, we will distinguish the two cases by writting:It will also be convenient to consider the direct sum of two modules labelled by and , which we will denote by:
- Finally, a useful tool that we will use throughout this paper is the character of a (possibly reducible) generalised Verma module :where and for with a basis of the weight space of , andi.e., the prefactor is absent for , and is the character of the irreducible representation ℓ. Any irreducible generalised Verma module can be defined as the quotient of the (freely generated) generalised Verma module by its maximal submodule (for some weight related to ). An important property that will be used extensively in this work is the fact that given two representation spaces V and W of the same algebra with respective characters and , the characters of the tensor product, direct sum or quotient of these two spaces obey:As a consequence, the character of an irreducible generalised Verma module takes the form:whenever possesses a submodule . For more details on characters of generalised Verma modules, see e.g., [10,101].
3. Higher-Order Higher-Spin Singletons
3.1. Unitary Higher-Spin Singletons
- : modules with ;
- : modules with ;
- with : modules with .
- If (and ), then:In this case, the structure of the maximal submodule is more involved, the maximal submodule can be defined through the sequence of quotients of generalized Verma modules:with and is an irreducible module. For more details on the structure of irreducible generalised Verma module, see the classification displayed in [108]. Their character read [10]:
- (i)
- It decomposes into a (infinite) single direct sum of (finite-dimensional) modules in which each irrep of appears only once (is multiplicity free) and with a different weight, i.e.,This was proven originally in [109] for the case where only the spin-0 and spin- singletons exist, and extended to arbitrary dimensions and for singletons of arbitrary spin in [5].
- (ii)
- It branches into a single irreducible module 8 of the subalgebras , or , in which case this branching rule reads:and where the module correspond to a massless field of spin in AdS. Conversely, singletons can be seen as the only , or modules that can be lifted to a module of (which is ). From this point of view, this property can be restated as “Singletons are the only (massless) particles, or gauge fields, in d-dimensional Minkowski, de Sitter or anti-de Sitter spacetime which also admit conformal symmetries”, as they are the only representations of the isometry algebra of the d-dimensional maximally symmetric spaces that can be lifted to a representation of the conformal algebra in d-dimensions. Again, this property was first proven in in [4] and later extended to arbitrary dimensions in [5,110]. This was revisited recently in [111].
- (i)
- This decomposition can be proven by showing that the character of the module can be rewritten in the form:which is indeed the character of the direct sum of modules displayed in (22). This was proven in [10], and in practice the idea is simply to use the property of the “universal” function that it can be rewritten as:and then perform the tensor product between the characters appearing in the character with . Let us to do that explicitely for , where we can take advantage of the exceptional isomorphism to deal with tensor products:This decomposition can be illustrated by drawing a “weight diagram”, representing the weight of modules as a function of the first component of their weights, see Figure 1 below.
- (ii)
- In order to prove the branching rule from to , we will compare the decomposition of the spin-s singleton on the one hand, obtained by branching 10 the components of the of these modules displayed in the previous item onto , to the decomposition of the module describing a massless field with spin . For the sake of brevity, we will only detail the low dimensional case of spin-s singletons which captures the idea of the proof, and leave the treatment of the arbitrary dimension case to Appendix B.1.Let us start by deriving the decomposition of the spin-s singleton module :Next, we need to derive the of a massless spin-s field corresponding to the module . To do so, we will rewrite its character in a way that makes this decomposition explicit:where we used the property (25) of the function , namelyThis proves that the decomposition of the module of a massless spin-s field in AdS reads:which coincide with the decomposition obtained after branching the spin-s singleton module onto , i.e., we indeed haveThis can be graphically seen by implementing the branching rule of the weight diagram in Figure 2. Indeed, the branching rule for the irrep is:which means that one should add on each line of the weight diagram (representing the modules appearing at fixed energy, or weight) in Figure 2 a dot at each value of to the left of the orignal one until is reached. By doing so, an infinite wedge whose tip has coordinates precisely corresponding to the weight diagram of a massless field of spin given by a rectangular Young diagram on maximal height and length s as can be seen from (40) for and in Appendix B.1 for arbitrary odd values of d.
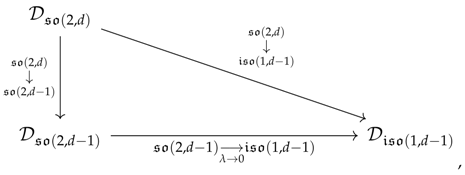
- From to . As far as the branching rule from to are concerned, it can be recovered, assuming that the following diagram is commutative:i.e., by combining the branching rule from to and an Inönü-Wigner contraction. That is to say, it is equivalent (i) to branch a representation from onto and then perform a Inönü-Wigner contraction by sending the cosmological constant λ to zero to obtain a representation of , and (ii) to branch the module onto to obtain the same module than previously. Under this assumption, we can use the branching rule (23) of the singleton module onto and then contracting it to a instead of deriving the branching rule from onto . The Inönü-Wigner contraction for massless fields in AdS (i.e., modules) is known as the Brink-Metsaev-Vasiliev mechanism [112], which was proven in [65,66,72]. This mechanism states that massless UIRs of spin given by a Young diagram contracts to the direct sum of massless UIRs of the Poincaré algebra with spin given by all of the Young diagrams obtained from the branching rule of except those where boxes in the first block of have been removed. Higher-spin singleton, as well as the massless module onto which they branch being labelled by a rectangular Young diagram, the BMV mechanism implies that they contract to a single i.e.,as shown in [5].
- From to . The generalised Verma modules are induced by, and decompose into, modules instead of in the case of . As a consequence, the method used previously consisting in relying on the common cannot be applied here and we will therefore refer to the original paper [5] for the proof of that branching rule.
3.2. Non-Unitary, Higher-Order Extension
3.3. Candidates for Higher-Spin Higher-Order Singletons
4. Flato-Frønsdal Theorem

- If they are of the same chirality ϵ:where and
- If they are of opposite chirality:Notice that in the above decomposition (109) of two singletons of opposite chirality, the irreps describing totally symmetric partially massless fields, i.e., of spin given by a single row Young diagram, only appear once despite what the notation would normally suggests.
- Partially massless fields of depth-τ and spin given by a two-row Young diagram which read:
- Massive fields of minimal energy Δ and spin given a two-row Young diagram which read:
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Branching Rules and Tensor Products of
Appendix A.1. Branching Rules for
Appendix A.2. Computing Tensor Products

- First, assign to the boxes of each rows of one of the Young diagrams (say μ) a label which keeps track of the order of the rows (for instance, if the labels are letters of the alphabet, then each of the boxes of the first row of μ are assigned the label “a”, each of the boxes of the second row of μ are assigned the label “b”, etc.);
- Then, glue the boxes of μ to λ in all possible ways such that the resulting diagram obey the following constraints:
- −
- Boxes in the same column should not have the same label;
- −
- When reading the row of the obtained Young diagram from right to left, and its columns from top to bottom, the number of boxes encountered should be decreasing with their label (i.e., less boxes of the second label are encountered than with the first label, less with the third than the second, etc.);
- −
- The resulting diagram should always be a legitimate Young diagram, i.e., the length of the rows is decreasing from top to bottom, and it is composed of at most d rows.
- (i)
- Branch each of the two Young diagrams into and pair them by number of boxes removed from the original ones until the products of one of these diagrams are exhausted;
- (ii)
- Compute the tensor product between these pairs of diagrams using the Littlewood-Richardson rule recalled above;
- (iii)
- Discard the Young diagrams which are not acceptable for , i.e., those for which the sum of the height of their first two columns is stricly greater than d.
 and
and  branching rule for these representations is:
branching rule for these representations is:




Appendix B. Technical Proofs
Appendix B.1. Proof of the Branching Rule for Unitary HS Singletons
Appendix B.2. Proof of the Branching Rule for Rectangular Partially Massless Fields
- The first piece, proportional to reads:Using the symmetry propertyof the characters, one can check that the previous sum reduces to a single contribution:For instance, for :The symmetry property (A71) implies that:hence we indeed obtain:
- The second piece, proportional to , also reduces to a single contribution upon using the same symmetry property (A71):
- Finally, the third piece (proportional to ) contains more contributions:Putting those three piece together yields:thereby proving the decomposition (A55) of the spin-s and depth-t RPM module. Finally, the of this module reads:thereby proving the branching rule:
References
- Metsaev, R.R. Continuous spin gauge field in (A)dS space. Phys. Lett. B 2017, 767, 458–464. [Google Scholar]
- Metsaev, R.R. Fermionic continuous spin gauge field in (A)dS space. Phys. Lett. B 2017, 773, 135–141. [Google Scholar]
- Bekaert, X.; Skvortsov, E.D. Elementary particles with continuous spin. Int. J. Mod. Phys. A 2017, 32, 1730019. [Google Scholar]
- Angelopoulos, E.; Flato, M.; Fronsdal, C.; Sternheimer, D. Massless Particles, Conformal Group and De Sitter Universe. Phys. Rev. D 1981, 23, 1278–1289. [Google Scholar]
- Angelopoulos, E.; Laoues, M. Masslessness in n-dimensions. Rev. Math. Phys. 1998, 10, 271–299. [Google Scholar]
- Iazeolla, C.; Sundell, P. A Fiber Approach to Harmonic Analysis of Unfolded Higher-Spin Field Equations. J. High Energy Phys. 2008, 2008, 022. [Google Scholar]
- Flato, M.; Fronsdal, C. One Massless Particle Equals Two Dirac Singletons. Lett. Math. Phys. 1978, 2, 421–426. [Google Scholar]
- Angelopoulos, E.; Laoues, M. Singletons on AdS(n). In Proceedings of the Conference Moshe Flato, Dijon, France, 5–8 September 1999; pp. 3–23. [Google Scholar]
- Vasiliev, M.A. Higher spin superalgebras in any dimension and their representations. J. High Energy Phys. 2004, 2004, 46. [Google Scholar]
- Dolan, F.A. Character formulae and partition functions in higher dimensional conformal field theory. J. Math. Phys. 2006, 47, 062303. [Google Scholar]
- Vasiliev, M.A. Equations of Motion of Interacting Massless Fields of All Spins as a Free Differential Algebra. Phys. Lett. B 1988, 209, 491–497. [Google Scholar]
- Vasiliev, M.A. Consistent equation for interacting gauge fields of all spins in (3+1)-dimensions. Phys. Lett. B 1990, 243, 378–382. [Google Scholar]
- Vasiliev, M.A. More on equations of motion for interacting massless fields of all spins in (3+1)-dimensions. Phys. Lett. B 1992, 285, 225–234. [Google Scholar]
- Vasiliev, M.A. Nonlinear equations for symmetric massless higher spin fields in (A)dS(d). Phys. Lett. B 2003, 567, 139–151. [Google Scholar]
- Bekaert, X.; Boulanger, N.; Sundell, P. How higher-spin gravity surpasses the spin two barrier. Rev. Mod. Phys. 2012, 84, 987–1009. [Google Scholar]
- Bekaert, X.; Cnockaert, S.; Iazeolla, C.; Vasiliev, M.A. Nonlinear higher spin theories in various dimensions. In Proceedings of the 1st Solvay Workshop Higher Spin Gauge Theories, Brussels, Belgium, 12–14 May 2004; pp. 132–197. [Google Scholar]
- Didenko, V.E.; Skvortsov, E.D. Elements of Vasiliev theory. arXiv, 2014; arXiv:1401.2975. [Google Scholar]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from noncritical string theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar]
- Sezgin, E.; Sundell, P. Massless higher spins and holography. Nucl. Phys. B 2002, 644, 303–370. [Google Scholar]
- Klebanov, I.R.; Polyakov, A.M. AdS dual of the critical O(N) vector model. Phys. Lett. B 2002, 550, 213–219. [Google Scholar]
- Giombi, S.; Klebanov, I.R. One Loop Tests of Higher Spin AdS/CFT. J. High Energy Phys. 2013, 2013, 68. [Google Scholar]
- Giombi, S.; Klebanov, I.R.; Tseytlin, A.A. Partition Functions and Casimir Energies in Higher Spin AdSd+1/CFTd. Phys. Rev. D 2014, 90, 024048. [Google Scholar]
- Sezgin, E.; Sundell, P. Holography in 4D (super) higher spin theories and a test via cubic scalar couplings. J. High Energy Phys. 2005, 2015, 44. [Google Scholar]
- Giombi, S.; Yin, X. Higher Spin Gauge Theory and Holography: The Three-Point Functions. J. High Energy Phys. 2010, 2010, 115. [Google Scholar]
- Giombi, S.; Yin, X. The Higher Spin/Vector Model Duality. J. Phys. A 2013, 46, 214003. [Google Scholar]
- Giombi, S. Higher spin—CFT duality. In Proceedings of the Theoretical Advanced Study Institute in Elementary Particle Physics: New Frontiers in Fields and Strings (TASI 2015), Boulder, CO, USA, 1–26 June 2015; pp. 137–214. [Google Scholar]
- Giombi, S.; Klebanov, I.R.; Tan, Z.M. The ABC of Higher-Spin AdS/CFT. arXiv, 2016; arXiv:1608.07611. [Google Scholar]
- Sleight, C. Interactions in Higher-Spin Gravity: A Holographic Perspective. Ph.D. Thesis, Ludwig Maximilian University of Munich, München, Germany, 2016. [Google Scholar]
- Sleight, C. Metric-like Methods in Higher Spin Holography. arXiv, 2017; arXiv:1701.08360. [Google Scholar]
- Bekaert, X.; Erdmenger, J.; Ponomarev, D.; Sleight, C. Towards holographic higher-spin interactions: Four-point functions and higher-spin exchange. J. High Energy Phys. 2015, 2015, 170. [Google Scholar]
- Ruhl, W. The Masses of gauge fields in higher spin field theory on AdS(4). Phys. Lett. B 2005, 605, 413–418. [Google Scholar]
- Manvelyan, R.; Ruhl, W. The Masses of gauge fields in higher spin field theory on the bulk of AdS(4). Phys. Lett. B 2005, 613, 197–207. [Google Scholar]
- Manvelyan, R.; Ruhl, W. The Off-shell behaviour of propagators and the Goldstone field in higher spin gauge theory on AdS(d+1) space. Nucl. Phys. B 2005, 717, 3–18. [Google Scholar]
- Sleight, C.; Taronna, M. Higher Spin Interactions from Conformal Field Theory: The Complete Cubic Couplings. Phys. Rev. Lett. 2016, 116, 181602. [Google Scholar]
- Bekaert, X.; Erdmenger, J.; Ponomarev, D.; Sleight, C. Quartic AdS Interactions in Higher-Spin Gravity from Conformal Field Theory. J. High Energy Phys. 2015, 2015, 149. [Google Scholar]
- Boulanger, N.; Kessel, P.; Skvortsov, E.D.; Taronna, M. Higher spin interactions in four-dimensions: Vasiliev versus Fronsdal. J. Phys. A 2016, 49, 095402. [Google Scholar]
- Skvortsov, E.D.; Taronna, M. On Locality, Holography and Unfolding. J. High Energy Phys. 2015, 2015, 44. [Google Scholar]
- Vasiliev, M.A. Current Interactions and Holography from the 0-Form Sector of Nonlinear Higher-Spin Equations. J. High Energy Phys. 2017, 2017, 111. [Google Scholar]
- Taronna, M. A note on field redefinitions and higher-spin equations. J. Phys. A 2017, 50, 075401. [Google Scholar]
- Sleight, C.; Taronna, M. Higher spin gauge theories and bulk locality: A no-go result. arXiv, 2017; arXiv:1704.07859. [Google Scholar]
- Bonezzi, R.; Boulanger, N.; de Filippi, D.; Sundell, P. Noncommutative Wilson lines in higher-spin theory and correlation functions of conserved currents for free conformal fields. J. Phys. A 2017, 50, 475401. [Google Scholar]
- Maldacena, J.; Zhiboedov, A. Constraining Conformal Field Theories with A Higher Spin Symmetry. J. Phys. A 2013, 46, 214011. [Google Scholar]
- Alba, V.; Diab, K. Constraining conformal field theories with a higher spin symmetry in d = 4. arXiv, 2013; arXiv:1307.8092. [Google Scholar]
- Alba, V.; Diab, K. Constraining conformal field theories with a higher spin symmetry in d > 3 dimensions. J. High Energy Phys. 2016, 2016, 44. [Google Scholar]
- Boulanger, N.; Ponomarev, D.; Skvortsov, E.D.; Taronna, M. On the uniqueness of higher-spin symmetries in AdS and CFT. Int. J. Mod. Phys. A 2013, 28, 1350162. [Google Scholar]
- Siegel, W. All Free Conformal Representations in All Dimensions. Int. J. Mod. Phys. A 1989, 4, 2015–2020. [Google Scholar]
- Leigh, R.G.; Petkou, A.C. Holography of the N = 1 higher spin theory on AdS(4). J. High Energy Phys. 2003, 2003, 11. [Google Scholar]
- Skvortsov, E.D. On (Un)Broken Higher-Spin Symmetry in Vector Models. In Higher Spin Gauge Theories; World Scientific: Singapore, 2015; pp. 103–137. [Google Scholar]
- Maldacena, J.; Zhiboedov, A. Constraining conformal field theories with a slightly broken higher spin symmetry. Class. Quant. Gravity 2013, 30, 104003. [Google Scholar]
- Boulanger, N.; Skvortsov, E.D. Higher-spin algebras and cubic interactions for simple mixed-symmetry fields in AdS spacetime. J. High Energy Phys. 2011, 2011, 63. [Google Scholar]
- Joung, E.; Mkrtchyan, K. Notes on higher-spin algebras: Minimal representations and structure constants. J. High Energy Phys. 2014, 2014, 103. [Google Scholar]
- Joseph, A. The minimal orbit in a simple Lie algebra and its associated maximal ideal. Ann. Sci. École Norm. Super. 1976, 9, 1–29. [Google Scholar]
- Bekaert, X.; Grigoriev, M. Manifestly conformal descriptions and higher symmetries of bosonic singletons. Symmetry Integr. Geom. Methods Appl. 2010, 6, 38. [Google Scholar]
- Labastida, J.M.F. Massless Particles in Arbitrary Representations of the Lorentz Group. Nucl. Phys. B 1989, 322, 185–209. [Google Scholar]
- Metsaev, R.R. Massless mixed symmetry bosonic free fields in d-dimensional anti-de Sitter space-time. Phys. Lett. B 1995, 354, 78–84. [Google Scholar]
- Metsaev, R.R. Arbitrary spin massless bosonic fields in d-dimensional anti-de Sitter space. In Supersymmetries and Quantum Symmetries; Springer: Berlin/Heidelberg, Germany, 1999; pp. 331–340. [Google Scholar]
- Metsaev, R.R. Fermionic fields in the d-dimensional anti-de Sitter space-time. Phys. Lett. B 1998, 419, 49–56. [Google Scholar]
- Burdik, C.; Pashnev, A.; Tsulaia, M. The Lagrangian description of representations of the Poincare group. Nucl. Phys. Proc. Suppl. 2001, 102, 285–292. [Google Scholar]
- Burdik, C.; Pashnev, A.; Tsulaia, M. On the Mixed symmetry irreducible representations of the Poincare group in the BRST approach. Mod. Phys. Lett. A 2001, 16, 731–746. [Google Scholar]
- Alkalaev, K.B.; Shaynkman, O.V.; Vasiliev, M.A. On the frame—Like formulation of mixed symmetry massless fields in (A)dS(d). Nucl. Phys. B 2004, 692, 363–393. [Google Scholar]
- Bekaert, X.; Boulanger, N. On geometric equations and duality for free higher spins. Phys. Lett. B 2003, 561, 183–190. [Google Scholar]
- Bekaert, X.; Boulanger, N. Mixed symmetry gauge fields in a flat background. In Proceedings of the 5th International Workshop on Supersymmetries and Quantum Symmetries (SQS’03), Dubna, Russia, 24–29 July 2003; pp. 37–42. [Google Scholar]
- Boulanger, N.; Iazeolla, C.; Sundell, P. Unfolding Mixed-Symmetry Fields in AdS and the BMV Conjecture: I. General Formalism. J. High Energy Phys. 2009, 2009, 13. [Google Scholar]
- Boulanger, N.; Iazeolla, C.; Sundell, P. Unfolding Mixed-Symmetry Fields in AdS and the BMV Conjecture: II. Oscillator Realization. J. High Energy Phys. 2009, 2009, 14. [Google Scholar]
- Skvortsov, E.D. Mixed-Symmetry Massless Fields in Minkowski space Unfolded. J. High Energy Phys. 2008, 2008, 4. [Google Scholar]
- Alkalaev, K.B.; Grigoriev, M.; Tipunin, I.Y. Massless Poincare modules and gauge invariant equations. Nucl. Phys. B 2009, 823, 509–545. [Google Scholar]
- Skvortsov, E.D. Gauge fields in (A)dS(d) within the unfolded approach: Algebraic aspects. J. High Energy Phys. 2010, 2010, 106. [Google Scholar]
- Skvortsov, E.D. Gauge fields in (A)dS(d) and Connections of its symmetry algebra. J. Phys. A 2009, 42, 385401. [Google Scholar]
- Campoleoni, A. Metric-like Lagrangian Formulations for Higher-Spin Fields of Mixed Symmetry. arXiv, 2010; arXiv:0910.3155v2. [Google Scholar]
- Alkalaev, K.B.; Grigoriev, M. Unified BRST description of AdS gauge fields. Nucl. Phys. B 2010, 835, 197–220. [Google Scholar]
- Alkalaev, K.B.; Grigoriev, M. Unified BRST approach to (partially) massless and massive AdS fields of arbitrary symmetry type. Nucl. Phys. B 2011, 853, 663–687. [Google Scholar]
- Campoleoni, A.; Francia, D. Maxwell-like Lagrangians for higher spins. J. High Energy Phys. 2013, 2013, 168. [Google Scholar]
- Metsaev, R.R. Cubic interaction vertices of massive and massless higher spin fields. Nucl. Phys. B 2006, 759, 147–201. [Google Scholar]
- Metsaev, R.R. Cubic interaction vertices for fermionic and bosonic arbitrary spin fields. Nucl. Phys. B 2012, 859, 13–69. [Google Scholar]
- Alkalaev, K. FV-type action for AdS5 mixed-symmetry fields. J. High Energy Phys. 2011, 2011, 31. [Google Scholar]
- Boulanger, N.; Skvortsov, E.D.; Zinoviev, Y.M. Gravitational cubic interactions for a simple mixed-symmetry gauge field in AdS and flat backgrounds. J. Phys. A 2011, 44, 415403. [Google Scholar]
- Alkalaev, K. Mixed-symmetry tensor conserved currents and AdS/CFT correspondence. J. Phys. A 2013, 46, 214007. [Google Scholar]
- Alkalaev, K. Massless hook field in AdS(d+1) from the holographic perspective. J. High Energy Phys. 2013, 2013, 18. [Google Scholar]
- Chekmenev, A.; Grigoriev, M. Boundary values of mixed-symmetry massless fields in AdS space. Nucl. Phys. B 2016, 913, 769–791. [Google Scholar]
- Bekaert, X.; Grigoriev, M. Higher order singletons, partially massless fields and their boundary values in the ambient approach. Nucl. Phys. B 2013, 876, 667–714. [Google Scholar]
- Brust, C.; Hinterbichler, K. Partially Massless Higher-Spin Theory. J. High Energy Phys. 2017, 2017, 086. [Google Scholar]
- Alkalaev, K.B.; Grigoriev, M.; Skvortsov, E.D. Uniformizing higher-spin equations. J. Phys. A 2015, 48, 015401. [Google Scholar]
- Brust, C.; Hinterbichler, K. Partially massless higher-spin theory II: One-loop effective actions. J. High Energy Phys. 2017, 2017, 126. [Google Scholar]
- Brust, C.; Hinterbichler, K. Free □k scalar conformal field theory. J. High Energy Phys. 2017, 2017, 66. [Google Scholar]
- Eastwood, M.; Leistner, T. Higher symmetries of the square of the Laplacian. In Symmetries and Overdetermined Systems of Partial Differential Equations; Springer: Berlin, Germany, 2008; pp. 319–338. [Google Scholar]
- Eastwood, M.G. Higher symmetries of the Laplacian. Ann. Math. 2005, 161, 1645–1665. [Google Scholar]
- Gover, A.R.; Silhan, J. Higher symmetries of the conformal powers of the Laplacian on conformally flat manifolds. J. Math. Phys. 2012, 53, 032301. [Google Scholar]
- Michel, J.-P. Higher symmetries of the Laplacian via quantization. Annales de L’institut Fourier 2014, 64, 1581–1609. [Google Scholar]
- Joung, E.; Mkrtchyan, K. Partially-massless higher-spin algebras and their finite-dimensional truncations. J. High Energy Phys. 2016, 2016, 3. [Google Scholar]
- Deser, S.; Nepomechie, R.I. Gauge Invariance Versus Masslessness in De Sitter Space. Ann. Phys. 1984, 154, 396–420. [Google Scholar]
- Deser, S.; Nepomechie, R.I. Anomalous Propagation of Gauge Fields in Conformally Flat Spaces. Phys. Lett. B 1983, 132, 321–324. [Google Scholar]
- Higuchi, A. Symmetric Tensor Spherical Harmonics on the N Sphere and Their Application to the De Sitter Group SO(N,1). J. Math. Phys. 1987, 28, 1553–1566. [Google Scholar]
- Deser, S.; Waldron, A. Partial masslessness of higher spins in (A)dS. Nucl. Phys. B 2001, 607, 577–604. [Google Scholar]
- Skvortsov, E.D.; Vasiliev, M.A. Geometric formulation for partially massless fields. Nucl. Phys. B 2006, 756, 117–147. [Google Scholar]
- Basile, T.; Bekaert, X.; Boulanger, N. Mixed-symmetry fields in de Sitter space: A group theoretical glance. J. High Energy Phys. 2017, 2017, 81. [Google Scholar]
- Gwak, S.; Kim, J.; Rey, S.-J. Massless and Massive Higher Spins from Anti-de Sitter Space Waveguide. J. High Energy Phys. 2016, 2016, 24. [Google Scholar]
- Gwak, S.; Kim, J.; Rey, S.-J. Higgs Mechanism and Holography of Partially Massless Higher Spin Fields. In Proceedings of the International Workshop on Higher Spin Gauge Theories, Singapore, 4–6 November 2015; pp. 317–352. [Google Scholar]
- Basile, T.; Bekaert, X.; Boulanger, N. Flato-Fronsdal theorem for higher-order singletons. J. High Energy Phys. 2014, 2014, 131. [Google Scholar]
- Beccaria, M.; Bekaert, X.; Tseytlin, A.A. Partition function of free conformal higher spin theory. J. High Energy Phys. 2014, 2014, 113. [Google Scholar] [Green Version]
- Bekaert, X. Singletons and their maximal symmetry algebras. In Proceedings of the 6th Modern Mathematical Physics Meeting: Summer School and Conference on Modern Mathematical Physics, Belgrade, Serbia, 14–23 September 2010; pp. 71–89. [Google Scholar]
- Fernando, S.; Günaydin, M. Massless conformal fields, AdSd+1/CFTd higher spin algebras and their deformations. Nucl. Phys. B 2016, 904, 494–526. [Google Scholar]
- Laoues, M. Some Properties of Massless Particles in Arbitrary Dimensions. Rev. Math. Phys. 1998, 10, 1079–1109. [Google Scholar]
- Dirac, P.A.M. A Remarkable representation of the 3 + 2 de Sitter group. J. Math. Phys. 1963, 4, 901–909. [Google Scholar]
- Ferrara, S.; Fronsdal, C. Conformal fields in higher dimensions. In Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories, Proceedings of the 9th Marcel Grossmann Meeting, MG’9, Rome, Italy, 2–8 July 2000; World Scientific: Singapore, 2000; pp. 508–527. [Google Scholar]
- Enright, T.; Howe, R.; Wallach, N. A classification of unitary highest weight modules. In Representation Theory of Reductive Groups; Springer: Berlin, Germany, 1983; pp. 97–143. [Google Scholar]
- Shaynkman, O.V.; Tipunin, I.Y.; Vasiliev, M.A. Unfolded form of conformal equations in M dimensions and o (M + 2) modules. Rev. Math. Phys. 2006, 18, 823–886. [Google Scholar]
- Ehrman, J.B. On the unitary irreducible representations of the universal covering group of the 3 + 2 deSitter group. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1957; Volume 53, pp. 290–303. [Google Scholar]
- Metsaev, R.R. All conformal invariant representations of d-dimensional anti-de Sitter group. Mod. Phys. Lett. A 1995, 10, 1719–1731. [Google Scholar]
- Barnich, G.; Bekaert, X.; Grigoriev, M. Notes on conformal invariance of gauge fields. J. Phys. A 2015, 48, 505402. [Google Scholar]
- Brink, L.; Metsaev, R.R.; Vasiliev, M.A. How massless are massless fields in AdS(d). Nucl. Phys. B 2000, 586, 183–205. [Google Scholar]
- Artsukevich, A.Y.; Vasiliev, M.A. Dimensional Degression in AdS(d). Phys. Rev. D 2009, 79, 045007. [Google Scholar]
- Dolan, L.; Nappi, C.R.; Witten, E. Conformal operators for partially massless states. J. High Energy Phys. 2001, 2001, 16. [Google Scholar]
- Bae, J.-B.; Joung, E.; Lal, S. A note on vectorial AdS5/CFT4 duality for spin-j boundary theory. J. High Energy Phys. 2016, 2016, 77. [Google Scholar]
- Vasiliev, M.A. Bosonic conformal higher-spin fields of any symmetry. Nucl. Phys. B 2010, 829, 176–224. [Google Scholar]
- Bekaert, X.; Boulanger, N. The Unitary representations of the Poincare group in any spacetime dimension. In Proceedings of the 2nd Modave Summer School in Theoretical Physics, Modave, Belgium, 6–12 August 2006. [Google Scholar]
- Fulton, W.; Harris, J. Representation Theory: A First Course; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1991. [Google Scholar]
- Fuchs, J.; Schweigert, C. Symmetries, Lie Algebras and Representations: A Graduate Course for Physicists; Cambridge Monographs on Mathem; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
| 1 | In the sense that for every UIRs of the lowest energy type, i.e., in the discrete series of representations, a realisation on a space of solutions of a wave equation is known. It should be noted however that the recent works [1,2] uncovered the existence of “continuous spin” fields on AdS which do not fall into the discrete series, but might correspond to module induced from the non-compact subalgebra (instead of the maximal compact subalgebra ) as noticed in [3]. |
| 2 | See e.g., [6] where those properties were studied using the harmonic expansion of fields in (A)dS spacetimes. |
| 3 | See also [47] where the authors derived the bulk counterpart of this theorem. |
| 4 | Singletons of spin- do not appear here due to the fact that the free CFT based on these fields do not possess a conserved current of spin-2, i.e., a stress-energy tensor and therefore are not covered by the theorem derived in [46]. This can be seen for instance from the decomposition of the tensor product of two spin-s singletons spelled out in [10], where one can check that there are no currents of spin lower than . |
| 5 | Notice that by changing the boundary condition of fields in the bulk opens the possibility of having an HS theory dual to an interacting CFT, see for instance [22,25,28,49,50]. From the CFT point of view, this corresponds to the modification of the previously mentioned Maldacena-Zhiboedov theorem studied by the same authors in [51]. Instead of the existence of at least one conserved higher spin current, it is assumed that the CFT possesses a parameter N together with a tower of single trace, approximately conserved currents of all even spin , such that the conservation law gets corrected by terms of order . As a consequence, the anomalous dimensions of these higher spin currents are of order , which translates into the fact that the dual higher spin fields in the bulk acquire masses through radiative corrections, thereby leading to changes in their boundary conditions. |
| 6 | Notice that this is true only for . For the AdS case however, due to the fact that the annihilator of the scalar and the spin- singleton are isomorphic (i.e., , see e.g., [6] for more details), the HS algebra is isomorphic to and is therefore known. This translates into the fact that the two corresponding HS theory have almost the same spectrum of fields, the only difference being the mass of the bulk scalar field. |
| 7 | |
| 8 | Or at most two, which is the case of the scalar singleton as will be illustrated later (in Proposition 1). |
| 9 | Actually, it was even adopted as a definition of singletons in [8]. |
| 10 | The branching rules for irreps are recalled in Appendix A.1. |
| 11 | Although mentionned briefly in [8] as “multipleton”. |
| 12 | |
| 13 | |
| 14 | A scalar module possesses a submodule only if , whereas a spin one-half module possesses a submodule only if . In other words, only the and modules are defined as quotients, see the classification in [108]. |
| 15 | This technique was originally used in [10] (see appendix D) in order to derive the decomposition of the unitary singleton modules. We merely adapt it here to the non-unitary case. |




© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basile, T. A Note on Rectangular Partially Massless Fields. Universe 2018, 4, 4. https://doi.org/10.3390/universe4010004
Basile T. A Note on Rectangular Partially Massless Fields. Universe. 2018; 4(1):4. https://doi.org/10.3390/universe4010004
Chicago/Turabian StyleBasile, Thomas. 2018. "A Note on Rectangular Partially Massless Fields" Universe 4, no. 1: 4. https://doi.org/10.3390/universe4010004
APA StyleBasile, T. (2018). A Note on Rectangular Partially Massless Fields. Universe, 4(1), 4. https://doi.org/10.3390/universe4010004