Cosmological Bounce and Some Other Solutions in Exponential Gravity
Abstract
:1. Introduction
2. The Cosmological Set Up in the Two Frame
2.1. The Jordan Frame
2.2. The Einstein Frame
3. Description of a Bouncing Scenario
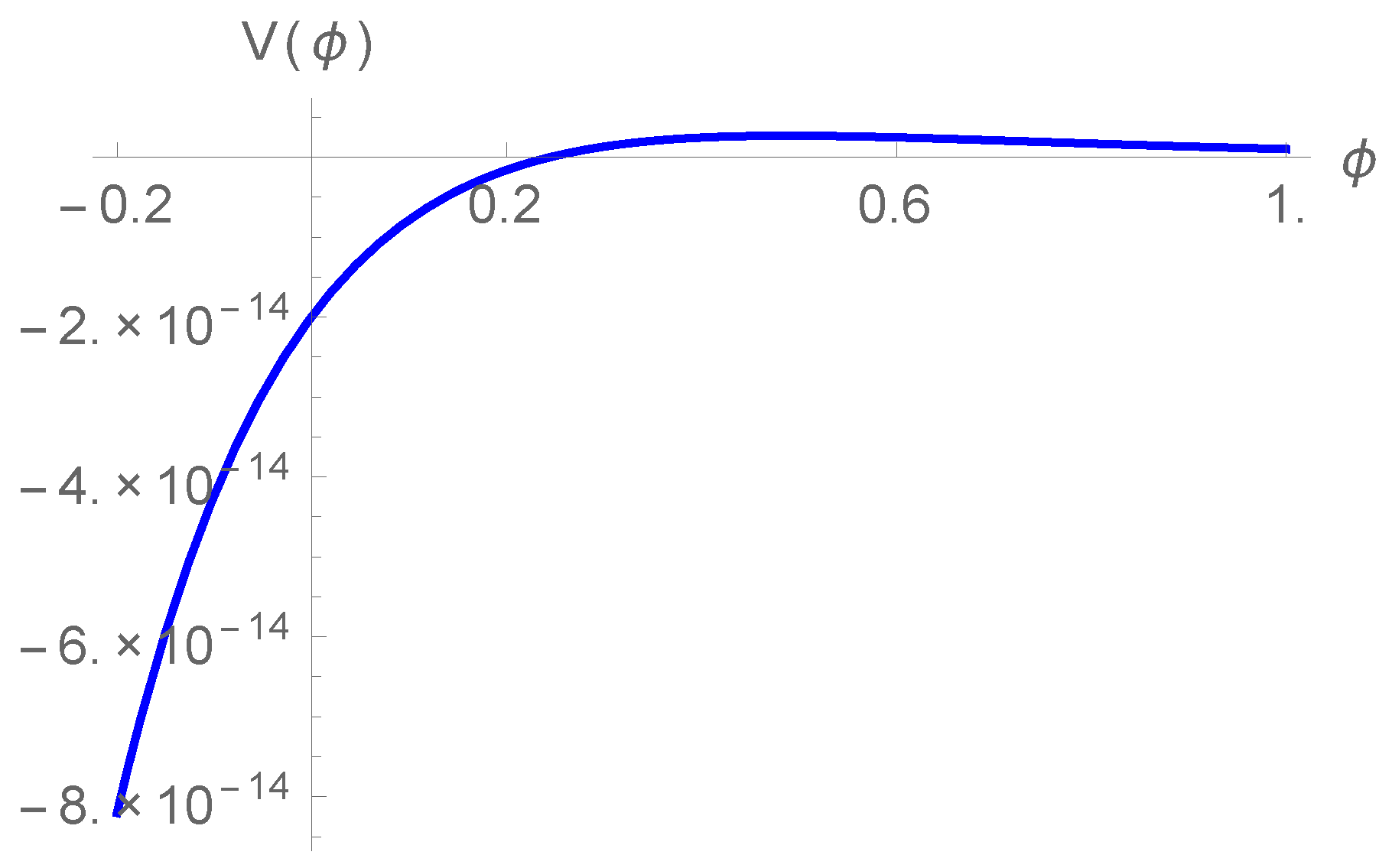
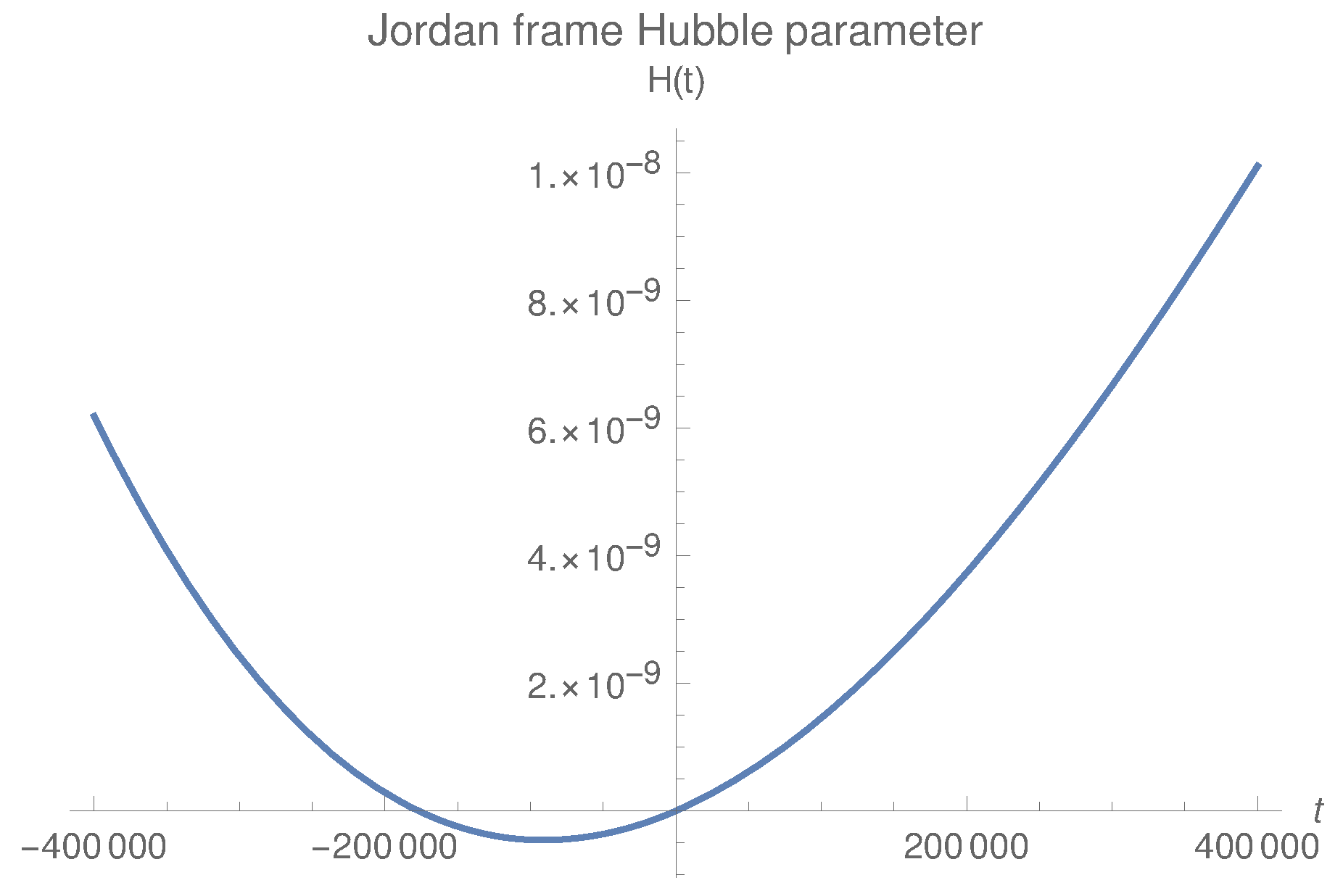
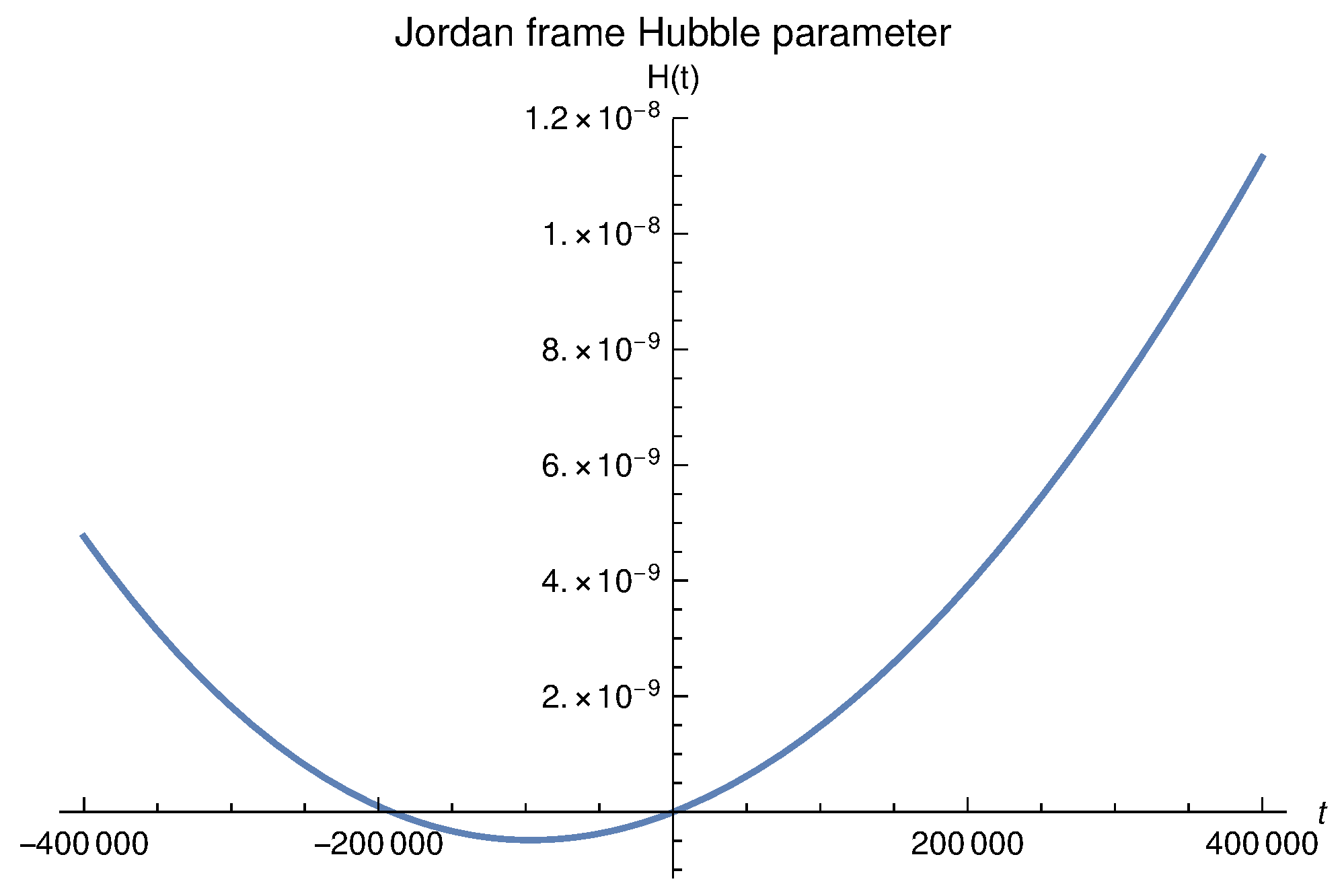
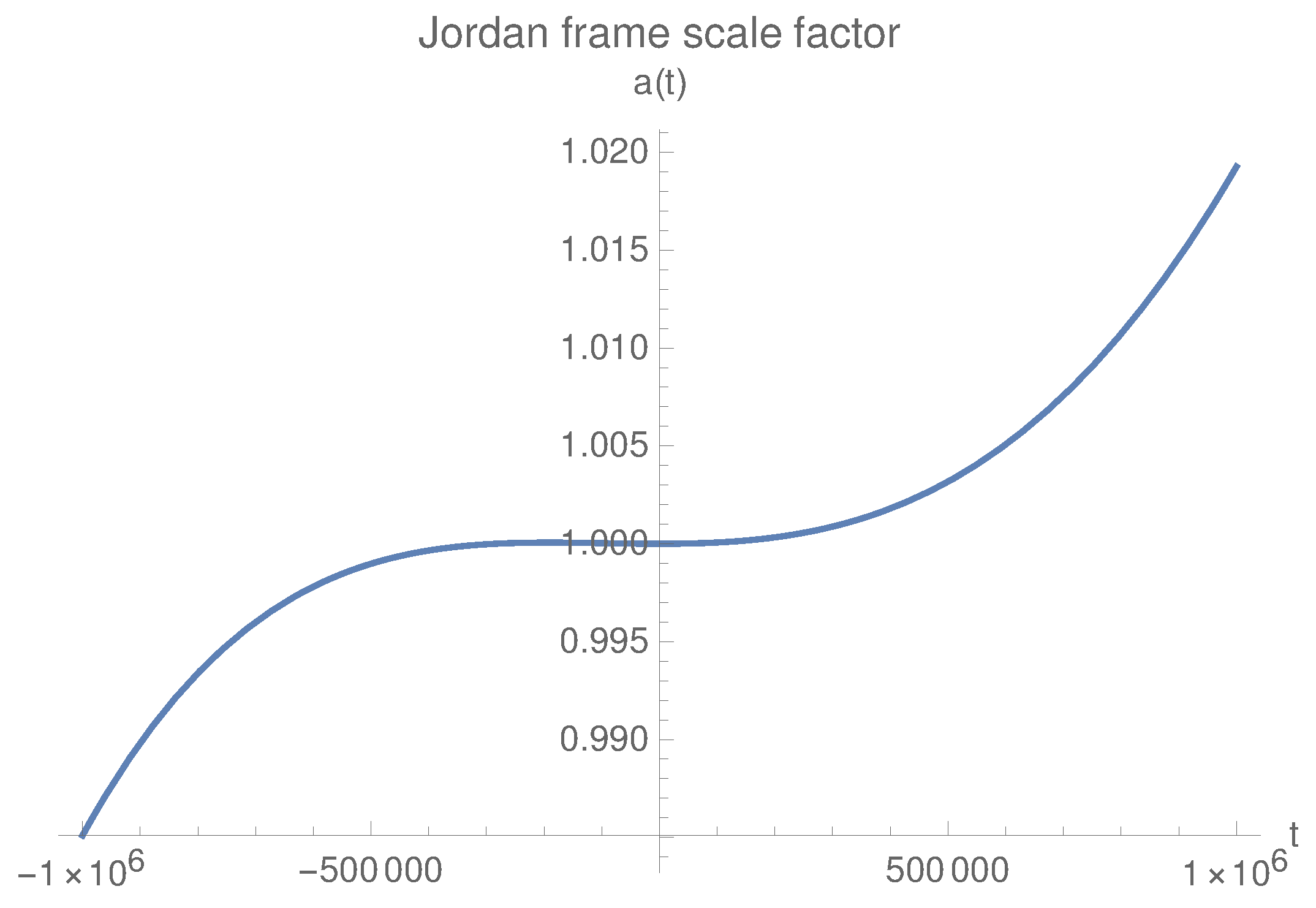
4. Bounce in Exponential Gravity
5. Evolution of Metric Perturbations through the Bounce
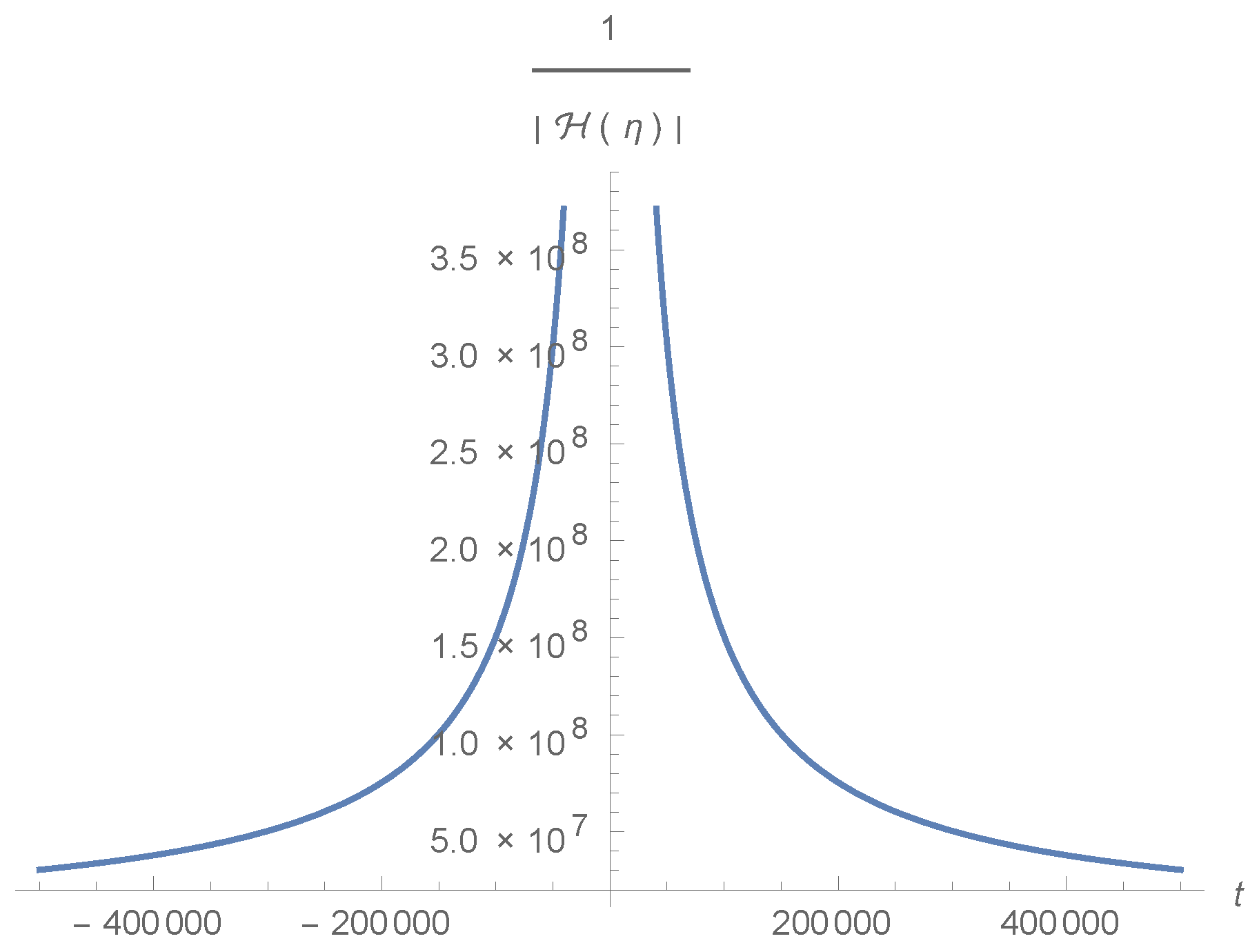
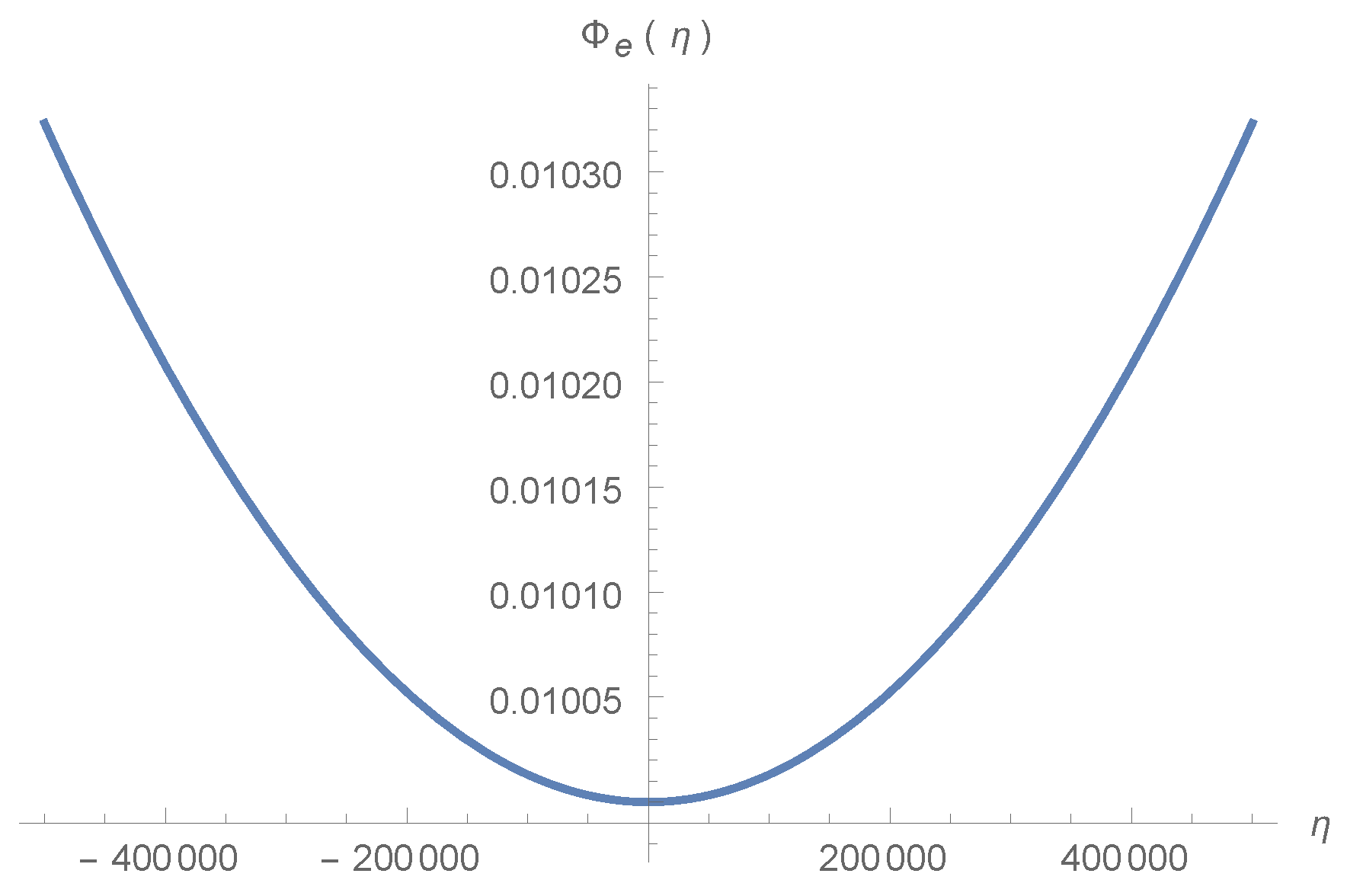
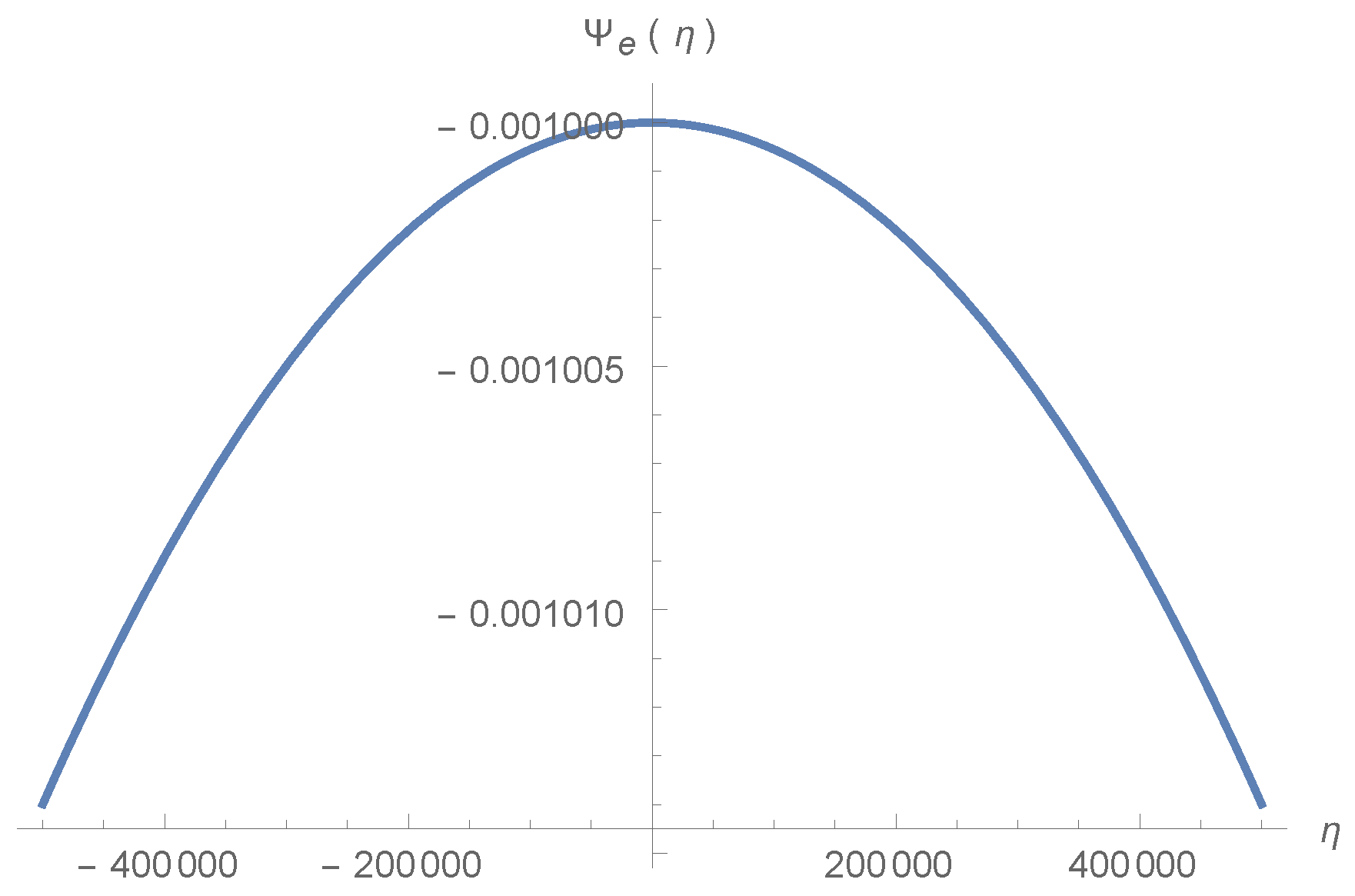
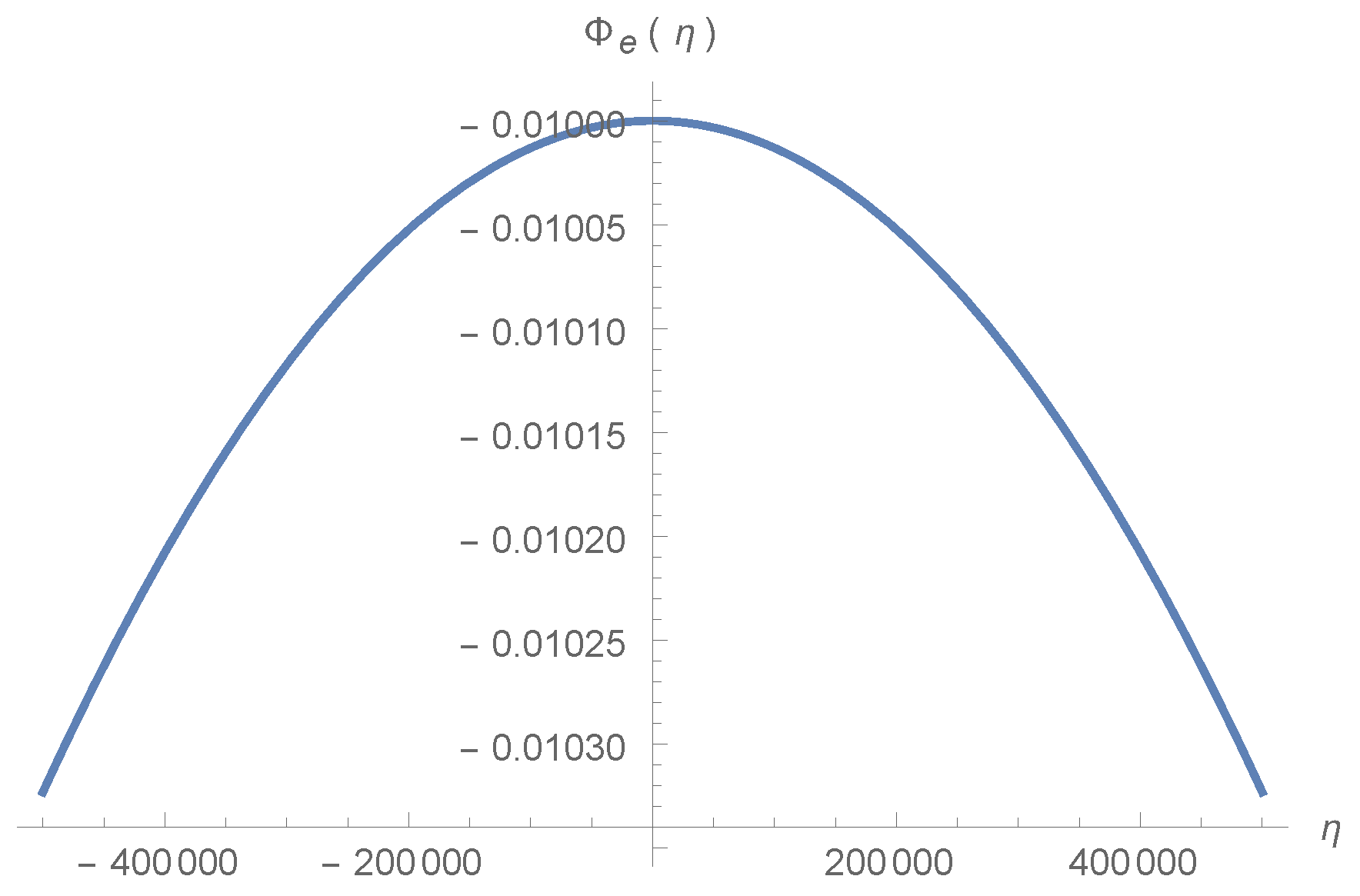
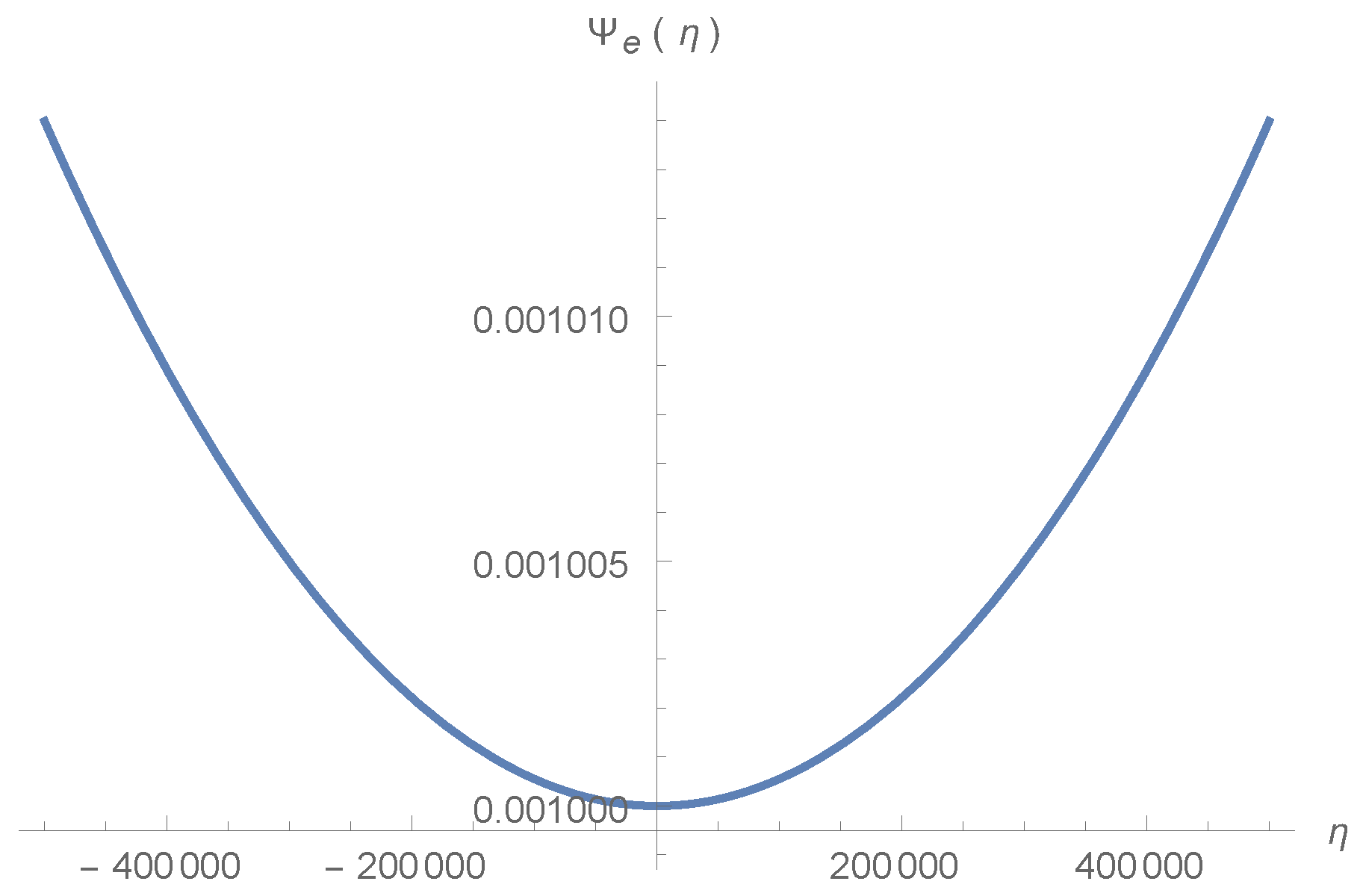
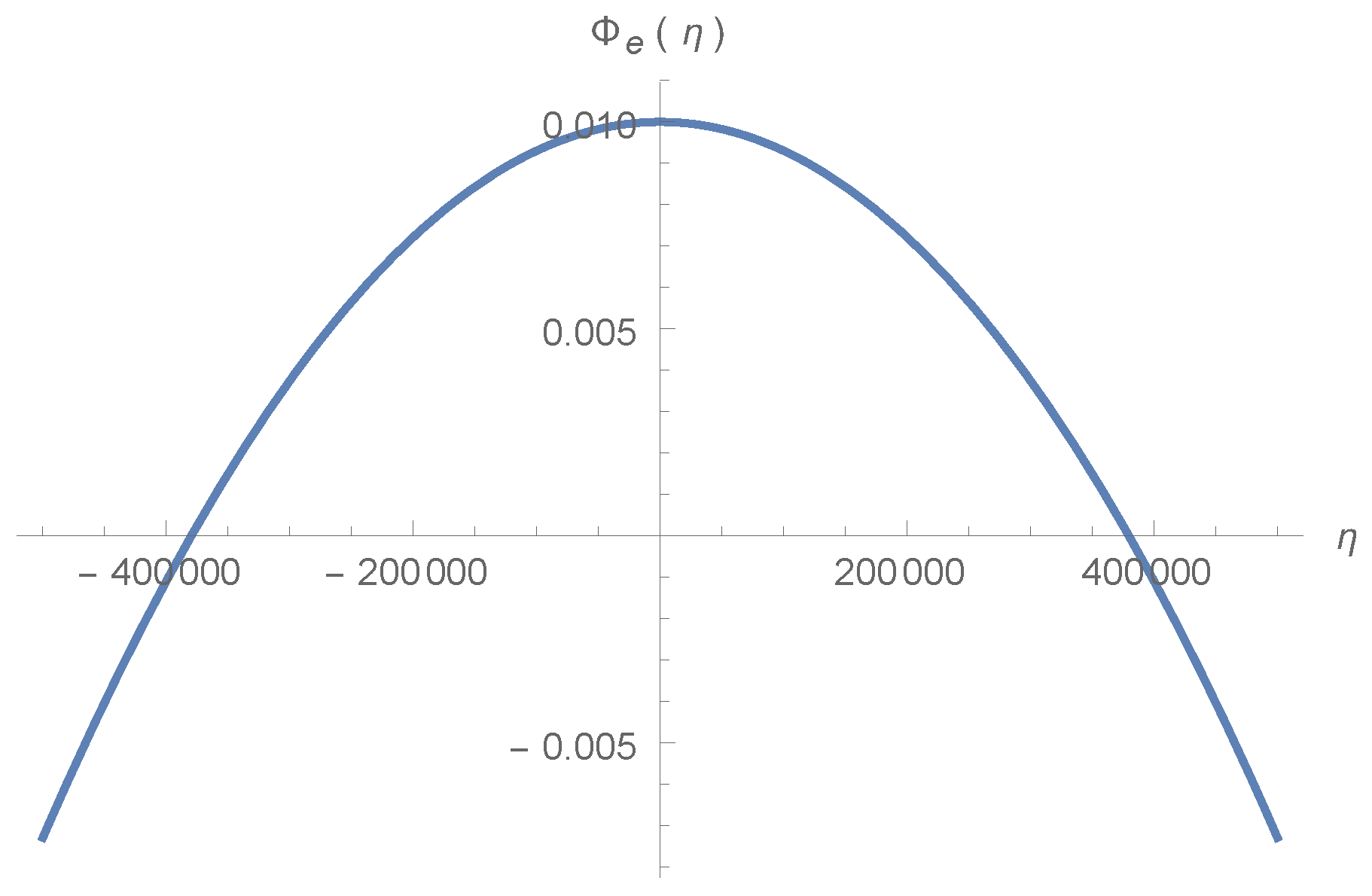
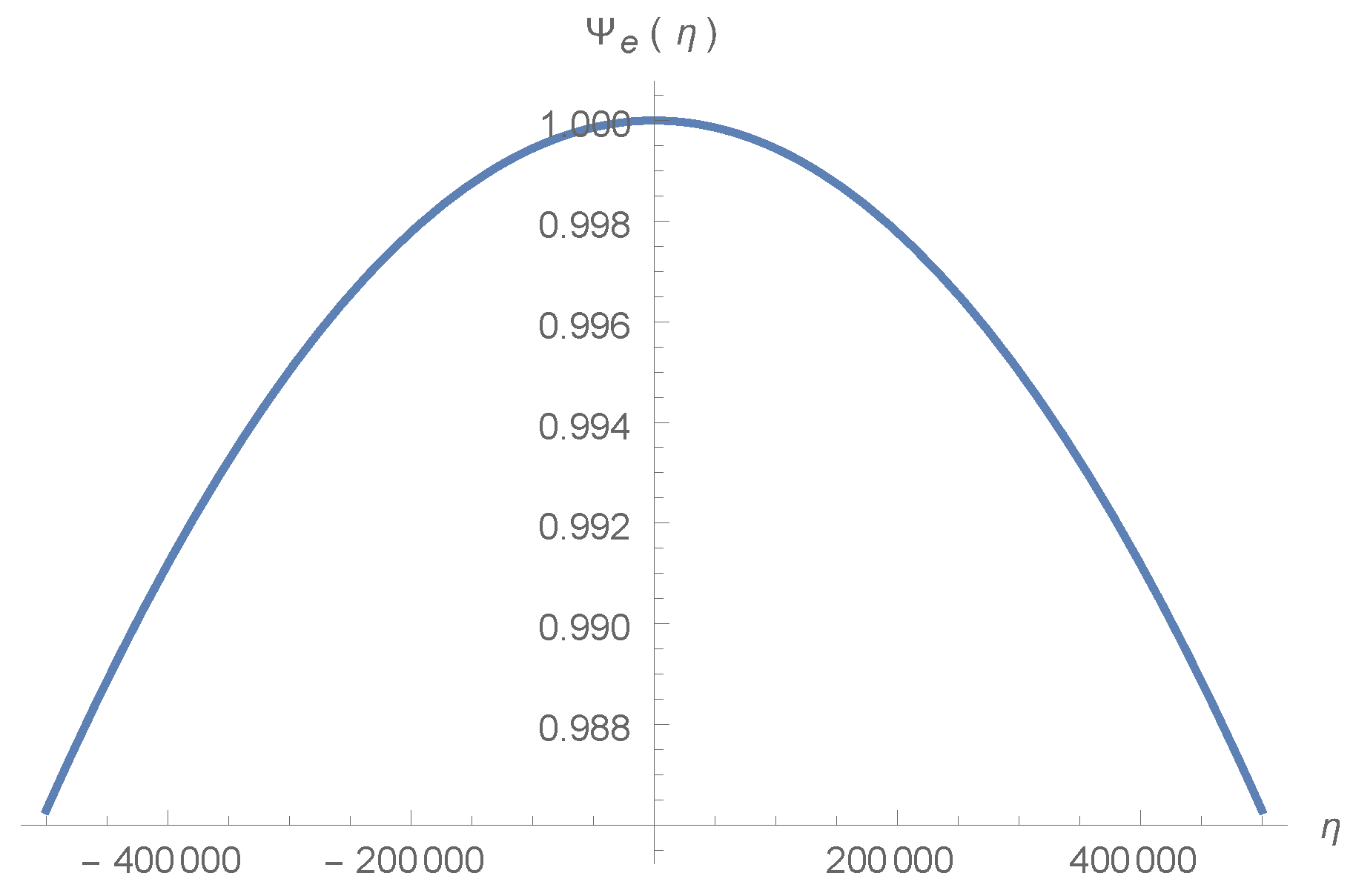
5.1. Scalar Perturbation Evolution through Bounce
- , , , .
- , , , .
- , , , .
- , , , .
5.2. Brief Comments about Tensor Perturbations through Bounce
6. Two Exact Solutions in Exponential Gravity
6.1. Exact Exponential Bouncing Solution
6.2. Exact de-Sitter Solution
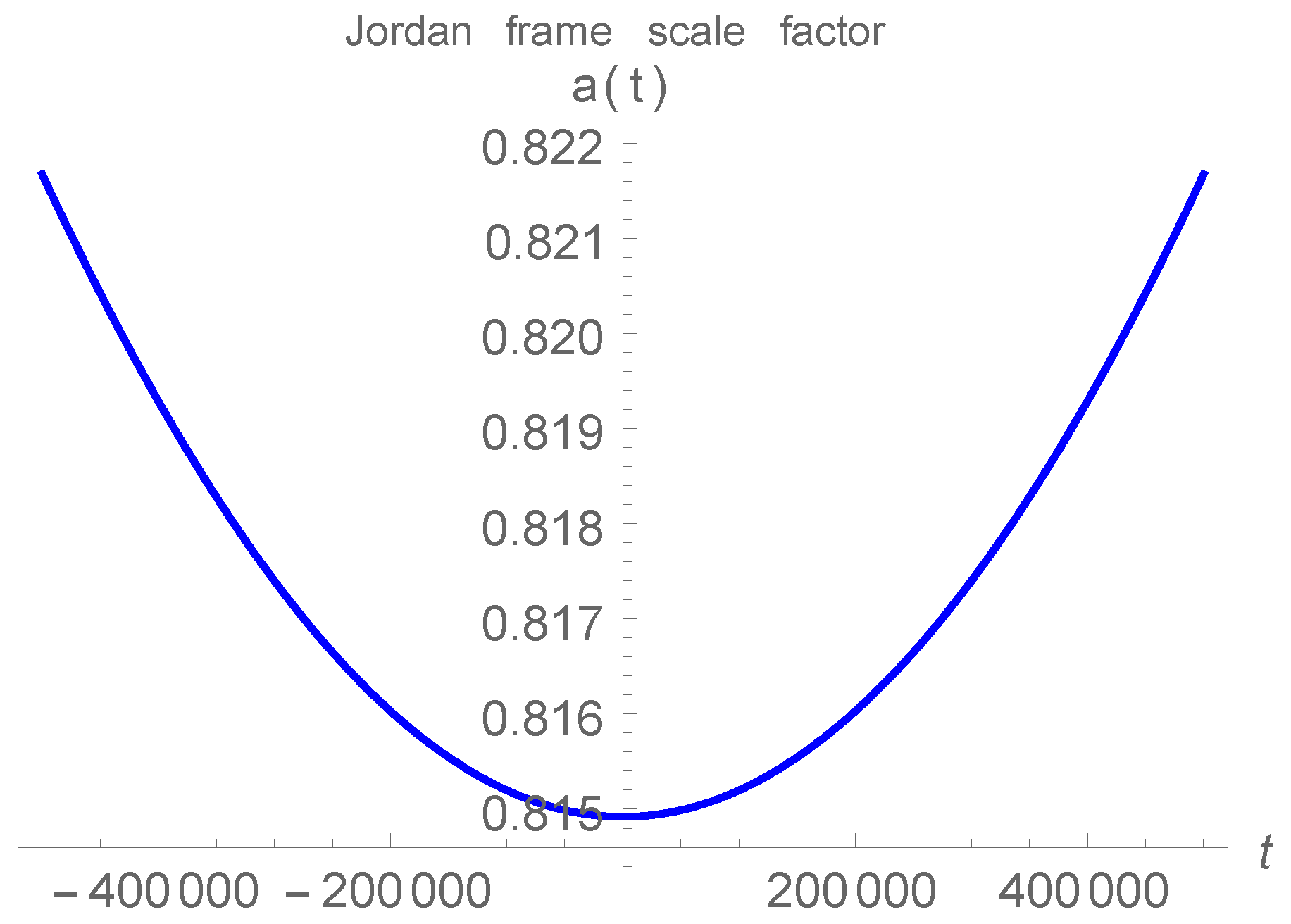
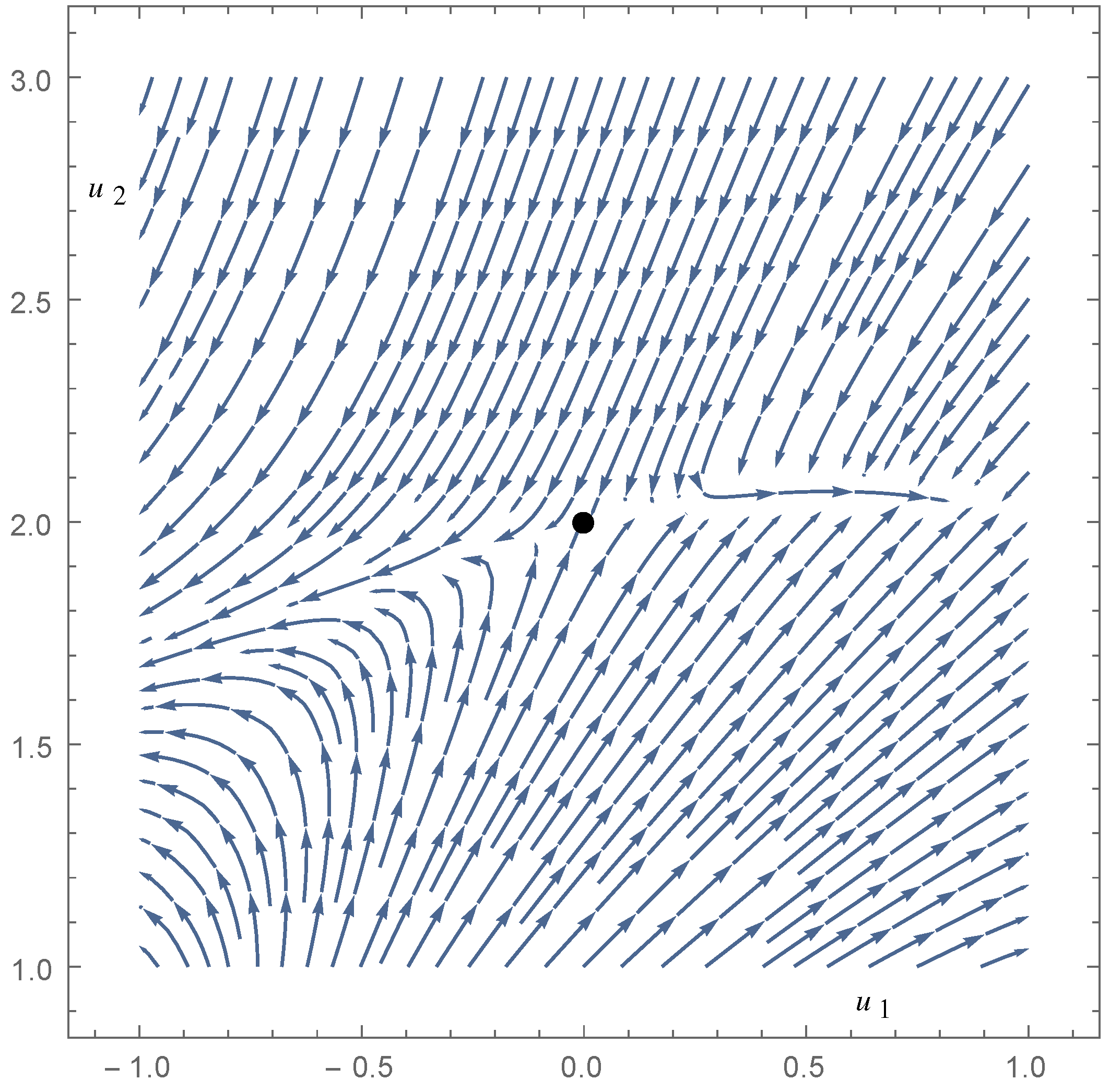
7. New Solutions in Exponential Gravity
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kragh, H. Cyclic models of the relativistic universe: The early history. Einstein Stud. 2018, 14, 183–204. [Google Scholar]
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopædia Inflationaris. Phys. Dark Univ. 2014, 5–6, 75–235. [Google Scholar] [CrossRef]
- Borde, A.; Vilenkin, A. Singularities in inflationary cosmology: A Review. Int. J. Mod. Phys. D 1996, 5, 813–824. [Google Scholar] [CrossRef]
- Novello, M.; Bergliaffa, S.E.P. Bouncing Cosmologies. Phys. Rep. 2008, 463, 127–213. [Google Scholar] [CrossRef]
- Battefeld, D.; Peter, P. A Critical Review of Classical Bouncing Cosmologies. Phys. Rep. 2015, 571, 1–66. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Odintsov, S.D.; Shapiro, I.L. Effective Action in Quantum Gravity; IOP: Bristol, UK, 1992; 413p. [Google Scholar]
- Vilkovisky, G.A. Effective action in quantum gravity. Class. Quantum Gravity 1992, 9, 895. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef] [PubMed]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Ruzmaikina, T.; Ruzmaikin, A. Quadratic Corrections to the Lagrangian Density of the Gravitational Field and the Singularity. Sov. Phys. J. Exp. Theor. Phys. 1970, 30, 372. [Google Scholar]
- Cai, Y.F.; Saridakis, E.N. Non-singular Cyclic Cosmology without Phantom Menace. J. Cosmol. 2011, 17, 7238–7254. [Google Scholar]
- Saridakis, E.N.; Banerjee, S.; Myrzakulov, R. Bounce and cyclic cosmology in new gravitational scalar-tensor theories. Phys. Rev. D 2018, 98, 063513. [Google Scholar] [CrossRef]
- Paul, N.; Chakrabarty, S.N.; Bhattacharya, K. Cosmological bounces in spatially flat FRW spacetimes in metric f(R) gravity. J. Cosmol. Astropart. Phys. 2014, 2014, 009. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Chakrabarty, S. Intricacies of Cosmological bounce in polynomial metric f(R) gravity for flat FLRW spacetime. J. Cosmol. Astropart. Phys. 2016, 2016, 030. [Google Scholar] [CrossRef]
- Bamba, K.; Makarenko, A.N.; Myagky, A.N.; Nojiri, S.; Odintsov, S.D. Bounce cosmology from F(R) gravity and F(R) bigravity. J. Cosmol. Astropart. Phys. 2014, 2014, 008. [Google Scholar] [CrossRef]
- Carloni, S.; Dunsby, P.K.S.; Solomons, D.M. Bounce conditions in f(R) cosmologies. Class. Quantum Gravity 2006, 23, 1913–1922. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Non-singular exponential gravity: A simple theory for early- and late-time accelerated expansion. Phys. Rev. D 2011, 83, 086006. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Exponential Inflation with F(R) Gravity. Phys. Rev. D 2018, 97, 064001. [Google Scholar] [CrossRef]
- Oikonomou, V.K. An Exponential F(R) Dark Energy Model. Gen. Relativ. Gravit. 2013, 45, 2467–2481. [Google Scholar] [CrossRef]
- Cai, Y.F.; Marciano, A.; Wang, D.G.; Wilson-Ewing, E. Bouncing cosmologies with dark matter and dark energy. Universe 2016, 3, 1. [Google Scholar] [CrossRef]
- Cai, Y.F. Exploring Bouncing Cosmologies with Cosmological Surveys. Sci. China Phys. Mech. Astron. 2014, 57, 1414–1430. [Google Scholar] [CrossRef]
- Barrow, J.D.; Cotsakis, S. Inflation and the Conformal Structure of Higher Order Gravity Theories. Phys. Lett. B 1988, 214, 515–518. [Google Scholar] [CrossRef]
- Matsumoto, J. Cosmological perturbations in F(R) gravity. Phys. Rev. D 2013, 87, 104002. [Google Scholar] [CrossRef]
- Cai, Y.F.; Easson, D.A.; Brandenberger, R. Towards a Nonsingular Bouncing Cosmology. J. Cosmol. Astropart. Phys. 2012, 2012, 020. [Google Scholar] [CrossRef]
- Kobayashi, T. Generic instabilities of nonsingular cosmologies in Horndeski theory: A no-go theorem. Phys. Rev. D 2016, 94, 043511. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Wan, Y.; Li, H.G.; Qiu, T.; Piao, Y.S. The Effective Field Theory of nonsingular cosmology. J. High Energy Phys. 2017, 2017, 090. [Google Scholar] [CrossRef]
- Raveendran, R.N.; Chowdhury, D.; Sriramkumar, L. Viable tensor-to-scalar ratio in a symmetric matter bounce. J. Cosmol. Astropart. Phys. 2018, 2018, 030. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Sá¡ez-Chillán Gámez, D.; Sharov, G.S. Is exponential gravity a viable description for the whole cosmological history? Eur. Phys. J. C 2017, 77, 862. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmidt, H.J. Exact cosmological solutions of nonlinear F(R) gravity. arXiv, 1998; arXiv:gr-qc/9808060. [Google Scholar]
- Wei, H.; Li, H.Y.; Zou, X.B. Exact cosmological solutions of f(R) theories via Hojman symmetry. Nucl. Phys. B 2016, 903, 132–149. [Google Scholar] [CrossRef]
- Bari, P.; Bari, P.; Chakraborty, S.; Bhattacharya, K. Causal horizons in a bouncing universe. Gen. Relat. Gravit. 2018, 50, 118. [Google Scholar] [CrossRef]
- Amendola, L.; Gannouji, R.; Polarski, D.; Tsujikawa, S. Conditions for the cosmological viability of f(R) dark energy models. Phys. Rev. D 2007, 75, 083504. [Google Scholar] [CrossRef]
- Carloni, S.; Troisi, A.; Dunsby, P.K.S. Some remarks on the dynamical systems approach to fourth order gravity. Gen. Relat. Gravit. 2009, 41, 1757–1776. [Google Scholar] [CrossRef] [Green Version]
- Carloni, S.; Dunsby, P.K.S.; Capozziello, S.; Troisi, A. Cosmological dynamics of R**n gravity. Class. Quantum Gravity 2005, 22, 4839–4868. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Autonomous dynamical system approach for f(R) gravity. Phys. Rev. D 2017, 96, 104049. [Google Scholar] [CrossRef]
| 1. | The reader can consult Ref. [5] for a review on singularities in inflationary cosmology. |
| 2. | We are not calling this condition as the weak energy condition as the energy conditions are generally stated in the Einstein frame. |
| 3. | We want to remind the reader at this point that a prime on f implies a derivative with respect to R where as a prime on implies a derivative with respect to . |
| 4. | We call the conditions as intermediate instead of initial conditions. The reason being that we impose our conditions on the dynamical system at and look at the system at both negative and positive times. |
| 5. | The new conventions which are at odds with our previous convention becomes necessary as conformal time is involved in the discussions. From the next section we will use the old conventions. |





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bari, P.; Bhattacharya, K.; Chakraborty, S. Cosmological Bounce and Some Other Solutions in Exponential Gravity. Universe 2018, 4, 105. https://doi.org/10.3390/universe4100105
Bari P, Bhattacharya K, Chakraborty S. Cosmological Bounce and Some Other Solutions in Exponential Gravity. Universe. 2018; 4(10):105. https://doi.org/10.3390/universe4100105
Chicago/Turabian StyleBari, Pritha, Kaushik Bhattacharya, and Saikat Chakraborty. 2018. "Cosmological Bounce and Some Other Solutions in Exponential Gravity" Universe 4, no. 10: 105. https://doi.org/10.3390/universe4100105
APA StyleBari, P., Bhattacharya, K., & Chakraborty, S. (2018). Cosmological Bounce and Some Other Solutions in Exponential Gravity. Universe, 4(10), 105. https://doi.org/10.3390/universe4100105




