Towards a Unified Quark-Hadron-Matter Equation of State for Applications in Astrophysics and Heavy-Ion Collisions
Abstract
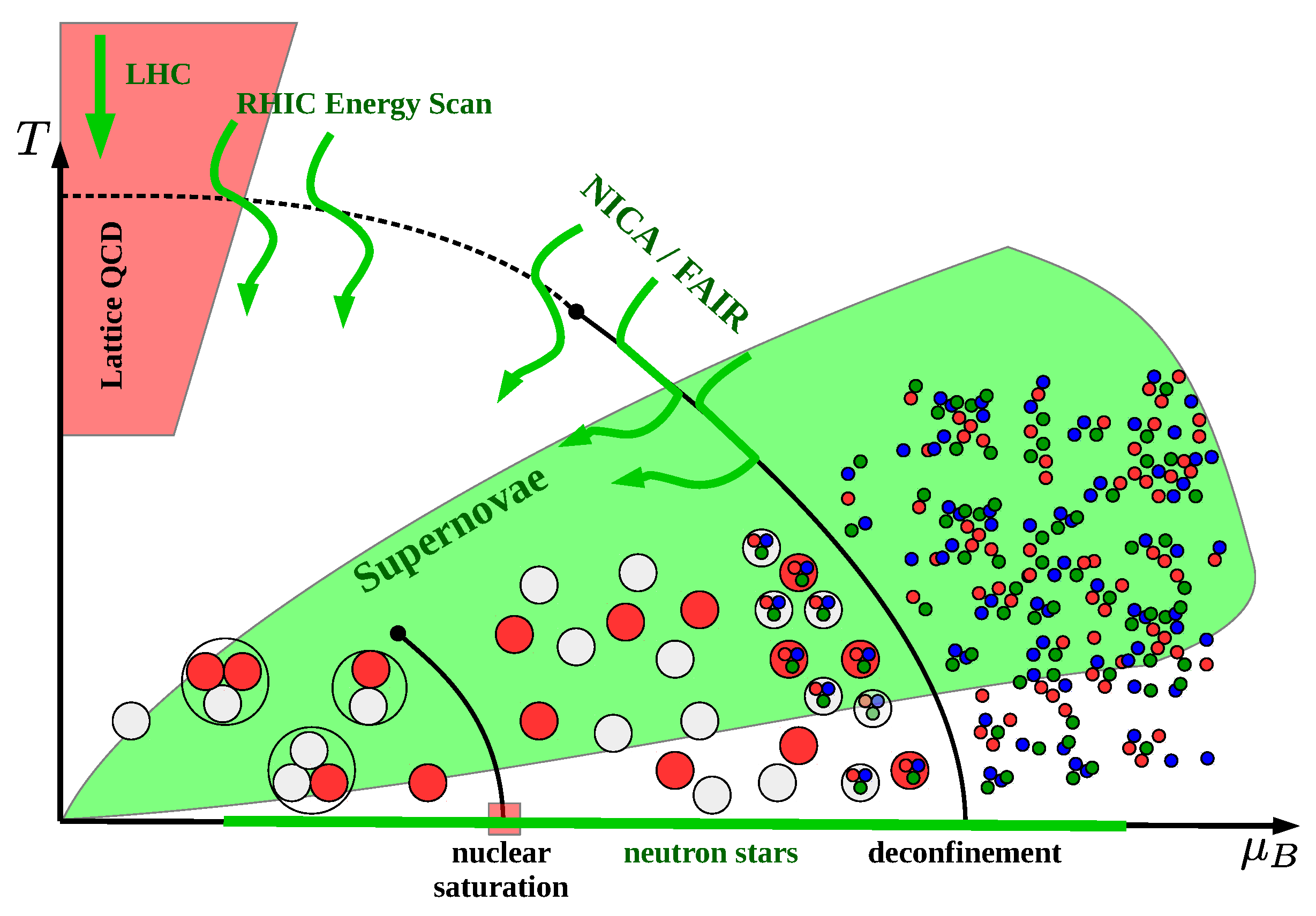
:1. Introduction
2. Quantum Statistical Approach and the Cluster Virial Expansion

3. —Derivable Approach to the Cluster Virial Expansion for Nuclear Matter
3.1. Generalized Beth-Uhlenbeck EoS from the Φ−Derivable Approach
3.2. Deuterons in Nuclear Matter
4. Cluster Virial Expansion for Quark-Hadron Matter within the Derivable Approach
4.1. Relativistic Density Functional Approach to Nuclear Matter
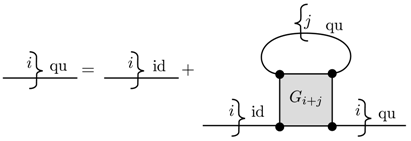
4.2. Quark Pauli Blocking in Hadronic Matter
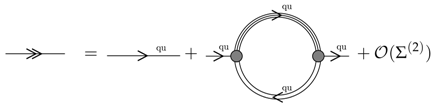
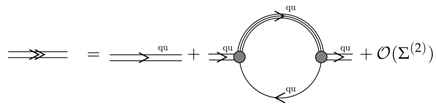

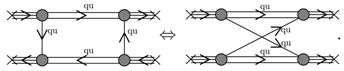
4.3. Mott Dissociation of Pions in Quark Matter
4.4. Relativistic Density Functional Approach to Quark Matter
5. Applications in Core-Collapse Supernovae and Neutron Stars
5.1. Heavy Nuclear Clusters with
5.2. Light Nuclear Clusters with
5.3. Homogeneous Matter at Supersaturation Density and Phase Transition to Quark Matter
6. Cluster Formation and Quark Deconfinement Transition in Heavy-Ion Collisions
6.1. Light Cluster Formation and Symmetry Energy in Low-Energy Heavy-Ion Collisions
6.2. Deconfinement Transition in Relativistic Heavy-Ion Collisions
- Can the success of the thermal statistical model in describing the production of nuclear clusters as measured by the ALICE experiment at LHC [134] be interpreted so that they freeze out directly when hadronizing the QGP so that they may be viewed as preformed multiquark systems already in the QGP?
- What are the necessary ingredients to understand chemical freezeout of hadrons and clusters kinetically [135]?
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Natowitz, J.B.; Hagel, K.; Ma, Y.; Murray, M.; Qin, L.; Wada, R.; Wang, J. Limiting temperatures and the equation of state of nuclear matter. Phys. Rev. Lett. 2002, 89, 212701. [Google Scholar] [CrossRef] [PubMed]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Baym, G.; Kadanoff, L.P. Conservation Laws and Correlation Functions. Phys. Rev. 1961, 124, 287–299. [Google Scholar] [CrossRef]
- Baym, G. Selfconsistent approximation in many body systems. Phys. Rev. 1962, 127, 1391–1401. [Google Scholar] [CrossRef]
- Kraeft, W.D.; Kremp, D.; Ebeling, W.; Röpke, G. Quantum Statistics of Charged Particle Systems; Springer: Berlin, Germany, 1986. [Google Scholar]
- Weinhold, W.; Friman, B.; Nörenberg, W. Thermodynamics of Delta resonances. Phys. Lett. B 1998, 433, 236–242. [Google Scholar] [CrossRef]
- Weinhold, W. Thermodynamik mit Resonanzzuständen. Ph.D. Thesis, Technischen Universität Darmstadt, Darmstadt, Germany, 1998. [Google Scholar]
- Zimmermann, R.; Stolz, H. The Mass Action Law in Two-Component Fermi Systems Revisited Excitons and Electron-Hole Pairs. Phys. Status Solidi 1985, 131, 151–164. [Google Scholar] [CrossRef]
- Röpke, G.; Münchow, L.; Schulz, H. On the phase stability of hot nuclear matter and the applicability of detailed balance equations. Phys. Lett. B 1982, 110, 21–24. [Google Scholar] [CrossRef]
- Röpke, G.; Münchow, L.; Schulz, H. Particle clustering and Mott transitions in nuclear matter at finite temperature. Nucl. Phys. A 1982, 379, 536–552. [Google Scholar] [CrossRef]
- Röpke, G.; Schmidt, M.; Münchow, L.; Schulz, H. Particle clustering and Mott transition in nuclear matter at finite temperature (II). Nucl. Phys. A 1983, 399, 587–602. [Google Scholar] [CrossRef]
- Schmidt, M.; Röpke, G.; Schulz, H. Generalized Beth-Uhlenbeck approach for hot nuclear matter. Ann. Phys. 1990, 202, 57–99. [Google Scholar] [CrossRef]
- Röpke, G. Correlations and Clustering in Dilute Matter. In Nuclear Particle Correlations and Cluster Physics; Schröder, W., Ed.; World Scientific: Singapore, 2017; pp. 31–69. [Google Scholar]
- Röpke, G.; Blaschke, D.; Ivanov, Y.B.; Karpenko, I.; Rogachevsky, O.V.; Wolter, H.H. Medium effects on freeze-out of light clusters at NICA energies. Phys. Part. Nucl. Lett. 2018, 15, 225–229. [Google Scholar] [CrossRef]
- Beth, E.; Uhlenbeck, G. The quantum theory of the non-ideal gas. II. Behaviour at low temperatures. Physica 1937, 4, 915–924. [Google Scholar] [CrossRef]
- Röpke, G.; Bastian, N.U.; Blaschke, D.; Klähn, T.; Typel, S.; Wolter, H.H. Cluster virial expansion for nuclear matter within a quasiparticle statistical approach. Nucl. Phys. A 2013, 897, 70–92. [Google Scholar] [CrossRef]
- Röpke, G. Nuclear matter equation of state including two-, three-, and four-nucleon correlations. Phys. Rev. C 2015, 92, 054001. [Google Scholar] [CrossRef]
- Röpke, G. Clustering in nuclear environment. J. Phys. 2014, 569, 012031. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Schwenk, A. Cluster formation and the virial equation of state of low-density nuclear matter. Nucl. Phys. A 2006, 776, 55–79. [Google Scholar] [CrossRef]
- Blaschke, D. Cluster virial expansion for quark and nuclear matter. In Proceedings of the XXII International Baldin Seminar on High Energy Physics Problems, JINR Dubna, Russia, 15–20 September 2014. [Google Scholar]
- Vanderheyden, B.; Baym, G. Selfconsistent approximations in relativistic plasmas: Quasiparticle analysis of the thermodynamic properties. J. Stat. Phys. 1998, 93, 843–861. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Iancu, E.; Rebhan, A. Approximately selfconsistent resummations for the thermodynamics of the quark gluon plasma. 1. Entropy and density. Phys. Rev. D 2001, 63, 065003. [Google Scholar] [CrossRef]
- Uhlenbeck, G.E.; Beth, E. The quantum theory of the non-ideal gas I. Deviations from the classical theory. Physica 1936, 3, 729–745. [Google Scholar] [CrossRef]
- Typel, S. Variations on the excluded-volume mechanism. Eur. Phys. J. A 2016, 52, 16. [Google Scholar] [CrossRef]
- Röpke, G.; Blaschke, D.; Schulz, H. Pauli Quenching Effects in a Simple String Model of Quark/Nuclear Matter. Phys. Rev. D 1986, 34, 3499–3513. [Google Scholar] [CrossRef]
- Blaschke, D.; Röpke, G. Pauli Quenching for Hadrons in Nuclear Matter: A Quark Substructure Effect. Dubna Preprint 1988, unpublished. [Google Scholar]
- Vautherin, D.; Brink, D.M. Hartree-Fock calculations with Skyrme’s interaction. 1. Spherical nuclei. Phys. Rev. C 1972, 5, 626–647. [Google Scholar] [CrossRef]
- Blaschke, D.; Tovmasian, T.; Kämpfer, B. Predicting Stable Quark Cores in Neutron Stars From a Unified Description of Quark—Hadron Matter. Sov. J. Nucl. Phys. 1990, 52, 675–678. [Google Scholar]
- Klähn, T.; Blaschke, D. Strange Matter in Compact Stars. EPJ Web Conf. 2018, 171, 08001. [Google Scholar] [CrossRef]
- Bastian, N.U.F.; Blaschke, D.B.; Cierniak, M.; Fischer, T.; Kaltenborn, M.A.R.; Marczenko, M.; Typel, S. Strange matter prospects within the string-flip model. EPJ Web Conf. 2018, 171, 20002. [Google Scholar] [CrossRef]
- Dubinin, A.; Blaschke, D.; Friesen, A.; Turko, L. Pauli Blocking Effect Within the Relativistic Pion Gas. Acta Phys. Pol. Suppl. 2017, 10, 903. [Google Scholar] [CrossRef]
- Blaschke, D.; Röpke, G. Quark exchange contribution to the effective meson meson interaction potential. Phys. Lett. B 1993, 299, 332–337. [Google Scholar] [CrossRef]
- Barnes, T.; Swanson, E.S. A Diagrammatic approach to meson meson scattering in the nonrelativistic quark potential model. Phys. Rev. D 1992, 46, 131–159. [Google Scholar] [CrossRef]
- Blaschke, D.; Buballa, M.; Dubinin, A.; Röpke, G.; Zablocki, D. Generalized Beth—Uhlenbeck approach to mesons and diquarks in hot, dense quark matter. Ann. Phys. 2014, 348, 228–255. [Google Scholar] [CrossRef]
- Hüfner, J.; Klevansky, S.P.; Zhuang, P.; Voss, H. Thermodynamics of a quark plasma beyond the mean field: A generalized Beth-Uhlenbeck approach. Ann. Phys. 1994, 234, 225–244. [Google Scholar] [CrossRef]
- Zhuang, P.; Hüfner, J.; Klevansky, S.P. Thermodynamics of a quark—Meson plasma in the Nambu-Jona- Lasinio model. Nucl. Phys. A 1994, 576, 525–552. [Google Scholar] [CrossRef]
- Yamazaki, K.; Matsui, T. Quark-Hadron Phase Transition in the PNJL model for interacting quarks. Nucl. Phys. A 2013, 913, 19–50. [Google Scholar] [CrossRef]
- Wergieluk, A.; Blaschke, D.; Kalinovsky, Y.L.; Friesen, A. Pion dissociation and Levinson`s theorem in hot PNJL quark matter. Phys. Part. Nucl. Lett. 2013, 10, 660–668. [Google Scholar] [CrossRef]
- Blaschke, D.; Dubinin, A.; Buballa, M. Polyakov-loop suppression of colored states in a quark-meson-diquark plasma. Phys. Rev. D 2015, 91, 125040. [Google Scholar] [CrossRef]
- Kitazawa, M.; Kunihiro, T.; Nemoto, Y. Emergence of soft quark excitations by the coupling with a soft mode of the QCD critical point. Phys. Rev. D 2014, 90, 116008. [Google Scholar] [CrossRef]
- Blaizot, J.P. Quantum fields at finite temperature and density. J. Korean Phys. Soc. 1992, 25, S65–S98. [Google Scholar]
- Kaltenborn, M.A.R.; Bastian, N.U.F.; Blaschke, D.B. Quark-Nuclear Hybrid Equation of State with Excluded Volume Effects. Phys. Rev. D 2017, 96, 056024. [Google Scholar] [CrossRef]
- Khvorostukin, A.S.; Skokov, V.V.; Toneev, V.D.; Redlich, K. Lattice QCD constraints on the nuclear equation of state. Eur. Phys. J. C 2006, 48, 531–543. [Google Scholar] [CrossRef]
- Kapusta, J.I. Finite Temperature Field Theory. In Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Horowitz, C.J.; Piekarewicz, J. Quark models of nuclear matter: 1. Basic models and ground state properties. Nucl. Phys. A 1992, 536, 669–696. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Piekarewicz, J. Nuclear to quark matter transition in the string flip model. Phys. Rev. C 1991, 44, 2753–2764. [Google Scholar] [CrossRef]
- Benic, S.; Blaschke, D.; Alvarez-Castillo, D.E.; Fischer, T.; Typel, S. A new quark-hadron hybrid equation of state for astrophysics—I. High-mass twin compact stars. Astron. Astrophys. 2015, 577, A40. [Google Scholar] [CrossRef]
- Hebeler, K.; Schwenk, A. Chiral three-nucleon forces and neutron matter. Phys. Rev. C 2010, 82, 014314. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Constraints on Neutron Star Radii Based on Chiral Effective Field Theory Interactions. Phys. Rev. L 2010, 105, 161102. [Google Scholar] [CrossRef] [PubMed]
- Holt, J.W.; Kaiser, N.; Weise, W. Chiral nuclear dynamics with three-body forces. Prog. Part. Nucl. Phys. 2012, 67, 353–358. [Google Scholar] [CrossRef]
- Sammarruca, F.; Chen, B.; Coraggio, L.; Itaco, N.; Machleidt, R. Dirac-Brueckner-Hartree-Fock versus chiral effective field theory. Phys. Rev. C 2012, 86, 054317. [Google Scholar] [CrossRef]
- Tews, I.; Krüger, T.; Hebeler, K.; Schwenk, A. Neutron Matter at Next-to-Next-to-Next-to-Leading Order in Chiral Effective Field Theory. Phys. Rev. Lett. 2013, 110, 032504. [Google Scholar] [CrossRef] [PubMed]
- Krüger, T.; Tews, I.; Hebeler, K.; Schwenk, A. Neutron matter from chiral effective field theory interactions. Phys. Rev. C 2013, 88, 025802. [Google Scholar] [CrossRef]
- Coraggio, L.; Holt, J.W.; Itaco, N.; Machleidt, R.; Sammarruca, F. Reduced regulator dependence of neutron-matter predictions with perturbative chiral interactions. Phys. Rev. C 2013, 87, 014322. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 448. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Fischer, T.; Bastian, N.U.; Blaschke, D.; Cerniak, M.; Hempel, M.; Klähn, T.; Martínez-Pinedo, G.; Newton, W.G.; Röpke, G.; Typel, S. The state of matter in simulations of core-collapse supernovae—Reflections and recent developments. Publ. Astron. Soc. Austral. 2017, 34, 67. [Google Scholar] [CrossRef]
- Typel, S.; Röpke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Hempel, M.; Schaffner-Bielich, J.; Typel, S.; Röpke, G. Light clusters in nuclear matter: Excluded volume versus quantum many-body approaches. Phys. Rev. C 2011, 84, 055804. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Yamada, S.; Suzuki, H.; Chiba, S. Neutrino signals from the formation of black hole: A probe of equation of state of dense matter. Phys. Rev. Lett. 2006, 97, 091101. [Google Scholar] [CrossRef] [PubMed]
- Fischer, T.; Whitehouse, S.C.; Mezzacappa, A.; Thielemann, F.K.; Liebendörfer, M. The neutrino signal from protoneutron star accretion and black hole formation. Astron. Astrophys. 2009, 499, 1–15. [Google Scholar] [CrossRef]
- O’Connor, E.; Ott, C.D. Black Hole Formation in Failing Core-Collapse Supernovae. Astrophys. J. 2011, 730, 70. [Google Scholar] [CrossRef]
- Steiner, A.W.; Hempel, M.; Fischer, T. Core-collapse Supernova Equations of State Based on Neutron Star Observations. Astrophys. J. 2013, 774, 17. [Google Scholar] [CrossRef]
- Marek, A.; Janka, H.T.; Müller, E. Equation-of-state dependent features in shock-oscillation modulated neutrino and gravitational-wave signals from supernovae. Astron. Astrophys. 2009, 496, 475–494. [Google Scholar] [CrossRef]
- Suwa, Y.; Takiwaki, T.; Kotake, K.; Fischer, T.; Liebendörfer, M.; Sato, K. On the Importance of the Equation of State for the Neutrino-driven Supernova Explosion Mechanism. Astrophys. J. 2013, 764, 99. [Google Scholar] [CrossRef]
- Nagakura, H.; Iwakami, W.; Furusawa, S.; Okawa, H.; Harada, A.; Sumiyoshi, K.; Yamada, S.; Matsufuru, H.; Imakura, A. Simulations of Core-Collapse Supernovae in Spatial Axisymmetry with Full Boltzmann Neutrino Transport. Astrophys. J. 2018, 854, 136. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Swesty, F. A Generalized equation of state for hot, dense matter. Nucl. Phys. A 1991, 535, 331–376. [Google Scholar] [CrossRef]
- Shen, H.; Toki, H.; Oyamatsu, K.; Sumiyoshi, K. Relativistic equation of state of nuclear matter for supernova and neutron star. Nucl. Phys. A 1998, 637, 435–450. [Google Scholar] [CrossRef]
- Fischer, T.; Hempel, M.; Sagert, I.; Suwa, Y.; Schaffner-Bielich, J. Symmetry energy impact in simulations of core-collapse supernovae. Eur. Phys. J. A 2014, 50, 46. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the Symmetry Parameters of the Nuclear Interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Tews, I.; Lattimer, J.M.; Ohnishi, A.; Kolomeitsev, E.E. Symmetry Parameter Constraints from A Lower Bound on the Neutron-Matter Energy. Astrophys. J. 2017, 848, 105. [Google Scholar] [CrossRef]
- Thielemann, F.K.; Brachwitz, F.; Höflich, P.; Martinez-Pinedo, G.; Nomoto, K. The physics of type Ia supernovae. New Astron. Rev. 2004, 48, 605–610. [Google Scholar] [CrossRef]
- Fischer, T.; Whitehouse, S.; Mezzacappa, A.; Thielemann, F.K.; Liebendörfer, M. Protoneutron star evolution and the neutrino driven wind in general relativistic neutrino radiation hydrodynamics simulations. Astron. Astrophys. 2010, 517, A80. [Google Scholar] [CrossRef]
- Hempel, M.; Schaffner-Bielich, J. Statistical Model for a Complete Supernova Equation of State. Nucl. Phys. A 2010, 837, 210–254. [Google Scholar] [CrossRef]
- Juodagalvis, A.; Langanke, K.; Hix, W.R.; Martínez-Pinedo, G.; Sampaio, J.M. Improved estimate of electron capture rates on nuclei during stellar core collapse. Nucl. Phys. A 2010, 848, 454–478. [Google Scholar] [CrossRef]
- Bruenn, S.W. Stellar core collapse: Numerical model and infall epoch. Astrophys. J. Suppl. 1985, 58, 771–841. [Google Scholar] [CrossRef]
- Langanke, K.; Martinez-Pinedo, G.; Müller, B.; Janka, H.T.; Marek, A. Effects of Inelastic Neutrino-Nucleus Scattering on Supernova Dynamics and Radiated Neutrino Spectra. Phys. Rev. Lett. 2008, 100, 011101. [Google Scholar] [CrossRef] [PubMed]
- Fuller, G.M.; Meyer, B.S. High-temperature neutrino-nucleus processes in stellar collapse. Astrophys. J. 1991, 376, 701–716. [Google Scholar] [CrossRef]
- Fischer, T.; Langanke, K.; Martínez-Pinedo, G. Neutrino-pair emission from nuclear de-excitation in core-collapse supernova simulations. Phys. Rev. C 2013, 88, 065804. [Google Scholar] [CrossRef]
- Schatz, H.; Gupta, S.; Möller, P.; Beard, M.; Brown, E.F.; Deibel, A.T.; Gasques, L.R.; Hix, W.R.; Keek, L.; Lau, R.; et al. Strong neutrino cooling by cycles of electron capture and β- decay in neutron star crusts. Nature 2014, 505, 62–65. [Google Scholar] [CrossRef] [PubMed]
- Haensel, P.; Zdunik, J.L. Non-equilibrium processes in the crust of an accreting neutron star. Astron. Astrophys. 1990, 227, 431–436. [Google Scholar]
- Brown, E.F.; Bildsten, L.; Rutledge, R.E. Crustal Heating and Quiescent Emission from Transiently Accreting Neutron Stars. Astrophys. J. 1998, 504, L95–L98. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L. Models of crustal heating in accreting neutron stars. Astron. Astrophys. 2008, 480, 459–464. [Google Scholar] [CrossRef]
- Fischer, T.; Martínez-Pinedo, G.; Hempel, M.; Huther, L.; Röpke, G.; Typel, S.; Lohs, A. Expected impact from weak reactions with light nuclei in corecollapse supernova simulations. In Proceedings of the 13th International Symposium on Origin of Matter and Evolution of Galaxies, Beijing, China, 24–27 June 2015. [Google Scholar]
- Röpke, G. Light nuclei quasiparticle energy shifts in hot and dense nuclear matter. Phys. Rev. C 2009, 79, 014002. [Google Scholar] [CrossRef]
- Röpke, G. Parametrization of light nuclei quasiparticle energy shifts and composition of warm and dense nuclear matter. Nucl. Phys. A 2011, 867, 66–80. [Google Scholar] [CrossRef]
- Fischer, T. Constraining the supersaturation density equation of state from core-collapse supernova simulations—Excluded volume extension of the baryons. Eur. Phys. J. A 2016, 52, 54. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The Equation of State from Observed Masses and Radii of Neutron Stars. Astrophys. J. 2010, 722, 33–54. [Google Scholar] [CrossRef]
- Suleimanov, V.; Poutanen, J.; Revnivtsev, M.; Werner, K. Neutron star stiff equation of state derived from cooling phases of the X-ray burster 4U 1724-307. Astrophys. J. 2011, 742, 122. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The Neutron Star Mass-Radius Relation and the Equation of State of Dense Matter. Astrophys. J. 2013, 765, L5. [Google Scholar] [CrossRef]
- Fodor, Z.; Katz, S. Critical point of QCD at finite T and mu, lattice results for physical quark masses. J. High Energy Phys. 2004, 0404, 050. [Google Scholar] [CrossRef]
- Ratti, C.; Thaler, M.A.; Weise, W. Phases of QCD: Lattice thermodynamics and a field theoretical model. Phys. Rev. D 2006, 73, 014019. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabó, K. Fluctuations of conserved charges at finite temperature from lattice QCD. J. High Energy Phys. 2012, 1, 138. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Mukherjee, S.; Petreczky, P.; Schmidt, C.; Smith, D.; et al. Freeze-Out Conditions in Heavy Ion Collisions from QCD Thermodynamics. Phys. Rev. Lett. 2012, 109, 192302. [Google Scholar] [CrossRef] [PubMed]
- Borsányi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Szabó, K.K. Full result for the QCD equation of state with 2 + 1 flavors. Phys. Lett. B 2014, 730, 99–104. [Google Scholar] [CrossRef]
- Kurkela, A.; Fraga, E.S.; Schaffner-Bielich, J.; Vuorinen, A. Constraining neutron star matter with Quantum Chromodynamics. Astrophys. J. 2014, 789, 27. [Google Scholar] [CrossRef]
- Farhi, E.; Jaffe, R. Strange Matter. Phys. Rev. D 1984, 30, 2379. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. 1. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Klevansky, S. The Nambu-Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649–708. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rept. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Klähn, T.; Fischer, T. Vector Interaction Enhanced Bag Model for Astrophysical Applications. Astrophys. J. 2015, 810, 134. [Google Scholar] [CrossRef]
- Klähn, T.; Fischer, T.; Hempel, M. Simultaneous chiral symmetry restoration and deconfinement - Consequences for the QCD phase diagram. Astrophys. J. 2017, 836, 89. [Google Scholar] [CrossRef]
- Fischer, T.; Bastian, N.U.F.; Wu, M.R.; Typel, S.; Klähn, T.; Blaschke, D.B. High-density phase transition paves the way for supernova explosions of massive blue-supergiant stars. arXiv 2017, arXiv:1712.08788. [Google Scholar]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure. In Astrophysics and Space Science Library; Springer: Berlin, Germany, 2007. [Google Scholar]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parametrized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef]
- Zdunik, J.L.; Haensel, P. Maximum mass of neutron stars and strange neutron-star cores. Astron. Astrophys. 2013, 551, A61. [Google Scholar] [CrossRef]
- Alford, M.G.; Han, S.; Prakash, M. Generic conditions for stable hybrid stars. Phys. Rev. D 2013, 88, 083013. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Ayriyan, A.; Bastian, N.U.; Blaschke, D.; Grigorian, H.; Maslov, K.; Voskresensky, D.N. How robust is a third family of compact stars against pasta phase effects? Phys. Rev. C 2018, 97, 045802. [Google Scholar] [CrossRef]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, 97, 084038. [Google Scholar] [CrossRef]
- Blaschke, D.; Chamel, N. Phases of dense matter in compact stars. arXiv 2018, arXiv:1803.01836. [Google Scholar]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-wave constraints on the neutron-star-matter Equation of State. Phys. Rev. Lett. 2017, 120, 17270. [Google Scholar] [CrossRef] [PubMed]
- Röpke, G. Nuclear matter EoS including few-nucleon correlations. Nuovo Cim. C 2017, 39, 392. [Google Scholar]
- Kuhrts, C.; Beyer, M.; Danielewicz, P.; Röpke, G. Medium corrections in the formation of light charged particles in heavy ion reactions. Phys. Rev. C 2001, 63, 034605. [Google Scholar] [CrossRef]
- Bastian, N.U.; Batyuk, P.; Blaschke, D.; Danielewicz, P.; Ivanov, Y.B.; Karpenko, I.; Röpke, G.; Rogachevsky, O.; Wolter, H.H. Light cluster production at NICA. Eur. Phys. J. A 2016, 52, 244. [Google Scholar] [CrossRef]
- Bastian, N.U.; Blaschke, D.; Röpke, G. Light cluster production at NICA. Acta Phys. Pol. Suppl. 2017, 10, 899. [Google Scholar] [CrossRef]
- Kowalski, S.; Natowitz, J.B.; Shlomo, S.; Wada, R.; Hagel, K.; Wang, J.; Materna, T.; Chen, Z.; Ma, Y.G.; Qin, L.; et al. Experimental determination of the symmetry energy of a low density nuclear gas. Phys. Rev. C 2007, 75, 014601. [Google Scholar] [CrossRef]
- Kowalski, S.; Natowitz, J.B.; Shlomo, S.; Wada, R.; Hagel, K.; Wang, J.; Materna, T.; Chen, Z.; Ma, Y.G.; Qin, L.; et al. Symmetry energy of dilute warm nuclear matter. Phys. Rev. Lett. 2010, 104, 202501. [Google Scholar]
- Wada, R. The Nuclear Matter Symmetry Energy at 0.03 ≤ ρ/ρ0 ≤ 0.2. Phys. Rev. C 2012, 85, 064618. [Google Scholar] [CrossRef]
- Hagel, K.; Natowitz, J.B.; Röpke, G. The equation of state and symmetry energy of low density nuclear matter. Eur. Phys. J. A 2014, 50, 39. [Google Scholar] [CrossRef]
- Typel, S.; Wolter, H.H.; Röpke, G.; Blaschke, D. Effects of the liquid-gas phase transition and cluster formation on the symmetry energy. Eur. Phys. J. A 2014, 50, 17. [Google Scholar] [CrossRef]
- Li, B.A.; Chen, L.W.; Ko, C.M. Recent Progress and New Challenges in Isospin Physics with Heavy-Ion Reactions. Phys. Rept. 2008, 464, 113–281. [Google Scholar] [CrossRef]
- Qin, L. Laboratory Tests of Low Density Astrophysical Equations of State. Phys. Rev. Lett. 2012, 108, 172701. [Google Scholar] [CrossRef] [PubMed]
- Hagel, K.; Wada, R.; Qin, L.; Natowitz, J.B.; Shlomo, S.; Bonasera, A.; Röpke, G.; Typel, S.; Chen, Z.; Huang, M.; et al. Experimental Determination of In-Medium Cluster Binding Energies and Mott Points in Nuclear Matter. Phys. Rev. Lett. 2012, 108, 062702. [Google Scholar] [CrossRef] [PubMed]
- Hempel, M.; Hagel, K.; Natowitz, J.; Röpke, G.; Typel, S. Constraining supernova equations of state with equilibrium constants from heavy-ion collisions. Phys. Rev. C 2015, 91, 045805. [Google Scholar] [CrossRef]
- Batyuk, P.; Blaschke, D.; Bleicher, M.; Ivanov, Y.B.; Karpenko, I.; Merts, S.; Nahrgang, M.; Petersen, H.; Rogachevsky, O. Event simulation based on three-fluid hydrodynamics for collisions at energies available at the Dubna Nuclotron-based Ion Collider Facility and at the Facility for Antiproton and Ion Research in Darmstadt. Phys. Rev. C 2016, 94, 044917. [Google Scholar] [CrossRef]
- Batyuk, P.; Blaschke, D.; Bleicher, M.; Ivanov, Y.B.; Karpenko, I.; Malinina, L.; Merts, S.; Nahrgang, M.; Petersen, H.; Rogachevsky, O. Three-fluid Hydrodynamics-based Event Simulator Extended by UrQMD final State interactions (THESEUS) for FAIR-NICA-SPS-BES/RHIC energies. In Proceedings of the 6th International Conference on New Frontiers in Physics (ICNFP 2017), Kolymbari, Greece, 17–26 August 2017. [Google Scholar]
- Ivanov, Y.B. Alternative Scenarios of Relativistic Heavy-Ion Collisions: I. Baryon Stopping. Phys. Rev. C 2013, 87, 064904. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Alternative Scenarios of Relativistic Heavy-Ion Collisions: II. Particle Production. Phys. Rev. C 2013, 87, 064905. [Google Scholar] [CrossRef]
- Ivanov, Y.B. Alternative Scenarios of Relativistic Heavy-Ion Collisions: III. Transverse Momentum Spectra. Phys. Rev. C 2014, 89, 024903. [Google Scholar] [CrossRef]
- Typel, S.; Blaschke, D. A Phenomenological Equation of State of Strongly Interacting Matter with First-Order Phase Transitions and Critical Points. Universe 2018, 4, 32. [Google Scholar] [CrossRef]
- Bastian, N.U.; Blaschke, D. Towards a new quark-nuclear matter EoS for applications in astrophysics and heavy-ion collisions. J. Phys. 2016, 668, 012042. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. arXiv 2017, arXiv:1710.09425. [Google Scholar]
- Blaschke, D.; Jankowski, J.; Naskret, M. Formation of hadrons at chemical freeze-out. arXiv 2017, arXiv:1705.00169. [Google Scholar]
| 1 | Note that the interaction in nuclear systems is strong. However, the perturbation expansion is performed with respect to the imaginary part of the self-energy that is assumed to be small. Most of the interaction is already taken into account in the self-consistent determination of the quasiparticle energies. With increasing density, the Fermi energy will dominate the potential energy so that the correlations are suppressed. A quasiparticle description can be used to calculate the nuclear structure. |
| 2 | A Padé approximation of the nucleon quasiparticle shifts, applicable in a wide temperature range, can be found in Ref. [14]. |
| 3 | For odd A, are the fermionic Matsubara frequencies and for even A, the bosonic ones. |
| 4 | |
| 5 | Recently, a thermodynamically consistent generalization of the excluded-volume improved RDF approach to the hadronic EoS has been suggested which employs a density- and temperature-dependent excluded volume parameter. Within this setting, a second first-order phase transition with a critical endpoint in the QCD phase diagram has been obtained [132]. Such a formulation may be most convenient, e.g., for Bayesian studies of the structure of the QCD phase diagram to be extracted from data of heavy-ion collision experiments. |










| Low Density Limit | High Density Modification (Medium Effects) |
| (1) elementary particles | |
| Ideal Fermi gas: | Quasiparticle quantum liquid: |
| neutrons, protons | mean-field approximation |
| (electrons, neutrinos,…) | Skyrme, Gogny, RMF |
| (2) bound state formation | |
| Nuclear statistical equilibrium: | Chemical equilibrium of quasiparticle clusters: |
| ideal mixture of all bound states | medium modified bound state energies |
| chemical equilibrium, mass action law | self-energy and Pauli blocking |
| (3) continuum contributions | |
| Second virial coefficient: | Generalized Beth-Uhlenbeck formula: |
| account of continuum correlations () | medium modified binding energies, |
| scattering phase shifts, Beth-Uhlenbeck Eq. | medium modified scattering phase shifts |
| (4) chemical & physical picture | |
| Cluster virial approach: | Correlated medium: |
| all bound states (clusters) | phase space occupation by all bound states |
| scattering phase shifts of all pairs | in-medium correlations, quantum condensates |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bastian, N.-U.F.; Blaschke, D.; Fischer, T.; Röpke, G. Towards a Unified Quark-Hadron-Matter Equation of State for Applications in Astrophysics and Heavy-Ion Collisions. Universe 2018, 4, 67. https://doi.org/10.3390/universe4060067
Bastian N-UF, Blaschke D, Fischer T, Röpke G. Towards a Unified Quark-Hadron-Matter Equation of State for Applications in Astrophysics and Heavy-Ion Collisions. Universe. 2018; 4(6):67. https://doi.org/10.3390/universe4060067
Chicago/Turabian StyleBastian, Niels-Uwe F., David Blaschke, Tobias Fischer, and Gerd Röpke. 2018. "Towards a Unified Quark-Hadron-Matter Equation of State for Applications in Astrophysics and Heavy-Ion Collisions" Universe 4, no. 6: 67. https://doi.org/10.3390/universe4060067
APA StyleBastian, N.-U. F., Blaschke, D., Fischer, T., & Röpke, G. (2018). Towards a Unified Quark-Hadron-Matter Equation of State for Applications in Astrophysics and Heavy-Ion Collisions. Universe, 4(6), 67. https://doi.org/10.3390/universe4060067






