Physical Justifications and Possible Astrophysical Manifestations of the Projective Theory of Relativity ^†

Abstract

The ‘projective theory of relativity’ is a theory developed historically by Oswald Veblen and Banesh Hoffmann, Jan Arnoldus Schouten and David van Dantzig. This theory differs radically from Kaluza-Klein/conformal type theories of spacetime, although it shares with these theories geometric aspects in five-dimensional spaces. The peculiarity of the projective geometries involved in this theory was that it is based on spaces coordinated by five so-called ‘homogeneous coordinates.’ Since then, no physical observables could be ascribed to these five homogeneous coordinates and, in particular, during the elaboration of this theory which consequently fell completely into oblivion. We will present how this projective theory of relativity can be fully justified physically from the causal structures and localizing protocols involved in so-called ‘relativistic localizing systems’ that extend ‘relativistic positioning systems.’ We explain the correspondence between ‘homogeneous coordinates’ of the projective theory of relativity and the physical observables defined in relativistic localizing systems. Then, possible astrophysical manifestations will be presented based on projective effects, invariance of interactions, or observations with respect to projective transformations.

1. Reference Systems—Relativistic Positioning vs. Localizing Systems

As demonstrated in previous works [1,2,3], the physical justification of the ‘projective geometry of spacetime, and thus the validity of the ‘projective theory of relativity’ [4,5,6], is completely deduced from peculiar characteristics of the physical observables that are expressed in relativistic localizing protocols of spacetime events. These protocols are explicitly implemented in the so-called ‘relativistic localizing systems’ (RLS) [1,2,3] that are extensions of the so-called ‘relativistic positioning systems’ (RPS) [7,8,9,10,11,12,13,14]. The latter have been designed to correct the current, first generation, non-relativistic positioning systems such as the GPS, Galileo, Glonass, Beidou, or IRNSS. These new, second generation, relativistic positioning systems not only answer the question of possible technological improvements to current positioning systems but also very fundamental questions in spacetime physics. For example, in special or general relativity, particular protocols have historically been devised to construct physical observables associated with the position in space at a given time relative to a reference frame. But all are based, in particular, on a convention of simultaneity [15] that is not inherently relativistic because, as it is well known, simultaneity is relative to one frame and only one. Relativistic positioning systems solve this difficulty by freeing themselves from the need to define a notion of simultaneity in one way or another. Then, moreover, relativistic observables are obtained from RLSs without, in particular, the use of any geometric symmetry criteria and can then be applied to, for example, the determination of a genuine relativistic quantum field theory. Only constraints resulting from causal axiomatics are really necessary and better still, it is not even necessary to make hypotheses about the geometric, differential nature and even about the existence or not of these spacetime characteristics. The latter are the results of the relativistic localizing protocol, detailed in the present section, which ultimately only involves causal orders of information exchanges [16]. To put it succinctly, these are processes of code geometrization.

Besides, it should also be noted that the ‘projective theory of relativity’ is not a particular string theory. String theories all have a pseudo-Riemannian, base spacetime manifold whose geometry follows the axiomatics of Euclidean geometry. In the present case of the projective theory of relativity, the pseudo-Riemannian spacetime manifold follows the axiomatics of projective geometry. It is therefore a geometric theory with a radically different basic axiomatics and, moreover, it is not a string theory upon such projective geometry. Also, we ought to indicate that there are alternative theories to the projective theory of relativity, in particular, the so-called Fantappié-Arcidiacono one developed by Licata, Chiatti, and Benedetto [17,18,19,20,21].

But then, the question is to know what other manifestations of the projective geometry of spacetime could appear, and in particular in astrophysics. Two results have previously been obtained on this subject [22]: A foliation of spacetime with a structure similar to those of black holes, and fits of galactic rotational velocity curves. These results are presented briefly in Section 2, Section 3 and Section 4 but their difficult interpretations are discussed in Section 5 in greater depth and in a new way both from a mathematical point of view and from the point of view of physical implications and meanings.

In order to give some details about these RLSs, we recall briefly in this introductory section some definitions and principles of how reference systems, RPSs, and RLSs strongly differ and work, and why RPSs are relativistic unlike current positioning systems such as the GPS.

Basically, a ‘reference system’ (RS) is a set of procedures for creating a ‘reference frame’ (RF) from which space and time coordinates can be ascribed to “geographic” locations belonging to a given, extended material body such as, for examples, Earth, Moon, Mars, etc. The RS named WGS84 ( World Geodetic System 1984) is the set of procedures used by the GPS for Earth. The set of procedures used by Galileo is named ITRS (International Terrestrial Reference System). Beside, the RF of the reference systems WGS84 is called merely WGS84 Reference frame defined in a very similar way to the ITRF (International Terrestrial Reference Frame). For Galileo, the RF is named GTRF09v1 (Galileo Terrestrial Reference Frame 2009 ver. 1), which is a particular frame among those provided by the ITRS (International Terrestrial Reference System).

The reference system WGS84 has three main features: a Cartesian system of coordinates also called grid of [Cartesian] coordinates provided by the particular terrestrial frame called the ‘WGS84 Reference frame’ as indicated above, a reference oblate ellipsoid called the ‘datum’ from which a zero altitude can be somehow defined for Earth’s surface, and a gravitational, nominal mean sea level equipotential surface called the ‘ geoid’ which is defined from the EGM96 (Earth Gravitational Model 1996).

Now, a positioning system (PS) is the physical realization of a grid of coordinates, i.e., a “physical grid”. Let us note that the circles of latitude (parallels) and longitude (meridians) have no physical counterparts; unless we can find a very improbable way to draw lines with, for instance, colored pigments on the whole of Earth’s surface. Actually, electromagnetic signals are used which “draw” a grid of coordinates varying in time called emission grid. Each coordinated “line” are then electromagnetically “stamped” by so-called time stamps. Actually, these grids of coordinates are physically achieved by signages in space and time which assume existence of physical media for digital informations. Such physical media are well known for road networks for instance with milestones. In the case of PSs, physical media are electromagnetic fields carrying digital informations, which are dates also known as ‘time stamps’ broadcast by clocks on board satellites.

Now, what are the differences between “classical” and relativistic PSs? At the present days, all positioning systems (GPS, Galileo, Beidou, etc.) are classical PSs because the time stamps must be corrected for the relativistic effects such as time dilatation for instance. Without these corrections, the grids provided by current PSs which are grids of light coordinates, i.e., emission grids, do not correspond to the grids of null geodesics defined from the systems of reference (e.g., WGS84). More precisely, the process of positioning is a transitive process: the users are positioned relative to satellites of the PSs and the satellites are positioned with respect to the RF via ground stations. Then, the users are positioned in the RF. But, relativistic corrections must be made regularly over time between the space (satellites) and control (reference frame/ground stations) segments by uploading to the satellites, ephemerids, and orbits, corrected by ground calculations and from which the time stamps transmitted to users are modified.

These calculation processes carried out in ground stations and uploaded to satellites are eliminated in the case of RPSs. It is through a process known as ‘auto-location’ [14], entirely relativistic and autonomous, that the correct ephemerids and orbits of satellites are continuously and permanently determined in time without intermediate calculations of relativistic corrections. Let us note that ground stations as “ancillary ground satellites" must be included as crucial parts in the auto-location process. Thus, the relationship between the space and control segments becomes entirely relativistic in nature and defines somehow a unique “space-control segment”. But RPSs do not have this only advantage. They have the following properties according to Coll [14]: They are (1) ‘generic’, i.e., they can be constructed whatever is the given spacetime class, (2) (gravity-)‘free’, i.e., no knowledge of the gravitational field is necessary, and (3) ‘immediate’, i.e., users can know their coordinates with respect to the given RF without delay.

Also, Coll and Tarantola have extended the characteristics of the RPSs to ‘galactic positioning systems’ [23]. The first experimental result implementing this protocol was performed by Ruggiero et al. [24,25] using astronomical data from pulsars used to replace satellites. This galactic positioning protocol has also been very recently and successfully implemented on board the ISS by Winternitz et al. [26] without any reference to the work of Coll, Tarantola, Ruggiero et al., which we quote to do them justice.

Finally, it can be noted that these RPSs only work if we own “GPS/Galileo/Beidou ...receivers” and, obviously, we cannot locate an event that is not itself a “receiver carrier”. To put it succinctly, we cannot locate a star relatively to the terrestrial RS since this would imply that the star “holds” a GPS receiver. What we need for is precisely a RLS that avoids completely the need for any kind of receivers. Roughly speaking, a RLS is a “radar” system, relativistically localizing events in spacetime and localizing them in an emission grid provided by an underlying RPS.

Basically, a RLS is made of five satellites, four of them providing an underlying RPS. These five satellites exchange time stamps so that each can self-locate in the emission grid of the underlying RPS. In addition, they also have the particularity of being made up of completely “spherical retinas”. These retinas have their own coordinate systems to locate directions of incident light rays as “light points” on their surfaces. Typically, for example, these coordinates are the two angles corresponding to latitude and longitude. Each of these retinas can be considered as celestial spheres on which the directions where the other four satellites are located are visualized by points and, possibly as well the direction of events to be located in the emission grid after localization (see Figure 1); which is naturally the goal. Hence, on each retina, there are four points associated with the other four satellites, and they constitute a projective frame for $P{\mathbb{R}}^2$.

But in addition, these four points are also linked at each instant to pairs of time stamps evolving over time and used in the underlying auto-locating process. As a result, we can translate pairs of angle values into pairs of time stamps that provide additional coordinates for each projective point on the retinas (see Figure 2) associated with an event. More precisely, this angles/time stamps translation makes it possible to assign pairs of time stamps to each event detected on the retinas. Actually, four pairs of time stamps only are necessary.

Then, from a reconstruction process, we can assign to each detected event four time stamps from which the event can be located in the emission grid of the underlying RPS. This is a kind of generalization of the now well-known reconstruction process from which 3D views can be obtained from two 2D pictures. From this reconstruction process based on four projective 2D pictures, we get a projective 4D spacetime, i.e., the geometric structure of spacetime is the projective space $P{\mathbb{R}}^4$. This structure is intrinsic and fully relativistic. No hypothesis is made as to the geometric nature of the Riemannian differentiable manifold of spacetime. In particular, no Lorentzian metric is assumed as well as a possible temporal orientation of spacetime. Only the existence of a minimal causal axiomatics [16] and the complete characterization of the intrinsic projective geometry of the “retinas” are necessary. In other words, the geometric projective structure of the spacetime manifold is emergent from the relativistic localizing protocol as the result of a process of conversion from exchanged codes to a projective geometry of spacetime.

2. The Admisssible Lorentzian Metric

2.1. The Underlying Hyperbolic Geometry

As indicated in previous section, the spacetime manifold we denote by $\mathcal{M}$ is an emergent geometric structure arising somehow “naked”, i.e., neither time orientation nor any Lorentzian metric are really defined on the emergent spacetime manifold $\mathcal{M}$ from localization; appart the fundamental, projective ground structure. Nevertheless, we can start with a few following geometric assumptions about the geometric structure of $\mathcal{M}$ [22]: (1) The spacetime manifold $\mathcal{M}$ is time-orientable and simply connected, (2) we provide $\mathcal{M}$ with an Euclidean metric $d{s}^2$ such that $(\mathcal{M},d{s}^2)$ is the four-dimensional hyperbolic space ${\mathcal{H}}^4\subset P{\mathbb{R}}^4$1, (3) to each event $e\in \mathcal{M}$, a system of four Riemann normal coordinates $\left(u_p^i\right)\equiv p\in \mathcal{M}$ can be attached such that $u_e^{\alpha }=0$ ($i=1,\dots ,4$)2, (4) the coordinates $u^i$ are assumed to be the inhomogeneous coordinates of the local projective geometry of ${\mathcal{H}}^4$, and (5) to the inhomogeneous coordinates $u^i$ there corresponds five homogeneous coordinates $U^{\alpha }$ ($\alpha =0,1,\dots ,4$).

Unlike what is usually done in such similar circumstances, it is an “underlying” hyperbolic space ${\mathcal{H}}^4$ that is considered here because this space is simply connected contrarily to anti-de Sitter spaces $Ad{S}_n$; all the more so as anti-de Sitter spaces are not subspaces of projective spaces $P{\mathbb{R}}^n$ but of Euclidean spaces ${\mathbb{R}}^{n+1}$. We recall that ${\mathcal{H}}^4$ is defined from a quadratic form Q and a metric $d{S}^2$ on ${\mathbb{R}}^5$ such that $Q\left(U\right)\equiv {\left(U^0\right)}^2-{\sum }_{i=1}^4{\left(U^i\right)}^2$ and $d{S}^2\equiv {\sum }_{i=1}^4{\left(d{U}^i\right)}^2-{\left(d{U}^0\right)}^2$. More precisely, we have the following.

Definition 1.

The hyperbolic space ${\mathcal{H}}^4\subset P{\mathbb{R}}^4$ is the open set of lines in ${\mathbb{R}}^5$ generated by points $U\in {\mathbb{R}}^5$ such that $Q\left(U\right)>0$ and equiped with the metric $d{s}^2$ (see below).

Futhermore, defining from Q the section $\sigma :\left(u^i\right)\in {\mathbb{R}}^4⟶\left(U^{\alpha }\right)\in {\mathbb{R}}^5$ such that $U^0=\sigma {\left(u\right)}^0\equiv \sqrt{1+{\sum }_{i=1}^4{\left(u^i\right)}^2}$ and $U^i=\sigma {\left(u\right)}^i\equiv u^i$ $(i=1,\dots ,4)$, then, the Euclidean metric $d{s}^2$ can be defined as the pull-back of $d{S}^2$ by $\sigma$, i.e., $d{s}^2\equiv {\sigma }^{*}\left(d{S}^2\right)$. Then, we obtain

$$d{s}^2=\frac{{\sum }_{i=1}^4{\left(d{u}^i\right)}^2+{\sum }_{i=1<j}^4{(u^{j}d{u}^i-u^{i}d{u}^j)}^2}{1+{\sum }_{i=1}^4{\left(u^i\right)}^2},$$

(1)

which is the Euclidean metric defined on ${\mathbb{R}}^4\simeq \mathcal{M}$ and defining completely ${\mathcal{H}}^4$ as a Riemannian manifold embedded in $P{\mathbb{R}}^4$. To complete the description of ${\mathcal{H}}^4$, we ought to mention that the restricted Lorentz group $S{O}^{+}(1,4)\subset PGL(5,{\mathbb{R}}^{})=SL(5,{\mathbb{R}}^{})$ acts transitively on ${\mathcal{H}}^4$ via homographies $\left[\mathfrak{A}\right]$ defined from linear actions $\mathfrak{A}\equiv \left({\mathfrak{A}}_{\beta }^{\alpha }\right)$ on ${\mathbb{R}}^5$. More precisely, we have $u^{\prime }=\left[\mathfrak{A}\right]\left(u\right)$ whenever $U^{\prime }=\mathfrak{A}.U$, i.e., in indexed notation $(\alpha =0,\dots ,4;i=1,\dots ,4)$:

$$u^{\prime }=\left[\mathfrak{A}\right]\left(u\right)⟺u^i=\frac{{\mathfrak{A}}_0^i+{\sum }_{j=1}^4{\mathfrak{A}}_j^i{u}^j}{{\mathfrak{A}}_0^0+{\sum }_{k=1}^4{\mathfrak{A}}_k^0{u}^k}\mathrm{whenever}{U}^{\prime }=\mathfrak{A}.U⟺U^{\prime \alpha }={\sum }_{\beta =0}^4{\mathfrak{A}}_{\beta }^{\alpha }{U}^{\beta }.$$

(2)

Then, Q and $d{S}^2$ are invariant with respect to linear maps $\mathfrak{A}\in S{O}^{+}(1,4)$ whereas $d{s}^2$ is invariant with respect to homographies $\left[\mathfrak{A}\right]$, i.e., we have ${\left[\mathfrak{A}\right]}^{*}\left(d{s}^2\right)=d{s}^2$.

2.2. The Pseudo-Hyperbolic Space and the Admissible Lorentzian Metric

To recover an admissible Lorentzian metric $d{\tau }^2$ instead of the Euclidean metric $d{s}^2$ on $\mathcal{M}$, we use the assumption that $\mathcal{M}$ is time orientable, i.e., we can find a nowhere non-vanishing, everywhere defined vector field on $\mathcal{M}$. We assume that this vector field exists and that it is the dual of the differential 1-form $d{u}^1\in T^{*}\mathcal{M}$. Then, $\mathcal{M}$ becomes time-oriented and $d{\tau }^2$ is defined by formula: $d{\tau }^2\equiv {\left(d{u}^1\right)}^2-d{s}^2$. Also, $d{\tau }^2$ is the pull-back by $\sigma$ of a metric $d{T}^2$ on ${\mathbb{R}}^5$, i.e., we have $d{\tau }^2\equiv {\sigma }^{*}\left(d{T}^2\right)$ where $d{T}^2\equiv 2{\left(d{U}^1\right)}^2-d{S}^2={\sum }_{k=0}^1{\left(d{U}^k\right)}^2-{\sum }_{i=2}^4{\left(d{U}^i\right)}^2$. Clearly, this last metric $d{T}^2$ is the metric defined on the anti-de Sitter space $Ad{S}_4\subset {\mathbb{R}}^5$ of signature $(2,2)$ and which is defined from the quadratic form $\Lambda$ on ${\mathbb{R}}^5$ such that $\Lambda \left(U\right)\equiv Q\left(U\right)+2{\left(U^1\right)}^2={\sum }_{k=0}^1{\left(U^k\right)}^2-{\sum }_{i=2}^4{\left(U^i\right)}^2$. Then, $Ad{S}_4$ is the set of points U such that $\Lambda \left(U\right)=-k^2=cst<0$. Nevertheless, we must not consider $Ad{S}_4\subset {\mathbb{R}}^5$ which is not simply connected but a simply connected subspace of $P{\mathbb{R}}^4$ that we call the pseudo-hyperbolic space ${\mathcal{H}}^{1,3}$. Let us note also that if $Q\left(U\right)>0$ then, necessarily, we have $\Lambda \left(U\right)>0$ which forbids to consider $Ad{S}_4$.

Definition 2.

The pseudo-hyperbolic space ${\mathcal{H}}^{1,3}\subset P{\mathbb{R}}^4$ is the open set of lines in ${\mathbb{R}}^5$ generated by points $U\in {\mathbb{R}}^5$ such that $Q\left(U\right)>0$ and equiped with the metric $d{\tau }^2$.

Then, the orthochronous pseudo-orthogonal group $S{O}^{+}(2,3)\subset PGL(5,{\mathbb{R}}^{})$ is the group of invariance of the quadratic form $\Lambda$ and the metric $d{T}^2$. This group $S{O}^{+}(2,3)$ acts by linear maps $\mathfrak{A}$ on $\Lambda$ and $d{T}^2$. In return, this involves to restrict $S{O}^{+}(2,3)$ to the subgroup $S{O}^{+}(1,4)\cap S{O}^{+}(2,3)\equiv \left[{\widehat{G}}_{\tau }^{+}\right]$ in order to simultaneously keep an invariance of Q defining ${\mathcal{H}}^4$ and ${\mathcal{H}}^{1,3}$. Nevertheless, the metric $d{\tau }^2$ is no more invariant with respect to homographies $\left[\mathfrak{A}\right]$.

Let $\pi :{\mathbb{R}}^5⟶P{\mathbb{R}}^4$ be the projective map such that, in particular, $\pi {\left(U\right)}^i=U^i/U^0$ whenever $U^0\ne 0$, and $\mathfrak{a}:{\mathbb{R}}^4⟶B^4$ the embedding such that $\mathfrak{a}\equiv \pi \circ \sigma$ and where $B^4\subset {\mathbb{R}}^4$ is the four-dimensional open ball. Then, we define the representation $〚〛$ of homographies such that $〚\mathfrak{A}〛={\mathfrak{a}}^{-1}\circ \left[\mathfrak{A}\right]\circ \mathfrak{a}$ where $\left[\mathfrak{A}\right]\in \left[{\widehat{G}}_{\tau }^{+}\right]$. Then, $d{\tau }^2$ is invariant with respect to $〚\mathfrak{A}〛$. More precisely, it can be shown that $〚\mathfrak{A}{〛}^{*}\left(d{\tau }^2\right)=d{\tau }^2$ where $\mathfrak{A}\in {\widehat{G}}_{\tau }^{+}$.

3. The Singular Pseudo-Hyperbolic Space and the Foliation

In the previous section, we have shown that the metric $d{\tau }^2$ is invariant with respect to the $〚\mathfrak{A}〛$ action (where $\mathfrak{A}\in {\widehat{G}}_{\tau }^{+}$). Nevertheless, we can define another Lorentzian metric $d{\widehat{h}}^2$ invariant with respect to the $\left[\mathfrak{A}\right]$ action. However, this new metric $d{\widehat{h}}^2$ is no more defined on ${\mathbb{R}}^4$ but only on the four-dimensional open ball $B^4\subset {\mathbb{R}}^4$. Actually, $d{\widehat{h}}^2$ is defined to be such that $d{\widehat{h}}^2={\mathfrak{a}}^{-1*}\left(d{\tau }^2\right)$ with ${\left[\mathfrak{A}\right]}^{*}\left(d{\widehat{h}}^2\right)=d{\widehat{h}}^2$. In addition, this metric $d{\widehat{h}}^2$ is totally discontinuous although bounded on the boundary $\mathring{B}\equiv \partial {\overline{B}}^4=S^3$ of ${\overline{B}}^4$. Now, let $I:\left(u^i\right)\in {\overline{B}}^{4*}⟶(u^i/R^2)\in {\mathbb{R}}^4-B^4$ be the inversion map in the 3-sphere $S^3$ where ${\overline{B}}^{4*}\equiv {\overline{B}}^4-\left\{0\right\}$ and $R^2\equiv {\sum }_{j=1}^4{\left(u^j\right)}^2$. This inversion commutes with $\left[\mathfrak{A}\right]$, i.e., we have $I\circ \left[\mathfrak{A}\right]=\left[\mathfrak{A}\right]\circ I$.

Then, from I, we can define the metric $d{\check{h}}^2$ on ${\mathbb{R}}^4-{\overline{B}}^4$ such that $d{\check{h}}^2\equiv I^{-1*}\left(d{\widehat{h}}^2\right)$. Then, we obtain a metric $d{h}^2\equiv (d{\check{h}}^2,d{\widehat{h}}^2)$ on $B^4\cup ({\mathbb{R}}^4-{\overline{B}}^4)\equiv {\mathbb{R}}^4-S^3$ which is invariant with respect to the $\left[\mathfrak{A}\right]$ action. We can partially only bypass this discontinuity issue on $S^3$ defining a particular class of conformal metrics $d{\nu }^2$ from $d{h}^2$.

For this purpose, we define first the functions $q\left(u\right)$ and $\Xi \left(q\right)$ such that

$$q\left(u\right)\equiv 1+2\frac{{\left(u^1\right)}^2}{1-{\sum }_{i=1}^4{\left(u^i\right)}^2},\Xi \left(q\right)\equiv \frac{C\left(q\right)}{q^{5/4}},$$

(3)

where $C\left(q\right)$ is a continuous function such that $C(+\infty )\ne 0$ whenever $u^1\ne 0$ and bounded on $[1,+\infty ]$. It is important to note that the function q is invariant with respect to homographie in $\left[{\widehat{G}}_{\tau }^{+}\right]$, i.e., $q\left(\right[\mathfrak{A}\left]\right(u\left)\right)=q\left(u\right)$ for any $\mathfrak{A}\in {\widehat{G}}_{\tau }^{+}$.

As a result, we can define metrics $d{\widehat{\nu }}^2\equiv \Xi {\left(q\right)}^{2}d{\widehat{h}}^2$ on ${\overline{B}}^4-S^2$ with their associated metrics $d{\check{\nu }}^2\equiv I^{-1*}\left(d{\widehat{\nu }}^2\right)$ on ${\mathbb{R}}^4-(B^4\cup S^2)$. As a consequence, we obtain metrics $d{\nu }^2\equiv (d{\check{\nu }}^2,d{\widehat{\nu }}^2)$ on ${\mathbb{R}}^4-S^2$ where $S^2$ is the spatial 2-sphere, i.e., such that $u^1=0$ and ${\sum }_{k=2}^4{\left(u^k\right)}^2=1$. These two metrics are invariant with respect to ${\widehat{G}}_{\tau }^{+}$. In particular, we have $〚\mathfrak{A}{〛}^{*}\left(d{\widehat{\nu }}^2\right)\equiv \Xi {\left(q\left(\left[\mathfrak{A}\right]\left(u\right)\right)\right)}^2〚\mathfrak{A}{〛}^{*}\left(d{\widehat{h}}^2\right)=d{\widehat{\nu }}^2$ for any $\mathfrak{A}\in {\widehat{G}}_{\tau }^{+}$.

Then, we call singular pseudo-hyperbolic space ${\mathcal{H}}_s^{1,3}$ the space ${\mathbb{R}}^4-S^2$ equipped with the metric field $d{\nu }^2$. Then, we deduce: (1) an invariance of ${\mathcal{H}}_s^{1,3}$ with respect to homographic action of group ${\widehat{G}}_{\tau }^{+}$, and (2) a class of conformal metrics $d{\nu }^2$ projectively invariant and singular (discontinuous) only on the spacelike equatorial sphere $S^2\subset S^3$.

But also, in addition, we obtain a particular foliation from the group action ${\widehat{G}}_{\tau }^{+}$ on ${\mathcal{H}}_s^{1,3}$. The group action defines orbits in ${\mathcal{H}}_s^{1,3}$ which are: (1) the three-dimensional, disjoint, simply connected and connected north and south hemispheres $H_{\alpha }^{3+}$ ($u^1>0$) and $H_{\alpha }^{3-}$ ($u^1<0$) of 3-ellipsoids $S_{\alpha }^3$ such that ${\alpha }^2{\left(u^1\right)}^1+{\sum }_{k=2}^4{\left(u^k\right)}^2=1$ where ${\alpha }^2>1$, and the spacelike leaf $H_{\infty }^3\equiv B^4\cap (\left\{0\right\}\times {\mathbb{R}}^3)$ (i.e., the open ball $B^3$), and (2) their corresponding “inverted” leaves $I\left(H_{\alpha }^{3+}\right)$, $I\left(H_{\alpha }^{3-}\right)$ and the spacelike leaf $I\left(H_{\infty }^3\right)\equiv {\mathbb{R}}^3-{\overline{B}}^3$.

This foliation [22] can be represented by the following Figure 3.

4. Similar Black Hole Structures and a Simple, Modified Newton’s Law

The previous foliation indicates a structure very similar to that of a black hole. Nevertheless, there is no central singularity in that case; only a so-called ‘closed trapped surface’ which is the equatorial spacelike 2-sphere $S^2\subset \left\{0\right\}\times {\mathbb{R}}^3$ on which the metrics $d{\nu }^2$ are discontinuous. This suggests a first manifestation of projective invariance in an alternative black hole model essentially based on termodynamical/non-ergodic trapping effects by spherical shock front possibly stabilized by this foliation and localized on the equatorial spacelike 2-sphere.

A second possible manifestation of projective geometry could be a modification of the Newton’s law of gravitation. Indeed, it can be shown that due to invariance with respect to the group ${\widehat{G}}_{\tau }^{+}$, we can deduce [22] a modified force of gravitation $\overrightarrow{\mathbf{F}}$ such that

$$\overrightarrow{\mathbf{F}}\left(r\right)=\mathcal{G}m{m}^{\prime }\frac{{\left(\alpha +\beta r\right)}^2}{r^2}\overrightarrow{\mathbf{v}},$$

(4)

where $\mathcal{G}$ is the constant of gravitation, r is the distance between the two masses m and $m^{\prime }$, $\overrightarrow{\mathbf{v}}$ is the unit vector on the line joining the two masses and $\alpha$ and $\beta$ are two parameters. A priori, we should have $\alpha \simeq 1$ and $\beta \simeq 0$ to be close to the (non-modified) Newtons’s law. Nevertheless, the cases $\alpha =0$ and $\beta \ne 0$ are perfectly acceptable within the context of this “projective modification”. Moreover, it is important to note that these two parameters $\alpha$ and $\beta$ are not fixed, universal constants. They depend on physical contexts of observation of the two masses. Indeed, what is characteristic of projective geometry in physics is the existence of geometric perspectives with its lines of horizons and vanishing points. In dimension 3, the modified images resulting from the perspective viewpoints are distinct according to the position of the observers, the dimensions of the objects observed and their reciprocal geometric relationships. The situation present in dimension 4 is here perfectly similar although it is expressed geometrically in addition with dimensions of time, energy or force.

Hence, if, for instance, an observer looks at these two masses as stellar objetcs in a galaxy, necessarily the two parameters $\alpha$ and $\beta$ in the modified Newton’s law will depend on the relative distance between the observer and the given galaxy, and the extension of the latter. This is very disconcerting from the point of view of classical physics, which is not in projective spaces but Euclidean for which these dimension effects and dependence on the distance to observer do not really exist. Also, because the $u^1$-time is a cosmological time orienting spacetime, considering galactic dimensions, the two parameters $\alpha$ and $\beta$ should depend on the difference of cosmological times between the galaxy and observers and its cosmological distance from the observers; in addition to characteristic times and lengths of the given galaxy.

Then, as a result, we have the following rotational velocity fields (constant $\mathcal{G}$ being set to 1)

$$v\left(r\right)\equiv \sqrt{\left|\beta +\frac{\alpha }{r}\right|M\left(r\right)},$$

(5)

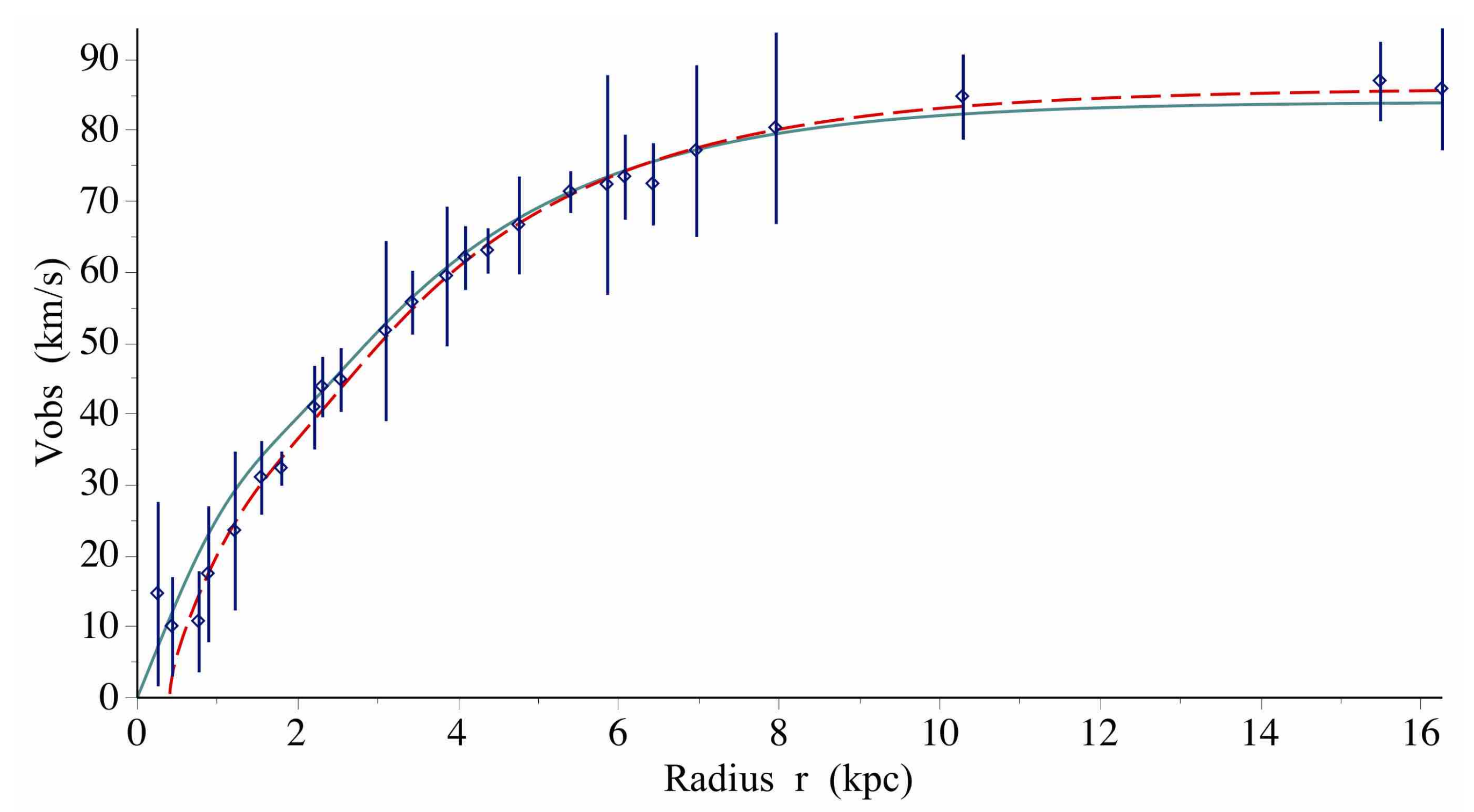
where $M\left(r\right)$ is the mass enclosed in a sphere of radius r. Fits of rotational velocity curves have been obtained for around 10 galaxies [22] recorded in the SPARC astronomical database and 18 galaxies from the THINGS database. In the first “SPARC case”, no mass models were used to deduce the masses $M\left(r\right)$ for each galaxy, and in the second “THINGS case”, Formula (5) was given without theoretical or physical justifications and from a pure phenomenological viewpoint just because of the quality of the fits obtained. Moreover, in the “SPARC case”, the masses have been deduced from galactic surface brightness data. On the contrary, in the “THINGS case”, no such galactic surface brightness data were available and thus various mass models were tested. In addition, the implicit following constraint was imposed [27] (see Formula (17)): $\alpha \equiv 1+R_0\beta$, where $R_0$ is the galactic scale length (in that case, as indicated above, $R_0$ could depend on cosmological times/distances as well as $\beta$). In full generality, such constraint is not always satisfied, e.g., $\alpha =0$ and $\beta >0$. We obtain such null value for $\alpha$ to make the best fit of the rotational velocity curve of the dwarf galaxy LSBC F583-01 (see Figure 4). In that limit case, we obtain the odd relation $v\left(r\right)\simeq \sqrt{M\left(r\right)}$, but well justified in the present projective framework.

5. Conclusions—Interpretations and Physical Perspectivities

At the heart of projective geometry is the notion of geometric perspective as illustrated in Figure 5 below.

It is clear, reasoning on the basis of this figure, that the viewpoint of the observer plays an important role in the representation of the object observed as well as its dimensions. The same will apply to laws and physical objects subject to projective geometry and they will therefore depend on the views of observers and the characteristic dimensions involved in these laws or physical objects. These dimensions will involve temporal and/or spatial characteristics. We are therefore in physical situations that are not in this case geometric representations only of what is observed but which actually manifest genuine physical effects. This would therefore be particularly apparent in the variations in $\alpha$ and $\beta$ parameters depending on the observers and galaxies observed. In particular, this would imply that the $\alpha$ and $\beta$ parameters would vary depending on the observer for the same galaxy. This seems rather shocking although in fact it is impossible for us, in the current state of technology, to change our viewpoints as observers over distances comparable or larger than the galactic dimensions; and therefore to actually observe these variations of $\alpha$ and $\beta$.

If we take the reasoning a little further, it would also mean that the dynamics of a galaxy would depend on the observer; but on condition, in this case, that the observer’s mass, or physical influence, is significant in relation to the masses and physical phenomena contained or involved in the galaxy under consideration. We are therefore led to suggest that the $\alpha$ and $\beta$ parameters are very specific to each galaxy but that they vary only slightly depending on the selected observers whose physical influence is weak or vanishing. Another alternative would be to consider observers without influence on galactic dynamics but that the observation of a galaxy by an observer is done from a geometric perspective which is equivalently translated into a modification of Newton’s law applied to the dynamics of the considered galaxy. Conversely, considering, for example, the case of stars in a galaxy, each of these stars would interact gravitationally with the others via a modified Newtonian force with $\alpha$ and $\beta$ parameters that would be specific to that star in that galaxy. In other words, it would also be necessary to consider a dynamic of these various modified Newton’s laws, i.e., a dynamic of the $\alpha$ and $\beta$ parameters. Such a dynamic would therefore remain to be determined. Only in the absence of knowledge of such a dynamic, or even its existence, such a modification of Newton’s law presents a conceptual weakness in the state of the suggested physical projective model.

But also, in another way, it can be said that Newton’s law is no longer universal. This loss of universality manifests with parameters $\alpha$ and $\beta$ that depend on geometric/physical characteristics at the origin of the Cartesian coordinates chosen to express Formula (4). This also means that this origin has a physical content. The fits of galaxies were done considering that this origin coincides with the galactic center. In other words, these parameters depend on large scale structures. The latter can be mass distributions or spacetime curvature at the galactic center which could be considered somehow as a “geometrical synthesis” of the mass distribution around this center. Besides, we can note that because projective geometry is locally an affine geometry to which points at infinity are added, most of the definitions of projective geometrical objects are dependent on a common, given, and arbitrarily fixed origin (e.g., a galactic center), contrarily to geometrical objects in Euclidean geometry.

Actually, in particular, considering that the $\alpha$ and $\beta$ parameters depend on, for instance, the curvature, this means that we have a kind of dynamical feedback process: First, the universal Newton’s law bends spacetime, and then, the resulting non-vanishing local curvature modifies the Newton’s initial law to remain compatible with projective geometry. It is rather the opposite that could surprise us: That the change in spacetime curvature has no effects on the universality of certain physical laws. Indeed, why does the Newton’s law not change with topological/geometrical changes induced by the curvature changes it produces? Roughly speaking, universality would refer to Euclidean aspects and Newton’s law is clearly expressed only within the framework of Euclidean geometry. As a result, there would be a dynamical relationship between the shape of, for instance, a galaxy and the way the Newton’s law is modified via the $\alpha$ and $\beta$ parameters; a kind of renormalization process to recover a global projective invariance of the system “galaxy plus internal, gravitational interactions”.

Beside, such Formula (4) for gravitational force seems also at first sight simply impossible, because the force does not fall when the distance goes to infinity. The introduced modification can help to describe the rotational curves of spiral galaxies, but Formula (4) with parameters fixed from the rotational curves (with nonzero value for $\beta$) leads to completely impossible gravitational effects at larger distances. However, projective spaces are topologically compact spaces meaning that the projective geometry cannot be considered with an infinite extension from the chosen origin imposing a limit on the modifications of the Newton’s law. Therefore, such modifications could be unavailable at very large scales/distances. As indicated in previous papers [1,2,3], we have a ‘generalised Cartan space(time)’ locally homeomorphic to local four-dimensional (compact) projective spaces.

Also, what appears at first glance to be a major conceptual weakness of this projective approach could be a very big advantage. Indeed, Newton’s law modified according to Formula (4) is only the simplest possible modification of Newton’s law compatible with projective invariance, rotational invariance and time and space splitting. In fact, we have shown that there is an infinite number of particular possible modifications to this law that are compatible with projective invariance. And one of the most general ways to present these modifications is to actually consider the $\alpha$ and $\beta$ parameters as scalar fields. Therefore, an interpretation of these two scalar fields (in fact, a 2-dimensional vector field) would be to consider them as effective, “massless dark matter” fields. Therefore we would be confronted with a modified Newton’s law incorporating such dynamic fields. And this would then have to be compared with the great variability of the situations encountered with galaxies having or not having dark matter within them; and for the moment remaining undetectable as a massive field. We would then have a mixed model of modified Newton’s law parameterized by an effective, ‘massless dark matter’ field which would be the signature of the loss of universality of the Newton’s law within a projective geometry framework.