On the Constant-Roll Inflation with Large and Small ηH
Abstract
:1. Introduction
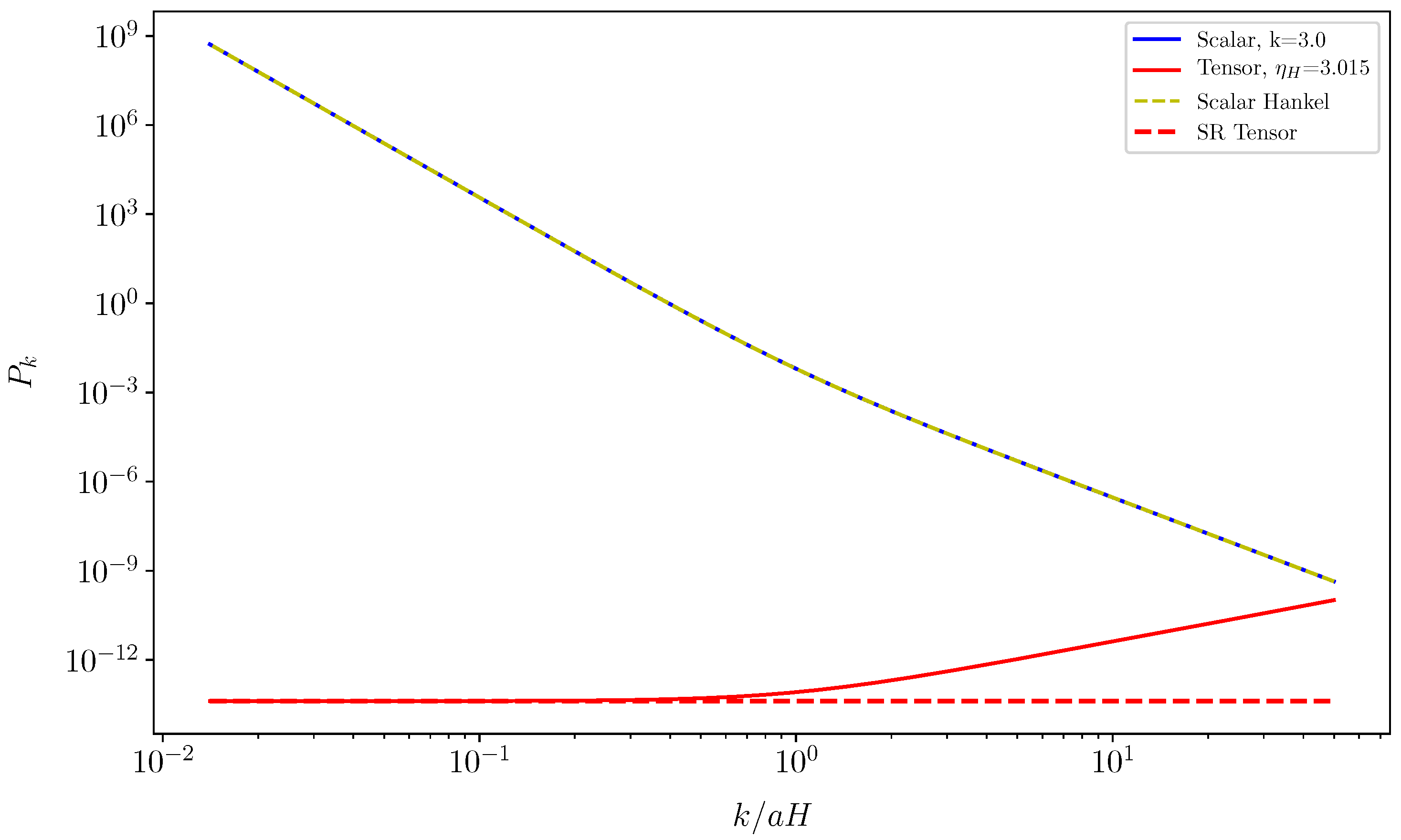
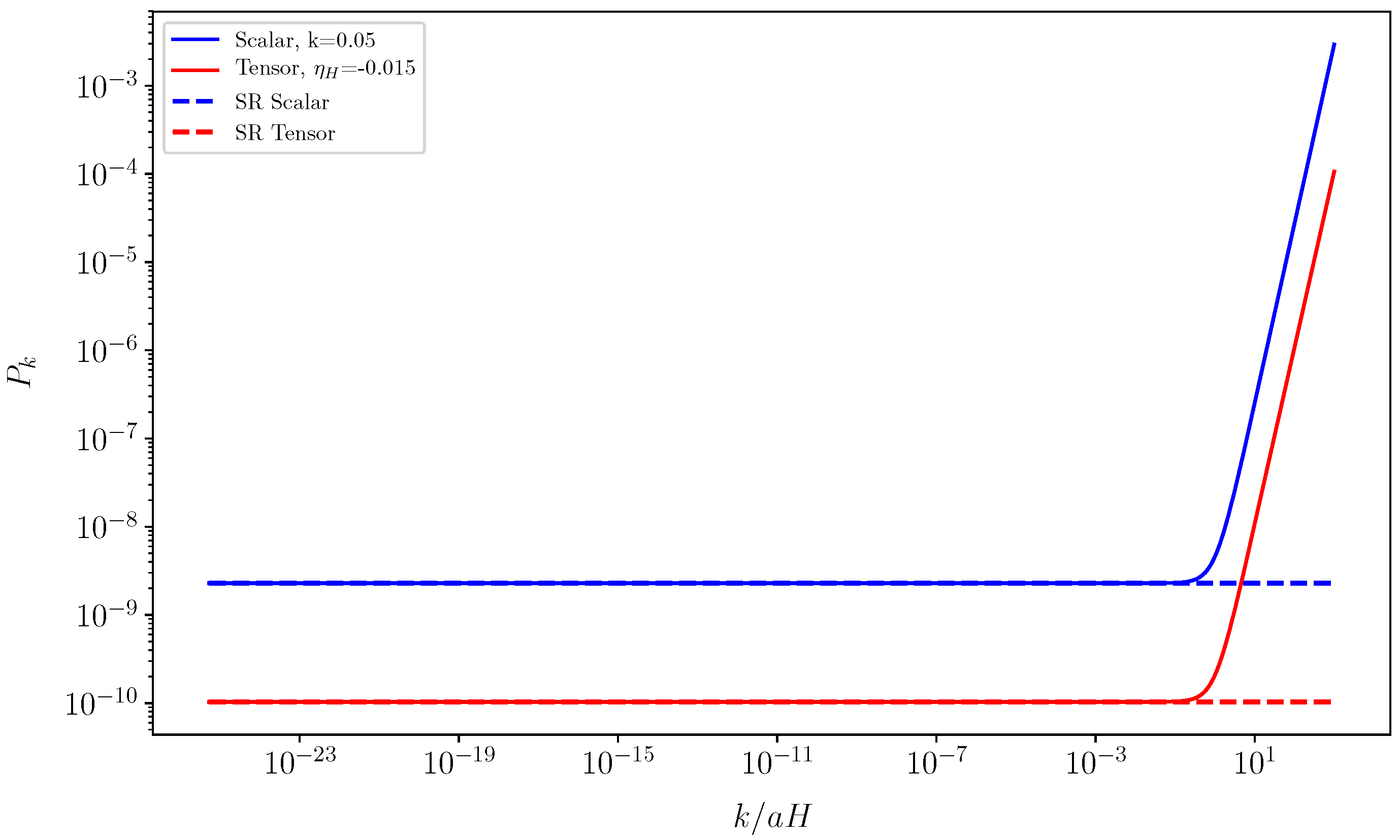
2. The Constant-Roll Inflation
2.1. The Constant-Roll Models
2.2. The Duality between the Slow-Roll and the Ultra Slow-Roll Inflation
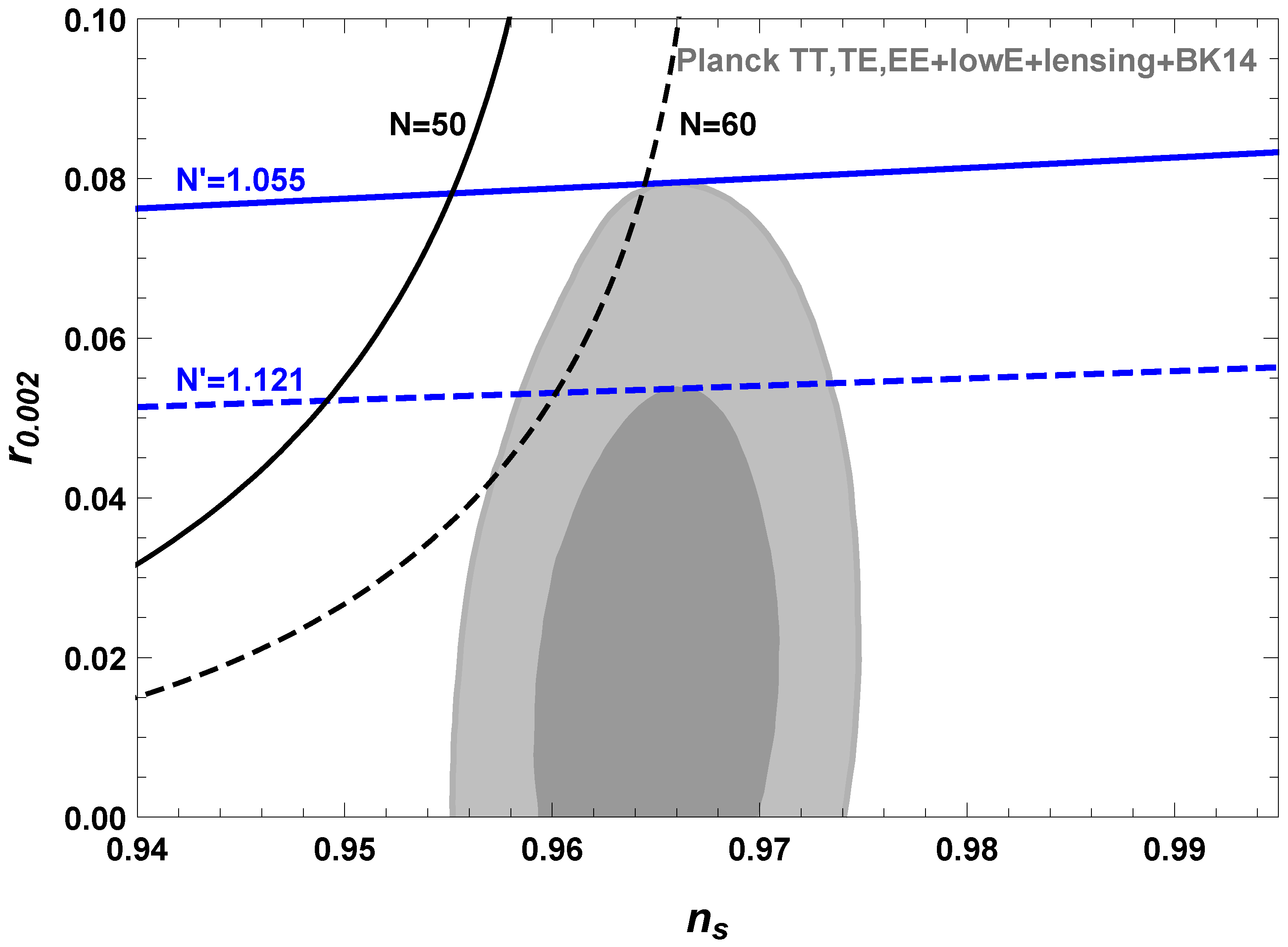
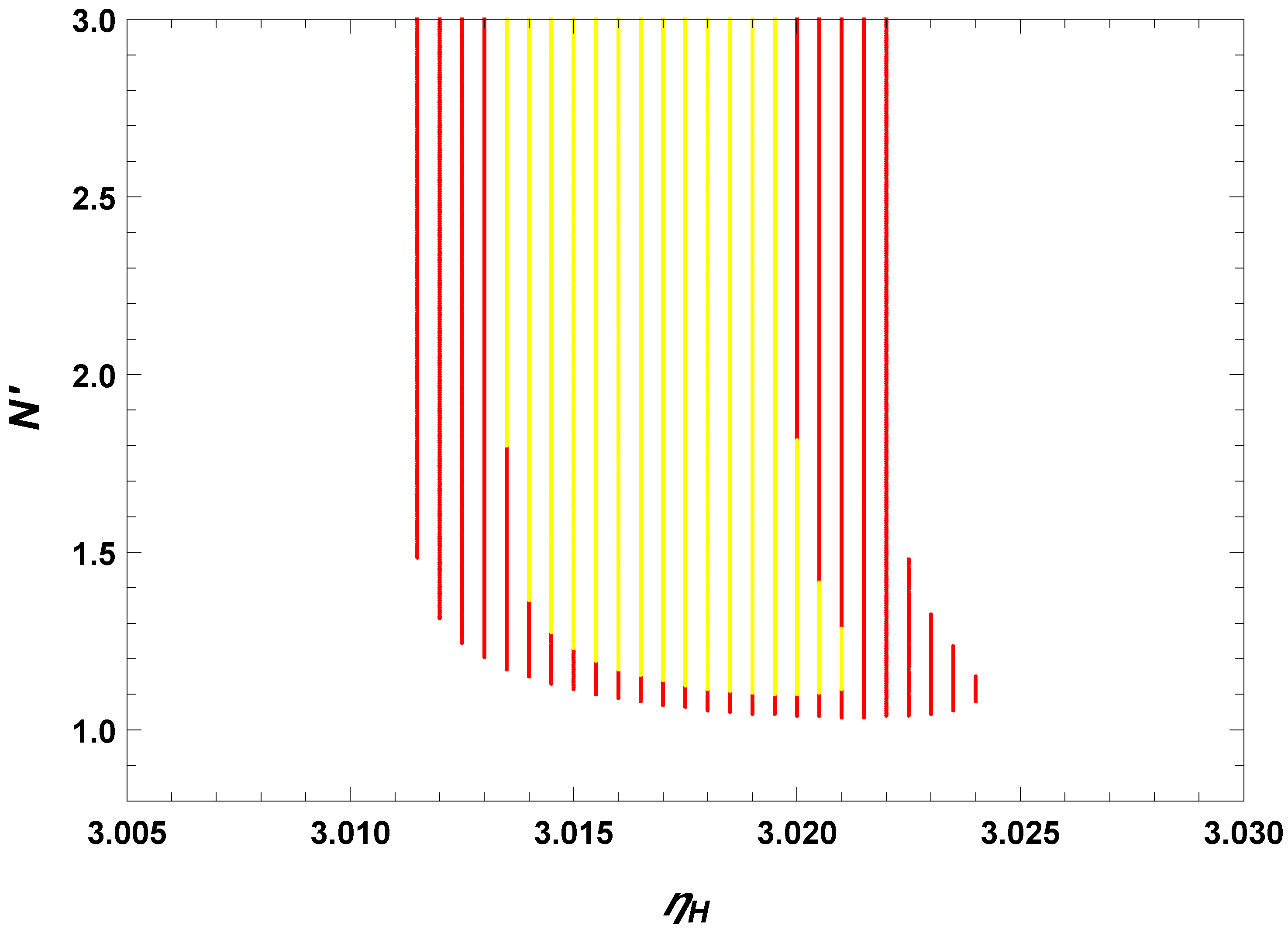
3. The Observational Constraints
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220–1223. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Chibisov, G.V. Quantum Fluctuation and Nonsingular Universe. JETP Lett. 1981, 33, 532–535. (In Russian) [Google Scholar]
- Hawking, S.W. The Development of Irregularities in a Single Bubble Inflationary Universe. Phys. Lett. B 1982, 115, 295–297. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Dynamics of Phase Transition in the New Inflationary Universe Scenario and Generation of Perturbations. Phys. Lett. B 1982, 117, 175–178. [Google Scholar] [CrossRef]
- Guth, A.H.; Pi, S.Y. Fluctuations in the New Inflationary Universe. Phys. Rev. Lett. 1982, 49, 1110–1113. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. arXiv 2018, arXiv:1807.06211. [Google Scholar]
- Array, K. BICEP2/Keck Array x: Constraints on Primordial Gravitational Waves using Planck, WMAP, and New BICEP2/Keck Observations through the 2015 Season. Phys. Rev. Lett. 2018, 121, 221301. [Google Scholar]
- Martin, J.; Motohashi, H.; Suyama, T. Ultra Slow-Roll Inflation and the non-Gaussianity Consistency Relation. Phys. Rev. D 2013, 87, 023514. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A.; Yokoyama, J. Inflation with a constant rate of roll. J. Cosmol. Astropart. Phys. 2015, 1509, 018. [Google Scholar] [CrossRef]
- Tsamis, N.C.; Woodard, R.P. Improved estimates of cosmological perturbations. Phys. Rev. D 2004, 69, 084005. [Google Scholar] [CrossRef] [Green Version]
- Kinney, W.H. Horizon crossing and inflation with large eta. Phys. Rev. D 2005, 72, 023515. [Google Scholar] [CrossRef]
- Leach, S.M.; Liddle, A.R. Inflationary perturbations near horizon crossing. Phys. Rev. D 2001, 63, 043508. [Google Scholar] [CrossRef] [Green Version]
- Leach, S.M.; Sasaki, M.; Wands, D.; Liddle, A.R. Enhancement of superhorizon scale inflationary curvature perturbations. Phys. Rev. D 2001, 64, 023512. [Google Scholar] [CrossRef] [Green Version]
- Jain, R.K.; Chingangbam, P.; Sriramkumar, L. On the evolution of tachyonic perturbations at super-Hubble scales. J. Cosmol. Astropart. Phys. 2007, 0710, 003. [Google Scholar] [CrossRef]
- Namjoo, M.H.; Firouzjahi, H.; Sasaki, M. Violation of non-Gaussianity consistency relation in a single field inflationary model. Europhys. Lett. 2013, 101, 39001. [Google Scholar] [CrossRef]
- Yi, Z.; Gong, Y. On the constant-roll inflation. J. Cosmol. Astropart. Phys. 2018, 1803, 052. [Google Scholar] [CrossRef]
- Tzirakis, K.; Kinney, W.H. Inflation over the hill. Phys. Rev. D 2007, 75, 123510. [Google Scholar] [CrossRef]
- Morse, M.J.P.; Kinney, W.H. Large-η constant-roll inflation is never an attractor. Phys. Rev. D 2018, 97, 123519. [Google Scholar] [CrossRef]
- Lin, W.C.; Morse, M.J.P.; Kinney, W.H. Dynamical Analysis of Attractor Behavior in Constant Roll Inflation. J. Cosmol. Astropart. Phys. 2019, 1909, 063. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A. Constant-roll inflation: confrontation with recent observational data. Europhys. Lett. 2017, 117, 39001. [Google Scholar] [CrossRef]
- Galvez Ghersi, J.T.; Zucca, A.; Frolov, A.V. Observational Constraints on Constant Roll Inflation. J. Cosmol. Astropart. Phys. 2019, 1905, 030. [Google Scholar] [CrossRef]
- Gao, Q. The observational constraint on constant-roll inflation. Sci. China Phys. Mech. Astron. 2018, 61, 070411. [Google Scholar] [CrossRef] [Green Version]
- Germani, C.; Prokopec, T. On primordial black holes from an inflection point. Phys. Dark Univ. 2017, 18, 6–10. [Google Scholar] [CrossRef] [Green Version]
- Motohashi, H.; Hu, W. Primordial Black Holes and Slow-Roll Violation. Phys. Rev. D 2017, 96, 063503. [Google Scholar] [CrossRef]
- Di, H.; Gong, Y. Primordial black holes and second order gravitational waves from ultra-slow-roll inflation. J. Cosmol. Astropart. Phys. 2018, 1807, 007. [Google Scholar] [CrossRef]
- Lu, Y.; Gong, Y.; Yi, Z.; Zhang, F. Constraints on primordial curvature perturbations from primordial black hole dark matter and secondary gravitational waves. arXiv 2019, arXiv:1907.11896. [Google Scholar]
- Motohashi, H.; Starobinsky, A.A. f(R) constant-roll inflation. Eur. Phys. J. C 2017, 77, 538. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Reheating in Constant-roll F(R) Gravity. Mod. Phys. Lett. A 2017, 32, 1750172. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Inflation with a Smooth Constant-Roll to Constant-Roll Era Transition. Phys. Rev. D 2017, 96, 024029. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Constant-roll Inflation in F(R) Gravity. Class. Quant. Grav. 2017, 34, 245012. [Google Scholar] [CrossRef]
- Dimopoulos, K. Ultra slow-roll inflation demystified. Phys. Lett. B 2017, 775, 262–265. [Google Scholar] [CrossRef]
- Ito, A.; Soda, J. Anisotropic Constant-roll Inflation. Eur. Phys. J. C 2018, 78, 55. [Google Scholar] [CrossRef]
- Karam, A.; Marzola, L.; Pappas, T.; Racioppi, A.; Tamvakis, K. Constant-Roll (Quasi-)Linear Inflation. J. Cosmol. Astropart. Phys. 2018, 1805, 011. [Google Scholar] [CrossRef]
- Fei, Q.; Gong, Y.; Lin, J.; Yi, Z. The reconstruction of tachyon inflationary potentials. J. Cosmol. Astropart. Phys. 2017, 1708, 018. [Google Scholar] [CrossRef]
- Cicciarella, F.; Mabillard, J.; Pieroni, M. New perspectives on constant-roll inflation. J. Cosmol. Astropart. Phys. 2018, 1801, 024. [Google Scholar] [CrossRef]
- Anguelova, L.; Suranyi, P.; Wijewardhana, L.C.R. Systematics of Constant Roll Inflation. J. Cosmol. Astropart. Phys. 2018, 1802, 004. [Google Scholar] [CrossRef]
- Gao, Q.; Gong, Y.; Fei, Q. Constant-roll tachyon inflation and observational constraints. J. Cosmol. Astropart. Phys. 2018, 1805, 005. [Google Scholar] [CrossRef]
- Mohammadi, A.; Saaidi, K. Constant-roll approach to non-canonical inflation. arXiv 2018, arXiv:1803.01715. [Google Scholar]
- Pattison, C.; Vennin, V.; Assadullahi, H.; Wands, D. The attractive behavior of ultra-slow-roll inflation. J. Cosmol. Astropart. Phys. 2018, 1808, 048. [Google Scholar] [CrossRef]
- Liddle, A.R.; Parsons, P.; Barrow, J.D. Formalizing the slow roll approximation in inflation. Phys. Rev. D 1994, 50, 7222–7232. [Google Scholar] [CrossRef]
- Mukhanov, V.F. Gravitational Instability of the Universe Filled with a Scalar Field. JETP Lett. 1985, 41, 493–496. [Google Scholar]
- Sasaki, M. Large Scale Quantum Fluctuations in the Inflationary Universe. Prog. Theor. Phys. 1986, 76, 1036. [Google Scholar] [CrossRef]
- Cheng, S.L.; Lee, W.; Ng, K.W. Numerical study of pseudoscalar inflation with an axion-gauge field coupling. Phys. Rev. D 2016, 93, 063510. [Google Scholar] [CrossRef] [Green Version]
- Cheng, S.L.; Lee, W.; Ng, K.W. Superhorizon curvature perturbation in ultraslow-roll inflation. Phys. Rev. D 2019, 99, 063524. [Google Scholar] [CrossRef] [Green Version]
- Byrnes, C.T.; Cole, P.S.; Patil, S.P. Steepest growth of the power spectrum and primordial black holes. J. Cosmol. Astropart. Phys. 2019, 1906, 028. [Google Scholar] [CrossRef]
- Passaglia, S.; Hu, W.; Motohashi, H. Primordial black holes and local non-Gaussianity in canonical inflation. Phys. Rev. D 2019, 99, 043536. [Google Scholar] [CrossRef] [Green Version]
| 1. | For the ultra-slow-roll inflation, can be very small because it decreases with time. |
| 2. | In Equation (25), we add the missing factor 2. |
| 3. | For the potential, solutions other than the constant-roll inflation also exist. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Gong, Y.; Yi, Z. On the Constant-Roll Inflation with Large and Small ηH. Universe 2019, 5, 215. https://doi.org/10.3390/universe5110215
Gao Q, Gong Y, Yi Z. On the Constant-Roll Inflation with Large and Small ηH. Universe. 2019; 5(11):215. https://doi.org/10.3390/universe5110215
Chicago/Turabian StyleGao, Qing, Yungui Gong, and Zhu Yi. 2019. "On the Constant-Roll Inflation with Large and Small ηH" Universe 5, no. 11: 215. https://doi.org/10.3390/universe5110215
APA StyleGao, Q., Gong, Y., & Yi, Z. (2019). On the Constant-Roll Inflation with Large and Small ηH. Universe, 5(11), 215. https://doi.org/10.3390/universe5110215




