1. Introduction
According to observational evidences from various sources it has been established that our universe entered a dark energy-dominated era and began a period of accelerated expansion roughly billion years ago [
1]. In order to provide an explanation, physicists follow two main directions. The first is to maintain general relativity as the gravitational theory and introduce new, exotic fluids in the universe content, dubbed as the dark energy sector [
2,
3]. The second way is to modify the gravitational sector, constructing extended theories of gravity that possess general relativity as a particular limit, but which, in general, present extra degrees of freedom, capable of describing the universe behavior [
4,
5,
6,
7,
8].
However, both approaches can be quantified by the introduction of an equation-of-state parameter for the dark energy perfect fluid (effective in the case of modified gravity), namely
, where
,
are respectively the pressure and the energy density. Hence, introducing various parametrizations of
allows us to describe the universe evolution in a phenomenological way, even if the microphysical origin of the cause of acceleration is unknown. Following this, a large number of parametrizations have been introduced in recent years, namely the one-parameter dark energy parametrizations [
9,
10], or the two-parameter family, such as the Chevallier–Polarski–Linder (CPL) parametrization [
11,
12], the Linear parametrization [
13,
14,
15], the Logarithmic parametrization [
16], the Jassal–Bagla–Padmanabhan parametrization (JBP) [
17], the Barboza–Alcaniz (BA) parametrization [
18], etc. (see for instance [
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47] and the references therein).
In most of the above dark energy equation-of-state parametrizations with a two-parameter description, one sets the “pivoting redshift” to zero, namely the point in which the two parameters describing
are uncorrelated. However, due to possible rotational correlations between the two parameters of the two-parameter models, in principle one could avoid setting the pivoting redshift to zero straightaway, and let it as a free parameter [
48,
49,
50].
In the present work we are interested in investigating the observational constraints on the most well-known parametrization, namely the CPL one, incorporating however the pivoting redshift as an extra parameter, assuming it to be either fixed or free. The motivation of this choice is to examine if the evolution of the dark energy equation of state can be better described by introducing more freedom in this parametrization. A first examination towards this direction was performed in [
51], however in the present work we provide a robust analysis with the latest cosmological data. In particular, we will use data from cosmic microwave background (CMB), baryon acoustic oscillations (BAO), redshift space distortion (RSD), weak lensing (WL), joint light curve analysis (JLA), and cosmic chronometers (CC), while we will include a Gaussian prior on the Hubble constant value. Among all the datasets mentioned above, some are related to the background evolution, such as JLA and CC, while CMB data play a very important role concerning the information of the model at the level of perturbations.
The plan of the work is as follows: In
Section 2 we present the basic equations of a parametrized dark energy model at the background and perturbative levels.
Section 3 describes the various data sets used in this work. In
Section 4 we perform the observational confrontation, extracting the constraints on the model parameters and on various cosmological quantities. In
Section 5 we proceed to a comparison of the various generalized CPL parametrization, with and without pivoting redshift. Finally, we summarize the obtained results in
Section 6.
2. Dynamical Dark Energy with Pivoting Redshift
In this section we briefly review the basic equations for a non-interacting cosmological scenario both at background and perturbative levels, and we introduce the pivoting redshift dark energy parametrization. We consider the homogeneous and isotropic Friedmann–Lemaître–Robertson–Walker (FLRW) line element
where
is the scale factor and
corresponds to open, closed, and flat geometry, respectively. Additionally, we consider that the universe is filled with baryons, cold dark matter, radiation, and the (effective) dark energy fluid. Hence, the evolution of the universe is determined by the Friedmann equations, which are written as
where
G is Newton’s gravitational constant and
is the Hubble function, with dots denoting derivatives with respect to the cosmic time
t. Moreover, in the above equations we have introduced the total energy density and pressure of the universe, reading as
and
, with the symbols
corresponding to radiation, baryon, cold dark matter, and dark energy fluid, respectively. In the following we focus our analysis on the spatially flat case (
), which is the one favored by observations.
In the case where the above sectors do not present mutual interactions, we can write the conservation equation of each fluid as
where
is known as the equation-of-state parameter of the
i-th fluid (
). For radiation,
, for baryons
, for cold dark matter
, and
is time dependent in general. Thus, using the conservation Equation (
4), one could easily extract that
,
,
, where
(
) is the present value of
(
). In the case of the dark energy fluid, the solution of (
4) is
where
is the current value of
and
is the value of the scale factor today which is set to unity by definition. Thus, inserting the evolution laws of the different components of the universe, one can explicitly express the Hubble function (
2) as:
From the expression (
5) one can deduce that the evolution of the dark energy component is highly dependent on the form of its equation-of-state parameter
. In the simplest case where
the dark energy fluid evolves as
. Nevertheless, for dynamical
one may consider various parametrizations in terms of the scale factor or the redshift
z, where
. Thus, in the literature one can find many forms of such parametrizations.
One of the well known parametrizations of the dark energy equation-of-state parameter is the Chevallier–Polarski–Linder (CPL) one, given by [
11,
12]
where
is the current value of
and
at
. One can see that the CPL parametrization can be generalized by introducing a new parameter
in the following way [
48,
49,
50]
where
,
and
. The parameter
describes the dark energy equation-of-state at
. In the case where the extra parameter
, we obtain
, and thus we recover the standard CPL model (
7). The parameter
is called the “pivoting redshift” or decorrelation redshift with
its corresponding scale factor, and indicates the point in which the two parameters describing
, i.e.,
and
, are uncorrelated, minimizing the error on
. Essentially,
marks the point in which
is most tightly constrained, given the data [
48,
49,
50]. We note that the pivot redshift is chosen in such a way so that the parameters
and
become uncorrelated. In particular, it is known that in the above parametrization
, and thus
, depend on the probing method, the fiducial scenario, and the imposed priors [
48]. Hence, in principle one could avoid setting
straightaway, and let it as a free parameter. Thus,
can be more precisely determined than
, and actually it is indeed the most precisely determined value of
. In this work we are interested in investigating the generalized CPL parametrization (
8), namely incorporating the pivoting redshift as an extra parameter, assuming it to be either fixed or free.
We proceed by providing the cosmological equations at the perturbation level. In the synchronous gauge the perturbed FLRW metric reads as
where
is the unperturbed and
the perturbed metric, and
is the conformal time. Using the above perturbed metric one can solve the conservation equations
. Thus, for a mode with wavenumber
k the perturbed equations can be written as [
52,
53,
54]
where primes denote derivatives with respect to the conformal time, and
is the conformal Hubble factor. Additionally,
is the density perturbation for the
i-th fluid,
is the divergence of the
i-th fluid velocity,
is the trace of the metric perturbations
, and
is the anisotropic stress of the
i-th fluid. Note that in the following we set
for all
i, since we assume zero anisotropic stress for all fluids. If we denote the sound speed of the
i-th fluid by
, then it is given by the relation
and the adiabatic speed of sound of the
i-th fluid is given by
, which is related to the equation of state as
. For barotropic fluids,
and in addition if
constant, then
. Now, for the dark energy fluid with equation of state
, if it is assumed to be purely adiabatic, then
, that means we have an imaginary value of
and hence there appear instabilities in the perturbations. To fix this problem, it is necessary to impose
and it is natural to set
by hand [
55].
3. Observational Data
In this section we present the various observational data sets that are going to be used in order to confront dark energy parametrizations with pivoting redshift. In our analysis we incorporate the data by varying nine cosmological parameters: the baryon energy density
(where
is the actual baryon density and
is the critical density
1 of the universe), the cold dark matter energy density
, the reionization optical depth
, the spectral index of the scalar perturbations
, the logarithm of the amplitude of the primordial power spectrum
, the ratio between the sound horizon and the angular diameter distance at decoupling
, the two free parameters of the extended CPL parametrization (
8), namely,
and
, and the pivot redshift
. Furthermore, we explore all parameters within the range of the conservative flat priors shown in
Table 1.
Let us now present in detail the data sets that we will use.
Cosmic microwave background (CMB): We constrain the parameters by analyzing the full range of the 2015 Planck temperature and polarization power spectra (
) [
56,
57]. This dataset is identified as the Planck TTTEEE + lowTEB. At the time of writing only the Planck 2015 likelihood was publicly available, however we do not expect the conclusions of this paper to change significantly given the similarities between the Planck 2015 and Planck 2018 results [
58,
59].
Baryon acoustic oscillations (BAO): We consider the baryon acoustic oscillations as was done in [
60]. They are the 6 dF Galaxy Survey (6dFGS) measurement at
[
61], the Main Galaxy Sample of Data Release 7 of Sloan Digital Sky Survey (SDSS-MGS) at
[
62], and the CMASS and LOWZ samples from the Data Release 12 (DR12) of the Baryon Oscillation Spectroscopic Survey (BOSS) at
and at
[
63].
Redshift space distortion (RSD): We add two redshift space distortion data. In particular, we include the data from CMASS and LowZ galaxy samples. The CMASS sample consists of 777,202 galaxies having the effective redshift of
[
64], whereas the LOWZ sample consists of 361,762 galaxies having an effective redshift of
[
64].
Weak lensing (WL): We include the cosmic shear data from the Canada–France–Hawaii Telescope Lensing Survey (CFHTLenS) [
65,
66,
67].
Joint light curve analysis (JLA): We consider the joint light curve analysis sample [
68] consisting of 740 luminosity distance measurements of Supernovae Type Ia data in the redshift interval
.
Cosmic chronometers (CC): We add the thirty measurements of the cosmic chronometers in the redshift interval
. The CC data have been summarized in [
69].
We include a Gaussian prior on the Hubble constant value from Riess et al. [
70] (i.e.,
), referred to as HST.
In order to incorporate statistically the several combinations of datasets and extract the observational constraints, we use our modified version of the publicly available Monte Carlo Markov Chain package
Cosmomc [
71], which is an efficient Monte Carlo algorithm equipped with a convergence diagnostic based on the Gelman and Rubin statistic [
72]. It implements an efficient sampling of the posterior distribution using the fast/slow parameter decorrelations [
73] and additionally it includes the support for the Planck data release 2015 Likelihood Code [
57]
2.
5. Statistical Comparison of All Parametrizations
In this section we proceed to a comparison of the various generalized CPL parametrizations, with and without the pivoting redshift. Hence, for completeness we perform a similar observational confrontation with the previous section for the standard CPL parametrization, namely without pivoting redshift (i.e.,
), and we summarize the results in
Table 9.
We can now perform the model comparison following the summarizing tables given above, namely
Table 2 (varying
),
Table 3 (
),
Table 4 (
),
Table 5 (
),
Table 6 (
),
Table 7 (
),
Table 8 (
), and
Table 9 (no pivoting redshift, i.e.,
).
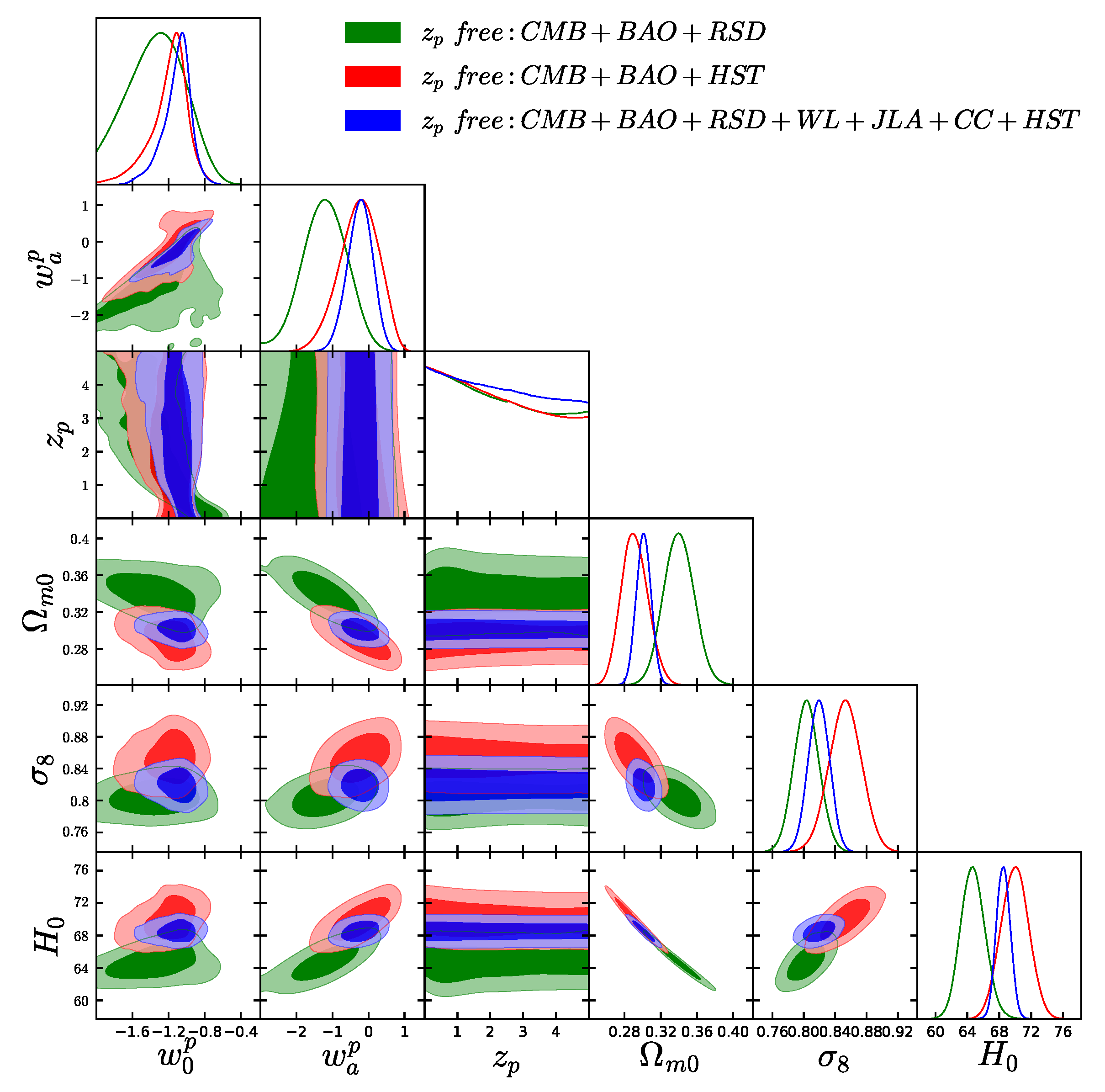
First of all, from all the analyses we find that the CMB data alone do not provide stringent constraints on the free parameters, however, we observe that the addition of any external datasets leads to a refinement of the constraints by reducing their error bars in a significant way. Furthermore, we find that the CMB + BAO + RSD combination returns slightly different constraints compared to the remaining two datasets, nevertheless for this combination we find an interesting pattern in the parameter, where we observe that with increasing , eventually approaches towards the cosmological constant value and finally for large () it crosses the boundary. Concerning the remaining two datasets, namely CMB + BAO + HST and CMB + BAO + RSD + WL + JLA + CC + HST, we find that the cosmological constraints are similar, with the best constraints definitely achieved for the final combination. Thus, in this section we focus on the observational datasets CMB + BAO + RSD and CMB + BAO + RSD + WL + JLA + CC + HST, in order to provide a statistical comparison between the cosmological models for free and fixed pivoting redshift .
In order to proceed towards the statistical comparisons of the models, in
Table 10 we depict the constraints on the basic model parameters for different values of
(free and fixed). Furthermore, in
Figure 9 we present the one-dimensional marginalized posterior distributions for the free parameters. In particular, the upper part of
Figure 9 corresponds to the CMB + BAO + RSD dataset, while the lower part to the full combination CMB + BAO + RSD + WL + JLA + CC + HST. From both parts of
Figure 9 we can clearly notice that all parameters present the same behavior independently of the pivoting redshift
, apart from
and
. Hence, in order to examine in more detail the effect of
on
,
, in
Figure 10 we depict the contour plots in the
plane for various
, for the combinations CMB + BAO + RSD (left panel of
Figure 10) and CMB + BAO + RSD + WL + JLA + CC + HST (right panel of
Figure 10).
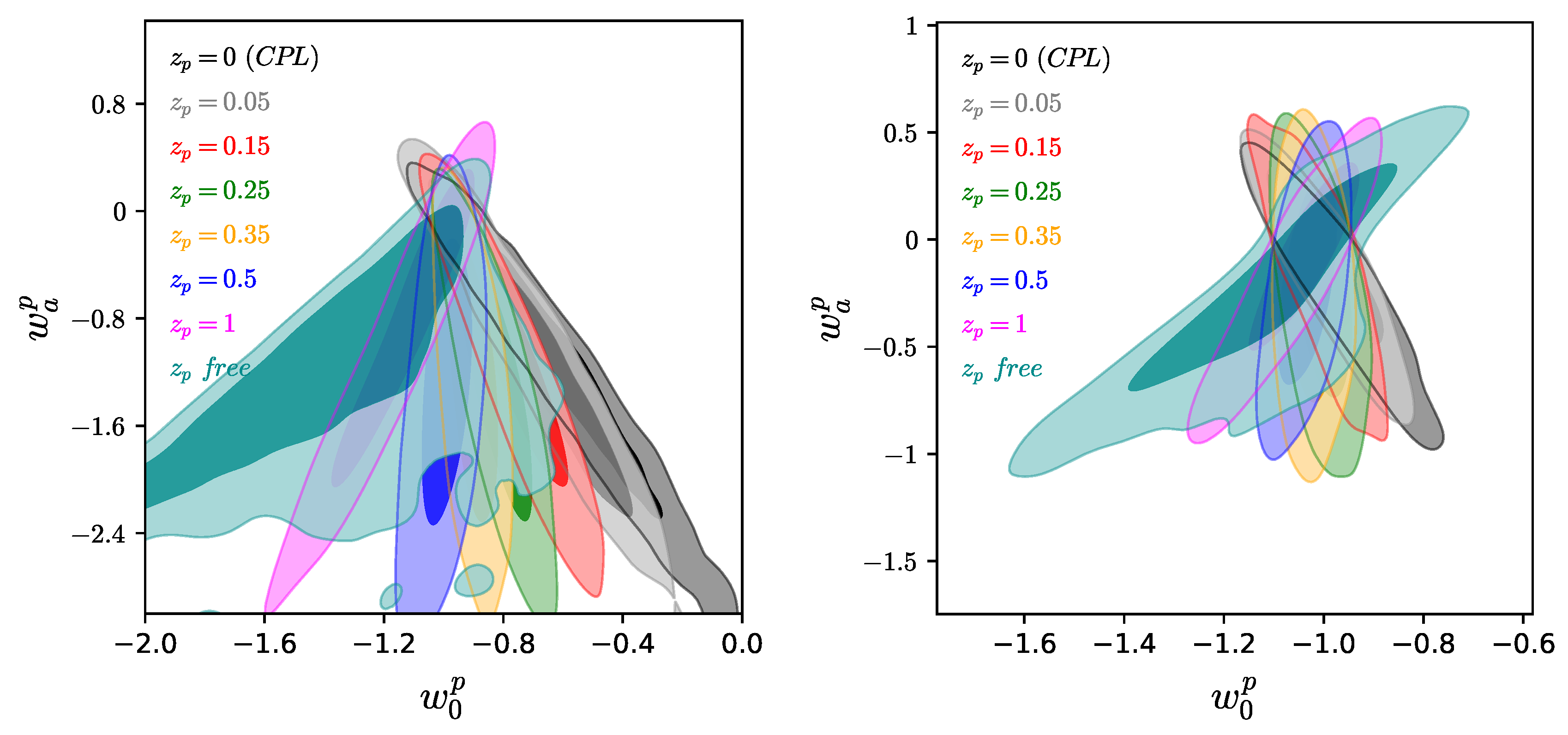
As we observe in
Figure 10 for both datasets, by changing the values of
the correlations between
and
change significantly. In particular, starting from a negative correlation present for
(the original CPL parametrization), increasing the
values leads to a rotation of the direction of the degeneracy between these two parameters. Therefore, we find a positive correlation for
, as well as in the case where
is left free. Finally, we can identify the value of the pivoting redshift for which
and
are no more correlated, and this is approximately
for both datasets (the contours corresponding to
(yellow) are vertical, showing no degeneracy). The changing of the correlations from negative to positive is one of the main results of this work.
Lastly, in order to provide the obtained results in a more transparent way, in
Figure 11 we provide the whisker plot for the equation-of-state parameter at present, namely
, for all the examined cases of the generalized CPL parametrization (see
Table 11 for the numerical values of
at 68% CL that we have extracted using the values of
,
through
, and the corresponding pivot redshift).
6. Concluding Remarks
Dynamical dark energy parametrizations are an effective approach to understanding the evolution of the universe, without needing to know the microphysical origin of the dark energy and whether it corresponds to new fields or to gravitational modification. Hence, a large number of such dark energy equation-of-state parametrizations have been introduced in the literature, with the Chevallier–Polarski–Linder (CPL) being one of the most studied.
However, in most of the above two-parameter parametrizations one considers the “pivoting redshift” to correspond to zero, namely the point in which the two parameters describing are uncorrelated, minimizing the error on this. Due to possible rotational correlations between the two parameters, in principle one could avoid setting the pivoting redshift to zero straightaway, handling it as a free parameter.
In the present work we investigated the observational constraints on such a generalized CPL parametrization, namely incorporating the pivoting redshift as an extra parameter, assuming it to be either fixed or free. For this, we used various data combinations from cosmic microwave background (CMB), baryon acoustic oscillations (BAO), redshift space distortion (RSD), weak lensing (WL), joint light curve analysis (JLA), and cosmic chronometers (CC), and we additionally included a Gaussian prior on the Hubble constant value. We considered two different cases, namely one in which is handled as a free parameter, and one in which it is fixed to a specific value. For the later case we considered various values of , in order to examine how the fixed value affects the results.
For the case of free
, we found that for all data combinations
always remains unconstrained, and there is a degeneracy with the dark energy equation of state
(see
Figure 2). On the other hand, in the case where
is fixed we did not find any degeneracy in the parameter space, as expected. In particular, the mean values of
lie always in the phantom regime, and for higher values of
(
),
at more than 1
while for lower values of
(
) the quintessence regime is also allowed at 1
.
The inclusion of any external data set to sole CMB data, such as BAO + RSD, BAO + HST, and BAO + RSD + WL + JLA + CC + HST, significantly improves the CMB constraints by reducing the error bars on the various quantities. For instance, irrespectively of the different fixed values, the CMB data always return high values for the present Hubble constant with large error bars, which both decrease for the combined data cases.
Concerning the constraints on
, for the CMB + BAO + RSD dataset we saw that they depend on the values of
. In particular, for low
(
) the mean values of
are always quintessential, while for
the mean value of
lies in the phantom regime. Nevertheless, a common characteristic is that for all
values
is allowed within 68% CL (note that for
within 68% CL
is strictly greater than
). Furthermore, for the CMB + BAO + HST dataset we saw that the obtained
-values for different
are in better agreement with the cosmological constant. Additionally, for the last full combination of CMB + BAO + RSD + WL + JLA + CC + HST, we also found that
is consistent with the cosmological constant, independently of the
values. As expected, compared to all the analyses performed in this work, the cosmological constraints obtained for the full data combination, namely CMB + BAO + RSD + WL + JLA + CC + HST, are much more stringent, as it was summarized in the whisker plot of
Figure 11.
Finally, in the above analysis we were able to reveal a correlation between the parameters
and
for different
(see
Figure 10). In particular, we found that with increasing
the correlations between
and
change from negative to positive (the direction of degeneracy is rotating from negative to positive), and for the case
,
and
are uncorrelated. Hence,
has a special interest because for this particular value of the redshift the aforementioned parameters become uncorrelated. This is one of the main results of the present work. Since the pivoting redshift is defined as the point in which
and
are considered uncorrelated, and having found that this is not true for
but for
indeed justifies why a non-zero pivoting redshift needs to be taken into account.