Study of Jet Shape Observables in Au+Au Collisions at s N N = 200 GeV with JEWEL

Abstract

Nuclear–nuclear collisions at energies attainable at the large accelerators RHIC and the LHC are an ideal environment to study nuclear matter under extreme conditions of high temperature and energy density. One of the most important probes of such nuclear matter is the study of production of jets. In this article, several jet shape observables in Au+Au collisions at the center of mass energy per nucleon–nucleon pair of $\sqrt{s_{NN}}$ = 200 GeV simulated in the Monte Carlo generator JEWEL are presented. Jets were reconstructed using the anti-$k_T$ algorithm and their shapes were studied as a function of the jet-resolution parameter R, transverse momentum $p_T$ and collision centrality.

1. Introduction

The study of production of jets is one of the most important probes of nuclear matter under extreme conditions of high temperature and energy density. The jet is a collimated spray of hadrons originating from fragmentation of a hard parton created in the initial stage of the nucleus–nucleus collision and can be used for tomography of the nuclear matter (Figure 1). As jets mostly conserve the energy and the direction of the originating parton, they are measured in particle detectors and studied to determine the properties of the original quarks.

To probe the complimentary aspects of the jet fragmentation and constrain theoretical description of jet–medium interactions, different observables related to shapes of jets are studied at the CERN Large Hadron Collider (LHC) [2,3,4]. It is important to perform similar measurements at lower collision energies at the Relativistic Heavy Ion Collider (RHIC) taking advantage of new high statistics data. The jet substructure observables are the perfect tool to understand what is happening when the particles interact with Quark–Gluon Plasma (QGP) medium. This article is focused on two jet shape observables: the girth and momentum dispersion that will be described in more detail below.

2. Jet Shape Observables

The first radial moment (alternatively angularity or girth), g, probes the radial distribution of radiation inside a jet. It is defined as

$$g=\sum _{i\in jet}\frac{p_{\mathrm{T}}^{\mathrm{i}}}{p_{\mathrm{T},\mathrm{jet}}}|\Delta R_{\mathrm{i},\mathrm{jet}}|.$$

(1)

Here $p_{\mathrm{T}}^{\mathrm{i}}$ represents the momentum of the ith jet constituent and $\Delta R_{\mathrm{i},\mathrm{jet}}$ is the distance in $\eta \times \varphi$ plane between the constituent i and the jet axis [5], where $\eta$ is the pseudorapidity and $\varphi$ is the azimuthal angle. This type of shape is sensitive to the radial energy profile or broadening of the jet. In the collinear limit for the polar angle $\theta \to$ 0 the radial moment becomes equivalent to jet broadening.

The next observable is momentum dispersion, $p_{T}D$. It measures the second moment of the constituent $p_{\mathrm{T}}$ distribution in the jet and is connected to hardness or softness of the jet fragmentation. It means that in the case of a large number of constituents and softer momentum the $p_{\mathrm{T}}D$ tends to 0, while in the opposite situation the $p_{\mathrm{T}}D$ will be close to 1. Its definition is given by the equation:

$$p_{T}D=\frac{\sqrt{{\sum }_{i\in jet}{p}_{\mathrm{T},\mathrm{i}}^2}}{{\sum }_{i\in jet}{p}_{\mathrm{T},\mathrm{i}}}.$$

(2)

These two jet shape observables are infrared and collinear (IRC) safe. It means that if one modifies an event by a collinear splitting or the addition of a soft emission, the set of hard jets that are found in the event should remain unchanged [6].

3. The Anti-${\mathit{k}}_{\mathit{T}}$ Algorithm

Jets are commonly reconstructed using the anti-$k_T$ clustering algorithm [7]. The anti-$k_T$ algorithm is a sequential-clustering algorithm. The algorithm is based on successive pair-wise recombination of particles and it works as follows. Firstly, the distance, $d_{ij}$, between particles i and j is found as

$$d_{ij}=\min (k_{ti}^{-2},k_{tj}^{-2})\frac{{\Delta }_{ij}^2}{R^2},$$

(3)

where ${\Delta }_{ij}^2={(y_i-y_j)}^2+{({\varphi }_i-{\varphi }_j)}^2$ and $k_{ti}$ or $k_{tj}$, $y_i$, ${\varphi }_i$ and R stand for the transverse momenta, rapidity, azimuth, and radius parameter of particle i respectively. Secondly, the algorithm calculates the distance, $d_{iB}$ between the entity i and the beam B as

$$d_{iB}=k_{ti}^{-2}.$$

(4)

The next step of the anti-$k_T$ jet algorithm is to find the minimum distance, $d_{min}$, between the distances $d_{ij}$ and $d_{iB}$. In case the smallest distance is $d_{ij}$, the algorithm performs a recombination of the entities. In other situation i is called to be a jet and is subsequently removed from the list. All these steps are repeated until no particles are left.

4. JEWEL

Jet Evolution With Energy Loss (JEWEL) is a Monte Carlo event generator that describes the Quantum Chromodynamics (QCD) evolution of jets in vacuum and in a medium in a perturbative approach [8,9,10]. In this section, the simulation in JEWEL will be described. For this research 50 million events were simulated for the interaction in vacuum and 20 million events for the interaction in medium. The simulation was made for 0–10% central and 60–80% peripheral Au+Au collisions with additional “recoils on/off” option for interaction with medium. “Recoils on” option in JEWEL keeps the thermal partons recoiling against interactions with the jet in the event and let them hadronize together with the jet, while the “recoils off” option ignore the medium response [11]. All events were required to have the center-of-mass (CMS) energy $\sqrt{s_{\mathrm{NN}}}$ = 200 GeV.

Table 1. Parameters of the JEWEL vacuum simulation for central and peripheral collisions [8].

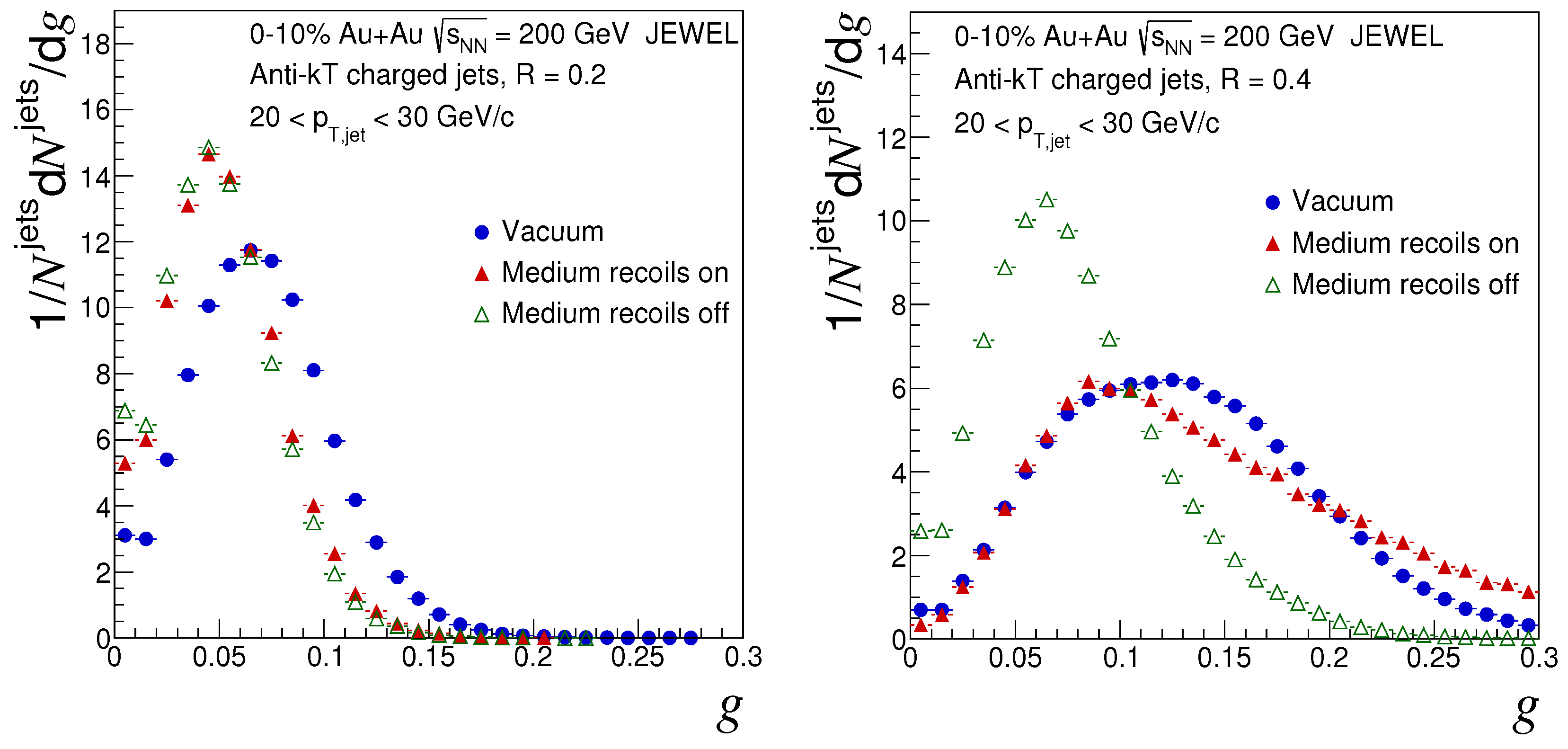
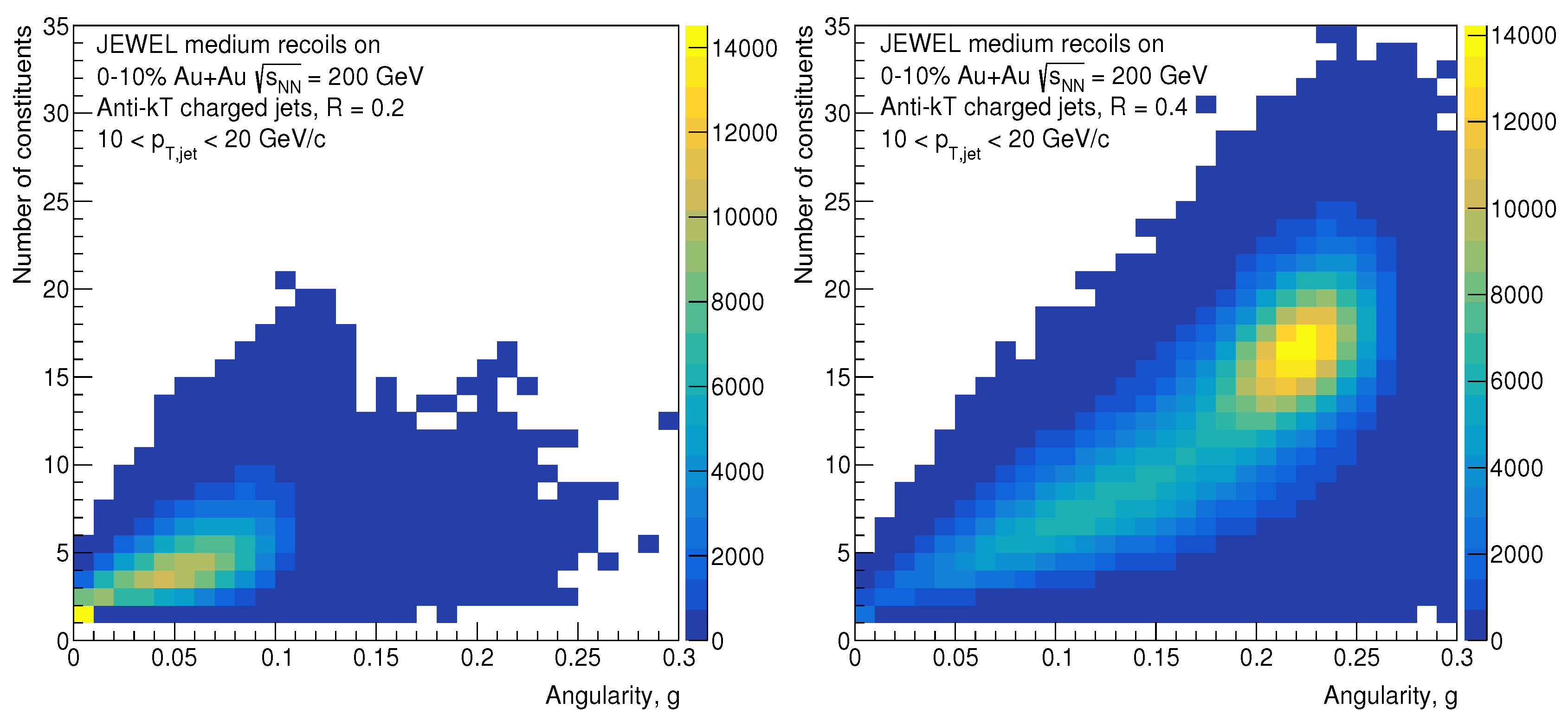
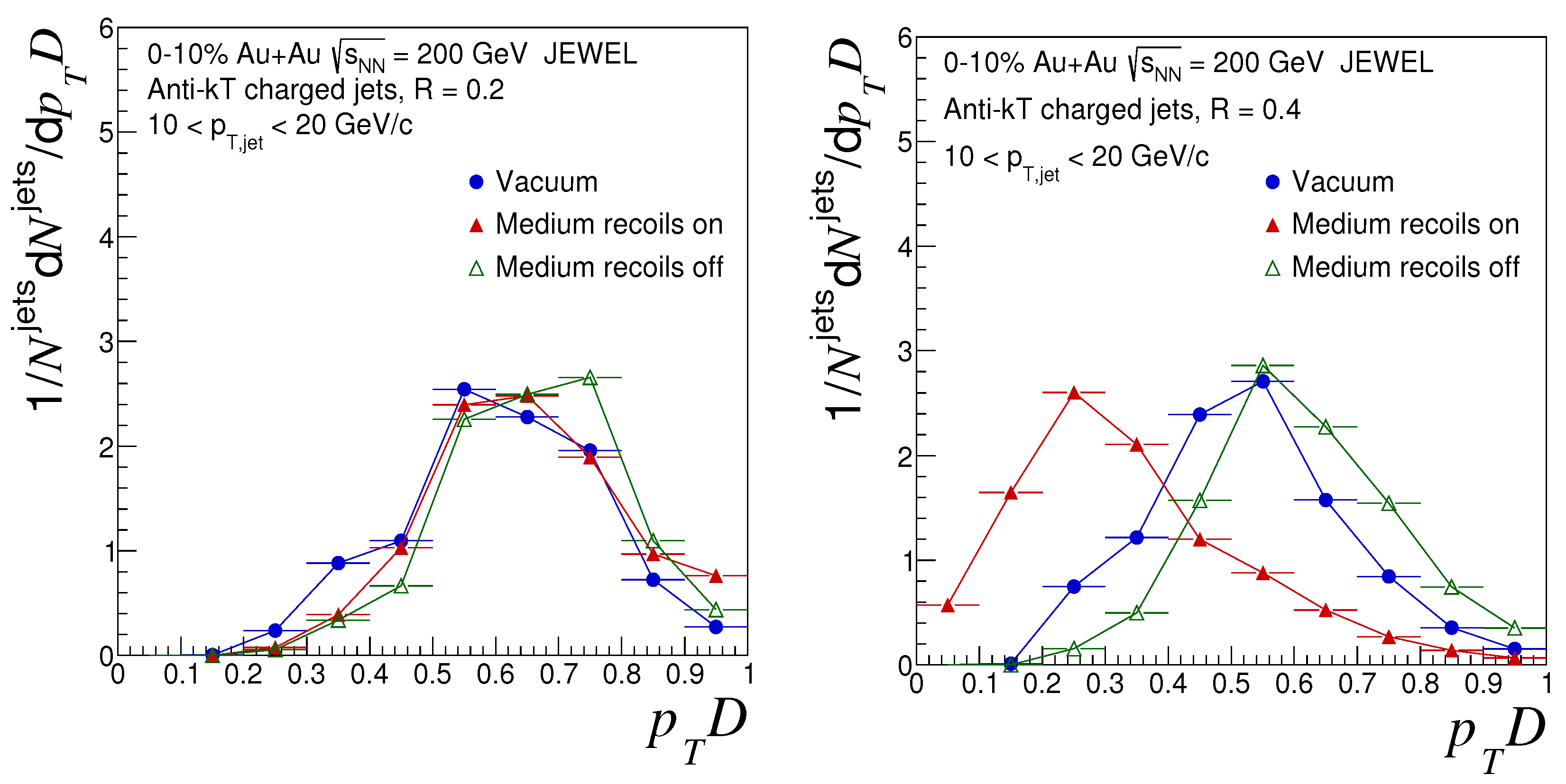
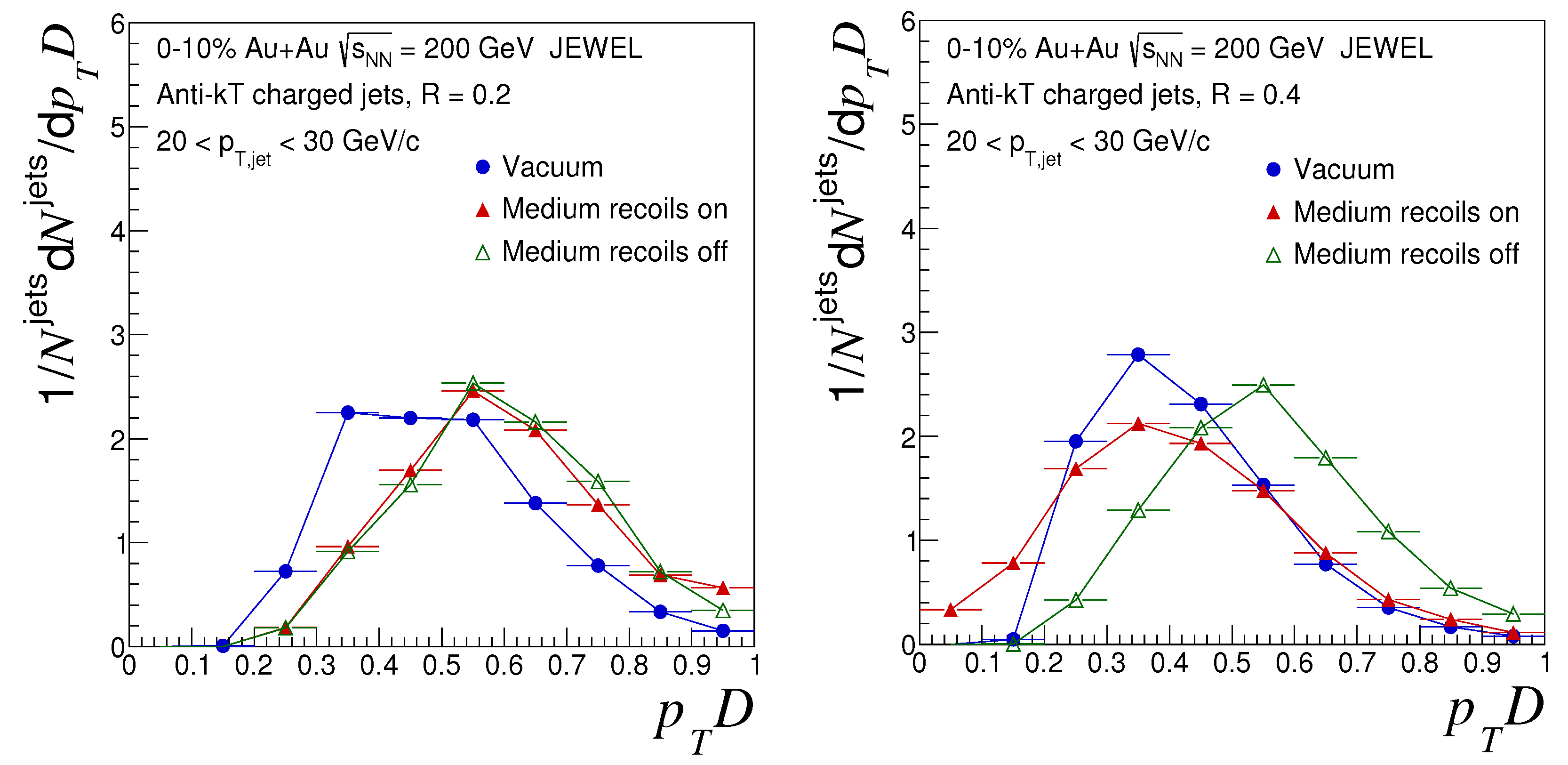
Name of Parameter	Name in JEWEL	Value
Parton Distribution Function set	PDFSET	10,100
Number of events	NEVENT	100,000
Mass number of Au nucleus	MASS	197
The CMS energy of the colliding system	SQRTS, [GeV]	200
Minimum $p_T$ in matrix element	PTMIN, [GeV]	3
Maximum $p_T$ in matrix element	PTMAX, [GeV]	−1
The rapidity range	ETAMAX	2.5

contains the parameters used for the vacuum model. Additional parameters for the simulation with the medium can be found in

Table 2. Parameters of the JEWEL simulation with medium for central and peripheral “recoils on/off” collisions [8].

Name of Parameter	Name in JEWEL	Value
The initial (mean) temperature	TI, [GeV]	0.28
The initial time ${\tau }_i$	TAUI, [fm]	0.6
An integer mass number of colliding nuclei	A	197
The lower end of centrality range	CENTRMIN, [%]	0	60
The upper end of centrality range	CENTRMAX, [%]	10	80
The switch of keeping recoils	KEEPRECOLIS	T	F
The nucleus–nucleus cross-section	SIGMANN, [fm${}^2$]	4.2

.

A resolution parameter, R, quantifies the size of the jet. For this study values of the resolution parameter were chosen to be R = 0.2 and R = 0.4, respectively. The charged particles were simulated in pseudorapidity ${\eta }_{cent}$ = 2.5 and full azimuth. Jets were reconstructed with the anti-$k_T$ algorithm included in FastJet software package [12].

5. Results

In this section, only the JEWEL results for central Au+Au collisions at $\sqrt{s_{NN}}$ = 200 GeV are presented as they are more appealing from the physical point of view. The jet shape observables are calculated for different values of the resolution parameter R and charged jet $p_{\mathrm{T}}$ separately for vacuum and medium with “recoils on/off” option. The distributions will be further compared to the results and the JEWEL simulation from the ALICE collaboration [13].

Figure 2 shows the measured jet shape distributions in 0–10% central Pb–Pb collisions at $\sqrt{s_{\mathrm{NN}}}$ = 2.76 TeV for anti-$k_T$ charged jets at ALICE compared to JEWEL simulation with and without recoils [13]. As the resolution parameter is small, R = 0.2, the effects of medium recoils are also small. It means that the measurement is constrained by purely radiative aspects of the JEWEL shower modification. A good agreement between the data and the model, especially in momentum dispersion, can be observed.

Figure 3 and Figure 4 compare the distributions of angularity for vacuum and medium “recoils on/off” central Au+Au collisions in two different $p_T$ ranges 10 < $p_T$ < 20 GeV/c and 20 < $p_T$ < 30 GeV/c, respectively. As it can be seen, the first radial moment has the same behavior for R = 0.2 as the results from the ALICE experiment (Figure 2). Nevertheless, peaks for the medium “recoils on” and medium “recoils off” simulation of angularity with R = 0.4 are shifted to the right and left, respectively. Distributions for medium “recoils on” collisions with R = 0.4 have a longer tail than others. Also, the spike for g = 0.01 in the case of jets with 10 < $p_T$ < 20 GeV/c can be observed for both resolution parameters. That signals the presence of jets with only one constituent. To probe this, the dependence of the number of constituents on the angularity is shown in Figure 5. It can be clearly seen that there is a larger number of particles for R = 0.4 than for R = 0.2 jets.

Figure 6 and Figure 7 compare the results for the momentum dispersion for jets with 10 < $p_T$ < 20 GeV/c and 20 < $p_T$ < 30 GeV/c, respectively. As for previous observable, there is a better agreement between the models in 20 < $p_T$ < 30 GeV/c$p_T$ range. However, in contradiction to the ALICE results, the obtained distributions for the momentum dispersion start form $p_{T}D$ = 0 (for R = 0.4 in central and peripheral collisions) and $p_{T}D$ = 0.1 (for R = 0.2 in central collisions) instead of $p_{T}D$ = 0.3. That can be a consequence of the use of different centrality ranges. Also, a shift of the distribution to lower values for the central medium “recoils on” setting for R = 0.4 and 10 < $p_T$ < 20 GeV/c can be observed.

6. Conclusions

In this article, the results of study of two jet shape observables, girth and momentum dispersion, in central Au+Au collisions at CMS energy of 200 GeV per nucleon–nucleon pair with the JEWEL Monte Carlo generator were presented. The jet shapes were calculated using the anti-k${}_T$ jet finding algorithm implemented in the FastJet software package. The chosen observables were studied as a function of the transverse momentum, jet-resolution parameter, and collision centrality. All the obtained results have the same behavior as the results from the ALICE collaboration [13]. In this study, it was shown that the spike in the girth results for g = 0.01 for jets with $p_T$ 10–20 GeV/c for both values of resolution parameter, R = 0.2 and R = 0.4, (Figure 3) is due to presence of jets with only one constituent (Figure 5). As for the momentum dispersion, the obtained distributions (Figure 6 and Figure 7) are wider in comparison to the ALICE results.

One of the goals of future work is to perform the background subtraction similarly to the ALICE experiment. It is expected that after the background subtraction the points for medium “recoils on/off” and vacuum models will be closer to each other.