Observing the Dark Sector †
Abstract
:1. Introduction
2. Galaxy Surveys
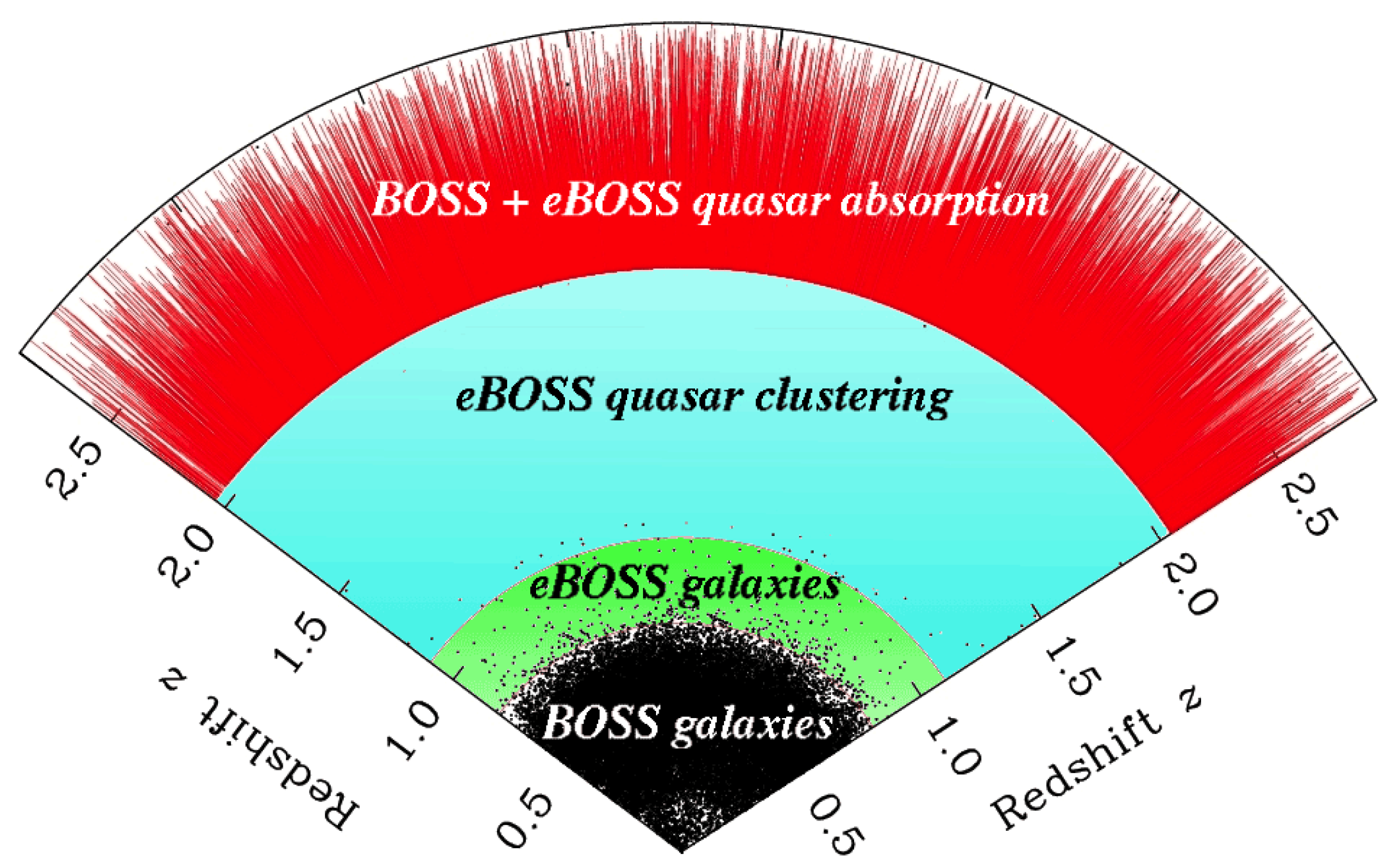
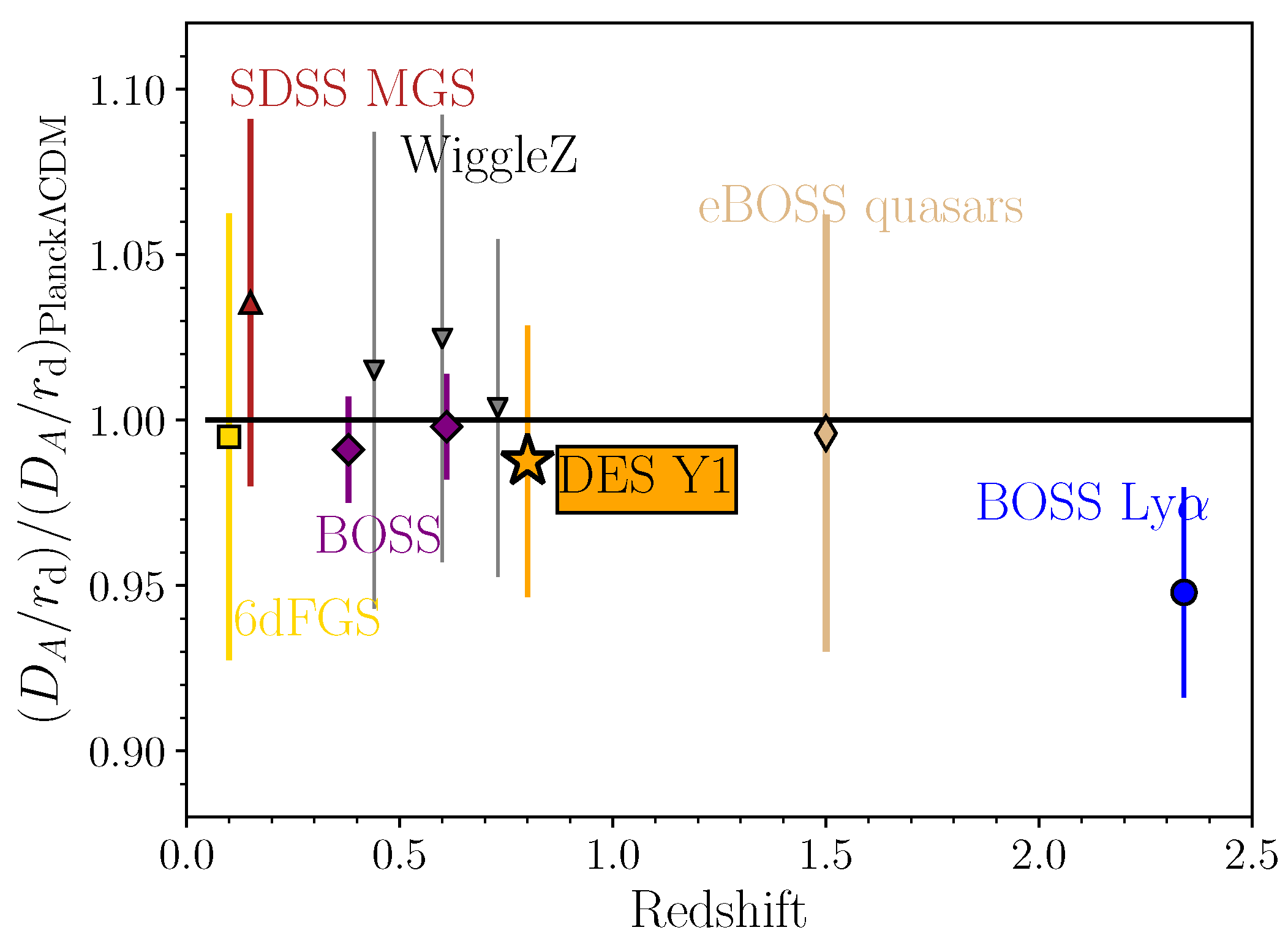
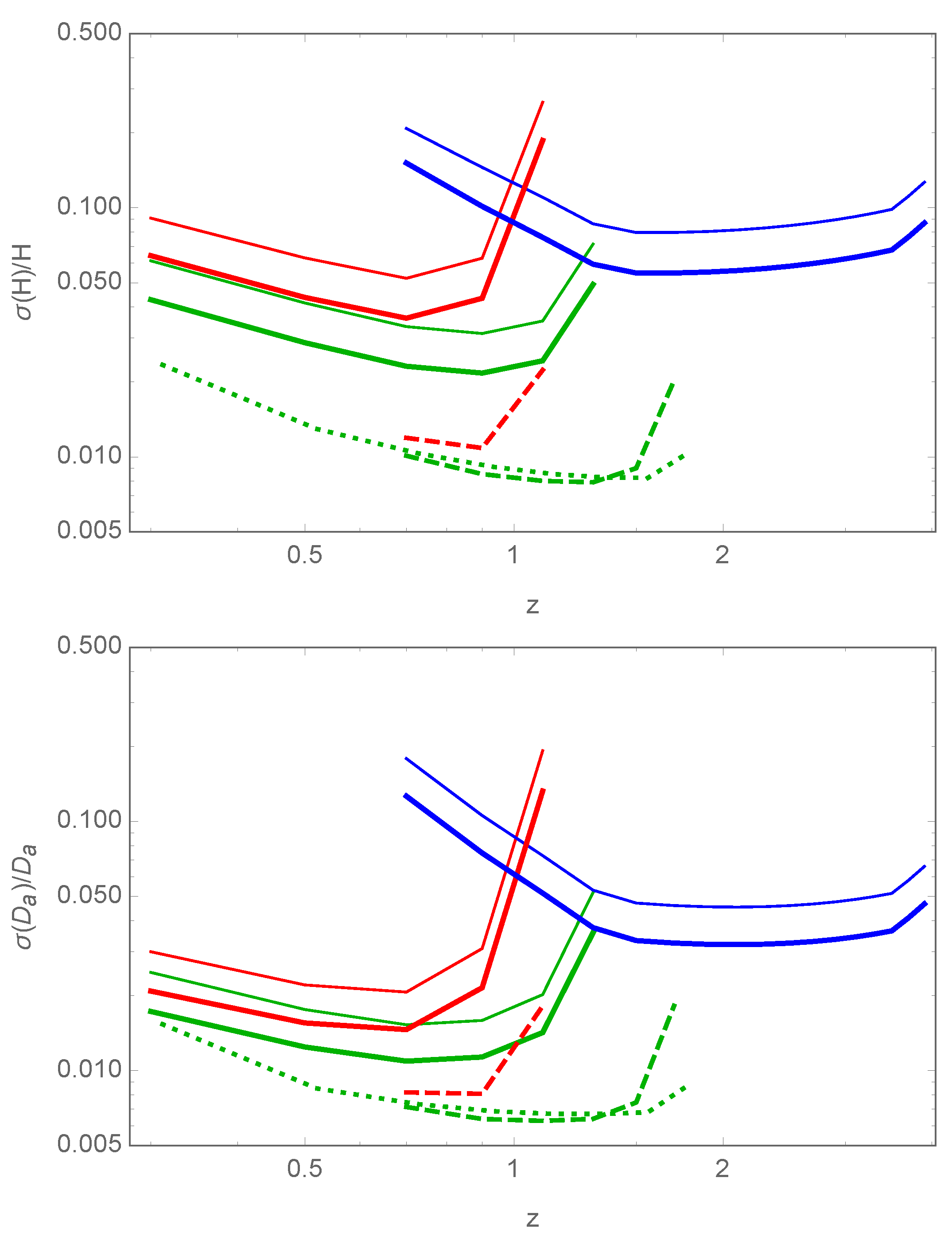
2.1. Extended Baryon Oscillation Spectroscopic Survey
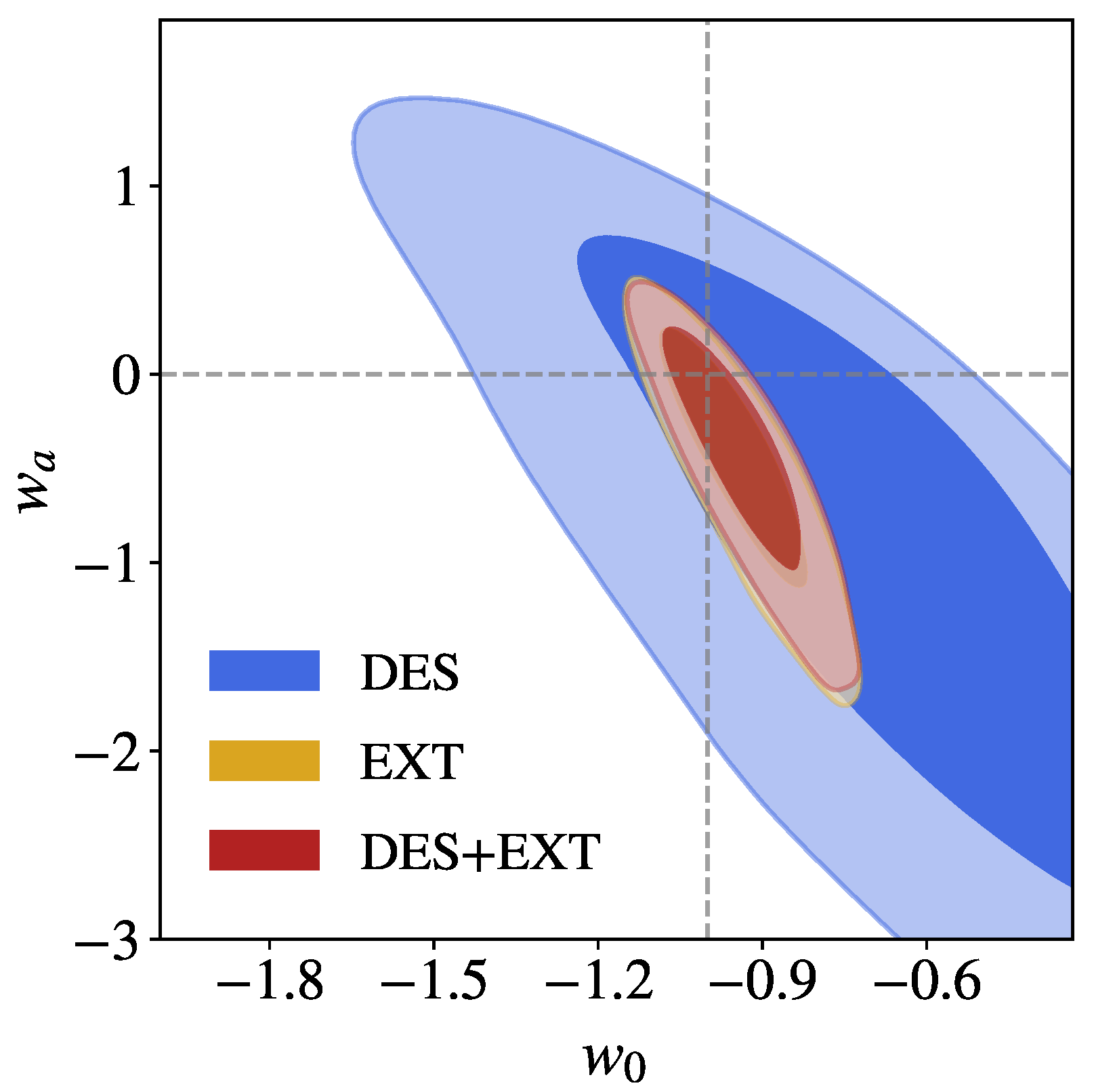
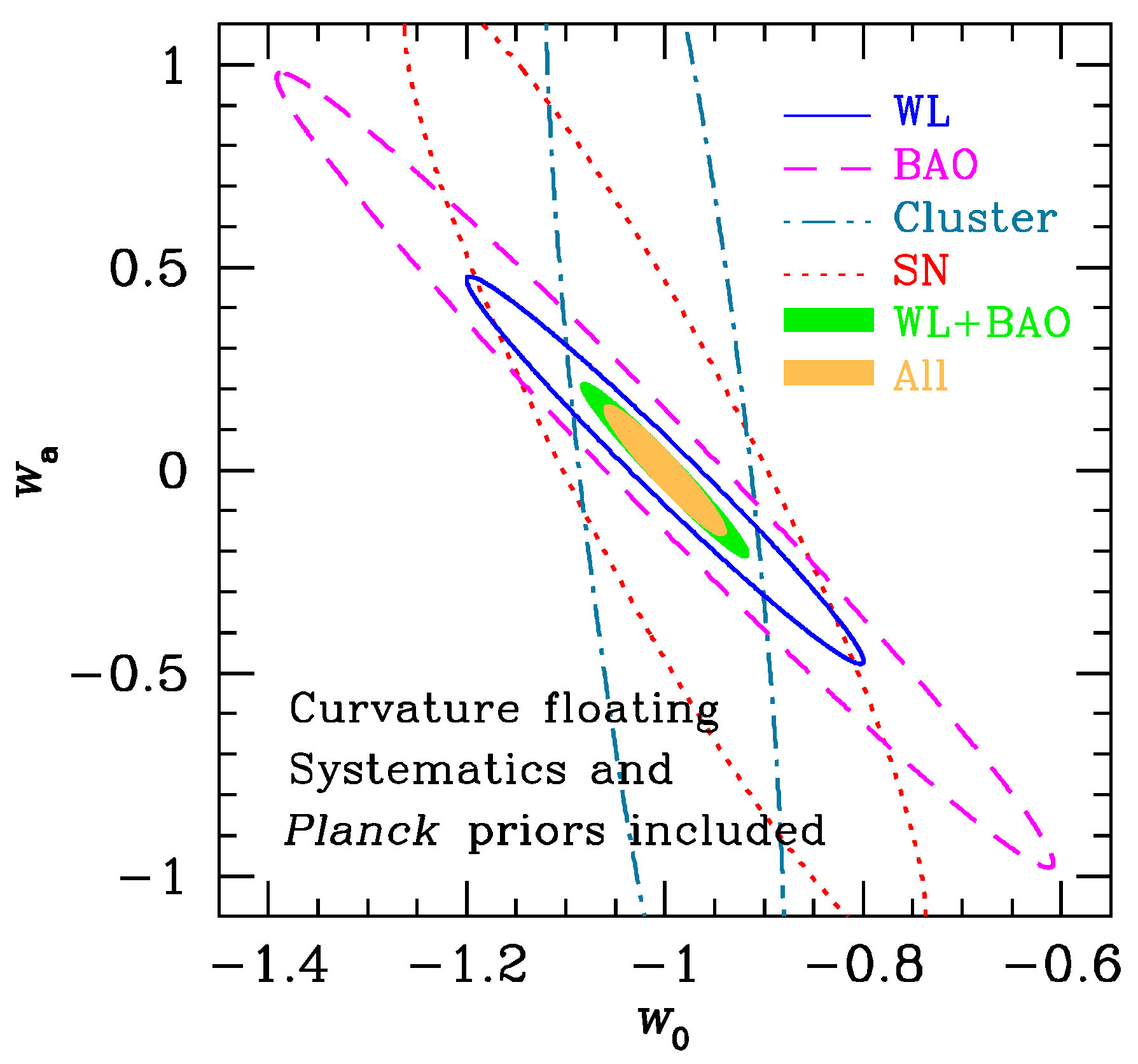
2.2. Dark Energy Survey
- Produced the largest contiguous mass map of the Universe;
- Discovered nearly a score of Milky Way dwarf satellites and other Milky Way structures;
- Measured weak lensing cosmic shear, galaxy clustering and cross-correlations with CMB lensing and with clusters detected via X-ray and the Sunyaev-Zeldovich effect;
- Measured light curves for large numbers of type Ia supernovae and discovered a number of super-luminous supernovae (SLSN) including the highest-redshift SLSN so far;
- Discovered a number of redshift quasars (also known as QSOs or quasi-stellar objects);
- Discovered a number of strongly lensed galaxies and QSOs;
- Discovered a number of interesting objects in the outer Solar System;
- Found optical counterparts of GW events
- Distribution of 300 million galaxies, including measurements of the Baryon Acoustic Oscillation;
- Weak gravitational lensing of galaxies;
- Supernovae of type Ia;
- Counts of clusters of galaxies.
- “Shape catalogue”: 26M galaxies for cosmic shear measurements (source galaxies) divided into 4 redshift bins;
- “Position catalogue”: 650,000 luminous red galaxies (lens galaxies) for clustering measurements divided into 5 redshift bins.
- Spatial curvature;
- The effective number of neutrinos species;
- Time-varying equation of state of dark energy, see Equation (1);
- Tests of gravity.
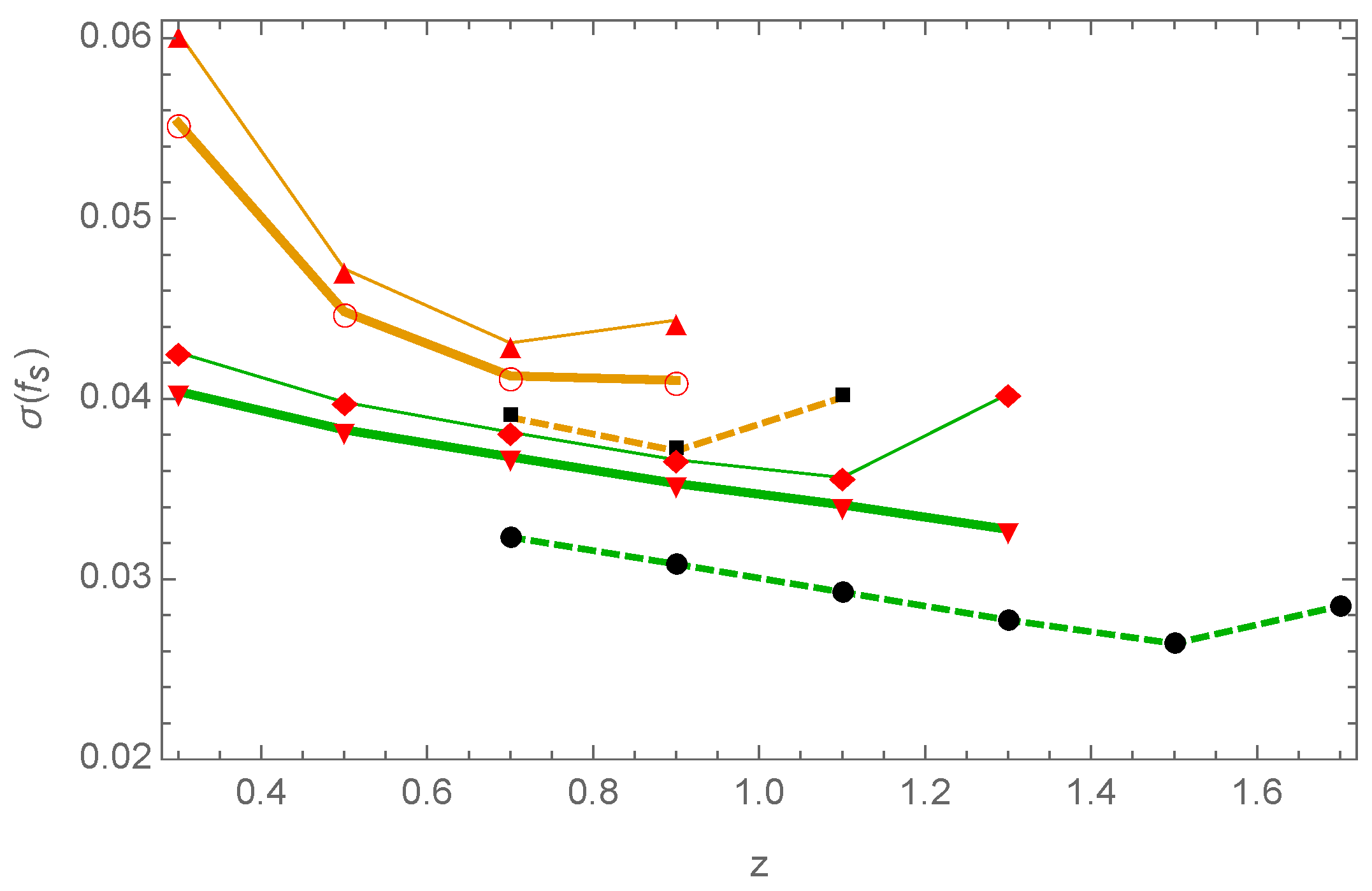
2.3. Javalambre Physics of the Accelerating Universe Astrophysical Survey
2.4. Dark Energy Spectroscopic Instrument
2.5. Euclid Consortium
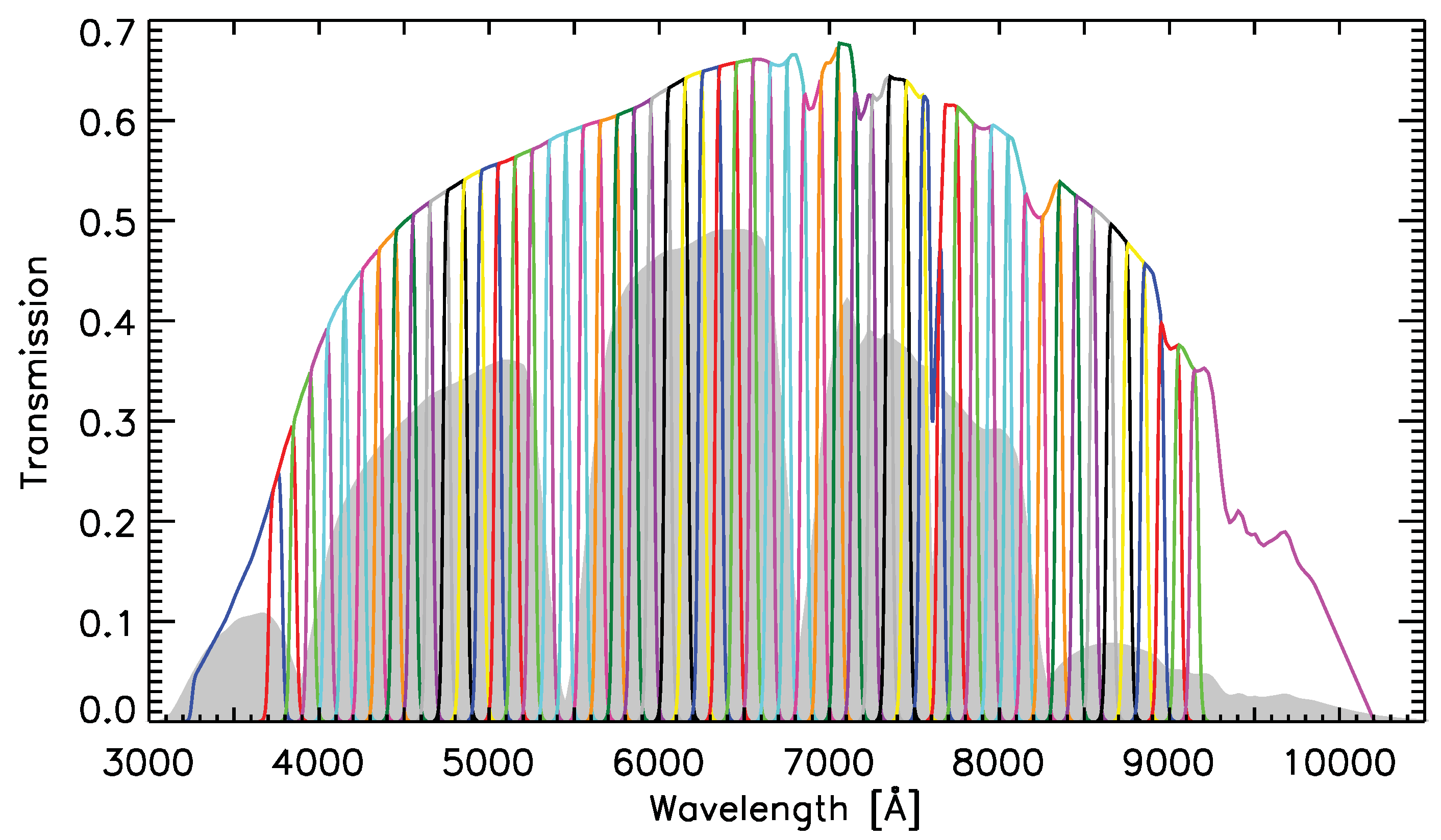
2.6. Large Synoptic Survey Telescope
- Theory and Joint Probes,
- Weak Lensing,
- Large Scale Structure,
- Supernovae,
- Strong Lensing,
- Photometric Redshifts.
- Weak gravitational lensing: the bending/distortion of the light of distant sources from dark and baryonic matter along the line of sight. Tomographic weak lensing measurements will yield percent-level constraints on the nature of the dark sector and modified gravity.
- Large-scale structure: the vast number of galaxies that will be detected by LSST will allow us to measure the Baryonic Acoustic Oscillations and the distance-redshift relation with percent-level precision.
- Type Ia Supernovae: LSST will discover tens of thousands of well-measured supernova light curves up to over the full ten-year survey, yielding an accurate determination of the luminosity distance-redshift relation.
- Galaxy clusters: LSST will measure the masses of ∼20,000 clusters with a precision of , which will give information about their distribution as a function of redshift.
- Strong gravitational lensing: LSST will produce a sample of ∼2600 time-delayed lensing systems, an increase of two orders of magnitude compared to present-day samples. Angular-displacement, morphological-distortion and time-delay information will allow us to constrain the massive lensing objects.
3. Square Kilometer Array
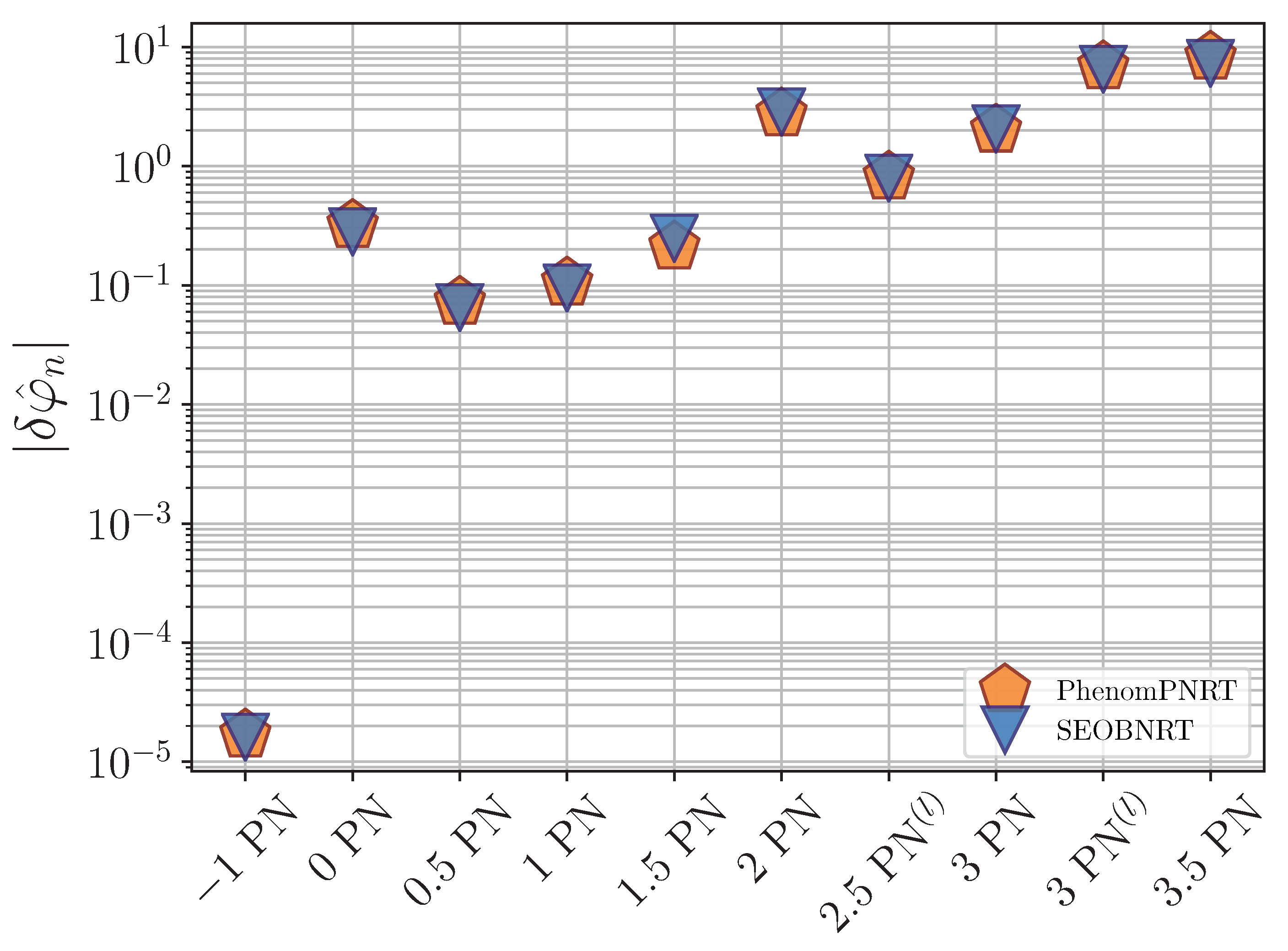
4. Gravitational Wave Surveys
Future Detectors
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed Type Ia Supernovae from Pan-STARRS1 and Cosmological Constraints from The Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.-H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Kazin, E.A.; Koda, J.; Blake, C.; Padmanabhan, N.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.J.; et al. The WiggleZ Dark Energy Survey: Improved distance measurements to z = 1 with reconstruction of the baryonic acoustic feature. Mon. Not. R. Astron. Soc. 2014, 441, 3524–3542. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. arXiv 2018, arXiv:1807.06209. [Google Scholar]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. 2013, 208, 19. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Alarcon, A.; Aleksić, J.; Allam, S.; Allen, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; et al. Dark Energy Survey year 1 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2018, 98, 043526. [Google Scholar] [CrossRef] [Green Version]
- Köhlinger, F.; Viola, M.; Joachimi, B.; Hoekstra, H.; van Uitert, E.; Hildebrandt, H.; Choi, A.; Erben, T.; Heymans, C.; Joudaki, S.; et al. KiDS-450: The tomographic weak lensing power spectrum and constraints on cosmological parameters. Mon. Not. R. Astron. Soc. 2017, 471, 4412–4435. [Google Scholar] [CrossRef]
- Krauss, L.M.; Turner, M.S. The Cosmological constant is back. Gen. Rel. Gravity 1995, 27, 1137–1144. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef] [Green Version]
- Salvatore Capozziello, Rocco D’Agostino, and Orlando Luongo. Extended Gravity Cosmography. 2019.
- Feng, J.L. Dark Matter Candidates from Particle Physics and Methods of Detection. Ann. Rev. Astron. Astrophys. 2010, 48, 495–545. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Li, X.; Wang, S.; Wang, Y. Dark Energy. Commun. Theor. Phys. 2011, 56, 525–604. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, A.; Bernstein, G.; Cahn, R.; Freedman, W.L.; Hewitt, J.; Hu, W.; Huth, J.; Kamionkowski, M.; Kolb, E.W.; Knox, L.; et al. Report of the Dark Energy Task Force. arXiv 2006, arXiv:astro-ph/0609591. [Google Scholar] [Green Version]
- Luongo, O.; Muccino, M. Speeding up the universe using dust with pressure. Phys. Rev. 2018, D98, 103520. [Google Scholar] [CrossRef]
- Aviles, A.; Gruber, C.; Luongo, O.; Quevedo, H. Cosmography and constraints on the equation of state of the Universe in various parametrizations. Phys. Rev. D 2012, 86, 123516. [Google Scholar] [CrossRef]
- Ata, M.; Baumgarten, F.; Bautista, J.; Beutler, F.; Bizyaev, D.; Blanton, M.R.; Blazek, J.A.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; et al. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: First measurement of baryon acoustic oscillations between redshift 0.8 and 2.2. Mon. Not. R. Astron. Soc. 2018, 473, 4773–4794. [Google Scholar] [CrossRef]
- Blanton, M.R.; Bershady, M.A.; Abolfathi, B.; Albareti, F.D.; Allende Prieto, C.; Almeida, A.; Alonso-García, J.; Anders, F.; Anderson, S.F.; Andrews, B.; et al. Sloan Digital Sky Survey IV: Mapping the Milky Way, Nearby Galaxies and the Distant Universe. Astron. J. 2017, 154, 28. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Avila, S.; Banerji, M.; Baxter, E.; Bechtol, K.; Becker, M.R.; Bertin, E.; Blazek, J.; Bridle, S.L.; et al. Dark Energy Survey Year 1 Results: Constraints on Extended Cosmological Models from Galaxy Clustering and Weak Lensing. arXiv 2018, arXiv:1810.02499. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Alarcon, A.; Allam, S.; Andrade-Oliveira, F.; Annis, J.; Avila, S.; Banerji, M.; Banik, N.; Bechtol, K.; et al. Dark Energy Survey Year 1 Results: Measurement of the Baryon Acoustic Oscillation scale in the distribution of galaxies to redshift 1. Mon. Not. R. Astron. Soc. 2017, 483, 4866–4883. [Google Scholar]
- Benitez, N.; Dupke, R.; Moles, M.; Sodre, L.; Cenarro, J.; Marin-Franch, A.; Taylor, K.; Cristobal, D.; Fernandez-Soto, A.; Mendes de Oliveira, C.; et al. J-PAS: The Javalambre-Physics of the Accelerated Universe Astrophysical Survey. arXiv 2014, arXiv:1403.5237. [Google Scholar]
- Ascaso, B.; Benítez, N.; Dupke, R.; Cypriano, E.; Lima-Neto, G.; López-Sanjuan, C.; Varela, J.; Alcaniz, J.S.; Broadhurst, T.; Cenarro, A.J.; et al. An Accurate Cluster Selection Function for the J-PAS Narrow-Band wide-field survey. Mon. Not. R. Astron. Soc. 2016, 456, 4291–4304. [Google Scholar] [CrossRef]
- Abramo, L.R.; Leonard, K.E. Why multi-tracer surveys beat cosmic variance. Mon. Not. R. Astron. Soc. 2013, 432, 318–326. [Google Scholar] [CrossRef]
- Abramo, L.R.; Secco, L.F.; Loureiro, A. Fourier analysis of multitracer cosmological surveys. Mon. Not. R. Astron. Soc. 2016, 455, 3871–3889. [Google Scholar] [CrossRef]
- Abramo, R.; Universidade de São Paulo: São Paulo, Brazil. Private communication, 2018.
- Aghamousa, A.; Aguilar, J.; Ahlen, S.; Alam, S.; Allen, L.E.; Allende Prieto, C.; Annis, J.; Bailey, S.; Balland, C.; Ballester, O.; et al. DESI Final Design Report. 1. Science, Targeting, and Survey Design. arXiv 2016, arXiv:1611.00036. [Google Scholar]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Auguères, J.-L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A.; et al. Euclid Definition Study Report. arXiv 2011, arXiv:1110.3193. [Google Scholar]
- Amendola, L.; Appleby, S.; Avgoustidis, A.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Rel. 2018, 21, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abell, P.A.; Allison, J.; Anderson, S.F.; Andrew, J.R.; Angel, J.R.P.; Armus, L.; Arnett, D.; Asztalos, S.J.; Axelrod, T.S.; Bailey, S.; et al. LSST Science Book, version 2.0. arXiv 2009, arXiv:0912.0201. [Google Scholar]
- Bull, P.; Camera, S.; Raccanelli, A.; Blake, C.; Ferreira, P.G.; Santos, M.G.; Schwarz, D.J. Measuring baryon acoustic oscillations with future SKA surveys. PoS 2015, AASKA14, 024. [Google Scholar]
- Raccanelli, A.; Bull, P.; Camera, S.; Blake, C.; Ferreira, P.; Maartens, R.; Santos, M.; Bacon, D.; Doré, O.; Viel, M.; et al. Measuring redshift-space distortion with future SKA surveys. PoS 2015, AASKA14, 031. [Google Scholar]
- Santos, M.G.; Alonso, D.; Bull, P.; Silva, M.; Yahya, S. HI galaxy simulations for the SKA: Number counts and bias. PoS 2015, AASKA14, 021. [Google Scholar]
- Yahya, S.; Bull, P.; Santos, M.G.; Silva, M.; Maartens, R.; Okouma, P.; Bassett, B. Cosmological performance of SKA HI galaxy surveys. Mon. Not. R. Astron. Soc. 2015, 450, 2251–2260. [Google Scholar] [CrossRef]
- Bull, P. Extending cosmological tests of General Relativity with the Square Kilometre Array. Astrophys. J. 2016, 817, 26. [Google Scholar] [CrossRef]
- Bull, P.; Camera, S.; Kelley, K.; Padmanabhan, H.; Pritchard, J.; Raccanelli, A.; Riemer-Sørensen, S.; Shao, L.; Andrianomena, S.; Athanassoula, E.; et al. Fundamental Physics with the Square Kilometer Array. arXiv 2018, arXiv:1810.02680. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Harry, G.M. Advanced LIGO: The next generation of gravitational wave detectors. Class. Quantum Gravity 2010, 27, 084006. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quantum Gravity 2015, 32, 024001. [Google Scholar] [CrossRef]
- Aso, Y.; Michimura, Y.; Somiya, K.; Ando, M.; Miyakawa, O.; Sekiguchi, T.; Tatsumi, D.; Yamamoto, H. Interferometer design of the KAGRA gravitational wave detector. Phys. Rev. D 2013, 88, 043007. [Google Scholar] [CrossRef] [Green Version]
- Somiya, K. Detector configuration of KAGRA: The Japanese cryogenic gravitational-wave detector. Class. Quantum Gravity 2012, 29, 124007. [Google Scholar] [CrossRef]
- Schutz, B.F. Networks of gravitational wave detectors and three figures of merit. Class. Quantum Gravity 2011, 28, 125023. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Prospects for Observing and Localizing Gravitational-Wave Transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Rel. 2018, 21, 3. [Google Scholar] [CrossRef] [PubMed]
- Coulter, D.A.; Foley, R.J.; Kilpatrick, C.D.; Drout, M.R.; Piro, A.L.; Shappee, B.J.; Siebert, M.R.; Simon, J.D.; Ulloa, N.; Kasen, D.; et al. Swope Supernova Survey 2017a (SSS17a), the Optical Counterpart to a Gravitational Wave Source. Science 2017, 358, 1556. [Google Scholar] [CrossRef] [PubMed]
- LIGO Scientific Collaboration. LIGO Algorithm Library—LALSuite; Free Software (GPL): Boston, MA, USA, 2018. [Google Scholar]
- Creminelli, P.; Vernizzi, F. Dark Energy after GW170817 and GRB170817A. Phys. Rev. Lett. 2017, 119, 251302. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence. Astrophys. J. 2017, 851, L35. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. arXiv 2018, arXiv:1811.12907. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101, Erratum in 2018, 121, 129901. [Google Scholar] [CrossRef]
- Vallisneri, M.; Kanner, J.; Williams, R.; Weinstein, A.; Stephens, B. The LIGO Open Science Center. J. Phys. Conf. Ser. 2015, 610, 012021. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Binary Black Hole Mergers in the first Advanced LIGO Observing Run. Phys. Rev. 2016, X6, 041015, Erratum in 2018, X8, 039903. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Tests of General Relativity with GW170817. arXiv 2018, arXiv:1811.00364. [Google Scholar]
- Husa, S.; Khan, S.; Hannam, M.; Pürrer, M.; Ohme, F.; Forteza, X.J.; Bohé, A. Frequency-domain gravitational waves from nonprecessing black-hole binaries. I. New numerical waveforms and anatomy of the signal. Phys. Rev. D 2016, 93, 044006. [Google Scholar] [CrossRef] [Green Version]
- Bohé, A.; Shao, L.; Taracchini, A.; Buonanno, A.; Babak, S.; Harry, I.W.; Hinder, I.; Ossokine, S.; Pürrer, M.; Raymond, V.; et al. Improved effective-one-body model of spinning, nonprecessing binary black holes for the era of gravitational-wave astrophysics with advanced detectors. Phys. Rev. D 2017, 95, 044028. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [Green Version]
- Schutz, B.F. Determining the Hubble Constant from Gravitational Wave Observations. Nature 1986, 323, 310–311. [Google Scholar] [CrossRef]
- Pozzo, W.D. Inference of the cosmological parameters from gravitational waves: Application to second generation interferometers. Phys. Rev. D 2012, 86, 043011. [Google Scholar] [CrossRef]
- Soares-Santos, M.; Palmese, A.; Hartley, W.; Annis, J.; Garcia-Bellido, J.; Lahav, O.; Doctor, Z.; Fishbach, M.; Holz, D.E.; Lin, H.; et al. First measurement of the Hubble constant from a dark standard siren using the Dark Energy Survey galaxies and the LIGO/Virgo binary-black-hole merger GW170814. Astrophys. J. 2019, in press. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quantum Gravity 2010, 27, 194002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Ackley, K.; Adams, C.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Exploring the Sensitivity of Next Generation Gravitational Wave Detectors. Class. Quantum Gravity 2017, 34, 044001. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star Formation History. Ann. Rev. Astron. Astrophys. 2014, 52, 415–486. [Google Scholar] [CrossRef]
- Vitale, S.; Farr, W.M. Measuring the star formation rate with gravitational waves from binary black holes. arXiv 2018, arXiv:1808.00901. [Google Scholar]
- Mendonça, J.; Sturani, R. Cosmological model selection from standard siren detections by third generation gravitational wave obervatories. arXiv 2019, arXiv:1905.03848. [Google Scholar]
- Klein, A.; Barausse, E.; Sesana, A.; Petiteau, A.; Berti, E.; Babak, S.; Gair, J.; Aoudia, S.; Hinder, I.; Ohme, F.; et al. Science with the space-based interferometer eLISA: Supermassive black hole binaries. Phys. Rev. D 2016, 93, 024003. [Google Scholar] [CrossRef] [Green Version]
- Evans, M.; Sturani, R.; Vitale, S.; Hall, E. Unofficial sensitivity curves (ASD) for aLIGO, Kagra, Virgo, Voyager, Cosmic Explorer and ET. Technical Report. 2018. Available online: https://dcc.ligo.org/LIGO-T1500293/public (accessed on 20 November 2018).
| 1 | See Luongo and Muccino [16] for the case of dark matter with a non-vanishing pressure. |
| 2 | See Aviles et al. [17] for alternative parametrizations. |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |













© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marra, V.; Rosenfeld, R.; Sturani, R. Observing the Dark Sector. Universe 2019, 5, 137. https://doi.org/10.3390/universe5060137
Marra V, Rosenfeld R, Sturani R. Observing the Dark Sector. Universe. 2019; 5(6):137. https://doi.org/10.3390/universe5060137
Chicago/Turabian StyleMarra, Valerio, Rogerio Rosenfeld, and Riccardo Sturani. 2019. "Observing the Dark Sector" Universe 5, no. 6: 137. https://doi.org/10.3390/universe5060137
APA StyleMarra, V., Rosenfeld, R., & Sturani, R. (2019). Observing the Dark Sector. Universe, 5(6), 137. https://doi.org/10.3390/universe5060137




