Detecting the Hadron-Quark Phase Transition with Gravitational Waves
Abstract
1. Introduction
2. GW170817—The Long-Awaited Event
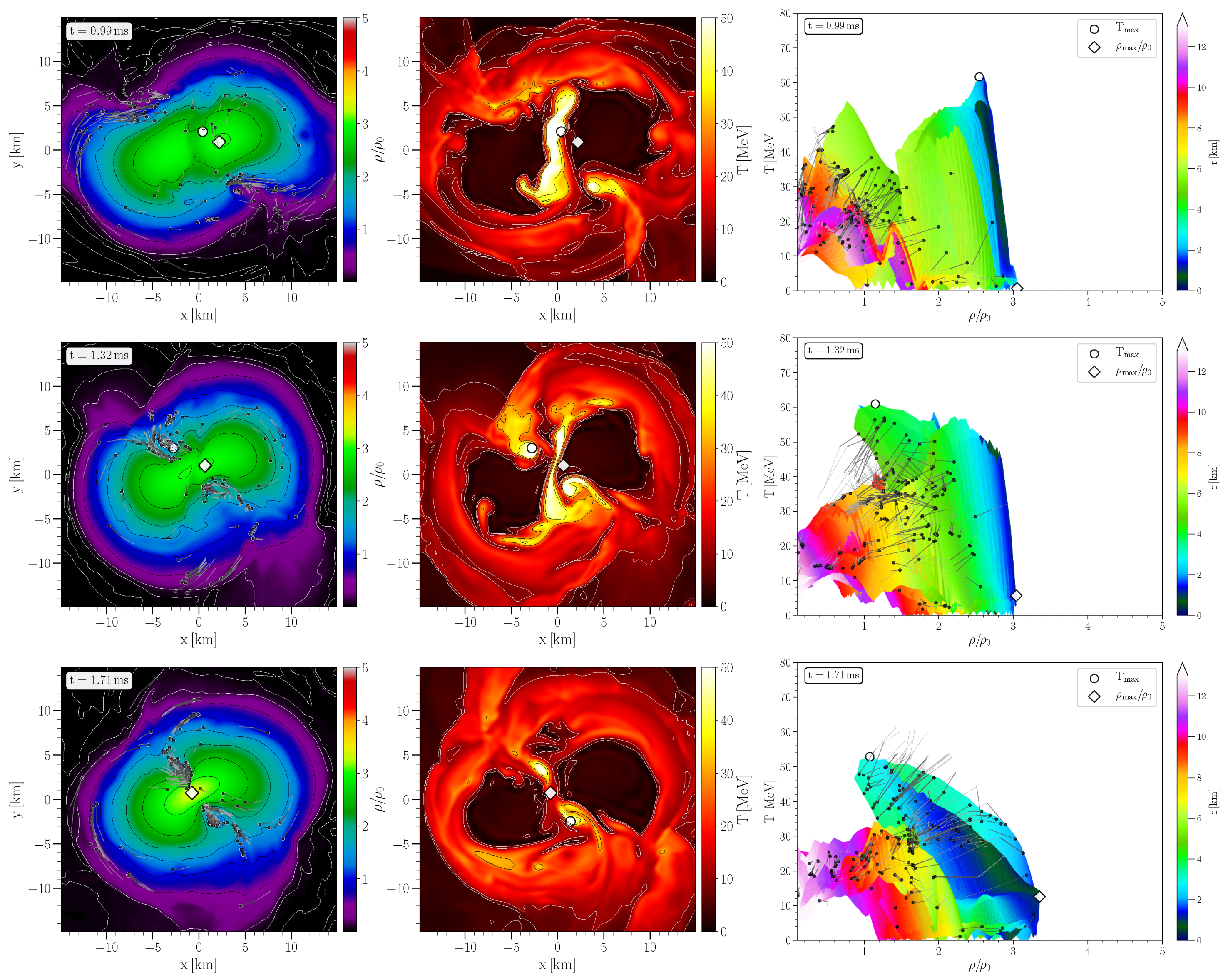
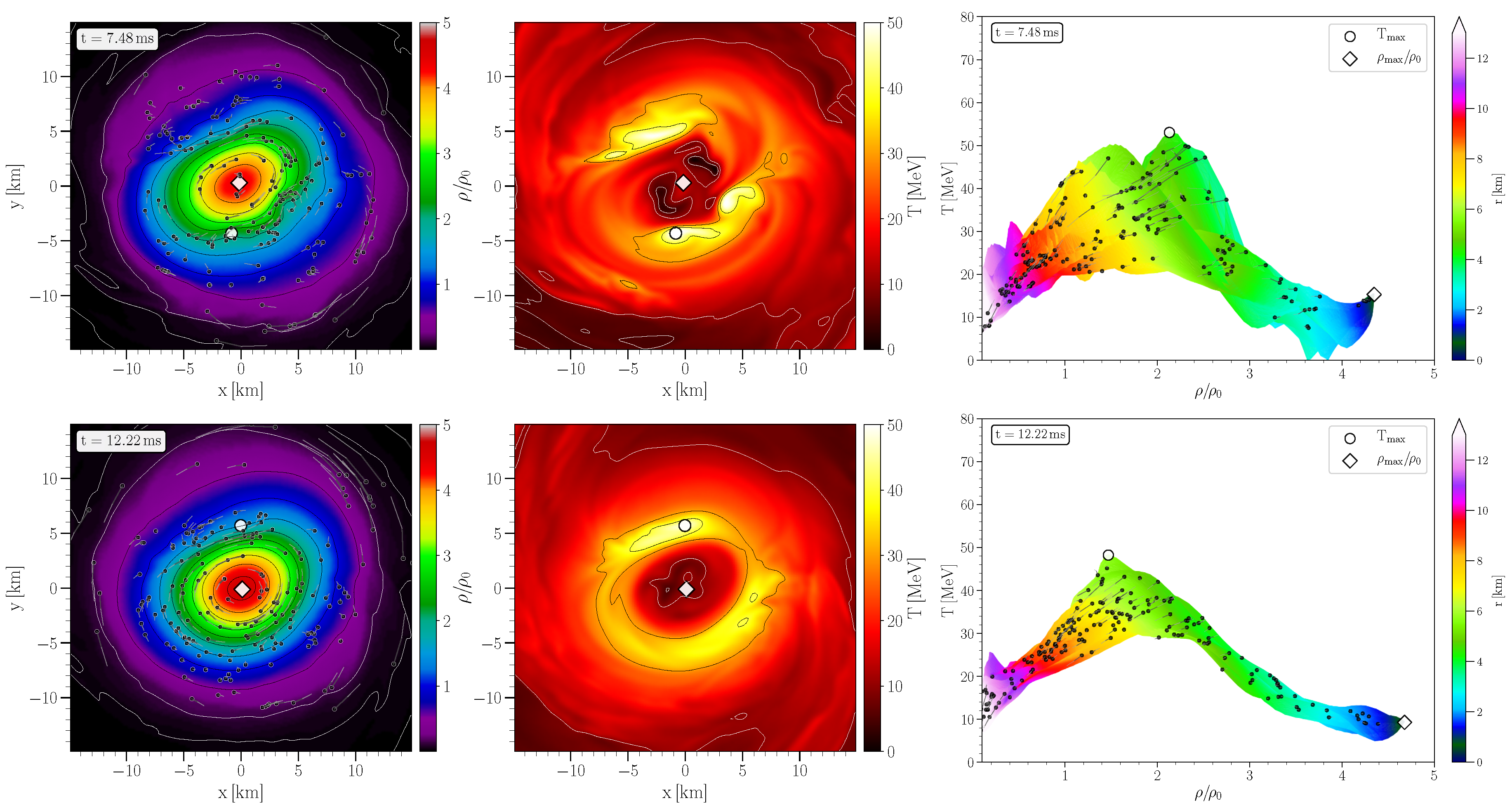
3. Hypermassive Neutron Stars and the QCD Phase Diagram
4. Detecting the Hadron-Quark Phase Transition with Gravitational Waves
5. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gammie, C.F.; et al. [Event Horizon Telescope Collaboration]. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- Akiyama, K.; et al. [Event Horizon Telescope Collaboration]. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. Lett. 2019, 875, L5. [Google Scholar]
- Akiyama, K.; et al. [Event Horizon Telescope Collaboration]. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. Lett. 2019, 875, L6. [Google Scholar]
- Abbott, B.P.; et al. [The LIGO Scientific Collaboration and Virgo Collaboration]. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; et al. [The LIGO Scientific Collaboration and Virgo Collaboration]. GWTC-1: A gravitational-wave transient catalog of compact binary mergers observed by LIGO and Virgo during the first and second observing runs. arXiv 2018, arXiv:1811.12907. [Google Scholar]
- Abbott, B.P.; et al. [The LIGO Scientific Collaboration and Virgo Collaboration]. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; et al. [The LIGO Scientific Collaboration and Virgo Collaboration]. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Troja, E.; Piro, L.; van Eerten, H.; Wollaeger, R.T.; Im, M.; Fox, O.D.; Butler, N.R.; Cenko, S.B.; Sakamoto, T.; Fryer, C.L.; et al. The X-ray counterpart to the gravitational-wave event GW170817. Nature 2017, 551, 71–74. [Google Scholar] [CrossRef]
- Abbott, B.P.; et al. [The LIGO Scientific Collaboration, Virgo Collaboration, Gamma-Ray Burst Monitor and INTEGRAL]. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Blanchet, L. Gravitational Radiation from Post-Newtonian Sources and Inspiralling Compact Binaries. Living Rev. Relat. 2006, 9, 2. [Google Scholar] [CrossRef]
- Schäfer, G.; Jaranowski, P. Hamiltonian formulation of general relativity and post-Newtonian dynamics of compact binaries. Living Rev. Relat. 2018, 21, 7. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Chapter The Effective-One-Body Approach to the General Relativistic Two Body Problem. In Astrophysical Black Holes; Springer International Publishing: Cham, Switzerland, 2016; pp. 273–312. [Google Scholar]
- Bohé, A.; Shao, L.; Taracchini, A.; Buonanno, A.; Babak, S.; Harry, I.W.; Hinder, I.; Ossokine, S.; Pürrer, M.; Raymond, V. Improved effective-one-body model of spinning, nonprecessing binary black holes for the era of gravitational-wave astrophysics with advanced detectors. Phys. Rev. D 2017, 95, 044028. [Google Scholar]
- Rezzolla, L.; Giacomazzo, B.; Baiotti, L.; Granot, J.; Kouveliotou, C.; Aloy, M.A. The Missing Link: Merging Neutron Stars Naturally Produce Jet-like Structures and Can Power Short Gamma-ray Bursts. Astrophys. J. Lett. 2011, 732, L6. [Google Scholar] [CrossRef]
- Drout, M.R.; Piro, A.L.; Shappee, B.J.; Kilpatrick, C.D.; Simon, J.D.; Contreras, C.; Coulter, D.A.; Foley, R.J.; Siebert, M.R.; Morrell, N.; et al. Light curves of the neutron star merger GW170817/SSS17a: Implications for r-process nucleosynthesis. Science 2017, 358, 1570–1574. [Google Scholar] [CrossRef] [PubMed]
- Bovard, L.; Martin, D.; Guercilena, F.; Arcones, A.; Rezzolla, L.; Korobkin, O. On r-process nucleosynthesis from matter ejected in binary neutron star mergers. Phys. Rev. D 2017, 96, 124005. [Google Scholar] [CrossRef]
- Hanauske, M.; Takami, K.; Bovard, L.; Rezzolla, L.; Font, J.A.; Galeazzi, F.; Stöcker, H. Rotational properties of hypermassive neutron stars from binary mergers. Phys. Rev. D 2017, 96, 043004. [Google Scholar] [CrossRef]
- Hanauske, M.; Steinheimer, J.; Bovard, L.; Mukherjee, A.; Schramm, S.; Takami, K.; Papenfort, J.; Wechselberger, N.; Rezzolla, L.; Stöcker, H. Concluding Remarks: Connecting Relativistic Heavy Ion Collisions and Neutron Star Mergers by the Equation of State of Dense Hadron- and Quark Matter as signalled by Gravitational Waves. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 878, p. 012031. [Google Scholar]
- Hanauske, M.; Yilmaz, Z.S.; Mitropoulos, C.; Rezzolla, L.; Stöcker, H. Gravitational waves from binary compact star mergers in the context of strange matter. In Proceedings of the 17th International Conference on Strangeness in Quark Matter (SQM 2017), Utrecht, The Netherlands, 10–15 July 2017; p. 20004. [Google Scholar]
- Alford, M.G.; Bovard, L.; Hanauske, M.; Rezzolla, L.; Schwenzer, K. Viscous Dissipation and Heat Conduction in Binary Neutron-Star Mergers. Phys. Rev. Lett. 2018, 120, 041101. [Google Scholar] [CrossRef]
- Hanauske, M.; Bovard, L. Neutron star mergers in the context of the hadron-quark phase transition. J. Astrophys. Astron. 2018, 39, 45. [Google Scholar] [CrossRef]
- Hanauske, M.; Steinheimer, J.; Motornenko, A.; Vovchenko, V.; Bovard, L.; Most, E.; Papenfort, L.; Schramm, S.; Stöcker, H. Neutron Star Mergers: Probing the EoS of Hot, Dense Matter by Gravitational Waves. Particles 2019, 2, 4. [Google Scholar] [CrossRef]
- Hanauske, M.; Bovard, L.; Steinheimer, J.; Motornenko, A.; Vovchenko, V.; Schramm, S.; Dexheimer, V.; Papenfort, J.; Most, E.R.; Stöcker, H. MAGIC—How MAtter’s extreme phases can be revealed in Gravitational wave observations and in relativistic heavy Ion Collision experiments. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019. [Google Scholar]
- The LIGO Scientific Collaboration; the Virgo Collaboration. Tests of General Relativity with GW170817. arXiv 2018, arXiv:1811.00364. [Google Scholar]
- Creminelli, P.; Vernizzi, F. Dark Energy after GW170817 and GRB170817A. Phys. Rev. Lett. 2017, 119, 251302. [Google Scholar] [CrossRef] [PubMed]
- Copeland, E.J.; Kopp, M.; Padilla, A.; Saffin, P.M.; Skordis, C. Dark Energy after GW170817 Revisited. Phys. Rev. Lett. 2019, 122, 061301. [Google Scholar] [CrossRef]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-star Radius Constraints from GW170817 and Future Detections. Astrophys. J. Lett. 2017, 850, L34. [Google Scholar] [CrossRef]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. Astrophys. J. Lett. 2018, 852, L25. [Google Scholar] [CrossRef]
- Margalit, B.; Metzger, B. Constraining the Maximum Mass of Neutron Stars From Multi-Messenger Observations of GW170817. arXiv 2017, arXiv:1710.05938. [Google Scholar] [CrossRef]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. arXiv 2017, arXiv:1712.00451. [Google Scholar] [CrossRef]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New Constraints on Radii and Tidal Deformabilities of Neutron Stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Constraining the nuclear equation of state with GW170817. arXiv 2018, arXiv:1804.08583. [Google Scholar]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GW170817: Measurements of neutron star radii and equation of state. arXiv 2018, arXiv:1805.11581. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. Properties of the binary neutron star merger GW170817. arXiv 2018, arXiv:1805.11579. [Google Scholar] [CrossRef]
- Christian, J.E.; Zacchi, A.; Schaffner-Bielich, J. Signals in the tidal deformability for phase transitions in compact stars with constraints from GW170817. arXiv 2018, arXiv:1809.03333. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. Lett. 2018, 852, L29. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; the Virgo Collaboration. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Raithel, C.A.; Özel, F.; Psaltis, D. Tidal Deformability from GW170817 as a Direct Probe of the Neutron Star Radius. Astrophys. J. Lett. 2018, 857, L23. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef] [PubMed]
- Montaña, G.; Tolós, L.; Hanauske, M.; Rezzolla, L. Constraining twin stars with GW170817. Phys. Rev. D 2019, 99, 103009. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; The Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. Search for post-merger gravitational waves from the remnant of the binary neutron star merger GW170817. arXiv 2017, arXiv:1710.09320. [Google Scholar]
- Baiotti, L.; Rezzolla, L. Binary neutron-star mergers: A review of Einstein’s richest laboratory. Rep. Prog. Phys. 2017, 80, 096901. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Hotokezaka, K.; Fromm, S.A.; Bernuzzi, S.; Roberts, L.F. Binary Neutron Star Mergers: Mass Ejection, Electromagnetic Counterparts, and Nucleosynthesis. Astrophys. J. Lett. 2018, 869, 130. [Google Scholar] [CrossRef]
- Takami, K.; Rezzolla, L.; Baiotti, L. Spectral properties of the post-merger gravitational-wave signal from binary neutron stars. Phys. Rev. D 2015, 91, 064001. [Google Scholar] [CrossRef]
- Clark, J.A.; Bauswein, A.; Stergioulas, N.; Shoemaker, D. Observing gravitational waves from the post-merger phase of binary neutron star coalescence. Class. Quantum Gravity 2016, 33, 085003. [Google Scholar] [CrossRef]
- Chatziioannou, K.; Clark, J.A.; Bauswein, A.; Millhouse, M.; Littenberg, T.B.; Cornish, N. Inferring the post-merger gravitational wave emission from binary neutron star coalescences. Phys. Rev. D 2017, 96, 124035. [Google Scholar] [CrossRef]
- Torres-Rivas, A.; Chatziioannou, K.; Bauswein, A.; Clark, J.A. Observing the post-merger signal of GW170817-like events with improved gravitational-wave detectors. Phys. Rev. D 2019, 99, 044014. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Dietrich, T.; Tichy, W.; Brügmann, B. Mergers of binary neutron stars with realistic spin. Phys. Rev. D 2014, 89, 104021. [Google Scholar] [CrossRef]
- Kastaun, W.; Ciolfi, R.; Endrizzi, A.; Giacomazzo, B. Structure of Stable Binary Neutron Star Merger Remnants: Role of Initial Spin. Phys. Rev. D 2016, 96, 043019. [Google Scholar] [CrossRef]
- Dietrich, T.; Bernuzzi, S.; Ujevic, M.; Tichy, W. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of the stars’ rotation. Phys. Rev. D 2017, 95, 044045. [Google Scholar] [CrossRef]
- Chaurasia, S.V.; Dietrich, T.; Johnson-McDaniel, N.K.; Ujevic, M.; Tichy, W.; Brügmann, B. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of large eccentricities. Phys. Rev. D 2018, 98, 104005. [Google Scholar] [CrossRef]
- Papenfort, L.J.; Gold, R.; Rezzolla, L. Dynamical ejecta and nucleosynthetic yields from eccentric binary neutron-star mergers. Phys. Rev. D 2018, 98, 104028. [Google Scholar] [CrossRef]
- Dietrich, T.; Ujevic, M.; Tichy, W.; Bernuzzi, S.; Brügmann, B. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of the mass ratio. Phys. Rev. D 2017, 95, 024029. [Google Scholar] [CrossRef]
- Dietrich, T.; Ujevic, M. Modeling dynamical ejecta from binary neutron star mergers and implications for electromagnetic counterparts. Class. Quantum Gravity 2017, 34, 105014. [Google Scholar] [CrossRef]
- Siegel, D.M.; Ciolfi, R. Electromagnetic Emission from Long-lived Binary Neutron Star Merger Remnants. I. Formulation of the Problem. Astrophys. J. 2016, 819, 14. [Google Scholar] [CrossRef]
- Siegel, D.M.; Ciolfi, R. Electromagnetic Emission from Long-lived Binary Neutron Star Merger Remnants. II. Lightcurves and Spectra. Astrophys. J. 2016, 819, 15. [Google Scholar] [CrossRef]
- Bauswein, A.; Stergioulas, N. Semi-analytic derivation of the threshold mass for prompt collapse in binary neutron-star mergers. Mon. Not. R. Astron. Soc. 2017, 471, 4956–4965. [Google Scholar] [CrossRef]
- Shibata, M.; Kiuchi, K. Gravitational waves from remnant massive neutron stars of binary neutron star merger: Viscous hydrodynamics effects. Phys. Rev. D 2017, 95, 123003. [Google Scholar] [CrossRef]
- Kastaun, W.; Ciolfi, R.; Giacomazzo, B. Structure of stable binary neutron star merger remnants: A case study. Phys. Rev. D 2016, 94, 044060. [Google Scholar] [CrossRef]
- The Einstein Toolkit Consortium. Available online: einsteintoolkit.org (accessed on 20 June 2019).
- Brown, D.; Diener, P.; Sarbach, O.; Schnetter, E.; Tiglio, M. Turduckening black holes: An analytical and computational study. Phys. Rev. D 2009, 79, 044023. [Google Scholar] [CrossRef]
- Löffler, F.; Faber, J.; Bentivegna, E.; Bode, T.; Diener, P.; Haas, R.; Hinder, I.; Mundim, B.C.; Ott, C.D.; Schnetter, E.; et al. The Einstein Toolkit: A Community Computational Infrastructure for Relativistic Astrophysics. Class. Quantum Gravity 2012, 29, 115001. [Google Scholar] [CrossRef]
- Nakamura, T.; Oohara, K.; Kojima, Y. General Relativistic Collapse to Black Holes and Gravitational Waves from Black Holes. Prog. Theor. Phys. Suppl. 1987, 90, 1–218. [Google Scholar] [CrossRef]
- Shibata, M.; Nakamura, T. Evolution of three-dimensional gravitational waves: Harmonic slicing case. Phys. Rev. D 1995, 52, 5428–5444. [Google Scholar] [CrossRef]
- Baumgarte, T.W.; Shapiro, S.L. Numerical integration of Einstein’s field equations. Phys. Rev. D 1999, 59, 024007. [Google Scholar] [CrossRef]
- Alcubierre, M.; Brügmann, B.; Diener, P.; Koppitz, M.; Pollney, D.; Seidel, E.; Takahashi, R. Gauge conditions for long-term numerical black hole evolutions without excision. Phys. Rev. D 2003, 67, 084023. [Google Scholar] [CrossRef]
- Pollney, D.; Reisswig, C.; Rezzolla, L.; Szilágyi, B.; Ansorg, M.; Deris, B.; Diener, P.; Dorband, E.N.; Koppitz, M.; Nagar, A.; et al. Recoil velocities from equal-mass binary black-hole mergers: A systematic investigation of spin-orbit aligned configurations. Phys. Rev. D 2007, 76, 124002. [Google Scholar] [CrossRef]
- Rezzolla, L.; Zanotti, O. Relativistic Hydrodynamics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Font, J.A. Numerical Hydrodynamics and Magnetohydrodynamics in General Relativity. Living Rev. Relat. 2008, 6, 4. [Google Scholar] [CrossRef] [PubMed]
- Radice, D.; Rezzolla, L.; Galeazzi, F. Beyond second-order convergence in simulations of binary neutron stars in full general-relativity. Mon. Not. R. Astron. Soc. L. 2014, 437, L46–L50. [Google Scholar] [CrossRef]
- Radice, D.; Rezzolla, L.; Galeazzi, F. High-order fully general-relativistic hydrodynamics: New approaches and tests. Class. Quantum Gravity 2014, 31, 075012. [Google Scholar] [CrossRef]
- Schnetter, E.; Hawley, S.H.; Hawke, I. Evolutions in 3D numerical relativity using fixed mesh refinement. Class. Quantum Gravity 2004, 21, 1465–1488. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Swesty, F.D. A Generalized Equation of State for Hot, Dense Matter. Nucl. Phys. A 1991, 535, 331–376. [Google Scholar] [CrossRef]
- Bovard, L.; Rezzolla, L. On the use of tracer particles in simulations of binary neutron stars. Class. Quantum Gravity 2017, 34, 215005. [Google Scholar] [CrossRef]
- Rezzolla, L.; Takami, K. Gravitational-wave signal from binary neutron stars: A systematic analysis of the spectral properties. Phys. Rev. D 2016, 93, 124051. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Dexheimer, V.; Hanauske, M.; Schramm, S.; Stöcker, H.; Rezzolla, L. Signatures of quark-hadron phase transitions in general-relativistic neutron-star mergers. arXiv 2018, arXiv:1807.03684. [Google Scholar] [CrossRef]
- Dexheimer, V.A.; Schramm, S. Novel approach to modeling hybrid stars. Phys. Rev. C 2010, 81, 045201. [Google Scholar] [CrossRef]
- Bauswein, A.; Bastian, N.U.F.; Blaschke, D.B.; Chatziioannou, K.; Clark, J.A.; Fischer, T.; Oertel, M. Identifying a first-order phase transition in neutron star mergers through gravitational waves. arXiv 2018, arXiv:1809.01116. [Google Scholar] [CrossRef] [PubMed]
- Fischer, T.; Bastian, N.U.F.; Wu, M.R.; Typel, S.; Klähn, T.; Blaschke, D.B. High-density phase transition paves the way for supernova explosions of massive blue-supergiant stars. arXiv 2017, arXiv:1712.08788. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanauske, M.; Bovard, L.; Most, E.; Papenfort, J.; Steinheimer, J.; Motornenko, A.; Vovchenko, V.; Dexheimer, V.; Schramm, S.; Stöcker, H. Detecting the Hadron-Quark Phase Transition with Gravitational Waves. Universe 2019, 5, 156. https://doi.org/10.3390/universe5060156
Hanauske M, Bovard L, Most E, Papenfort J, Steinheimer J, Motornenko A, Vovchenko V, Dexheimer V, Schramm S, Stöcker H. Detecting the Hadron-Quark Phase Transition with Gravitational Waves. Universe. 2019; 5(6):156. https://doi.org/10.3390/universe5060156
Chicago/Turabian StyleHanauske, Matthias, Luke Bovard, Elias Most, Jens Papenfort, Jan Steinheimer, Anton Motornenko, Volodymyr Vovchenko, Veronica Dexheimer, Stefan Schramm, and Horst Stöcker. 2019. "Detecting the Hadron-Quark Phase Transition with Gravitational Waves" Universe 5, no. 6: 156. https://doi.org/10.3390/universe5060156
APA StyleHanauske, M., Bovard, L., Most, E., Papenfort, J., Steinheimer, J., Motornenko, A., Vovchenko, V., Dexheimer, V., Schramm, S., & Stöcker, H. (2019). Detecting the Hadron-Quark Phase Transition with Gravitational Waves. Universe, 5(6), 156. https://doi.org/10.3390/universe5060156





