Impact of the Nuclear Equation of State on the Stability of Hybrid Neutron Stars
Abstract
1. Introduction
2. vBag
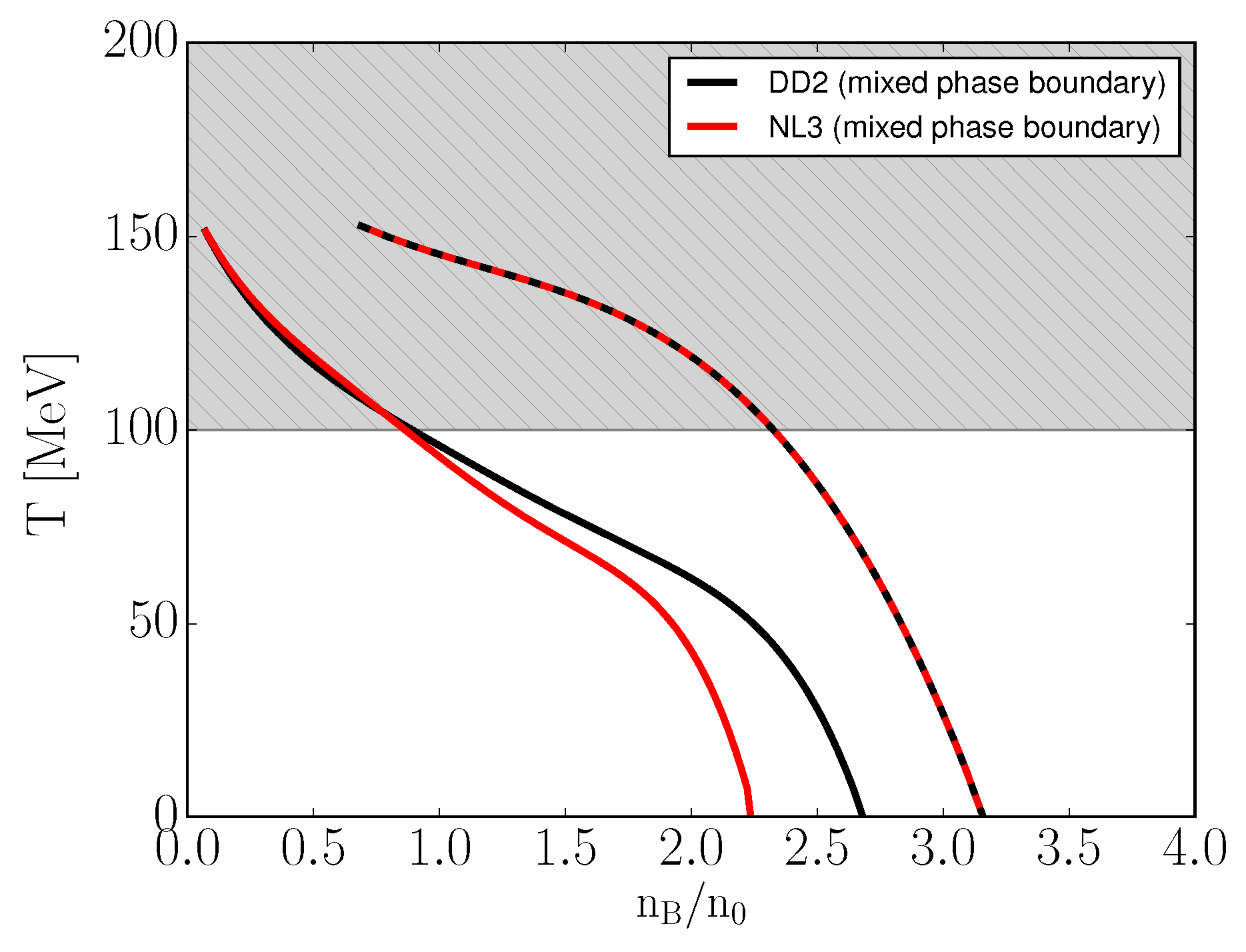
3. The Phase Diagram
4. Hybrid Neutron Stars
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roberts, C.D. Three Lectures on Hadron Physics. J. Phys. Conf. Ser. 2016, 706, 022003. [Google Scholar] [CrossRef]
- Fodor, Z.; Katz, S.D. Critical point of QCD at finite T and mu, lattice results for physical quark masses. JHEP 2004, 2004, 050. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Szabo, K.K. The Order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef] [PubMed]
- Bazavov, A.; Ding, H.-T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Maezawa, Y.; Mukherjee, S.; Ohno, H.; Petreczky, P.; et al. The QCD Equation of State to from Lattice QCD. Phys. Rev. D 2017, 95, 054504. [Google Scholar] [CrossRef]
- Guenther, J.N.; Bellwied, R.; Borsanyi, S.; Fodor, Z.; Katz, S.D.; Pasztor, A.; Ratti, C.; Szabó, K.K. The QCD equation of state at finite density from analytical continuation. Nucl. Phys. A 2017, 967, 720–723. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.-T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Karthik, N.; Laermann, E.; Lahiri, A.; Larsen, R.; Li, S.-T.; et al. Chiral crossover in QCD at zero and non-zero chemical potentials. arXiv 2018, arXiv:1812.08235. [Google Scholar] [CrossRef]
- Bastian, N.U.F.; Blaschke, D.; Fischer, T.; Röpke, G. Towards a Unified Quark-Hadron Matter Equation of State for Applications in Astrophysics and Heavy-Ion Collisions. Universe 2018, 4, 67. [Google Scholar] [CrossRef]
- Dexheimer, V.A.; Schramm, S. A Novel Approach to Model Hybrid Stars. Phys. Rev. C 2010, 81, 045201. [Google Scholar] [CrossRef]
- Steinheimer, J.; Schramm, S.; Stocker, H. An Effective chiral Hadron-Quark Equation of State. J. Phys. G 2011, 38, 035001. [Google Scholar] [CrossRef]
- Marczenko, M.; Sasaki, C. Net-baryon number fluctuations in the Hybrid Quark-Meson-Nucleon model at finite density. Phys. Rev. D 2018, 97, 036011. [Google Scholar] [CrossRef]
- Marczenko, M.; Blaschke, D.; Redlich, K.; Sasaki, C. Chiral symmetry restoration by parity doubling and the structure of neutron stars. Phys. Rev. D 2018, 98, 103021. [Google Scholar] [CrossRef]
- Cleymans, J.; Gavai, R.V.; Suhonen, E. Quarks and Gluons at High Temperatures and Densities. Phys. Rept. 1986, 130, 217. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Fischer, T.; Bastian, N.U.; Blaschke, D.; Cierniak, M.; Hempel, M.; Klähn, T.; Martínez-Pinedo, G.; Newton, W.G.; Röpke, G.; Typel, S. The state of matter in simulations of core-collapse supernovae—Reflections and recent developments. Publ. Astron. Soc. Aust. 2017, 34, 67. [Google Scholar] [CrossRef]
- Farhi, E.; Jaffe, R.L. Strange Matter. Phys. Rev. D 1984, 30, 2379. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Klähn, T.; Fischer, T. Vector interaction enhanced bag model for astrophysical applications. Astrophys. J. 2015, 810, 134. [Google Scholar] [CrossRef]
- Klähn, T.; Fischer, T.; Hempel, M. Simultaneous chiral symmetry restoration and deconfinement—Consequences for the QCD phase diagram. Astrophys. J. 2017, 836, 89. [Google Scholar] [CrossRef]
- Fischer, T.; Klähn, T.; Hempel, M. Consequences of simultaneous chiral symmetry breaking and deconfinement for the isospin symmetric phase diagram. Eur. Phys. J. A 2016, 52, 225. [Google Scholar] [CrossRef]
- Cierniak, M.; Klähn, T.; Fischer, T.; Bastian, N.U. Vector-Interaction-Enhanced Bag Model. Universe 2018, 4, 30. [Google Scholar] [CrossRef]
- Qin, S.x.; Chang, L.; Chen, H.; Liu, Y.x.; Roberts, C.D. Phase diagram and critical endpoint for strongly-interacting quarks. Phys. Rev. Lett. 2011, 106, 172301. [Google Scholar] [CrossRef] [PubMed]
- Fischer, C.S.; Luecker, J.; Welzbacher, C.A. Phase structure of three and four flavor QCD. Phys. Rev. D 2014, 90, 034022. [Google Scholar] [CrossRef]
- Rusnak, J.J.; Furnstahl, R.J. Two point fermion correlation functions at finite density. Z. Phys. A Hadrons Nucl. 1995, 352, 345–350. [Google Scholar] [CrossRef]
- Roberts, C.D.; Schmidt, S.M. Dyson-Schwinger equations: Density, temperature and continuum strong QCD. Prog. Part. Nucl. Phys. 2000, 45, S1–S103. [Google Scholar] [CrossRef]
- Gutierrez-Guerrero, L.X.; Bashir, A.; Cloet, I.C.; Roberts, C.D. Pion form factor from a contact interaction. Phys. Rev. C 2010, 81, 065202. [Google Scholar] [CrossRef]
- Munczek, H.J. Dynamical chiral symmetry breaking, Goldstone’s theorem and the consistency of the Schwinger-Dyson and Bethe-Salpeter Equations. Phys. Rev. D 1995, 52, 4736–4740. [Google Scholar] [CrossRef]
- Bender, A.; Roberts, C.D.; Von Smekal, L. Goldstone theorem and diquark confinement beyond rainbow ladder approximation. Phys. Lett. B 1996, 380, 7–12. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rept. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Ebert, D.; Feldmann, T.; Reinhardt, H. Extended NJL model for light and heavy mesons without q- anti-q thresholds. Phys. Lett. B 1996, 388, 154–160. [Google Scholar] [CrossRef]
- Typel, S.; Röpke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Konig, J.; Ring, P. A New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997, 55, 540–543. [Google Scholar] [CrossRef]
- Motohiro, Y.; Kim, Y.; Harada, M. Asymmetric nuclear matter in a parity doublet model with hidden local symmetry. Phys. Rev. C 2015, 92, 025201. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the Symmetry Parameters of the Nuclear Interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Kortelainen, M.; McDonnell, J.; Nazarewicz, W.; Reinhard, P.G.; Sarich, J.; Schunck, N.; Stoitsov, M.V.; Wild, S.M. Nuclear energy density optimization: Large deformations. Phys. Rev. C 2012, 85, 024304. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- Guillot, S. First results on the equation of state constraints from NICER. In Proceedings of the Neutron Stars and Their Environments Workshop MODE-SNR-PWN, Orléans, France, 8–10 April 2019. [Google Scholar]
- Arzoumanian, Z.; Adam, B.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year Data Set: High-precision timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. 2018, 235, 37. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. A very massive neutron star: Relativistic Shapiro delay measurements of PSR J0740+6620. arXiv 2019, arXiv:1904.06759. [Google Scholar]
- Bauswein, A.; Bastian, N.U.F.; Blaschke, D.B.; Chatziioannou, K.; Clark, J.A.; Fischer, T.; Oertel, M. Identifying a first-order phase transition in neutron star mergers through gravitational waves. Phys. Rev. Lett. 2019, 122, 061102. [Google Scholar] [CrossRef]
- Benic, S.; Blaschke, D.; Alvarez-Castillo, D.E.; Fischer, T.; Typel, S. A new quark-hadron hybrid equation of state for astrophysics - I. High-mass twin compact stars. Astron. Astrophys. 2015, 577, A40. [Google Scholar] [CrossRef]
- Schaffner-Bielich, J.; Greiner, C.; Diener, A.; Stoecker, H. Detectability of strange matter in heavy ion experiments. Phys. Rev. C 1997, 55, 3038–3046. [Google Scholar] [CrossRef]
- Weissenborn, S.; Chatterjee, D.; Schaffner-Bielich, J. Hyperons and massive neutron stars: Vector repulsion and SU(3) symmetry. Phys. Rev. C 2012, 85, 065802. [Google Scholar] [CrossRef]
- Fortin, M.; Oertel, M.; Providência, C. Hyperons in hot dense matter: What do the constraints tell us for equation of state? Publ. Astron. Soc. Austral. 2018, 35, 44. [Google Scholar] [CrossRef]
- Witten, E. Cosmic Separation of Phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L.; Schaeffer, R. Strange quark stars. Astron. Astrophys. 1986, 160, 121–128. [Google Scholar]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cierniak, M.; Fischer, T.; Bastian, N.-U.; Klähn, T.; Salinas, M. Impact of the Nuclear Equation of State on the Stability of Hybrid Neutron Stars. Universe 2019, 5, 186. https://doi.org/10.3390/universe5080186
Cierniak M, Fischer T, Bastian N-U, Klähn T, Salinas M. Impact of the Nuclear Equation of State on the Stability of Hybrid Neutron Stars. Universe. 2019; 5(8):186. https://doi.org/10.3390/universe5080186
Chicago/Turabian StyleCierniak, Mateusz, Tobias Fischer, Niels-Uwe Bastian, Thomas Klähn, and Marc Salinas. 2019. "Impact of the Nuclear Equation of State on the Stability of Hybrid Neutron Stars" Universe 5, no. 8: 186. https://doi.org/10.3390/universe5080186
APA StyleCierniak, M., Fischer, T., Bastian, N.-U., Klähn, T., & Salinas, M. (2019). Impact of the Nuclear Equation of State on the Stability of Hybrid Neutron Stars. Universe, 5(8), 186. https://doi.org/10.3390/universe5080186






