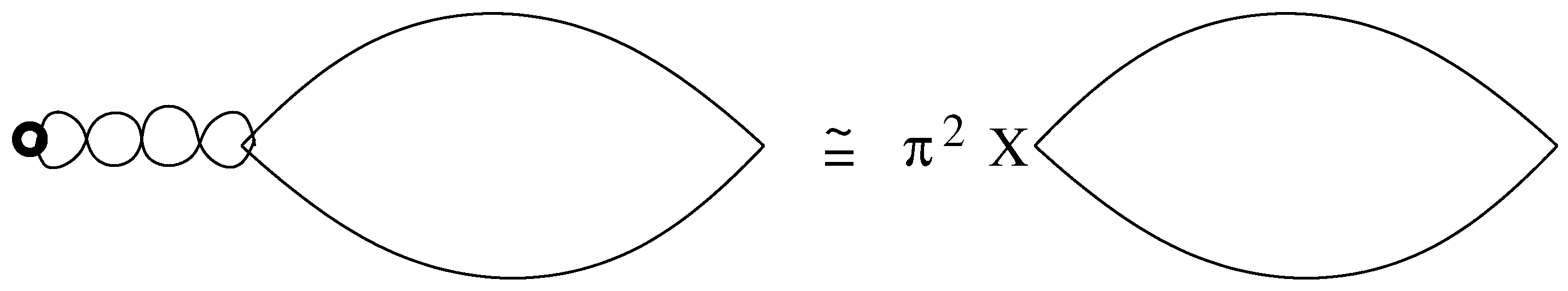Review of Charmonium and Bottomonium Quark State Production via Relativistic Heavy Ion Collisions

Abstract

This is a review of the production of heavy quark states via relativistic heavy ion collisions in RHIC. The heavy quarks here are c, charm quark, and b, bottom quark. The states are charmonium meson states $\Psi \left(nS\right)$, with n = 1,2 and upsilon meson states ${\rm Y}\left(mS\right)$, with m = 1,2,3. Quantum Chromodynamics (QCD) sum rules were used to derive the result that the $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ are mixed hybrid states, which increase their production cross sections. We also review the $\Psi \left(nS\right)$ and ${\rm Y}\left(mS\right)$ production cross sections via Cu-Cu and Au-Au collisions, which are very important for this review of the production of heavy quark states in RHIC. The possible detection of the Quark Gluon Plasma (QGP) is also reviewed.

1. Introduction

First we review Quantum Chromodynamics (QCD).

The elementary fermions, with quantum spin 1/2, are quarks. There are three generations of quarks (u,d), (c,s), (t,b). The u(up), d(down), and s(strange) quarks have small masses and are not needed in this review. The t(top) quark has a very large mass, with $m_t\simeq$ 173 GeV, while $m_b\simeq$ 4.18 GeV [1].

The elementary boson, the gluon (g), has quantum spin 1, like the photon. The photon has an electromagnetic interaction U(1) with quarks while the gluon has a strong interaction SU(3) with quarks. Since the strong interaction is approximately 100 times larger than the electromagnetic interaction, perturbation theory does not work. Therefore Feynman diagrams used for Quantum Electrodynamics cannot be used for Quantum Chromodynamics as the higher order diagrams are larger than the lower order diagrams [2].

One nonperturbative QCD method involves Lattice Gauge Theory. The article by Andreas S. Kronfelld [3] gives a detailed description of how Lattice Gauge Theory can calculate QCD interactions using computers.

Another nonperturbative theory, which is used in our review of mixed hybrid heavy quark mesons, is the method of QCD sum rules. This method, developed by M.A. Shifman, A.I. Vainstein, and V.I. Zakharov [4], does not require large computers.

Standard mesons consist of a quark and antiquark:$|q\overline{q}>$. A top quark meson $|t\overline{t}>$ is so massive that none have been detected. The charmonium mesons are $\Psi \left(nS\right)$, with n = 1,2. The upsilon mesons are ${\rm Y}\left(mS\right)$, with m = 1, 2, 3. It was the method of QCD sum rules that showed that the $\Psi \left(2S\right)$ charmonium quark meson and the ${\rm Y}\left(3S\right)$ bottomonium quark mesons are mixed hybrid states, while all the other $\Psi \left(nS\right)$ and ${\rm Y}\left(mS\right)$ are standard charmonium and bottomonium meson states. QCD, charmonium, bottomonium meson states were reviewed by N. Brambilla et.al. [5] and recent theoretical progress by A. Rothkopf [6].

The production of $\Psi \left(nS\right)$ and ${\rm Y}\left(mS\right)$ cross sections via Cu-Cu and Au-Au collisions is an extension of the theory [7] for p-p to Cu-Cu and Au-Au collisions. In Ref [7] the color octet model [7,8,9,10] was used.

In Section 4, it is reviewed that experiments confirmed that the $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ are mixed normal and hybrid states by the ratios of $\Psi \left(2S\right)$ to $J/\Psi \left(1S\right)$ and ${\rm Y}\left(3S\right)$ to ${\rm Y}\left(1S\right)$ cross sections.

In Section 5, heavy quark state production in the color octet model via A-A collisions is reviewed, with the gluon distribution function $f_g$ needed for RHIC. The heavy quarks are c, charm quark, and b, bottom quark. The states are charmonium states $\Psi \left(nS\right)$, with n = 1, 2 and upsilon states ${\rm Y}\left(mS\right)$, with m = 1, 2, 3. The $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ are mixed hybrid states, which increased their production cross sections. We also review the $\Psi \left(nS\right)$ and ${\rm Y}\left(mS\right)$ production cross sections via Cu-Cu and Au-Au collisions, which is very important for this review of the production of heavy quark states via RHIC.

In Section 6 Cosmological Phase Transitions and the possible detection of the Quark Gluon Plasma (QGP) via RHIC by the production of heavy quark hybrid states are reviewed.

2. Quantum Chromodynamics (QCD)

In Quantum Chromodynamics (QCD) the elementary particles are quarks (Fermions) and gluons (Bosons).

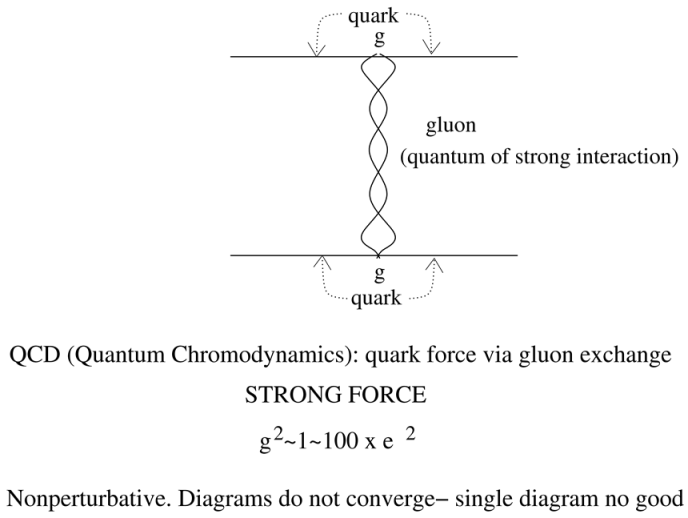
Strong interactions are produced by quarks exchanging gluons, as illustrated in the figure below.

Color: Quarks have three colors. Color is due to the strong interaction, as electric charge is due to the electromagnetic interaction. A quark and antiquark can form a gluon, which has color.

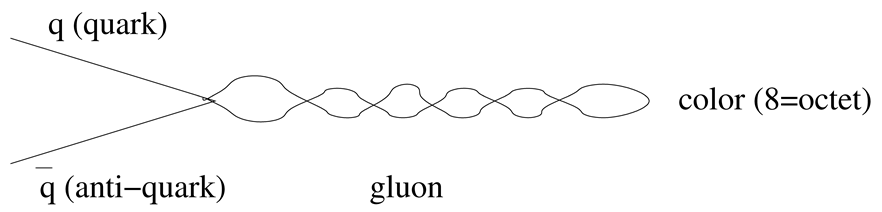
Note that particles with color, like gluons and quarks, cannot move freely in space. Particles which can move freely are baryons, like the proton and neutron, and mesons, which have no total color. The heavy quarks in this review are charm c and bottom b.

Light mesons, such as the $\pi$, consist of light quarks $u,d$ and antiquarks $\overline{u},\overline{d}$. We do not need them in this Review.

3. Review of Mixed Hybrid Heavy Quark Mesons and the Color Octet Model

In this section the hybrid heavy quark mesons and the color octet models are reviewed.

The Method of QCD Sum Rules and Mixed Hybrid Heavy Quark Mesons

The starting point of the method of QCD sum rules [4] for finding the mass of a state A is the correlator,

$${\Pi }^A\left(x\right)=⟨|T\left[J_A\left(x\right)J_A\left(0\right)\right]|⟩,$$

(1)

with $|⟩$ the vacuum state and the current $J_A\left(x\right)$ creating the states with quantum numbers A:

$$J_A\left(x\right)|⟩=c_A|A⟩+\sum _n{c}_n|n;A⟩,$$

(2)

where $|A⟩$ is the lowest energy state with quantum numbers A, and the states $|n;A⟩$ are higher energy states.

The QCD sum rule is obtained by evaluating ${\Pi }^A$ in two ways. First, after a Fourier transform to momentum space, a dispersion relation gives the left-hand side (lhs) of the sum rule:

$$\Pi {\left(q\right)}_{\mathrm{lhs}}^A=\frac{\mathrm{Im}{\Pi }^A\left(M_A\right)}{\pi (M_A^2-q^2)}+{\int }_{s_o}^{\infty }ds\frac{\mathrm{Im}{\Pi }^A\left(s\right)}{\pi (s-q^2)}$$

(3)

where $M_A$ is the mass of the state A (assuming zero width) and $s_o$ is the start of the continuum.

Next ${\Pi }^A\left(q\right)$ is evaluated by an operator product expansion (O.P.E.), giving the right-hand side (rhs) of the sum rule

$$\Pi {\left(q\right)}_{\mathrm{rhs}}^A=\sum _k{c}_k\left(q\right)⟨0|{\mathcal{O}}_k|0⟩,$$

(4)

where $c_k\left(q\right)$ are the Wilson coefficients and $⟨0\left|{\mathcal{O}}_k\right|0⟩$ are gauge invariant operators.

A Borel transform, $\mathcal{B}$, replaces the q variable by the Borel mass, $M_B$,

$$\mathcal{B}=\underset{q^2,n\to \infty }{lim}\frac{1}{(n-1)!}{\left(q^2\right)}^n{(-\frac{d}{d{q}^2})}^n{|}_{q^2/n=M_B^2}.$$

(5)

The final QCD sum rule has the form

$$\mathcal{B}\Pi {\left(q\right)}_{\mathrm{lhs}}^A=\mathcal{B}\Pi {\left(q\right)}_{\mathrm{rhs}}^A.$$

(6)

Using the method of QCD sum rules it was shown [11] that the $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ are approximately 50-50 mixtures of standard quarkonium and hybrid quarkonium states:

$$\begin{gathered} |\Psi \left(2S\right)>=-0.7|c\overline{c}\left(2S\right)>+\sqrt{1-0.5}|c\overline{c}g\left(2S\right)> \\ |{\rm Y}\left(3S\right)>=-0.7|b\overline{b}\left(3S\right)>+\sqrt{1-0.5}|b\overline{b}g\left(3S\right)>, \end{gathered}$$

(7)

with a 10% uncertainty [12] in the QCD sum rule estimate of the mixing probabilitiy, while

$$\begin{gathered} |J/\Psi \left(1S\right)>=|c\overline{c}\left(1S\right)> \\ |{\rm Y}\left(nS\right)>=|b\overline{b}\left(nS\right)>, \end{gathered}$$

(8)

for $n\ne 3$.

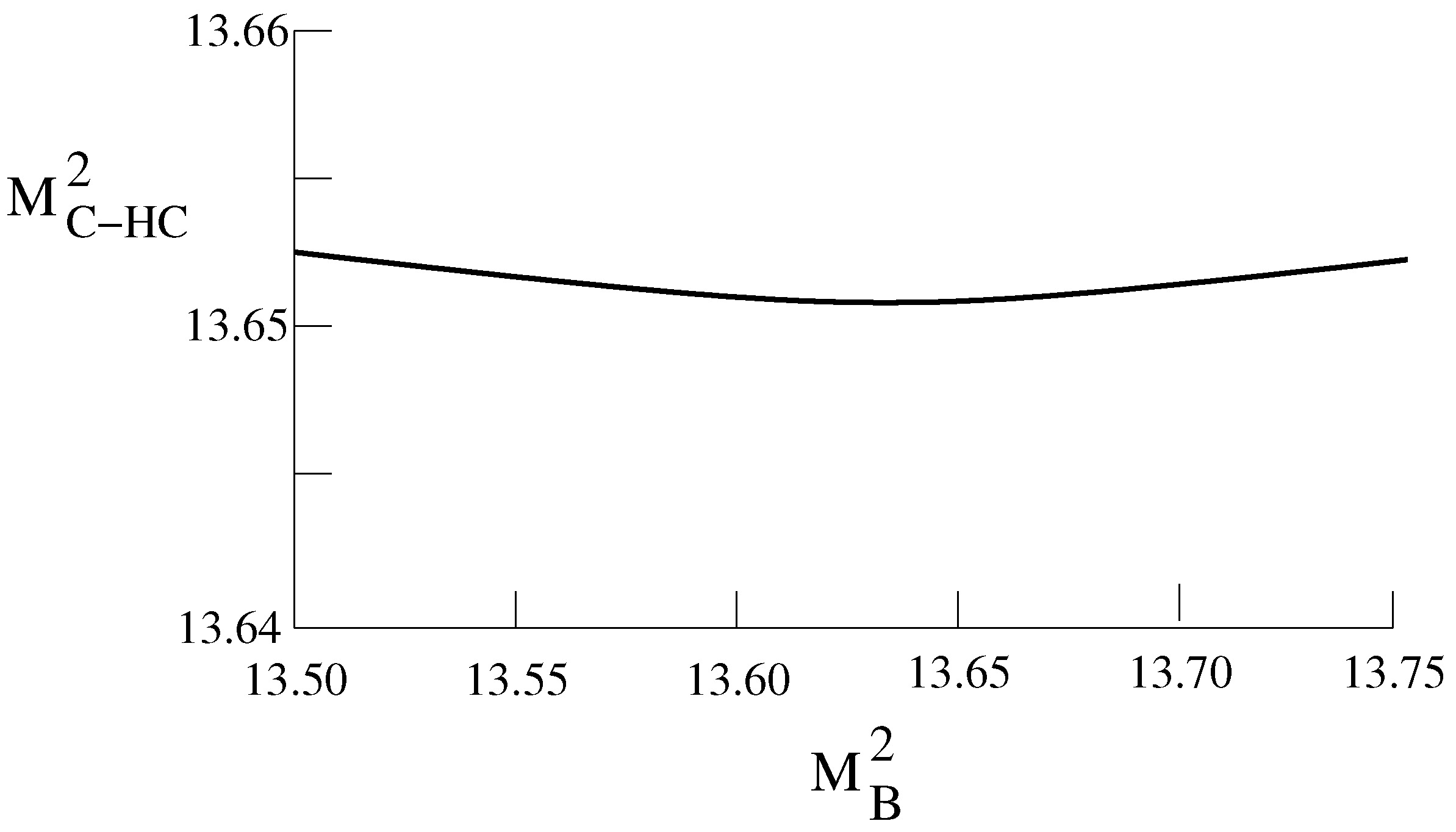
For the $\Psi \left(2S\right)$ state, about a 50-50 meson-hybrid meson [11], the mass of the lowest-energy mixed charmonium-hybrid is shown in Figure 1.

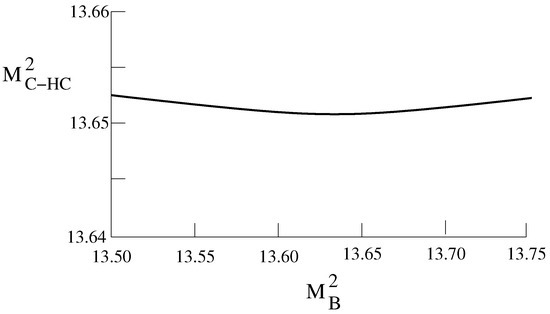
Figure 1. Mixed charmoniun-hybrid charmonium mass = 3.69 GeV [11].

Therefore, in Ref [11] the mass of the lowest energy mixed charmonium-hybrid charmonium was found to be about the mass of the $\Psi \left(2S\right)$ state, 3.69 GeV.

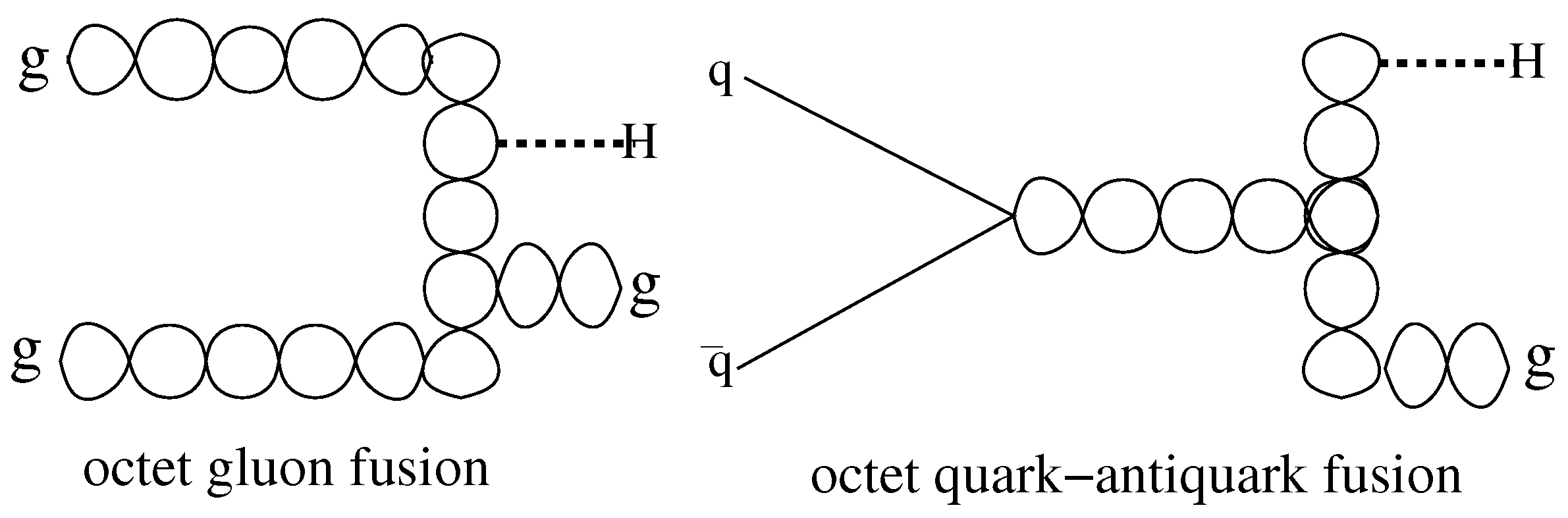
The cross sections for charmonium and bottomonium production in the color octet model, explained in Ref [13], are based on the cross sections obtained from the matrix elements for quark-antiquark and gluon-gluon octet fusion to a hadron H, illustrated in Figure 2.

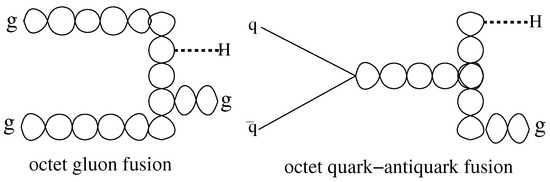
Figure 2. Gluon and quark–antiquark color octet fusion producing hadron H.

With $q\overline{q}$ models pp cross section ratios are [7] $\sigma \left(2S\right)/\sigma \left(1S\right)\simeq 0.039$,$\sigma \left(3S\right)/\sigma \left(1S\right)\simeq 0.0064$. On the other hand, for gluonic interactions with quarks there is an enhancement factor of ${\pi }^2$, for purely hybrid states, as illustrated in Figure 2. For states that are approximately 50% hybrid, this gives an enhancement factor of ${\pi }^2/4$, with a 10% uncertainty, which accounts for the enhanced cross section ratios discussed above, in Ref [7], and in Figure 3.

Figure 3. External field method for $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ states.

4. QCD Sum Rules and Mixed Heavy Quark Hybrid Meson States

The starting point of the method of QCD sum rules [4] is the correlator

$${\Pi }^A\left(x\right)=⟨|T\left[J_A\left(x\right)J_A\left(0\right)\right]|⟩,$$

(9)

with $|⟩$ the vacuum state and the current $J_A\left(x\right)$ creates the states with quantum numbers A. For the charmonium states, $J_A=J_c$ is

$$J_c=f{J}_{c\overline{c}}+\sqrt{1-f^2}{J}_{c\overline{c}g},$$

(10)

where $J_{c\overline{c}}$ creates a normal charmonium state and $J_{c\overline{c}g}$ creates a hybrid state with an active gluon. As discussed in the previous subsection $f\simeq -\sqrt{2}$ for the $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ and $f\simeq 1.0$ for the other charmonium and bottomonium states [11].

Experimental Verification that the $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ are Mixed Hybrid Heavy Quark Mesons

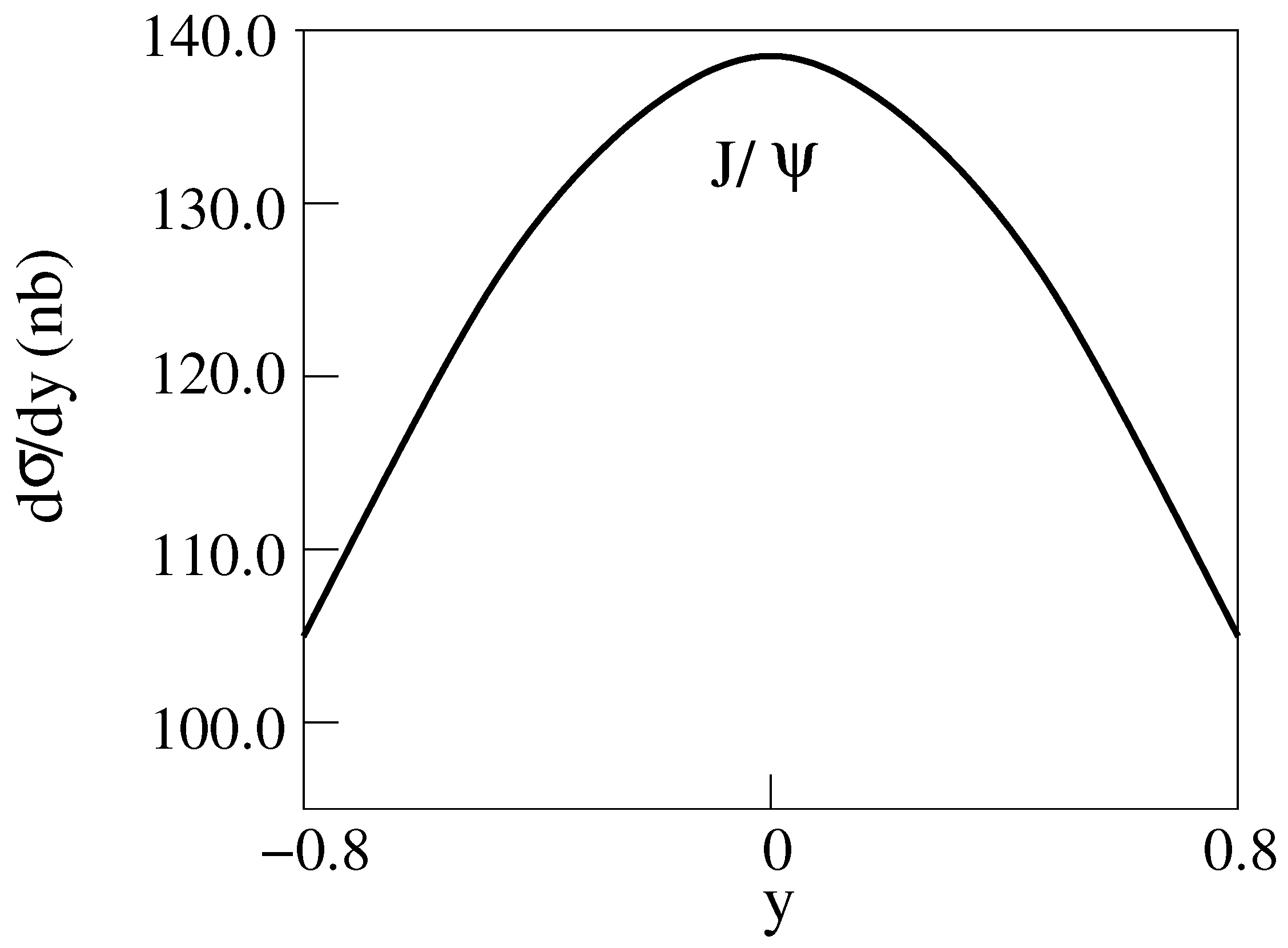
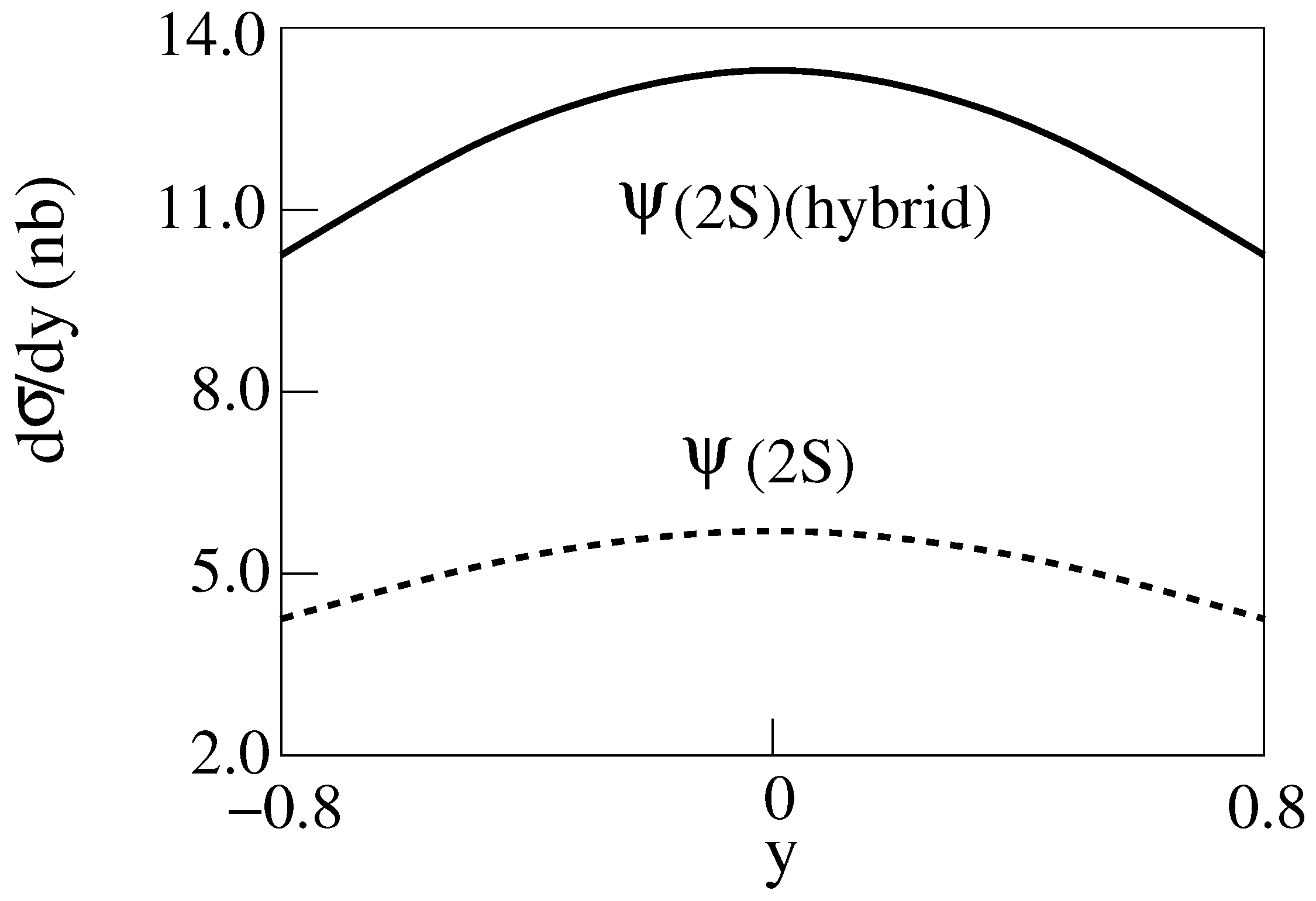
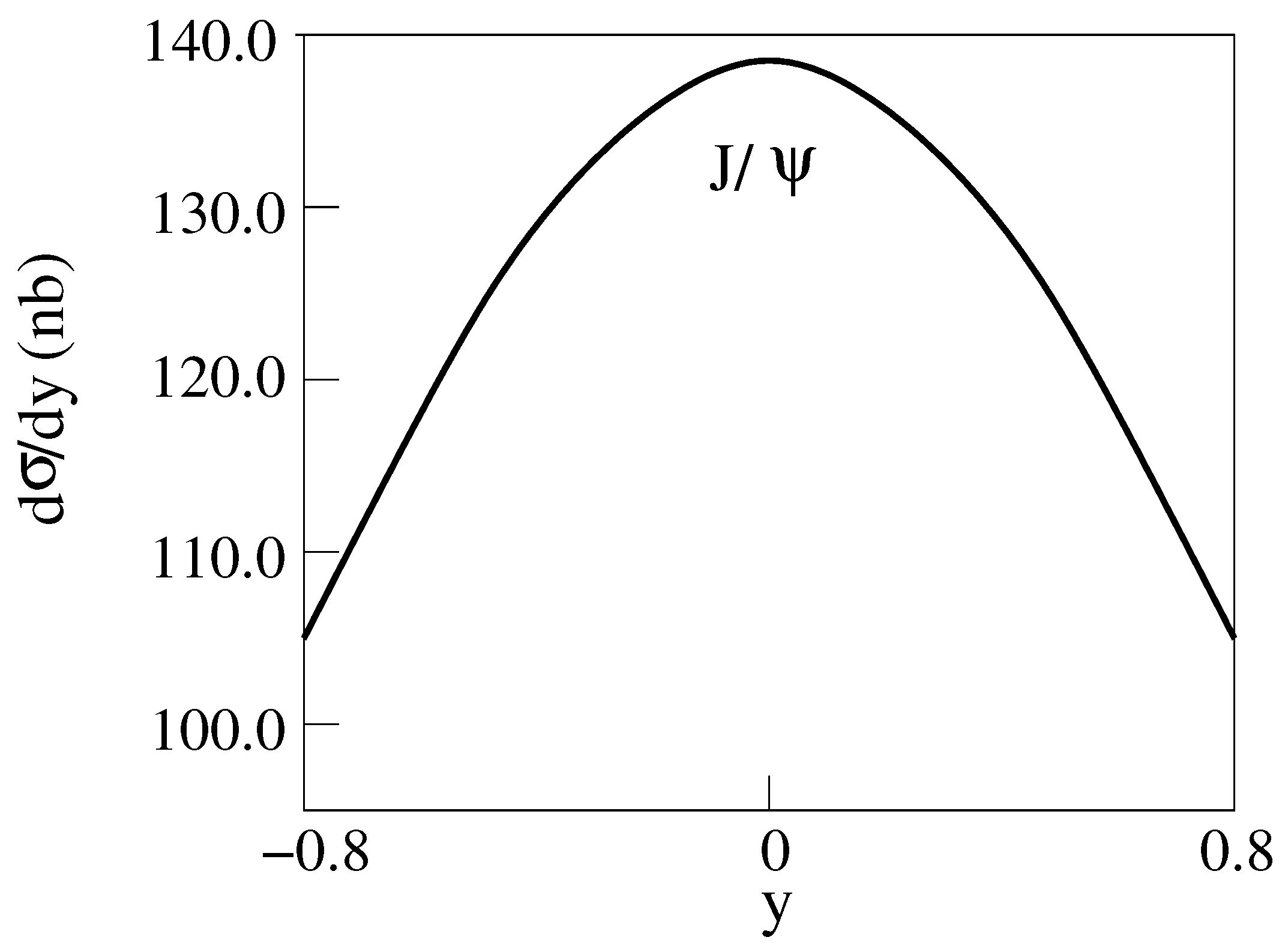
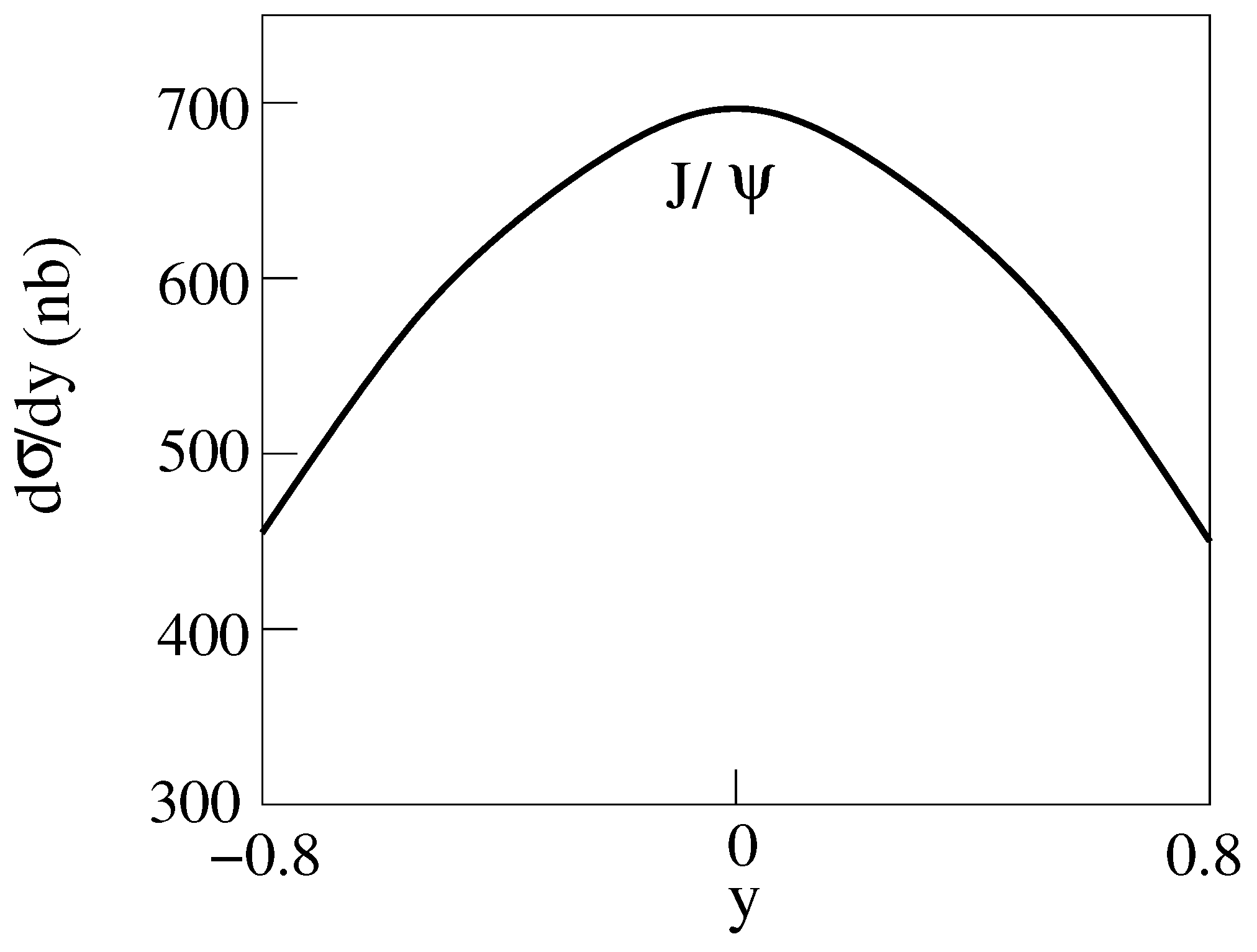
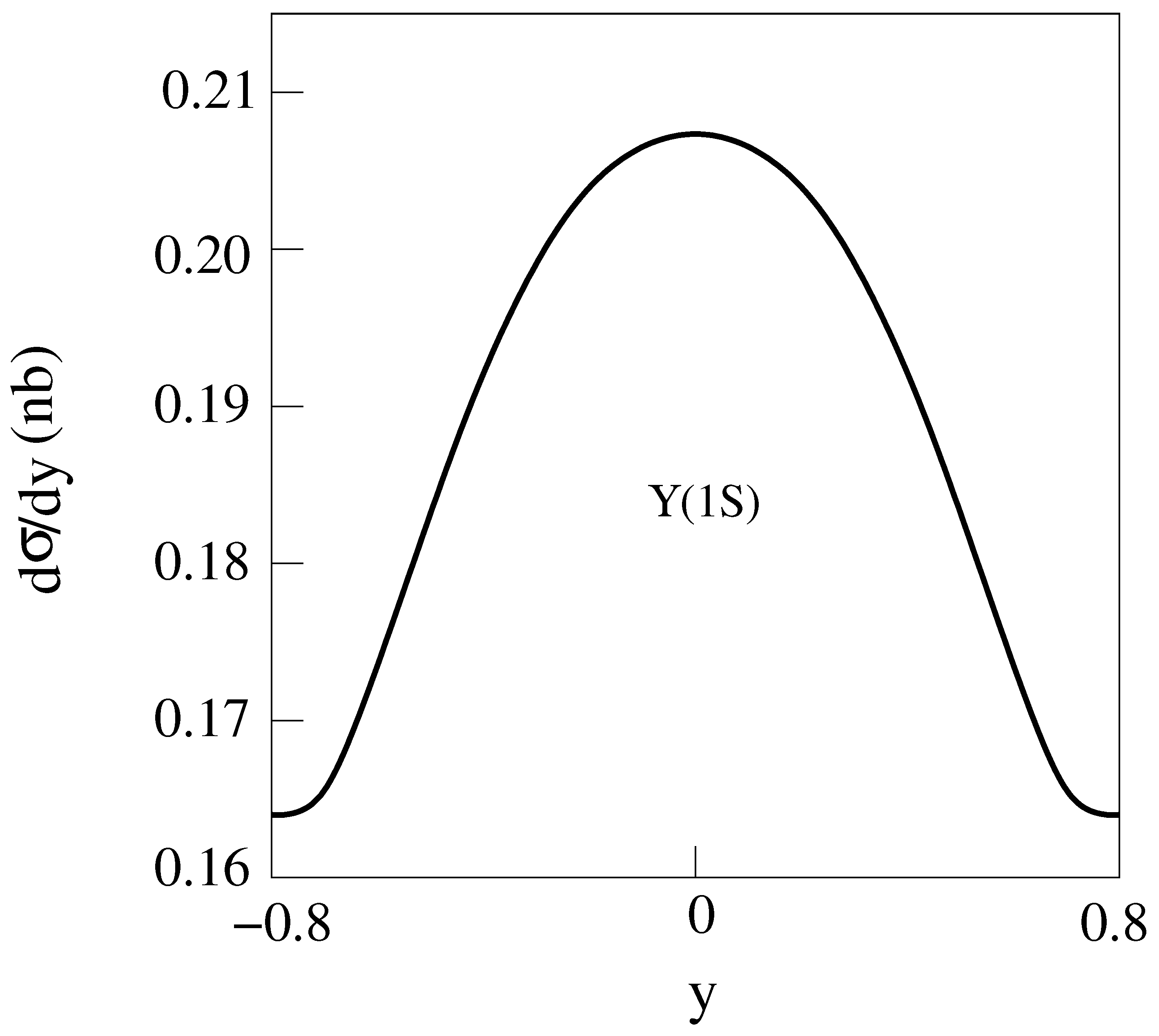
$\Psi$ and ${\rm Y}$ production Cu-Cu Collisions for E = 200 GeV [14] are shown in Figure 4, Figure 5, Figure 6 and Figure 7. The dashed curves are for the standard model.

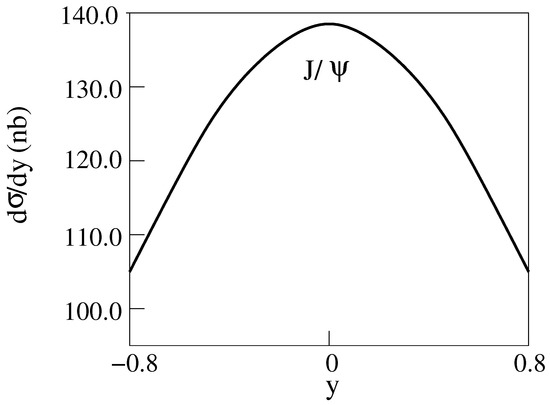
Figure 4. d$\sigma$/dy for E = 200 GeV Cu-Cu collisions producing $J/\Psi$ [14].

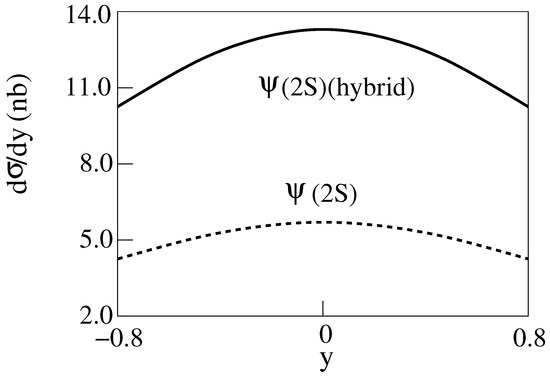
Figure 5. d$\sigma$/dy for E = 200 GeV Cu-Cu collisions producing $\Psi \left(2S\right)$ [14].

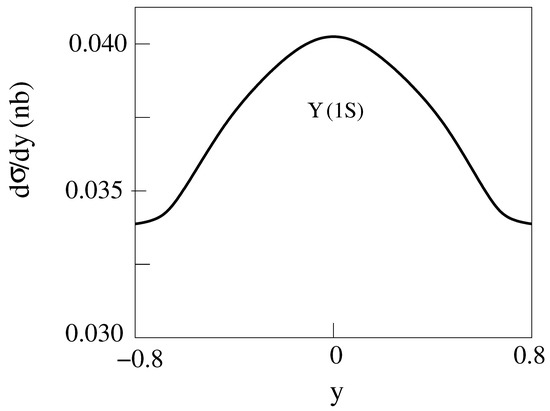
Figure 6. d$\sigma$/dy for E = 200 GeV Cu-Cu collisions producing ${\rm Y}\left(1S\right)$ [14].

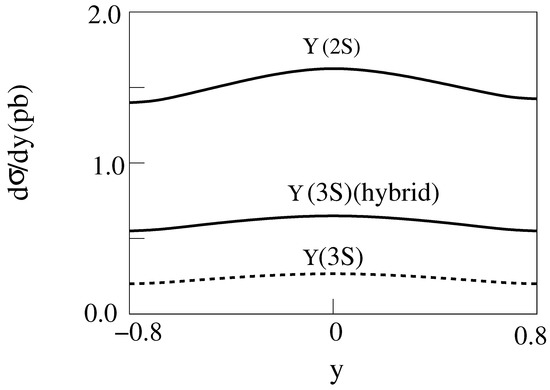
Figure 7. d$\sigma$/dy for Cu-Cu collisions producing ${\rm Y}\left(2S\right),{\rm Y}\left(3S\right)$ [14].

Tests of the mixed hybrid theory for $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ states using ratios of cross sections for Cu-Cu Collisions at E = 200 GeV: Since the absolute magnitude of d$\sigma$/dy for production of $\Psi \left(2S\right)$ states via Cu-Cu collisions is not certain, due to uncertainty in the normalization of the states, the tests of the theory [14] were carried out using ratios of cross sections, which can be compared to experiments.

From Figure 1 and Figure 2 the ratios of $\Psi \left(2S\right)$ to $J/\Psi \left(1S\right)$ for the standard model (st) and the mixed hybrid theory (hy) for A-A (including Cu-Cu) collisions are

$$\begin{array}{ll}{\sigma (\Psi \left(2S\right))/\sigma (J/\Psi \left(1S\right))|}_{st-A--A}& \simeq 0.27\\ \sigma (\Psi \left(2S\right))/\sigma {(J/\Psi \left(1S\right))|}_{hy-A--A}& \simeq 0.52\pm 0.05,\end{array}$$

while the experimental result [15] is

$$\sigma (\Psi (2S\left)\right)/\sigma (J/\Psi (1S)\simeq 0.59,$$

which shows that the mixed hybrid theory for the $\Psi \left(2S\right)$ state is consistent with experiment, while the standard $|c\overline{c}\left(2S\right)>$ is not.

From studies of heavy quark state production in p-p collisions theoretical results for the nature of ${\rm Y}\left(3S\right)$ state found [7]

$$\begin{array}{ll}\sigma ({\rm Y}(3S\left)\right)/\sigma ({\rm Y}(1S\left)\right)& \simeq 0.04\mathrm{standard}\\ \sigma ({\rm Y}(3S\left)\right)/\sigma ({\rm Y}(1S\left)\right)& \simeq 0.147-0.22\mathrm{hybrid}\end{array}$$

(11)

compared to the experimental result [16]

$$\sigma ({\rm Y}(3S\left)\right)/\sigma ({\rm Y}(1S\left)\right)\simeq 0.12-0.16$$

(12)

Therefore, the ${\rm Y}\left(3S\right)$ state as well as the $\Psi \left(2S\right)$ state has been shown to be a heavy quark mixed hybrid state.

5. $\mathit{J}/\mathsf{\Psi }$, $\mathsf{\Psi }\left(\mathbf{2}\mathit{S}\right)$ and $\mathsf{{\rm Y}}\left(\mathit{nS}\right)$ Production in Cu-Cu and Au-Au Collisions with $\sqrt{{\mathit{s}}_{\mathit{pp}}}$ = 200 GeV

The differential rapidity cross section for the production of a heavy quark state with in the color octet model in A-A collisions is given by

$$\frac{d{\sigma }_{AA\to \Phi }}{dy}=R_{AA}^E{N}_{bin}^{AA}<\frac{d{\sigma }_{pp}\to \Phi }{dy}>,$$

(13)

where $R_{AA}^E$ is the product of the nuclear modification factor $R_{AA}$ and $S_{\Phi }$, the dissociation factor after the state $\Phi$ (a charmonium or bottomonium state) is formed. $N_{bin}^{AA}$ is the number of binary collisions in the A-A collision, and $<\frac{d{\sigma }_{pp\to \Phi (\lambda =0)}}{dy}>$ is the differential rapidity cross section for $\Phi$ production via nucleon–nucleon collisions in the nuclear medium.

Experimental studies show that for $\sqrt{s_{pp}}$ = 200 GeV $R_{AA}^E\simeq 0.5$ both for Cu-Cu [17] and Au-Au [18]. The number of binary collisions are $N_{bin}^{AA}$ = 51.5 for Cu-Cu [19] and 258 for Au-Au. The differential rapidity cross section for pp collisions for $\sqrt{s_{pp}}$ = 200 GeV in terms of $f_g$ [7], the gluon distribution function is

$$<\frac{d{\sigma }_{pp\to \Phi (\lambda =0)}}{dy}>=A_{\Phi }\frac{1}{x\left(y\right)}{f}_g(\overline{x}\left(y\right),2m)f_g(a/\overline{x}\left(y\right),2m)\frac{dx}{dy},$$

(14)

with

$$f_g\left(x\right)\simeq 275.14-6167.6x+36871.3x^2,$$

(15)

with

$$x\left(y\right)=0.5\left[\frac{m}{s}(expy-exp(-y))+\sqrt{{(\frac{m}{s}(expy-exp(-y)))}^2+4a}\right],$$

(16)

and

$$\begin{array}{lll}\overline{x}\left(y\right)& =& x\left(y\right)(1+\frac{{\xi }_g^2(A^{1/3}-1)}{Q^2})\\ x\left(y\right)& =& 0.5\left[\frac{m}{\sqrt{s_{pp}}}(expy-exp(-y))+\sqrt{{(\frac{m}{\sqrt{s_{pp}}}(expy-exp(-y)))}^2+4a}\right],\end{array}$$

(17)

with [19] ${\xi }_g^2=.12Ge{V}^2$. For $J/\Psi$$Q^2=10Ge{V}^2$, so $\overline{x}=1.058x$ for Au and $\overline{x}=1.036x$ for Cu, while for ${\rm Y}\left(1S\right)$ $Q^2=100Ge{V}^2$, so $\overline{x}=1.006x$ for Au and $\overline{x}=1.004x$ for Cu.

From this we find the differential rapidity cross sections as shown in the following figures for $J/\Psi ,\Psi \left(2S\right)$ and ${\rm Y}\left(1S\right),{\rm Y}\left(2S\right),{\rm Y}\left(3S\right)$ production via Cu-Cu and Au-Au collisions at RHIC (E = 200 GeV), with $\Psi \left(2S\right),{\rm Y}\left(3S\right)$ enhanced by ${\pi }^2/4$ as discussed above. The absolute magnitudes are uncertain, and the shapes and relative magnitudes are our main prediction.

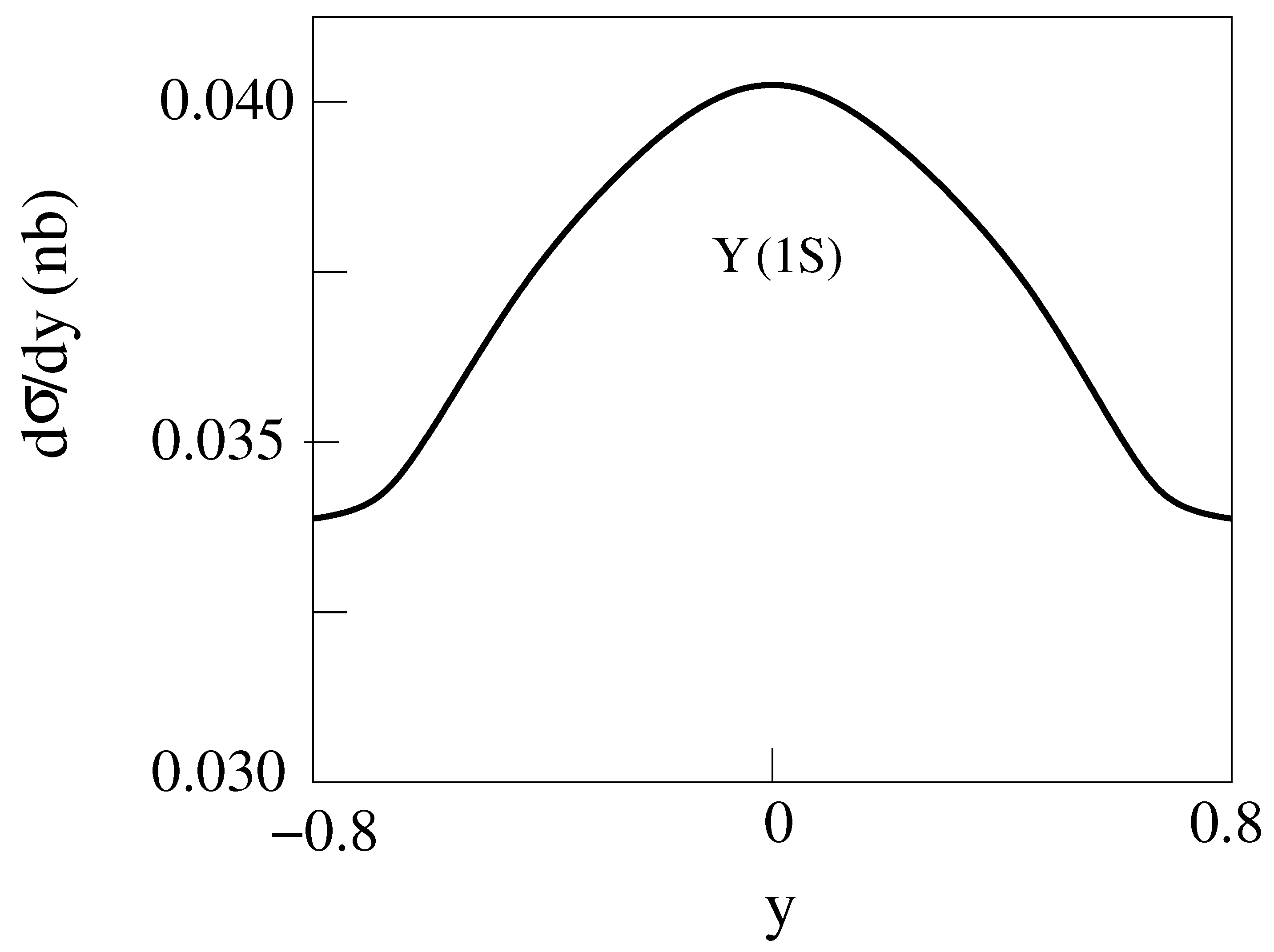
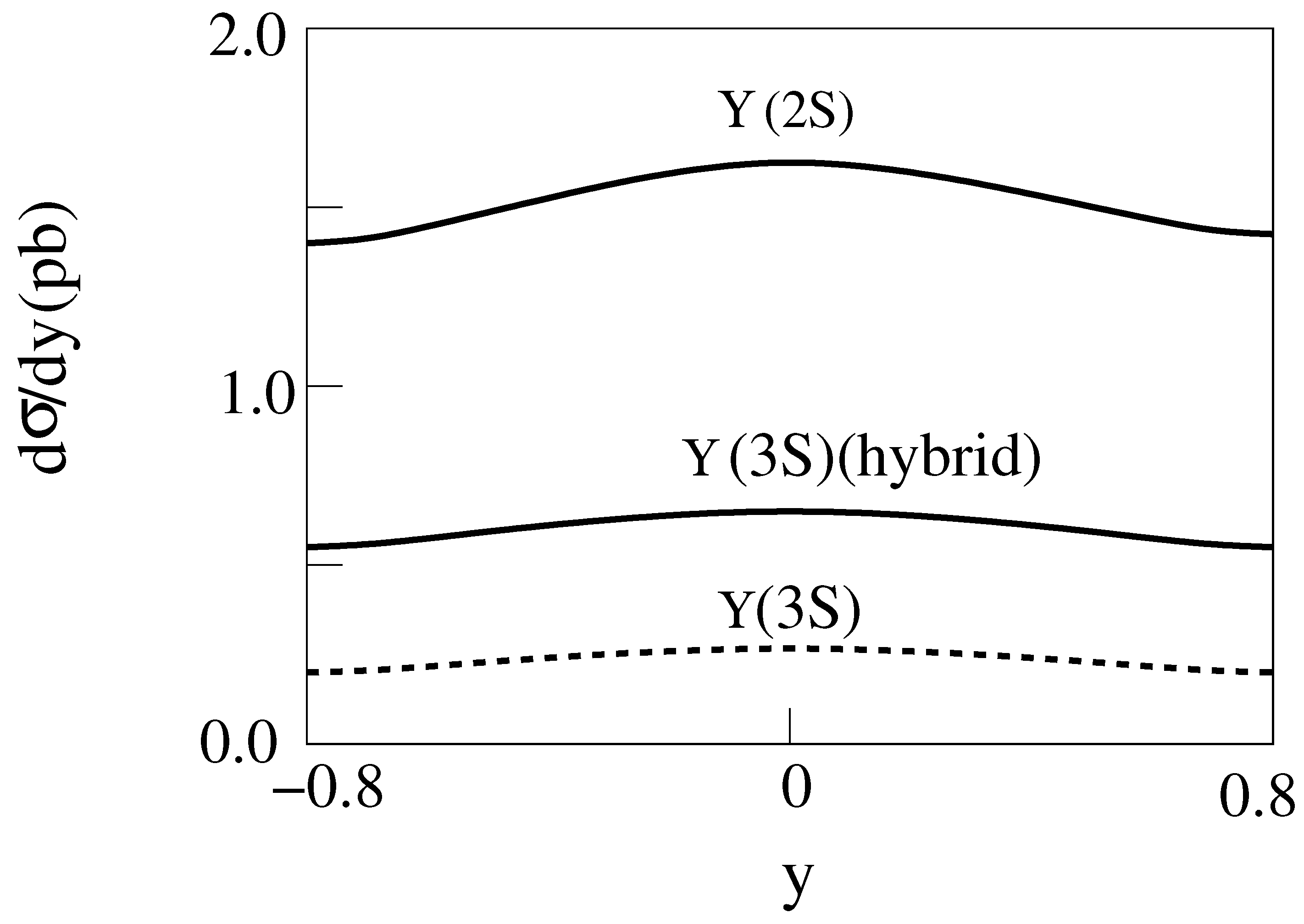
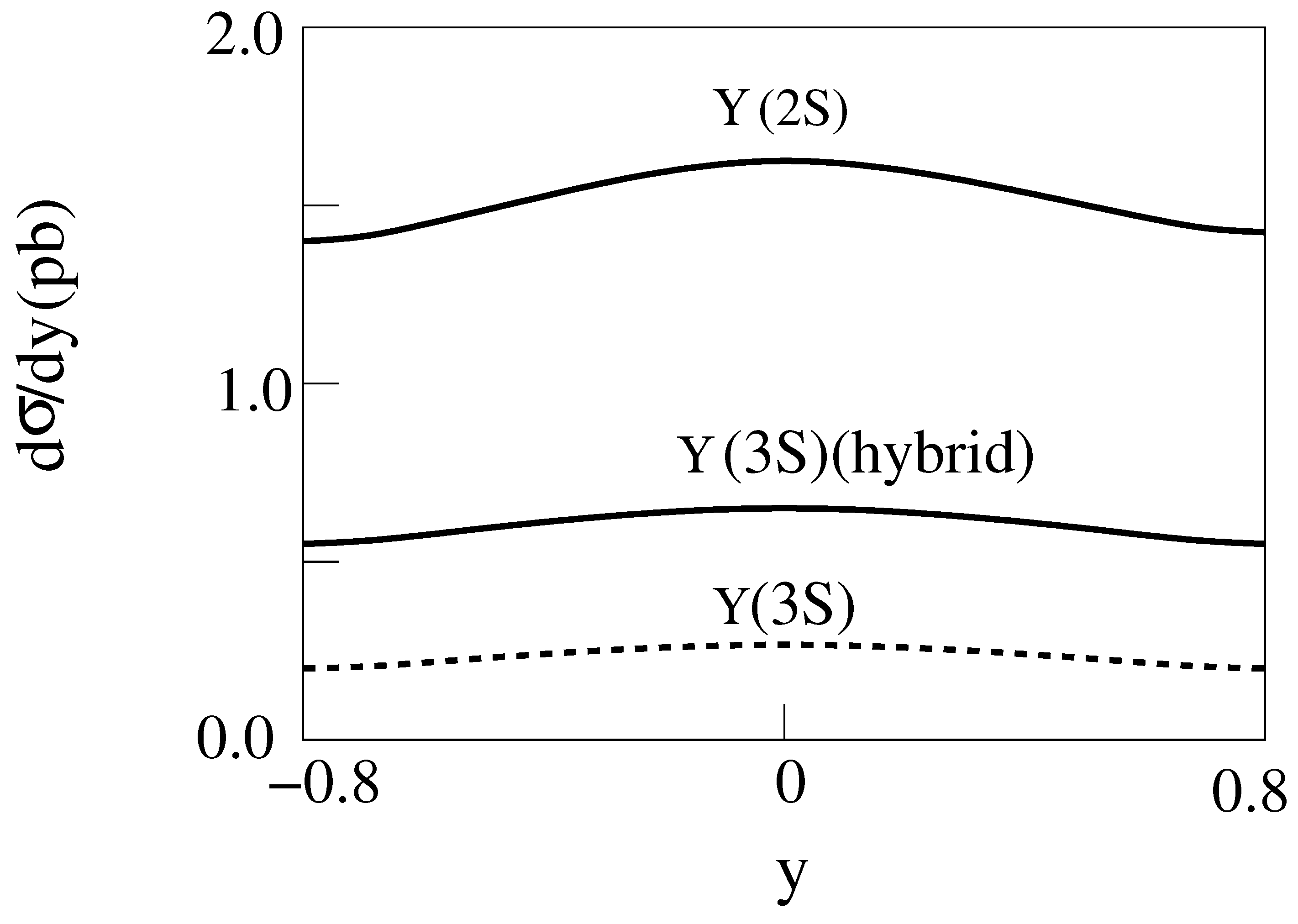
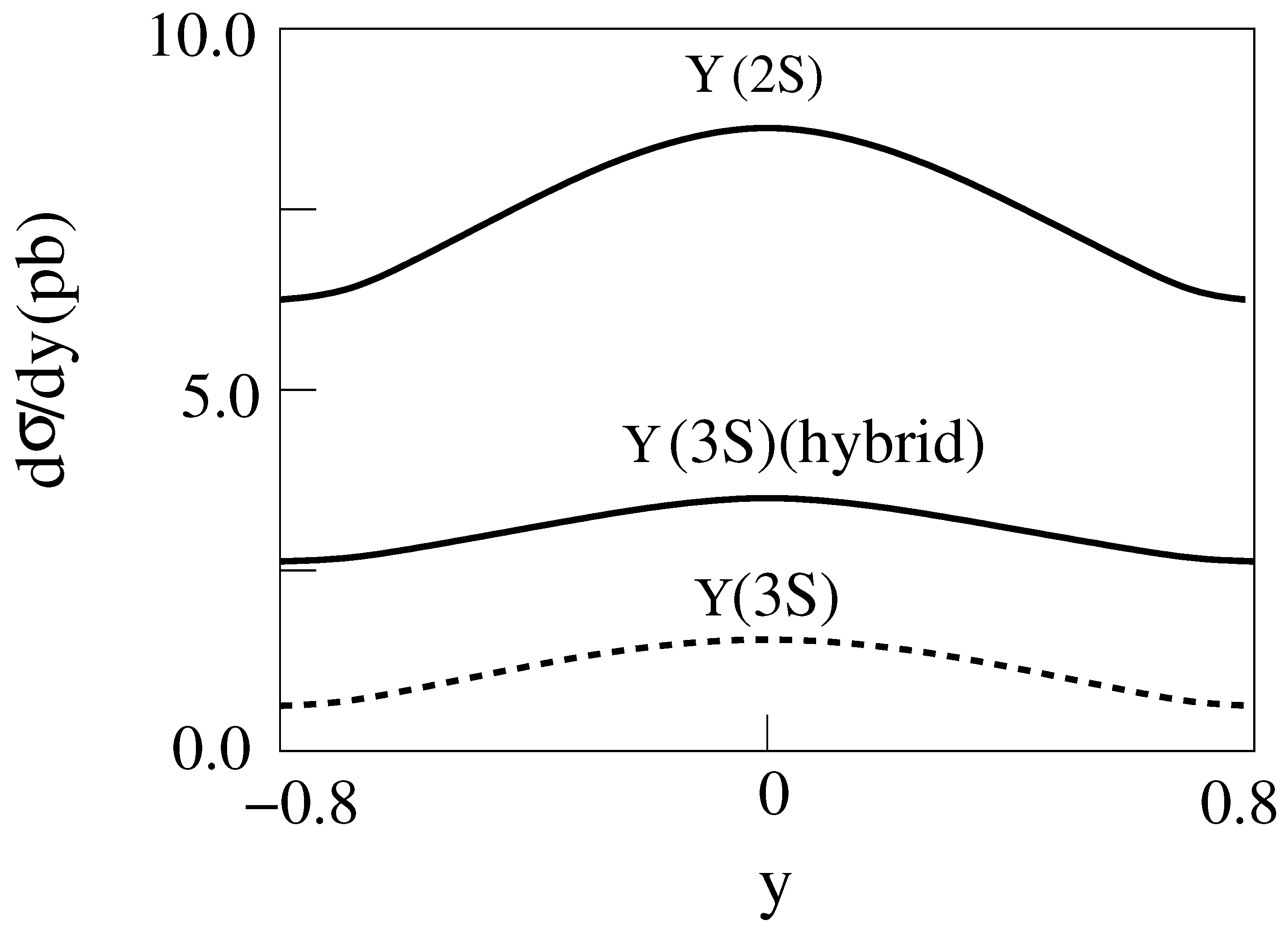
The differential cross sections d$\sigma$/dy are shown for $\Psi \left(mS\right)$ and ${\rm Y}\left(1nS\right)$ with m = 1,2 and n = 1,2,3 in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15.

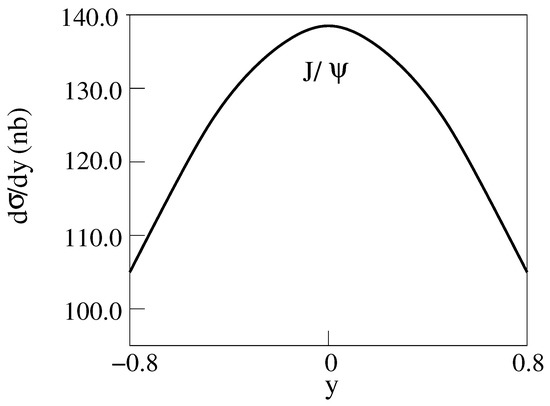
Figure 8. d$\sigma$/dy for 2 m = 3 GeV, E = 200 GeV Cu-Cu collisions producing $J/\Psi$ with $\lambda =0$ [14].

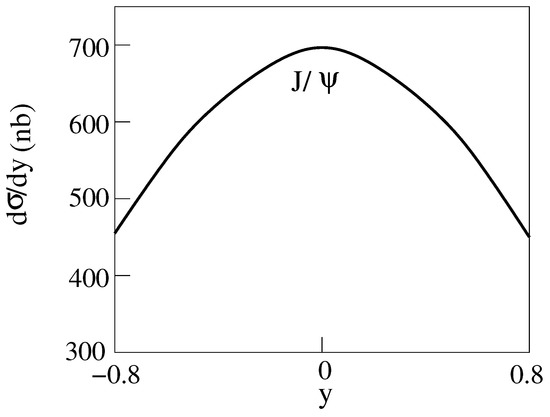
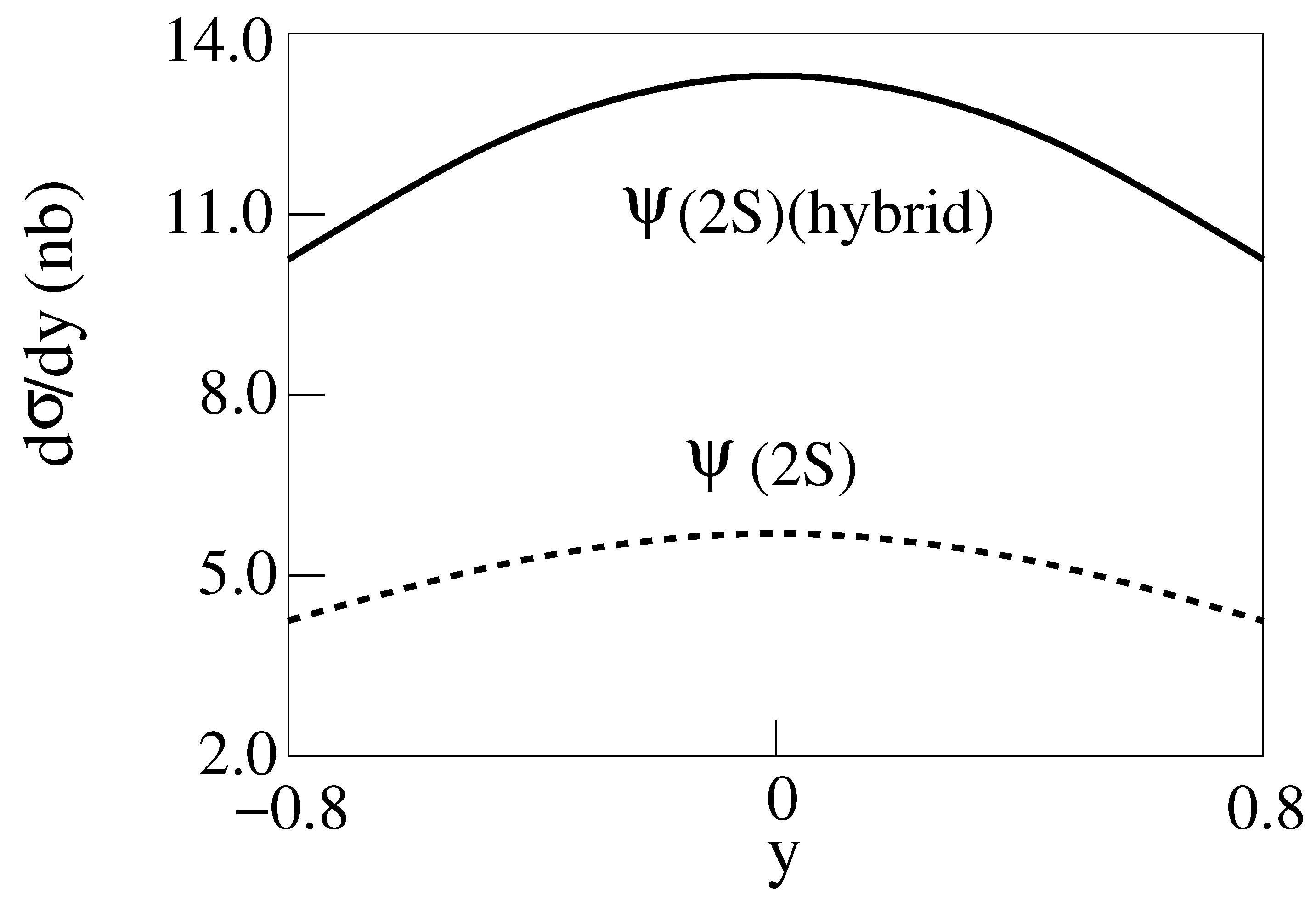
Figure 9. d$\sigma$/dy for 2 m = 3 GeV, E = 200 GeV Au-Au collisions producing $J/\Psi$ with $\lambda =0$ [14].

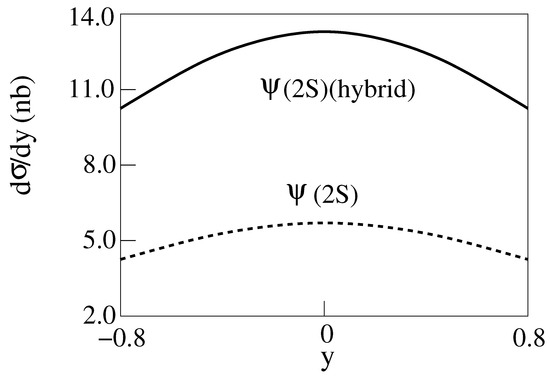
Figure 10. d$\sigma$/dy for 2 m = 3 GeV, E = 200 GeV Cu-Cu collisions producing $\Psi \left(2S\right)$ with $\lambda =0$. The dashed curve is for the standard $c\overline{c}$ model [14].

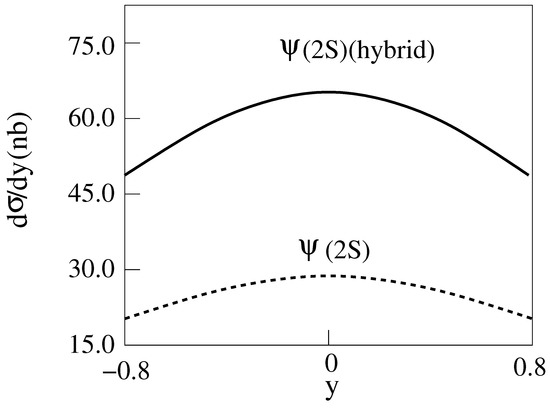
Figure 11. d$\sigma$/dy for 2 m = 3 GeV, E = 200 GeV Au-Au collisions producing $\Psi \left(2S\right)$ with $\lambda =0$. The dashed curve is for the standard $c\overline{c}$ model [14].

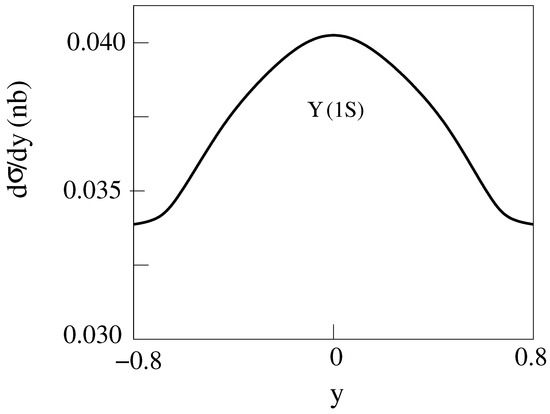
Figure 12. d$\sigma$/dy for 2 m = 10 GeV, E = 200 GeV Cu-Cu collisions producing ${\rm Y}\left(1S\right)$ with $\lambda =0$ [14].

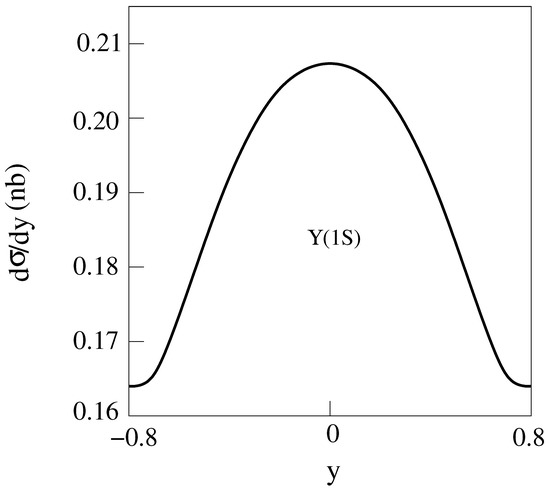
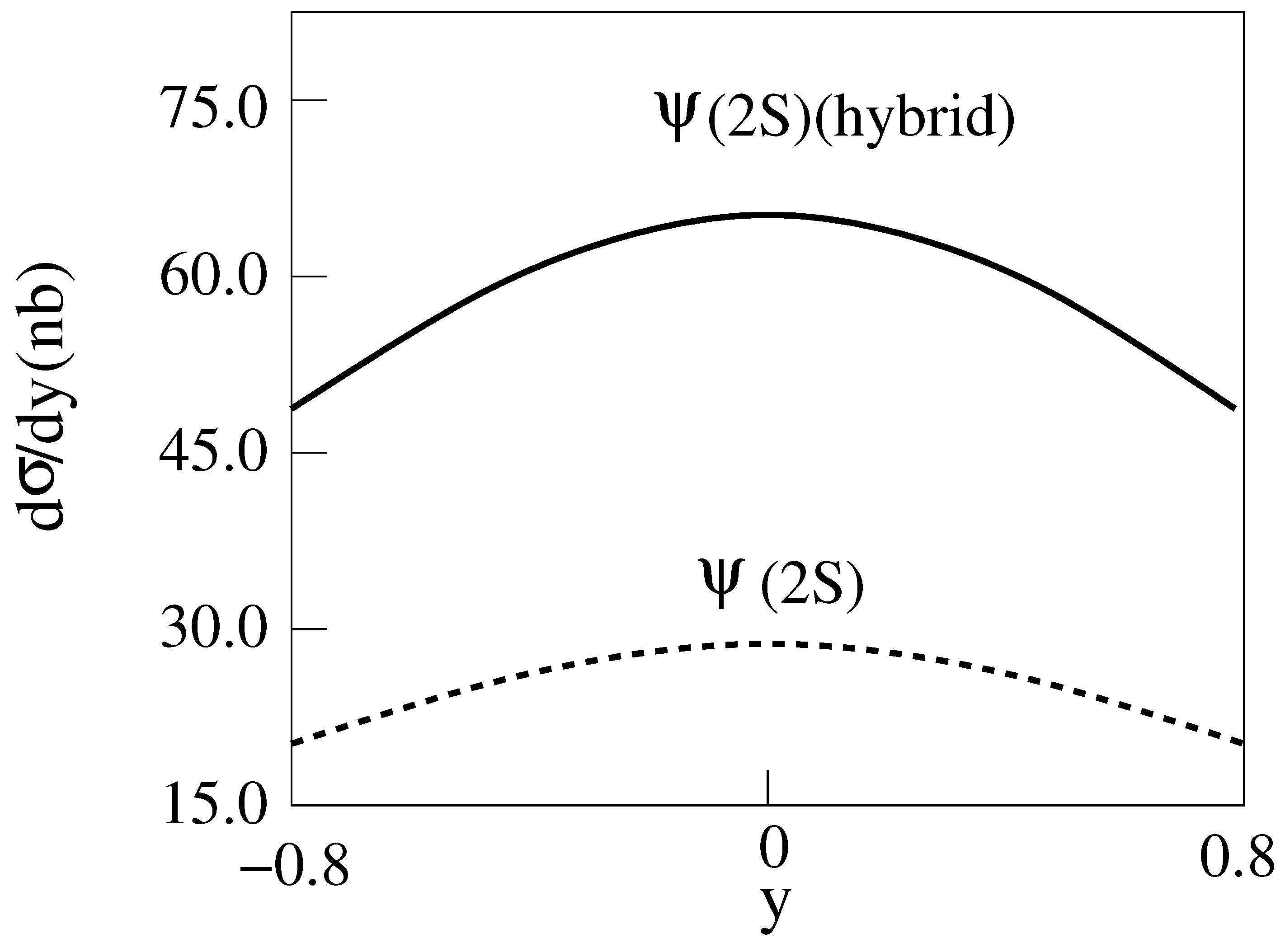
Figure 13. d$\sigma$/dy for 2 m = 10 GeV, E = 200 GeV Au-Au collisions producing ${\rm Y}\left(1S\right)$ with $\lambda =0$ [14].

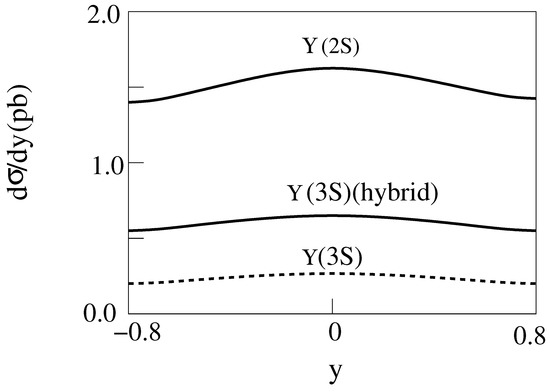
Figure 14. d$\sigma$/dy for 2 m = 10 GeV, E = 200 GeV Cu-Cu collisions producing ${\rm Y}\left(2S\right),{\rm Y}\left(3S\right)$ with $\lambda =0$. For ${\rm Y}\left(3S\right)$ the dashed curve is for the standard $b\overline{b}$ model [14].

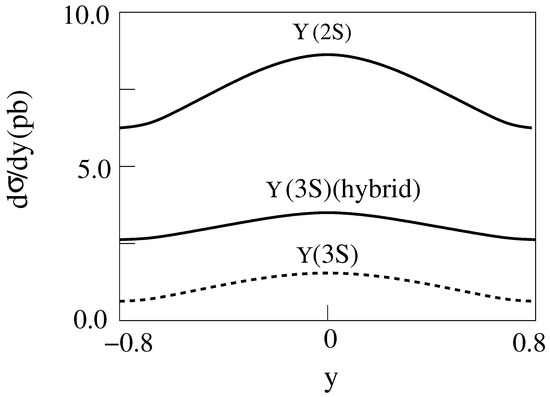
Figure 15. d$\sigma$/dy for 2 m = 10 GeV, E = 200 GeV Au-Au collisions producing ${\rm Y}\left(2S\right),{\rm Y}\left(3S\right)$ with $\lambda =0$. For ${\rm Y}\left(3S\right)$ the dashed curve is for the standard $b\overline{b}$ model [14].

6. Cosmological Phase Transitions

Let us define $|0,T>$ the state of the Universe with a temperature T since there is thermal equilibrium with no flow of thermal energy.

If there is a Cosmological first order phase transition, then there is a critical temperature $T_c$, and with the operator A depending on the phase transition.

$$<0,T\left|A\right|0,T{>}_{T<T_c}-<0,T\left|A\right|0,T{>}_{T>T_c}=\Delta A$$

$$\Delta A=\mathrm{latent}\mathrm{heat}\mathrm{of}\mathrm{the}\mathrm{phase}\mathrm{transition}.$$

The Electroweak Phase Transition (EWPT) occured at the time $t\simeq {10}^{-11}$ s. The critical temperature of the EWPT is $T_c$(EWPT) ≃ 125 GeV. For the EWPT the operator A is $\varphi$, the Higgs field, and

$$<0,T\left|\varphi \right|0,T{>}_{T<T_c}-<0,T\left|\varphi \right|0,T{>}_{T>T_c}=\Delta \varphi$$

$$=\mathrm{Higgs}\mathrm{Mass}\simeq 125\mathrm{GeV}=\mathrm{the}\mathrm{latent}\mathrm{heat}\mathrm{of}\mathrm{the}\mathrm{EWPT}.$$

During the EWPT:

(1)

all particles except the photon got their mass,

(2)

magnetic fields were created,

(3)

baryogenesis occured: more quarks than antiquarks.

The EWPT is reviewed in detail in Ref [20]. Next we discuss the QCDPT.

The QCD phase transition, QCDPT, occured at the time $t\simeq {10}^{-5}$ s, with the critical temperature for the QCDPT $T_c^{QCDPT}\simeq$ 150 MeV. The Latent Heat for the QCD Phase Transition (QCDPT) is the Quark Condensate, which we now define.

$$\begin{array}{ccc}\hfill q\left(x\right)& =& \mathrm{quark}\mathrm{field}\hfill \\ \hfill \overline{q}\left(x\right)& =& \mathrm{antiquark}\mathrm{field}\hfill \\ \hfill |0,T>& =& \mathrm{vacuum}\mathrm{state}\mathrm{temperature}=\mathrm{T}\hfill \\ \hfill <0,T\left|\overline{q}\left(x\right)q\left(x\right)\right|0,T>& =& \mathrm{quark}\mathrm{condensate}\hfill \\ & =& \mathrm{vacuum}\mathrm{expectation}\mathrm{value}\mathrm{of}\overline{\mathrm{q}}\left(\mathrm{x}\right)\mathrm{q}\left(\mathrm{x}\right)\hfill \end{array}$$

The quark condensate $<0,T|\overline{q}\left(x\right)q\left(x\right)|0,T>$ changes during the QCDPT:

$$\begin{array}{ccc}\hfill <0,T|\overline{q}\left(x\right)q\left(x\right)|0,T>& =& 0\mathrm{in}\mathrm{quark}\mathrm{gluon}\mathrm{plasma}\mathrm{phase}\mathrm{T}>{\mathrm{T}}_{\mathrm{c}}^{\mathrm{QCDPT}}\hfill \\ & \simeq & {\left(.23GeV\right)}^3\mathrm{in}\mathrm{hadron}\mathrm{phase}\mathrm{T}<{\mathrm{T}}_{\mathrm{c}}^{\mathrm{QCDPT}}\hfill \end{array}$$

Therefore

$$\Delta <0,T|\overline{q}{\left(x\right)q\left(x\right)|0,T>=\mathrm{latent}\mathrm{heat}\mathrm{of}\mathrm{the}\mathrm{QCDPT}=\left(.23\mathrm{GeV}\right)}^3$$

6.1. Detection of the QGP via Hybrid Mesons Produced by RHIC

As discussed above, during the evolution of the early universe there were two important Cosmological Phase Transitions: The Electorpeak Phase Transition when all particles except the photon got their mass, and the QCD phase transition, QCDPT, the transition from a universe with dense matter with quarks and gluons, called the quark gluon plasma (QGP), to our universe with protons and neutrons and other hadrons. The QCDPT is reviewed since hybrid mesons and RHIC are essential for the detection of the QGP.

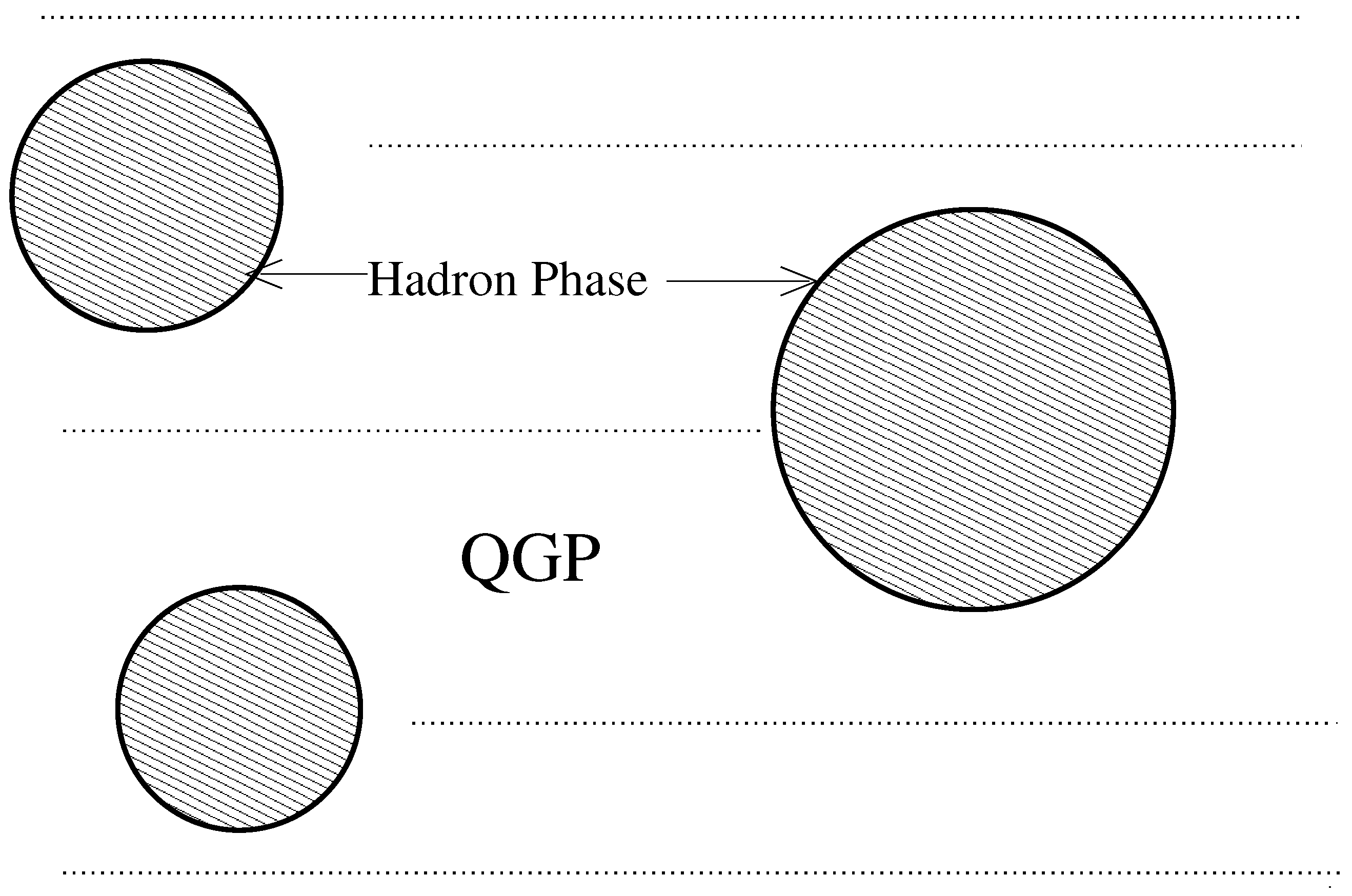
The critical temperature $T_c^{QCDPT}\simeq$ 150 MeV. During the time that $T=T_c^{QCDPT}$ bubbles of our universe nucleated within the QGP, as shown in Figure 16.

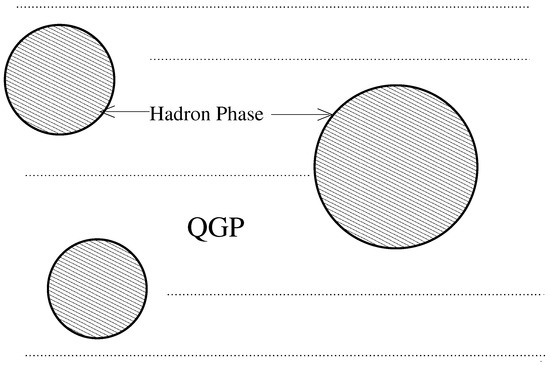
Figure 16. Hadron phase forming within the Quark Gluon Plasma (QGP) during the Quantum Chromodynamics Phase Transition (QCDPT).

6.2. Creation and Detection of the QGP via A-A Collisions

A main goal of the study of heavy quark state production in A-A colisions is the detection of the Quark Gluon Plasma (QGP).

The energy of the atomic nuclei must be large enough so just after the nuclei collide the temperature is that of the unverse about ${10}^{-5}$ seconds after the Big Bang, when the universe was too hot for protons or neutrons and consisted of quarks and gluons (the constituents of proton and nucleons)—the QGP.

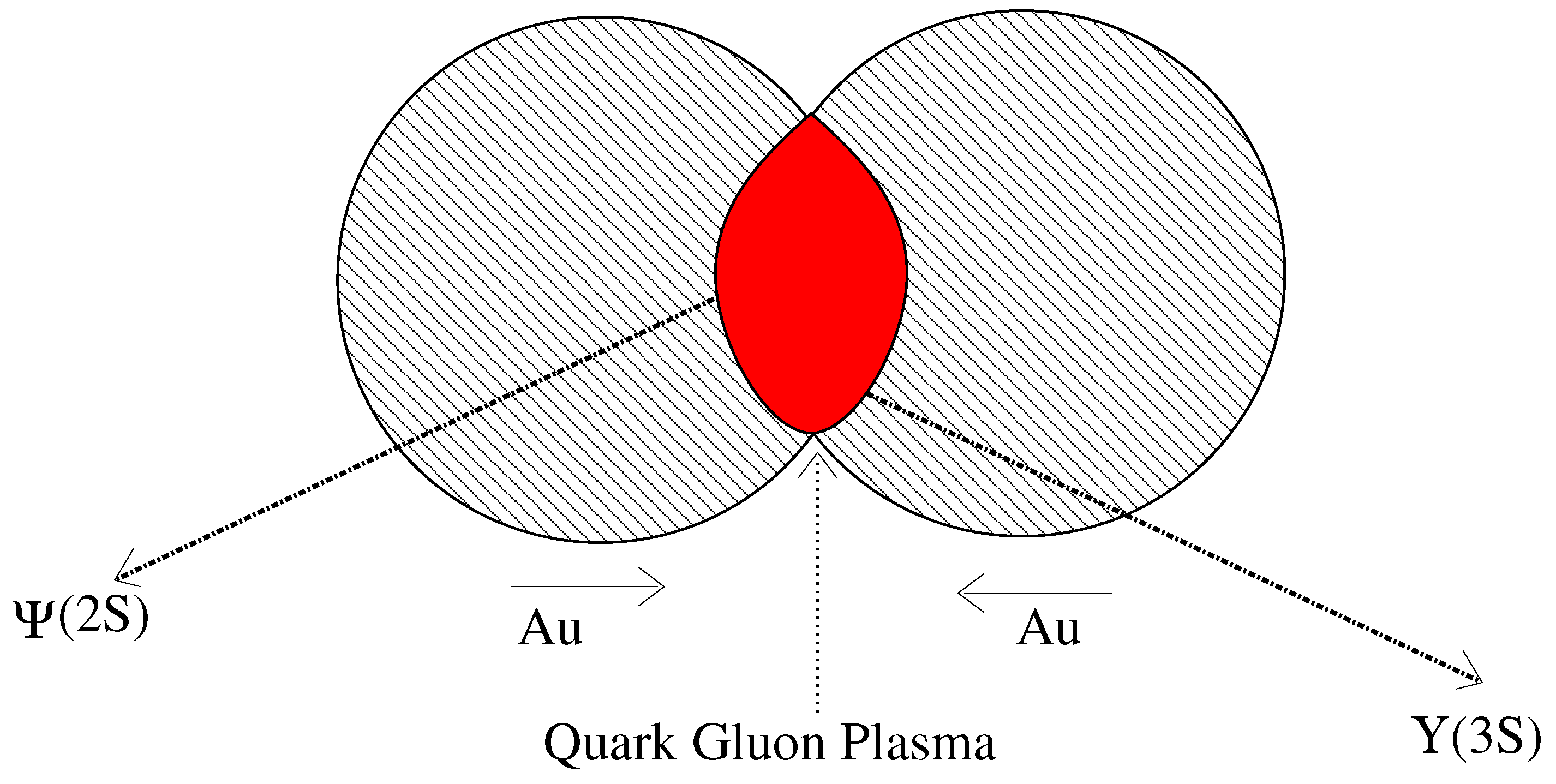
As Figure 17 illustrates for Au-Au collisions, the emission of mixed hybrid mesons, the $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ as discussed above, with active gluons, could be a signal of the formation of the QGP.

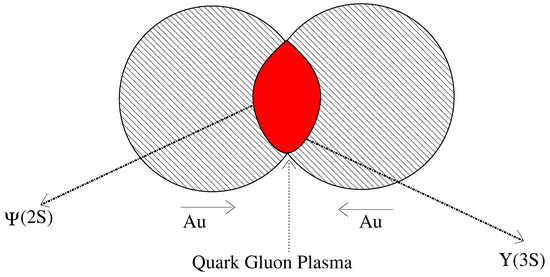
Figure 17. Au-Au collisions producing $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ from the QGP.

As discussed above the detection of the heavy quark mixed hybrid mesons $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ produced in Au-Au collisions is an experimental challenge.

7. Conclusions

After a brief review of Quantum Chromodynamics QCD, Sum Rules were used to show that the $\Psi \left(2S\right),{\rm Y}\left(3S\right)$ are mixed hybrid states [11].

The conclusion from QCD sum rules that the $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ meson states are approxumastely half normal and half hybrid states was confirmed by the ratios of cross sections of $\Psi \left(2S\right)$ to $J/\Psi \left(1S\right)$ for Cu-Cu Collisions and ${\rm Y}\left(3S\right)$ to ${\rm Y}\left(1S\right)$ for p-p collisions compared to experimental results.

In our next section, the production of $\Psi \left(mS\right)$ and ${\rm Y}\left(nS\right)$, with m = 1, 2 and n = 1, 2, 3, in Cu-Cu and Au-Au collisions with $\sqrt{s_{pp}}$ = 200 GeV was reviewed, with experimental tests expected in the future.

In our final section the creation of the QGP via A-A collisions and possible detection of the QGP via the emission of mixed hybrid mesons was reviewed. Since $\Psi \left(2S\right)$ and ${\rm Y}\left(3S\right)$ are mixed hybrid states their production and detection in A-A collisions could provide evidence for the creation of the QGP.