1. Introduction
The results of the solar and atmospheric neutrino oscillation experiments were recognized by a recent Nobel prize. The Mikheyev–Smirnov–Wolfenstein (MSW) effect is an essential component needed for the interpretation of these neutrino oscillation experiments [
1,
2] (for a historical account of neutrino oscillations in matter, see [
3]). Therefore, the mixing of the neutrino mass eigenstates in vacuum and in dense matter seem to be well established in describing the propagation of neutrinos from source to detecting devices. These effects were mostly considered in electron plasma [
4,
5], such as the Sun or supernovae, and their use is extended to condensed matter, such as the Earth crust and inner layers [
6,
7,
8]. However, to our best knowledge, the variation of the electron density inside condensed matter has not yet been considered. A simple estimate of the electron density and neutrino potential inside a medium-Z nucleus, such as
Si, shows that it is more than two orders of magnitude larger than that existing in the Sun’s core [
9,
10]. One could then ask if these high electron densities can produce additional mixing of the mass eigenstates that need to be considered in the interpretation of neutrino production and detection phenomenology.
The effect of the matter-induced neutrino potential on the neutrino mixing in matter is traditionally analyzed using the local in-medium mass eigenstates with modified effective masses and mixings [
11,
12,
13]. This approach relies on the separation of the neutrino wavelength scale from the much larger neutrino oscillation and matter density variation scales. In reality, there are no such local mass eigenstates in matter (the neutrino potential is a timelike component of a vector and modifies the energy but not the mass), but the analysis of the evolution of the vacuum mass eigenstates in finite matter medium is complicated by the various scales involved. However, the results based on local, in-medium, mass eigenstates seem to be valid. One of the issues related to the introduction of the fictitious in-matter mass eigenstates is that one assumes that the neutrinos produced via weak interactions in dense matter (e.g., in the Sun’s core) are emitted as in-matter mass eigenstates. The transition to vacuum is usually described by the long-scale evolution of the amplitudes (for an example, see Reference [
14]), which may or may not be adiabatic. In this article, we investigate if the results of this approach (see also Reference [
9]) can be extended to the analysis of the effects of nonadiabatic transitions of the neutrinos through condensed matter, where the electron densities near the atomic nuclei are orders of magnitude larger than those in the Sun’s core. In our analysis, we use the evolution of the flavor amplitudes (see Equation (
11) below), thus avoiding the complicated evolution of the fictitious in-medium mass eigenstates.
2. Neutrino Oscillations in Condensed Matter
It is now widely accepted that the flavor neutrinos participating in the weak interaction are coherent superpositions of vacuum mass eigenstates. For the neutrino fields, the mixing reads:
where index
indicates a flavor state (electron, muon, tau, …),
j designates mass eigenstates (1, 2, 3, …,
), and
are elements of the vacuum neutrino mixing (PMNS) matrix. Here, the dots indicate sterile flavors, or high mass eigenstates, with
being the number of mass eigenstates. If one discards the existence of the low-mass sterile neutrinos, the coupling to the higher mass eigenstates is then very small, and the sum over
j in Equation (
1) is reduced to
. This mixing leads to violations of the flavor number, and it is reflected in the outcome of the neutrino oscillation experiments. These experiments are mostly analyzed in terms of neutrino states:
which are dominated by the larger components of the fields. Neutrino states are used to analyze the matter effects, also known as Mikheyev–Smirnov–Wolfenstein effects [
15]. Neutrino mixing is affected in matter by the neutrino optical potential. The general relation between the neutrino optical potential (in
) and the electron density
(in cm
) is:
where the minus–plus sign corresponds to (anti)neutrinos,
is Fermi’s constant, and
is the proton mass (
g). Above, we used Equation (2.8) of [
13], where the equivalent matter density times the electron fraction
was replaced with
. In atoms, just considering the electron density of two electrons in the lowest
state of a Hydrogen-like atom (the higher s-states contribute very little,
,
n being the principal quantum number), one gets:
where
Z is the atomic number and
r is the radial distance from the atomic nuclei in pm (
m). Electron Density Functional Theory (DFT) calculations [
16,
17] (for example, see
Figure 1 of Reference [
9]) show that this approximation is very good at and near the nuclei, where the main transition takes place.
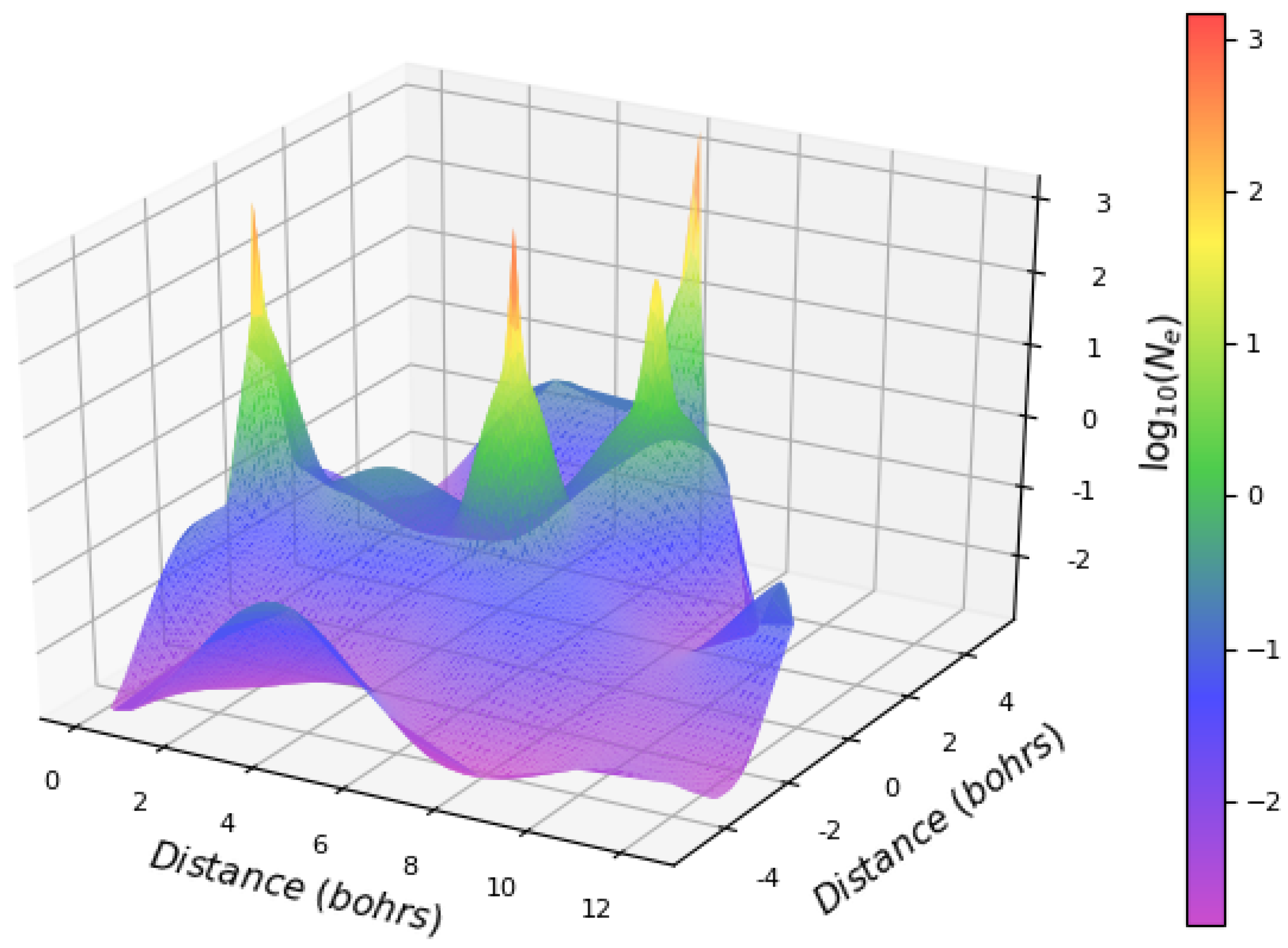
Figure 1 shows the result of a DFT calculation for the electron density in the cell of quartz crystal, one of the most common in the Earth’s crust. The results show that 85% of the electron density in the cell resides in the spikes (defined as larger than the average density of 0.1 atomic units), while only 15% is located in the volume that has lower-than-average density. In addition, the values of the electron density near the peaks are very well described by Equation (
4). These high electron densities near the nuclei are much larger than those in the Sun’s core for all atoms with an atomic number greater than 5. As an example, for atoms with
, the electron density at the nucleus is four orders of magnitude larger than that in the Sun’s core.
Therefore, it should be interesting to investigate the effects of these large electron densities on the neutrino mixing in atomic weak interactions. To solve this problem, one needs to consider the evolution of mixing for three (or more) neutrino mass eigenstates, which can be described by the coupled Dirac equations:
where
are Dirac spinors for the (perturbed) vacuum mass eigenstates,
are the corresponding neutrino masses,
is the momentum in the direction of the beam, and
and
are Dirac matrices [
19]. Here,
is the neutral current potential generated mostly by neutrons, i.e.,
where
is the local neutron density in cm
(here and below we neglect the neutral current contributions from protons and electrons, which cancel out in the limit of average constant densities). The neutral current potential is the same for all three active neutrinos, and therefore can be neglected in the analysis of neutrino oscillations (as is the main momentum term in the underlying Dirac equations). However, if the sterile neutrinos are present, the neutral current potential needs to be considered [
20].
In Equation (
5), the Dirac spinors
can be viewed as components of some flavor neutrino normalized superposition of mass eigenstates spinors:
where
indicates the known active neutrino flavors—electron, muon, and tau. Here, we consider the traditional approach [
14] of separating the neutrino wavelength scale from the neutrino oscillation and matter density variation scales by considering a Schroedinger-like equation for the amplitudes, assuming that the
spinors are free spinors.
The vector of 3 flavor amplitudes is denoted as
, and then the Schroedinger-like evolution equation for the flavor amplitudes in matter reads:
where
,
,
are the masses of the vacuum mass eigenstates, and
is the magnitude of momentum (
for relativistic neutrinos). The general requirement for the validity of the above evolution equation is that the neutrino wavelength be smaller than the length over which there is a significant change of the optical potential created by a varying electron density [
13,
14]:
In the case of the potential created by the atomic electron density, Equations (
3) and (
4), this condition reads:
which is satisfied for neutrino energies larger than 1 MeV, and for all atomic numbers larger than that of oxygen.
In constant electron density, Equation (
8) is usually solved by diagonalizing the in-matter Hamiltonian,
, assuming that the solution describes in-matter mass eigenstates that have in-matter mixing matrices and masses, and using these effective masses and mixings in the standard vacuum oscillation formulae [
14]. We will call this the eigenvalues method. In this approach, Equation (
4) suggests that the electron density inside the atomic nucleus is much larger than that in the Sun’s core and, therefore, the (anti)neutrinos are emitted in the (lower)higher mass eigenstates. Solutions to this problem for one single atom were discussed in Reference [
9]. Here, we are interested to see if there are any effects of the electron density “spikes” around the atomic nuclei in bulk condensed matter. For that, we integrate Equation (
8), which we rewrite in dimensionless form:
Here,
s is the normalized propagation length,
,
is the unit length defined as
,
,
, and
. The mass differences
were taken from Reference [
21], and
in Equation (
11) takes into account the normal(inverted) mass ordering,
(
). In the calculation, we use a number
N of density spikes, entering
via
. Shown in
Figure 2 are different density profiles: Gaussians in blue, exponential in red, and a combination of the two of them in black. Each density profile represents the electron density near an atomic nucleus multiplied by twice the proton mass. Given that the Gaussians are normalized to unity, an additional normalization factor
was used to recover the flat average density of matter
:
where, for an easier comparison with solar density, we used the local equivalence between the average electron density
and average mass density
:
We use a similar relation for related to the normalization of the Gaussian spikes in the electron density. The number of intervals N can be chosen appropriately to describe the large peak values of the Gaussians.
To integrate Equation (
8), we used the ZVODE routine from the SciPy ODE package, which implements a complex version of the VODE algorithm [
22]. Given that the electron density spikes are extremely narrow, we tried different widths for the density profiles shown in
Figure 2. In an attempt to get good accuracy of the solution, we divided the width of each density spike by about 100 integration steps, and required for each step an absolute tolerance of
from ZVODE routine.
The results in
Figure 3 show a significant difference between the solution of the integration method using the spiked density profile (in black) and the “exact” eigenvalues solution corresponding to the equivalent flat electron density (in dark green). As one can see from the figure, there is little effect at 1300 km that corresponds to the Deep Underground Neutrino Experiment (DUNE)/Long-Baseline Neutrino Facility (LBNF) experiment baseline, but it would have been significant for 7330 km, which is the distance between Fermilab and Gran Sasso or that from CERN to Sanford lab in South Dakota. However, when increasing the accuracy in the ZVODE routine to
, the difference between the two curves in
Figure 3 disappeared. This situation emphasized once again the danger of relying solely on numerical analysis. In addition, the needed accuracy of
being close to the numerical round-off error for double precision further emphasizes the difficulty of the numerical problem. We also extensively checked this aspect using Julia’s Differential Equations package, which has a much richer set of routines that can integrate stiff and nonstiff systems of complex differential equations, and the behavior was similar to that we experience with ZVODE.
Therefore, we tried using a more direct analysis to understand this result, which will be presented in the next section.
3. The Iterations Algorithm
Previous work on neutrino oscillation probabilities in matter includes perturbative expansions [
20,
23,
24,
25]. The most used approach is to diagonalize the Hamiltonian in matter, and use perturbation theory to identify main contributing terms. In the process, one uses the S-matrix approach for the propagation of the amplitudes. For example, for Equation (
11), the corresponding S-matrix is given by:
where the
T operator in front of the exponential indicates an ordered position-dependence of the integrals when the matrix exponential is expanded (similar to the time-ordered product). The S-matrix can be used to calculate the probability of measuring neutrino flavor
at distance
s assuming that flavor
was emitted at
[
23]:
In the case of constant electron density,
in Equation (
11) does not depend on the integration variable
s, and one can use the diagonalization methods and/or perturbative expansions [
20,
23,
24,
25]. Alternatively, one can directly integrate Equation (
11).
Here, we propose using the matrix solution to Equation (
11) in a different way: we divide the
s interval in
N small pieces
(for example, equally spaced
), for which we consider the
Hamiltonian to be constant:
where the diagonal matrices
and
can be identified by comparing with Equation (
11). The solution to Equation (
11) can be written as:
Given that the
are small, one can show that the matrices
can be approximated by:
Moreover, given that matrices
and
are diagonal, then:
and:
where
is calculated with the average electron density in the interval
. Using Equations (
17)–(
20), one can iteratively find the S-matrix and the associated probabilities of Equation (
15). We will call this approach the iterations method. In the proof of Equation (
18), one needs the transformations forth and back between the flavor amplitudes and the mass eigenstates amplitudes:
The condition for small
used in Equation (
18) suggests that one needs a large number of iterations to obtain good accuracy. Our numerical implementation indicates that even 10–15 factors in Equation (
17) would provide a 0.1% accuracy when compared with the “exact” eigenvalues method.
Figure 4 shows the difference between the iterations method described above when only 15 iterations are used, and the exact eigenvalues method solution. Increasing N to 150 reduces the absolute difference to less than
.
The iterations method described above works as well for smoothly varying average electron (matter) densities.
Figure 5 shows the results of the above method (red curve) compared with the solution obtained by directly integrating Equation (
8) for a varying density through the Earth’s crust for the DUNE/LBNF experiment, similar to that described in Reference [
26] (blue curve). The electron neutrino appearance probability is calculated for a muon neutrino beam of 0.8 GeV. The two curves are overlapping if the artificial 0.005 shift to the red curve is removed (the estimated error used for both algorithms is about
).
The iterations algorithm is very efficient, while in almost all cases one can use a equally spaced grid (
), and the product of the matrices
in Equation (
18) can be precalculated. Therefore, the right-hand side of Equation (
18) can be easily calculated at any iteration step in Equation (
17) by multiplying each raw of the precalculated matrix with the corresponding diagonal element in
(Equation (
19)). One can conclude that the algorithm is very simple and efficient, features that become even more important when it is extended to the light sterile neutrino(s) case (see
Section 5). In addition, it is faster than a direct integration method for the case of varying matter densities: in a comparison with the integration algorithm used in Reference [
26] (see Reference [19] in [
26]) for the same matter density profile used in
Figure 5, we observed a factor of 20 less iterations needed, equivalent to a speedup of about 20, under the same accuracy. A simple way of understanding this improvement relative to the direct integration of Equation (
11) is that Equation (
18) includes some partial integration information through the exponential factors in the diagonal matrices
and
.
4. The Connection to the Integration Method
The iterations algorithm described above can also be used to understand the results of
Section 2. To see that, one can consider the electron density in condensed matter composed of N spikes clustered around the atomic nuclei. One can further approximate the spikes with Dirac delta functions, which are normalized to unity and multiplied by the constant given in Equation (
12). Then, when integrating Equation (
8) on each
segment, one can (i) transform the flavor amplitudes into mass-eigenstate amplitudes with
(for example, see Equation (
21)), (ii) freely propagate the mass-eigenstate amplitudes using
, (iii) transform the mass-eigenstate amplitudes into flavor amplitudes with
U, and (iv) integrate Equation (
8) over the Dirac delta spikes. For the last step, one can assume that in the vicinity of a Dirac delta spike only the term proportional with
in Equation (
8) survives:
Given that the Dirac delta function norm in Equation (
12) is proportionate to
, then
in the interval
, and the solution to the above equation becomes:
where
are the
s coordinates before and after the delta spike in the
interval, and
is calculated with the average electron density of Equation (
13). Therefore, the result of integrating the full vector of amplitudes over the Dirac delta spikes is:
Putting together all the steps of the algorithm described above, one gets for the S-matrix factors entering Equation (
17):
which is the same as in Equation (
18) with the definitions (
19)–(
20) for
and
. This completes the proof that justifies the use of an average electron density, rather than its large variation around the atomic nuclei. For smooth changes of the average electron density one can use a typical coarse-graining argument.
5. The Case of Light Sterile Neutrinos
Recent short-baseline neutrino oscillations investigation [
27] seems to confirm older suspicions that one or more sterile neutrinos may be present. A vigorous short-baseline neutrino program to settle this issue is underway at Fermilab [
28]. Therefore, we consider extending our algorithm for neutrino oscillations in varying electron density by including the effect of sterile neutrinos. Here, we consider one sterile neutrino and a fourth mass eigenstate with a mass of about 1 eV. Then, in all above equations, a new sterile flavor with its amplitude
needs to be included, and the
PMNS mixing matrix
should be extended to four rows and four columns (the extension to more sterile neutrino and mass eigenstates is straightforward). One could find compact formulae for the
matrix elements [
20,
29], but to avoid typos in the lengthy equations and given that we are mainly interested in numerical calculations, we can obtain the 4-dimensional
matrix using six
rotations:
Here,
are the mixing angles and
are the CP-violating phases. The
are
matrices that represent rotations in two direction,
, such that the
and
matrix elements are
and the
matrix elements are
(the
matrix elements being its complex conjugate). Then, Equations (
11) and (
15)–(
20) can be extended using:
Here,
and
, where
given in Equation (
6) is proportional with the neutron density in nuclei. Given that the neutron density inside a nucleus is orders of magnitude larger than the electron density at the nucleus, the spikes in
are much larger than those in
. For example, in typical atoms in the Earth’s, the maximum electron-induced optical potential is about
, while the neutron-induced optical potential is about
eV. In addition, the slope of the neutron density in nuclei is much steeper, and the validity of the extension of Equation (
11) can only be justified for neutrino energies above 1.5 GeV (see Equation (
9)). For those energies, the algorithm of
Section 3 can be easily extended using the definitions (
26) and (
27). Extending the analysis of
Section 4, one can conclude that the use of average density in the
and
terms entering Equation (
27) is granted. Then, the average scaled potentials,
and
, are similar in magnitude, and the
and
matrices in the S-matrix Equation (
25) become:
Using matrices (
26) and (
28) in the iterations algorithm formula, Equation (
25), can be used to calculate the S-matrix and the transition probability.
For neutrino energies lower than 1.5 GeV, the
extension of Equation (
5) needs to be used. In that case, the widely different mass scales would make the analysis intractable. However, if one artificially increases the mass and the potential scales close to the neutrino energy scale, one can directly integrate the
extension of Equation (
5). A preliminary numerical analysis suggests that using average macroscopic electron and neutron densities provides the same oscillation probabilities as using the spiked densities. Alternatively, one can consider the S-matrix for the
extension of Equation (
5) and treat the neutron density spikes around the atomic nuclei as in
Section 4 above. This analysis will be reported separately.
Finally, the extension of our algorithm to more light sterile neutrinos, e.g., 3 + 2, is simple and straightforward. One only needs to calculate the
mixing matrix by extending the definition given in Equation (
26), and to extend the
,
,
, and
matrices, Equations (
27) and (
28), by adding the appropriate diagonal matrix elements.